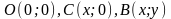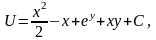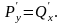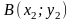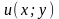Как найти потенциальную функцию

Определение
6.
Векторное
поле

называется потенциальным,
если

не зависит от пути, соединяющего точки
A
и
B.

Если

не зависит от пути интегрирования, то

При
этом функция

называется потенциальной
функцией
поля

.

Вычисление
потенциальной функции

Если

,
то существует функция

,
для которой

.
Для вычисления функции

используем криволинейный интеграл

,
не зависящий от пути интегрирования.
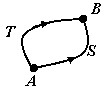
Путь AB
выбираем любой, соединяющий точки

и

;
например, ломаную линию ACB,
где

(рис. 3). Тогда

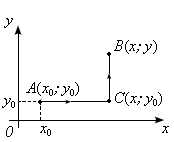
Рис.
3

Итак,

Пример.
Найти потенциальную функцию

по её полному дифференциалу:

Проверим
условие полного дифференциала:

– выполняется.

Способ
1.
Если

,
то

Следовательно,

Способ
2.
Выберем в качестве пути интегрирования
ломаную OCB,
где


(рис.
4)

Рис.
4

Итак:

где
C
– произвольная постоянная.

6. Вычисление криволинейного интеграла, независящего от пути интегрирования

Интеграл

не зависит от пути интегрирования, если

Тогда значение интеграла будет зависеть
от координат начала пути – точка A
и конца пути – точка B.
При этом интеграл записывают следующим
образом:

Чтобы его вычислить, можно использовать
два способа.

Способ
1.

где

– потенциальная функция.

Но
так как

,
то

Следовательно

Способ
2.
Можно вычислить интеграл, выбрав любой
путь интегрирования, соединяющий точки

и

.
Наиболее рационально выбрать путь ACB
(рис. 3)
–
ломаную линию, звенья которой параллельны
осям координат, т.е. взять точку

или
,
тогда путь интегрирования будет состоять
из двух отрезков: AC
и
CB,
при
этом интеграл будет равен сумме двух
интегралов 
по
AC
и
CB.
0

Пример.
Вычислить интеграл

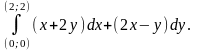
Способ
1 (рис.
5).

Рис.
5

Способ
2.

,

где


функция, для которой
.

Значит:

Ответ:
8.

§ 4. Поверхностные интегралы

1. Поверхностный интеграл I рода

Пусть
функция

непрерывна на гладкой поверхности S,
заданной функцией

непрерывно дифференцируемой в каждой
точке области D
R².

Определение.
Поверхностным
интегралом I
рода
от функции

по поверхности S
называется предел интегральной суммы

при условиях:

1)

и

(стягиваясь в точку);

2)
предел интегральной суммы существует
и не зависит ни от способа разбиения
поверхности S
на n
частей, ни от выбора точек

на этих частях, т.е.

где

– площадь i-й
части поверхности

– дифференциал поверхности S,
вычисляемый по формуле:

Если
проекция поверхности S
на плоскость OXY
однозначна и совпадает с областью D,
то поверхностный интеграл I рода
вычисляется по формуле:

Замечание
1.
Если прямая, параллельная оси OZ

и проходящая через внутреннюю точку
области
D,
пересекает
поверхность
S
в
более
чем одной точке,
то
поверхность
S
разбивается
на части так, чтобы прямая, параллельная
оси
OZ,
пересекала
поверхность
S
только в одной точке.
Далее интегрирование следует выполнить
по каждой из полученных частей.

Замечание
2.
Поверхностный интеграл I рода не зависит
от того, по какой стороне поверхности
он берётся.

Замечание
3.
Физический
смысл поверхностного интеграла I рода
зависит

от
физического смысла данного скалярного
поля, т.е. от

,
он может определять массу, распределенную
на данной поверхности, электрический
заряд и т.д.

Замечание
4.
Если функция

равна единице во всех точках поверхности
S,
то поверхностный интеграл I рода

равен площади поверхности
S.
Следовательно,
справедлива формула:

где
D
–
проекция поверхности S
на
плоскость
OXY,

–
функция, задающая поверхность S.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Definition/Summary

Given a vector field ##vec F(x,y,z)## that has a potential function, how do you find it?

Equations

$$nabla phi(x,y,z) = vec F(x,y,z)$$ $$nabla times vec F(x,y,z) = vec 0$$

Extended explanation

Suppose we are given a vector field ##vec F(x,y,z)=langle f(x,y,z),g(x,y,z),h(x,y,z)rangle## that has a potential function ##phi## and we wish to recover the potential function. We know that we must have##nabla phi =vec F##, so ##phi_x = f,, phi_y=g,, phi_z = h##. This means we can recover ##phi## by integrating the components of ##vec F##.

To look at a particular example, consider $$vec F =langle 2xz^3+e^z,-zsin(yz),3x^2z^2-ysin(yz)+xe^zrangle$$Our unknown potential function ##phi## must satisfy$$phi_x=2xz^3+e^z,, phi_y=-zsin(yz),,phi_z=3x^2z^2-ysin(yz)+xe^z$$Students often solve this type of problem by taking the anti-partial derivative of each equation:$$phi = int 2xz^3+e^z,partial x = x^2z^3+xe^z$$ $$phi = int -zsin(yz), partial y=cos(yz)$$ $$phi = int 3x^2z^2-ysin(yz)+xe^z, partial z=x^2z^3+cos(yz)+xe^z$$

where I have used the ##partial## symbol in the integrals to emphasize that it is an anti-partial derivative in each case. I have also left off the “constants” of integration. Looking at these results, one may observe that the function ##phi## can be discerned by “taking the new part of each result but not repeating”. For example, you keep the ##cos(yz)## from the second integral, but you don’t keep the ##xe^z## and ##cos(yz)## from the last integral because you already have them. So using this method, we get$$phi(x,y,z) = x^2z^3+cos(yz)+xe^z$$and it is easy to check that ##nabla phi = vec F##.

The problem with this method is at the last step where you build the formula for ##phi## by inspection of the three antiderivatives above. Exactly what you are looking for in the inspection and the rules for building the potential function are not well defined and can lead to wrong answers. To demonstrate this, consider the 2-D example $$vec F(x,y) = langle P(x,y),Q(x,y)rangle= langle 2cos(2x)cos^2(y),-sin(2x)sin(2y)rangle$$ Here it is easy to see that ##Q_x=P_y## so there is no doubt there is a potential function ##phi(x,y)##. So, using the above method:$$phi = int 2cos(2x)cos^2(y), partial x = sin(2x)cos^2(y)$$ $$phi = int -sin(2x)sin(2y),partial y =frac{sin(2x)cos(2y)} 2$$Since these terms are different, we keep both of them, giving $$phi(x,y) = sin(2x)cos^2(y)+frac{sin(2x)cos(2y)} 2$$ Unfortunately, for this ##phi##, if you calculate it, you get $$phi_x = 2cos(2x)cos^2(y) +cos(2x)cos(2y) ne P(x,y)$$ so this is not the correct potential function.

So the “integrate all three components and build the potential from them” method is unreliable, even though it frequently works. Fortunately, the proper way to work such problems is just as easy and always works. So, let’s look at the first example above. Doing the first integral correctly and not ignoring the constants of integration gives us$$phi = int 2xz^3+e^z,partial x = x^2z^3+xe^z + u(y,z)$$ where ##u## is an unknown function of the other variables, since we did an anti-partial derivative. Now we use this version of ##phi## to check ##phi_y = g##:$$phi_y = frac partial {partial y}( x^2z^3+xe^z )+u_y(y,z)= 0 +u_y(y,z) =zsin(yz)$$so we get$$u(y,z) = int zsin(yz)partial y = -cos(yz) + v(z)$$where now the constant of integration depends only on ##z##. Putting this value for ##u## in our formula for ##phi## gives$$phi = x^2z^3+xe^z -cos(yz) + v(z)$$Now all that remains is to take the partial of this with respect to ##z## and set it equal to the third component ##h(x,y,z)##:$$phi_z=3x^2z^2+xe^z+ysin(yz)+v'(z)=3x^2z^2-ysin(yz)+xe^z$$This implies ##v'(z)=0## so ##v## is a constant, which can be ignored. So we get our final version:$$phi = x^2z^3+xe^z -cos(yz)$$It is the same answer, but there is no guesswork building the potential function.

Now let’s try this method on the 2D example that didn’t work before. Our first integration gives$$phi = int 2cos(2x)cos^2(y), partial x = sin(2x)cos^2(y) + w(y)$$Differentiating this with respect to ##y## and setting the result equal to the second component gives$$phi_y=sin(2x)(-2)sin(y)cos(y)+w'(y)=-sin(2x)sin(2y)$$This tells us that ##w'(y)=0## since ##2sin(y)cos(y)=sin(2y)##. So ##w## is constant and can be ignored. This leaves us with the correct potential function$$phi = sin(2x)cos^2(y)$$unlike the first method.

See these for more examples:

https://www.physicsforums.com/threads/intermediate-math-challenge-august-2018.952511/ (problem #4)

https://www.physicsforums.com/threads/basic-math-challenge-august-2018.952503/ (problem #4)

https://www.physicsforums.com/threads/intermediate-math-challenge-july-2018.950690/ (problem #3)

Comment Thread

Как показать что поле вектора потенциально

Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!

Контакты

Администратор, решение задач
Роман

Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym

Решение задач
Андрей

facebook:
dniprovets25

Специальные векторные поля

Специальные векторные поля

1. Услуги проектирования
2. Теория поля
3. Специальные векторные поля

Специальные векторные поля

Потенциальное векторное поле

Определение потенциального поля

Векторное поле $bar < a >(mathbf < textit < M >> )$ называется потенциальным в области $mathbf < textit < V >> $, если существует такое скалярное поле $varphi (M)$, что $bar < a >(mathbf < textit < M >> )=gradvarphi (M)$ для $forall Min V$. Поле $varphi (M)$ называется потенциалом поля $bar < a >(mathbf < textit < M >> )$.

Свойства потенциального поля

1. Потенциал определён с точностью до произвольной постоянной $gradvarphi = grad(varphi +C)$.
2. Разность потенциалов в двух точках $M_1 in V,,M_2 in V$ определена однозначно.
3. Если поле $bar < a >(mathbf < textit < M >> )$ потенциально, то линейный интеграл этого поля по любой кривой $mathop < AB >limits^cup $, целиком лежащей в $mathbf < textit < V >> $, определяется только начальной и конечной точками этой кривой и не зависит от формы кривой. $W=intlimits_ < mathop < AB >limits^cup >< bar < a >dbar < r >> =intlimits_ < mathop < AB >limits^cup >< Pdx+Qdy+Rdz= >=intlimits_ < mathop < AB >limits^cup >< frac < partial varphi >< partial x >dx+frac < partial varphi >< partial y >dy+frac < partial varphi >< partial z >dz > =intlimits_ < mathop < AB >limits^cup >< dvarphi >=left. < varphi (P) >right|_A^B =varphi (B)-varphi (A)$. Эта формула, как и в плоском случае, является обобщением формулы Ньютона-Лейбница для потенциального поля.
4. Циркуляция потенциального в области $mathbf < textit < V >> $ поля по любому контуру, лежащему в $mathbf < textit < V >> $, равна нулю.
5. Векторная линия потенциального поля в каждой точке $mathbf < textit < M >> $ ортогональна эквипотенциальной поверхности < т.е. поверхности уровня потенциала >, проходящей через точку $mathbf < textit < M >> $.
6. Ротор потенциального векторного поля равен нулю: $ rotgradvarphi =left| < begin< l >,,bar < i >,,,bar < j >,,bar < k >\ frac < partial >< partial x >,,frac < partial >< partial y >,frac < partial >< partial z >\ frac < partial varphi >< partial x >,frac < partial varphi >< partial y >,frac < partial varphi >< partial z >\ end >right|=left( < frac < partial ^2varphi >< partial ypartial z >-frac < partial ^2varphi >< partial zpartial y >>right)bar < i >+left( < frac < partial ^2varphi >< partial zpartial x >-frac < partial ^2varphi >< partial xpartial z >>right)bar < j >+left( < frac < partial ^2varphi >< partial xpartial y >-frac < partial ^2varphi >< partial ypartial x >>right)bar < k >=0. $

Введём определение безвихревого поля: поле $bar < a >(mathbf < textit < M >> )$, ротор которого в каждой точке равен нулю, называется безвихревым.

Мы доказали, что потенциальное поле необходимо безвихрево. Дальше мы займёмся достаточными условиями потенциальности.

Достаточные условия потенциальности

Теорема

Если область $mathbf < textit < V >> $ и поле $bar < a >(mathbf < textit < M >> )$ удовлетворяют следующим условиям:

то $bar < a >(mathbf < textit < M >> )$ — потенциальное в $mathbf < textit < V >> $ поле.

Доказательство. Напомним определение односвязной области: область < на плоскости, в пространстве >называется односвязной, если любой замкнутый контур, лежащий в этой области, можно непрерывной деформацией стянуть в точку, не выходя при этом за пределы области. Нам при доказательстве теоремы придётся строить поверхности, натянутые на контуры, определение односвязности как раз гарантирует, что такие поверхности существуют и ими могут служить поверхности, образующиеся при деформации контура в точку.

1. Докажем, что если выполняются условия теоремы, то линейный интеграл поля $bar < a >(mathbf < textit < M >> )$ по любой кривой $mathop < AB >limits^cup $, целиком лежащей в $mathbf < textit < V >> $, определяется только начальной и конечной точками этой кривой и не зависит от её формы. Пусть$mathbf < textit < ASB >> $ и $mathbf < textit < ATB >> $ — два пути, соединяющие точки $mathbf < textit < A >> $ и $mathbf < textit < B >> $. Вместе они образуют замкнутый контур $mathbf < textit < ASBTA >> $. Пусть $sigma $ — кусочно-гладкая поверхность, натянутая на этот контур. Тогда по формуле Стокса $ointlimits_ < ASBTA >< bar < a >cdot dbar < r >> =iintlimits_sigma < rotbar < a >cdot bar < n >d > sigma =0$, так как $rotbar < a >(M)=0$. Но $ointlimits_ < ASBTA >< bar < a >cdot dbar < r >> =ointlimits_ < ASB >< bar < a >cdot dbar < r >> +ointlimits_ < BTA >< bar < a >cdot dbar < r >> =ointlimits_ < ASB >< bar < a >cdot dbar < r >> -ointlimits_ < ATB >< bar < a >cdot dbar < r >> = 0Rightarrowointlimits_ < ASB >< bar < a >cdot dbar < r >> = ointlimits_ < ATB >< bar < a >cdot dbar < r >> $
2. Докажем, что если мы фиксируем точку $M_0 in V$ и возьмём $varphi (M)=intlimits_ < mathop < M_0 M >limits^cup >< bar < a >dbar < r >> $, то $bar < a >(M)=gradvarphi (M)$, т.е. определённая таким образом функция $varphi (M)$ действительно является потенциалом поля $bar < a >(mathbf < textit < M >> )$.

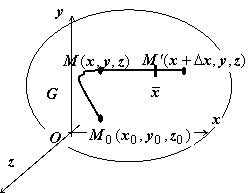
Это доказательство полностью повторяет доказательство теоремы пункта Вычисление криволинейного интеграла второго рода в случае, когда выполняются условия независимости от формы пути.

Действительно, пусть $M(x,y,z)in G, < M >'(x+Delta x,y,z)in G.$ Тогда $varphi (M)=intlimits_ < mathop < M_0 M >limits^cup > < Pdx+Qdy+Rdz >,varphi ( < M >’)=intlimits_ < mathop < M_0 M < M >’ > limits^cup > < Pdx+Qdy >+Rdz=intlimits_ < mathop < M_0 M >limits^cup > < Pdx+Qdy+Rdz >+\+intlimits_ < mathop < M < M >’ > limits^cup > < Pdx+Qdy >+RdzRightarrow varphi (x+Delta x,y,z)=varphi (x,y,z)+intlimits_x^ < x+Delta x > < P(x,y,z)dx >Rightarrow $

< на $MM’ y=const,z=const$ >$Rightarrow Delta _x varphi (x,y,z)=varphi (x+Delta x,y,z)-varphi (x,y,z)=intlimits_x^ < x+Delta x > < P(x,y,z)dx >= P(bar x,y,z)Delta x$

$Rightarrow frac < Delta _x varphi > < Delta x >=P(bar < x >,y,z)$. Точка $bar < x >$ удовлетворяет условиям $x Огравление $Rightarrow $

Электронная библиотека

В теории поля и ее приложениях рассматриваются так называемые потенциальные поля.

Определение. Поле вектора называется потенциальным, если вектор является градиентом некоторой скалярной функции :

(поле в этом случаи называют также безвихревым или градиентным).

Функция называется потенциальной функцией поля. Часто говорят, что скалярная функция называется скалярным потенциалом поля.

Замечание. В литературе дается определение потенциального поля и так, что . Знак «минус» перед берётся для удобства. Это не имеет принципиального значения. При изучении понятия потенциального векторного поля надо уточнять, каким образом вводится понятие потенциального поля. В частности, для электрического поля:

Знак «минус» перед имеет здесь физический смысл, он означает, что в направлении вектора напряженности электрический потенциал убывает (рис. 1.45).

Если – потенциальная функция вектора , то , где , тоже будет потенциальной, так как .

Поле не всякого вектора является потенциальным. Возникает задача: по какому признаку установить, будет ли поле потенциальным? Следующая теорема дает утвердительный ответ и, что важно, приводит к методу нахождения этой функции.

Теорема: Для того чтобы поле было потенциальным, необходимо и достаточно, чтобы вихрь этого поля равнялся нулю:

Доказательство. Необходимость. Дано, что — потенциальное поле. Тогда, согласно определению (1.111), , т.е.

Отсюда заключаем, что

Найдем вихрь поля:

Что и требовалось доказать.

Достаточность. Дано, что , т.е.

Это есть условие полного дифференциала функции [6], т.е.

Следовательно, искомая функция (потенциальная) может быть найдена так:

Полный дифференциал функции :

Отсюда поле вектора — потенциально.

Замечание 1. Потенциальное поле обладает рядом особенностей:

а) Потенциальное поле характеризуется лишь одной скалярной функцией , в то время как любое векторное поле определяется тройкой скалярных функций .

б) Циркуляция в потенциальном поле по любому контуру равна нулю.

Это следует из теоремы Стокса:

в) В потенциальном поле криволинейный интеграл не зависит от формы пути интегрирования (доказано при рассмотрении условия независимости криволинейного интеграла от формы пути интегрирования).

При нахождении потенциальной функции в качестве начальной точки берут начало координат, если эта точка принадлежит области, в которой ищется потенциальная функция – это упрощает вычисления; согласно замечанию криволинейный интеграл не зависит от формы пути интегрирования, поэтому удобно брать путь – ломаную (см. рис. 1.46), тогда:

Если найти , то должны получить вектор . Это Можно считать проверкой.

Итог: Криволинейный интеграл потенциального поля на пути равен разности потенциальной функции в конечной и начальной точках этого пути:

другими словами, для потенциального поля имеет место формула Ньютона-Лейбница. Она позволит по известной потенциальной функции найти криволинейный интеграл второго рода (роль первообразной здесь играет потенциальная функция поля ).

Проверить, будет ли поле вектора потенциальным? В случаи его потенциальности найти потенциальную функцию.

Решение. Найдем вихрь этого поля:

Согласно признаку потенциальности поле – потенциальное. Следовательно, существует потенциальная функция, которую найдем, используя формулу (1.115):

В общем случае, если — произвольная точка, то

Задачи для упражнений

1) Найти потенциал поля .

2) Будет ли поле вектора потенциальным? В случае потенциальности найти u(х, y, z)

3) Условия прежние:

Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00