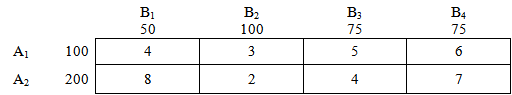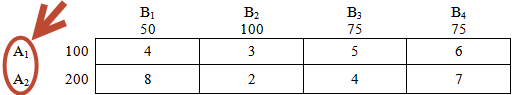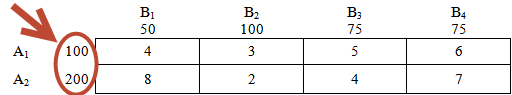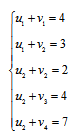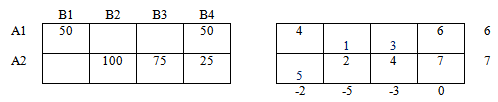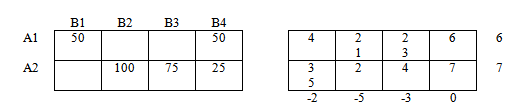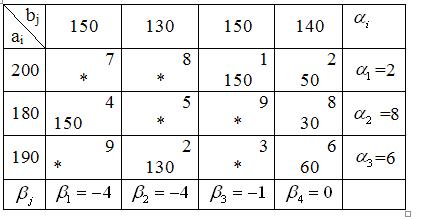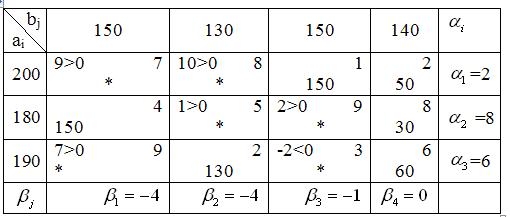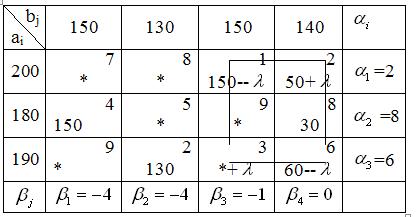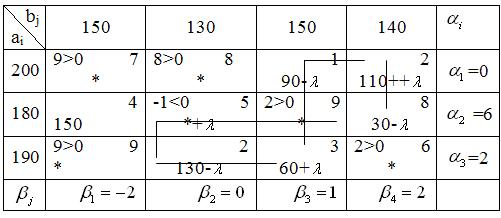Как найти потенциалы в транспортной задаче

Одна из самых распространенных и востребованных оптимизационных задач в логистике — транспортная задача. В классическом виде она предполагает нахождение оптимального (т. е. сопряженного с минимальными затратами) плана грузоперевозок.

Например, у нас есть сеть розничных магазинов, которым требуется определенное количество товаров. Также имеется ряд складов поставщиков, где требуемые товары хранятся. При этом на каждом складе различный объем запасов этих товаров. Кроме этого нам известны тарифы — затраты на перевозку 1 товара от каждого склада к каждому магазину.

Возникает необходимость разработать такой план перевозок, чтобы магазины получили требуемое количество товаров с наименьшими затратами на транспортировку. Вот именно в таких случаях (и во множестве других) приходится решать транспортную задачу.

Теоретический материал по транспортной задаче

Транспортная задача (задача Монжа — Канторовича) — математическая задача линейного программирования специального вида о поиске оптимального распределения однородных объектов из аккумулятора к приемникам с минимизацией затрат на перемещение.

Для простоты понимания рассматривается как задача об оптимальном плане перевозок грузов из пунктов отправления (например, складов) в пункты потребления (например, магазины), с минимальными общими затратами на перевозки.

Математическая модель транспортной задачи имеет следующий вид:

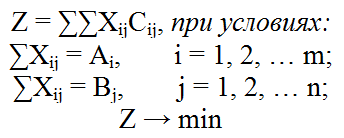
где: Z — затраты на перевозку грузов;

X — объем груза;

C — стоимость (тариф) перевозки единицы груза;

A — запас поставщика;

B — запрос потребителя;

m — число поставщиков;

n — число потребителей.

Общий план решения транспортной задачи методом потенциалов

Решить транспортную задачу можно различными методами, начиная от симплекс-метода и простого перебора, и заканчивая методом графов. Один из наиболее применяемых и подходящих для большинства случаев методов — итерационное улучшение плана перевозок.

Суть его в следующем: находим некий опорный план и проверяем его на оптимальность (Z → min). Если план оптимален — решение найдено. Если нет — улучшает план столько раз, сколько потребуется, пока не будет найден оптимальный план.

Ниже приведен алгоритм решения транспортной задачи в самом общем виде:

1. Построение транспортной таблицы.
2. Проверка задачи на закрытость.
3. Составление опорного плана.
4. Проверка опорного плана на вырожденность.
5. Вычисление потенциалов для плана перевозки.
6. Проверка опорного плана на оптимальность.
7. Перераспределение поставок.
8. Если оптимальное решение найдено, переходим к п. 9, если нет — к п. 5.
9. Вычисление общих затрат на перевозку груза.
10. Построение графа перевозок.

Подробная инструкция по решению транспортной задачи

1. Построение транспортной таблицы

Заполняем транспортную таблицу с исходными данными, где указываем запасы материалов, имеющиеся на складах поставщиков (A_i), и потребности заводов (B_j) в этих материалах.

В нижний правый угол ячеек таблицы заносим значение тарифов на перевозку груза (C_ij).

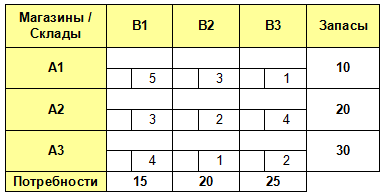
2. Проверка задачи на закрытость

Обозначим суммарный запас груза у всех поставщиков символом A, а суммарную потребность в грузе у всех потребителей — символом B.

Тогда:

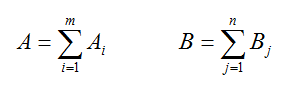
Транспортная задача называется закрытой, если A = B . Если же A ≠ B , то транспортная задача называется открытой. В случае закрытой задачи от поставщиков будут вывезены все запасы груза, и все заявки потребителей будут удовлетворены. В случае открытой задачи для ее решения придется вводить фиктивных поставщиков или потребителей.

Проверим задачу на закрытость:

A = 10 + 20 + 30 = 60.

B = 15 + 20 + 25 = 60.

A = B, следовательно данная транспортная задача — закрытая.

3. Составление опорного плана

Составляет предварительный (опорный) план перевозок. Он не обязательно должен быть оптимальный. Это просто своеобразный «черновик» или «набросок», итерационно улучшая который мы постепенно придем к оптимальному плану.

Есть разные методы нахождения опорного плана. Наиболее распространены следующие:

Выберите один из методов и пройдите по ссылке в его описании, чтобы посмотреть как в данном примере был составлен опорный план и заполнена транспортная таблица.

4. Проверка опорного плана на вырожденность

Клетки таблицы, в которые записаны отличные от нуля перевозки, называются базисными, а остальные (пустые) — свободными.

План называется вырожденным, если количество базисных клеток в нем меньше, чем m + n — 1. Если во время решения задачи получился вырожденный план, то его необходимо пополнить, проставив в недостающем числе клеток нулевую перевозку и превратив, тем самым, эти клетки в базисные (общий баланс и суммарная стоимость перевозок плана при этом не изменятся).

Проводить пополнение плана, выбирая клетки произвольно, нельзя. План должен быть ациклическим!

План называется ациклическим, если его базисные клетки не содержат циклов. Циклом в транспортной таблице называется несколько клеток, соединенных замкнутой ломаной линией так, чтобы две соседние вершины ломаной были расположены либо в одной строке, либо в одном столбце. Ниже приведен пример цикла:

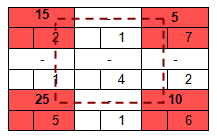
Ломаная линия может иметь точки самопересечения, но не в клетках цикла.

В нашем примере количество базисных клеток = 5; m + n — 1 = 3 + 3 — 1 = 5.

Следовательно, первоначальный план перевозок — невырожденный (5 = 5).

5. Вычисление потенциалов для плана перевозки

Для анализа полученных планов и их последующего улучшения удобно ввести дополнительные характеристики пунктов отправления и назначения, называемые потенциалами.

Этот метод улучшения плана перевозок называется методом потенциалов. Есть другие методы итерационного улучшения плана перевозок, но здесь мы их рассматривать не будем.

Итак, сопоставим каждому поставщику A_i и каждому потребителю B_j соответствующие величины U_i и V_j так, чтобы для всех базисных клеток плана было выполнено следующее соотношение: U_i + V_j = C_ij.

Добавим к транспортной таблице дополнительную строку и столбец для U_i и V_j.

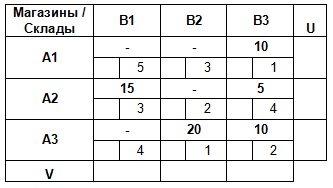
Предположим, что U₁ = 0.

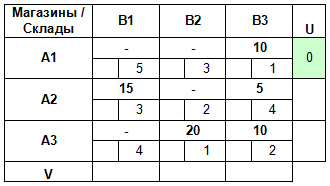
Тогда мы сможем найти V₃ = C₁₃ — U₁ = 1 — 0 = 1.

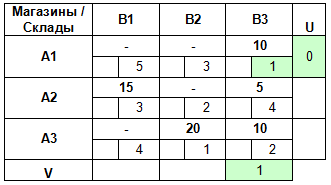
Зная V₃, мы теперь можем найти U₃:

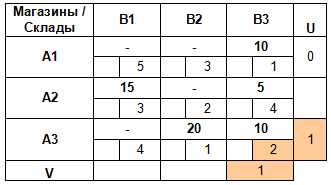
По аналогии вычисляем все оставшиеся потенциалы:

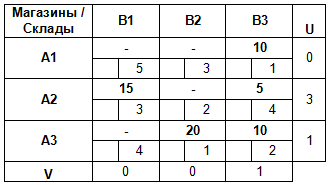
6. Проверка плана на оптимальность методом потенциалов

Для каждой свободной клетки плана вычислим разности ΔC_ij = C_ij — (U_i + V_j ), и запишем полученные значения в левых нижних углах соответствующих ячеек.

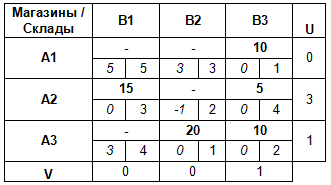
План является оптимальным, если все разности ΔC_ij ≥ 0.

В данном случае план — неоптимальный (ΔC₂₂ < 0), и его следует улучшить путем перераспределения поставок.

7. Перераспределение поставок

Найдем ячейку с наибольшей по абсолютной величине (т. е. без учета знака, по модулю) отрицательной разностью ΔC_ij и построим цикл, в котором кроме этой клетки все остальные являются базисными. Такой цикл всегда существует и единственен.

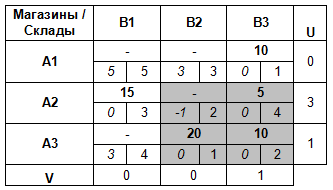
Отметим ячейку с отрицательной разностью ΔC_ij знаком «+», следующую знаком «—», и так далее, поочередно.

Затем находим минимальное значение груза в ячейках цикла имеющих знак «-» (здесь это 5) и вписываем его в свободную ячейку со знаком «+». Затем последовательно обходим все ячейки цикла, поочередно вычитая и прибавляя к ним минимальное значение (в соответствии со знаками, которыми эти ячейки помечены: где минус — вычитаем, где плюс — прибавляем).

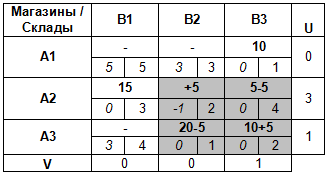
Получим новый опорный план перевозок:

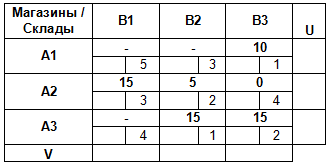
Так как базисных клеток стало больше, чем m + n — 1, то базисную клетку с нулевым значением делаем свободной:

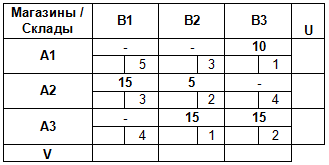
Снова вычисляем значения потенциалов и разности ΔC_ij:

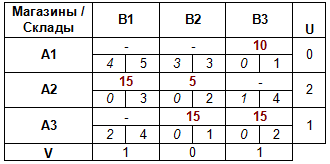
На этот раз все разности ΔC_ij ячеек положительные, следовательно, найдено оптимальное решение.

8. Если оптимальное решение найдено, переходим к п. 9, если нет — к п. 5.

В нашем примере оптимальное решение найдено, поэтому переходим к пункту 9.

9. Вычисление общих затрат на перевозку груза

Вычислим общие затраты на перевозку груза (Z), соответствующие найденному нами оптимальному плану, по формуле:

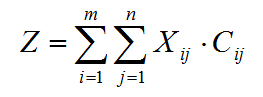
То есть нужно перемножить значения объемов грузоперевозок на соответствующие им тарифы.

Z_min = 10 ⋅ 1 + 15 ⋅ 3 + 5 ⋅ 2 + 15 ⋅ 1 + 15 ⋅ 2 = 110 ден. ед.

В результате общие затраты на доставку всей продукции для оптимального решения составляют 110 ден. ед.

10. Построение графа перевозок

Найдя оптимальный план перевозок, построим граф. Вершинами графа будут «склады» и «магазины». В вершинах укажем соответствующие объемы запасов и потребностей. Дугам, соединяющим вершины графа, будут соответствовать ненулевые перевозки. Каждую такую дугу подпишем, указав объем перевозимого груза.

В результате получится граф, аналогичный изображенному ниже:

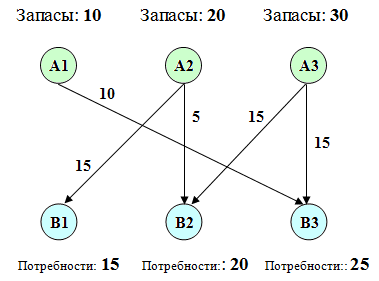
Все, транспортная задача решена. Поздравляю!

Практическое применение транспортной задачи

Транспортная задача применяется во многих случаях. В частности:

• оптимизация поставок сырья и материалов на производственные предприятия;
• оптимизация доставок товаров со складов в розничные магазины;
• оптимизация пассажирских перевозок.

Это далеко не полный перечень возможностей прикладного использования транспортной задачи.

© Копирование любых материалов статьи допустимо только при указании прямой индексируемой ссылки на источник: Галяутдинов Р.Р.

Транспортная задача линейного программирования

Прочие статьи цикла

Транспортная задача линейного программирования относится к перечню классических задач, решаемых в практике деятельности людей. Эта задача методами классической математики не решается. В задаче необходимо отыскивать экстремум целевой функции. В задаче целевая функция – линейная. Ограничения на переменные (их может быть очень много) описываются также линейными зависимостями. Казалось бы чего проще. Но как раз ограничения и порождают трудности, связанные не просто с поиском max и min при отсутствии ограничений, а с необходимостью учета таких ограничений. Искать требуется не просто экстремум, а условный экстремум. Методы решения задачи позволяют учитывать особенности структуры задачи и даже отказаться от симплексного метода решения в чистом виде.

I. Основные параметры, термины и обозначения

Для ощущения масштаба задачи приведу парочку изображений того, что рассматривается в транспортной задаче линейного программирования.

Зеленый цвет — пассажирские суда, желтые — грузовые, розовый — частные яхты, оранжевый — танкеры и др. Аналогичная картина наблюдается и для авиационных перевозок, перевозок по железной дороге или автотранспортом. Изображения получены в начальном периоде Пандемии короновируса, что привело к огромным пробкам в узостях мирового Океана (Панамский, Суэцкий и др. каналы). Танкеры отправили отстаиваться на рейде, экипажам судов на берег сойти не разрешалось. Это форс-мажорные обстоятельства, которые в теории должны рассматриваться и учитываться специальным образом, что пока к сожалению перевозчиков не сделано.

В теории в тексте задачи Хичкока ничего не говорится о равенстве имеющегося общего запаса судов в портах отправления и общей потребности в судах в портах прибытия (назначения). Если такого равенства нет, то система ограничений несовместна. В случае равенства

транспортная задача называется «сбалансированной». Задачи, в которых условие баланса не задано, должны быть приведены к «сбалансированному» виду. Это можно выполнить использованием «фиктивных» перевозок. Рассматриваем два случая:

Метод содержит три последовательных этапа:

1. Формирование опорного плана;

2. Проверка опорного плана на оптимальность;

3. Переход к новому опорному плану, если предыдущий не оптимален.

II. Формирование опорного плана перевозок

Затем, если a₁ > b₁, то определяется остаток (a₁ – b₁) продукта на первом пункте отправления и его запас реализуется на 2-м пункте назначения. Остаток потребностей 2-го пункта назначения удовлетворяется за счет 2-го пункта отправления, остатки которого направляются в 3-й пункт назначения и т.д. Ниже метод будет иллюстрирован числовым примером.

Пример 1. Построение опорного плана методом Северо-Западного угла

Заданы значения: m = 3, n = 4; a₁ = 60, a₂ = 80, a₃ =100, b₁ = 40,b₂ = 60, b₃ = 80, b₄ = 60. Слева в таблице приведены d_ij удельные стоимости перевозок; справа — В_ij стоимости совместно с предложениями a_i и потребностями b_{j .}

Требуется найти план Х [m,n] перевозок, удовлетворяющий условиям на целевую функцию Q и переменные х_ij задачи Q.

РЕШЕНИЕ Построить исходный опорный план способом северо-западного угла. Строим симплексную таблицу:                                        Таблица 3.   Опорный план задачи

Q = d₁₁∙x₁₁ + d₁₂∙x₁₂ + d₂₂∙x₂₂ + d₂₃ ∙x₂₃+ d₃₃ ∙x₃₃+ d₃₄ ∙x₃₄ = = 5∙40 + 2∙20 + 10∙40 + 2∙40 + 8∙40 + 5∙60 = 200+40+400 + 80 + 320+ 300 = 1340 ед

Коэффициенты d_ij называются фиктивными или косвенными стоимостями; их выражают через косвенные величины α и β, d’_ij = α_i +β_j . Здесь параметры α_i и ( — β_j ), по аналогии с механикой называют потенциалами i-го пункта отправления и j-го пункта прибытия. Значения потенциалов определяется из системы линейных уравнений: α_i + β_j = d_ij Каждому из таких уравнений соответствует какая-либо базисная переменная х_ij Система уравнений с потенциалами содержит m+n неизвестных потенциалов, число же уравнений равняется числу базисных ячеек таблицы, т.е. (m + n – 1). Следовательно, один из потенциалов можно задать произвольно, положив его равным, например, нулю.

Решая далее систему уравнений для потенциалов, находим значения потенциалов строк и столбцов, все фиктивные стоимости d_ij и коэффициенты γ_ij. Если для всех свободных клеток γ_rs ≤ 0, то перевод в базис любой свободной переменной не уменьшит значения целевой функции и, следовательно, выбранный опорный план не является оптимальным. Если же некоторые γ_rs >0, то данный план можно улучшить путем перевода в базис свободной переменной, соответствующей max γ_rs, а также путем исключения из базиса, принадлежащей ему переменной, первой обращающейся в нуль. Переход к новому опорному плану и поиск оптимального плана рассмотрим на примере. Другой способ формирования опорного плана предложен Фогелем. Этот способ при первом чтении можно пропустить, так как дальше он в тексте не используется.

Пример 2. Способ аппроксимации Фогеля

В большинстве случаев этот способ дает опорный план наиболее близкий к оптимальному. Удобен для матриц большой размерности. Используется концепция штрафов, взимаемых за выбор не самого оптимального с точки зрения транспортных издержек маршрута. Штраф по каждой строке и каждому столбцу определяется из анализа маршрутов с различными показателями издержек (как разность двух различных уровней транспортных издержек). Первой заполняется клетка матрицы (таблицы), в которой фиксируется самый крупный штраф. После заполнения клетки штрафы пересчитываются и так до тех пор, пока все ресурсы не будут распределены. Исходные данные для этого примера заполняют таблицу слева вверху.

Этапы алгоритма: 1.     Вычисление разностей в каждой строке и в каждом столбце между наименьшей стоимостью и ближайшей к ней по величине. Разности по строкам записываются справа в столбце разностей, разности по столбцам – внизу в строке разностей. Например, для строк А₁ разность равна А₁В₂ – А₁В₃ = 38 – 24 = 14 и т. д.

ТАБЛИЦА 2 — Метод Фогеля для получения опорного плана транспортной задачи

2.     Поиск из всех разностей, как по строкам, так и по столбцам максимальный. В нашем примере максимальная разность равна 38 и находится в строке А₂. Обведем максимальную разность рамкой.

3.     Размещение в клетку, где находится наименьшая стоимость (А₂В₂ = 18) (строка с наибольшей разностью), максимально возможного количества ресурсов. Оно равно 20, т.е. всему ресурсу отправителя А₂. Поскольку все ресурсы отправителя А₂ исчерпаны, строку А₂ исключаем из дальнейших расчетов, для чего отметим все клетки этой строки точками.

4.     Вычисление разностей столбцам и строкам, не принимая во внимание стоимость в клетках, имеющих ресурсы и клетках с точкой (исключенную строку или столбец) и определение максимальной разности в строке или столбце (В₃ = 76).

5.     Поиск минимального элемента в строке или в столбце с максимальной разностью (А₁В₃ = 24) и размещения в данную клетку максимально возможного количества ресурса, возвращение к этапу №4 и т.д. Окончательно

ЦФ Q=23∙19 + 7∙3 + 20∙18 + 2∙10 + 14∙24 + 1∙100 +3∙48 = = 437 + 21 + 360 + 20 +3 36 + 100 + 272 =1546 ед. Это значение соответствует опорному плану Фогеля.

III. Транспортная задача линейного программирования

Как основной метод решения транспортной задачи – используется метод потенциалов. Ни симплексный метод, ни распределительный метод здесь не рассматриваются. У них имеются свои плюсы и минусы, но объем изложения достаточно велик. Возможно этому позднее я уделю внимание и время, но пока отвечаю на пожелание читателя Хабра.

Пример 3 — Транспортная задача. Метод потенциалов

Исходные данные задачи удобно представить двумя матрицами.

ТАБЛИЦА — Исходные данные

Базисные n + m – 1 = 3 + 4 – 1 = 6 переменные:  
x₁₁ =70, x₁₂ = 20, x₂₂ = 10, x₂₃ = 20, x₂₄ = 0, x₃₄ = 40.
Остальные переменные nm – n + m – 1 = 12 – 6 = 6 свободные:
x₁₃ = x₁₄ = x₂₁ = x₂₄ = x₃₁= x₃₂ = 0 .
Суммарная стоимость перевозок для опорного плана получает представление:
Q = d₁₁ ∙x₁₁ + d₁₂∙x₁₂ + d₂₂∙x₂₂ + d₂₃∙x₂₃+ d₂₄∙x₂₄+ d₃₄∙x₃₄ =
=2∙70 + 3∙20 + 3∙10 + 1∙20 + 2∙0 + 2∙40 = 140 + 60 + 30 + 20 + 0 +80  = 330 ед.

2. Проверка опорного плана на оптимальность

Формируем матрицу фиктивных стоимостей D'[m, n] и матрицу Г [m, n].

Выделяем в Г [m, n] свободные ячейки, содержащие γ_rs. Проверяем наличие положительных переменных γ_i,j > 0. Так как в матрице (в свободных ячейках) имеем γ₃₂ = 2 > 0, то исходный опорный план может быть улучшен, он не является оптимальным.

3. Переход к новому (улучшенному) опорному плану

Переменную x₃₂ =x следует ввести в базис.  Обозначим ее предварительно через x без индексов. С учетом того, что х должна быть положительна х > 0. Найдем значение max x при условии сохранения баланса перевозок. Для этого воспользуемся начальным опорным планом. Будем добавлять переменную х в ячейки таблицы так, чтобы сохранялись условия баланса перевозок

Обозначим ее предварительно через x без индексов. С учетом того, что х должна быть положительна х > 0. Найдем значение max x при условии сохранения баланса перевозок. Для этого воспользуемся начальным опорным планом. Будем добавлять переменную х в ячейки таблицы так, чтобы сохранялись условия баланса перевозок   Очевидно, что наибольшее x определяется теми x_ij в базисных клетках, из которых этот х вычитается. Следовательно, x₁₁ = min{х₂₂, х₃₄} = {10, 40} = 10. При x >10 перевозка х₂₂ становится отрицательной. Переменную х₂₂ исключаем из базиса и переводим ее в разряд свободных переменных. Далее повторяются рекурсивно три пункта алгоритма.

1. Получаем из модифицированного плана новый опорный план

   В нем объемы перевозок распределены иначе чем в начальном опорном плане.

Суммарная стоимость перевозок для этого опорного плана получает представление:
Q = d₁₁ ∙x₁₁ + d₁₂∙x₁₂ + d₂₃∙x₂₃ + d₃₂∙x₃₂ + d₂₄∙x₂₄+ d₃₄∙x₃₄ =
=2∙70 + 3∙20 + 2∙10 + 1∙20 + 1∙10 + 2∙30 = 140 + 60 + 20 + 20 + 10 + 60  = 310 ед. Затраты на перевозки при этом плане уменьшились на 330 – 310 = 20 ед.

Является ли найденный опорный план оптимальным? Ответ может быть получен после составления и решения системы уравнений для потенциалов.

2. Проверка опорного плана на оптимальность

Формируем матрицу фиктивных стоимостей D'[m, n] и матрицу Г [m, n].

Свободные ячейки матрицы Г [m, n] содержат γ_i,j > 0 (γ₁₄ = 1>0). План не оптимален.

3. Переход к новому (улучшенному) опорному плану

Из свободных переменных с x_ij > 0, выбираем одну x₁₄  для введения ее в базис. Обозначим ее как и ранее через x без индексов. С учетом того, что х должна быть положительна х > 0. Найдем значение max x при условии сохранения баланса перевозок. Для этого воспользуемся очередным опорным планом. Будем добавлять переменную х в ячейки таблицы так, чтобы сохранялись условия баланса перевозок  

Очевидно, что наибольшее x определяется теми x_ij в базисных клетках, из которых этот х вычитается. Следовательно, x₁₁ = min{х₁₂, х₃₄} = {20, 30} = 20. При х₁₂ >20 перевозка х₁₂ становится отрицательной. Переменную х₁₂ исключаем из базиса и переводим ее в разряд свободных переменных. Переходим к новой итерации

1. Получаем из модифицированного плана новый опорный план.

В нем объемы перевозок распределены иначе чем в предшествующем опорном плане.

Суммарная стоимость перевозок для этого опорного плана получает представление:
Q = d₁₁ ∙x₁₁ + d₁₄∙x₁₄ + d₂₃∙x₂₃ + d₃₂∙x₃₂ + d₂₄∙x₂₄+ d₃₄∙x₃₄ =
=2∙70 + 3∙20 + 1∙20 + 2∙10 + 1∙30 + 2∙10 = 140 + 60 + 20 + 20 + 30 + 20  = 290 ед. Затраты на перевозки при этом плане уменьшились на 310 – 290 = 20 ед. Является ли найденный опорный план оптимальным? Ответ может быть получен после составления и решения системы уравнений для потенциалов.

2. Проверка опорного плана на оптимальность

Определим систему уравнений для потенциалов и вычислим их значения:
α₁ + β₁ = d₁₁ = 2;
α₁ + β₄ = d₁₄ = 3;
α₂ + β₃ = d₂₃ = 1;
α₂ + β₄ = d₂₄ = 2;
α₃ + β₂ = d₃₂ = 1;
α₃ + β₄ = d₃₄ = 2. Каждое из этих значений соответствует одной базисной ячейке. Одну из неизвестных в системе можно задавать произвольно. Пусть β₁ = 0. Тогда после решения системы получены значения потенциалов: α₁= 2, α₂= 2, α₃= 2, β₁ =0, β₂=1, β₃ =–1, β₄ =0.

Формируем матрицу фиктивных стоимостей D'[m, n] и матрицу Г [m, n].

При переходе к новому опорному плану проверяем наличие положительных свободных переменных γ_i,j >0. Но таких переменных не оказалось. Отсюда следует вывод, что полученный последним модифицированный план является оптимальным и ему соответствует значение линейной формы
Q’= 2∙70 + 3∙20 + 1∙20 + 2∙10 + 1∙30 + 2∙10 = 290.

Заключение

Вся теория исследования операций с позиций математики решает неклассические задачи оптимизации целевых функций. Отличие от классики в том, что те ограничения на переменные, которые исследователи вынуждены накладывать в рамках моделей, созданы и вызваны реальностью. Отыскивать требуется экстремумы функций при многих ограничениях, так называемые условные экстремумы. Классика не позволяет этого делать. Взятие производных и приравнивание их нулю «не видит» ограничений. Лучшее, что там имеется это функция Лагранжа, но ее использование также весьма ограничено. Транспортные задачи – частный, но важный случай в исследовании операций. Надеюсь, что читатель разобравшись в приведенных примерах, лучше стал понимать логику задачи и сумеет самостоятельно постигать интересующие его вопросы по другим публикациям в учебниках и журнальных статьях.

Литература

Этот
метод используется при решении
транспортной задачи, суть которой
заключается в определении оптимального
плана перевозок некоторого однородного
груза из

пунктов отправления

в

пунктов потребления
.

Рассмотрим
транспортную задачу, в которой критерием
оптимальности является минимальность
транспортных расходов по перевозке
грузов.

Экономико-математическая
модель такой задачи содержит системы
линейных уравнений:

,

,

условие
неотрицательности переменных

и целевую функцию

.

Следует иметь в
виду, что:

1. Всякое неотрицательное
   решение системы линейных уравнений,
   определяемое матрицей
   
   называется допустимым
   планом транспортной задачи.

2. Ранг матрицы,
   составленной из коэффициентов при
   неизвестных системы основных ограничений
   задачи, на единицу меньше числа уравнений,
   т.е. равен
   .
   Следовательно, число линейно независимых
   уравнений равно
   
   и они определяют вектора, вошедшие в
   базис, а соответствующие им
   
   переменных будут являться базисными.

3. Допустимый план
   транспортной задачи, имеющий не более
   
   отличных от нуля величин
   ,
   называется опорным.

4. Если в опорном
   плане число отличных от нуля компонент
   в точности равно
   ,
   то план является невырожденным,
   если меньше, то план является вырожденным.

5. План, при котором
   целевая функция принимает свое
   минимальное значение, называется
   оптимальным
   планом транспортной задачи.

6. Для решения
   транспортной задачи необходимо и
   достаточно, чтобы суммарные запасы
   груза в пунктах отправления были равны
   сумме заявок пунктов назначения:

.

1. Модель транспортной
   задачи, удовлетворяющей этому условию,
   называется закрытой.
   Если же указанное условие не выполняется,
   то модель называется открытой.

В случае превышения
запаса над заявками

,

вводится фиктивный

пункт назначения с потребностью

и соответствующие тарифы считаются
равными нулю:
.

При

водится фиктивный

пункт отправления с запасами груза

и соответствующие тарифы считаются
равными нулю:
.

1. Наилучшим
   элементом
   матрицы тарифов С
   называется наименьший
   тариф, если
   решается задача на минимум, наибольший
   тариф –
   если решается задача на максимум целевой
   функции.

Рассмотрим один
из методов построения начального
опорного плана – метод наименьших
тарифов.

Алгоритм построения
начального опорного плана методом
наименьших тарифов включает следующие
этапы:

а) среди тарифов
определяется наименьший;

б) клетка с выбранным
тарифом заполняется величиной, равной
максимально возможному объему груза с
учетом ограничений по строке и столбцу.
При этом либо весь груз вывозится от
соответствующего поставщика, либо
полностью удовлетворяется заявка
потребителя. Если одновременно весь
груз вывозится от некоторого поставщика
и полностью удовлетворяется заявка
рассматриваемого потребителя, то в
клетку с наименьшим тарифом, принадлежащей
строке или столбцу, которые содержат
упомянутых поставщика или потребителя,
вводят нуль.

в) из оставшихся
тарифов вновь находится наилучший
(наименьший), и процесс продолжается до
тех пор, пока не будет распределен весь
груз.

Если модель
транспортной задачи открытая и введены
фиктивный поставщик или потребитель,
то распределение осуществляется сначала
для действительных поставщиков и
потребителей, и в последнюю очередь
нераспределенный груз направляется от
фиктивного поставщика или к фиктивному
потребителю.

1. Дальше полученный
   план проверяется на оптимальность. Для
   этого используется метод потенциалов,
   суть которого состоит в следующем.

План

транспортной задачи будет оптимальным,
если существует система

чисел
,
называемых потенциалами
поставщиков и потребителей
соответственно, удовлетворяющая
условиям:

Потенциалы

и

обозначают оплату за перевозку единицы
груза в пунктах потребления (поставщиками)
и назначения (потребителями) соответственно,
поэтому их сумма равна транспортному
тарифу
.

Введем так
называемое превышение
клетки таблицы

.

Тогда признак
оптимальности
опорного плана транспортной задачи,
которая исследуется на минимум, можно
сформулировать следующим образом.

Если

для заполненных клеток и

для свободных клеток, то рассматриваемый
план является оптимальным.

Алгоритм оценки
оптимальности плана транспортной задачи
методом потенциалов включает следующие
этапы.

1. Построение
   начального плана.

2. Определение
   значения целевой функции
   путем суммирования произведений тарифов
   на объем запланированного к перевозке
   груза по всем заполненным клеткам
   таблицы.

3. Проверка условия
   оптимальности.
   Определяются потенциалы
   
   и
   .
   Для каждой заполненной клетки таблицы
   записываются уравнение
   .
   Получается система
   
   уравнений с
   
   переменными.

Т.к. число переменных
больше числа уравнений
,
то система является неопределенной и
имеет бесконечное множество решений.
Поэтому одному из неизвестных потенциалов

и

задают произвольное значение, например,
для простоты вычислений полагают
.
Тогда остальные потенциалы определяются
из приведенных уравнений.

В транспортную
таблицу добавляются дополнительная
строка и столбец, куда заносятся
потенциалы.

Определяются
превышения свободных клеток
.

Если все

(решается задача на минимум целевой
функции) для свободных клеток, то
оптимальный план найден. Если хотя бы
одно превышение свободной клетки

(решается задача на минимум целевой
функции), то план не является оптимальным,
его можно улучшить, осуществив
перераспределение груза.

1. Построение
   нового опорного плана.
   Из всех положительных превышений
   свободных клеток выбирается наибольшая
   (если поставлена задача на минимум).
   Клетку, которой соответствует наибольшее
   превышение, следует заполнить, т.е.
   направить груз. Заполняя выбранную
   клетку, необходимо изменить объемы
   поставок, записанных в ряде других
   заполненных и связанных с заполняемой
   клеткой так называемым циклом.

Циклом,
или прямоугольным
контуром,
в таблице транспортной задачи называется
ломаная линия, вершины которой расположены
в заполненных клетках таблицы, а звенья
– вдоль строк и столбцов, причем в каждой
вершине цикла встречаются ровно два
звена, одно из которых находится в
строке, другое – в столбце. Если ломаная
линия, образующая цикл, пересекается,
то точки пересечения не являются
вершинами. Для каждой свободной клетки
таблицы можно построить единственный
цикл.

Вершинам цикла,
начиная от вершины, находящейся в
свободной клетке, присваиваем поочередно
знаки «+»
и «–».

Из объемов груза,
стоящих в минусовых клетках, выбираем
наименьший. Перераспределяем его по
циклу, прибавляя к соответствующим
объемам груза, стоящим в плюсовых клетках
и вычитая из объемов, стоящих в минусовых
клетках таблицы. В результате клетка,
которая ранее была свободной, становится
заполненной, а одна из заполненных
клеток цикла становится свободной.

Полученный новый
опорный план проверяется на оптимальность,
т.е. возвращаемся к третьему этапу
алгоритма.

Примечания.

1. Если в минусовых
   клетках цикла находятся два (или
   несколько) одинаковых минимальных
   значения
   ,
   то при перераспределении объемов груза
   освобождается только одна клетка (с
   наибольшим тарифом
   ),
   а в остальных клетках проставляются
   нули. Таким образом, во вновь полученном
   опорном плане число занятых клеток
   будет равно
   .

2. Если в оптимальном
   плане транспортной задачи превышение
   свободной клетки равно нулю (),
   то задача имеет множество оптимальных
   планов. Для клетки с нулевым превышением
   можно построить цикл и перераспределить
   груз. В результате полученный оптимальный
   план будет иметь такое же значение
   целевой функции.

3. Значение целевой
   функции на каждой итерации можно
   рассчитывать следующим образом:

(задача решается
на минимум),

где
величина
перемещаемого по циклу объема груза;

превышение свободной
клетки, в которую направляется груз при
переходе к новому плану;

значение целевой
функции на
той
итерации;

значение целевой
функции на предыдущей итерации.

Пример. На
три базы

поступил однородный и делимый груз в
количествах, соответственно равных 39,
36, 38 ед. Этот груз требуется перевезти
в три магазина

в количествах соответственно 27, 35, 33 ед.
Стоимость доставки единицы груза из
каждого пункта отправления в соответствующие
пункты назначения задана матрицей
тарифов (ден. ед. за ед. груза):

.

Необходимо составить
план перевозок груза с минимальными
транспортными издержками.

Решение. 1.
Проверим
необходимое и достаточное условие
разрешимости задачи:

,

.

Как видно, суммарные
запасы груза на базах превышают суммарную
потребность в пунктах назначения.
Следовательно, модель исходной
транспортной задачи является открытой.

Чтобы получить
закрытую модель, введем дополнительный
(фиктивный пункт назначения

с потребностью груза, равной 18 ед. (113 –
95). Тарифы перевозки единицы груза с баз

к

полагаем равными нулю.

Занесем данные в
таблицу перевозок.

27	35	33	18
	39	8		7		0
	36		5		0	— 4
	38	7			0	— 2
	5	10	7	0

Используя метод
наименьшей стоимости, построим начальный
опорный план транспортной задачи.

Среди тарифов из
всей таблицы наименьшим является
,
поэтому в клетку

направляем максимально возможное
количество груза. Оно равно
.
Тогда

и с базы

не вывезен груз в количестве 9 ед., а
потребность магазина

удовлетворена полностью. Столбец таблицы

выходит из рассмотрения. Из оставшихся
тарифов таблицы наименьшим является
.
Поэтому в клетку

направляем максимально возможное
количество груза, равное
.
Тогда строка

выходит из рассмотрения, поскольку с
базы

вывезен весь груз, а потребность третьего
магазина не удовлетворена на 24 ед. Из
оставшихся тарифов наилучший

и
.
Но

относится ко второй строке
,
а она вышла из рассмотрения. В клетку

направляем количество груза, равное
.
При этом потребность третьего магазина
удовлетворена, а с третьей базы не
вывезены 14 ед. груза. Третий столбец

выходит из рассмотрения. Из оставшихся
тарифов наилучшими являются

и
,
которые соответственно принадлежат
столбцам

и
,
вышедшим из рассмотрения. Аналогично,
тариф

принадлежит столбцу

и поэтому наилучшим теперь будет
.
В клетку

направляем груз в количестве 14 ед.,
который оставался на базе
.
Строка

выходит из рассмотрения. Остался один
тариф
.
В клетку

направляем груз в количестве

ед., поскольку потребность магазина

ранее была не удовлетворена на 21 ед. (35
– 14). На базе

остались не вывезенными 18 ед. (39 – 21)
груза. Направим их фиктивному потребителю,
т.е. от

18 е. груза в клетку
.

В результате
получен начальный опорный план

,

который является
допустимым, поскольку потребности всех
магазинов удовлетворены, а грузы с баз
по возможности вывезены.

2. Подсчитаем
число заполненных клеток таблицы
перевозок, их 6 и должно быть
.
Следовательно, опорный план является
невырожденным.

3. Определяем
значение целевой функции начального
опорного плана:

ден. ед.

4.
Проверим
оптимальность полученного плана. Найдем
потенциалы

по заполненным клеткам перевозок, в
которых

(превышение
=0),
полагая, что
.
Решим систему уравнений:

Занесем найденные
значения потенциалов в таблицу перевозок
и вычислим превышения свободных клеток:

;

;

;

;

;

.

Начальный опорный
план

не является оптимальным, т.к.
,
поэтому переходим к его улучшению.

5. Выбираем
свободную клетку с максимальным
положительным превышением (в нашем
примере только одна свободная клетка
имеет положительное превышение
).
Для этой клетки

построим цикл перераспределения груза.
Для этого в клетку

поставим знак «+»,
а в остальных вершинах многоугольника
чередующиеся знаки «–»,
«+»,«–».
Цикл приведен в таблице перевозок.

Из чисел
,
стоящих в минусовых клетках, выбираем
наименьшее, т.е.
.
Прибавляем 9 к объемам грузов, стоящих
в плюсовых клетках, и вычитаем 9 из
,
стоящих в минусовых клетках. В результате
получим новый опорный план.

27	35	33	18
	39	8		7		10
	36				0	5
	38	7			0	8
	— 4	0	— 3	— 10

6.
Определим
значение целевой функции

ден. ед.

7.
Проверяем
оптимальность плана

методом потенциалов, для этого находим
потенциалы

по заполненным клеткам таблицы, где
,
полагая, что
:

Затем рассчитываем
превышение свободных клеток:

;

;

;

;

;

.

Поскольку все
превышения свободных клеток неположительны,
то план

является оптимальным, но не единственным.
Последнее следует из того, что клетка

имеет нулевое превышение и для нее можно
построить цикл перераспределения
,
который позволяет установить альтернативный
оптимальный план

.

Значение целевой
функции при этом плане

ден. ед.,

т.е. совпадает со
значением
,
которое является минимальным.

Анализ плана. С
первой базы необходимо направить 21 ед.
груза в третий магазин, со второй базы
направить 27 ед. и 9 ед. в первый и второй
магазины соответственно, а груз с третьей
базы следует вывозить во второй и третий
магазины в количестве 26 и 12 ед.
соответственно. При этом на первой базе
останется 18 ед. груза. Общая стоимость
доставки груза потребителям будет
минимальной и составит 487 ден. ед.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

В данной статье разберемся с решением транспортной задачи. Все действия будем выполнять пошагово с очень подробными пояснениями. Дадим определение, аналогичное тому, которое дано в ваших учебниках или лекциях. Определение: Транспортная задача — это математическая задача линейного программирования специального вида о поиске оптимального распределения однородных объектов с минимизацией затрат на перемещение.

Чтобы не загромождать страницу большим объемом пояснений, разобью весь материал на несколько частей — блоков.

Ну, начнем! Далее Вводная часть, с которой желательно ознакомиться.

Вводная часть, с которой желательно ознакомиться

Существует несколько методов решения транспортной задачи. Мы будем подробно рассматривать два из них:

• решение транспортной задачи методом потенциалов (рассмотрен в данной статье)
• решение транспортной задачи с использованием симплекс метода.

Решение задачи методом потенциалов происходит в несколько этапов:

1. Определение опорного решения.
2. Применение к найденному опорному решению самого метода потенциалов.
3. Проверка единственности решения.

Определение опорного плана, в свою очередь, можно выполнить несколькими способами. Мы рассмотрим два из них:

• метод северо-западного угла
• метод минимальных стоимостей

(не путать с методами решения самой транспортной задачи!!!)

О чем говорится в определении транспортной задачи?

У нас есть некоторый груз, который находится на складах: склад 1, склад 2, …, склад  — это пункты отправления.

Этот груз нам необходимо развести по магазинам: магазин 1, магазин 2, …, магазин k — это пункты назначения.

Нам выгоднее как можно эффективнее выполнить работу, т.е. найти такой вариант перевозки, при котором затраты будут минимальными.

Рассмотрим пример решения транспортной задачи подробно. 

Транспортная задача задается следующей таблицей:  

Далее, что означают числа в условии транспортной задачи?

Что означают числа в условии транспортной задачи?

Рассмотрим постановку транспортной задачи, т.е. что дано в условии и переведем ее с математического языка на язык, понятный нам.

Это наши «склады» — пункты отправления: два склада с товаром: А₁ и А₂

Это объем товара — количество груза, соответственно на складах А₁ и А₂:

Далее имеем дело с пунктами назначения — с «магазинами». В нашем случае их 4 штуки: В₁, В₂, В₃ и В₄.

И соответственно потребности каждого из магазинов — потребности пунктов назначения:

 

Числа внутри таблицы — матрица стоимостей, или по другому, расценки перевозки 1 единицы груза из соответствующих пунктов. Эти значения также могут интерпритироваться как расстояния между соответствующими пунктами. Подробности — в условии решаемой задачи.

 

Например, для перевозки 1 единицы груза из пункта отправления («склада») А₂ в пункт назначения («магазин») В₃ надо заплатить 4 условные единицы стоимости, например 4 руб.

 

Аналогично, мы заплатим 6 рублей за перевозку 1 единицы груза из «склада» А₁ в «магазин» В₄. 

 

Или та же самая задача может быть задана сразу в более понятном виде: 

 

Возможна текстовая постановка задачи. В этом случае необходимо самим заполнять все ячейки таблицы, исходя из заданных в условии значений. 

Далее — Методы определения первоначального плана транспортной задачи.

Методы определения первоначального плана транспортной задачи.

Рассмотрим самый распространенный метод получения опорного плана — метод северо-западного угла.

Называется он так потому, что заполнение таблицы начинается с самой верхней левой (северо-западной) ячейки. 

Перед тем, как распределять ресурсы по «магазинам», проверим, равны ли общие потребности имеющимся ресурсам?

Потребности:  50 + 100 + 75 + 75 = 300

Ресурсы:        100 + 200 = 300

 

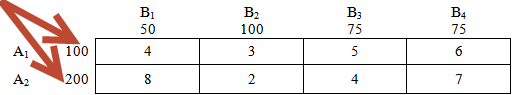
Потребности = Ресурсам

В этом случае говорят, что транспортная задача закрытая. Решение открытой транспортной задачи рассмотрим чуть позже. 

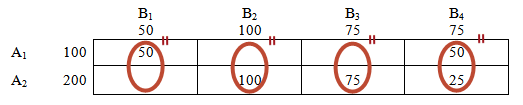
Начнем нахождение опорного решения:

Заполним клетку (1;1).

В магазин В₁ требуется 50 единиц товара. Со склада А₁ отправим в этот магазин 50 единиц.

Потребности магазина В₁ выполнены, следовательно, нет необходимости везти туда груз со склада А₂. 

На складе А₁ еще осталось 50 единиц груза. Эти остатки можем направить в магазин В₂. Ресурсы склада А₁ исчерпаны. 

Переходим к складу А₂. 

Так как потребности магазина В₁ выполнены полностью, рассмотрим магазин В₂, которому требуется 100-50=50 единиц товара. Направим их туда.

 

Заметим, на складе А₂ осталось еще 200-50=150 единиц груза, которые мы распределим по магазинам В₃ и В₄, полностью удовлетворяя и их потребности. 

Склады пусты! 

Потребности магазинов в товаре полностью выполнены! 

Получен опорный (первоначальный) план транспортной задачи. 

 

Рассмотрели северо-западный метод построения первоначального плана (опорного решения).

Далее опишем метод минимальных стоимостей получения опорного плана.

Метод минимальных стоимостей получения опорного плана

Суть метода состоим в том, чтобы в первую очередь направлять груз в те пункты, где «расценки» в матрице стоимостей минимальны. Если клеток с наименьшими тарифами несколько, то заполняется любая из них.

 

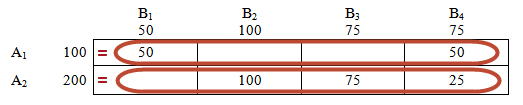
Направляем 100 единиц груза из склада А₂ в магазин В₂.

Остатки на складе А₂ — 100 единиц. Потребности магазина В₂ выполнены.

Груз со склада А₂ отправим в магазин, у которого стоимость перевозки ниже — магазин В₃, так как  мин(4;7)=4 

Размер поставки равен потребности магазина — 75. Остатки со склада 200-100-75=25 перенесем  в магазин В₄.

 

Остается только раскидать груз со склада А₁ по магазинам: В₁ — 50 единиц, В₄ —  75-25=50 единиц.

Получили два опорных плана: методом северо-западного угла и методом минимальных стоимостей.

Первый опорный план (по методу северо-западного угла):

Второй опорный план (по методу минимальных стоимостей):

Далее проверим правильность вычисления первоначального плана.

Проверка правильности вычисления первоначального плана

Перед тем как перейти к дальнейшему решению задачи проверим условие:

Правило: 

Количество заполненных клеток (базисных клеток) в первоначальном плане ВСЕГДА должно быть равно m + n — 1, где m — количество строк, n — количество столбцов

В нашем случае условие выполняется: 2 + 4 — 1 = 5

Что же делать, если количество заполненных ячеек меньше необходимого?

Подробно об этом с разбором примеров в статье Вырожденность опорного плана транспортной задачи. Как избавиться?

Во избежании случайных вычислительных ошибок проверим, равны ли суммарные значения каждой строки и каждого столбца соответствующим значениям условия.

100 = 50 + 50

200 = 100 + 75 + 25

По столбцам:

Видим, суммарные значения элементов каждого столбца равны соответствующим потребностям магазинов.

Несмотря на то, что опорные планы разные, оба приведут к одному оптимальному решению или же к решениям, имеющим одну стоимость перевозки. 

Далее применим метод потенциалов к обоим опорным планам и сравним получившиеся ответы.

Метод потенциалов решения транспортной задачи — шаг 1.

Описанную ниже последовательность действий будем повторять несколько раз, с каждым шагом приближаясь к оптимальному решению. Начнем с проверки опорного плана на оптимальность.

Выпишем матрицу стоимостей, данную в условии задачи.

Далее строим рядом две таблицы. Размерность таблиц как и в матрице стоимостей:

количество строк = количеству складов, количество столбцов = количеству магазинов. 

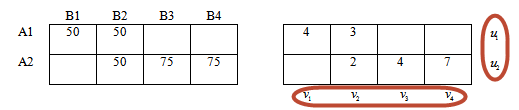
Заполняем первую — левую таблицу в соответствии с полученным опорным планом.

 

Переходим в правую таблицу.

Переносим из матрицы стоимостей значения, которые соответствуют занятым клеткам левой таблицы.

В матрице стоимости эти значения подчеркнуты. 

 

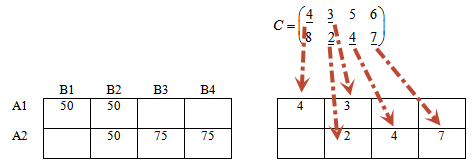
Припишем каждой строке правой таблице потенциалы u₁, u₂. Каждому столбцу — потенциалы v₁, v₂, v₃, v₄.

Для вычисления этих потенциалов в некоторых учебниках составляют систему и из нее определяют неизвестные (покажу на данном шаге).

Мы будем определять значения потенциалов непосредственно из правой таблицы.  

Составим систему уравнений по следующему правилу: 

Каждое из значений в ячейке (правая таблица) равно сумме потенциалов соответствующей строки и соответствующего столбца. 

Например: значение 4 находится в 1-й строке и 1-м столбце. Тогда сумма потенциалов 1-й строки (u₁) и 1-ого столбца(v₁) равна 4.

 

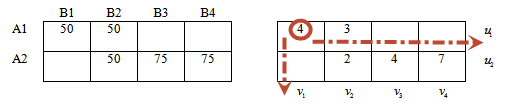
Первое уравнение системы: u₁ + v₁ = 4 

Рассмотрим следующее значение таблицы.  

Значение 3 находится в первой строке (потенциал u₁), втором столбце (потенциал v₂). 

Второе уравнение системы: u₁ + v₂ = 3

Аналогично для каждого значения таблицы составим уравнение.

Получим систему уравнений:

Для того, чтобы система имела единственное решение, примем значение одного из потенциалов равным нулю.

Для удобства в качестве этого потенциала всегда будем брать v₄. 

 

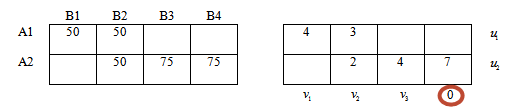
Тогда система уравнений будет выглядеть: 

 

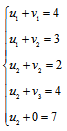
Решим систему уравнений и получим значения потенциалов:

 

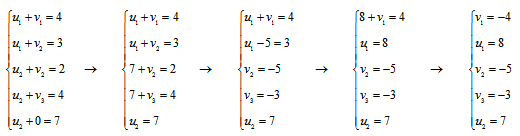
Наглядно:

 

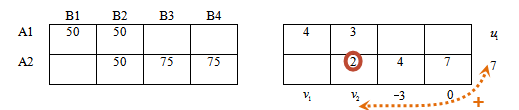
Так как система очень проста, то значения потенциалов можно получить и устно. 

Покажем подробно:

 

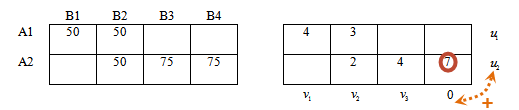
Сумма отмеченных потенциалов равна 7, следовательно, потенциал u₂ = 7

Значение 4 базисной ячейки находится во 2-й строке, 3-м столбце, тогда рассмотрим сумму соответствующих потенциалов.

v₃ + 7 = 4 откуда v₃ = -3

Далее все аналогично:

Значение 2 равно сумме потенциалов 2-й строки и 2-го столбца:

2 = v₂ + 7 откуда v₂ = -5

u₁ — 5 = 3, откуда u₁ = 8

 

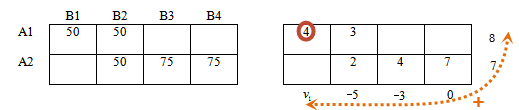
v₁ + 8 = 4, откуда v₁ = -4 

В итоге получили:

 

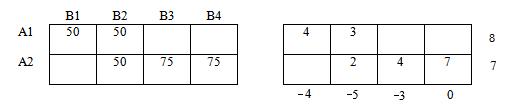
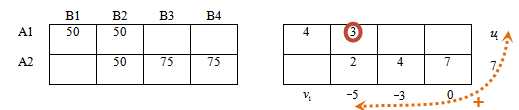
Далее приступим к заполнению пустых ячеек (свободные ячейки) правой таблицы. 

Свободные ячейки подчиняются тому же правилу суммирования потенциалов.

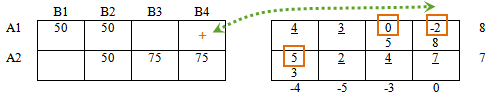
Вычислим оценочную матрицу, по которой узнаем, оптимален ли рассматриваемый план.

Из каждого элемента матрицы стоимостей вычтем соответствующий элемент правой таблицы: 

—

=

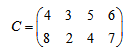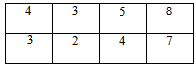Получили оценочную матрицу. Заметим, что в базисных ячейках всегда получим нули.

Критерий оптимальности:

если в оценочной матрице нет отрицательных элементов, то решение оптимально, в противном случае решение не оптимально. 

Согласно критерию оптимальности, решение выше не оптимально, так как в оценочной таблице присутствует отрицательное значение.

Дабы не загромождать решение множеством таблиц, оценочная матрица в нашем решении будет «вписана» в правую таблицу.

Подчеркнутые значения — базисные ячейки, как сказано выше, значения оценочной матрицы в базисных ячейках равны нулю, нули писать не будем. Выделенные значения — значения оценочной матрицы в свободных ячейках, среди них ищем отрицательные значения. 

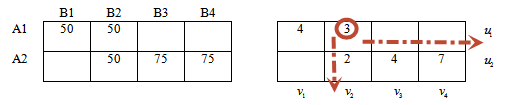
Для перехода к следующему опорному решению выполним следующее (построим цикл пересчета):

— найдем среди отрицательных значений оценочной матрицы максимальный по модулю (или по другому, минимальный среди отрицательных) 

— в соответствующей ячейке левой таблицы ставим знак » + «

В нашем примере наименьшее отрицательное значение -2.

Знак » + » ставим в ячейке 1-й строки, 4-го столбца левой таблицы — ячейка соответствующая значению (-2).

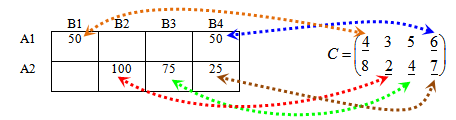
Необходимо расставить чередующиеся значения «+ » и » — » в левой таблице так, чтобы получился замкнутый цикл и выполнялись правила:

— остальные знаки цикла (все кроме уже поставленного первого » + «) ставим только в заполненных (базисных) ячейках таблицы,

— если в строке есть «плюс» («минус»), то в этой строке должен быть и «минус» («плюс»),

— если в столбце есть » плюс» («минус»), то в этом столбце должен быть и «минус» («плюс»).

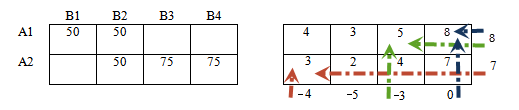
Применим к нашей таблице:

В столбце В₄ есть «плюс», следовательно в этом столбце должен быть и «минус». 

 

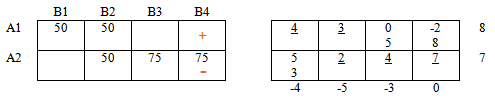
Аналогично, в строке А₂ есть «минус», следовательно должен быть и «плюс». 

Если мы поставим этот «плюс» в столбце В3, то цепочка порвется, так как в этом же столбце невозможно поставить «минус» — нет заполненной ячейки. 

Ставим » + » в столбце В2 и продолжаем чередовать знаки. 

 

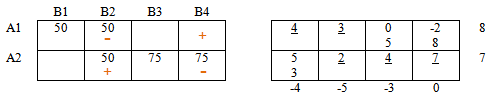
Получили замкнутый цикл чередующихся знаков. Цикл пересчета найден!

Далее обратимся к ячейкам, содержащим «минусы». Среди значений этих ячеек найдем минимальное:  Δ = мин {50;75} = 50 

К  «плюсам» прибавим найденное Δ = 50, в ячейках с «минусами» — вычтем Δ = 50.

Ячейка, в которой находилось значение  Δ = 50 останется пустой. В ячейке в которой мы поставили первый плюс появится значение, равное Δ = 50.

Общее количество заполненных (базисных) ячеек при пересчете не должно изменится! 

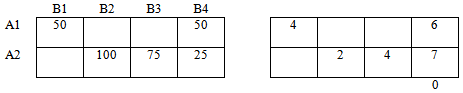
Получили следующий опорный план: 

 

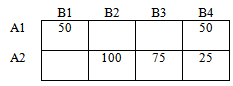
Вычислим стоимость перевозки на первом шаге.

Для этого найдем сумму произведений значений опорного плана и матрицы стоимостей.

S₁ = 50 · 4 + 100 · 2 + 75 · 4 + 25 · 7 + 50 · 6 = 1275 

На первом шаге решения транспортной задачи получили опорный план:

 

Общая стоимость перевозки S₁ = 1275

Метод потенциалов — шаг 2

Алгоритм проверки плана на оптимальность и построение цикла пересчета очень подробно расписан в шаге 1. 

Далее решение задачи будем излагать менее детально.

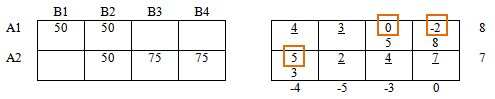
Для полученного опорного решения строим вспомогательную — правую таблицу и заполняем значениями из матрицы стоимостей базисные ячейки.

Вычисляем потенциалы строк и столбцов:

По правилу суммирования соответствующих потенциалов, заполняем свободные ячейки.

Вычисляем оценочные значения в свободных ячейках.

Для этого из значений матрицы стоимостей вычитаем найденные значения соответствующих свободных ячеек.

Среди оценочных значений нет отрицательных, следовательно план перевозки оптимален.

Получили оптимальный план. Итоговая стоимость перевозки S₁ = 1275

Примеры решения транспортных задач:

Закрытая транспортная задача размерностью 2х2

Закрытая транспортная задача размерностью 3х4

Закрытая транспортная задача размерностью 2х3

Закрытая транспортная задача размерностью 4х5

Пример.

1. Проверим, является ли данная задача замкнутой.

Подсчитаем суммарные запасы груза и суммарные потребности заказчиков

, .

Поскольку , модель транспортной задачи замкнутая, и задача имеет оптимальный план.

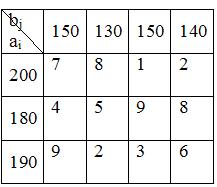
2. Построим первый опорный план транспортной задачи методом северо-западного угла.

Начинаем заполнение распределительной таблицы с верхней левой клетки, то есть построение исходного опорного плана начинаем с удовлетворения потребностей первого потребителя b1 за счет запасов первого поставщика a1. Для этого сравниваем запас a1 = 200 с потребностями b1 = 150. Так как a1 > b1, то потребности b1 полностью удовлетворяем за счет a1, и в первую клетку помещаем min (200, 150)=150. У первого поставщика осталось 50 единиц груза. Так как потребности первого получателя груза полностью удовлетворены, исключим из рассмотрения первый столбец, заполнив в нем оставшиеся клетки точками. Далее заполняем таблицу по строкам слева направо и сверху вниз. Следующая самая верхняя левая незаполненная клетка – (1,2). Потребителю b2 поставляем 50 единиц груза, оставшихся у первого поставщика. Поскольку от первого поставщика весь груз вывезен, заполняем оставшиеся клетки первой строки точками. Второму получателю, пока что, недопоставлено 80 единиц груза. Следующая незаполненная клетка – (2,2). Потребителю b2 отправляем недостающие 80 единиц груза, при этом его потребности полностью удовлетворены, поэтому оставшиеся клетки во втором столбце заполняем точками. У второго поставщика a2 осталось еще 100 единиц груза. Аналогичным образом заполняем оставшиеся клетки, пока не удовлетворим всех потребителей и не вывезем все запасы груза у поставщиков.

В результате распределения груза получим первый опорный план, в котором x11 = 150, x12 = 50, x22 = 80, x23 = 100, x33 = 50, x34 = 140. Эти переменные соответствуют заполненным клеткам и являются базисными, остальные переменные, соответствующие клеткам с точками, являются свободными (значения свободных переменных равны нулю). Первый опорный план можно представить в матричном виде

Число заполненных клеток k = 6. Это число должно равняться рангу системы ограничений r = m + n – 1 = 3 + 4 – 1 = 6. Так как k = r = 6, то построенный план является невырожденным. Подсчитаем затраты на перевозку по этому плану

.

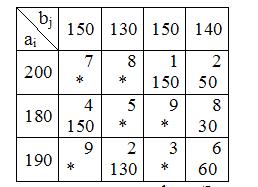
3. Построим первое опорное решение транспортной задачи методом минимальной стоимости (минимального тарифа).

Найдем клетку с минимальным тарифом. Это клетка (1,3) с тарифом

C13 =1. Построение исходного опорного плана начинаем с занесения поставки груза в клетку с наименьшей стоимостью c13. Заполняем клетку x13 = 150. Оставшиеся клетки третьего столбца заполняем точками, так как потребности третьего получателя полностью удовлетворены. У первого поставщика осталось 50 единиц груза. Ищем следующую клетку с минимальным тарифом. Таких клеток две: c14 =2, c32 =2. Заполним сначала клетку (3,2). Поставим в нее x32=min (190, 130)=130. Второй столбец заполняем точками. У третьего поставщика осталось 60 единиц груза. Ищем следующую клетку с наименьшим тарифом – это клетка (1,4). В нее помещаем 50 единиц груза, min(50,140)=50. Первую строку заполняем точками, так как от первого поставщика вывезен весь груз. Четвертому получателю недопоставлено 90 единиц. Аналогичным образом распределяем весь имеющийся груз и получаем первый опорный план перевозок.

Подсчитаем затраты на перевозку по этому плану.

.

Итак, в каждой строке и в каждом столбце таблицы заполнена хотя бы одна клетка, циклов по заполненным клеткам нет, число заполненных клеток m+n-1=6, следовательно, план опорный и невырожденный.

4. Проверка первого опорного плана (решения) на оптимальность. Метод потенциалов

После построения исходного опорного плана приступаем к проверке его на оптимальность методом потенциалов, который заключается в последовательном улучшении опорных планов транспортной задачи на основе информации, полученной с помощью чисел, называемых потенциалы поставщиков и потребителей (, — двойственные переменные, то есть переменные задачи, двойственной к транспортной). Потенциалы находим из условия , где cij — тарифы заполненных клеток. Будем проверять на оптимальность первый опорный план, построенный методом минимального тарифа. В двойственной задаче одна свободная переменная, поэтому возьмем одну любую из двойственных переменных и приравняем ее к нулю. Возьмем, например,(выгоднее брать в качестве нулевой переменной ту, которая соответствует строке или столбцу с наибольшим количеством заполненных клеток).

В таблице в дополнительном столбце справа помещаем потенциалы отправителей , а в строке снизу – потенциалы получателей. Составим систему уравнений для определения потенциалов:

Из этой системы находим

Считаем оценки для свободных клеток:

Запишем получившиеся оценки в левом верхнем углу свободных клеток.

Так как среди оценок имеются отрицательные , то данный план не является оптимальным. Его можно улучшить перераспределением поставок. Для этого выбираем свободную клетку с наименьшим отрицательным значением (наибольшим по абсолютной величине). В данном случае это клетка (3,3).

Сроим цикл пересчета, начиная с клетки (3,3), в которую нужно поместить поставку груза (её отмечают знаком «+»), и двигаясь по занятым клеткам (в данном случае это клетки (3,4), (1,4), (1,3)), поочередно отмечая их знаками «-», «+». Если в клетку (3,3) добавили +, то в смежных по циклу клетках необходимо вычесть для сохранения баланса перевозок по третьей строке и третьему столбцу. Звенья цикла должны быть параллельны строкам или столбцам таблицы, причем в каждой вершине цикла встречаются ровно два звена, одно из которых находится в строке, а другое – в столбце. Количество вершин в цикле должно быть четно. В результате построения цикла в соответствующих строках и столбцах должно быть парное количество знаков «-», «+».

Определяем величину поставки в клетку (3,3), как минимальную величину из поставок, стоящих в отрицательных клетках, то есть . Перераспределяем по циклу поставки на величину . Значение записываем в незанятую клетку (3,3), отмеченную знаком «+», двигаясь по циклу, прибавляем эту величину к поставкам в клетках со знаком «+», вычитаем в клетках со знаком «-».

В результате получаем новое опорное решение или новый опорный план, в котором клетки с грузом, равным величине , становятся свободными.

Если освобождается больше одной клетки, то есть число заполненных клеток меньше числа m + n — 1, то такой план называется вырожденными, и для определения потенциалов необходимо ввести недостающее количество нулевых элементов в число основных базисных переменных. Свободные клетки заполняют нулевыми поставками так, чтобы они не образовывали цикл по заполненным клеткам, и чтобы в каждой строке и в каждом столбце находилась хотя бы одна заполненная клетка. Проверим новый опорный план на оптимальность. Пусть =0. Тогда найдем все остальные потенциалы, рассматривая только заполненные клетки и помня, что для них , то есть что сумма потенциалов должна быть равна тарифу, стоящему на пересечении соответствующих потенциалам строки и столбца.

Число заполненных клеток k=m+n-1, следовательно, план невырожденный. Найдем оценки Для всех клеток с точками, где стоят свободные переменные. Данный опорный план не является оптимальным, так как не все оценки для свободных клеток , а именно, .

Возьмем клетку (2,2) за начало цикла пересчета. Цикл будет проходить по клеткам (2,2), (3,2), (3,3), (1,3), (1,4), (2,4) и опять вернется в (2,2).

Ищем количество единиц груза , перераспределяемых по циклу пересчета, как минимум по клеткам, помеченных знаком минус. Получаем новый опорный план

Проверяем данный опорный план на оптимальность

Полученный опорный план является оптимальным, так как все оценки для свободных клеток . Выписываем оптимальный план: x11 = 0; x12 = 0; x13 = 60; x14 =140; x21 = 150; x22 = 30; x23 = 0; x24 = 0; x31 = 0; x32 = 100; x33 = 90; x34 = 0. Или в матричной форме

Высчитываем минимальные затраты на транспортировку продукции:

< Предыдущая		Следующая >