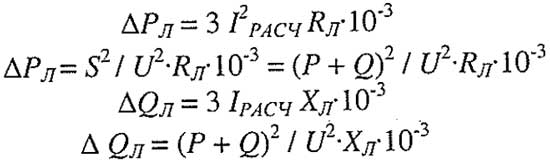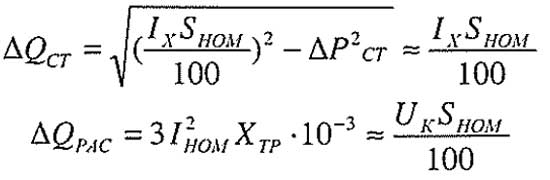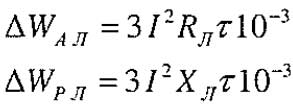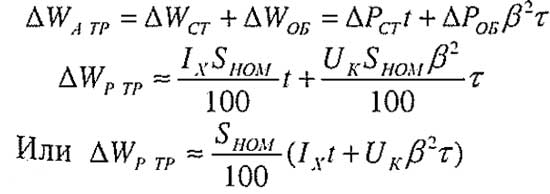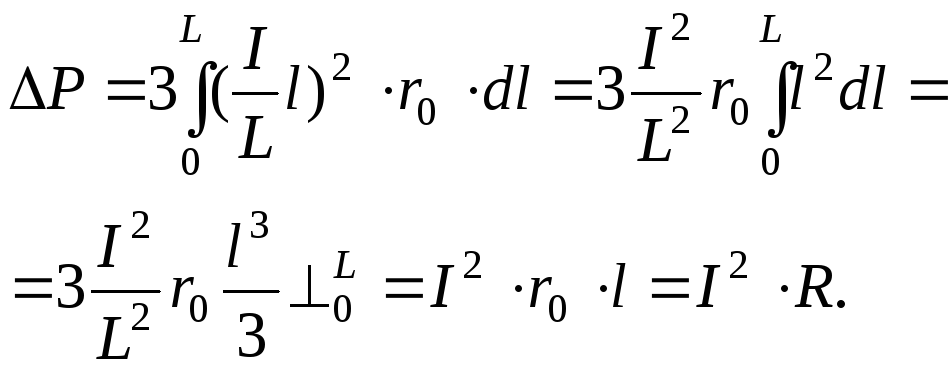Как найти потери нагрузки

При передаче электрической энергии от генераторов электростанций до потребителя около 12-18% всей вырабатываемой электроэнергии теряется в проводниках воздушных и кабельных линий, а также в обмотках и стальных сердечниках силовых трансформаторов.

При проектировании нужно стремиться к уменьшению потерь электроэнергии на всех участках энергосистемы, поскольку потери электроэнергии ведут к увеличению мощности электростанций, что в свою очередь влияет на стоимость электроэнергии.

В сетях до 10кВ потери мощности в основном обусловлены нагревом проводов от действия тока.

Потери мощности в линии.

Потери активной мощности (кВт) и потери реактивной мощности  (кВАр) можно найти по следующим формулам:

где Iрасч – расчетный ток данного участка линии, А;

Rл – активное сопротивление линии, Ом.

Потери мощности в трансформаторах.

Потери мощности в силовых трансформаторах состоят из потерь, не зависящих и зависящих от нагрузки. Потери активной мощности (кВт) в трансформаторе можно определить по следующей формуле:

Потери активной мощности в трансформаторе

где ?Рст – потери активной мощности в стали трансформатора при номинальном напряжении. Зависят только от мощности трансформатора и приложенного к первичной обмотке трансформатора напряжения. ?Рст приравнивают  ?Рх;

?Рх— потери холостого хода трансформатора;

?Роб – потери в обмотках при номинальной нагрузке трансформатора, кВт; ?Роб приравнивают  ?Рк.

?Рк– потери короткого замыкания;

?=S/Sном – коэффициент загрузки трансформатора равен отношению фактической нагрузки трансформатора к его номинальной мощности;

Потери реактивной мощности трансформатора (кВАр) можно определить по следующей формуле:

где ?Qст – потери реактивной мощности на намагничивание, кВАр. ?Qст приравнивают ?Qх.

?Qх – намагничивающая мощность холостого хода трансформатора;

?Qрас – потери реактивной мощности рассеяния в трансформаторе при номинальной нагрузке.

Значения ?Рст(?Рх) и ?Роб(?Рк) приведения в каталогах производителей силовых трансформаторов. Значения ?Qст(?Qх) и ?Qрас  определяют по данным каталогов из следующих выражений:

где Iх – ток холостого хода трансформатора, %;

Uк – напряжение короткого замыкания, %;

Iном – номинальный ток трансформатора, А;

Xтр – реактивное сопротивление трансформатора;

Sном – номинальная мощность трансформатора, кВА.

Потери электроэнергии.

На основании потерь мощности можно посчитать потери электроэнергии. Здесь следует быть внимательными. Нельзя посчитать потери электроэнергии умножив потери мощности при какой либо определенной нагрузке на число часов работы линии. Этого делать не стоит, т.к в течение суток или сезона потребляемая нагрузка изменяется и таким образом мы получим необоснованно завышенное значение.

Чтобы правильно посчитать потери электроэнергии используют метод, основанный на понятиях времени использования потерь и времени использовании максимума нагрузки.

Время максимальных потерь ? – условное число часов, в течение которых максимальный ток, протекающий в линии, создает потери энергии, равные действительным потерям энергии в год.

Временем использования максимальной нагрузки или временем использования максимума Тмах называют условное число часов, в течение которых линия, работая с  максимальной нагрузкой, могла бы передать потребителю за год столько энергии, сколько при работе по действительному переменному графику. Пусть W(кВт*ч) – энергия  переданная по линии за некоторый промежуток времени,  Рмах(кВт) -максимальная нагрузка, тогда время использования  максимальной нагрузки:

Тмах=W/Рмах

На основании статистических данных для отдельных групп электроприемников были получены следующие значения Тмах:

• Для внутреннего освещения – 1500—2000 ч;
• Наружного освещения – 2000—3000 ч;
• Промышленного предприятия односменного – 2000—2500 ч;
• Двухсменного – 3000—4500 ч;
• Трехсменного   – 3000—7000 ч;

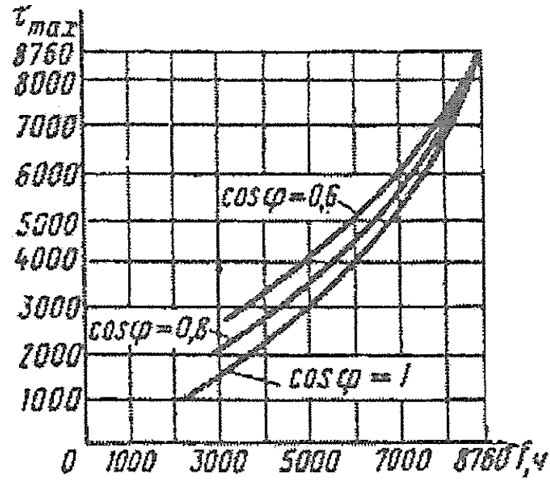
Время потерь ? можно найти по графику, зная Тмах и коэффициент мощности.

Теперь зная ? можно посчитать потери электроэнергии в линии и в трансформаторе.

Потери энергии в линии:

Потери энергии в трансформаторе:

где ?Wатр –общая потеря активной энергии (кВт*ч) в трансформаторе;

?Wртр –общая потеря реактивной энергии (кВАр*ч) в трансформаторе.

Расчёт потерь напряжения в кабеле

• Online расчёт заземления
• Online расчёт сечения кабеля по мощности и току

Потеря напряжения в кабеле — величина, равная разности между установившимися значениями действующего напряжения, измеренными в двух точках системы электроснабжения (по ГОСТ 23875-88). Этот параметр необходимо знать при производстве любых электромонтажных работ — начиная от видеонаблюдения и ОПС и заканчивая системами электроснабжения промышленных объектов.

При равенстве сопротивлений Zп1=Zп2=Zп3 и Zн1=Zн2=Zн3 ток в нулевом проводе отсутствует (Рис.1), поэтому для трёхфазных линий потери напряжения рассчитываются для одного проводника.

В двух- и однофазных линиях, а также в цепи постоянного тока, ток идёт по двум проводникам (Рис.2), поэтому вводится коэффициент 2 (при условии равенства Zп1=Zп2).

Доступна Windows-версия программы расчёта потерь напряжения

Пояснения к расчёту

Расчёт потерь линейного (между фазами) напряжения в кабеле при трёхфазном переменном токе производится по формулам:

Для расчёта потерь фазного напряжения U=220 В; 1 фаза.

P — активная мощность передаваемая по линии, Вт;
Q — реактивная мощность передаваемая по линии, ВАр;
R — удельное активное сопротивление кабельной линии, Ом/м;
X — удельное индуктивное сопротивление кабельной линии, Ом/м;
L — длина кабельной линии, м;
Uл — линейное напряжение сети, В;
Uф — фазное напряжение сети, В.

ВСЕ РАСЧЁТЫ

Лекция № 7

Потери мощности и электроэнергии в элементах сети

План.

1. Потери мощности
   в элементах сети.

2. Расчет потерь
   мощности в линиях электропередач.

3. Расчет потерь
   мощности в ЛЕП с равномерно распределенной
   нагрузкой.

4. Расчет потерь
   мощности в трансформаторах.

5. Приведенные и
   расчетные нагрузки потребителей.

6. Расчет потерь
   электроэнергии.

7. Мероприятия по
   снижению потерь мощности.

Потери мощности в элементах сети

Для
количественной характеристики работы
элементов электрической сети
рассматриваются ее рабочие режимы.
Рабочий
режим
– это установившееся электрическое
состояние, которое характеризуется
значениями токов, напряжений, активной,
реактивной и полной мощностей.

Основной целью
расчета режимов является определение
этих параметров, как для проверки
допустимости режимов, так и для обеспечения
экономичности работы элементов сетей.

Определение
значений токов в элементах сети и
напряжений в ее узлах начинается с
построения картины распределения полной
мощности по элементу, т.е. с определения
мощностей в начале и конце каждого
элемента. Такую картину называют
потокораспределением.

Рассчитывая
мощности в начале и в конце элемента
электрической сети, учитывают потери
мощности в сопротивлениях элемента и
влияние его проводимостей.

Расчет потерь мощности в линиях электропередач

Потери активной
мощности на участке ЛЕП (см. рис. 7.1)
обусловлены активным сопротивлением
проводов и кабелей, а также несовершенством
их изоляции. Мощность, теряемая в активных
сопротивлениях трехфазной ЛЕП и
расходуемая на ее нагрев, определяется
по формуле:

,

где
полный,
активный и реактивный токи в ЛЕП;

P, Q, S
– активная, реактивная и полная
мощности в начале или конце ЛЕП;

U– линейное напряжение в начале или
конце ЛЕП;

R
– активное сопротивление одной
фазы ЛЕП.

Потери активной
мощности в проводимостях ЛЕП обусловлены
несовершенством изоляции. В воздушных
ЛЕП – появлением короны и, в очень
незначительной степени, утечкой тока
по изоляторам. В кабельных ЛЕП –
появлением тока проводимости а его
абсорбции. Рассчитываются потери по
формуле:

,

где U– линейное напряжение в начале или
конце ЛЕП;

G
– активная проводимость ЛЕП.

При проектировании
воздушных ЛЕП потери мощности на корону
стремятся свести к нулю, выбирая такой
диаметр провода, когда возможность
возникновения короны практически
отсутствует.

Потери реактивной
мощности на участке ЛЕП обусловлены
индуктивными сопротивлениями проводов
и кабелей. Реактивная мощность, теряемая
в трехфазной ЛЕП, рассчитывается
аналогично мощности, теряемой в активных
сопротивлениях:

Генерируемая
емкостной проводимостью зарядная
мощность ЛЕП рассчитывается по формуле:

,

где U– линейное напряжение в начале или
конце ЛЕП;

B
– реактивная проводимость ЛЕП.

Зарядная мощность
уменьшает реактивную нагрузку сети и
тем самым снижает потери мощности в
ней.

Расчет потерь мощности в леп с равномерно распределенной нагрузкой

В линиях местных
сетей ()
потребители одинаковой мощности могут
располагаться на одинаковом расстоянии
друг от друга (например, источники
света). Такие ЛЕП называются линиями с
равномерно распределенной нагрузкой
(см. рис. 7.2).

В равномерно
нагруженной линии трехфазного переменного
тока длиной L
с суммарной токовой нагрузкойIплотность тока на единицу длины составитI/L. При погонном
активном сопротивленииr₀
потери активной мощности составят:

Если бы нагрузка
была сосредоточена в конце, то потери
мощности определялись бы как:

.

Сравнивая приведенные
выражения, видим, что потери мощности
в линии с равномерно распределенной
нагрузкой в 3 раза меньше.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #