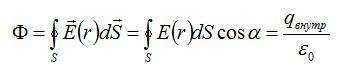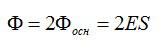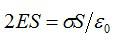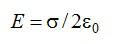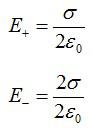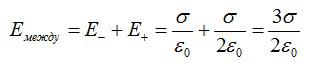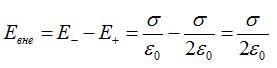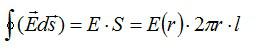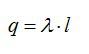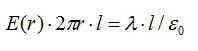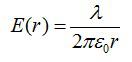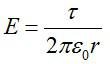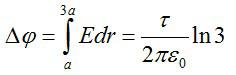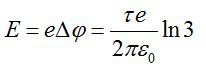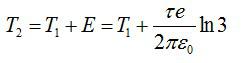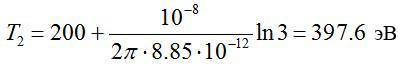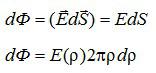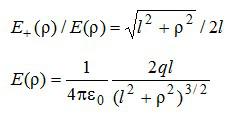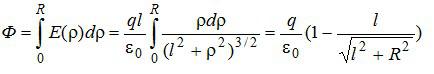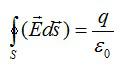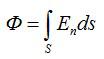Как найти поток через окружность

Поток векторного поля: теория и примеры

Понятие потока векторного поля и его вычисление как поверхностного интеграла

Своим названием поток векторного поля обязан задачам гидродинамики о потоке жидкости. Поток векторного поля может быть вычислен в виде поверхностного интеграла, который выражает общее количество жидкости, протекающей в единицу времени через некоторую поверхность в направлении вектора скорости течения жидкости в данной точке. Понятие потока векторного поля обобщается также на магнетический поток, поток электричества, поток тепла через заданную поверхность и другие. Поток векторного поля может быть вычислен в виде поверхностного интеграла как первого, так и второго рода и далее мы дадим его вывод через эти интегралы.

Пусть в некоторой области пространства задано векторное поле

и поверхность σ, в каждой точке M которой определён единичный вектор нормали . Пусть также направляющие косинусы этого вектора — непрерывные функции координат x, y, z точки M.

Определение потока векторного поля. Потоком W поля вектора через поверхность σ называется поверхностный интеграл

.

Обозначим как a n проекцию вектора на на единичный вектор . Тогда поток можем записать как поверхностный интеграл первого рода

.

.

поток векторного поля можно вычислить и как поверхностный интеграл второго рода

.

Направление и интенсивность потока векторного поля

Поток векторного поля зависит от местоположения поверхности σ. Если поверхность размещена так, что во всех её точках вектор поля образует с вектором нормали поверхности острый угол, то проекции вектора a n положительны и, таким образом поток W также положителен (рисунок ниже). Если же поверхность размещена так, что во всех её точках вектор образует с вектором нормали поверхности тупой угол, то поток W отрицателен.

Через каждую точку поверхности проходит одна векторная линия, поэтому поверхность σ пересекает бесконечное множество векторных линий. Однако условно можно принять, что поверхность σ пересекает некоторое конечное число векторных линий. Поэтому можно считать, что поток векторного поля — это число векторных линий, пересекающих поверхность σ. Чем интенсивнее поток векторного поля, тем более плотно расположены векторные линии и в результате получается бОльший поток жидкости.

Если поток векторного поля — поле скорости частиц текущей жидкости через поверхность σ, то поверхностный интеграл равен количеству жидкости, протекающей в единицу времени через поверхность σ. Если рассматривать магнетическое поле, которое характеризуется вектором магнетической индукции , то поверхностный интеграл называется магнетическим потоком через поверхность σ и равен общему количеству линий магнетической индукции, пересекающих поверхность σ. В случае электростатического поля интеграл выражает число линий электрической силы, пересекающих поверхность σ. Этот интеграл называется потоком вектора интенсивности электростатического поля через поверхнсть σ. В теории теплопроводности рассматривается стационарный поток тепла через поверхность σ. Если k — коэффициент теплопроводности, а u(M) — температура в данной области, то поток тепла, протекающего через поверхность σ в единицу времени, определяет интеграл .

Вычисление потока векторного поля: примеры

Пример 1. Вычислить поток векторного поля через верхнюю сторону треугольника, образованного пересечением плоскости с координатными плоскостями. Решить задачу двумя способами: 1) через поверхностный интеграл первого рода; 2) через поверхностный интеграл второго рода.

1) Поверхностью σ является треугольник ABC , а её проекцией на ось xOy — треугольник AOB .

Координатами вектора нормали данной поверхности являются коэффициенты при переменных в уравнении плоскости:

.

Длина вектора нормали:

.

Единичный вектор нормали:

.

Из выражения единичного вектора нормали следует, что направляющий косинус . Тогда .

Теперь можем выразить поток векторного поля в виде поверхностного интеграла первого рода и начать решать его:

Выразим переменную «зет»:

Продолжаем вычислять интеграл и, таким образом, поток векторного поля:

Получили ответ: поток векторного поля равен 64.

2) Выражая поток векторного поля через поверхностный интеграл второго рода, получаем

.

Представим этот интеграл в виде суммы трёх интегралов и каждый вычислим отдельно. Учитывая, что проекция поверхности на ось yOz является треугольник OCB , который ограничивают прямые y = 0 , z = 0 , y + 3z = 6 или y = 6 − 3z и в точках поверхности 2x = 6 − y − 3 , получаем первый интеграл и вычисляем его:

Проекцией поверхности на ось xOz является треугольник OAC , который ограничен прямыми x = 0 , z = 0 , 2x + 3z = 6 или . По этим данным получаем второй интеграл, который сразу решаем:

Проекцией поверхности на ось xOy является треугольник OAB , который ограничен прямыми x = 0 , y = 0 , 2x + y = 6 . Получаем третий интеграл и решаем его:

Осталось только сложить все три интеграла:

.

Получили ответ: поток векторного поля равен 64. Как видим, он совпадает с ответом, полученным в первом случае.

Пример 2. Вычислить поток векторного поля через верхнюю сторону треугольника, образованного пересечением плоскости с координатными плоскостями. Решить задачу двумя способами: 1) через поверхностный интеграл первого рода; 2) через поверхностный интеграл второго рода.

Решение. Данная поверхность представляет собой треугольник ABC , изображённый на рисунке ниже.

1) Коэффициенты при x , y и z из уравнения плоскости являются координатами вектора нормали плоскости, которые нужно взять с противоположным знаком (так как вектор нормали верхней стороны треугольника образует с осью Oz острый угол, так что третья координата вектора нормали плоскости должна быть положительной). Таким образом, вектор нормали запишется в координатах так:

.

Длина этого вектора:

,

единичный вектор нормали (орт):

.

Скалярное произведение векторного поля и единичного нормального вектора:

Поток векторного поля, таким образом, представим в виде поверхностного интеграла первого рода

.

Выразим «зет» и продифференцируем то, что уже можно продифференцировать:

2) Представим поток векторного поля в виде поверхностного интеграла второго рода:

.

Первый и второй интегралы берём со знаком «минус», так как вектор нормали поверхности образует с осями Ox и Oy тупой угол.

Вычисляем первый интеграл:

Вычисляем второй интеграл:

Вычисляем третий интеграл:

Складываем три интеграла и получаем тот же самый результат:

.

Пример 3. Вычислить поток векторного поля через внешнюю сторону параболоида в первом октанте, отсечённую плоскостью z = 9 .

Поток векторного поля представим в виде поверхностного интеграла второго рода:

Второй интеграл берём со знаком минус, так как нормальный вектор поверхности образует с осью Oz тупой угол. Вычисляем первый интеграл:

Вычисляем второй интеграл:

В сумме получаем искомый поток векторного поля:

.

Примеры решений задач по теории поля

В этом разделе вы найдете готовые задания разного типа по векторному анализу (теории поля):

Примеры: базовые понятия теории поля

Задача 1. Проверить, что поле $f=(3x+y^2)i+2xy j$ потенциально и восстановить потенциал.

Задача 2. Найти дивергенцию и ротор векторного поля $overline=(3x-y) overline+(6z+5x) overline$

Задача 4. Вычислить потенциальную функцию векторного поля

Поток поля через поверхность

Циркуляция векторного поля

с помощью формулы Стокса и непосредственно (положительным направлением обхода контура считать то, при котором точка перемещается по часовой стрелке, если смотреть из начала координат).

Задача 12. Найти циркуляцию вектора $F$ вдоль ориентированного контура $L$. $$ overline = (3x-1) overline+ (y-x+z)overline+4z overline, $$ $L$ — контур треугольника $ABCA$, где $A,B,C$ точки пересечения плоскости $2x-y-2z+2=0$ соответственно с осями координат $Ox, Oy, Oz$.

Работа векторного поля

Задача 13. Найдите работу векторного поля $A=(2xy-y; x^2+x)$ по перемещению материальной точки вдоль окружности $x^2+y^2=4$ из $M (2; 0)$ в $К(-2; 0)$.

Задача 14. Вычислить работу векторного поля силы $overline = xz overline -overline+y overline$ при движении материальной точки по пути $L: x^2+y^2+z^2=4$, $z=1 (y ge 0)$ от точки $M(sqrt(3);0;1)$ до точки $N(-sqrt(3);0;1)$.

Типовой расчет по теории поля

Задание 15.
А) Найти поток векторного поля $F$ через внешнюю поверхность пирамиды, отсекаемой плоскостью $(p)$ двумя способами: непосредственно и по формуле Гаусса-Остроградского.
Б) Найти циркуляцию вектора $F$ по контуру треугольника двумя способами: по определению и по формуле Стокса.

$$ overline = z overline+ (x+y)overline+y overline, quad (p): 2x+y+2z=2. $$

Помощь с решением заданий

Если вам нужна помощь с решением задач и контрольных по этой и другим темам математического анализа, обращайтесь в МатБюро. Стоимость подробной консультации от 150 рублей , оформление производится в Word, срок от 1 дня.

Как найти поток через окружность

Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!

Контакты

Администратор, решение задач
Роман

Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym

Решение задач
Андрей

facebook:
dniprovets25

источники:

http://www.matburo.ru/ex_ma.php?p1=mafield

http://yukhym.com/ru/integrirovanie-funktsii/formula-ostrograds-kogo-gaussa-potok-vektornogo-polya.html

1. Определение потока векторного поля

Рассмотрим
векторное поле
,
где проекции— непрерывные функции в некоторой области
(V). Возьмем некоторую
гладкую (кусочно гладкую) двустороннюю
ориентированную поверхность (S)
(то есть двустороннюю поверхность с
выбранным на ней направлением нормали).

Определение.ПотокомПвекторного полячерез двустороннюю ориентированную
поверхность (S)
называется поверхностный интеграл
первого рода по поверхности (S):

.
(1.3)

Здесь
—
орт нормали к выбранной стороне (S);ds– элемент площади
поверхности (S).

Замечание.В
случае замкнутой поверхности ее
ориентируют, направляя нормаль изнутри
области (V) наружу.
Сторона с положительным направлением
нормали называется положительной
стороной поверхности.

Для
потока можно дать следующие записи
через поверхностные интегралы первого
и второго рода
:

(1.3)

где
,,— то есть— проекции площадкина плоскостиOyz,Oxz,Oxyсоответственно.

Пример.Вычислить поток векторного поля—
радиус-вектор точки)
через полную поверхность прямого
кругового цилиндра с высотойHи радиусом основанияR(см. рис.1).

Р

Рис.1.

ешение.Так как поверхность (S)
есть объединение поверхностейи,
то поэтому для потокаП(по свойству
аддитивности) имеем:.
На боковой поверхностинормальпараллельна плоскостиOxy;
следовательно,и поток=.
На нижнем основаниинормальпараллельна
осиOz:.
Тогдаи;
на стороненормальи,
т.е.и.Искомый
поток.
Обратим внимание на то, что.
Ниже увидим, что это не случайно.

2. Способы вычисления потока

1.
Метод проектирования.Пусть поверхность
(S) задана явным
уравнением.
В этом случае орти.
Для потокаП получим формулу:

.
(1.4)

Замечание 1.При проектировании на другие плоскости
в подынтегральную функцию в формуле
(1.4) следует добавить (множителем) проекциюна координатную ось, перпендикулярную
плоскости проектирования.

В формуле (1.4) ()
– область на плоскостиOxy,
в которую проектируется поверхность
(S); произведениеdxdyберется со знаком +, если уголмежду осью Ozи
нормальюострый, и минус, если уголтупой. Символозначает, что в подынтегральную функцию
вместоzнадо подставить.

Замечание 2.Аналогичные формулы можно записать,
если проектировать поверхность (S)
на плоскостиOxzилиOyz.

Замечание 3.В
случае неявного задания поверхности
(S)вектор.

Пример
1.Найти поток векторного полячерез верхнюю сторону треугольникаАВСс вершинами в точках,,(см. рис.2).

Р

Рис.2.

ешение.Составим уравнение
плоскости (поверхности (S)),
проходящей через три заданные точки:

,

откуда
.
Поверхность (S)
проектируется на плоскостьOxyв область,.
Из условия следует, что нормальобразует острый угол с осьюOz.
Имеем=;
произведениеdxdy,
берем со знаком “+”. Тогда по формуле
(1.4)

.

Пример 2.Вычислить полячерез замкнутую поверхность (S),
ограниченную цилиндроми плоскостями,.
Положительной стороной (по определению)
считаем внешнюю сторону замкнутой
поверхности.

Решение.Поверхность (S) кусочно
гладкая. Разобъем ее на три части
(см.
рис.3):.
В связи с этим.
1 )Для поверхностиz=0 и.

Т

Рис.3.

огда.
Проекцияповерхности (S) на
плоскостьOxyесть
полукруг,.
С учетом направления нормалидля потокаполучим:.
Переходя к полярным координатам, найдем.2)
Дляи.
Поверхностьпроектируется на плоскостьOxyв область ()
(см.п.1), и поток

=.3)Для,

и
=.
Однозначно поверхностьпроектируется на плоскостьOyzв область (),
ограниченную линиями.

Исключая отсюда
x, найдем проекцию
этой линии на плоскостьOyz:.
Для потока получим (напомним Замечание
1: следует учесть, что в этом случае

=.
4) Для потокаполучим.

2.
Метод проектирования на все три
координатные плоскости. Пусть
поверхность (S)
однозначно проектируется на все три
координатные плоскости: (D_xy):z=z(x,y);;.Для
потокаП в этом случае имеем (вторая
формула из (1.3)):

(1.5)

В (1.5) знаки проекций
dydz,dxdz,dxdyвыбираются в
соответствии с сформулированным выше
правилом.

Пример 3.Найти
поток векторачерез часть внешней стороны сферы,
заключенной в первом октанте.

Решение.Имеем.
С учетом того, что поверхность расположена
в первом октанте, проекцииdydz,dxdz,dxdyберем со знаком “+”. По формуле (1.5).
Из уравнения сферы имеем:;;и

.
Очевидно,
.
Вычислим этот интеграл в полярной
системе координат:===.
Следовательно,.

3.
Применение формулы Гаусса-Остроградского.Приведем соответствующую теорему.

Теорема.Если
в некоторой областипроекции полянепрерывны и имеют непрерывные частные
производные,
то поток векторачерез произвольную замкнутую кусочно
гладкую поверхность (S),
расположенную целиком в области,
равен тройному интегралу от суммыпо области (V),
ограниченной поверхностью (S):

(1.6)

—
формула Гаусса-Остроградского.

Замечание.
Подынтегральная функция в тройном
интеграле (1.6) называется дивергенцией
(расходимостью) поля
;
обозначается.

Пример 4.
Вычислить поток векторачерез
замкнутую поверхность,.

Решение. По
формуле (1.6).
Для вычисления этого интеграла применим
сферическую систему координат:,,;.
Таким образом,

.

Пример 5.Используя формулу Гаусса-Остроградского
(1.6), вычислить поток полячерез верхнюю сторону части поверхности,
расположенную над плоскостьюOxy.

Решение.Для
того, чтобы можно было применить формулу
(1.6), замкнем снизу данную поверхность
куском плоскостиOxy,
который ограничен окружностью,z = 0 . Вычислим
подынтегральную функцию, стоящую под
знаком тройного интеграла:.
Отсюда следует, что потокП=0. По
свойству аддитивности,
откуда искомый поток.
Уравнение поверхностии.
Таким образом,— потокчерез поверхностьz=0 численно равен площади круга;
искомый поток.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

We have that the flux of ${bf F}(x,y)=(F_x(x,y),F_y(x,y))$ through a given closed curve $gamma$ is
$$int_{gamma} ({bf F} cdot {bf n}) ds$$
where ${bf n}$ is the outward unit normal vector field to $gamma$.

If $gamma$ is the circle of radius $r$ centred at the origin then the outer normal is given by ${bf n}=(cos(t),sin(t))$, hence
$$int_{gamma} ({bf F} cdot {bf n}) ds=int_0^{2pi}[F_x(rcos(t),rsin(t))cos(t)+F_y(rcos(t),rsin(t))sin(t)] (rdt).$$

In your case, $r=1$, $F_x(x,y)=a_{11}x+a_{12}y$ and $F_y(x,y)=a_{21}x+a_{22}y$.
Now you can compute the above integral and find a formula in terms of the elements of the matrix $A$.

By the Divergence Theorem you will find that the flux is

$$int_D nabla cdot {bf F} , dA =
int_D (a_{11}+a_{22}) , dA=(a_{11}+a_{22})|D|=pi(a_{11}+a_{22})$$
where $D$ is the interior of $gamma$.

Примеры решений задач по теории поля

В этом разделе вы найдете готовые задания разного типа по векторному анализу (теории поля):

Примеры: базовые понятия теории поля

Задача 1. Проверить, что поле $f=(3x+y^2)i+2xy j$ потенциально и восстановить потенциал.

Задача 2. Найти дивергенцию и ротор векторного поля $overline{a}=(3x-y) overline{i}+(6z+5x) overline{k}$

Задача 3. Дано скалярное поле $u(x,y,z)$ и векторное поле $overline{a}(x,y,z)$. Найти $grad u$, $div overline{a}$, $rot overline{a}$ в точке $M(1;5;-2)$.

$$u=frac{sqrt{x}}{y}-frac{yz}{x+sqrt{y}}, quad
overline{a}=yzoverline{i} +xzoverline{j} +xyoverline{k}$$

Задача 4. Вычислить потенциальную функцию векторного поля

$$overline{a}=left( frac{x}{y}+ycos x right)overline{i} +left(-frac{x^2}{2y^2}+sin xright)overline{j}.$$

Поток поля через поверхность

Задача 5. Найти поток векторного поля $overline{a}=2x overline{i}+y overline{j}-2z overline{k}$ через часть плоскости $P: 2x+y/2+z=1$, расположенную в первом октанте (нормаль образует острый угол с осью $Oz$).

Задача 6. Найти поток векторного поля $overline{a}$ через часть поверхности $S$, вырезаемую плоскостями $P_1, P_2$ (нормаль внешняя к замкнутой поверхности, образуемой данными поверхностями).

$$ overline{a}=(x^3+xy^2)overline{i}+(y^3+x^2y)overline{j}+z^2overline{k},\
S: x^2+y^2=1, P_1^ z=0; P_2: z=3$$

Задача 7. Найти поток векторного поля $overline{a}$ через замкнутую поверхность $S$ (нормаль внешняя).

$$ overline{a}=xoverline{i}+zoverline{j}-yoverline{k},\
S: z=4-2(x^2+y^2), z=2(x^2+y^2).$$

Задача 8. Найти поток векторного поля $overline{a}=x^3overline{i}+y^3overline{j}+z^3overline{k}$ через замкнутую поверхность $S: x^2+y^2+z^2=1$ (нормаль внешняя).

Задача 9. Найти поток векторного поля $overline{a}$ через часть плоскости $S$, вырезанную плоскостью $P: z=1$ непосредственно и с помощью формулы Гаусса-Остроградского (нормаль внешняя к замкнутой поверхности).

$$overline{a}=(x+xy^2) overline{i} + (y-yx^2)overline{j}+(z-3)overline{k}, quad S: x^2+y^2=z^2 (z geq 0).$$

Циркуляция векторного поля

Задача 10. Найти модуль циркуляции векторного поля $overline{a}=xyoverline{i}+yzoverline{j}+zxoverline{k}$ вдоль контура

$$x^2+y^2=9, x+y+z=1.$$

Задача 11. Найдите циркуляцию вектора $overline{a}=(x^2-y) overline{i}+ xoverline{j}+ overline{k}$ по контуру

$$x^2+y^2=1;\
z=1$$

с помощью формулы Стокса и непосредственно (положительным направлением обхода контура считать то, при котором точка перемещается по часовой стрелке, если смотреть из начала координат).

Задача 12. Найти циркуляцию вектора $F$ вдоль ориентированного контура $L$.
$$ overline{F} = (3x-1) overline{i}+ (y-x+z)overline{j}+4z overline{k}, $$
$L$ — контур треугольника $ABCA$, где $A,B,C$ точки пересечения плоскости $2x-y-2z+2=0$ соответственно с осями координат $Ox, Oy, Oz$.

Работа векторного поля

Задача 13. Найдите работу векторного поля $A=(2xy-y; x^2+x)$ по перемещению материальной точки вдоль окружности $x^2+y^2=4$ из $M (2; 0)$ в $К(-2; 0)$.

Задача 14. Вычислить работу векторного поля силы $overline{F} = xz overline{i} -overline{j}+y overline{k}$ при движении материальной точки по пути $L: x^2+y^2+z^2=4$, $z=1 (y ge 0)$ от точки $M(sqrt(3);0;1)$ до точки $N(-sqrt(3);0;1)$.

Типовой расчет по теории поля

Задание 15.
А) Найти поток векторного поля $F$ через внешнюю поверхность пирамиды, отсекаемой плоскостью $(p)$ двумя способами: непосредственно и по формуле Гаусса-Остроградского.
Б) Найти циркуляцию вектора $F$ по контуру треугольника двумя способами: по определению и по формуле Стокса.

$$ overline{F} = z overline{i}+ (x+y)overline{j}+y overline{k}, quad (p): 2x+y+2z=2. $$

Помощь с решением заданий

Если вам нужна помощь с решением задач и контрольных по этой и другим темам математического анализа, обращайтесь в МатБюро. Стоимость подробной консультации от 150 рублей, оформление производится в Word, срок от 1 дня.

Полезные ссылки

• Учебник с примерами онлайн по теории поля
• Функции нескольких переменных — задачи с решениями

Теорема Гаусса выражает связь между потоком вектора напряженности электрического поля через замкнутую поверхность и алгебраической суммой зарядов, заключенных в объеме, ограниченном этой поверхностью. О примерах использования теоремы Гаусса на практике поговорим в этой статье.

Присоединяйтесь к нам в телеграме, чтобы не только решать задачи, но и быть в курсе актуальных новостей для студентов всех специальностей.

Задачи на теорему Гаусса с решением

Если вам нужно сначала освежить теоретические знания, читайте подробную теорию по теореме Гаусса в нашем справочнике. Ну а перед решением задач не забудьте повторить памятку и на всякий случай держите под рукой полезные формулы.

Кстати, при решении задач на теорему Гаусса придется довольно часто брать интегралы. Хотите научиться делать это по-быстрому? У нас уже есть отдельная статья и видео на эту тему.

Задача на теорему Гаусса №1: напряженность поля плоскости

Условие

Определите напряженность поля бесконечной заряженной плоскости. Поверхностная плотность заряда сигма.

Решение

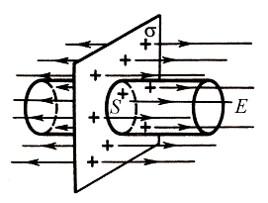
Линии напряженности перпендикулярны рассматриваемой плоскости и направлены в обе стороны от неё. Выберем в качестве гауссовой поверхности цилиндр с основанием, параллельным плоскости:

По теореме Гаусса:

Поток сквозь цилиндр равен сумме потоков сквозь боковую поверхность цилиндра и потокам сквозь оба его основания. Поток сквозь боковую поверхность равен нулю, так как линии напряженности параллельны ей:

Согласно теореме Гаусса:

Отсюда:

Ответ: см. выше.

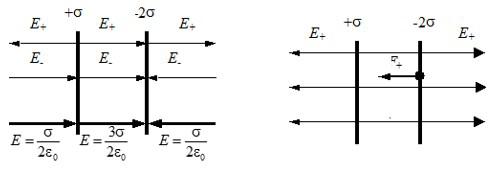
Задача на теорему Гаусса №2: напряженность поля двух пластин

Условие

Электрическое поле создано двумя параллельными заряженными тонкими пластинами с поверхностными плотностями заряда + сигма  и -2 сигма. Площадь каждой пластины S, расстояние между пластинами d можно считать значительно меньшим их продольных размеров. Какова напряженность электрического поля, созданного этими пластинами?

Решение

Для электрического поля действует принцип суперпозиции: результирующее поле равно векторной сумме отдельных полей каждой пластины. Из предыдущей задачи мы знаем формулу, по которой вычисляется напряженность поля тонкой заряженной пластины, запишем для каждой из них:

Векторы напряженности между пластинами совпадают по направлению, результирующая напряженность равна:

Справа и слева от пластин, во внешней области, векторы направлены в разные стороны:

Для наглядности приведем рисунок:

Ответ: см. выше.

Задача на теорему Гаусса №3: напряженность электрического поля бесконечной нити

Условие

Определить напряженность электрического поля, создаваемую бесконечной тонкой нитью, равномерно заряженной с линейной плотностью заряда лямбда.

Решение

Напряженность будем искать при помощи теоремы Гаусса. Наша задача – определить зависимость напряженности от расстояния от нити. В качестве поверхности выберем цилиндр с боковыми стенками, параллельными нити. Будем учитывать только поток вектора напряженности через боковую поверхность, так как поток через основания цилиндра равен нулю:

Заряд нити внутри рассматриваемой поверхности равен заряду отрезка нити длиной l:

По теореме Гаусса:

Отсюда:

Ответ: см. выше.

Задача с применением теоремы Гаусса №4

Условие

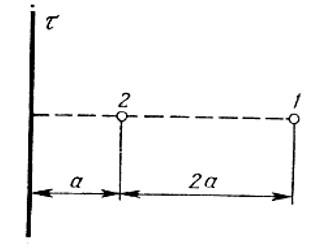
Электрическое поле создано бесконечной заряженной прямой линией с равномерно распределённым зарядом (τ = 10 нКл/м). Определить кинетическую энергию Т2 электрона в точке 2, если в точке 1 его кинетическая энергия Т1 = 200 эВ. Расстояние точки 2 от линии равно а = 0,5 см, точки 1 – b=1,5 см.

Решение

Ранее рассмотренные задачи были примерами вычисления полей с помощью теоремы Гаусса. Теперь рассмотрим задачу, которая решается сиспользованием этой информации. Из предыдущей задачи возьмем выражение для напряженности поля заряженной нити:

Разность потенциалов поля в двух точках будет равна:

При прохождении этой разницы потенциалов электрон приобретёт кинетическую энергию:

Конечная энергия частицы будет равна:

Получим:

Ответ: 397.6 эВ.

Задача на теорему Гаусса №5: поток электрического поля

Условие

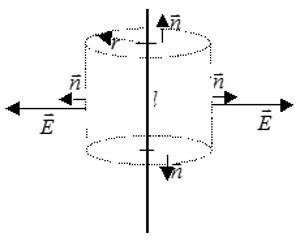
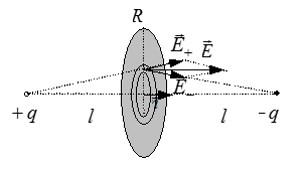
Два точечных заряда q и –q расположены на расстоянии 2l друг от друга. Найти поток вектора напряженности через круг радиуса R. Плоскость круга проходит через его середину и перпендикулярна отрезку прямой, соединяющей заряды.

Решение

Рассмотрим элементарный поток результирующего электрического поля через бесконечно малую кольцевую зону круга: 

В записи потока учтено, что вектор напряженности перпендикулярен поверхности круга. Выразим напряженность электрического поля через «ро», используя подобие треугольников, показанных на рисунке:

Вычисление потока сводится к взятию интеграла:

Ответ: см. выше.

Примеры применения теоремы Гаусса можно найти не только в электростатике, но и в других областях физики.

Вопросы на теорему Гаусса

Вопрос 1. Сформулируйте теорему Гаусса.

Ответ. Теорема Гаусса гласит:

Поток вектора напряженности электростатического поля через замкнутую поверхность равен алгебраической сумме зарядов внутри поверхности, деленной на эпсилон нулевое (электрическую постоянную).

Вопрос 2. Что такое поток вектора напряженности?

Ответ. Поток вектора напряженности – скалярная физическая величина, определяемая как число линий вектора напряженности, пронизывающих некоторую поверхность S. Поток напряженности электрического поля через поверхность S конечного размера определяется как алгебраическая сумма элементарных потоков:

Вопрос 3. Что такое силовые линии напряженности?

Ответ. Это линии, с помощью которых используются для графического представления поля:

• касательная к силовой линии в каждой точке пространства направлена вдоль вектора поля;
• густота силовых линий пропорциональна напряженности поля в данной точке;
• поток вектора напряженности пропорционален числу силовых линий, пронизывающих поверхность.

Вопрос 4. Где начинаются и где заканчиваются силовые линии?

Ответ. Силовые линии начинаются и заканчиваются на зарядах, оставаясь непрерывными в пустом пространстве.

Вопрос 5. Верно ли утвержление: теорема Гаусса справедлива только для неподвижных зарядов.

Ответ. Нет, так как заряд частицы не зависит от ее скорости.

Нужна помощь в решении задач и других студенческих заданий? Обратитесь в профессиональный студенческий сервис за качественным решением проблем.