Поток векторного поля: теория и примеры
Понятие потока векторного поля и его вычисление как поверхностного интеграла
Своим названием поток векторного поля обязан задачам гидродинамики о потоке жидкости. Поток векторного поля может быть вычислен в виде поверхностного интеграла, который выражает общее количество жидкости, протекающей в единицу времени через некоторую поверхность в направлении вектора скорости течения жидкости в данной точке. Понятие потока векторного поля обобщается также на магнетический поток, поток электричества, поток тепла через заданную поверхность и другие. Поток векторного поля может быть вычислен в виде поверхностного интеграла как первого, так и второго рода и далее мы дадим его вывод через эти интегралы.
Пусть в некоторой области пространства задано векторное поле
и поверхность σ, в каждой точке M которой определён единичный вектор нормали . Пусть также направляющие косинусы этого вектора — непрерывные функции координат x, y, z точки M.
Определение потока векторного поля. Потоком W поля вектора через поверхность σ называется поверхностный интеграл
.
Обозначим как a n проекцию вектора на на единичный вектор . Тогда поток можем записать как поверхностный интеграл первого рода
.
.
поток векторного поля можно вычислить и как поверхностный интеграл второго рода
.
Направление и интенсивность потока векторного поля
Поток векторного поля зависит от местоположения поверхности σ. Если поверхность размещена так, что во всех её точках вектор поля образует с вектором нормали поверхности острый угол, то проекции вектора a n положительны и, таким образом поток W также положителен (рисунок ниже). Если же поверхность размещена так, что во всех её точках вектор образует с вектором нормали поверхности тупой угол, то поток W отрицателен.
Через каждую точку поверхности проходит одна векторная линия, поэтому поверхность σ пересекает бесконечное множество векторных линий. Однако условно можно принять, что поверхность σ пересекает некоторое конечное число векторных линий. Поэтому можно считать, что поток векторного поля — это число векторных линий, пересекающих поверхность σ. Чем интенсивнее поток векторного поля, тем более плотно расположены векторные линии и в результате получается бОльший поток жидкости.
Если поток векторного поля — поле скорости частиц текущей жидкости через поверхность σ, то поверхностный интеграл равен количеству жидкости, протекающей в единицу времени через поверхность σ. Если рассматривать магнетическое поле, которое характеризуется вектором магнетической индукции , то поверхностный интеграл называется магнетическим потоком через поверхность σ и равен общему количеству линий магнетической индукции, пересекающих поверхность σ. В случае электростатического поля интеграл выражает число линий электрической силы, пересекающих поверхность σ. Этот интеграл называется потоком вектора интенсивности электростатического поля через поверхнсть σ. В теории теплопроводности рассматривается стационарный поток тепла через поверхность σ. Если k — коэффициент теплопроводности, а u(M) — температура в данной области, то поток тепла, протекающего через поверхность σ в единицу времени, определяет интеграл .
Вычисление потока векторного поля: примеры
Пример 1. Вычислить поток векторного поля через верхнюю сторону треугольника, образованного пересечением плоскости с координатными плоскостями. Решить задачу двумя способами: 1) через поверхностный интеграл первого рода; 2) через поверхностный интеграл второго рода.
1) Поверхностью σ является треугольник ABC , а её проекцией на ось xOy — треугольник AOB .
Координатами вектора нормали данной поверхности являются коэффициенты при переменных в уравнении плоскости:
.
Длина вектора нормали:
.
Единичный вектор нормали:
.
Из выражения единичного вектора нормали следует, что направляющий косинус . Тогда .
Теперь можем выразить поток векторного поля в виде поверхностного интеграла первого рода и начать решать его:
Выразим переменную «зет»:
Продолжаем вычислять интеграл и, таким образом, поток векторного поля:
Получили ответ: поток векторного поля равен 64.
2) Выражая поток векторного поля через поверхностный интеграл второго рода, получаем
.
Представим этот интеграл в виде суммы трёх интегралов и каждый вычислим отдельно. Учитывая, что проекция поверхности на ось yOz является треугольник OCB , который ограничивают прямые y = 0 , z = 0 , y + 3z = 6 или y = 6 − 3z и в точках поверхности 2x = 6 − y − 3 , получаем первый интеграл и вычисляем его:
Проекцией поверхности на ось xOz является треугольник OAC , который ограничен прямыми x = 0 , z = 0 , 2x + 3z = 6 или . По этим данным получаем второй интеграл, который сразу решаем:
Проекцией поверхности на ось xOy является треугольник OAB , который ограничен прямыми x = 0 , y = 0 , 2x + y = 6 . Получаем третий интеграл и решаем его:
Осталось только сложить все три интеграла:
.
Получили ответ: поток векторного поля равен 64. Как видим, он совпадает с ответом, полученным в первом случае.
Пример 2. Вычислить поток векторного поля через верхнюю сторону треугольника, образованного пересечением плоскости с координатными плоскостями. Решить задачу двумя способами: 1) через поверхностный интеграл первого рода; 2) через поверхностный интеграл второго рода.
Решение. Данная поверхность представляет собой треугольник ABC , изображённый на рисунке ниже.
1) Коэффициенты при x , y и z из уравнения плоскости являются координатами вектора нормали плоскости, которые нужно взять с противоположным знаком (так как вектор нормали верхней стороны треугольника образует с осью Oz острый угол, так что третья координата вектора нормали плоскости должна быть положительной). Таким образом, вектор нормали запишется в координатах так:
.
Длина этого вектора:
,
единичный вектор нормали (орт):
.
Скалярное произведение векторного поля и единичного нормального вектора:
Поток векторного поля, таким образом, представим в виде поверхностного интеграла первого рода
.
Выразим «зет» и продифференцируем то, что уже можно продифференцировать:
2) Представим поток векторного поля в виде поверхностного интеграла второго рода:
.
Первый и второй интегралы берём со знаком «минус», так как вектор нормали поверхности образует с осями Ox и Oy тупой угол.
Вычисляем первый интеграл:
Вычисляем второй интеграл:
Вычисляем третий интеграл:
Складываем три интеграла и получаем тот же самый результат:
.
Пример 3. Вычислить поток векторного поля через внешнюю сторону параболоида в первом октанте, отсечённую плоскостью z = 9 .
Поток векторного поля представим в виде поверхностного интеграла второго рода:
Второй интеграл берём со знаком минус, так как нормальный вектор поверхности образует с осью Oz тупой угол. Вычисляем первый интеграл:
Вычисляем второй интеграл:
В сумме получаем искомый поток векторного поля:
.
Поток вектора через площадку
Поток векторного поля: теория и примеры
Понятие потока векторного поля и его вычисление как поверхностного интеграла
Своим названием поток векторного поля обязан задачам гидродинамики о потоке жидкости. Поток векторного поля может быть вычислен в виде поверхностного интеграла, который выражает общее количество жидкости, протекающей в единицу времени через некоторую поверхность в направлении вектора скорости течения жидкости в данной точке. Понятие потока векторного поля обобщается также на магнетический поток, поток электричества, поток тепла через заданную поверхность и другие. Поток векторного поля может быть вычислен в виде поверхностного интеграла как первого, так и второго рода и далее мы дадим его вывод через эти интегралы.
Пусть в некоторой области пространства задано векторное поле
и поверхность σ, в каждой точке M которой определён единичный вектор нормали . Пусть также направляющие косинусы этого вектора — непрерывные функции координат x, y, z точки M.
Определение потока векторного поля. Потоком W поля вектора через поверхность σ называется поверхностный интеграл
.
Обозначим как a n проекцию вектора на на единичный вектор . Тогда поток можем записать как поверхностный интеграл первого рода
.
.
поток векторного поля можно вычислить и как поверхностный интеграл второго рода
.
Направление и интенсивность потока векторного поля
Поток векторного поля зависит от местоположения поверхности σ. Если поверхность размещена так, что во всех её точках вектор поля образует с вектором нормали поверхности острый угол, то проекции вектора a n положительны и, таким образом поток W также положителен (рисунок ниже). Если же поверхность размещена так, что во всех её точках вектор образует с вектором нормали поверхности тупой угол, то поток W отрицателен.
Через каждую точку поверхности проходит одна векторная линия, поэтому поверхность σ пересекает бесконечное множество векторных линий. Однако условно можно принять, что поверхность σ пересекает некоторое конечное число векторных линий. Поэтому можно считать, что поток векторного поля — это число векторных линий, пересекающих поверхность σ. Чем интенсивнее поток векторного поля, тем более плотно расположены векторные линии и в результате получается бОльший поток жидкости.
Если поток векторного поля — поле скорости частиц текущей жидкости через поверхность σ, то поверхностный интеграл равен количеству жидкости, протекающей в единицу времени через поверхность σ. Если рассматривать магнетическое поле, которое характеризуется вектором магнетической индукции , то поверхностный интеграл называется магнетическим потоком через поверхность σ и равен общему количеству линий магнетической индукции, пересекающих поверхность σ. В случае электростатического поля интеграл выражает число линий электрической силы, пересекающих поверхность σ. Этот интеграл называется потоком вектора интенсивности электростатического поля через поверхнсть σ. В теории теплопроводности рассматривается стационарный поток тепла через поверхность σ. Если k — коэффициент теплопроводности, а u(M) — температура в данной области, то поток тепла, протекающего через поверхность σ в единицу времени, определяет интеграл .
Вычисление потока векторного поля: примеры
Пример 1. Вычислить поток векторного поля через верхнюю сторону треугольника, образованного пересечением плоскости с координатными плоскостями. Решить задачу двумя способами: 1) через поверхностный интеграл первого рода; 2) через поверхностный интеграл второго рода.
1) Поверхностью σ является треугольник ABC , а её проекцией на ось xOy — треугольник AOB .
Координатами вектора нормали данной поверхности являются коэффициенты при переменных в уравнении плоскости:
.
Длина вектора нормали:
.
Единичный вектор нормали:
.
Из выражения единичного вектора нормали следует, что направляющий косинус . Тогда .
Теперь можем выразить поток векторного поля в виде поверхностного интеграла первого рода и начать решать его:
Выразим переменную «зет»:
Продолжаем вычислять интеграл и, таким образом, поток векторного поля:
Получили ответ: поток векторного поля равен 64.
2) Выражая поток векторного поля через поверхностный интеграл второго рода, получаем
.
Представим этот интеграл в виде суммы трёх интегралов и каждый вычислим отдельно. Учитывая, что проекция поверхности на ось yOz является треугольник OCB , который ограничивают прямые y = 0 , z = 0 , y + 3z = 6 или y = 6 − 3z и в точках поверхности 2x = 6 − y − 3 , получаем первый интеграл и вычисляем его:
Проекцией поверхности на ось xOz является треугольник OAC , который ограничен прямыми x = 0 , z = 0 , 2x + 3z = 6 или . По этим данным получаем второй интеграл, который сразу решаем:
Проекцией поверхности на ось xOy является треугольник OAB , который ограничен прямыми x = 0 , y = 0 , 2x + y = 6 . Получаем третий интеграл и решаем его:
Осталось только сложить все три интеграла:
.
Получили ответ: поток векторного поля равен 64. Как видим, он совпадает с ответом, полученным в первом случае.
Пример 2. Вычислить поток векторного поля через верхнюю сторону треугольника, образованного пересечением плоскости с координатными плоскостями. Решить задачу двумя способами: 1) через поверхностный интеграл первого рода; 2) через поверхностный интеграл второго рода.
Решение. Данная поверхность представляет собой треугольник ABC , изображённый на рисунке ниже.
1) Коэффициенты при x , y и z из уравнения плоскости являются координатами вектора нормали плоскости, которые нужно взять с противоположным знаком (так как вектор нормали верхней стороны треугольника образует с осью Oz острый угол, так что третья координата вектора нормали плоскости должна быть положительной). Таким образом, вектор нормали запишется в координатах так:
.
Длина этого вектора:
,
единичный вектор нормали (орт):
.
Скалярное произведение векторного поля и единичного нормального вектора:
Поток векторного поля, таким образом, представим в виде поверхностного интеграла первого рода
.
Выразим «зет» и продифференцируем то, что уже можно продифференцировать:
2) Представим поток векторного поля в виде поверхностного интеграла второго рода:
.
Первый и второй интегралы берём со знаком «минус», так как вектор нормали поверхности образует с осями Ox и Oy тупой угол.
Вычисляем первый интеграл:
Вычисляем второй интеграл:
Вычисляем третий интеграл:
Складываем три интеграла и получаем тот же самый результат:
.
Пример 3. Вычислить поток векторного поля через внешнюю сторону параболоида в первом октанте, отсечённую плоскостью z = 9 .
Поток векторного поля представим в виде поверхностного интеграла второго рода:
Второй интеграл берём со знаком минус, так как нормальный вектор поверхности образует с осью Oz тупой угол. Вычисляем первый интеграл:
Вычисляем второй интеграл:
В сумме получаем искомый поток векторного поля:
.
Теорема Гаусса
Для полноценного описания электростатического поля заданной системы зарядов в вакууме достаточно экспериментально подтвержденного закона Кулона и принципа суперпозиции. Но при этом существует возможность свойства электростатического поля охарактеризовать в ином обобщенном виде, не опираясь на утверждения касательно кулоновского поля точечного заряда.
Поток вектора напряженности
Зададим новую физическую величину, описывающую электрическое поле – поток Φ вектора напряженности электрического поля. Предположим, что в пространстве, содержащем заданное электрическое поле, имеется некая достаточно малая площадка Δ S .
Элементарный поток вектора напряженности (через площадку S ) – это физическая величина, равная произведению модуля вектора E → , площади Δ S и косинуса угла α между вектором и нормалью к площадке:
Δ Φ = E Δ S cos α = E n Δ S.
В данной формуле E n является модулем нормальной составляющей поля E → .
Рисунок 1 . 3 . 1 . Иллюстрация элементарного потока Δ Φ .
Теперь возьмем для рассмотрения некую произвольную замкнутую поверхность S . Разобьем заданную поверхность на площадки небольшого размера Δ S i , рассчитаем элементарные потоки Δ Φ i поля через эти малые площадки, после чего найдем их сумму, что в итоге даст нам поток Φ вектора через замкнутую поверхность S (рис. 1 . 3 . 2 ):
Φ = ∑ ∆ Φ i = ∑ E m ∆ S i
Когда речь идет о поверхности замкнутого типа, всегда используется внешняя нормаль.
Рисунок 1 . 3 . 2 . Расчет потока Ф через произвольную замкнутую поверхность S .
Теорема Гаусса. Доказательство
Теорема или закон Гаусса для электростатического поля в вакууме является одним из основных электродинамических законов.
Поток вектора напряженности электростатического поля E → через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε 0 .
Уравнение Гаусса имеет вид:
Φ = 1 ε 0 ∑ q в н у т р
Докажем указанную теорию: для этого исследуем сферическую поверхность (или поверхность шара) S . В центре заданной поверхности расположен точечный заряд q . Любая точка сферы обладает электрическим полем, перпендикулярным поверхности сферы и равным по модулю:
E = E n = 1 4 π ε 0 · q R 2 ,
где R является радиусом сферы.
Поток Φ через поверхность шара запишется, как произведение E и площади сферы 4 π R 2 . Тогда: Φ = 1 ε 0 q .
Следующим нашим шагом будет окружение точечного заряда произвольной поверхностью S замкнутого типа; зададим также вспомогательную сферу R 0 (рис. 1 . 3 . 3 ).
Рисунок 1 . 3 . 3 . Поток электрического поля точечного заряда через произвольную поверхность S , окружающую заряд.
Возьмем для рассмотрения конус с малым телесным углом Δ Ω при вершине. Рассматриваемый конус задаст на сфере малую площадку Δ S 0 , а на поверхности S – площадку Δ S . Элементарные потоки Δ Φ 0 и Δ Φ через эти площадки являются одинаковыми. В самом деле:
Δ Φ 0 = E 0 Δ S 0 , Δ Φ = E Δ S cos α = E Δ S ‘ ,
где выражением Δ S ‘ = Δ S cos α определяется площадка, которая задастся конусом с телесным углом Δ Ω на поверхности сферы радиуса n .
Поскольку ∆ S 0 ∆ S ‘ = R 0 2 r 2 , то ∆ Φ 0 = ∆ Φ . Из полученного следует вывод о том, что полный поток электрического поля точечного заряда через произвольную поверхность, охватывающую заряд, равен потоку Φ 0 через поверхность вспомогательной сферы:
Так же мы можем продемонстрировать, что, когда замкнутая поверхность S не охватывает точечный заряд q , поток Φ равен нулю. Этот случай проиллюстрирован на рис. 1 . 3 . 2 . Все силовые линии электрического поля точечного заряда пронизывают замкнутую поверхность S насквозь. Внутри поверхности S зарядов нет, т.е. в этой области не наблюдается обрыва или зарождения силовых линий.
Обобщение теоремы Гаусса на случай произвольного распределения зарядов является следствием из принципа суперпозиции. Поле любого распределения зарядов возможно записать в виде векторной суммы электрических полей точечных зарядов. Поток Φ системы зарядов через произвольную замкнутую поверхность S сложится из потоков Φ i электрических полей отдельных зарядов. Когда заряд q i расположен внутри поверхности S , он дает вклад в поток, равный q i ε 0 . В случае расположения заряда снаружи поверхности его вклад в поток есть нуль.
Так, мы доказали теорему Гаусса.
Теорема Гаусса, по сути, есть следствие закона Кулона и принципа суперпозиции. Однако, взяв за изначальную аксиому утверждения теоремы, следствием станет закон Кулона, в связи с чем теорему Гаусса порой называют альтернативной формулировкой закона Кулона.
Опираясь на теорему Гаусса, в определенных случаях легко определить напряженность электрического поля вокруг заряженного тела (при наличии заранее угаданных симметрии заданного распределения зарядов и общей структуры поля).
Применение теоремы Гаусса
В качестве примера можно рассмотреть задачу, в которой необходимо вычислить поле тонкостенного полого однородно заряженного длинного цилиндра с радиусом R . Такая задача имеет осевую симметрию, и из соображений симметрии электрическое поле должно иметь направление по радиусу. Таким образом, чтобы иметь возможность применить теорему Гаусса, оптимально выбрать поверхность замкнутого типа S в виде соосного цилиндра некоторого радиуса r и длины l , закрытого с обоих торцов (рис. 1 . 3 . 4 ).
Рисунок 1 . 3 . 4 . Иллюстрация поля однородно заряженного цилиндра. O O ‘ – ось симметрии.
Если r ≥ R , то весь поток вектора напряженности пройдет через боковую поверхность цилиндра, поскольку поток через оба основания есть нуль. Формула площади боковой поверхности цилиндра запишется как: 2 π r l . Применим закон Гаусса и получим:
Φ = E 2 π r l = τ l ε 0 .
В указанном выражении τ является зарядом длины цилиндра. Далее можно записать:
Данное выражение не имеет зависимости от радиуса R заряженного цилиндра, а значит оно применимо и к полю длинной однородно заряженной нити.
Чтобы найти напряженность поля внутри заряженного цилиндра, необходимо создать замкнутую поверхность для случая r R . В соответствии с симметрией задачи поток вектора напряженности через боковую поверхность цилиндра должен быть, и в этом случае он равен Φ = E 2 π r l . Исходя из гауссовской теоремы, этот поток находится в пропорции к заряду, расположенному внутри замкнутой поверхности. Заряд этот равен нулю, откуда вытекает, что электрическое поле внутри однородно заряженного длинного полого цилиндра тоже есть нуль.
Точно так же теорема и формула Гаусса применимы для определения электрического поля в иных случаях, когда распределение зарядов охарактеризовано какой-либо симметрией, к примеру, симметрией относительно центра, плоскости или оси. Во всех этих случаях необходимо выбирать замкнутую гауссову поверхность подходящей формы.
К примеру, в случае центральной симметрии поверхность оптимально выбрать в виде сферы, у которой центр расположен в точке симметрии. Когда мы имеем симметрию относительно оси, подходящим видом замкнутой поверхности будет соосный цилиндр, закрытый с обоих торцов (аналогично рассмотренному выше примеру).
При отсутствии симметрии и невозможности угадать общую структуру поля, теорема Гаусса не сможет быть применена для упрощения решения задачи по определению напряженности поля.
Разберем еще пример распределения зарядов при наличии симметрии: нахождение поля равномерно заряженной плоскости (рис. 1 . 3 . 5 ).
Рисунок 1 . 3 . 5 . Поле равномерно заряженной плоскости. σ – поверхностная плотность заряда. S – замкнутая гауссова поверхность.
Здесь гауссову поверхность S оптимально задать как цилиндр некой длины, замкнутый с обоих концов. Ось цилиндра является перпендикуляром к заряженной плоскости; в свою очередь, торцы цилиндра находятся на одинаковом расстоянии от нее. В соответствии с симметрией поле равномерно заряженной плоскости должно везде иметь направление по нормали. Применим теорему Гаусса и получим:
2 E ∆ S = σ ∆ S ε 0 или E = σ 2 ε 0 .
Здесь σ является поверхностной плотностью заряда или зарядом, приходящимся на единицу площади.
Выражение, которое мы получили для электрического поля однородно заряженной плоскости, возможно использовать и для плоских заряженных площадок конечного размера: здесь расстояние от точки, в которой мы определяем напряженность поля, до заряженной площадки должно быть значимо меньше размеров площадки.
Поток вектора через площадку
Экспериментально установленные закон Кулона и принцип суперпозиции позволяют полностью описать электростатическое поле заданной системы зарядов в вакууме. Однако, свойства электростатического поля можно выразить в другой, более общей форме, не прибегая к представлению о кулоновском поле точечного заряда.
Введем новую физическую величину, характеризующую электрическое поле – поток Φ вектора напряженности электрического поля. Пусть в пространстве, где создано электрическое поле, расположена некоторая достаточно малая площадка . Произведение модуля вектора на площадь и на косинус угла α между вектором и нормалью к площадке называется элементарным потоком вектора напряженности через площадку (рис. 1.3.1):
где – модуль нормальной составляющей поля
| Рисунок 1.3.1.
Рассмотрим теперь некоторую произвольную замкнутую поверхность . Если разбить эту поверхность на малые площадки Δ, определить элементарные потоки Δ поля через эти малые площадки, а затем их просуммировать, то в результате мы получим поток вектора через замкнутую поверхность (рис. 1.3.2): В случае замкнутой поверхности всегда выбирается внешняя нормаль .
|
Статья содержит базовое определение потока напряженности, теорему Остроградского — Гаусса вместе с доказательством. Как всегда, теория закрепляется на практике с помощью задач.
Поток вектора напряжённости электрического поля. Теорема Остроградского — Гаусса.
Определение. Потоком вектора напряженности Ф электрического поля через площадку S называется скалярная физическая величина, равная произведению площади S на нормальную составляющую напряжённости электрического поля E⏊.

, где n — вектор нормали к поверхности S, α — угол между нормалью n и вектором напряжённости E.

Теорема (Остроградского — Гаусса). Поток вектора напряжённости электрического поля в вакууме сквозь произвольную замкнутую поверхность, проведённую в поле, пропорционален алгебраической сумме электрических зарядов, заключённых внутри этой поверхности:
Доказательство. Рассмотрим поток вектора напряжённости через площадку ΔS (рис. 3.1).

С учетом напряжённости поля точечного заряда:


Как известно, телесный угол Ω по определению равен:
, где S — площадь, на которую опирается телесный угол, а r — расстояние до центра.

Применив это к нашему случаю, можно записать


Полный поток через сферу найдём, просуммировав все телесные углы. Так как полный телесный угол Ω = 4π, то получим
Так как поток ΔФ не зависит от положения заряда q, то получаем выражение, которое называется теоремой Остроградского — Гаусса.

С помощью теоремы Остроградского — Гаусса можно вычислять поля для некоторых симметричных случаев, в которых напряжённость поля одинакова во всех частях фигуры.
Пример 1 (Поле равномерно заряженной сферы). Окружим сферу радиуса R замкнутой поверхностью радиуса r > R (рис. 3.2).

Воспользовавшись теоремой Остроградского — Гаусса и определением потока, получим:

Поле сферы совпадает с полем точечного заряда за пределами сферы и равно нулю внутри сферы (так как все заряды находятся на поверхности).

Пример 2 (Поле бесконечной равномерно заряженной плоскости с поверхностным зарядом σ). Так как плоскость бесконечная, то во всех точках вектор E одинаков и направлен перпендикулярно поверхности. Густота линий (следовательно, и E тоже) не зависит от расстояния до плоскости — поле однородно.
Для нахождения E рассмотрим сферу радиуса R. Вне сферы поле равно 0, а внутри

Рассмотрим поле на расстояние r = R + x, x << R. Это поле равно E = σ / ε₀ и создается близлежащим к сфере малым участком (поле Eпл) и полем E₁, создаваемым остальными участками сферы. Участок должен быть настолько малым, чтобы его можно было считать плоским. С другой стороны, характерные размеры этого участка должны быть много больше расстояния x (чтобы этот малый плоский участок можно было считать бесконечной плоскостью). Другими словами, должно выполняться следующее соотношение:

где S — площадь малого участка сферы.
По разные стороны от поверхности поле E₁ одно и тоже, а поле Eпл меняет знак (рис. 3.3).

Следовательно, можно составить систему уравнений:

, из которой находим

Пример 3 (Поле бесконечного равномерно заряженного цилиндра радиуса R).
Окружим цилиндр замкнутой поверхностью в виде такого же цилиндра радиуса r > R (рис. 3.4).

Для удобства выберем некоторый участок длины L и заряда q и найдём для него поток двумя способами:

, где τ —линейная плотность заряженного цилиндра. Внутри цилиндра поля нет!
Замечание.Внутри всех проводящих замкнутых фигур поля нет! Это следует из того, что все заряды проводящих фигур сосредоточены на поверхности. Если представить, что внутри проводящего тела появятся поля, то должен потечь и ток, но этого не наблюдается в статически заряженных проводящих телах.
Пример 4 (Поле однородно заряженного диэлектрического шара радиуса R с зарядом q). Если выбрать контур радиуса r ≥ R, то решение дословно повторяет пример 1.

При r < R

, где q₁ — заряд, ограниченный замкнутым шаром радиуса r. Для нахождения q₁ найдём сначала объёмную плотность заряда ρ:

А затем найдём заряд q₁:

Подставив соответствующие выражение в (3.1), получим

В итоге получим:

Замечание. Простой проверкой убеждаемся, что при r = R оба выражения приводят к одному и тому же результату, что показывает, что функция E(r) в данном случае непрерывна.
Примеры решения задач
Задача 3.1. Воздух при напряженности более чем E₀ = 3 · 10⁶ В/м перестает быть хорошим диэлектриком и может проводить электрический ток. Найти, какой максимальный заряд можно поместить на металлический шар радиуса R = 1 м.
Решение. Максимальная напряжённость будет достигаться на поверхности шара, поэтому она не должна превышать заданного значения E₀.

Как видно из задачи, заряд 1 Кл — это очень большой заряд, и так сильно зарядить тела привычных размеров невозможно!
Задача 3.2. Найти распределение напряжённости в заряженной пластине толщиной h с объёмной плотностью заряда ρ. Какое максимальное значение напряжённости поля будет достигнуто, если соединить две пластины вместе (рис. 3.5)?

Решение. Сначала разберёмся, как в каждой толстой пластине зависит напряжённость электрического поля от x, где x — расстояние от середины пластины.
Для этого окружим часть пластины замкнутым контуром толщиной 2x, проходящим через центр пластины.
При x < h/2:

Тогда при x > h/2

Тогда, если соединить две пластины вместе, получим:

Задачи для самостоятельного решения
Задача 1. Напряжённость поля до бесконечно проводящей заряженной плоскости равна E₁, а после пластины — E₂. Найти поверхностную плотность заряда на пластине. Считать, что поле в обоих случаях направлено перпендикулярно заряженной пластине.
Задача 2. Две пересекающиеся под углом α и заряженные поверхностной плотностью заряда σ бесконечные пластины делят пространство на четыре области. Найти напряжённость в каждой из областей.
Список литературы
- Белолипецкий С. Н., Еркович О. С., Казаковцева В. А., Цвецинская Т. С. Задачник по физике. М., 2005.
- Задачи по физике / Под ред. Савченко О. Я. Новосибирск, 1999.
- Козел С. М., Слободянин В. П. Всероссийские олимпиады по физике. 1992–2001. М., 2002.
- Савченко Н. Е. Решение задач по физике. М., 2011.
- Черноуцан А. Учебно-справочное пособие для старшеклассников и абитуриентов. М., 2000.
Итак, на примерах мы показали, что, если
силовые линии однородного электрического
поля напряженностью
пронизывают некоторую площадкуS,
топоток вектора напряженности(число силовых линий через площадку)
будет определяться формулой
где En– произведение векторана нормаль
к данной площадке (рисунок 2.5).
Рисунок 2.5
Полное число силовых линий, проходящих
через поверхность S,
называется потоком вектора
напряженности ФЕ
через эту поверхность.
Элементарный поток вектора напряженности
через площадку dS(рис.
5) определится соотношением:
,
где
–
проекцияна направление нормали
.
В векторной форме можно записать
– скалярное произведение двух
векторов, где вектор.
Таким образом, поток вектора
есть скаляр, который в зависимости от
величины углаα может быть как
положительным, так и отрицательным.
Полный поток вектора напряженности
через любую площадку Sможно определить тогда,
а поток через замкнутую поверхность,
окружающую заряд или заряженное тело
равен.
Так как напряженность поля, созданного
в любой точке пространства зависит от
величины заряда, создающего это поле,
то поток вектора напряженности
электростатического поля через любую
площадку, находящуюся в этом поле также
зависит от величины заряда.
Рассмотрим примеры, изображенные на
рисунках 2.6 и 2.7.
Рисунок 2.6
Рисунок 2.7
Для рисунка 2.6 – поверхность А1
окружает положительный заряд и поток
здесь направлен наружу, т.е.ПоверхностьА2– окружает
отрицательный заряд, здесьи направлен внутрь. Общий поток через
поверхностьАравен нулю.
Для рисунка 2.7 – поток будет не равен
нулю, если суммарный заряд внутри
поверхности не равен нулю. Для этой
конфигурации поток через поверхность
Аотрицательный.
Таким образом, поток вектора напряженности
зависит от заряда.
2.3. Теорема Остроградского – Гаусса (теорема Гаусса)
К.Ф. Гаусс (1777–1855) выдающийся немецкий
математик, астроном и физик в 1839г.
предложил теорему, которая устанавливает
связь потока вектора напряженности
электрического поля череззамкнутую поверхность со значением
зарядаq, находящегося
внутри этой поверхности.Эта теорема
выведена математически для векторного
поля любой природы русским математиком
М.В. Остроградским (1801-1862), а затем
независимо от него применительно к
электростатическому полю – К.Гауссом.
Теорема Остроградского – Гаусса
(теорема Гаусса): поток вектора
напряженности электрического поля
через замкнутую поверхность в вакууме
равен алгебраической сумме заключенных
внутри этой поверхности зарядов, деленной
на
:
.
Докажем эту теорему. Пусть поле создается
точечным зарядом q.
Окружим заряд замкнутой поверхностьюSпроизвольной формы.
Разобьем замкнутую поверхность на
элементарные площадкиdS, к каждой из которых проведем вектор
нормали.
Э
поток вектора напряженности через
площадкуdS(рис. 2.8)
определится соотношением:
,
где
–проекция
на направление нормали
.
Тогда,
где— элементарный телесный угол, под которым
элементвиден из места положения заряда. Вычислим
поток вектора напряженности через
замкнутую поверхностьSот точечного зарядаq,
находящегося внутри этой поверхности.

так как
,
то
.
Как видно, поток вектора напряженности
выходящий из поверхности не зависит от
формы поверхности, охватывающей заряд
и пропорционален величине заряда.
Если заряд находится вне замкнутой
поверхности, то суммарный поток через
любые элементарные площадки dS1иdS2,
находящиеся внутри телесного углаdΩ(рис. 2.9) равен сумме потоков напряженности
выходящего из этой поверхности
(положительный поток) и входящего в нее
(отрицательный поток).
Тогда
,
следовательно, поток напряженности
электрического поля через любую
поверхностьS, не
охватывающую заряды равен нулю, т.е.ФЕ=0.
Пусть внутри замкнутой поверхности
имеется зарядов, тогда алгебраическим
суммированием (согласно принципу
суперпозиции) находим, что общий поток
вектора напряженности через замкнутую
поверхность равен
.
Теорема доказана.
Таким образом теорему Гаусса можно
сформулировать следующим образом: поток
вектора напряженности электрического
поля через замкнутую поверхность в
вакууме равен алгебраической сумме
заключенных внутри этой поверхности
зарядов, деленной на
:
(1),
Если заряд распределен внутри замкнутой
поверхности непрерывно с объемной
плотностью
,
то теорема Гаусса имеет вид:
(2)
где интеграл справа берется по объему
V, охватываемому поверхностьюS.
Необходимо обратить внимание на следующее
обстоятельство: в то время как само поле
зависит от конфигурации всех зарядов,
потоксквозь произвольную замкнутую поверхность
определяется только алгебраической
суммой зарядов внутри поверхностиS.
Это значит, чтоесли передвинуть заряды
внутри замкнутой поверхности, тоизменится всюду, и на поверхностиS, апоток вектора
через эту поверхность останется прежним.
Таким образом, чтобы рассчитать
поле, созданное какой-то конфигурацией
зарядов в данной точке, нужно через эту
точку провести замкнутую поверхность
произвольной формы и рассчитать поток
вектора напряженности через эту
поверхность. Так как по теореме
Гаусса поток вектора напряженности
электрического поля через замкнутую
поверхность в вакууме равен алгебраической
сумме заключенных внутри этой поверхности
зарядов, деленной на
,
то, зная величину заряда, находящегося
внутри замкнутой поверхности можно
найти напряженность поля в интересующей
нас точке пространства.
Рассмотрим примеры применения теоремы
Гаусса.
Соседние файлы в папке физ1
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Слайд 6Если оказывается удобным проектировать поверхность S на координатные плоскости yOz
или xOz, то для вычисления потока П пользуются соответственно формулами:
(4)
или
(5)
Формула
(4) применяется в случае, когда поверхность S проектируется взаимно однозначно в область Dyz плоскости yOz, а значит, ее можно задать уравнением x=φ(y,z); cosα находится как коэффициент при орте i в формуле

Слайд 14Задача 1.
Найти поток вектора а =i через площадку, перпендикулярную
оси Ох, имеющую форму прямоугольника со сторонами, равными 1 и
2 (см. рис.), в положительном направлении оси Ох.
Решение. Согласно определению потока вектора через поверхность S, будем иметь
В нашем случае а=i, п0 =i, так что
Замечание. Выбрав единичный вектор (орт) нормали к площадке S так, что n0= – i, получили бы П = –2.
Учитывая то, что площадь прямоугольника равна 2, получим

Слайд 15Задача 2.
Вычислить поток векторного поля а = r, где
r — радиус-вектор, через прямой круговой цилиндр с высотой h,
радиусом основания R и осью Оz.
Решение. Поверхность S состоит из боковой поверхности σ1, верхнего основания σ2 и нижнего основания σ3 цилиндра.
Искомый поток П в силу свойства аддитивности будет равен
где П1, П2, П3 — потоки данного поля через σ1, σ2, σ3 соответственно.
На боковой поверхности σ1 цилиндра внешняя нормаль n0 параллельна плоскости хОу, и поэтому

Слайд 16На верхнем основании σ2 нормаль n0 параллельна оси и поэтому
можно положить п0 = k. Тогда
На нижнем основании σ3 вектор
а =r перпендикулярен к нормали n0 = -k. Поэтому

Слайд 17Решение. Так как нормаль n к сфере коллинеарна радиусу-вектору r,
то можно взять
Но на сфере S имеем |r| = R,
значит

Слайд 18Искомый поток П будет равен
Так как площадь сферы

Слайд 19Решение. Уравнение плоскости, в которой лежит треугольник АВС, имеет вид
x+y+z=1, откуда z=1-x-y.
Треугольник АВС проектируется взаимно однозначно на плоскость xOy
в область Dxy, которой является треугольник ОАВ.
По условию нормаль n0 к плоскости, в которой лежит треугольник АВС, образует острый угол γ с осью Oz, поэтому

Слайд 20Найдем скалярное произведение
Вычислим искомый поток

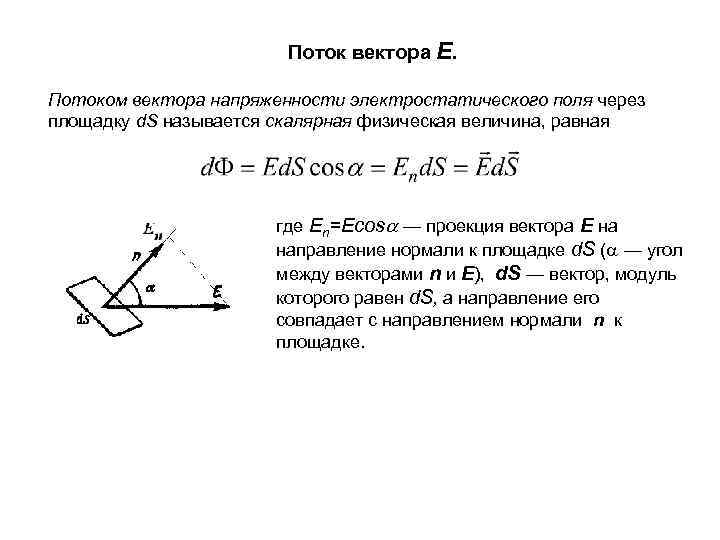
Поток вектора E. Потоком вектора напряженности электростатического поля через площадку d. S называется скалярная физическая величина, равная где En=Ecos — проекция вектора E на направление нормали к площадке d. S ( — угол между векторами n и E), d. S — вектор, модуль которого равен d. S, а направление его совпадает с направлением нормали n к площадке.
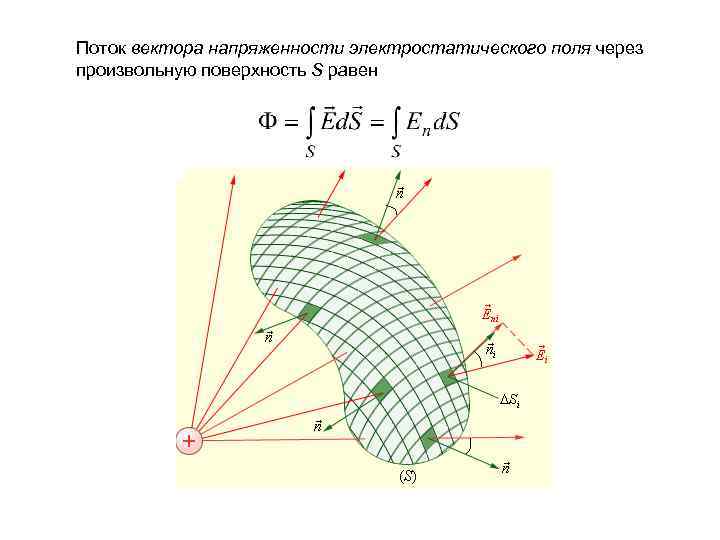
Поток вектора напряженности электростатического поля через произвольную поверхность S равен
Теорема Гаусса (в интегральной форме): поток вектора E сквозь замкнутую поверхность равен алгебраической сумме зарядов внутри этой поверхности, деленной на 0. Продемонстрируем это на примере точечного заряда. Окружим его замкнутой сферической поверхностью. Поток вектора напряженности сквозь сферическую поверхность радиуса r, охватывающую точечный заряд q, находящийся в ее центре, равен
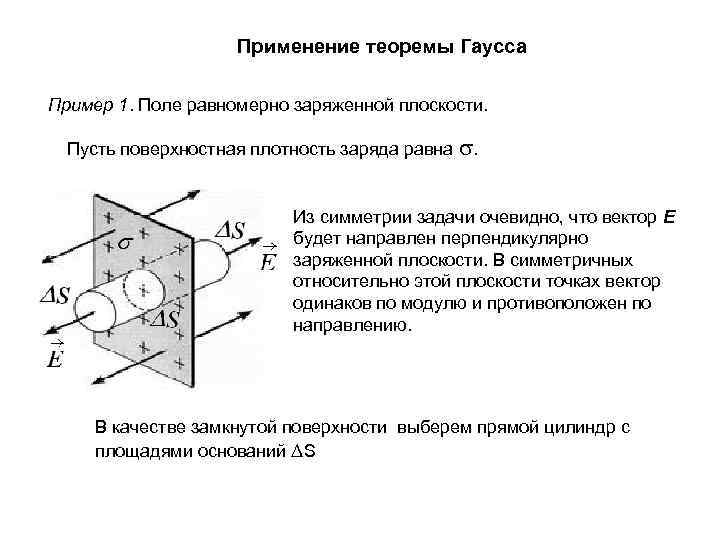
Применение теоремы Гаусса Пример 1. Поле равномерно заряженной плоскости. Пусть поверхностная плотность заряда равна . Из симметрии задачи очевидно, что вектор E будет направлен перпендикулярно заряженной плоскости. В симметричных относительно этой плоскости точках вектор одинаков по модулю и противоположен по направлению. В качестве замкнутой поверхности выберем прямой цилиндр с площадями оснований S
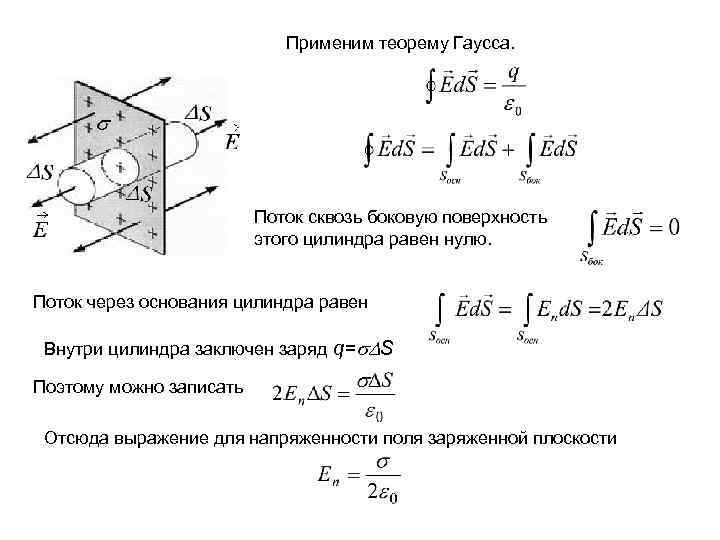
Применим теорему Гаусса. Поток сквозь боковую поверхность этого цилиндра равен нулю. Поток через основания цилиндра равен Внутри цилиндра заключен заряд q= S Поэтому можно записать Отсюда выражение для напряженности поля заряженной плоскости
В полученной формуле нет зависимости от расстояния до плоскости, следовательно такое поле является однородным. Полученный результат справедлив только для бесконечной плоской поверхности.
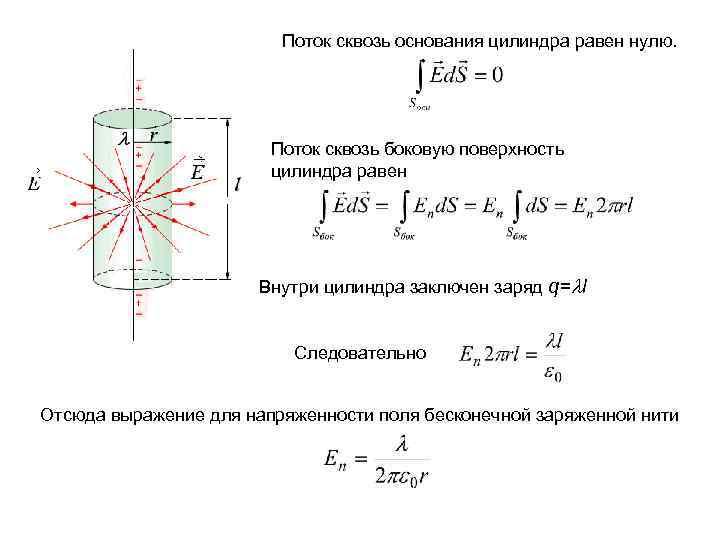
Пример 2. Поле бесконечной заряженной нити. Пусть линейная плотность заряда нити равна . Из соображений симметрии следует, что поле имеет радиальный характер: вектор E в каждой точке перпендикулярен нити, а модуль вектора E зависит только от расстояния r до нити. Выберем замкнутую поверхность в форме прямого цилиндра. Применим теорему Гаусса.
Поток сквозь основания цилиндра равен нулю. Поток сквозь боковую поверхность цилиндра равен Внутри цилиндра заключен заряд q= l Следовательно Отсюда выражение для напряженности поля бесконечной заряженной нити
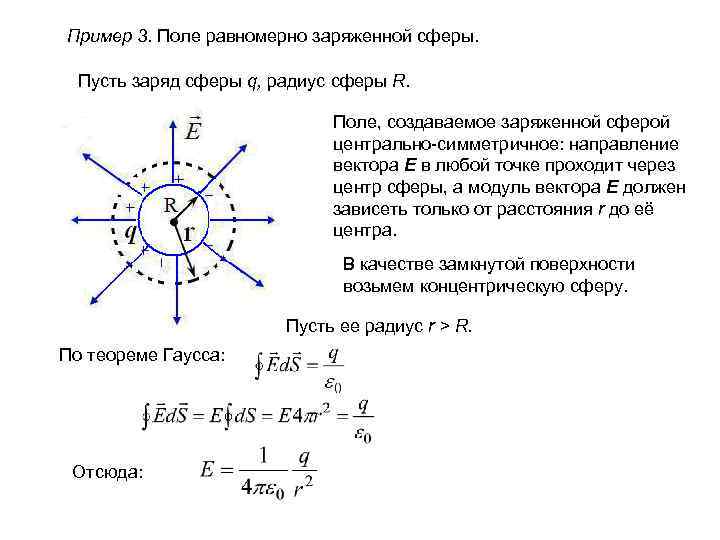
Пример 3. Поле равномерно заряженной сферы. Пусть заряд сферы q, радиус сферы R. Поле, создаваемое заряженной сферой центрально-симметричное: направление вектора E в любой точке проходит через центр сферы, а модуль вектора E должен зависеть только от расстояния r до eё центра. В качестве замкнутой поверхности возьмем концентрическую сферу. Пусть ее радиус r > R. По теореме Гаусса: Отсюда:
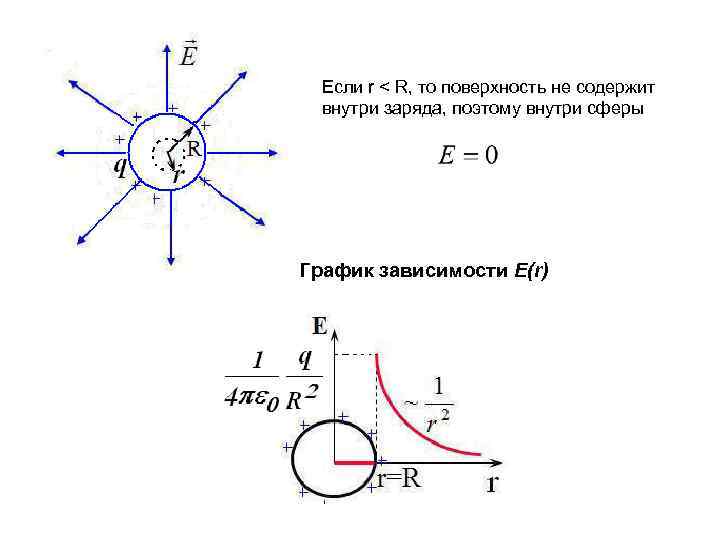
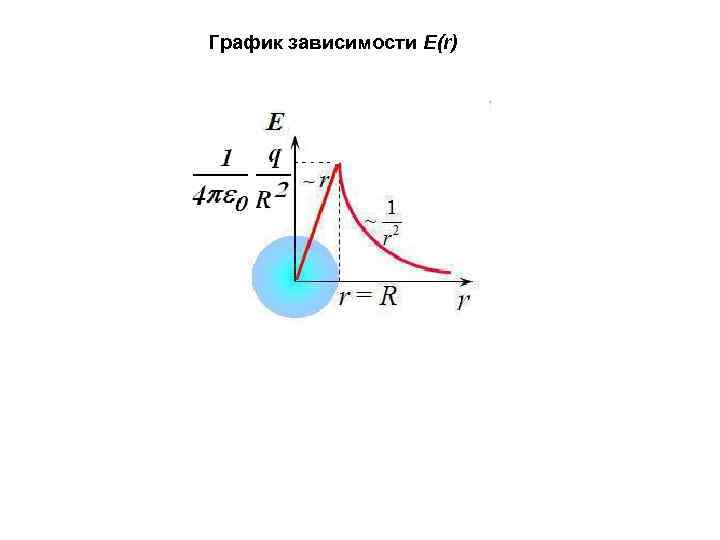
Если r < R, то поверхность не содержит внутри заряда, поэтому внутри сферы График зависимости E(r)
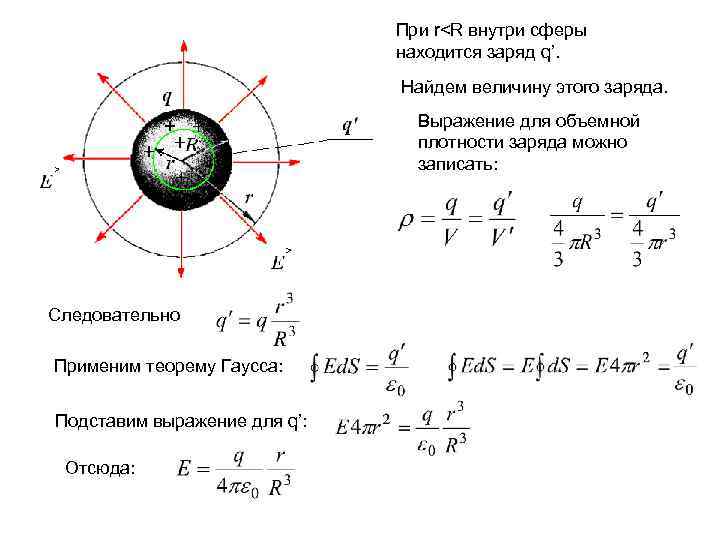
Пример 4. Поле равномерно заряженного шара. Пусть заряд q равномерно распределен по шару радиусом R. В качестве замкнутой поверхности снова возьмем концентрическую сферу. Пусть ее радиус r > R. По теореме Гаусса: Отсюда:
При r
График зависимости E(r)
Общие выводы. Полученные в этих примерах результаты можно было бы найти с использованием принципа суперпозиции, но использование теоремы Гаусса позволяет решать эти задачи более простым путем. Применение теоремы Гаусса для расчета полей эффективно лишь в тех случаях, где поле обладает специальной симметрией (плоской, цилиндрической или сферической).
Дифференциальная форма теоремы Гаусса. Пусть поверхность S охватывает заряженную область объемом V, с объемной плотностью заряда (x, y, z). Суммарный заряд области можно представить как — среднее значение объемной плотности заряда. Запишем теорему Гаусса Устремим объем области к нулю V 0, тогда (x, y, z). Обозначим предел левой части выражения, как div. E –называется дивергенцией вектора E
С учетом этого, получим Эта формула выражает теорему Гаусса в дифференциальной форме.
Дивергенция вектора. Дивергенция представляет собой скалярную функцию координат. Если компоненты вектора E заданы как Ex(x, y, z), Eу(x, y, z), Ez(x, y, z), то дивергенцию можно найти по формуле: Определим векторный дифференциальный оператор набла . В декартовых координатах Тогда