Статья содержит базовое определение потока напряженности, теорему Остроградского — Гаусса вместе с доказательством. Как всегда, теория закрепляется на практике с помощью задач.
Поток вектора напряжённости электрического поля. Теорема Остроградского — Гаусса.
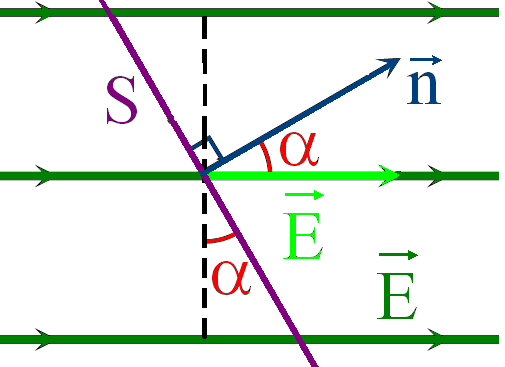
Определение. Потоком вектора напряженности Ф электрического поля через площадку S называется скалярная физическая величина, равная произведению площади S на нормальную составляющую напряжённости электрического поля E⏊.

, где n — вектор нормали к поверхности S, α — угол между нормалью n и вектором напряжённости E.

Теорема (Остроградского — Гаусса). Поток вектора напряжённости электрического поля в вакууме сквозь произвольную замкнутую поверхность, проведённую в поле, пропорционален алгебраической сумме электрических зарядов, заключённых внутри этой поверхности:
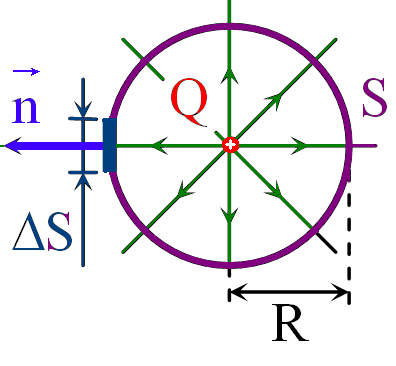
Доказательство. Рассмотрим поток вектора напряжённости через площадку ΔS (рис. 3.1).

С учетом напряжённости поля точечного заряда:


Как известно, телесный угол Ω по определению равен:
, где S — площадь, на которую опирается телесный угол, а r — расстояние до центра.

Применив это к нашему случаю, можно записать


Полный поток через сферу найдём, просуммировав все телесные углы. Так как полный телесный угол Ω = 4π, то получим
Так как поток ΔФ не зависит от положения заряда q, то получаем выражение, которое называется теоремой Остроградского — Гаусса.

С помощью теоремы Остроградского — Гаусса можно вычислять поля для некоторых симметричных случаев, в которых напряжённость поля одинакова во всех частях фигуры.
Пример 1 (Поле равномерно заряженной сферы). Окружим сферу радиуса R замкнутой поверхностью радиуса r > R (рис. 3.2).

Воспользовавшись теоремой Остроградского — Гаусса и определением потока, получим:

Поле сферы совпадает с полем точечного заряда за пределами сферы и равно нулю внутри сферы (так как все заряды находятся на поверхности).

Пример 2 (Поле бесконечной равномерно заряженной плоскости с поверхностным зарядом σ). Так как плоскость бесконечная, то во всех точках вектор E одинаков и направлен перпендикулярно поверхности. Густота линий (следовательно, и E тоже) не зависит от расстояния до плоскости — поле однородно.
Для нахождения E рассмотрим сферу радиуса R. Вне сферы поле равно 0, а внутри

Рассмотрим поле на расстояние r = R + x, x << R. Это поле равно E = σ / ε₀ и создается близлежащим к сфере малым участком (поле Eпл) и полем E₁, создаваемым остальными участками сферы. Участок должен быть настолько малым, чтобы его можно было считать плоским. С другой стороны, характерные размеры этого участка должны быть много больше расстояния x (чтобы этот малый плоский участок можно было считать бесконечной плоскостью). Другими словами, должно выполняться следующее соотношение:

где S — площадь малого участка сферы.
По разные стороны от поверхности поле E₁ одно и тоже, а поле Eпл меняет знак (рис. 3.3).

Следовательно, можно составить систему уравнений:

, из которой находим

Пример 3 (Поле бесконечного равномерно заряженного цилиндра радиуса R).
Окружим цилиндр замкнутой поверхностью в виде такого же цилиндра радиуса r > R (рис. 3.4).

Для удобства выберем некоторый участок длины L и заряда q и найдём для него поток двумя способами:

, где τ —линейная плотность заряженного цилиндра. Внутри цилиндра поля нет!
Замечание.Внутри всех проводящих замкнутых фигур поля нет! Это следует из того, что все заряды проводящих фигур сосредоточены на поверхности. Если представить, что внутри проводящего тела появятся поля, то должен потечь и ток, но этого не наблюдается в статически заряженных проводящих телах.
Пример 4 (Поле однородно заряженного диэлектрического шара радиуса R с зарядом q). Если выбрать контур радиуса r ≥ R, то решение дословно повторяет пример 1.

При r < R

, где q₁ — заряд, ограниченный замкнутым шаром радиуса r. Для нахождения q₁ найдём сначала объёмную плотность заряда ρ:

А затем найдём заряд q₁:

Подставив соответствующие выражение в (3.1), получим

В итоге получим:

Замечание. Простой проверкой убеждаемся, что при r = R оба выражения приводят к одному и тому же результату, что показывает, что функция E(r) в данном случае непрерывна.
Примеры решения задач
Задача 3.1. Воздух при напряженности более чем E₀ = 3 · 10⁶ В/м перестает быть хорошим диэлектриком и может проводить электрический ток. Найти, какой максимальный заряд можно поместить на металлический шар радиуса R = 1 м.
Решение. Максимальная напряжённость будет достигаться на поверхности шара, поэтому она не должна превышать заданного значения E₀.

Как видно из задачи, заряд 1 Кл — это очень большой заряд, и так сильно зарядить тела привычных размеров невозможно!
Задача 3.2. Найти распределение напряжённости в заряженной пластине толщиной h с объёмной плотностью заряда ρ. Какое максимальное значение напряжённости поля будет достигнуто, если соединить две пластины вместе (рис. 3.5)?

Решение. Сначала разберёмся, как в каждой толстой пластине зависит напряжённость электрического поля от x, где x — расстояние от середины пластины.
Для этого окружим часть пластины замкнутым контуром толщиной 2x, проходящим через центр пластины.
При x < h/2:

Тогда при x > h/2

Тогда, если соединить две пластины вместе, получим:

Задачи для самостоятельного решения
Задача 1. Напряжённость поля до бесконечно проводящей заряженной плоскости равна E₁, а после пластины — E₂. Найти поверхностную плотность заряда на пластине. Считать, что поле в обоих случаях направлено перпендикулярно заряженной пластине.
Задача 2. Две пересекающиеся под углом α и заряженные поверхностной плотностью заряда σ бесконечные пластины делят пространство на четыре области. Найти напряжённость в каждой из областей.
Список литературы
- Белолипецкий С. Н., Еркович О. С., Казаковцева В. А., Цвецинская Т. С. Задачник по физике. М., 2005.
- Задачи по физике / Под ред. Савченко О. Я. Новосибирск, 1999.
- Козел С. М., Слободянин В. П. Всероссийские олимпиады по физике. 1992–2001. М., 2002.
- Савченко Н. Е. Решение задач по физике. М., 2011.
- Черноуцан А. Учебно-справочное пособие для старшеклассников и абитуриентов. М., 2000.
Поток вектора напряжённости электрического поля
Поток
вектора напряжённости электрического
поля
(N)
—
это
скалярная физическая величина,
характеризующая распределение
электрического поля по поверхности
некоторой площади, равная произведению
модуля вектора напряженности (
)
на площадь поверхности (S)
и на косинус угла (
)
между вектором напряженности (
)
и нормали (перпендикуляра) (
)
|
|
однородное |
Поток может быть
положительным и отрицательным, в
зависимости от величины угла ,
определяемой направлением нормали к
поверхности.
Геометрический
смысл потока
вектора
напряжённости
Так как модуль
напряжённости определяется числом
линий напряжённости, пронизывающих
единицу площади поверхности перпендикулярной
линиям напряжённости, то поток
вектора напряжённости через поверхность
площадью S
пропорционален числу линий напряжённости,
проходящих через данную поверхность.
Поток вектора
напряжённости
через неплоскую
поверхность
|
|
Вся поверхность |
,
где Ni
– поток вектора напряжённости через
один из элементов площади;
k
– количество таких элементов.
Поток вектора напряжённости через замкнутую поверхность
При определении
потока вектора напряжённости через
замкнутую поверхность за положительное
направление нормали применяется внешняя
нормаль (нормаль, направленная наружу
области, охватываемой поверхностью).
Если замкнутая
поверхность не охватывает заряда, то
поток сквозь неё равен нулю, так как
число линий напряженности, входящих в
поверхность, равно числу линий, выходящих
из неё.
Теорема Остроградского ─ Гаусса
Для вычисления
модуля напряжённости электростатических
полей, источником которых являются
заряженные тела различной формы, широко
используется теорема Остроградского
─ Гаусса.
|
Поток вектора |
|
Доказательство
Воспользуемся
полем положительного точечного заряда
Q. Окружим этот заряд
сферой площадью S и радиусом
R, центр которой совпадает
с точкой нахождения заряда Q.
|
|
В каждой точке,
|
Найдём поток
напряжённости через поверхность, данной
сферы, для этого разобьём её на малые
элементы, найдя потоки вектора
напряжённости через каждый элемент.
Затем просуммируем алгебраически (с
учетом знака) эти потоки.
;
,
так как
,
то
,
;
следовательно,
.
Так как
,
,
;
то
.
|
Если заряд |
Теорема доказана.
Полученный результат
будет справедлив для замкнутой поверхности
любой формы при любом расположении
любого числа зарядов внутри этой
поверхности (в этом случае Q
– алгебраическая сумма зарядов,
находящихся внутри замкнутой поверхности).
Применим теорему
Остроградского ─ Гаусса для нахождения
модуля вектора напряжённости
электростатических полей некоторых
заряженных тел.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
21.04.2015625.62 Кб361.docx
- #
- #
- #
- #
- #
- #
- #
- #
Содержание книги
Предыдующая страница
§9. Электрическое поле и его свойства
9.5. Поток вектора напряженности электрического поля. Теорема Гаусса
Как и для любого векторного поля важно рассмотреть свойства потока электрического поля. Поток электрического поля определяется традиционно.
Выделим малую площадку площадью ΔS, ориентация которой задается единичным вектором нормали (~vec n) (рис. 157).
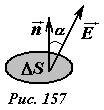
В пределах малой площадки электрическое поле можно считать однородным [1], тогда поток вектора напряженности ΔФE определяется как произведение площади площадки на нормальную составляющую вектора напряженности
(~Delta Phi_E = E cos alpha Delta S = (vec E cdot vec n) Delta S = E_n Delta S) . (1)
где (~(vec E cdot vec n) = E cos alpha) — скалярное произведение векторов (~vec E) и (~vec n); En — нормальная к площадке компонента вектора напряженности.
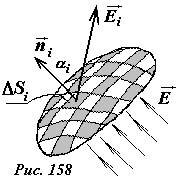
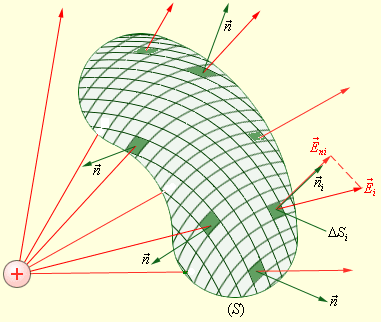
В произвольном электростатическом поле поток вектора напряженности через произвольную поверхность, определяется следующим образом (рис. 158):
- — поверхность разбивается на малые площадки ΔS (которые можно считать плоскими);
- — определяется вектор напряженности (~vec E) на этой площадке (который в пределах площадки можно считать постоянным);
- — вычисляется сумма потоков через все площадки, на которые разбита поверхность
-
(~Phi = Delta Phi_1 + Delta Phi_2 + Delta Phi_3 + ldots = sum_{i} {Delta Phi_i} = sum_{i} {E_i cos alpha_i Delta S_i}) .
Эта сумма называется потоком вектора напряженности электриче-ского поля через заданную поверхность. Трудно найти явный физический смысл этой величины, но как мы указывали, поток векторного поля является полезной вспомогательной математической величиной.
Рассмотрим электрическое поле точечного заряда Q (рис. 159). Это поле обладает сферической симметрией — модуль вектора напряженности зависит только от расстояния для заряда, в любой точке вектор напряженности направлен радиально, вдоль прямой, соединяющей заряд с точкой наблюдения.
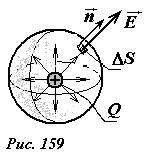
Окружим заряд сферой, произвольного радиуса R, центр которой совпадает с точечным зарядом. Во всех точках поверхности сферы вектор напряженности электрического поля направлен вдоль нормали к поверхности сферы (поэтому угол между ними равен нулю), его модуль постоянен и по закону Ш. Кулона равен
(~E = frac{Q}{4 pi varepsilon_0 R^2}) .
Выделим на поверхности сферы малую площадку площадью ΔSi, поток вектора напряженности через эту площадку равен
(~Delta Phi_i = frac{Q}{4 pi varepsilon_0 R^2} Delta S_i) .
Так как модуль вектора напряженности во всех точках сферы одинаков, суммирование потоков через поверхность сферы, сводится к суммированию площадей участков, на которые разбивается сфера. Вычислим поток вектора напряженности
(~Phi_E = sum_{i} {frac{Q}{4 pi varepsilon_0 R^2} Delta S_i} = frac{Q}{4 pi varepsilon_0 R^2} sum_{i} {Delta S_i} = frac{Q}{4 pi varepsilon_0 R^2} cdot 4 pi R^2 = frac{Q}{varepsilon_0}) , (2)
здесь (~sum_{i} {Delta S_i} = 4 pi R^2) — площадь поверхности сферы. Обратите внимание, что этот поток не зависит от радиуса сферы. Итак, поток вектора напряженности электрического поля точечного заряда через поверхность сферы равен отношению заряда к электрической постоянной.
Для обобщения полученного результата, вспомним теоремы о потоке несжимаемой жидкости. Самое важное — распределение скоростей от то-чечного источника, описывается такой же зависимостью, как и напряжен-ность электрического поля, созданного точечным источником. Следовательно, и потоки этих векторных полей подчиняются одинаковым законам. Поэтому, мы не будем подробно доказывать каждое утверждение, только приведем его основные этапы.
- Выражение для суммарного потока (3) вывод можно обобщить для любой замкнутой поверхности, окружающей точечный заряд.
- Поток вектора напряженности электрического поля точечного заряда через любую замкнутую поверхность, окружающую заряд, равен величине заряда, деленного на электрическую постоянную[~Phi_E = frac{Q}{varepsilon_0}] (рис. 160)
-
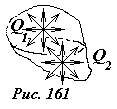
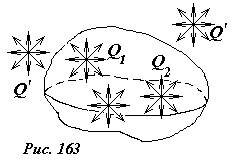
- Пусть внутри поверхности находится несколько зарядов (рис. 161). Так как для вектора напряженности электрического поля электрического поля справедлив принцип суперпозиции, то такой же принцип будет справедлив и для потока вектора напряженности. Следовательно, поток вектора напряженности электрического поля, созданного системой зарядов Q1, Q2, …, через любую замкнутую поверхность, окружающую заряды, равен сумме зарядов, деленную на электрическую постоянную ε0[~Phi_E = frac{Q_1}{varepsilon_0} + frac{Q_2}{varepsilon_0} + ldots]
-
- Если заряд Q´ находится вне замкнутой поверхности (рис. 162), то поток вектора напряженности поля, созданного этим зарядом через эту поверхность равен нулю: ФE = 0.
-
Наконец, можно объединить эти положения и сформулировать теорему о потоке вектора напряженности электрического поля (рис. 163): поток вектора напряженности электрического поля через любую замкнутую поверхность равен сумме зарядов, находящихся внутри этой поверхности, деленную на электрическую постоянную ε0:
(~Phi_E = frac{Q_1 + Q_2 + ldots}{varepsilon_0})
Эта важнейшая теорема впервые сформулирована немецким математиком К. Гауссом и носит его имя (теорема Гаусса).
В отличие от напряженности поля, которая является точечной характеристикой поля (определена в каждой точке поля), поток этого вектора есть характеристика некоторого объема (усредненной, интегральной) характеристикой. Если в некоторой части пространства электрическое поле отсутствует (напряженность равна нулю), то и поток вектора напряженности через любую поверхность, находящуюся в этой части также равен нулю. Обратное утверждение не верно — если поток вектора напряженности равен нулю, то из этого не следует, что поле отсутствует. Единственный вывод, который можно сделать из равенства потока нулю — внутри рассматриваемой поверхности суммарный заряд равен нулю.
Заряды, находящиеся вне рассматриваемой замкнутой поверхности, создают электрическое поле, в том числе и внутри объема, ограниченного рассматриваемой поверхностью. Только суммарный поток поля созданного этими зарядами равен нулю («сколько втекает — столько вытекает»). Можно сказать, что заряды вне поверхности, перераспределяют поток поля, создаваемый зарядами внутри поверхности (рис. 164).
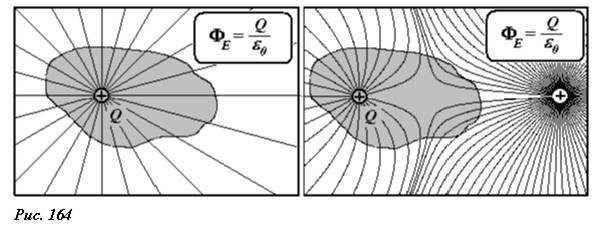
Теорема Гаусса строго доказывается на основании закона Ш. Кулона, поэтому она не несет нового физического содержания. Из теоремы Гаусса, легко выводится формула закона Ш. Кулона. Поэтому с точки зрения физики, теорема Гаусса и закон Кулона эквиваленты, это один и тот же физический закон, облаченный в разные математические оболочки.
Примечания
- ↑ Электрическое поле называется однородным, если во всех точках вектор напряженности постоянен, как по величине, так и по направлению — обычное определение однородности, как для любого поля.
Следующая страница
Поток вектора напряженности электрического поля
Андрей Геннадьевич Блохин
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Определение
Потоком вектора $overrightarrow{a} $через поверхность $S$ называют алгебраическую величину${ Ф}_a$, которая определяется следующим образом:
[Ф_a=intlimits_S{overrightarrow{a}doverrightarrow{S}} left(1right).]
При этом знак потока зависит от выбора направления нормали к элементарной площадке $dS$.
Элементарный поток вектора напряженности
Обратимся к электрическому полю. Модуль напряженности равен количеству силовых линий, которые пересекают поверхность площадь, которой равна единице, причем поверхность должна быть перпендикулярна линиям поля в данном месте. Количество линий поля, которые пересекают вышеназванную поверхность, называются потоком вектора напряженности. Если выделить элементарную площадку поверхности (dS), построить нормаль к этой площадке $overrightarrow{n}$, при этом угол между направлением вектора нормали и направлением вектора напряженности составит $alpha $, то элементарный поток вектора напряженности ($dФ_E$) можно записать как:
[dФ_E=EdScosalpha =overrightarrow{E}cdot doverrightarrow{S} left(2right),]
где
[doverrightarrow{S}=overrightarrow{n}dS left(3right).]
В уравнении (3) $overrightarrow{n}$ единичная нормаль к площадке $dS$.
Если рассматривать какую — либо произвольную поверхность $S$, то в соответствии с определением потока вектора (1) можно записать, что поток вектора напряженности ($Ф_E$):
[Ф_E=intlimits_S{overrightarrow{E}cdot doverrightarrow{S}} left(4right).]
Направление нормали
Как и в общем случае, поток вектора напряженности алгебраическая величина. Знак потока зависит от конфигурации поля и направления вектора — нормали $overrightarrow{n}$. Направление нормали условно. Можно сказать, что интеграл в уравнении (4) характеризует суммарную мощность источников вектора $overrightarrow{E}$, коими являются заряды, внутри объема, который ограничивает поверхность $S$.
Принято считать, что если имеют дело с замкнутой поверхностью, то нормаль имеет положительное направление наружу. Поток вектора напряженности в случае замкнутой поверхности записывают через криволинейный интеграл по замкнутой поверхности:
[Ф_E=ointlimits_S{overrightarrow{E}cdot doverrightarrow{S}} left(5right).]
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Пример 1
Задание: Напряженность электростатического поля задана формулой в декартовых координатах:
[overrightarrow{E}=frac{xoverrightarrow{i}+yoverrightarrow{j}}{x^2+y^2},]
где $overrightarrow{i}, overrightarrow{j}$ — единичные орты осей OX и OY. Найдите поток вектора $overrightarrow{E}$ через сферическую поверхность, если ее радиус равен $R$, а ее центр находится в начале координат.
Решение:
В качестве основы для решения используем определение потока вектора напряженности, а именно:
[Ф_E=intlimits_S{overrightarrow{E}cdot doverrightarrow{S}} left(1.1right), ]
где $doverrightarrow{S}=overrightarrow{n}dS$, $dS-$ элементарный участок поверхности сферы, $overrightarrow{n}$ — нормаль к этому участку.
Запишем выражение для нормали к поверхности сферы, в виде:
[overrightarrow{n}=frac{xoverrightarrow{i}+yoverrightarrow{j}+zoverrightarrow{k}}{sqrt{x^2+y^2+z^2}} left(1.2right).]
Подставим уравнение (1.2) в (1.1), используем выражение для напряжённости поля из условий задачи, найдем интеграл, при этом при нахождении произведения в подынтегральном выражении, учитываем, что $overrightarrow{i},overrightarrow{j},overrightarrow{k}$- ортогональные единичные векторы.
[Ф_E=intlimits_S{overrightarrow{E}cdot overrightarrow{n}dS}=intlimits_S{frac{xoverrightarrow{i}+yoverrightarrow{j}}{x^2+y^2}cdot frac{xoverrightarrow{i}+yoverrightarrow{j}+zoverrightarrow{k}}{sqrt{x^2+y^2+z^2}}dS}=intlimits_S{frac{x^2+y^2}{x^2+y^2sqrt{x^2+y^2+z^2}}} dS=intlimits_S{frac{dS}{sqrt{R^2}}}=frac{1}{R} intlimits_S{dS=frac{4pi R^2}{R}}=4pi R.]
Ответ: $Ф_E=4pi R.$
«Поток вектора напряженности электрического поля» 👇
Пример 2
Задание: Определите поток вектора напряженности через поверхность сферы, если внутри нее находится два точечных заряда $+q_1$ и ${-q}_2$.
Решение:
В качестве основы для решения можно взять формулу для потока вектора напряженности в виде:
[Ф_E=overrightarrow{E}cdot Soverrightarrow{n}=EScosalpha left(2.1right),]
где $alpha $ — угол между нормалью к поверхности, через который ищем поток и вектором напряженности. Поле точечного заряда имеет сферическую симметрию (рис.1). Следовательно, вектор напряженности поля и вектор — нормаль будут сонаправлены ($cosalpha ={cos 0 }=1$). На рис. 1 изображено поле положительного заряда.
Рис. 1
Результирующая напряженность поля может быть найдена в соответствии с принципом суперпозиции полей двух зарядов, с учетом знаков.
Запишем выражение для модуля напряженности поля, которое создает первый заряд:
[E_1=kfrac{q_1}{r^2}left(2.2right).]
Для второго заряда:
[E_2=kfrac{q_2}{r^2}left(2.3right).]
Найдем модуль результирующей напряженности, учитывая, что положительный заряд — исток поля, а отрицательный — сток поля, то есть направления полей противоположны:
[E=E_1-E_2=kfrac{q_1}{r^2}-kfrac{q_2}{r^2} left(2.4right).]
Если мы ищем поток через сферу, которая имеет радиус R, то выражение (2.4) примет вид:
[E=kfrac{q_1-q_2}{R^2} left(2.5right).]
Площадь поверхности сферы (S) заданного радиуса равна:
[S=4pi R^2left(2.6right).]
В таком случае, подставим выражения (2.6) и (2.5) в (2.1), учтем, что $cosalpha ={cos 0 }=1$, получим:
[Ф_E=kfrac{q_1-q_2}{R^2} 4 pi R^2=frac{q_1-q_2}{4pi {varepsilon }_0R^2}4 pi R^2=frac{q_1-q_2}{varepsilon_0}.]
Ответ: $Ф_E=frac{q_1-q_2}{{varepsilon }_0}.$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 03.12.2022