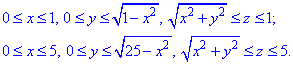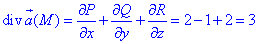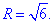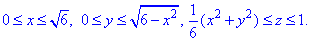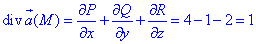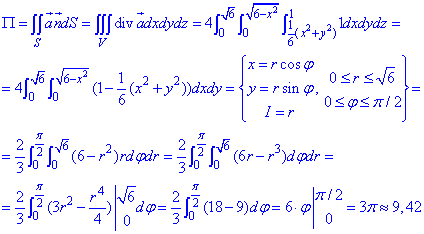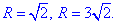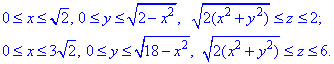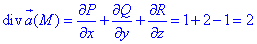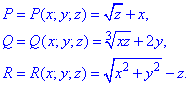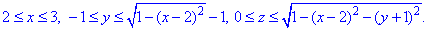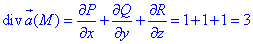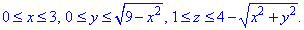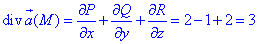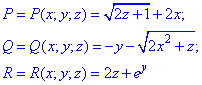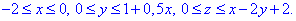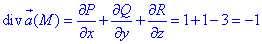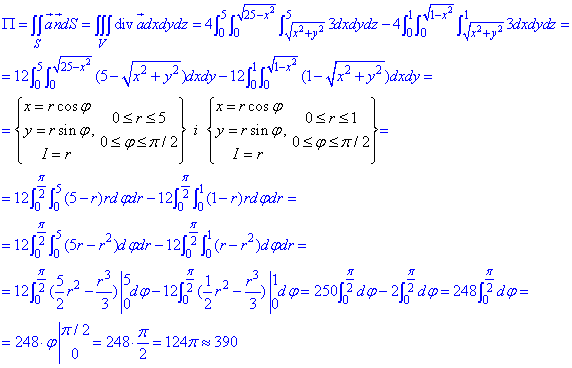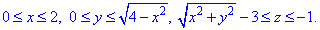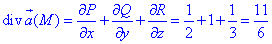На предыдущем уроке проанализированы более простые примеры на вычисления потока векторного поля. Здесь задания усложняются поверхностью интегрирования, которая ограничена как одним, так и двумя сечениями.
Как следствие, больше расчетов пределов интегрирования, более сложные двойные интегралы и сами вычисления.
Все важные переходы и приемы хорошо расписаны, а примеры отвечают учебным программам большинства ВУЗов Украины.
ЗАДАНИЕ 8.2 Найти поток векторного поля 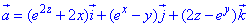
Решение: Поверхность x2+y2=z2 — описывает часть конуса с вершиной в начале координат, которое вытянуто вдоль оси Oz и ограничена плоскостями z=1, z=5.
В этом и следующих примерах для представления приведенны рисунки поверхности интегрирования и их проекции в декартовую плоскость
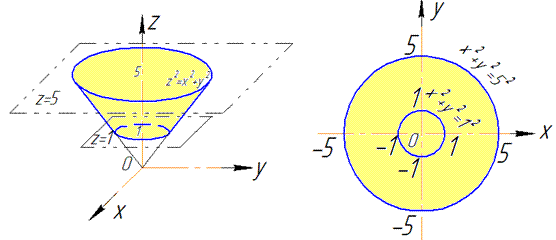
В силу симметрии нет необходимости интегрировать по кругу, достаточно найти пределы четверти круга :
Напоследок результирующий интеграл множим на четверку.
В примерах на интегрирование по поверхностям нужно быстро выполнять построение классических тел вращения.
Также необходимо правильно находить пересечения плоскостями, иначе правильного ответа не получите.
Вы должны уметь удачно учитывать симметричность функций, их четность или нечетность.
Вычислим дивергенцию векторного поля 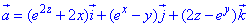
где функции являются соответствующими множителями при орте векторного поля
P=P(x;y;z)=e2z+2x, Q=Q(x;y;z)=ex-y, R=R(x;y;z)=2z-e2y.
За формулой Остроградського-Гаусса находим поток векторного поля 
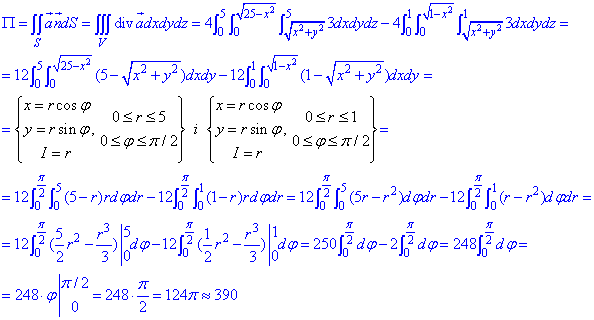
Без этого Вы остановитесь на середине интеграла и не будете знать, как возвести интеграл к конечному ответу.
ЗАДАНИЕ 8.4 Вычислить поток векторного поля 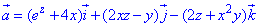
Решение: Поверхность x2+y2=6z — коловий параболоид с вершиной в начале координат, который вытянут вдоль оси Oz и ограничен плоскостью z=1.
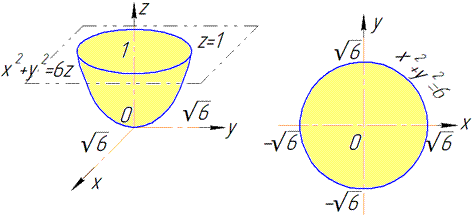
Как знать, что получим в перерезе плоскостью?
Кто хорошо читал теорию, тот делает это автоматически, а в целом в уравнение поверхности x2+y2=6z подставляем плоскость z=1.
В результате получим уравнение круга x2+y2=6.
Справа имеем квадрат радиуса, вот и весь анализ.
И такая схема справедлива для целого класса рассмотренных задач.
Как видим из рисунку четверть области V ограничена пределами:
Как и в предыдущем задании, здесь учитываем четность всех функций.
Это позволяет упростить само интегрирование и не разбивать доминирующий интеграл на несколько с одинаковым конечным значением.
Учитывая это, результат умножим на 4.
Но к нему еще следует дойти, потому сначала вычисляем дивергенцию векторного поля 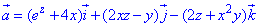
где функции P, Q, R принимают значение
P=P(x;y;z)=ez+4x, Q=Q(x;y;z)=2xz-y, R=R(x;y;z)=-2z-x2y.
Вычисляем поток векторного поля 
Для большинства приведенных примеров переход к полярной системе координат под интегралом позволяет упростить дальнейшее их нахождение. Детально останавливаться на этом не будем, в формуле выписаны все этапы интегрирования и замены, поэтому анализируйте самостоятельно.
ЗАДАНИЕ 8.7 Найти поток векторного поля 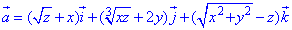
2(x2+y2)=z2, z=2, z=6 (нормаль внешна).
Решение: Уравнение 2(x2+y2) =z2 описывает конус с вершиной в начале координат (0;0;0) что вытянут вдоль оси Oz и ограничен плоскостями z=2, z=6 по условию.
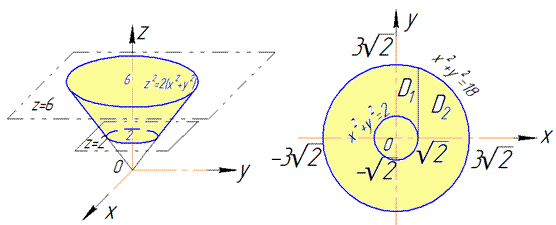
В силу симметрии рассматриваем четверть области V, которая ограничена поверхностями:
Результат интегрирования умножим на 4.
Определяем дивергенцию векторного поля 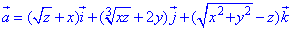
где функции задаются зависимостями
За формулой Остроградського-Гаусса находим поток поля 
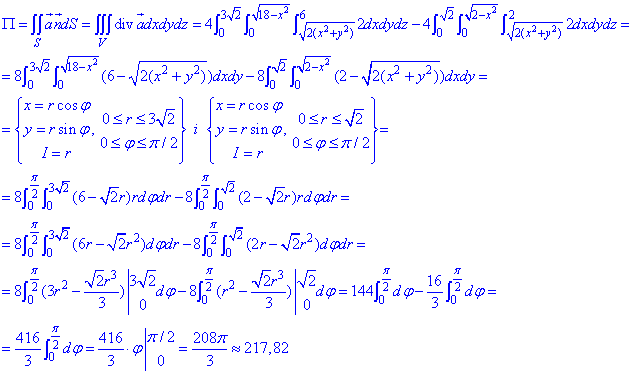
Применение перехода к полярной СК позволяет свести корневые функции к показательным.
ЗАДАНИЕ 8.8 Вычислить поток векторного поля 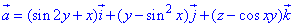
Решение: Сведем поверхность x2+y2+z2=4x-2y-4 к каноническому виду
x2-4x+4+y2+2y+1+z2=4+1-4, (x-2)2+(y+1)2+z2=1 — сфера с центром (2;-1;0) и радиусом R=1.
Ее график и проекция на плоскость Oxy приведены ниже
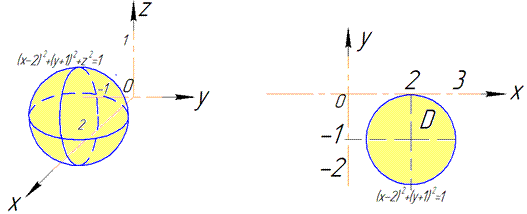
Здесь учли четность функций, поэтому интеграл будем множить на 8 (верхняя и нижняя полусферы).
Дивергенцию векторного поля 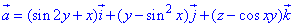
где P=P(x;y;z)=sin(2y)+x, Q=Q(x;y;z)=y-sin2(x), R=R(x;y;z)=z-cos(x*y).
Дальше интегрированием вычисляем поток векторного поля: 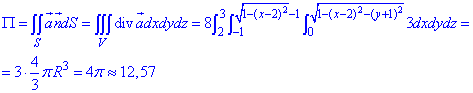
Так как здесь подинтегральная функция равна постоянной, то тройной интеграл не что иначе, как объем сферы с радиусом 1, разделенный на 8 (согласно упрощений).
На основе выше рассмотренных задач, попробуйте самостоятельно найти тройной интеграл и убедиться в правильности рассуждений.
ЗАДАНИЕ 8.14 Найти поток векторного поля 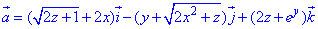
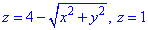
Решение: Поверхность 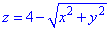
Графически поверхность интегрирования можно представить из следующих рисунков
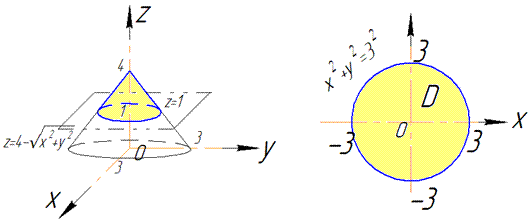
В силу симметрии четверть области V задается следующими пределами:
Не забываем, что при этом нужно интеграл кмножить на 4.
Находим дивергенцию поля 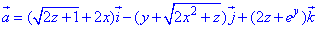
функции P, Q, R
Поток векторного поля 
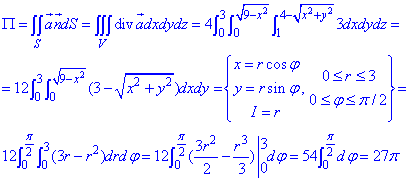
Потек равен П=27pi.
ЗАДАНИЕ 8.15 Вычислить поток векторного поля 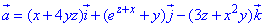
Решение: Уравнение 2y-x+z=2, -x/2+y/1+z/2=1— описывает плоскость, которая является одной из граней треугольной пирамиды.
Чтобы лучше это представить рассмотрите следующие рисунки к задаче.
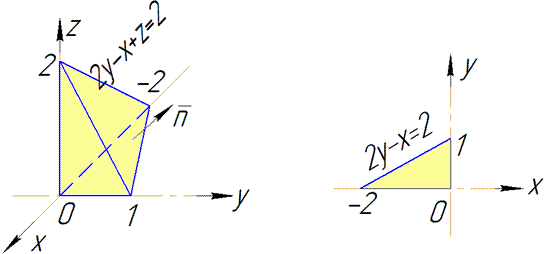
Такой анализ позволяет коректно расставить пределы интегрирования в тройном интеграле.
Вычисляем дивергенцию векторного поля 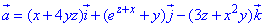
где P=P(x;y;z)=x+4yz, Q=Q(x;y;z)=ez+x+y, R=R(x;y;z)=-3z-x2y.
Вычисляем поток векторного поля 
Интеграл не из легких, поэтому внимательно разберите как расставленные пределы, проанализируйте эффективность замены переменных при упрощении повторного интеграла.
ЗАДАНИЕ 8.25 Вычислить поток векторного поля 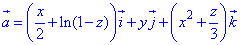
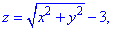
Решение: Анализ уравнения 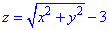
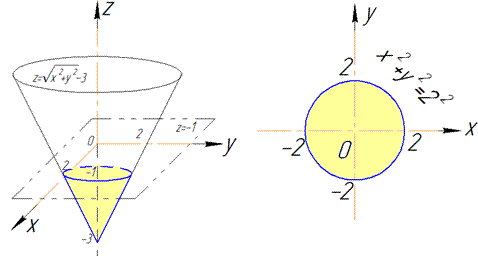
Четверть области V описываем следующими пределами:
Правильно найденные пределы интегрирования играют определяющую роль при интегрировании, поэтому помните что это одна из ответственных частей приведенных расчетов.
Результат интегрирования не забывайте множить на 4.
Дивергенцию поля 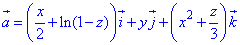
здесь учтено P=P(x;y;z)=x/2+ln(1-z), Q=Q(x;y;z)=y, R=R(x;y;z)=x2+z/3.
По формуле вычисляем поток векторного поля 
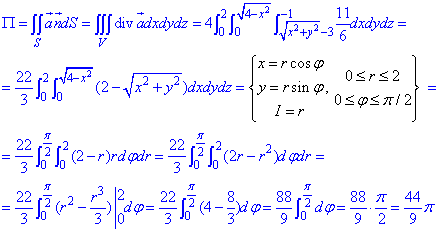
Будьте внимательные при расчетах, в первую очередь проверяйте правильность расстановки пределов интегрирования.
Хорошо заучите замену переменных, которая здесь приведена и применяйте ее в примерах, что подобные за конструкцией к рассмотренным.
При вычислении интегралов проверяйте себя на каждом шагу, наименьшая ошибка при переходах в начале приведет к неправильному ответу напоследок расчетов.
Примеры решений задач по теории поля
В этом разделе вы найдете готовые задания разного типа по векторному анализу (теории поля):
Спасибо за ваши закладки и рекомендации
Примеры: базовые понятия теории поля
Задача 1. Проверить, что поле $f=(3x+y^2)i+2xy j$ потенциально и восстановить потенциал.
Задача 2. Найти дивергенцию и ротор векторного поля $overline{a}=(3x-y) overline{i}+(6z+5x) overline{k}$
Задача 3. Дано скалярное поле $u(x,y,z)$ и векторное поле $overline{a}(x,y,z)$. Найти $grad u$, $div overline{a}$, $rot overline{a}$ в точке $M(1;5;-2)$.
$$u=frac{sqrt{x}}{y}-frac{yz}{x+sqrt{y}}, quad
overline{a}=yzoverline{i} +xzoverline{j} +xyoverline{k}$$
Задача 4. Вычислить потенциальную функцию векторного поля
$$overline{a}=left( frac{x}{y}+ycos x right)overline{i} +left(-frac{x^2}{2y^2}+sin xright)overline{j}.$$
Поток поля через поверхность
Задача 5. Найти поток векторного поля $overline{a}=2x overline{i}+y overline{j}-2z overline{k}$ через часть плоскости $P: 2x+y/2+z=1$, расположенную в первом октанте (нормаль образует острый угол с осью $Oz$).
Задача 6. Найти поток векторного поля $overline{a}$ через часть поверхности $S$, вырезаемую плоскостями $P_1, P_2$ (нормаль внешняя к замкнутой поверхности, образуемой данными поверхностями).
$$ overline{a}=(x^3+xy^2)overline{i}+(y^3+x^2y)overline{j}+z^2overline{k},\
S: x^2+y^2=1, P_1^ z=0; P_2: z=3$$
Задача 7. Найти поток векторного поля $overline{a}$ через замкнутую поверхность $S$ (нормаль внешняя).
$$ overline{a}=xoverline{i}+zoverline{j}-yoverline{k},\
S: z=4-2(x^2+y^2), z=2(x^2+y^2).$$
Задача 8. Найти поток векторного поля $overline{a}=x^3overline{i}+y^3overline{j}+z^3overline{k}$ через замкнутую поверхность $S: x^2+y^2+z^2=1$ (нормаль внешняя).
Задача 9. Найти поток векторного поля $overline{a}$ через часть плоскости $S$, вырезанную плоскостью $P: z=1$ непосредственно и с помощью формулы Гаусса-Остроградского (нормаль внешняя к замкнутой поверхности).
$$overline{a}=(x+xy^2) overline{i} + (y-yx^2)overline{j}+(z-3)overline{k}, quad S: x^2+y^2=z^2 (z geq 0).$$
Циркуляция векторного поля
Задача 10. Найти модуль циркуляции векторного поля $overline{a}=xyoverline{i}+yzoverline{j}+zxoverline{k}$ вдоль контура
$$x^2+y^2=9, x+y+z=1.$$
Задача 11. Найдите циркуляцию вектора $overline{a}=(x^2-y) overline{i}+ xoverline{j}+ overline{k}$ по контуру
$$x^2+y^2=1;\
z=1$$
с помощью формулы Стокса и непосредственно (положительным направлением обхода контура считать то, при котором точка перемещается по часовой стрелке, если смотреть из начала координат).
Задача 12. Найти циркуляцию вектора $F$ вдоль ориентированного контура $L$.
$$ overline{F} = (3x-1) overline{i}+ (y-x+z)overline{j}+4z overline{k}, $$
$L$ — контур треугольника $ABCA$, где $A,B,C$ точки пересечения плоскости $2x-y-2z+2=0$ соответственно с осями координат $Ox, Oy, Oz$.
Работа векторного поля
Задача 13. Найдите работу векторного поля $A=(2xy-y; x^2+x)$ по перемещению материальной точки вдоль окружности $x^2+y^2=4$ из $M (2; 0)$ в $К(-2; 0)$.
Задача 14. Вычислить работу векторного поля силы $overline{F} = xz overline{i} -overline{j}+y overline{k}$ при движении материальной точки по пути $L: x^2+y^2+z^2=4$, $z=1 (y ge 0)$ от точки $M(sqrt(3);0;1)$ до точки $N(-sqrt(3);0;1)$.
Типовой расчет по теории поля
Задание 15.
А) Найти поток векторного поля $F$ через внешнюю поверхность пирамиды, отсекаемой плоскостью $(p)$ двумя способами: непосредственно и по формуле Гаусса-Остроградского.
Б) Найти циркуляцию вектора $F$ по контуру треугольника двумя способами: по определению и по формуле Стокса.
$$ overline{F} = z overline{i}+ (x+y)overline{j}+y overline{k}, quad (p): 2x+y+2z=2. $$
Помощь с решением заданий
Если вам нужна помощь с решением задач и контрольных по этой и другим темам математического анализа, обращайтесь в МатБюро. Стоимость подробной консультации от 150 рублей, оформление производится в Word, срок от 1 дня.
Проконсультируем по задачам теории поля
Полезные ссылки
- Учебник с примерами онлайн по теории поля
- Функции нескольких переменных — задачи с решениями
1. Определение потока векторного поля
Рассмотрим
векторное поле
,
где проекции— непрерывные функции в некоторой области
(V). Возьмем некоторую
гладкую (кусочно гладкую) двустороннюю
ориентированную поверхность (S)
(то есть двустороннюю поверхность с
выбранным на ней направлением нормали).
Определение.ПотокомПвекторного полячерез двустороннюю ориентированную
поверхность (S)
называется поверхностный интеграл
первого рода по поверхности (S):
.
(1.3)
Здесь
—
орт нормали к выбранной стороне (S);ds– элемент площади
поверхности (S).
Замечание.В
случае замкнутой поверхности ее
ориентируют, направляя нормаль изнутри
области (V) наружу.
Сторона с положительным направлением
нормали называется положительной
стороной поверхности.
Для
потока можно дать следующие записи
через поверхностные интегралы первого
и второго рода
:

где
,
,
— то есть
— проекции площадки
на плоскостиOyz,Oxz,Oxyсоответственно.
П
—
радиус-вектор точки)
через полную поверхность прямого
кругового цилиндра с высотойHи радиусом основанияR(см. рис.1).
Р
Рис.1.
ешение.Так как поверхность (S)
есть объединение поверхностейи
,
то поэтому для потокаП(по свойству
аддитивности) имеем:.
На боковой поверхностинормаль
параллельна плоскостиOxy;
следовательно,и поток
=
.
На нижнем основаниинормаль
параллельна
осиOz:.
Тогдаи
;
на стороненормаль
и
,
т.е.и
.Искомый
поток.
Обратим внимание на то, что.
Ниже увидим, что это не случайно.
2. Способы вычисления потока
1.
Метод проектирования.Пусть поверхность
(S) задана явным
уравнением.
В этом случае орт
.
Для потокаП получим формулу:
.
(1.4)
Замечание 1.При проектировании на другие плоскости
в подынтегральную функцию в формуле
(1.4) следует добавить (множителем) проекциюна координатную ось, перпендикулярную
плоскости проектирования.
В формуле (1.4) ()
– область на плоскостиOxy,
в которую проектируется поверхность
(S); произведениеdxdyберется со знаком +, если уголмежду осью Ozи
нормальюострый, и минус, если угол
тупой. Символ
означает, что в подынтегральную функцию
вместоzнадо подставить.
Замечание 2.Аналогичные формулы можно записать,
если проектировать поверхность (S)
на плоскостиOxzилиOyz.
Замечание 3.В
случае неявного задания поверхности
(S)вектор
.
П
1.Найти поток векторного полячерез верхнюю сторону треугольникаАВСс вершинами в точках
,
,
(см. рис.2).
Р
Рис.2.
ешение.Составим уравнение
плоскости (поверхности (S)),
проходящей через три заданные точки:

откуда
.
Поверхность (S)
проектируется на плоскостьOxyв область,
.
Из условия следует, что нормальобразует острый угол с осьюOz.
Имеем=
;
произведениеdxdy,
берем со знаком “+”. Тогда по формуле
(1.4)

Пример 2.Вычислить полячерез замкнутую поверхность (S),
ограниченную цилиндроми плоскостями
,
.
Положительной стороной (по определению)
считаем внешнюю сторону замкнутой
поверхности.
Решение.Поверхность (S) кусочно
гладкая. Разобъем ее на три части
(см.
рис.3):.
В связи с этим.
1 )Для поверхностиz=0 и
.
Т
Рис.3.
огда.
Проекцияповерхности (S) на
плоскостьOxyесть
полукруг,
.
С учетом направления нормалидля потока
получим:
.
Переходя к полярным координатам, найдем.2)
Дляи
.
Поверхностьпроектируется на плоскостьOxyв область (
)
(см.п.1), и поток
=.3)Для
,
и
=
.
Однозначно поверхностьпроектируется на плоскостьOyzв область (
),
ограниченную линиями.
Исключая отсюда
x, найдем проекцию
этой линии на плоскостьOyz:.
Для потока получим (напомним Замечание
1: следует учесть, что в этом случае
=
.
4) Для потокаполучим
.
2.
Метод проектирования на все три
координатные плоскости. Пусть
поверхность (S)
однозначно проектируется на все три
координатные плоскости: (Dxy):z=z(x,y);;
.Для
потокаП в этом случае имеем (вторая
формула из (1.3)):

В (1.5) знаки проекций
dydz,dxdz,dxdyвыбираются в
соответствии с сформулированным выше
правилом.
Пример 3.Найти
поток векторачерез часть внешней стороны сферы
,
заключенной в первом октанте.
Решение.Имеем.
С учетом того, что поверхность расположена
в первом октанте, проекцииdydz,dxdz,dxdyберем со знаком “+”. По формуле (1.5).
Из уравнения сферы имеем:;
;
и
.
Очевидно,
.
Вычислим этот интеграл в полярной
системе координат:=
=
=

Следовательно,.
3.
Применение формулы Гаусса-Остроградского.Приведем соответствующую теорему.
Теорема.Если
в некоторой областипроекции поля
непрерывны и имеют непрерывные частные
производные,
то поток векторачерез произвольную замкнутую кусочно
гладкую поверхность (S),
расположенную целиком в области,
равен тройному интегралу от суммыпо области (V),
ограниченной поверхностью (S):
(1.6)
—
формула Гаусса-Остроградского.
Замечание.
Подынтегральная функция в тройном
интеграле (1.6) называется дивергенцией
(расходимостью) поля
;
обозначается.
Пример 4.
Вычислить поток векторачерез
замкнутую поверхность,
.
Решение. По
формуле (1.6).
Для вычисления этого интеграла применим
сферическую систему координат:,
,
;
.
Таким образом,
.
Пример 5.Используя формулу Гаусса-Остроградского
(1.6), вычислить поток полячерез верхнюю сторону части поверхности
,
расположенную над плоскостьюOxy.
Решение.Для
того, чтобы можно было применить формулу
(1.6), замкнем снизу данную поверхность
куском плоскостиOxy,
который ограничен окружностью,z = 0 . Вычислим
подынтегральную функцию, стоящую под
знаком тройного интеграла:.
Отсюда следует, что потокП=0. По
свойству аддитивности,
откуда искомый поток.
Уравнение поверхностии
.
Таким образом,— поток
через поверхностьz=0 численно равен площади круга
;
искомый поток.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
divergence calculator
Вычисление потока векторного поля на поверхности
Задача. Найти поток векторного поля
$$bar{a}=(x-y)cdotbar{i}+(x+y)cdotbar{j}+bar{k}$$
через часть цилиндрической поверхности
$$x^2+y^2=a^2,$$
расположенной между плоскостями
$$z=0,quad z=x.$$
Решение:
Поток находится по формуле:
$$prod=int int_{S} bar{a}cdot bar{n}, dS.$$
Найдем нормальный вектор (bar{n}) из уравнения (x^2+y^2=a^2):
$$bar{n} = frac{2xcdot bar{i}+2ycdot bar{j}}{sqrt{4x^2+4y^2}}=frac{x, bar{i}+y, bar{j}}{sqrt{x^2+y^2}}=frac{x, bar{i}+y, bar{j}}{a}.$$
Скалярное произведение векторов:
$$bar{a}cdot bar{n} = frac{x^2-xy}{a} + frac{xy+y^2}{a} = frac{x^2+y^2}{a} = frac{a^2}{a} = a.$$
Поскольку нам необходимо найти поток через цилиндрическую поверхность, то введем в качестве криволинейных координат (varphi) и (z).
Тогда (x=acdot cos varphi,quad y=acdot sin varphi,quad z=z,quad dS=a,dvarphi ,dz.)
Поток:
$$prod=int int_{S} a, dS = int int_{D} a^2,dvarphi ,dz=$$
$$=begin{vmatrix} -frac{pi}{2}leq varphi leq frac{pi}{2} \ 0leq zleq a, cos varphi end{vmatrix} =a^2intlimits_{-frac{pi}{2}}^{frac{pi}{2}}dvarphi intlimits_{0}^{a,cosvarphi}dz=$$
$$=a^2intlimits_{-frac{pi}{2}}^{frac{pi}{2}}left. z, right|_{0}^{a,cosvarphi},dvarphi=a^2intlimits_{-frac{pi}{2}}^{frac{pi}{2}}a,cosvarphi,dvarphi=$$
$$=a^3,left.sinvarphiright|_{-frac{pi}{2}}^{frac{pi}{2}}=a^3cdotleft(1-(-1)right)=2a^3.$$
Ответ:
$$prod=2a^3.$$
2016-03-14 • Просмотров [ 7119 ]