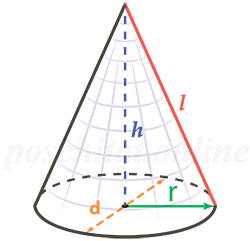
Площадь поверхности конуса
- Главная
- /
- Математика
- /
- Геометрия
- /
- Площадь поверхности конуса
Для того чтобы посчитать площадь поверхности конуса, просто воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
Площадь боковой поверхности конуса
=
=
Sб.пов =
0
Округление числа π: Округление ответа:
Площадь полной поверхности конуса
=
=
Sп.пов =
0
Округление числа π: Округление ответа:
Просто введите данные, и получите ответ.
Теория
Площадь боковой поверхности конуса через образующую
Чему равна площадь боковой поверхности конуса Sб.пов, если образующая l, а радиус основания r:
Формула
Sб.пов = π ⋅ r ⋅ l
через диаметр:
Sб.пов = π ⋅ l ⋅ d⁄2
Пример
Для примера посчитаем чему равна площадь боковой поверхности конуса, образующая которого l = 6 см, а радиус основания r = 3 см:
Sб.пов ≈ 3.14 ⋅ 6 ⋅ 3 ≈ 56.52 см²
Площадь боковой поверхности конуса через высоту
Чему равна площадь боковой поверхности конуса Sб.пов, если высота h, а радиус основания r:
Формула
Sб.пов = π ⋅ r ⋅ √r² + h²
через диаметр:
Sб.пов = π ⋅ d⁄2 ⋅ √(d/2)² + h²
Пример
Для примера посчитаем чему равна площадь боковой поверхности конуса, высота у которого h = 5 см, а радиус основания r = 2 см:
Sб.пов ≈ 3.14 ⋅ 2 ⋅ √2² + 5² ≈ 6.28 ⋅ √29 ≈ 33.82 см²
Площадь полной поверхности конуса через образующую
Чему равна площадь полной поверхности конуса Sп.пов, если образующая l, а радиус основания r:
Формула
Sп.пов = π ⋅ r ⋅ (r + l)
через диаметр:
Sп.пов = π ⋅ d⁄2 ⋅ (d⁄2 + l)
Пример
Для примера посчитаем чему равна площадь полной поверхности конуса, образующая которого l = 6 см, а радиус основания r = 3 см:
Sп.пов ≈ 3.14 ⋅ 3 ⋅ (3 + 6) ≈ 84.78 см²
Площадь полной поверхности конуса через высоту
Чему равна площадь полной поверхности конуса Sп.пов, если высота h, а радиус основания r:
Формула
Sп.пов = π ⋅ r ⋅ (r + √r² + h²)
через диаметр:
Sп.пов = π ⋅ d⁄2 ⋅ (d⁄2 + √(d/2)² + h²)
Пример
Для примера посчитаем чему равна площадь полной поверхности конуса, высота у которого h = 5 см, а радиус основания r = 2 см:
Sп.пов ≈ 3.14 ⋅ 2 ⋅ (2 + √2² + 5²) ≈ 6.28 ⋅ (2 + √29) ≈ 46.38 см²
См. также
Конус — это совокупность всех лучей, которые исходят из какой-либо точки пространства и пересекают плоскую поверхность.
Онлайн-калькулятор площади поверхности конуса
Точка, которая является началом этих лучей, называется вершиной конуса. В случае когда в основании конуса лежит многоугольник, конус превращается в пирамиду.
Конус состоит из некоторых элементов, знать которые необходимо для решения задач.
Образующая — отрезок, соединяющий точку, лежащую на окружности круга, который является основанием, и вершину конуса.
Высота — расстояние от плоскости основания до точки вершины конуса.
Виды конуса
Конус может быть нескольких видов:
Прямым, если его основанием является эллипс или круг. Причем вершина должна точно проектироваться в центр основания.
Косым — это тот случай, когда центр фигуры, лежащей в основании, не совпадает с проекцией вершины на это основание.
Круговым — соответственно, если основание — круг.
Усеченным — область конуса, которая будет лежать между основанием и сечением плоскости, параллельной основанию и пересекающей этот конус.
Формула площади поверхности конуса
Для нахождения полной площади поверхности конуса нужно найти сумму площади основания (или оснований, если конус усеченный) конуса и площади его боковой поверхности:
S=Sосн+SбокS=S_{text{осн}}+S_{text{бок}}
SоснS_{text{осн}} — площадь основания (оснований) конуса;
SбокS_{text{бок}} — площадь боковой поверхности конуса.
Рассмотрим примеры нахождения площади поверхности обычного прямого кругового конуса, а также усеченного этого же конуса.
Формула площади поверхности кругового конуса
Sосн=π⋅r2S_{text{осн}}=picdot r^2
Sбок=π⋅r⋅lS_{text{бок}}=picdot rcdot l
rr — радиус круга (основания) кругового конуса;
ll — длина образующей этого конуса.
Найти площадь поверхности кругового конуса, если радиус основания равен 3 (см.), а высота hh треугольника, путем вращения которого образовался данный конус, равна 4 (см.)
Решение
r=3r=3
h=4h=4
Образующую можно найти, если рассмотреть треугольник, катетами которого являются радиус и высота, а гипотенузой — сама образующая ll. По теореме Пифагора имеем:
l2=r2+h2l^2=r^2+h^2
l2=32+42l^2=3^2+4^2
l2=25l^2=25
l=5l=5
Вычислим площадь основания конуса:
Sосн=π⋅r2=π⋅32≈28.26S_{text{осн}}=picdot r^2=picdot 3^2approx28.26 (см. кв.)
Площадь боковой поверхности:
Sбок=π⋅r⋅l=π⋅3⋅5≈47.10S_{text{бок}}=picdot rcdot l=picdot 3cdot 5approx47.10 (см. кв.)
Полная площадь
S=Sосн+Sбок≈28.26+47.10=75.36S=S_{text{осн}}+S_{text{бок}}approx28.26+47.10=75.36 (см. кв.)
Ответ: 75.36 см. кв.
Формула площади поверхности усеченного кругового конуса
Для усеченного кругового конуса площадь боковой поверхности можно найти по формуле:
Sбок=π⋅l⋅(r+r′)S_{text{бок}}=picdot lcdot (r+r’)
ll — длина образующей конуса;
rr — радиус основания;
r′r’ — радиус круга, получаемый при усечении кругового конуса.
Условие возьмем из предыдущей задачи, добавив к нему только лишь радиус второго основания r′r’. Пусть он будет равен 2 (см.). Требуется вычислить полную площадь поверхности этого усеченного конуса.
Решение
l=5l=5
r=3r=3
r′=2r’=2
Оснований у нас теперь два, поэтому полная площадь оснований будет равна сумме площадей этих оснований с радиусами rr и r′r’:
Sосн=Sосн r+Sосн r’S_{text{осн}}=S_{text{осн r}}+S_{text{осн r’}}
Площадь основания радиуса rr:
Sосн r=π⋅r2=π⋅32≈28.26S_{text{осн r}}=picdot r^2=picdot 3^2approx28.26 (см. кв.)
Площадь основания радиуса r′r’:
Sосн r’=π⋅r′2=π⋅22≈12.56S_{text{осн r’}}=picdot r’^2=picdot 2^2approx12.56 (см. кв.)
Площадь боковой поверхности:
Sбок=π⋅l⋅(r+r′)=π⋅5⋅(3+2)≈78.50S_{text{бок}}=picdot lcdot (r+r’)=picdot 5cdot (3+2)approx78.50 (см. кв.)
Полная площадь:
S=Sосн+Sбок=Sосн r+Sосн r’+Sбок≈28.26+12.56+78.50=119,32S=S_{text{осн}}+S_{text{бок}}=S_{text{осн r}}+S_{text{осн r’}}+S_{text{бок}}approx28.26+12.56+78.50=119,32 (см. кв.)
Ответ: 119,32 см. кв.
Не знаете, как решить задачу по геометрии? Наши эксперты оперативно помогут вам с решением!
Тест по теме «Площадь поверхности конуса»
Как рассчитать площадь поверхности конуса
На данной странице калькулятор поможет рассчитать площадь поверхности конуса онлайн. Для расчета задайте высоту, радиус или образующую.
Конус — геометрическое тело, образованное вращением прямоугольного треугольника около одного из его катетов.
Образующая конуса — это отрезок, соединяющий вершину и границу основания.
Боковая поверхность через радиус и образующую
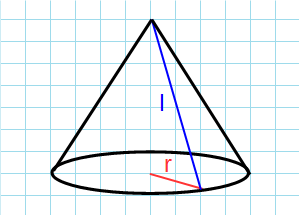
Формула боковой поверхности конуса через радиус и образующую:
π — константа равная (3.14); l — образующая конуса; r — радиус основания конуса.
Боковая поверхность через радиус и высоту
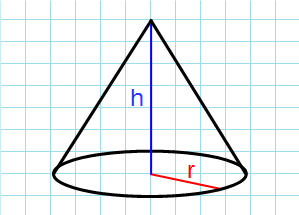
Формула боковой поверхности конуса через радиус и высоту:
π — константа равная (3.14); h — высота конуса; r — радиус основания конуса.
Полная площадь через радиус и образующую

Формула площади полной поверхности конуса через радиус и образующую:
π — константа равная (3.14); l — образующая конуса; r — радиус основания конуса.
Полная площадь через радиус и высоту

Формула полной площади поверхности конуса через радиус и высоту:
π — константа равная (3.14); h — высота конуса; r — радиус основания конуса.
Download Article
Download Article
The surface area of a cone is the sum of the lateral surface area and the base surface area. If you know the radius of the base and the slant height of the cone, you can easily find the total surface area using a standard formula. Sometimes, however, you might have the radius and some other measurement, such as the height or volume of the cone. In these instances, you can use the Pythagorean Theorem and the volume formula to derive the slant height, and thus the surface area of the cone.
-
1
-
2
Plug the value of the radius into the formula. This length should be given, or you should be able to measure it. Make sure you substitute for both
variables in the formula.
- For example, if the radius of the base of a cone is 5 cm, your formula will look like this:
.
Advertisement
- For example, if the radius of the base of a cone is 5 cm, your formula will look like this:
-
3
Plug the value of the slant height into the formula. This length should be given, or you should be able to measure it.
- For example, if the slant height of a cone is 10 cm, your formula will look like this:
.
- For example, if the slant height of a cone is 10 cm, your formula will look like this:
-
4
-
5
-
6
Add the lateral surface area and the base area of the cone. This will give you the total surface area of the cone, in square units.
- For example:
So, the surface area of a cone with a radius of 5 cm and a slant height of 10 cm is 235.5 square centimeters.
- For example:
Advertisement
-
1
-
2
-
3
Square the lengths of the radius and height, then add. Remember that squaring a number means to multiply it by itself.
-
4
Take the square root of each side of the equation. This will give you the length of the hypotenuse of the right triangle, which is equal to the slant height of the cone.[9]
-
5
-
6
Plug all the known values into the formula. The radius should be given, and you already calculated the slant height. Make sure you use the slant height in the surface area formula, not the (perpendicular) height. If you are not using a calculator, use 3.14 for
- For example, for a cone with a radius of 5 cm and a slant height of 13 cm, your formula will look like this:
.
- For example, for a cone with a radius of 5 cm and a slant height of 13 cm, your formula will look like this:
-
7
Multiply to find the lateral area and the base area. Then, add these products together. The sum will give you the total surface area of the cone in square units.[11]
Advertisement
-
1
-
2
Plug the known values into the formula. You should know the volume and the length of the radius. If not, you cannot use this method. If you are not using a calculator, use 3.14 for
.
- For example, if you know a cone has a volume of 950 cubic centimeters and a radius of 6 centimeters, your formula will look like this:
.
- For example, if you know a cone has a volume of 950 cubic centimeters and a radius of 6 centimeters, your formula will look like this:
-
3
-
4
Divide each side by the
coefficient. This will give you the value of
, which is the perpendicular height of the cone. You will need this information to find the slant height of the cone, which is necessary to know when solving for the surface area.
-
5
Set up the formula for the Pythagorean Theorem. The formula is
, where
and
equal the side lengths of a right triangle, and
equals the length of the hypotenuse (the side opposite the right angle).[15]
-
6
-
7
Solve for
. This will give you the length of the right triangle’s hypotenuse, which is also the slant height of the cone.
-
8
-
9
Plug all the known values into the formula. Make sure you use the slant height in the surface area formula, not the (perpendicular) height. If you are not using a calculator, use 3.14 for
- For example, for a cone with a radius of 6 cm and a slant height of 25.91 cm, your formula will look like this:
.
- For example, for a cone with a radius of 6 cm and a slant height of 25.91 cm, your formula will look like this:
-
10
Multiply to find the lateral area and the base area. Then, add these products together. The sum will give you the total surface area of the cone in square units.[17]
Advertisement
References
Add New Question
-
Question
What is the area of the base of a cone with a volume of 36 cubic inches and height of 9 inches?
The formula for volume of a cone is 1/3 x Base Area (i.e. area of a circle) x height.
Solution:
Volume = 1/3 x BA x H
36 = 1/3 x (BA)* x 9
36 x 3 = BA x 9 (we moved the 1/3 to the other side of the equation, hence it reciprocated)
108/9 = BA
Base area of the cone is 12 inches. -
Question
How do I show that slant height is 2r?
If you’re given the radius of the base and the height of the cone, you can do the Pythagorean theorem.
-
Question
How do I find the radius of the base of a cone given its surface area of 500 pi and height of 15 cm?
Assuming you are given the lateral surface area and the slant height, divide the lateral surface area by the product of pi and the slant height. If instead of the slant height you are given the perpendicular height, use Method 2 above to find the slant height, then multiply the slant height by pi, and divide that product into the lateral surface area to get the radius of the base.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
The Pythagorean theorem applies to the radius, perpendicular height, and slant height, with the slant height acting as the hypotenuse: (radius)2 + (perpendicular height)2 = (slant height)2.
Thanks for submitting a tip for review!
Advertisement
About This Article
Article SummaryX
To find the surface area of a cone if you know the length of the slant, use the formula (πrs)+πr^2. Put the value of the radius of the circle at the bottom of the cone into the formula where you see an “r” and be sure to square it where necessary. Then, insert the length of the slant into the formula for “s,” and multiply the radius, slant, and pi together. Once you have the first part of the equation, multiply pi by the radius squared. To get the total surface area, add the two values together, and be sure to record your answer in units squared! For help finding the surface area of a cone if you know the radius and the perpendicular height, or the radius and the volume, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 239,447 times.
Did this article help you?
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь поверхности прямого кругового конуса (боковую, полную и основания), а также разберем примеры решения задач для закрепления материала.
-
Формула вычисления площади конуса
- 1. Боковая поверхность
- 2. Основание
- 3. Полная площадь
- Примеры задач
Формула вычисления площади конуса
1. Боковая поверхность
Площадь (S) боковой поверхности конуса равняется произведению числа π на радиус основания и на длину образующей.
Sбок. = πRl
Образующая (l) соединяет вершину конуса и границу основания, другими словами, точку на окружности.
Примечание: в вычислениях значение числа π округляется до 3,14.
2. Основание
Основанием конуса является круг, площадь которого вычисляется так:
Sосн. = πR2
Учитывая то, что диаметр круга равняется двум его радиусам (d = 2R), данную формулу можно представить в виде:
Sосн. = π(d/2)2
3. Полная площадь
Для вычисления суммарной площади конуса следует сложить площади боковой поверхности и основания:
Sполн. = πRl + πR2 = πR(l + R)
Примеры задач
Задание 1
Вычислите площадь боковой поверхности конуса, если известно, что его радиус равен 16 см, а длина образующей – 5 см.
Решение:
Используем соответствующую формулу с известными нам величинами:
S = 3,14 ⋅ 16 см ⋅ 5 см = 251,2 см2.
Задание 2
Высота конуса равна 4 см, а его радиус – 3 см. Найдите суммарную площадь поверхности фигуры.
Решение:
Если рассмотреть конус в сечении, то можно заметить, что его высота, радиус и образующая представляют собой прямоугольный треугольник. Следовательно, воспользовавшись теоремой Пифагора, можно найти длину образующей (является гипотенузой):
l2 = (4 см)2 + (3 см)2 = 25 см2.
l = 5 см.
Осталось только использовать найденное и известные по условиям задачи значения, чтобы рассчитать площадь:
S = 3,14 ⋅ 3 см ⋅ (5 см + 3 см) = 75,36 см2.