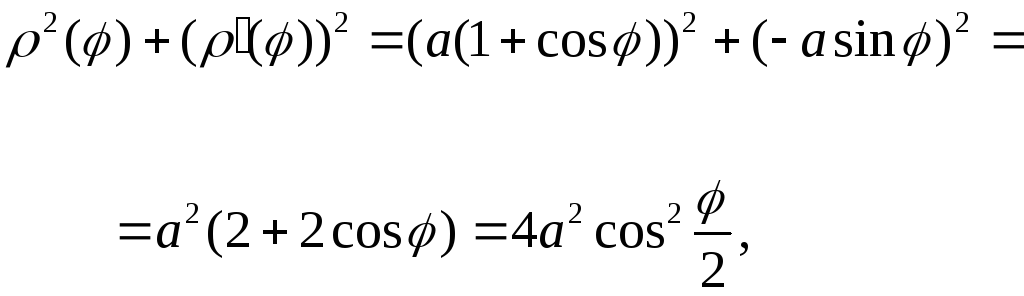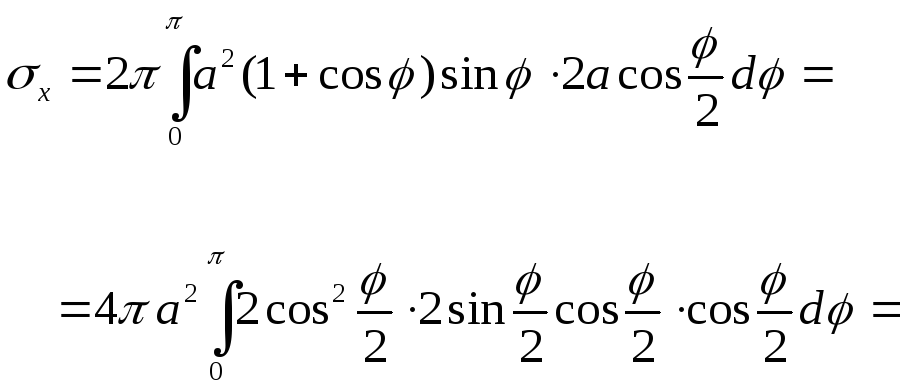Лучший ответ
|
|
 |
|
I Определения
Определение
1. Поверхность
вращения – это поверхность, которая
получается при вращении плоской линии
вокруг оси, лежащей в её плоскости и не
пересекающей её.
Ось вращения может
и пересекать линию, если это ось симметрии
линии. В этом случае рассматривают лишь
«половину» линии.
Впишем в кривую
произвольную ломанную и обозначим
длину наибольшего её звена. При вращении
этой ломанной вокруг оси мы получим
поверхность,
составленную из боковых поверхностей
усеченных конусов. Обозначим площадь
этой поверхности.
Определение
2. Конечный
предел
называют площадью поверхности вращения.
Можно показать,
что если линия
имеет длину, то поверхность, полученная
её вращением, имеет площадь.
II Общая формула
Линия
,
вращением которой вокруг оси абсцисс
получена поверхность, может быть задана
одним из следующих способов:
1) 2) 3)
Теорема.
Если функции, определяющие линию,
непрерывны вместе со своими производными,
то площадь поверхности вращения (вокруг
оси
)
определяется формулой:
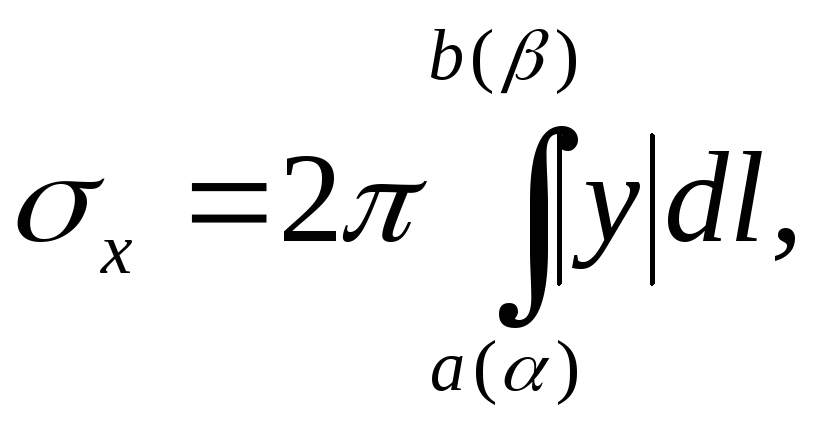
где
– подынтегральное выражение, фигурирующее
в соответствующей формуле для длины
дуги.
Идея
доказательства.
Пусть концы -го
звена ломанной имеют координаты
и .
Это звено при вращении вокруг оси
опишет
боковую поверхность усеченного конуса
с радиусами основанийи
и образующей
(длина
-го
звена). Для площади такой поверхности
известна формула
Вся ломанная даст
поверхность с площадью
Если, например,
имеющаяся кривая – это график функции
,
тогда
(см. §3, II). Также,
заменяя
на
получим
В этой сумме
нетрудно увидеть интегральную сумму,
которая в пределе даст интеграл из (1).
III Частные случаи и примеры
1) Найти площадь
сферического пояса, полученного вращением
дуги окружности ,
,
вокруг оси абсцисс.
Формула имеет вид
Проведём
предварительные вычисления:
,
.
Теперь вычисляем
площадь:
Сферический пояс
– это часть сферы, заключенная между
двумя параллельными плоскостями.
Полученный результат показывает, что
площадь сферического пояса зависит
лишь от расстояния между плоскостями,
и не зависит от их положения относительно
сферы.
2) Найти площадь
поверхности, полученной вращением
астроиды ,
вокруг оси
.
Общая формула
принимает вид
Астроида симметрична
относительно оси вращения. Поэтому
необходимо рассматривать лишь часть
её, например, для
.
Предварительные вычисления:
,
,
Так как
то, чтобы не «разбираться» с модулем,
воспользуемся симметрией астроиды
относительно оси
,
т.е. будем рассматривать:
3) Дуга кардиоиды
,
,
вращается вокруг полярной оси. Найти
объём тела вращения.
Формула (1) в этом
случае принимает вид:
Имеем для кардиоиды
Задачи
для самостоятельного решения.
1. Найти площадь
поверхности тора, полученного вращением
окруж-ности ,
,
вокруг оси
.
2. Круговой сегмент,
основание которого
,
высота,
вращается вокруг основания. Найти
площадь поверхности получающегося тела
вращения.
3. Первая арка
циклоиды
,
,
,
вращается: а) вокруг оси;
б) вокруг оси.
Найти площади получающихся поверхностей
вращения.
Соседние файлы в папке Лекции по мат.анализу
- #
- #
- #
- #
- #
- #
- #
Формулы объема
Объем и площадь шарового слоя и шарового пояса.
Объем шара равен 4/3π3 , а площадь сферы равна 4πr2.
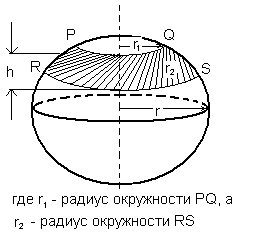
Шаровой слой — это часть шара между двумя параллельными плоскостями. На рисунке выше PQRS — шаровой слой.
Шаровой пояс — это сферическая поверхность шарового слоя.
Площадь шарового пояса на рисунке выше S=2 πhr;
Объем шарового слоя V=(πh/6)*(h2+3r12+3r22)
Пример1. Определение объема шарового слоя шара.
Определить объем шарового слоя шара с диаметром 50 см, если верхний и нижний диаметры слоя есть 25 и 40 см, а его высота 7,2 см.
Решение:
Как было сказано выше, объем шарового слоя
V=(πh/6)*(h2+3r12+3r22),
где h=7,2 см, r1= 25/2=12,5 см, r2=40/2=20 см
Следовательно, объем шарового слоя равен
V=(7,2π/6)*(7,22+3*12,52+3*202)=6483,18 см2 .
Пример 2. Определение площади шарового пояса.
Определить площадь шарового пояса из предыдущего примера.
Решение:
Площадь шарового пояса S=2πrh (как было определено выше), где радиус сферы r=50/2=25 см, а h=7,2 см.
Следовательно, площадь шарового пояса равна
S=2π*25*7,2=1130,4 см2
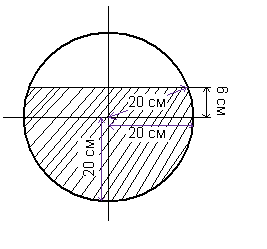
Пример 3. Определение объема заполнения сферического резервуара по уровню.
Сферический резервуар наполнен жидкостью до высоты 30 см. Определить объем жидкости в резервуаре (1л=1000 см3), если его внутренний диаметр равен 40 см.
Жидкость представлена в виде заштрихованной области в показанном на рис. ниже сечении.
Объем жидкости включает полусферу и шаровой пояс высотой 6 см.
Следовательно, объем жидкости есть V=(2/3)*πr3+(πh/6)*(h2+ 3r12+3r22), где
r2=40/2=20 см и r1=(202-62)1/2=19,1 см
Объем жидкости V=2/3 π *203+(6π)/6*(62+3*19,12+3*202)=24064,22 см3
Поскольку 1 литр =1000 см3, то количество литров жидкости равно
24064,22/1000=24,06422 л.
Площадь поверхности шарового слоя, формула
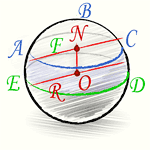
Шаровой слой — это часть шара, заключенная между двумя секущими параллельными плоскостями.
Шаровой пояс или Шаровая зона — это кривая поверхность шарового слоя. Круги ABC и DEF это основания шарового пояса. Расстояние между основаниями это высота шарового слоя.
Кривая поверхность шарового слоя равна произведению его высоты на окружность большого круга шара:
[ S = 2pi R h ]
(R — радиус большого круга шара, h=NO — высота шарового слоя)
Формулы шара, сферы
Вычислить, найти площадь поверхности шарового слоя по формуле (1)
Ссылки по теме
Площадь поверхности шарового слоя |
стр. 316 |
|---|