В данной публикации мы разберем варианты того, как можно вписать шар в цилиндр, а также, как исходя из этого определить его радиус (диаметр) и посчитать площадь поверхности.
- Формула расчета площади шара
- Способы вписать шар в цилиндр
- Примеры задач
Формула расчета площади шара
Для начала давайте вспомним общую формулу, по которой рассчитывается площадь поверхности шара:
S = 4 π R2
или S = 4 π (d/2)2, где d = 2R.
- R – радиус шара;
- d – его диаметр;
- π – число, приближенное значение которого равняется 3,14.
Способы вписать шар в цилиндр
Теперь давайте разберемся, каким образом можно вписать шар в цилиндр. В данном случае возможно несколько вариантов:
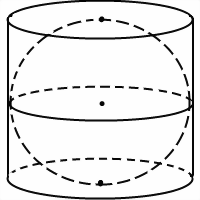
1. Шар касается оснований и боковой поверхности цилиндра
- радиус (диаметр) цилиндра является, в том числе, и радиусом (диаметром) шара;
- высота цилиндра – это диаметр шара.
2. Шар касается только оснований цилиндра
Радиус шара равен половине высоты цилиндра, а диаметр – полной высоте.
3. Шар касается только боковой поверхности цилиндра
Радиус (диаметр) цилиндра – это и есть радиус (диаметр) шара.
Примечание: Выяснив радиус или диаметр шара далее остается только воспользоваться формулой для расчета площади его поверхности.
Примеры задач
Задание 1
Шар вписан в цилиндр радиусом 15 см таким образом, что соприкасается и с основанием, и с боковой поверхностью последнего. Найдите площадь поверхности шара.
Решение:
Исходя из условий задачи, мы имеем дело с первым из трех описанных вариантов выше. А это значит, что радиус шара, также, равняется 15 см. Следовательно, площадь составляет:
S = 4 ⋅ 3,14 ⋅ (15 см)2 = 2826 см2.
Задание 2
Площадь поверхности шара равняется 1519,76 см2, и он вписан в цилиндр таким образом, что касается его оснований. Найдите высоту цилиндра.
Решение:
Для начала найдем радиус шара, которые равен:
Высота цилиндра равна двум радиусам шара или его диаметру (2-ой вариант, рассмотренный в разделе выше):
h = 2R = 2 ⋅ 11 см = 22 см.
Шар, вписанный в цилиндр, касается оснований цилиндра в их центрах, а боковой поверхности цилиндра — по параллельной основаниям окружности большого круга (то есть радиус этой окружности равен радиусу шара).
Если шар вписан в цилиндр, то цилиндр описан около шара.
В цилиндр можно вписать шар тогда и только тогда, когда цилиндр равносторонний, то есть его высота равна диаметру. Радиус вписанного в цилиндр шара R равен радиусу цилиндра r:
R=r.
Решение задач на шар, вписанный в цилиндр, чаще всего сводится к рассмотрению осевого сечения комбинации тел.
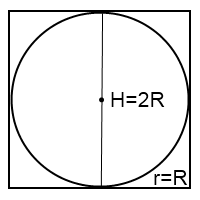
Это сечение представляет собой квадрат с вписанной в него окружностью. Сторона квадрата равна высоте цилиндра и диаметру шара:
H=2R
Найдем отношение объема цилиндра к объему вписанного в него шара. Объем шара
Объем цилиндра
Отсюда отношение объема шара к объему описанного около него цилиндра
Теперь найдем отношение площади поверхности цилиндра к площади вписанного шара. Площадь поверхности шара (площадь сферы)
Площадь полной поверхности цилиндра равна сумме площадей оснований и боковой поверхности:
Отсюда отношение площади поверхности вписанного шара к площади поверхности цилиндра
Шар, вписан в цилиндр. Значит сечение цилиндра — это квадрат. Достаточно знать либо диаметр цилиндра, либо его высоту, поскольку они должны быть равны. D = H.
Радиус шара соответственно равен R=D/2 = H/2.
А площадь поверхности Sшар = 4 pi R^2 = pi D^2 = pi H^2.
Почему-то в вопросе фигурирует ещё и площадь цилиндра.
Тоже определяется. Боковая площадь Sбок = pi D H = pi D^2 = pi H^2
Площадь одного основания Sосн = pi D^2/4 = pi H^2 / 4, двух оснований pi D^2 / 2=pi H^2 / 2
Полная площадь цилиндра Sполн= Sбок + 2*Sосн = 3 pi D^2 / 2 = 3 pi H^2 / 2
Найти площадь поверхности шара, вписанного в цилиндр
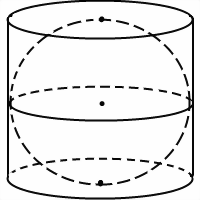
Шар, вписанный в цилиндр, касается оснований цилиндра в их центрах, а боковой поверхности цилиндра — по параллельной основаниям окружности большого круга (то есть радиус этой окружности равен радиусу шара).
Если шар вписан в цилиндр, то цилиндр описан около шара.
В цилиндр можно вписать шар тогда и только тогда, когда цилиндр равносторонний, то есть его высота равна диаметру. Радиус вписанного в цилиндр шара R равен радиусу цилиндра r: R=r.
Решение задач на шар, вписанный в цилиндр, чаще всего сводится к рассмотрению осевого сечения комбинации тел.
Площадь полной поверхности цилиндра равна сумме площадей оснований и боковой поверхности:
$$begin{aligned}
S_{2} &=S_{text {bok}}-2 S_{text {ocn}}=2 pi r H+2 pi r^{2}=\
&=2 pi R cdot 2 R+2 pi R^{2}=6 pi R^{2}
end{aligned}$$
где R — радиус площади основания цилиндра.
Отсюда отношение площади поверхности вписанного шара к площади поверхности цилиндра:
$$frac{S_{1}}{S_{2}}=frac{4 pi R^{2}}{6 pi R^{2}}=frac{2}{3}$$
Решили сегодня: раз, всего раз
Другие онлайн калькуляторы
- Найти радиус шара
- Вычислить радиус круга
- Нахождение площади треугольника 7-ю способами
- Посчитать поверхность правильной шестиугольной призмы
Вы поняли, как решать? Нет?
- Правила
- Комментарии
- Ответы на вопросы
Рассчитайте цену решения ваших задач


Калькулятор
стоимости
Решение контрольной
от 300 рублей
*
* Точная стоимость будет определена после загрузки задания для исполнителя
+Загрузить файл
Файлы doc, pdf, xls, jpg, png не более 5 МБ.

Шар вписан в цилиндр. Площадь поверхности шара равна 105. Найдите площадь полной поверхности цилиндра.
Решение.
Это задание ещё не решено, приводим решение прототипа.
Шар вписан в цилиндр. Площадь поверхности шара равна 111. Найдите площадь полной поверхности цилиндра.
Высота цилиндра равна диаметру шара, а радиус основания цилиндра равен радиусу шара (см. рис.).
Площадь основания цилиндра:
Площадь боковой поверхности цилиндра:
Площадь полной поверхности цилиндра:
Поскольку площадь поверхности шара дается формулой имеем:
Ответ: 166,5.