Как найти поверхностную плотность заряда через потенциал

По
принципу суперпозиции полей магнитная
индукция  в
произвольной точке магнитного поля
проводника с током  равна

 ,  
                                         (2.3)

где  –
магнитная индукция поля, создаваемого
элементом проводника длиной .

Интегрирование
производится по всей длине проводника L.

2.3.1. Магнитное поле прямолинейного тока

Рассчитаем
индукцию магнитного поля В,
создаваемую в точке А (рис. 2.2)
на расстоянии r₀ от
прямолинейного проводника с током:

;

;

.                
(2.4)

Выразим
переменные  и .
Из рис. 2.2 видно, что .
Дифференцируя это выражение, получаем:

.

Из
рис. 2.2 так же следует, что

.

Подставляя
значения  и r в
уравнение (2.4), имеем:

.                         
 (2.5)

Для
бесконечно длинного прямолинейного
проводника (₁ =
0, ₂ = )
уравнение (2.5) принимает вид:

 .                                        
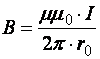
 (2.6)

9,
Уравне́ния
Ма́ксвелла — система
уравнений в дифференциальной или интегральной форме,
описывающих электромагнитное
поле и
его связь с электрическими
зарядами и токами в вакууме и сплошных
средах.
Вместе с выражением для силы
Лоренца,
задающим меру воздействия электромагнитного
поля на заряженные частицы, образуют
полную систему уравнений классической электродинамики,
называемую иногда уравнениями Максвелла —
Лоренца. Уравнения, сформулированныеДжеймсом
Клерком Максвеллом на
основе накопленных к середине XIX века
экспериментальных результатов, сыграли
ключевую роль в развитии представлений
теоретической физики и оказали сильное,
зачастую решающее, влияние не только
на все области физики, непосредственно
связанные с электромагнетизмом,
но и на многие возникшие впоследствии
фундаментальные теории, предмет которых
не сводился к электромагнетизму (одним
из ярчайших примеров здесь может
служитьспециальная
теория относительности).

10,
Электри́ческий заря́д (коли́чество
электри́чества)
— это физическая скалярная
величина,
определяющая способность тел быть
источником электромагнитных
полей и
принимать участие в электромагнитном
взаимодействии.
Впервые электрический заряд был введён
в законе
Кулона в 1785
году.

Единица
измерения заряда в Международной
системе единиц (СИ) — кулон —
электрический заряд, проходящий через
поперечное сечение проводника при силе
тока 1 Аза
время 1 с.
Заряд в один кулон очень велик. Если бы
два носителя заряда (q₁ = q₂ =
1 Кл) расположили в вакууме на
расстоянии 1 м,
то они взаимодействовали бы с силой9·10⁹ H,
то есть с силой, с которой гравитация
Земли притягивала бы предмет с массой
порядка 1 миллиона тонн.

Электрический
заряд замкнутой системы^[6] сохраняется
во времени и квантуется — изменяется
порциями, кратными элементарному
электрическому заряду,
то есть, другими словами, алгебраическая
сумма электрических зарядов тел или
частиц, образующих электрически
изолированную систему, не изменяется
при любых процессах, происходящих в
этой системе.

В
рассматриваемой системе могут
образовываться новые электрически
заряженные частицы, например, электроны —
вследствие явления ионизации атомов
или молекул, ионы — за счёт явления
электролитической диссоциации и др.
Однако, если система электрически
изолирована, то алгебраическая сумма
зарядов всех частиц, в том числе и вновь
появившихся в такой системе, всегда
равна нулю.

Закон
сохранения заряда —
один из основополагающих законов
физики. Закон
сохранения заряда был
впервые экспериментально подтверждён
в 1843
году великим
английским ученым Майклом
Фарадеем и
считается на настоящее время одним из
фундаментальных законов сохранения в
физике (подобно законам
сохранения импульса и энергии).
Всё более чувствительные экспериментальные
проверки закона сохранения заряда,
продолжающиеся и поныне, пока не выявили
отклонений от этого закона.

1. Точечный
   заряд. Закон Кулона – основной закон
   электростатики.

 Точечный
заряд –
это электрический
заряд,
когда размер тела, на котором этот заряд
сосредоточен, намного меньше расстояния
между заряженными телами.

Взаимодействие
двух покоящихся точечных зарядов
определяет основной закон электростатики
– закон
Кулона.
Этот закон экспериментально установил
в 1785 году французский физик Шарль
Огюстен Кулон (1736
– 1806). Формулировка закона Кулона
следующая:

Сила
взаимодействия двух
точечных неподвижных заряженных тел в
вакууме прямо пропорциональная
произведению модулей зарядов и обратно
пропорциональна квадрату расстояния
между ними.

Эта
сила взаимодействия называется кулоновская
сила,
и формула
закона Кулона будет
следующая: 

F
= k · (|q₁|
· |q₂|)
/ r² 

где
|q1|, |q2| – модули зарядов, r – расстояния
между зарядами, k – коэффициент
пропорциональности.

Коэффициент
k в СИ принято записывать в форме: 

k
= 1 / (4πε₀ε)

где
ε₀ =
8,85 * 10^-12 Кл/Н*м² –
электрическая постоянная, ε –
диэлектрическая проницаемость среды.

Для
вакуума ε = 1, k = 9 * 10⁹ Н*м/Кл².

Сила
взаимодействия неподвижных точечных
зарядов в вакууме: 

F
= [1 /(4πε₀)]
· [(|q₁|
· |q₂|)
/ r²] 

Если
два точечных заряда помещены в диэлектрик
и расстояние от этих зарядов до границ
диэлектрика значительно больше расстояния
между зарядами, то сила взаимодействия
между ними равна: 

F
= [1 /(4πε₀)]
· [(|q₁|
· |q₂|)
/ r²]
= k · (1 /π) · [(|q₁|
· |q₂|)
/ r²] 

1. Напряженность
   электрического поля. Принцип суперпозиции
   для напряженностей. Поле
   бесконечной равномерно заряженной
   нити.

Напряжённость
электрического поля. Силовой
характеристикой электрического поля
является вектор напряжённости
электрического поля E,
равный отношению вектора силы, действующей
в данной точке поля на пробный положительный
заряд, к величине этого заряда:

         
Напряжённость
в системе единиц СИ выражается в ньютонах
на кулон (Н/Кл).

Принцип
суперпозиции напряжённостей
электростатических полей. Из
принципа суперпозиции полей следует,
что сила, действующая на пробный заряд
со стороны других зарядов, равна
геометрической сумме всех действующих
на заряд сил по отдельности. Но если это
так, то напряжённости электрических
полей, равные отношениям сил к величине
пробного заряда, складываются подобно
силам.

Таким
образом, для электрических полей
справедлив принцип
суперпозиции в
следующей формулировке: напряжённость
результирующего электрического поля
есть геометрическая (векторная) сумма
напряжённостей полей, создаваемых
отдельными зарядами:

E = E₁ + E₂ + E₃ + …
         (5.3)

Применение
принципа суперпозиции для напряжённостей
позволяет существенно облегчить решение
многих задач электростатики.

1. Электрический
   диполь. Поле диполя.

Электрический
диполь —
система из двух равных по величине, но
противоположных по знаку точечных
электрических зарядов, расположенных
на некотором расстоянии друг от друга.

Расстояние
между зарядами называется плечом
диполя.

Основной
характеристикой диполя является
векторная величина, называемая электрическим
моментом диполя (P).

Электрическое
поле диполя

Диполь
является источником электрического
поля, силовые линии и эквипотенциальные
поверхности которого изображены на
рис. 13.1.

Рис.13.1. Диполь
и его электрическое поле

Центральная
эквипотенциальная поверхность
представляет собой плоскость, проходящую
перпендикулярно плечу диполя через его
середину. Все ее точки имеют нулевой
потенциал (φ =
0). Она делит электрическое поле диполя
на две половины, точки которых имеют
соответственно положительные (φ >
0) и отрицательные (φ <
0) потенциалы.

Абсолютная
величина потенциала зависит от дипольного
момента Р, диэлектрической проницаемости
среды ε и
от положения данной точки поля относительно
диполя. Пусть диполь находится в
непроводящей бесконечной среде и
некоторая точка А удалена от его центра
на расстояние r >> λ (рис.
13.2). Обозначим через α угол
между вектором Р и направлением на эту
точку. Тогда потенциал, создаваемый
диполем в точке А, определяется следующей
формулой:

Рис.13.2. Потенциал
электрического поля, созданного диполем

1. Линейная,
   поверхностная и объемная плотность
   заряда.

объемная
плотность заряда (r),  
поверхностная
плотность заряда (s)
и линейная
плотность заряда (t).

Для
линейного объекта (например, в случае
заряженногостержня) вводят понятие линейной
плотности заряда τ(рис.10.1,
в),

, где l –длина всего линейного объекта  (10.1.1)

где dq –
заряд, приходящий на единицу длины dl.

Если
объект двумерный (например, в случае
заряженного проводника) вводят поверхностную
плотность заряда(рис.10.1,
б)

 ,  (10.1.2)

где dq –
заряд, находящийся на элементе
поверхности ds.

Для
трехмерных объектов вводят объемные
плотности заряда(рис.10.1,а)

 ,  (10.1.3)

где dq –
заряд малого элемента заряженного тела
объемом dV.

1. Электростатическое
   поле наглядно можно изобразить с помощью
   силовых линий (линий напряженности). Силовыми
   линиями называют
   кривые, касательные к которым в каждой
   точке совпадают с вектором напряженности Е.

Силовые
линии являются условным понятием и
реально не существуют. Силовые линии
одиночного отрицательного и одиночного
положительного зарядов — это радиальные
прямые, выходящие от положительного
заряда или идущие к отрицательному
заряду.

Если
густота и направление силовых линий по
всему объему поля сохраняются неизменными,
такое электростатическое поле
считается однородным ( =
const). Например, заряд, распределенный
равномерно по бесконечной плоскости,
создает однородное электрическое поле,
силовые линии которого изображаются
равноотстоящими друг от друга параллельными
прямыми линиями.

Для
того чтобы силовые линии характеризовали
не только направление поля, но и значение
его напряженности, число
линий должно быть численно равно
напряженности поля Е.

Число
силовых линий ,
пронизывающих элементарную
площадку dS, перпендикулярную
к ним, определяет поток
вектора напряженности электростатического
поля:

где  —
проекция вектора Е на
направление нормали n к
площадке dS 

Соответственно
поток вектора Е сквозь
произвольную замкнутую поверхность S

На
разных участках поверхности S не
только величина, но и знак потока могут
меняться:

1)
при 

2)
при 

3)
при  это
означает, что линии скользят вдоль
поверхности, не пересекая ее.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Сосредоточенные и распределенные заряды

Заряды можно распределять по какой-либо области тел, тогда их называют распределенными. Когда же заряд целиком собран в одну точку, его называют точечным. Большинство школьных задач физики связано с точечными зарядами.

Сосредоточенный заряд

Электрический заряд, сосредоточенный в какой-либо точке пространства, называют точечным.

Рис. 1. Точечный заряд

Силу взаимодействия точечных зарядов можно вычислить, используя закон Кулона.

Распределенные заряды

Электрический заряд, так же, можно распределять по объему, площади, или длине. Такие заряды называют распределенными. Чтобы описать эти заряды, используют понятие плотности заряда.

Если заряд распределен по:
— объему, говорят о объемной плотности заряда;
— площади, употребляют поверхностную плотность;
— длине, используют линейную плотность.

Примечание: Плотности отрицательных зарядов записывают со знаком «минус».

Формула линейной плотности заряда

Рис. 2. Заряд распределен по длинному тонкому телу

[ large boxed {tau = frac{q}{L} } ]

( large q left(text{Кл} right) ) – заряд;

( large L left(text{м} right) ) – длина, по которой распределен заряд;

( large tau left(frac{text{Кл}}{text{м}} right) ) – линейная плотность заряда;

Формула поверхностной плотности заряда

Любая поверхность обладает площадью, распределяя по ней заряд, получим поверхностную его плотность.

Этот термин используют, например, для вычисления электрического поля заряженной плоскости, или плоского конденсатора (двух параллельных плоскостей).

Рис. 3. Заряд распределен по плоской поверхности

[ large boxed {sigma = frac{q}{S} } ]

( large S left(text{м}^{2} right) ) – площадь, по которой распределен заряд;

( large sigma left(frac{text{Кл}}{text{м}^{2}} right) ) – поверхностная плотность заряда;

Формула объемной плотности заряда

Функция, описывающая плотность распределения заряда в трехмерном пространстве, входит в одно из уравнений Максвелла.

Рис. 4. Заряд распределен по объему тела

[ large boxed {rho = frac{q}{V} } ]

( large V left(text{м}^{3} right) ) – объем, по которому распределен заряд;

( large rho left(frac{text{Кл}}{text{м}^{3}} right) ) – объемная плотность заряда;

Примечание:

Джеймс Клерк Максвелл (1831 — 1879) – талантливый шотландский математик и физик. Популяризатор науки, экспериментатор и конструктор научных приборов.

Описал электромагнитное взаимодействие с помощью своих уравнений (уравнения Максвелла). Система этих уравнений лежит в основе современной электродинамики.

Предсказал электромагнитные волны, обнаружил, что свет имеет электромагнитную природу и может создавать давление.

Занимался исследованиями в области молекулярной физики и термодинамики. Использовал математический аппарат статистики, получил температурное распределение скоростей молекул.

Проводил исследования в области астрономии и оптики, для планеты Сатурн провел анализ устойчивости колец.

Именно Максвелл заложил трехцветный принцип, который используется в цветной фотографии и телевидении.

Оценка статьи:

Загрузка…

0 Пользователей и 1 Гость просматривают эту тему.

---

---