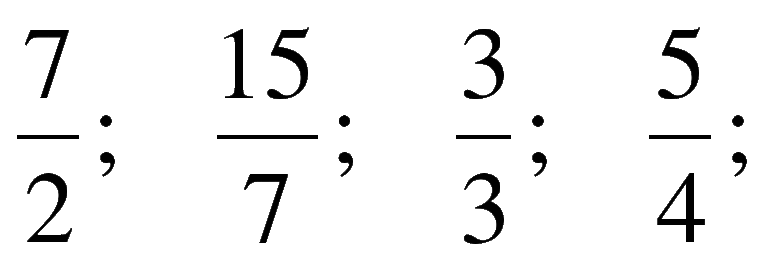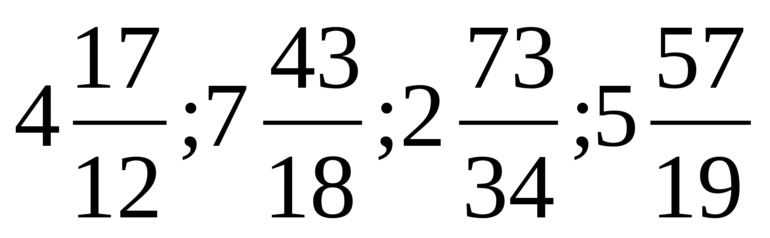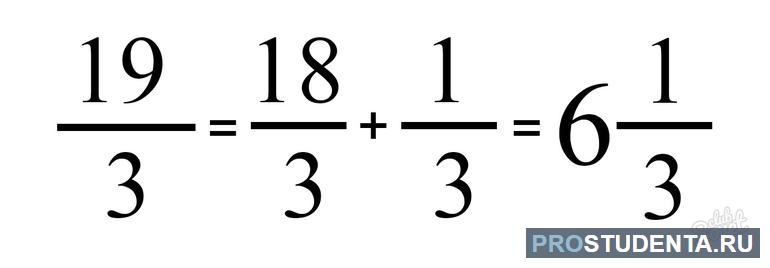Как найти правильную дробь от неправильной дроби

Перейти к содержанию

Общие сведения

Знакомить с дробями начинают в начальной школе. Чтобы ребёнок смог непросто заучить, а понять, что обозначает этот термин, применяют наглядный пример. В качестве его лучше использовать какое-либо круглое тело.

Пусть есть торт. Он один, поэтому представляет собой некое целое. Его можно разрезать на несколько равных частей. Например, 8. Получается, что из чего-то общего возможно выделить части. Количественно каждый кусок будет занимать 1/8 от пирога. Аналогично можно рассмотреть отрезок длиной 10 см. Каждый его 1 см будет составлять от целой длины 1/10.

Из 8 отрезанных кусочков 3 съели. На блюде осталось 5 одинаковых частей. По-другому их называют долями. Это изменение количества в математике произносят, как пять восьмых, то есть из целого после какого-то действия осталась определённая часть.

Записывать такое отношение принято в виде двух чисел, разделённых чертой. Называется она дробной и обозначает деление. Для примера с тортом выражение будет выглядеть как 1/8 и 5/8. Верхняя часть называется числитель и обозначает делимое, а нижняя — знаменатель, то есть делитель. Другими словами, первое число показывает, сколько частей взято, а нижнее, на какое число долей было разделено целое.

Такая дробь считается обыкновенной. Она может быть двух видов:

1. Правильной. Рациональное выражение, в котором числитель количественно меньше знаменателя. Например, 3 / 7; 15 / 32; 1 / 9.
2. Неправильной. Число, в котором значение делимого превышает величину делителя, либо равно ему — 6/4; 453/23; 5/1; 6/6.

Кроме обыкновенной дроби, выделяют ещё 2 типа выражений — десятичные и смешанные. Если первое есть не что иное, как запись рациональной дроби со знаменателем кратным десяти, то второе — число, состоящее из целой части и правильного выражения. Например, 3 8/9.

Понимается эта запись как сумма целого числа и дробного. То есть 3 + 8/9. Если выполнить операцию сложения, в ответе получится дробь, у которой числитель больше знаменателя. Любое смешанное выражение можно преобразовать в неправильное. Это утверждение справедливо и для обратного превращения. Например, запись 47/8 будет тождественной выражению 5 7/8.

Необходимость преобразования

С дробными числами можно выполнять различного вида математические действия: складывать, вычитать, перемножать и делить, возводить в степень и логарифмировать. Но при этом существует негласное правило, согласно которому все операции нужно выполнять только после приведения выражений к одному типу. Конечно, сложить или разделить смешанную дробь на неправильную возможно, но алгоритм действий будет нерациональным, что приведёт к появлению ошибок при вычислении.

Преобразовывать можно любую дробь. Из десятичной легко сделать правильную: 0,5 = 5/10. Из смешанной неправильную — 1 2/5 = 7 / 5. Эти операции выполняются и в обратную сторону. Единственным исключением является задача сделать из неправильной дроби правильную.

Запись, у которой делимое меньше делителя, нельзя представить как число с числителем меньше знаменателя. Но здесь на помощь и приходит смешанное выражение, то есть чтобы из неправильной дроби сделать правильную, нужно из первого числа выделить целую часть. В итоге получится выражение, состоящее из суммы двух чисел: неделимого и правильного.

Следует отметить ещё один важный момент. Перед тем как переводить дробь в неправильную или любую другую, нужно попробовать выполнить ряд упрощений. Это позволит в дальнейшем сложные вычисления заменить простыми. Выполнять упрощение возможно, основываясь на свойствах дробей:

• если числитель и знаменатель выражения умножить на один и тот же одночлен, смысл отношения от этого не изменится;
• делимое и делитель можно разделить на одинаковое число, при этом результат действия останется прежним.

Эти правила называют основным свойством дробного числа или операцией сокращения. Например, 18/6 = 3/1 = 3. Числитель и знаменатель был разделён на 3. Тот же результат будет получен, если делитель и делимое помножить на любое число: 18/6 = 18*2 /6*2 = 36 / 12 = 3. Действительно, правильность утверждения можно доказать простым анализом.

Пусть есть равенство: a/b = z. Нужно доказать, что a*n/b*n = z. Так как черта обозначает деление, используя связь между ним и умножением, исходное выражение можно переписать: a = b*n. Согласно свойствам числовых неравенств, обе части разрешается умножить на число, отличное от нуля. Тогда a*n = (b*z)*n. В соответствии с переместительным законом n и z можно поменять местами: a*n = (b*n)*z. Отсюда: z = a*n/(b*n). Что и нужно было доказать.

Алгоритм превращения

Переводить неправильную дробь в правильную или выполнять обратную операцию просто, если следовать алгоритму. Так как сделать это напрямую нельзя, то фактически получится преобразование в запись, содержащую целую и дробную часть.

Превратить неправильное выражение в смешанное можно по следующему алгоритму:

• упростить дробное отношение;
• выполнить умножение целой части на делитель дробной;
• сложить полученное произведение с числителем;
• сумму записать в делимое преобразованного выражения, а знаменатель оставить исходным.

Это упрощённый способ, быстро позволяющий выполнить перевод числа из одной формы в другую. Математическое равенство, описывающее это правило, будет выглядеть так: n a/b = ((n * b) + a)/b.

Чтобы преобразовать дробь по всем правилам, нужно сделать следующее. Так как смешанное отношение, по сути, является суммой целого и части, понадобится просто выполнить сложение. Для этого первое слагаемое представляют как неправильную дробь. Сделать это можно, разделив целое на единицу. Затем действуют по правилу сложения дробей, то есть находят общий знаменатель, дополнительные множители, выполняют складывание в числителе: n a/b = n/1 + a/b = ((n *b) + a)/b.

Из неправильной формы записи получить обычную дробь можно также через смешанную. Другими словами, представить выражение как сумму натурального числа и правильного отношения. Для этого необходимо выполнить 3 шага:

• разделить делимое на делитель;
• полученный остаток записать в числитель, а в знаменатель поставить исходное число, стоящее в делителе;
• частное приписать к выражению в виде целой доли.

На самом деле выполнять деление числителя на знаменатель часто довольно сложно, поэтому поступают следующим образом. Делимое представляют в виде суммы дробей, но таким образом, чтобы деление одной из них можно было выполнить без остатка, то есть, m / n = (k + c) / n = k / n + c / n. Где целое число k / n, а c / n правильная дробь.

Нужно отметить, что некоторые выражения можно превращать в другую форму, не записывая поочерёдно действия, а выполняя все преобразования в уме. Но на начальном этапе рекомендуется весь процесс расписывать пошагово, пока не будет получен необходимый опыт. А только уже после переходить к переводу в уме.

Примеры решения

Несмотря на то что операция по превращению довольно простая, для её успешного применения необходим опыт, поэтому следует потренироваться не только в простом преобразовании, но и увидеть полезность действий на практике. Вот некоторые примеры, рассчитанные на учащихся четвёртых классов, рекомендуемые к самостоятельному решению:

1. Выполнить перевод смешанной дроби в неправильную форму записи: 4 4/9 = (4*9 + 4)/9 = (36 + 4)/9 = 40/9; 5 7/15 = ((5*15) + 7)/15 = (75 + 7)/15 = 82/15; 2 3/5 = ((2*5)+3)/5 = (10 + 3)/5 = 13/5.
2. Перевести неправильное выражение в правильное. В соответствии с алгоритмом, нужно выделить целую часть. Для этого следует поделить числитель на знаменатель или выполнить ряд преобразований: 12/5 = (10+2)/5 = 10/5 + 2/5 = 2+2/5 = 2 2/5; 11/3 = (9+2)/3 = 3+2/3 = 3 2/3; 19/14 = (14+ 5)/14 = 14/14 + 5/14 = 1 + 5/14 = 1 5/14.
3. Решить уравнение: 1/12 + 3 2/4 + 19/12 — 2. Чтобы решить этот пример, необходимо свести все выражения к одной форме, то есть смешанную запись нужно привести к неправильному типу. 3 2 /24 = 3 + 2/24 = 3/1 + 2/24 = (24*3 + 2)/24 = 74/24. Полученное значение можно упростить, сократив обе части на 2: 74/24 = 37 / 12. Теперь исходное выражение примет вид: 1/12 + 37/12 + 19/12 — 2 = ((1+37+19)/12) — 2 = 57/12 — 2. Осталось преобразовать неправильную дробь в смешанную и рассчитать ответ: 57/12 — 2 = 9/12 + 48/12 — 2 = 4+9/12 — 2 = 2 + 9/12 = 2 9/12.

В интернете существуют сервисы, позволяющие в автоматическом режиме выполнять перевод из одной формы записи в другую. Чтобы воспользоваться услугами таких онлайн-калькуляторов, необязательно знать принцип преобразования. Доступ к услугам не требует регистрации или введения каких-либо персональных данных. Нужно просто иметь гаджет с подключённым интернетом и любой веб-браузер. Всё, что требуется от пользователя — ввести в предлагаемую форму исходную дробь и нажать кнопку «Рассчитать». Через несколько секунд на экран будет выведен ответ.

Кроме расчёта результата, многие такие математические сервисы дают возможность ознакомиться с подробным решением. Это хорошая возможность для учащихся закрепить полученные знания. Ведь можно не только проверить самостоятельное решение, но и понять, как получается тот или иной ответ. Причём на страницах сайтов содержится в кратком виде и теоретический материал с подробным описанием решения примеров.

Чтобы ответить на этот несложный вопрос, можно решить такую же несложную задачку:

Петя и Валя пришли в компанию сверстников. Всех вместе их стало 11. У Вали были с собой яблоки (но не много) и чтобы угостить всех Петя разрезал каждое на четыре части и раздал. Хватило всем и даже пять кусочков осталось.

Сколько яблок раздал Петя и сколько яблок осталось? Сколько их было всего?

Чтобы ответить, можно просто посчитать — 4 кусочка это 1 яблоко + 4 кусочка это еще 1 и три кусочка это три четверти. Вместе получилось 2 яблока и его 3/4.

А можно записать это математически

11 кусочков яблока это в нашем случае 11/4 — получили неправильную дробь, так как числитель больше знаменателя.

Чтобы выделить целую часть (преобразовать неправильную дробь в правильную), нужно числитель разделить на знаменатель, неполное частное (в нашем случае это 2) записать слева, остаток (3)оставить в числителе а знаменатель не трогать.

В результате получим 11/4 = 11:4 = 2 3/4 яблока раздал Петя.

Аналогично 5/4 = 1 1/4 яблок осталось.

(11+5)/4 = 16/4 = 4 яблока принесла Валя

Огромный блок математики посвящен работе с дробями или нецелыми числами. С ними очень часто встречаются и в жизни, поэтому знать, как работать с такими цифрами важно для любого человека. Математика – это наука, в которой ученик начинает с познания простых вещей и действий, а затем переходит к более сложным.

Знание и умение работать с подобными цифрами облегчит ему в дальнейшем работу с логарифмами, рациональными показателями и интегралами. С такими числами можно делать все то же самое, что и с обыкновенными: складывать дроби, делить, вычитать и умножать. Кроме этого, их можно сокращать. Работать с дробями просто, главное – это знать основные правила и методы их вычисления.

Основные понятия

Для того, чтобы понять, что это за значение такое, необходимо представить некий целый предмет. Допустим, что есть торт, который порезали на несколько одинаковых или равных кусков. Каждый кусочек будет называться долей.

[stop]Важно! В случае с дробями, есть некое целое число, которое состоит из равных долей – отдельных меньших чисел.[/stop]

Например, 10 состоит из 5 двоек, каждая двойка – это часть от десяти.

Доли имеют свои названия, в зависимости от их общего количества в целом числе: 10 может состоять из двух пятёрок или пяти двоек, в первом случае она будет называться  (одна вторая), а во втором —  (одна пятая). Следует помнить, что   равняется половине числа,  (одна третья) —  трети, а   (одна четвертая)  – четвертью. Их могут также изображать через черточку: ½, 1/3 или 1/5.

Цифру, написанную сверху горизонтальной линии или слева от наклонной, называют числителем – он показывает сколько долей взяли у целого числа, а цифра под линии или справа от нее – знаменатель, он показывает на сколько всего долей разделили. Например, торт разделили на 10 кусков и сразу отложили два из них для опоздавших гостей. Это будет 2/10 (две десятых), т.е. взяли 2 (числитель) куска от общих 10 (знаменатель).

Какие бывают доли, что такое неправильная дробь, что такое обыкновенная дробь? На эти вопросы легко ответить:

1. Обыкновенная – это такая, в котором числитель и знаменатель являются натуральными числами и записываются так:  или m/n;
2. Правильная дробь – это такая, которая по своей величине меньше единицы, а числитель меньше знаменателя: 5/7 (пять седьмых), 3/5 (три пятых);
3. Неправильная – это такая, которая больше или равна единице, а ее знаменатель меньше или равен числителю: 7/5 (семь пятых) или 19/3 (девятнадцать третьих);
4. Смешанная – это состоящая из целого и доли: 2 (две целых три пятых) или 5 (пять целых шесть двенадцатых) .

Смешанная цифра всегда может трансформироваться в неправильную дробь и наоборот.

Главное свойство гласит: при умножении, а также деления делимого и делителя на одинаковый множитель, в целом величина дроби не изменится. Это свойство делает возможным все операции с дробями.

Это интересно! Изучаем математику в игровой форме: как ребенку быстро выучить таблицу умножения

Как сократить?

Главное правило гласит, что долевую цифру можно сократить — поделить ее числитель и знаменатель на одинаковый делитель (отличный от 0) так, чтобы получилась новая цифра с меньшими параметрами, но равная исходной по величине. Исходя из этого правила можно понять, что дроби бывают сократимые и несократимые.

Пример сокращения дробей: 8/24 сократим, поделив ее параметры на 2. Получим: 8:2=4 и 24:2=12. В результате, исходная цифра превратится в 4/12 . Можно повторить операцию, вновь поделив числа: 4:2=2 и 12:2=6. Получим 2/6. Еще раз повторим операцию: 2:2=1 и 6:2=3. В итоге получится несократимая цифра 1/3, поскольку ее параметры уже нельзя разделить на одинаковый делитель. Любое сократимое число можно привести к несократимому.

[stop]Важно ! Если делимое или делитель представлены выражением  (, вначале каждое из выражений надо умножить на один множитель и дробь превратить в простую, сократив на этот множитель выражение: .[/stop]

Сокращать можно при умножении дробных выражений друг на друга: *. Сами по себе эти числа несократимые, но выполняя операцию умножения, можно сократить их по диагонали: * = =. Сокращать при умножении можно только крест-накрест: числитель первой со знаменателем второй, и наоборот.

Сокращать можно и смешанную цифру, т.е. целую часть и правильную дробь представить в виде неправильной. Для этого следует выполнить некоторые действия:

1. Имея 5, преобразуем его в неправильную дробь. Для этого знаменатель перемножим с его целой частью и приплюсуем к полученной цифре числитель: 5*9+1=46;
2. Сумма станет числителем неправильной доли, а его низ позаимствуем от первоначальной;
3. В итоге получаем: .

Справедливо и обратное действие: из неправильной дроби сделать смешанную. Для этого рассмотрим обратное действие с :

1. Разделим между собой верх и низ: 46:9=5,111111111111111;
2. Целый результат деления станет полной цифрой, а бесконечный остаток – верхом доли;
3. Знаменатель при этом останется неизмененным;
4. Получаем 5.

Таким способом сокращать дроби при любых операциях возможно. Можно сокращать значения ее делимого и делителя при умножении их на одинаковый множитель, и превращая из смешанного числа в долю, и наоборот.

Возможные действия

Все основные виды вычислений доступны при счете долей, как и с целыми цифрами: сложение, вычитание и прочие. Рассмотрим каждое действие по отдельности с примерами:

Сложение и вычитание

Складывать доли можно двумя путями, в зависимости от их делителя. Они бывают одинаковыми и разными. Рассмотрим пример складывания долей с одинаковыми делителями.

Для решения   +  необходимо по отдельности сложить делимое долей, а делитель не трогать: 1+1. Результатом станет цифра  , но поскольку она неправильная, то ее можно преобразовать в смешанную, разделив делимое на делитель: 2:2= 1. Неправильную долю всегда (!) следует приводить к правильной и несокращаемой, т. е. если ее делимое и делитель можно поделить на одинаковый множитель – это следует сделать в обязательно порядке.

В случае сложения долей с различными делителями, их необходимо изначально привести к одинаковому. Например, для решения :  необходимо:

1. Найти наименьшее общее кратное (НОК) для делителей. Здесь у делителей 2 и 3 меньшее кратное – 6.
2. НОК делят вначале на первый делитель, а затем на второй: 6:3=2 и 6:3=2. В данном случае полученные 2 и 3 – это первый и второй дополнительные множители.
3. Каждое слагаемое первоначального примера умножить на найденные множители:  +  =  + .
4. Далее складываем доли: .
5. Преобразуем: 1.

Вычитание осуществляется точно так же: в случае с одинаковыми делителями их не трогаем, а числители последовательно вычитаем:  — =  = . Если же знаменатели различные, то следует поступить, как и при сложении: найти НОК, множители, умножить доли, а затем вычесть уже доли с одинаковыми делителями.

Умножение и деление

При умножении необходимо последовательно перемножить их верх и низ между собой:   =  поскольку есть возможность сокращения на 6. В случае деления все несколько сложнее.

Для деления  следует:

1. Умножить первый множитель на долю, обратную второй, т. е. ;
2. Далее действует правило умножения: =  = , поскольку первоначальный результат можно сократить на 2.

[stop]Важно! Деление всегда можно заменить умножением, но только при соблюдении условия замены делителя на обратное ему число.[/stop]

Перевод смешанного числа в неправильную дробь

Выделение целой части из неправильной дроби


Чтобы правильно решать подобные примеры, следует запомнить главное свойство и правила сокращения. Что касается операций, то важно знать, как правильно складывать и умножать при одинаковых и разных знаменателях, поскольку делятся и вычитаются они по одинаковому принципу.

При решении примеров, связанных с дробными выражениями, часто приходится выполнять упрощения и различные арифметические операции. Зная, как перевести неправильную дробь в правильную, можно узнать, сколько целых частей содержится в числе, тем самым сделать вычисление проще. Такое действие актуально и при умножении или делении смешанных выражений. Метод преобразования довольно прост и не требует заучивания каких-либо сложных формул.

Оглавление:

• Общие сведения
• Способ деления
• Классический метод
• Преобразование на математическом калькуляторе

Общие сведения

При выполнении каких-либо математических расчётов часто приходится иметь дело с нецелыми числами. Одним из видов их записи является дробь. По сути, это отношение двух чисел. Пусть есть круг, разделённый на четыре равные части. Если в нём закрасить одну из них, то выполненное действие можно записать как ¼. То есть из целого выделили одну часть. Если закрасить два круга, то запись примет вид: 2/4. Фактически дробное выражение обозначает операцию обратную умножению, другими словами — деление.

Число, которое располагается слева, называют числителем. Он обозначает, сколько долей от целого была забрано. Поэтому его называют делимым. Число же, стоящее справа, называют знаменателем или делителем. Существует и другая форма записи — десятичная. В этом способе используют запятую, отделяя целую часть от десятичной. Например, ½ — это дробная запись, а 0,5 — десятичная. Причём эти две формы обозначения равнозначные. Так, если выполнить операцию деления, один разделить на два, то получится 0,5.

Существуют несколько типов дробей. По способу записи их разделяют на четыре вида:

1. Правильные — дробные числа, у которых значение числителя меньше чем знаменателя: x/y, где x < y.
2. Неправильные — дроби, в записи которых величина делимого превышает значение делителя: x/y, где x > y.
3. Смешанные — выражения, состоящие из целого и дробного числа. По сути, такая дробь обозначает их сумму: Z (X/Y) = Z + (X/Y).
4. Составные — содержат в записи несколько операций деления: (x/z)/y; (x/y)/(s/z).

Так как дроби — это способ записи чисел, то с ними можно выполнять любые математические действия. Например, складывать, вычитать, умножать, логарифмировать, возводить в степень и так далее. Причём для удобства выполнения операций часто приходится выполнять преобразования по переводу выражений из одного вида в другой.

Существуют специальные алгоритмы и правила, позволяющие как из неправильной дроби сделать правильную, так и преобразовать смешанное выражение.

Выполнение превращений относится к элементарным операциям и в ряде случаев позволяет значительно упростить решение примеров. Так, на первый взгляд, громоздкое выражение после преобразования становится простым и легко решаемым. При этом существуют и так называемые онлайн-калькуляторы. Это сервисы, выполняющие автоматический перевод из одного вида дроби в другой.

Способ деления

Любую неправильную дробь можно представить, как сумму натурального числа и правильного выражения. В отличие от записи, в которой числитель больше знаменателя, неправильное дробное выражение представляет собой число, которое больше либо равно единице. Одним из способов выполнить переход является простое деление. Выполнять его удобно с помощью метода «уголок».

Для этого сначала первую цифру числителя делят на знаменатель. Если результат действия не целое число, то операцию выполняют для двух первых знаков. То число, на которое числитель делится нацело, записывают под делителем. Это и будет значение целой доли. Затем определяют остаток. Вычисляют его по следующему алгоритму:

• умножают целое число на делитель;
• результат операции записывают под значением знаменателя;
• находят результат вычитания результата умножения из делимого.

Таким образом, первое число образует целую часть, второе записывают в числитель, а знаменатель оставляют без изменения. Например, 15/4. Так как 15 разделить на четыре без остатка нельзя, то подбирается ближайшее целое число. Им будет 12, так как 3 * 4 = 12. Если взять четыре, то при умножении получится 16, а это выражение уже превышает значение числителя. Затем из пятнадцати нужно вычесть двенадцать: 15 — 12 = 3. Все нужные вычисления выполнены, остаётся только записать правильно ответ: 3 (¾).

Вот ещё один пример. Преобразовать неправильную дробь: 78/32. По аналогии с предыдущим заданием превращение выполняют в два этапа. На первом находят целую составляющую, а на втором — дробную. Итак, ближайшее цело число к 78 при умножении на 32 будет 64: 32 * 2 = 64. Отсюда следует: 78 — 64 = 14. Значит, результат превращения будет иметь вид: 78/32 = 2 (14/32).

Как видно, ничего сложного в рассмотренном способе нет.

Главное — правильно подобрать число, на которое нацело делится числитель. Чаще всего им являются простые цифры. Но при этом, конечно же, всё зависит от конкретно рассматриваемого примера.

Классический метод

Этот способ считается классическим и обычно, если необходимо превратить неправильную дробь в выражение другого вида, используют его. Суть метода заключается в следующем. Пусть имеется неправильная дробь вида x/y, где икс превышает по значению игрек. Чтобы выполнить преобразование, нужно знать, что при делении числа само на себя получается единица. Например, 234/234 = 1, 6/6 = 1.

Используя это знание, исходную дробь нужно представить в виде суммы единицы и правильного выражения. Для этого в первом слагаемом в числителе пишут число, равняющееся знаменателю, то есть c/n = (n/n) + (?/n). Теперь нужно определить числитель во втором слагаемом.

По правилам сложения дробей с одинаковым знаменателем, при их суммировании последний остаётся без изменения, а над числителями выполняется нужное арифметическое действие. Таким образом, чтобы найти неизвестное, следует записать равенство: c/n = (n/n) + (?/n). Из правила сложения следует, что искомый числитель можно определить, как разницу между c и n. Теперь остаётся переписать исходную дробь как обычную смешанную: 1 ((c — n)/n).

Чтобы стало более понятно можно рассмотреть несколько конкретных примеров. Пусть нужно выполнить преобразование для дроби: 5/3. В соответствии с рассмотренным методом необходимо выражение представить в виде суммы: 3/3 + x/3. Теперь, чтобы найти неизвестное, следует из исходного числителя вычесть делимое, стоящее в первом слагаемом: 5 — 3 = 2. Значит, преобразование можно представить так: 5/3 = (3/3) + (2/3) = 1 + (2/3) = 1 (2/3).

Вот ещё один пример: 7/2 = (2/2) + (7 — 2)/2 = 1 + 5/2 = 1 + (2/2) + (3/2) = 1 + 1 + 2/2 + ½ = 3 (½). Как видно из второго примера, превратить дробь в неправильную не всегда получается в одно действие. В этом примере понадобилось три раза представлять выражение в виде суммы. Поэтому этот способ неудобно использовать при работе с длинными числами из-за большого числа выполняемых операций.

Следует отметить, что можно осуществлять и обратные действия, то есть переводить дробь в неправильную. Для этого целую часть нужно умножить на знаменатель дробной части, а после полученный результат сложить с числителем.

Полученная сумма будет являться числителем преобразованного выражения. Знаменатель же остаётся без изменения.

Например, 5 (4/7) = (5 * 7 + 4)/7 = 39/7.

Преобразование на математическом калькуляторе

Превращать неправильную дробь в правильную несложно. Но бывает так, что приходится иметь дело с большими числами. При этом преобразование может занять довольно длительное время. В таком случае хорошим выходом будет использовать математический калькулятор. Его принцип работы основан на алгоритмах превращения дроби из одного вида в другой. Это программа, занимающаяся расчётами, адаптирована под различные веб-браузеры и выполня ет вычисления в режиме реального времени.

Достоинства математических калькуляторов, умеющих преобразовывать дроби ещё и в том, что, кроме непосредственно результата действий, они выводят на экран подробное описание решения. Это помогает пользователю даже со слабой подготовкой научиться самостоятельно выполнять преобразования. Кроме этого, калькуляторы содержат необходимый минимум теоретической информации и даже примеры простых превращений. При этом они умеют выполнять и другие операции. Например, переводить смешанную дробь в неправильное число или выполнять какое-либо другое математическое действие.

Пользоваться математическими калькуляторами удобно будет как инженерам, которым необходимо быстро и правильно выполнить то или иное преобразование и учащимся.

Для первых это возможность не отвлекаться на расчёты и быть уверенным в правильности вычислений, а для вторых — подспорье в учёбе. Ведь с помощью такого калькулятора можно проверить самостоятельно полученный результат, а в случае необходимости найти и устранить ошибку.

Таким образом, чтобы преобразовать дробь можно применить два способа: классический и деления. Какой из них предпочтительно использовать зависит от конкретного примера. Но если вдруг перевод вызовет трудности, всегда можно воспользоваться программой для автоматического расчёта.