Содержание:
- Матрицы: основные определения и понятия
- Умножение матрицы на число
- Сложение и вычитание матриц
- Умножение матриц
- Транспонирование матрицы
- Минор и алгебраическое дополнение
- Вычисление определителя
- Нахождение обратной матрицы
- Нахождение ранга матрицы
Матрицы широко применяются в математике для
компактной записи СЛАУ или систем дифференциальных уравнений. Тогда количество
строк матрицы соответствует количеству уравнений системы, а количество столбцов равно количеству неизвестных. Матричный
аппарат позволяет свести решение громоздких СЛАУ к компактным
операциям над матрицами.
На практике, они позволяют не делать лишних операций и сократить время выполнения задач.
Поэтому, будущим специалистам очень важно понять теорию матриц и научиться решать задачи с ними.
Перед изучением примеров решения задач советуем изучить теоретический материал по матрицам, прочитать
все определения и свойства. Список тем находится в правом меню.
Примеры по темам:
- Матрицы: основные определения и понятия
- Умножение матрицы на число
- Сложение и вычитание матриц
- Умножение матриц
- Транспонирование матрицы
- Минор и алгебраическое дополнение
- Вычисление определителя
- Нахождение обратной матрицы
- Нахождение ранга матрицы
Матрицы: основные определения и понятия
Теоретический материал по теме — основные определения и понятия матриц.
Пример
Задание. Чему равен элемент $ a_{23} $
матрицы $ A=left( begin{array}{rrr}{1} & {4} & {0} \ {-1} & {3} & {7}end{array}right) $ ?
Решение. Находим элемент, который стоит на пересечении второй строки и третьего столбца:
Таким образом, $a_{23}=7$.
Ответ. $a_{23}=7$
Умножение матрицы на число
Теоретический материал по теме — умножение матрицы на число.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Пусть $A=left( begin{array}{r}{3} \ {-1}end{array}right)$ .
Найти матрицу 2$A$.
Решение. $2 A=2 cdot left( begin{array}{r}{3} \ {-1}end{array}right)=left( begin{array}{c}{2 cdot 3} \ {2 cdot(-1)}end{array}right)=left( begin{array}{r}{6} \ {-2}end{array}right)$
Ответ. $2 A=left( begin{array}{r}{6} \ {-2}end{array}right)$
Сложение и вычитание матриц
Теоретический материал по теме — сложение и вычитание матриц.
Пример
Задание. Найти $A+B$, если
$A=left( begin{array}{rrr}{1} & {-2} & {4} \ {2} & {0} & {-1}end{array}right)$,
$B=left( begin{array}{lll}{5} & {2} & {3} \ {4} & {6} & {2}end{array}right)$
Решение. $C=A+B=left( begin{array}{rrr}{1} & {-2} & {4} \ {2} & {0} & {-1}end{array}right)+left( begin{array}{lll}{5} & {2} & {3} \ {4} & {6} & {2}end{array}right)=$
$=left( begin{array}{rrr}{1+5} & {-2+2} & {4+3} \ {2+4} & {0+6} & {-1+2}end{array}right)=left( begin{array}{lll}{6} & {0} & {7} \ {6} & {6} & {1}end{array}right)$
Ответ. $C=left( begin{array}{lll}{6} & {0} & {7} \ {6} & {6} & {1}end{array}right)$
Пример
Задание. Найти матрицу $C=A-3 B$,
если $A=left( begin{array}{rr}{1} & {2} \ {2} & {-1} \ {3} & {0}end{array}right), B=left( begin{array}{rr}{-1} & {1} \ {1} & {2} \ {0} & {0}end{array}right)$
Решение. $C=A-3 B=left( begin{array}{rr}{1} & {2} \ {2} & {-1} \ {3} & {0}end{array}right)-3 cdot left( begin{array}{rr}{-1} & {1} \ {1} & {2} \ {0} & {0}end{array}right)=$
$left( begin{array}{rr}{1} & {2} \ {2} & {-1} \ {3} & {0}end{array}right)-left( begin{array}{rr}{-3} & {3} \ {3} & {6} \ {0} & {0}end{array}right)=left( begin{array}{cc}{1-(-3)} & {2-3} \ {2-3} & {-1-6} \ {3-0} & {0-0}end{array}right)=left( begin{array}{rr}{4} & {-1} \ {-1} & {-7} \ {3} & {0}end{array}right)$
Ответ. $C=left( begin{array}{rr}{4} & {-1} \ {-1} & {-7} \ {3} & {0}end{array}right)$
Умножение матриц
Теоретический материал по теме — умножение матриц.
Пример
Задание. Вычислить $A B$ и $B A$,
если $A=left( begin{array}{rr}{1} & {-1} \ {2} & {0} \ {3} & {0}end{array}right), B=left( begin{array}{ll}{1} & {1} \ {2} & {0}end{array}right)$
Решение. Так как $A=A_{3 times 2}$ , а
$B=B_{2 times 2}$ , то произведение возможно и результатом операции умножения будет матрица
$C=C_{3 times 2}$ , а это матрица вида $C=left( begin{array}{cc}{c_{11}} & {c_{12}} \ {c_{21}} & {c_{22}} \ {c_{31}} & {c_{32}}end{array}right)$ .
Вычисли элементы матрицы $C$ :
$ c_{11}=a_{11} cdot b_{11}+a_{12} cdot b_{21}=1 cdot 1+(-1) cdot 2=-1 $
$ c_{12}=a_{11} cdot b_{12}+a_{12} cdot b_{22}=1 cdot 1+(-1) cdot 0=1 $
$ c_{21}=a_{21} cdot b_{11}+a_{22} cdot b_{21}=2 cdot 1+0 cdot 2=2 $
$ c_{22}=a_{21} cdot b_{12}+a_{22} cdot b_{22}=2 cdot 1+0 cdot 0=2 $
$ c_{31}=a_{31} cdot b_{11}+a_{32} cdot b_{21}=3 cdot 1+0 cdot 2=3 $
$ c_{31}=a_{31} cdot b_{12}+a_{32} cdot b_{22}=3 cdot 1+0 cdot 0=3 $
Итак, $C=A B=left( begin{array}{rl}{-1} & {1} \ {2} & {2} \ {3} & {3}end{array}right)$ .
Выполним произведения в более компактном виде:
$=left( begin{array}{rrr}{1 cdot 1+(-1) cdot 2} & {1 cdot 1+(-1) cdot 0} \ {2 cdot 1+0 cdot 2} & {2 cdot 1+0 cdot 0} \ {3 cdot 1+0 cdot 2} & {3 cdot 1+0 cdot 0}end{array}right)=left( begin{array}{rr}{-1} & {1} \ {2} & {2} \ {3} & {3}end{array}right)$
Найдем теперь произведение $D=B A=B_{2 times 2} cdot A_{3 times 2}$. Так как
количество столбцов матрицы $B$ (первый сомножитель) не совпадает с
количеством строк матрицы $A$ (второй сомножитель), то данное произведение
неопределенно. Умножить матрицы в данном порядке невозможно.
Ответ. $A B=left( begin{array}{rr}{-1} & {1} \ {2} & {2} \ {3} & {3}end{array}right)$ .
В обратном порядке умножить данные матрицы невозможно, так как количество столбцов матрицы
$B$ не совпадает с
количеством строк матрицы $A$ .
Транспонирование матрицы
Теоретический материал по теме — транспонирование матрицы.
Пример
Задание. Найти матрицу $A^{T}$, если
$A=left( begin{array}{rl}{1} & {0} \ {-2} & {3}end{array}right)$
Решение. $A^{T}=left( begin{array}{rr}{1} & {0} \ {-2} & {3}end{array}right)^{T}=left( begin{array}{rr}{1} & {-2} \ {0} & {3}end{array}right)$
Ответ. $A^{T}=left( begin{array}{rr}{1} & {-2} \ {0} & {3}end{array}right)$
Минор и алгебраическое дополнение
Теоретический материал по теме — минор и алгебраическое дополнение.
Пример
Задание. Найти минор
$M_{23}$ к элементу
$a_{23}$ определителя
$left| begin{array}{rrr}{1} & {2} & {-1} \ {1} & {0} & {3} \ {7} & {8} & {4}end{array}right|$ .
Решение. Вычеркиваем в заданном определителе вторую строку и третий столбец:
тогда $M_{23}=left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|$
Ответ. $M_{23}=left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|$
Пример
Задание. Найти алгебраическое дополнение
$A_{23}$ к элементу
$a_{23}$ определителя
$left| begin{array}{rrr}{1} & {2} & {-1} \ {1} & {0} & {3} \ {7} & {8} & {4}end{array}right|$ .
Решение. $A_{23}=(-1)^{2+3} cdot M_{23}=(-1)^{5} cdot left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|=-left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|$
Ответ. $A_{23}=-left| begin{array}{ll}{1} & {2} \ {7} & {8}end{array}right|$
Вычисление определителя
Теоретический материал по теме — методы вычисления определителей.
Пример
Задание. Вычислить определитель второго порядка
$left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|$
Решение. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=11 cdot 5-(-2) cdot 7=55+14=69$
Ответ. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=69$
Пример
Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ методом треугольников.
Решение. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=3 cdot 1 cdot(-2)+4 cdot(-2) cdot(-1)+$
$+3 cdot 3 cdot 1-(-1) cdot 1 cdot 1-3 cdot(-2) cdot 3-4 cdot 3 cdot(-2)=54$
Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$
Пример
Задание. Вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$
Решение. Выполним следующие преобразования над строками определителя: из второй строки отнимем четыре
первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель,
равный данному.
$left| begin{array}{ccc}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=left| begin{array}{cccc}{1} & {2} & {3} \ {4-4 cdot 1} & {5-4 cdot 2} & {6-4 cdot 3} \ {7-7 cdot 1} & {8-7 cdot 2} & {9-7 cdot 3}end{array}right|=$
$=left| begin{array}{rrr}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {-6} & {-12}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {2 cdot(-3)} & {2 cdot(-6)}end{array}right|=0$
Определитель равен нулю, так как вторая и третья строки являются пропорциональными.
Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$
Пример
Задание. Вычислить определитель
$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|$ приведением его к треугольному виду.
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования
будет выполнять проще, если элемент $a_{11}$ будет
равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя,
приведет к тому, что он сменит знак на противоположный:
$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {2} & {-5} & {3} & {0} \ {-1} & {4} & {2} & {-3}end{array}right|$
Далее получим нули в первом столбце, кроме элемента $a_{11}$ ,
для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:
$Delta=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {2} & {5} & {-1}end{array}right|$
Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если
диагональный элемент будет равен $pm 1$ , то
вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на
противоположный знак определителя):
$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {3} & {-1} & {2} \ {0} & {2} & {5} & {-1}end{array}right|$
Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом:
к третьей строке прибавляем три вторых, а к четвертой — две вторых строки, получаем:
$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {-10} & {-10} \ {0} & {0} & {-1} & {-9}end{array}right|$
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под
главной диагональю, а для этого к последней строке прибавляем третью:
$Delta=-10 left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {-1} & {-9}end{array}right|=$
$=-10 cdot left| begin{array}{cccc}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {0} & {-8}end{array}right|=(-10) cdot 1 cdot(-1) cdot 1 cdot(-8)=-80$
Ответ. $Delta=-80$
Нахождение обратной матрицы
Теоретический материал по теме — нахождение обратной матрицы.
Пример
Задание. Для матрицы $A=left( begin{array}{ll}{7} & {4} \ {5} & {3}end{array}right)$
найти обратную методом присоединенной матрицы.
Решение. Приписываем к заданной матрице
$A$ справа единичную матрицу второго порядка:
$Aleft|E=left( begin{array}{ll|ll}{7} & {4} & {1} & {0} \ {5} & {3} & {0} & {1}end{array}right)right.$
От первой строки отнимаем вторую (для этого от элемента первой строки отнимаем соответствующий элемент второй строки):
$Aleft|E sim left( begin{array}{rr|rr}{2} & {1} & {1} & {-1} \ {5} & {3} & {0} & {1}end{array}right)right.$
От второй строки отнимаем две первых:
$Aleft|E sim left( begin{array}{rr|rr}{2} & {1} & {1} & {-1} \ {1} & {1} & {-2} & {3}end{array}right)right.$
Первую и вторую строки меняем местами:
$Aleft|E sim left( begin{array}{rr|r|rr}{1} & {1} & {-2} & {3} \ {2} & {1} & {1} & {-1}end{array}right)right.$
От второй строки отнимаем две первых:
$Aleft|E sim left( begin{array}{rr|rr}{1} & {1} & {-2} & {3} \ {0} & {-1} & {5} & {-7}end{array}right)right.$
Вторую строку умножаем на (-1), а к первой строке прибавляем вторую:
$Aleft|E sim left( begin{array}{rr|rr}{1} & {0} & {3} & {-4} \ {0} & {1} & {-5} & {7}end{array}right)right.$
Итак, слева получили единичную матрицу, а значит матрица, стоящая в
правой части (справа от вертикальной черты), является обратной к исходной.
Таким образом, получаем, что $A^{-1}=left( begin{array}{rr}{3} & {-4} \ {-5} & {7}end{array}right)$
Ответ. $A^{-1}=left( begin{array}{rr}{3} & {-4} \ {-5} & {7}end{array}right)$
Пример
Задание. Найти обратную матрицу для $A=left( begin{array}{ll}{1} & {1} \ {1} & {2}end{array}right)$
Решение. Шаг 1. Находим определитель: $Delta=left| begin{array}{ll}{1} & {1} \ {1} & {2}end{array}right|=2-1=1 neq 0$
Шаг 2. $A^{prime}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right)$
Шаг 3. $A^{-1}=frac{1}{Delta} cdot A^{prime}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right)$
Ответ. $A^{-1}=left( begin{array}{rr}{2} & {-1} \ {-1} & {1}end{array}right)$
Пример
Задание. Найти обратную матрицу к матрице $A=left( begin{array}{rrr}{1} & {0} & {2} \ {2} & {-1} & {1} \ {1} & {3} & {-1}end{array}right)$
Решение. Вычисляем определитель матрицы:
$Delta=left| begin{array}{rrr}{1} & {0} & {2} \ {2} & {-1} & {1} \ {1} & {3} & {-1}end{array}right|=1 cdot(-1) cdot(-1)+2 cdot 3 cdot 2+0 cdot 1 cdot 1-$
$-1 cdot(-1) cdot 2-3 cdot 1 cdot 1-2 cdot 0 cdot(-1)=1+12+0+2-3+0=12 neq 0$
Так как определитель не равен нулю, то матрица имеет обратную.
Обратная матрица $A^{-1}$ к матрице
$A$ находится по формуле:
$A^{-1}=frac{1}{Delta} cdot widetilde{A}^{T}$
Найдем союзную матрицу $check{A}$ , для этого вычислим алгебраические
дополнения к элементам матрицы $A$ :
$A_{11}=(-1)^{1+1} left| begin{array}{rr}{-1} & {1} \ {3} & {-1}end{array}right|=(-1) cdot(-1)-3 cdot 1=1-3=-2$
$A_{12}=(-1)^{1+2} left| begin{array}{rr}{2} & {1} \ {1} & {-1}end{array}right|=-[2 cdot(-1)-1 cdot 1]=-(-2-1)=3$
$A_{13}=(-1)^{1+3} left| begin{array}{rr}{2} & {-1} \ {1} & {3}end{array}right|=2 cdot 3-1 cdot(-1)=6+1=7$
$A_{21}=(-1)^{2+1} left| begin{array}{rr}{0} & {2} \ {3} & {-1}end{array}right|=-[0 cdot(-1)-3 cdot 2]=-(0-6)=6$
$A_{22}=(-1)^{2+2} left| begin{array}{rr}{1} & {2} \ {1} & {-1}end{array}right|=1 cdot(-1)-1 cdot 2=-1-2=-3$
$A_{23}=(-1)^{2+3} left| begin{array}{cc}{1} & {0} \ {1} & {3}end{array}right|=-[1 cdot 3-1 cdot 0]=-(3-0)=-3$
$A_{31}=(-1)^{3+1} left| begin{array}{rr}{0} & {2} \ {-1} & {1}end{array}right|=0 cdot 1-(-1) cdot 2=0+2=2$
$A_{32}=(-1)^{3+2} left| begin{array}{cc}{1} & {2} \ {2} & {1}end{array}right|=-[1 cdot 1-2 cdot 2]=-(1-4)=3$
$A_{33}=(-1)^{3+3} left| begin{array}{rr}{1} & {0} \ {2} & {-1}end{array}right|=1 cdot(-1)-2 cdot 0=-1-0=-1$
Таким образом, $tilde{A}=left( begin{array}{rrr}{-2} & {3} & {7} \ {6} & {-3} & {-3} \ {2} & {3} & {-1}end{array}right)$
Транспонируем эту матрицу (т.е. строки матрицы делаем столбцами с тем же номером):
$widetilde{A}^{T}=left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right)$
Итак, $A^{-1}=frac{1}{12} left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right)$
Ответ. $A^{-1}=frac{1}{12} left( begin{array}{rrr}{-2} & {6} & {2} \ {3} & {-3} & {3} \ {7} & {-3} & {-1}end{array}right)$
Нахождение ранга матрицы
Теоретический материал по теме — нахождение ранга матрицы.
Пример
Задание. Найти ранг матрицы $A=left( begin{array}{cccc}{0} & {4} & {10} & {1} \ {4} & {8} & {18} & {7} \ {10} & {18} & {40} & {17} \ {1} & {7} & {17} & {3}end{array}right)$
Решение. С помощью элементарных преобразований над ее строками приведем матрицу $A$ к
ступенчатому виду. Для этого вначале от третьей строки отнимем две вторых:
$A sim left( begin{array}{cccc}{0} & {4} & {10} & {1} \ {4} & {8} & {18} & {7} \ {2} & {2} & {4} & {3} \ {1} & {7} & {17} & {3}end{array}right)$
От второй строки отнимаем четвертую строку, умноженную на 4; от третьей — две четвертых:
$A sim left( begin{array}{rrrr}{0} & {4} & {10} & {1} \ {0} & {-20} & {-50} & {-5} \ {0} & {-12} & {-30} & {-3} \ {1} & {7} & {17} & {3}end{array}right)$
Ко второй строке прибавим пять первых, к третьей — три третьих:
$A sim left( begin{array}{cccc}{0} & {4} & {10} & {1} \ {0} & {0} & {0} & {0} \ {0} & {0} & {0} & {0} \ {1} & {7} & {17} & {3}end{array}right)$
Меняем местами первую и вторую строчки:
$A sim left( begin{array}{cccc}{0} & {0} & {0} & {0} \ {0} & {4} & {10} & {1} \ {0} & {0} & {0} & {0} \ {1} & {7} & {17} & {3}end{array}right)$
Далее четвертую и первую строки:
$A sim left( begin{array}{cccc}{1} & {7} & {17} & {3} \ {0} & {4} & {10} & {1} \ {0} & {0} & {0} & {0} \ {0} & {0} & {0} & {0}end{array}right) Rightarrow r a n g A=2$
Ответ. $operatorname{rang} A=2$
Пример
Задание. Найти ранг матрицы $A=left( begin{array}{rrrr}{1} & {2} & {-1} & {-2} \ {2} & {4} & {3} & {0} \ {-1} & {-2} & {6} & {6}end{array}right)$ ,
используя метод окаймления миноров.
Решение. Минорами минимального порядка являются миноры первого порядка, которые равны элементам
матрицы $A$ . Рассмотрим, например, минор
$M_{1}=1 neq 0$ . расположенный в первой строке и первом
столбце. Окаймляем его с помощью второй строки и второго столбца, получаем минор
$M_{2}^{1}=left| begin{array}{ll}{1} & {2} \ {2} & {4}end{array}right|=0$ ; рассмотрим еще один минор второго
порядка, для этого минор $M_{1}$ окаймляем при
помощи второй строки и третьего столбца, тогда имеем минор $M_{2}^{2}=left| begin{array}{rr}{1} & {-1} \ {2} & {3}end{array}right|=5 neq 0$ ,
то есть ранг матрицы не меньше двух. Далее рассматриваем миноры третьего порядка, которые окаймляют минор
$M_{2}^{2}$ . Таких миноров два: комбинация
третьей строки со вторым столбцом или с четвертым столбцом. Вычисляем эти миноры:
$M_{3}^{1}=left| begin{array}{rrr}{1} & {2} & {-1} \ {2} & {4} & {3} \ {-1} & {-2} & {6}end{array}right|=0$
так как содержит два пропорциональных столбца (первый и второй); второй минор
$M_{3}^{2}=left| begin{array}{rrr}{1} & {-1} & {-2} \ {2} & {3} & {0} \ {-1} & {6} & {6}end{array}right|$
преобразуем следующим образом: к первой строке прибавим третью, а ко второй две третьих:
$M_{3}^{2}=left| begin{array}{rrr}{0} & {5} & {4} \ {0} & {15} & {12} \ {-1} & {6} & {6}end{array}right|=0$
И так как первая и вторая строки пропорциональны, то минор равен нулю.
Таким образом, все окаймляющие миноры третьего порядка равны нулю. А, значит, ранг матрицы $A$
равен двум: $operatorname{rang} A=2$
Ответ. $operatorname{rang} A=2$
Читать первую тему — основные определения и понятия матриц,
раздела матрицы.
Если вы перешли к изучению данной темы, то уже знаете, что такое матрица и определитель матрицы, умеете находить определители второго, третьего и высших порядков, а также обратные матрицы. Если какая-то из этих тем вам незнакома, то следует изучить сначала ее.
Приступим к рассмотрению понятия матричного уравнения.
Матричные уравнения
Матричные уравнения устроены практически также как и числовые, только вместо чисел в них содержатся числовые матрицы. Как правило, типовое матричное уравнение состоит из нескольких матриц и некоторой неизвестной матрицы XX, которую и требуется найти.
Рассмотрим примеры наиболее простых матричных уравнений и их решения.
Пример 1
Решить матричное уравнение
(1234)+x=(1101)begin{pmatrix}1&2\3&4end{pmatrix}+x=begin{pmatrix}1&1\0&1end{pmatrix}.
Перенесем матрицу из левой части в правую:
x=(1101)−(1234)x=begin{pmatrix}1&1\0&1end{pmatrix}-begin{pmatrix}1&2\3&4end{pmatrix}.
Найдем разность матриц в правой части уравнения:
x=(1−11−20−31−4)x=begin{pmatrix}1-1&1-2\0-3&1-4end{pmatrix}.
Значит, x=(0−1−3−3)x=begin{pmatrix}0&-1\-3&-3end{pmatrix}.
Можно провести проверку:
(1234)+(0−1−3−3)=(1+02−13−34−3)=(1101)begin{pmatrix}1&2\3&4end{pmatrix}+begin{pmatrix}0&-1\-3&-3end{pmatrix}=begin{pmatrix}1+0&2-1\3-3&4-3end{pmatrix}=begin{pmatrix}1&1\0&1end{pmatrix},
(1101)=(1101)begin{pmatrix}1&1\0&1end{pmatrix}=begin{pmatrix}1&1\0&1end{pmatrix}.
Пример 2
Решить матричное уравнение (58−469−5)−12x=(341212)begin{pmatrix}5&8&-4\6&9&-5end{pmatrix}-frac{1}{2}x=begin{pmatrix}3&4&1\2&1&2end{pmatrix}.
Перенесем матрицу из левой части в правую:
−12x=(341212)−(58−469−5)-frac{1}{2}x=begin{pmatrix}3&4&1\2&1&2end{pmatrix}-begin{pmatrix}5&8&-4\6&9&-5end{pmatrix}.
Найдем разность матриц в правой части уравнения:
−12x=(3−54−81−(−4)2−61−92−(−5))-frac{1}{2}x=begin{pmatrix}3-5&4-8&1-(-4)\2-6&1-9&2-(-5)end{pmatrix},
−12x=(−2−45−4−87)-frac{1}{2}x=begin{pmatrix}-2&-4&5\-4&-8&7end{pmatrix}.
Умножим обе части уравнения на -2:
x=−2(−2−45−4−87)x=-2begin{pmatrix}-2&-4&5\-4&-8&7end{pmatrix},
x=(48−10816−14)x=begin{pmatrix}4&8&-10\8&16&-14end{pmatrix}.
Можно провести проверку:
(58−469−5)−12(48−10816−14)=(58−469−5)−(24−548−7)=(341212)begin{pmatrix}5&8&-4\6&9&-5end{pmatrix}-frac{1}{2}begin{pmatrix}4&8&-10\8&16&-14end{pmatrix}=begin{pmatrix}5&8&-4\6&9&-5end{pmatrix}-begin{pmatrix}2&4&-5\4&8&-7end{pmatrix}=begin{pmatrix}3&4&1\2&1&2end{pmatrix},
(341212)=(341212)begin{pmatrix}3&4&1\2&1&2end{pmatrix}=begin{pmatrix}3&4&1\2&1&2end{pmatrix}.
Такие уравнения элементарны, поэтому они довольно редко встречаются на практике.
Простейшие матричные уравнения
Обычно решение матричных уравнений сводится к одному из двух видов:
- A⋅X=BAcdot X=B;
- X⋅A=BXcdot A=B.
Рассмотрим, как решается каждое из этих уравнений.
| Уравнение вида A⋅X=BAcdot X=B | Уравнение вида X⋅A=BXcdot A=B |
|---|---|
| Для того чтобы разрешить данное уравнение относительно XX умножим обе его части на A−1A^{-1} слева: A−1⋅A⋅X=A−1⋅BA^{-1}cdot Acdot X=A^{-1}cdot B.
Так как A−1⋅A=EA^{-1}cdot A=E, то E⋅X=A−1⋅BEcdot X=A^{-1}cdot B, EE — единичная матрица. Так как E⋅X=XEcdot X=X, то X=A−1⋅BX=A^{-1}cdot B. |
Для того чтобы разрешить данное уравнение относительно XX умножим обе его части на A−1A^{-1} справа: X⋅A⋅A−1=B⋅A−1Xcdot Acdot A^{-1}=Bcdot A^{-1}.
Так как A⋅A−1=EAcdot A^{-1}=E, то X⋅E=B⋅A−1Xcdot E=Bcdot A^{-1}, EE — единичная матрица. Так как X⋅E=XXcdot E=X, то X=B⋅A−1X=Bcdot A^{-1}. |
Рассмотрим примеры решения простейших матричных уравнений вида A⋅X=BAcdot X=B.
Пример 1
Решить матричное уравнение (3728)⋅X=(4862)begin{pmatrix}3&7\2&8end{pmatrix}cdot X=begin{pmatrix}4&8\6&2end{pmatrix}. Выполнить проверку.
Уравнение имеет вид A⋅X=BAcdot X=B, где A=(3728)A=begin{pmatrix}3&7\2&8end{pmatrix}, B=(4862)B=begin{pmatrix}4&8\6&2end{pmatrix}.
Умножим обе части уравнения на A−1A^{-1} слева:
A−1⋅A⋅X=A−1⋅BA^{-1}cdot Acdot X=A^{-1}cdot B,
E⋅X=A−1⋅BEcdot X=A^{-1}cdot B, EE — единичная матрица,
X=A−1⋅BX=A^{-1}cdot B.
Найдем матрицу A−1A^{-1}.
∣3728∣=3⋅8−2⋅7=24−14=10≠0begin{vmatrix}3&7\2&8end{vmatrix}=3cdot8-2cdot7=24-14=10neq 0, значит для матрицы AA существует обратная матрица. Найдем ее методом элементарных преобразований.
Составим расширенную матрицу:
(3728∣1001)begin{pmatrix}left.begin{matrix}3&7\2&8end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}.
Вычтем из строки №1 строку №2:
(3728∣1001)∼(1−128∣1−101)begin{pmatrix}left.begin{matrix}3&7\2&8end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&-1\2&8end{matrix}right|begin{matrix}1&-1\0&1end{matrix}end{pmatrix}.
Прибавим к строке №2 строку №1, умноженную на -2:
(1−128∣1−101)∼(1−1010∣1−1−23)begin{pmatrix}left.begin{matrix}1&-1\2&8end{matrix}right|begin{matrix}1&-1\0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&-1\0&10end{matrix}right|begin{matrix}1&-1\-2&3end{matrix}end{pmatrix}.
Умножим строку №1 на 10:
(1−1010∣1−1−23)∼(10−10010∣10−10−23)begin{pmatrix}left.begin{matrix}1&-1\0&10end{matrix}right|begin{matrix}1&-1\-2&3end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}10&-10\0&10end{matrix}right|begin{matrix}10&-10\-2&3end{matrix}end{pmatrix}.
Прибавим к строке №1 строку №2, умноженную на 1:
(10−10010∣10−10−23)∼(100010∣8−7−23)begin{pmatrix}left.begin{matrix}10&-10\0&10end{matrix}right|begin{matrix}10&-10\-2&3end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}10&0\0&10end{matrix}right|begin{matrix}8&-7\-2&3end{matrix}end{pmatrix}.
Умножим строку №1 и №2 на 110frac{1}{10}:
(100010∣8−7−23)∼(1001∣810−710−210310)begin{pmatrix}left.begin{matrix}10&0\0&10end{matrix}right|begin{matrix}8&-7\-2&3end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0\0&1end{matrix}right|begin{matrix}frac{8}{10}&-frac{7}{10}\-frac{2}{10}&frac{3}{10}end{matrix}end{pmatrix}.
Значит, A−1=(810−710−210310)=110(8−7−23)A^{-1}=begin{pmatrix}frac{8}{10}&-frac{7}{10}\-frac{2}{10}&frac{3}{10}end{pmatrix}=frac{1}{10}begin{pmatrix}8&-7\-2&3end{pmatrix}.
A−1⋅B=110(8−7−23)⋅(4862)=110(−105010−10)=(−151−1)=XA^{-1}cdot B=frac{1}{10}begin{pmatrix}8&-7\-2&3end{pmatrix}cdotbegin{pmatrix}4&8\6&2end{pmatrix}=frac{1}{10}begin{pmatrix}-10&50\10&-10end{pmatrix}=begin{pmatrix}-1&5\1&-1end{pmatrix}=X.
Проверка:
(3728)⋅(−151−1)=(4862)begin{pmatrix}3&7\2&8end{pmatrix}cdotbegin{pmatrix}-1&5\1&-1end{pmatrix}=begin{pmatrix}4&8\6&2end{pmatrix}. — Верно.
Ответ: X=(−151−1)X=begin{pmatrix}-1&5\1&-1end{pmatrix}.
Пример 2
Решить матричное уравнение (0230)⋅X=(243−6)begin{pmatrix}0&2\3&0end{pmatrix}cdot X=begin{pmatrix}2&4\3&-6end{pmatrix}. Выполнить проверку.
Уравнение имеет вид A⋅X=BAcdot X=B, где A=(0230)A=begin{pmatrix}0&2\3&0end{pmatrix}, B=(243−6)B=begin{pmatrix}2&4\3&-6end{pmatrix}.
Умножим обе части уравнения на A−1A^{-1} слева:
A−1⋅A⋅X=A−1⋅BA^{-1}cdot Acdot X=A^{-1}cdot B,
E⋅X=A−1⋅BEcdot X=A^{-1}cdot B, EE — единичная матрица,
X=A−1⋅BX=A^{-1}cdot B.
Найдем матрицу A−1A^{-1}.
∣0230∣=0⋅0−3⋅2=0−6=−6≠0begin{vmatrix}0&2\3&0end{vmatrix}=0cdot0-3cdot2=0-6=-6neq 0, значит для матрицы AA существует обратная матрица. Найдем ее методом элементарных преобразований.
Составим расширенную матрицу:
(0230∣1001)begin{pmatrix}left.begin{matrix}0&2\3&0end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}.
Поменяем местами строки №1 и №2:
(0230∣1001)∼(3002∣0110)begin{pmatrix}left.begin{matrix}0&2\3&0end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}3&0\0&2end{matrix}right|begin{matrix}0&1\1&0end{matrix}end{pmatrix}.
Умножим строку №1 на 13frac{1}{3}, а строку №2 на 12frac{1}{2}:
(3002∣0110)∼(1001∣013120)begin{pmatrix}left.begin{matrix}3&0\0&2end{matrix}right|begin{matrix}0&1\1&0end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0\0&1end{matrix}right|begin{matrix}0&frac{1}{3}\frac{1}{2}&0end{matrix}end{pmatrix}.
Значит, A−1=(013120)=16(0230)A^{-1}=begin{pmatrix}0&frac{1}{3}\frac{1}{2}&0end{pmatrix}=frac{1}{6}begin{pmatrix}0&2\3&0end{pmatrix}.
A−1⋅B=16(0230)⋅(243−6)=16(6−12612)=(1−212)=XA^{-1}cdot B=frac{1}{6}begin{pmatrix}0&2\3&0end{pmatrix}cdot begin{pmatrix}2&4\3&-6end{pmatrix}=frac{1}{6}begin{pmatrix}6&-12\6&12end{pmatrix}=begin{pmatrix}1&-2\1&2end{pmatrix}=X.
Проверка:
(0230)⋅(1−212)=(243−6)begin{pmatrix}0&2\3&0end{pmatrix}cdotbegin{pmatrix}1&-2\1&2end{pmatrix}=begin{pmatrix}2&4\3&-6end{pmatrix}. — Верно.
Ответ: X=(1−212)X=begin{pmatrix}1&-2\1&2end{pmatrix}.
Рассмотрим примеры решения простейших матричных уравнений вида X⋅A=BXcdot A=B.
Пример 3
Решить матричное уравнение
X⋅(9711)=(201812)Xcdotbegin{pmatrix}9&7\1&1end{pmatrix}=begin{pmatrix}2&0\18&12end{pmatrix}. Выполнить проверку.
Уравнение имеет вид X⋅A=BXcdot A=B, где A=(9711)A=begin{pmatrix}9&7\1&1end{pmatrix}, B=(201812)B=begin{pmatrix}2&0\18&12end{pmatrix}.
Умножим обе части уравнения на A−1A^{-1} справа:
X⋅A⋅A−1=B⋅A−1Xcdot Acdot A^{-1}=Bcdot A^{-1},
X⋅E=B⋅A−1Xcdot E=Bcdot A^{-1}, EE — единичная матрица,
X=B⋅A−1X=Bcdot A^{-1}.
Найдем матрицу A−1A^{-1}.
∣9711∣=9⋅1−1⋅7=9−7=2≠0begin{vmatrix}9&7\1&1end{vmatrix}=9cdot1-1cdot7=9-7=2neq 0, значит для матрицы AA существует обратная матрица. Найдем ее методом элементарных преобразований.
Составим расширенную матрицу:
(9711∣1001)begin{pmatrix}left.begin{matrix}9&7\1&1end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}.
Поменяем строки №1 и №2 местами:
(9711∣1001)∼(1197∣0110)begin{pmatrix}left.begin{matrix}9&7\1&1end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&1\9&7end{matrix}right|begin{matrix}0&1\1&0end{matrix}end{pmatrix}.
Прибавим к строке №2 строку №1, умноженную на -9:
(1197∣0110)∼(110−2∣011−9)begin{pmatrix}left.begin{matrix}1&1\9&7end{matrix}right|begin{matrix}0&1\1&0end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&1\0&-2end{matrix}right|begin{matrix}0&1\1&-9end{matrix}end{pmatrix}.
Умножим строку №2 на −12-frac{1}{2}:
(110−2∣011−9)∼(1101∣01−1292)begin{pmatrix}left.begin{matrix}1&1\0&-2end{matrix}right|begin{matrix}0&1\1&-9end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&1\0&1end{matrix}right|begin{matrix}0&1\-frac{1}{2}&frac{9}{2}end{matrix}end{pmatrix}.
Прибавим к строке №1 строку №2, умноженную на -1:
(1101∣01−1292)∼(1001∣12−72−1292)begin{pmatrix}left.begin{matrix}1&1\0&1end{matrix}right|begin{matrix}0&1\-frac{1}{2}&frac{9}{2}end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0\0&1end{matrix}right|begin{matrix}frac{1}{2}&-frac{7}{2}\-frac{1}{2}&frac{9}{2}end{matrix}end{pmatrix}.
Значит, A−1=(12−72−1292)=12(1−7−19)A^{-1}=begin{pmatrix}frac{1}{2}&-frac{7}{2}\-frac{1}{2}&frac{9}{2}end{pmatrix}=frac{1}{2}begin{pmatrix}1&-7\-1&9end{pmatrix}.
B⋅A−1=(201812)⋅12⋅(1−7−19)=12(201812)⋅(1−7−19)=12(2−146−18)=(1−73−9)=XBcdot A^{-1}=begin{pmatrix}2&0\18&12end{pmatrix}cdot frac{1}{2}cdot begin{pmatrix}1&-7\-1&9end{pmatrix}=frac{1}{2}begin{pmatrix}2&0\18&12end{pmatrix}cdotbegin{pmatrix}1&-7\-1&9end{pmatrix}=frac{1}{2}begin{pmatrix}2&-14\6&-18end{pmatrix}=begin{pmatrix}1&-7\3&-9end{pmatrix}=X.
Проверка: (1−73−9)⋅(9711)=(201812).begin{pmatrix}1&-7\3&-9end{pmatrix}cdotbegin{pmatrix}9&7\1&1end{pmatrix}=begin{pmatrix}2&0\18&12end{pmatrix}. — Верно.
Ответ: X=(1−73−9)X=begin{pmatrix}1&-7\3&-9end{pmatrix}.
Пример 4
Решить матричное уравнение X⋅(1325)=(4−132)Xcdotbegin{pmatrix}1&3\2&5end{pmatrix}=begin{pmatrix}4&-1\3&2end{pmatrix}. Выполнить проверку.
Уравнение имеет вид X⋅A=BXcdot A=B, где A=(1325)A=begin{pmatrix}1&3\2&5end{pmatrix}, B=(4−132)B=begin{pmatrix}4&-1\3&2end{pmatrix}.
Умножим обе части уравнения на A−1A^{-1} справа:
X⋅A⋅A−1=B⋅A−1Xcdot Acdot A^{-1}=Bcdot A^{-1},
X⋅E=B⋅A−1Xcdot E=Bcdot A^{-1}, EE — единичная матрица,
X=B⋅A−1X=Bcdot A^{-1}.
Найдем матрицу A−1A^{-1}.
∣1325∣=1⋅5−2⋅3=5−6=−1≠0begin{vmatrix}1&3\2&5end{vmatrix}=1cdot5-2cdot3=5-6=-1neq 0, значит для матрицы AA существует обратная матрица. Найдем ее методом элементарных преобразований.
Составим расширенную матрицу:
(1325∣1001)begin{pmatrix}left.begin{matrix}1&3\2&5end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}.
Прибавим к строке №2 строку №1, умноженную на -2:
(1325∣1001)∼(130−1∣10−21)begin{pmatrix}left.begin{matrix}1&3\2&5end{matrix}right|begin{matrix}1&0\0&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&3\0&-1end{matrix}right|begin{matrix}1&0\-2&1end{matrix}end{pmatrix}.
Прибавим к строке №1 строку №2, умноженную на 3:
(130−1∣10−21)∼(100−1∣−53−21)begin{pmatrix}left.begin{matrix}1&3\0&-1end{matrix}right|begin{matrix}1&0\-2&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0\0&-1end{matrix}right|begin{matrix}-5&3\-2&1end{matrix}end{pmatrix}.
Умножим строку №2 на -1:
(100−1∣−53−21)∼(1001∣−532−1)begin{pmatrix}left.begin{matrix}1&0\0&-1end{matrix}right|begin{matrix}-5&3\-2&1end{matrix}end{pmatrix}sim begin{pmatrix}left.begin{matrix}1&0\0&1end{matrix}right|begin{matrix}-5&3\2&-1end{matrix}end{pmatrix}.
Значит, A−1=(−532−1)A^{-1}=begin{pmatrix}-5&3\2&-1end{pmatrix}.
B⋅A−1=(4−132)⋅(−532−1)=(−2213−117)=XBcdot A^{-1}=begin{pmatrix}4&-1\3&2end{pmatrix}cdotbegin{pmatrix}-5&3\2&-1end{pmatrix}=begin{pmatrix}-22&13\-11&7end{pmatrix}=X.
Проверка:
(−2213−117)⋅(1325)=(4−132)begin{pmatrix}-22&13\-11&7end{pmatrix}cdotbegin{pmatrix}1&3\2&5end{pmatrix}=begin{pmatrix}4&-1\3&2end{pmatrix}. — Верно.
Ответ: X=(−2213−117).X=begin{pmatrix}-22&13\-11&7end{pmatrix}.
Существует третий вид матричных уравнений: A⋅X⋅B=CAcdot Xcdot B=C, но в действительности он встречается редко.
Обе части уравнения умножим на A−1A^{-1} слева: A−1⋅A⋅X⋅B=A−1⋅CA^{-1}cdot Acdot Xcdot B=A^{-1}cdot C.
Зная, что A−1⋅A=EA^{-1}cdot A=E, получим: E⋅X⋅B=A−1⋅CEcdot Xcdot B=A^{-1}cdot C.
Поскольку E⋅X=XEcdot X=X, то X⋅B=A−1⋅CXcdot B=A^{-1}cdot C.
Обе части уравнения умножим на B−1B^{-1} справа: X⋅B⋅B−1=A−1⋅C⋅B−1Xcdot Bcdot B^{-1}=A^{-1}cdot Ccdot B^{-1}.
Зная, что B⋅B−1=EBcdot B^{-1}=E, получим: X⋅E=A−1⋅C⋅B−1Xcdot E=A^{-1}cdot Ccdot B^{-1}.
Поскольку X⋅E=XXcdot E=X, то X=A−1⋅C⋅B−1X=A^{-1}cdot Ccdot B^{-1}.

tr(A) = tr(AT ) .
4. При суммировании матриц их следы также суммируются:
tr(A + B) = tr(A) + tr(B) .
5. Хотя коммутативный (переместительный) закон умножения матриц, вообще говоря, не выполняется, однако:
tr(A B) = tr(B A) .
В частности, если А – матрица строка: A = (a1 a2 L an ) , то:
n
tr(A AT ) = tr(AT A) = ∑ai2
i=1
Основные вопросы темы
1.Определитель квадратной матрицы.
2.Вычисление определителя матриц 1, 2 и 3 порядка.
3.Вычисление определителя матриц произвольного порядка.
2.1Определитель квадратной матрицы.
Вначале дадим качественное определение: определителем квадратной матрицы размера n×n называется число, вычисляемое по строго определенному правилу и характеризующее определенные свойства матрицы. Эта характеристика широко используется для решения различных задач матричного анализа.
Определитель матрицы А обозначается как А , , или detA.
Правила вычисления определителей удобно рассмотреть, начиная с матриц первого, второго и третьего порядка.
2.2. Вычисление определителя матриц 1, 2 и 3 порядка.
Определитель матрицы первого порядка.
Определитель матрицы первого порядка A = (a11 ) равен элементу
1×1
матрицы a11 :
= A = a11 .
Определитель матрицы второго порядка.
15
|
Определитель матрицы второго порядка A |
a11 |
a12 |
вычисля- |
|
|
= |
||||
|
2×2 |
a22 |
|||
|
a21 |
ется по формуле:
|
= |
A |
= |
a11 |
a12 |
= a11a22 − a12 a21 . |
||
|
a21 |
a22 |
Таким образом, для того чтобы найти определитель второго порядка нужно из произведения элементов, составляющих главную диагональ матрицы, вычесть произведение элементов, составляющих ее вторую диагональ.
|
4 |
2 |
равен: |
||
|
Например, определитель матрицы A = |
||||
|
5 |
6 |
|||
|
= |
A |
= |
4 |
2 |
= 4 6 − 2 5 = 10 . |
|||||||
|
5 |
6 |
|||||||||||
|
2.2.3 Определитель матрицы третьего порядка |
a11 |
a12 |
a13 |
|||||||||
|
Определитель матрицы третьего порядка |
a22 |
вы- |
||||||||||
|
A = a21 |
a23 |
|||||||||||
|
3×3 |
a32 |
|||||||||||
|
a31 |
a33 |
числяется по формуле:
|
a11 |
a12 |
a13 |
= a11a22 a33 + a12 a23 a31 + a13 a21a32 − a13 a22 a31 − a12 a21a33 − a11a23 a32 . |
|||||
|
= |
A |
= |
a21 |
a22 |
a23 |
|||
|
a31 |
a32 |
a33 |
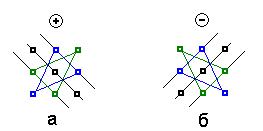
Правая часть данного равенства представляет собой алгебраическую сумму шести слагаемых, половина из которых берется со знаком ‘+’ , а другая половина – со знаком ‘–’. Каждое слагаемое содержит произведение трех элементов матрицы (по одному из каждого столбца и каждой строки). Правило определения элементов, входящих в каждое слагаемое, удобно представить в геометрической форме. Такое пред-
ставление носит название правило треугольников или правило Сарру-
са (см. рис. 2.1).
Рисунок 2.1. Графическая иллюстрация правила Сарруса.
16
Левая часть рисунка (рис. 2.1.а) отражает правило записи слагаемых со знаком ‘+’ :
—первое слагаемое представляет собой произведение членов матрицы, находящихся на главной диагонали;
—второе и третье слагаемые представляет собой произведение членов матрицы, входящих в треугольники с основаниями параллельными главной диагонали матрицы;
Аналогично находятся слагаемые со знаком ‘ – ’, с той лишь разницей, что все построения реализуются относительно дополнительной диагонали (рис. 2.1.б).
2.2.4Определитель квадратной матрицы произвольного порядка.
Правило вычисления определителя квадратной матрицы произвольного порядка определяется теоремой Лапласа. Однако, чтобы сформулировать эту теорему, необходимо познакомится еще с двумя понятиями: минор — Mij и алгебраическое дополнение — Aij элемента aij
матрицы А.
ОПРЕДЕЛЕНИЕ: Минором — Mij элемента aij матрицы А n-го порядка называется определитель матрицы (n-1)-го порядка, полученной из исходной матрицы путем вычеркивания строки и столбца, в которых находится элемент aij (т.е. i-ой строки и j-го столбца).
Например,
|
a11 |
a12 |
a13 |
a12 |
a13 |
= a12 a23 − a22 a13 . |
|||
|
M 31 = |
a21 |
a22 |
a23 |
= |
||||
|
a31 |
a32 |
a33 |
a22 |
a23 |
||||
ОПРЕДЕЛЕНИЕ: Алгебраическим дополнением — Аij элемента aij матрицы А n-го порядка называется минор этого элемента, взятый со знаком (− 1)i+ j :
Aij = (− 1)i+ j M ij .
Приведенные определения позволяют сформулировать теорему Лапласа, позволяющую вычислить определитель матрицы произвольного порядка.
17

Теорема Лапласа. Определитель квадратной матрицы равен сумме попарных произведений элементов произвольной строки (столбца) матрицы на их алгебраические дополнения:
n
A = ai1 Ai1 + ai2 Ai2 + ai3 Ai3 + K+ ain Ain = ∑ aik Aik , k =1
или
n
A = a1 j A1 j + a2 j A2 j + a3 j A3 j + K+ anj Anj = ∑akj Akj . k =1
Первое выражение определяет разложение определителя матрицы по элементам строки, второе – по элементам столбца.
ЗАМЕЧАНИЕ. Теорема Лапласа показывает, что определитель матрицы n-го порядка может быть вычислен через определители матриц более низкого — (n-1)-го порядка.
2.2.5 Свойства определителя матрицы.
Опираясь на теорему Лапласа, можно показать, что определитель матрицы обладает следующими свойствами.
1.При транспонировании матрицы, значение ее определителя не меняется:
A = AT .
2.При перестановке двух строк (столбцов) матрицы абсолютное значение определителя не меняется, а его знак меняется на противоположный.
3.Определитель матрицы, имеющей две пропорциональные строки (столбцы), равен нулю. В частности, определитель матрицы, имеющей две одинаковые строки (столбцы), равен нулю.
4.Общий множитель элементов отдельной строки (столбца) матрицы можно выносить за знак определителя. Из этого свойства,
вчастности, вытекает следующее равенство:
λА = λn A ,
где: n – порядок квадратной матрицы А; и λ – произвольное число.
5.Определитель матрицы не изменится, если к элементам одной строки (столбца) добавить элементы другой строки (столбца), предварительно умноженные на произвольное (не равное нулю) число.
6.Хотя произведение матриц не обладает законом коммутативности, однако:
18
A B = B A = А В ,
где А и В квадратные матрицы одного порядка.
7. Определитель единичной матрицы равен единице:
E = 1.
Учет указанных свойств часто значительно облегчает расчет определителя при использовании теоремы Лапласа. Действительно, согласно этой теореме значение определителя равно сумме попарных произведений элементов произвольной строки (столбца) матрицы на их алгебраические дополнения:
n
A = ai1 Ai1 + ai2 Ai2 + ai3 Ai3 + K+ ain Ain = ∑aik Aik , k =1
или:
n
A = a1 j A1 j + a2 j A2 j + a3 j A3 j + K+ anj Anj = ∑akj Akj . k =1
Отметим, что чем больше нулевых элементов содержит выбранная для расчета определителя строка (столбец), тем проще выполнить расчет, т.к. соответствующее слагаемое будет заведомо равно нулю. Поэтому, для вычислений целесообразно использовать строку (столбец), содержащую максимальное число нулевых элементов. Если таких строк (столбцов) нет, возможно выполнить ряд операций, которые согласно перечисленным ранее свойствам, не изменяют значение определителя, но увеличивают число нулевых элементов выбранной строки (столбца).
Пример. Вычислить определитель матрицы четвертого порядка
|
2 |
− 3 |
6 |
− 2 |
|||||
|
 |
= |
− 3 |
2 |
0 |
1 |
. |
||
|
3 |
− 1 |
4 |
2 |
|||||
|
− 8 |
2 |
− 3 |
3 |
Решение. Воспользуемся теоремой Лапласа, выбрав для разложения вторую строку, т.к. она содержит нулевой элемент. Попытаемся увеличить число нулевых элементов этой строки, воспользовавшись пятым свойством определителей. Прибавим ко второму столбцу – четвертый, предварительно умножив его на “-2” (согласно пятому свойству, значение определителя при этом не изменится). В результате получим:
19

|
2 |
1 |
6 |
− 2 |
|||||
|
 |
= |
− 3 |
0 |
0 |
1 |
. |
||
|
3 |
− 5 |
4 |
2 |
|||||
|
− 8 |
− 4 |
− 3 |
3 |
Число нулевых элементов второй строки — возросло. Теперь прибавим к первому столбцу – четвертый, предварительно умножив его на 3. В результате получим:
|
− 4 |
1 |
6 |
− 2 |
|||||
|
 |
= |
0 |
0 |
0 |
1 |
. |
||
|
9 |
− 5 |
4 |
2 |
|||||
|
1 |
− 4 |
− 3 |
3 |
Теперь, вторая строка содержит только один ненулевой элемент. Воспользуемся теоремой Лапласа, используя разложение определителя по второй строке:
|
B |
= b21 A21 + b22 A22 + b23 A23 + b24 A24 |
||||||||||
|
= 0 A21 + 0 A22 + 0 A23 + 1 A24 = |
|||||||||||
|
= A |
= (− 1)2+4 M |
= M |
− 4 |
1 |
6 |
||||||
|
24 |
24 |
= |
9 |
− 5 |
4 |
= −279 |
|||||
|
24 |
|||||||||||
|
1 |
− 4 |
− 3 |
ЗАМЕЧАНИЕ. Решение многих задач матричного анализа связано с проверкой равенства нулю определителя матрицы.
ОПРЕДЕЛЕНИЕ. Матрица А называется невырожденной (неособен-
ной), если ее определитель отличен от нуля. В противном случае она называется вырожденной (особенной).
Перечисленные выше свойства определителей позволяют сформулировать необходимое и достаточное условие равенства нулю опре-
делителя: Определитель матрицы равен нулю тогда и только тогда, когда матрица содержит линейно зависимые строки (столбцы).
Пример. Вычислить определитель матрицы четвертого порядка
|
5 |
3 |
8 |
1 |
||||
|
A |
= |
7 |
2 |
3 |
8 |
. |
|
|
10 |
6 |
16 |
2 |
||||
|
12 |
21 |
7 |
4 |
20
Соседние файлы в папке М
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
ОПРЕДЕЛЕНИЕ МАТРИЦЫ. ВИДЫ МАТРИЦ
Матрицей размером m
×n
называется совокупность m·n
чисел, расположенных в виде
прямоугольной таблицы из m
строк и n
столбцов. Эту таблицу
обычно заключают в круглые скобки. Например, матрица может иметь вид:
Для краткости матрицу можно обозначать одной заглавной буквой, например, А
или В
.
В общем виде матрицу размером m
×n
записывают так

Числа,
составляющие матрицу, называются элементами
матрицы
. Элементы матрицы удобно снабжать двумя индексами a ij
: первый указывает номер
строки, а второй – номер столбца. Например, a 23
– элемент стоит во 2-ой строке, 3-м столбце.
Если в матрице
число строк равно числу столбцов, то матрица называется квадратной
, причём число ее строк или столбцов называется порядком
матрицы. В приведённых выше
примерах квадратными являются вторая матрица – её порядок равен 3, и четвёртая
матрица – её порядок 1.
Матрица, в
которой число строк не равно числу столбцов, называется прямоугольной
. В примерах это первая матрица и третья.
Различаются также
матрицы, имеющие только одну строку или один столбец.
Матрица, у
которой всего одна строка , называется матрицей –
строкой
(или строковой), а матрица, у которой всего один столбец, матрицей – столбцом
.
Матрица, все
элементы которой равны нулю, называется нулевой
и обозначается (0), или просто 0. Например,

Главной диагональю
квадратной матрицы назовём диагональ, идущую
из левого верхнего в правый нижний угол.
Квадратная
матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю,
называется треугольной
матрицей.

Квадратная
матрица, у которой все элементы, кроме, быть может, стоящих
на главной диагонали, равны нулю, называется диагональной
матрицей. Например, или .
Диагональная
матрица, у которой все диагональные элементы равны единице, называется единичной
матрицей и обозначается буквой
E. Например, единичная матрица 3-го порядка имеет вид 
ДЕЙСТВИЯ НАД МАТРИЦАМИ
Равенство матриц
. Две матрицы A
и B
называются равными, если
они имеют одинаковое число строк и столбцов и их соответствующие элементы равны
a ij
= b ij
. Так если 

,
если a 11 = b 11 , a 12 = b 12 , a 21 = b 21
и a 22 = b 22
.
Транспонирование
. Рассмотрим произвольную матрицу A
из m
строк и n
столбцов. Ей можно
сопоставить такую матрицу B
из
n
строк и m
столбцов, у которой каждая
строка является столбцом матрицы A
с
тем же номером (следовательно, каждый столбец является строкой матрицы A
с тем же номером). Итак,
если 

Эту матрицу B
называют транспонированной
матрицей A
, а переход от A
к B транспонированием
.
Таким образом, транспонирование – это
перемена ролями строк и столбцов матрицы. Матрицу, транспонированную к матрице A
, обычно обозначают A T
.
Связь между матрицей A
и её транспонированной
можно записать в виде .
Например.
Найти матрицу транспонированную данной.
Сложение матриц.
Пусть матрицы A
и B
состоят из одинакового
числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры
.
Тогда для того, чтобы сложить матрицы A
и B
нужно к элементам матрицы A
прибавить элементы матрицы B
, стоящие на тех же местах.
Таким образом, суммой двух матриц A
и B
называется матрица C
, которая определяется по
правилу, например,
Примеры.
Найти сумму матриц:
Легко проверить,
что сложение матриц подчиняется следующим законам: коммутативному A+B=B+A
и ассоциативному (A+B
)+C
=A
+(B+C
).
Умножение матрицы на число.
Для того чтобы умножить
матрицу A
на число k
нужно каждый элемент
матрицы A
умножить на это число.
Таким образом, произведение матрицы A
на
число k
есть новая матрица, которая
определяется по правилу 
Для любых чисел a
и b
и
матриц A
и B
выполняются равенства:
Примеры.
Умножение матриц.
Эта операция осуществляется по своеобразному
закону. Прежде всего, заметим, что размеры матриц–сомножителей должны быть
согласованы. Перемножать можно только те матрицы, у которых число столбцов
первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки
первой равна высоте столбца второй). Произведением
матрицы A
не матрицу B
называется новая матрица C=AB
,
элементы которой составляются следующим образом:
Таким образом,
например, чтобы получить у произведения (т.е. в матрице C
) элемент, стоящий в 1-ой
строке и 3-м столбце c 13
, нужно в 1-ой матрице взять
1-ую строку, во 2-ой – 3-й столбец, и затем элементы строки умножить на
соответствующие элементы столбца и полученные произведения сложить. И другие
элементы матрицы-произведения получаются с помощью аналогичного произведения
строк первой матрицы на столбцы второй матрицы.
В
общем случае, если мы умножаем матрицу A = (a ij)
размера m
×n
на
матрицу B = (b ij)
размера n
×p
, то получим матрицу C
размера m
×p
, элементы которой вычисляются следующим образом: элемент c ij
получается в результате
произведения элементов i
-ой строки матрицы A
на соответствующие элементы j
-го
столбца матрицы B
и их сложения.
Из этого правила следует,
что всегда можно перемножать две квадратные матрицы одного порядка, в
результате получим квадратную матрицу того же порядка. В частности, квадратную
матрицу всегда можно умножить саму на себя, т.е. возвести в квадрат.
Другим важным
случаем является умножение матрицы–строки на матрицу–столбец, причём ширина
первой должна быть равна высоте второй, в результате получим матрицу первого
порядка (т.е. один элемент). Действительно,

Примеры.
Таким образом,
эти простые примеры показывают, что матрицы, вообще говоря, не перестановочны друг с другом, т.е. A∙B
≠ B∙A
. Поэтому при умножении
матриц нужно тщательно следить за порядком множителей.
Можно
проверить, что умножение матриц подчиняется ассоциативному и дистрибутивному
законам, т.е. (AB)C=A(BC)
и (A+B)C=AC+BC
.
Легко также
проверить, что при умножении квадратной матрицы A
на единичную матрицу E
того же порядка вновь получим матрицу A
, причём AE=EA=A
.
Можно
отметить следующий любопытный факт. Как известно произведение 2-х отличных от
нуля чисел не равно 0. Для матриц это может не иметь места, т.е. произведение
2-х не нулевых матриц может оказаться равным нулевой матрице.
Например
, если 
.
ПОНЯТИЕ ОПРЕДЕЛИТЕЛЕЙ
Пусть дана
матрица второго порядка – квадратная матрица, состоящая из двух строк и двух
столбцов 
Определителем второго порядка
, соответствующим данной
матрице, называется число, получаемое следующим образом: a 11 a 22 – a 12 a 21
.
Определитель обозначается
символом 
Итак, для того
чтобы найти определитель второго порядка нужно из произведения элементов
главной диагонали вычесть произведение элементов по второй диагонали.
Примеры.
Вычислить определители второго порядка.
Аналогично можно
рассмотреть матрицу третьего порядка и соответствующий ей определитель.
Определителем третьего порядка
, соответствующим данной
квадратной матрице третьего порядка, называется число, обозначаемое и
получаемое следующим образом:

Таким образом,
эта формула даёт разложение определителя третьего порядка по элементам первой
строки a 11 , a 12 , a 13
и сводит вычисление определителя третьего порядка к вычислению
определителей второго порядка.
Примеры.
Вычислить определитель третьего порядка.
Аналогично можно ввести понятия определителей
четвёртого, пятого и т.д. порядков, понижая их порядок разложением по элементам
1-ой строки, при этом знаки «+» и «–» у слагаемых чередуются.
Итак, в отличие
от матрицы, которая представляют собой таблицу чисел, определитель это число,
которое определённым образом ставится в соответствие матрице.
1-й курс, высшая математика, изучаем матрицы
и основные действия над ними. Здесь мы систематизируем основные операции, которые можно проводить с матрицами. С чего начать знакомство с матрицами? Конечно, с самого простого — определений, основных понятий и простейших операций. Заверяем, матрицы поймут все, кто уделит им хотя бы немного времени!
Определение матрицы
Матрица
– это прямоугольная таблица элементов. Ну а если простым языком – таблица чисел.
Обычно матрицы обозначаются прописными латинскими буквами. Например, матрица A
, матрица B
и так далее. Матрицы могут быть разного размера: прямоугольные, квадратные, также есть матрицы-строки и матрицы-столбцы, называемые векторами. Размер матрицы определяется количеством строк и столбцов. Например, запишем прямоугольную матрицу размера m
на n
, где m
– количество строк, а n
– количество столбцов.
Элементы, для которых i=j
(a11, a22, ..
) образуют главную диагональ матрицы, и называются диагональными.
Что можно делать с матрицами? Складывать/вычитать
, умножать на число
, умножать между собой
, транспонировать
. Теперь обо всех этих основных операциях над матрицами по порядку.
Операции сложения и вычитания матриц
Сразу предупредим, что можно складывать только матрицы одинакового размера. В результате получится матрица того же размера. Складывать (или вычитать) матрицы просто – достаточно только сложить их соответствующие элементы
. Приведем пример. Выполним сложение двух матриц A и В размером два на два.
Вычитание выполняется по аналогии, только с противоположным знаком.
На произвольное число можно умножить любую матрицу. Чтобы сделать это, нужно умножить на это число каждый ее элемент.
Например, умножим матрицу A из первого примера на число 5:
Операция умножения матриц
Перемножить между собой удастся не все матрицы. Например, у нас есть две матрицы — A и B. Их можно умножить друг на друга только в том случае, если число столбцов матрицы А равно числу строк матрицы В. При этом каждый элемент получившейся матрицы, стоящий в i-ой строке и j-м столбце, будет равен сумме произведений соответствующих элементов в i-й строке первого множителя и j-м столбце второго
. Чтобы понять этот алгоритм, запишем, как умножаются две квадратные матрицы:
И пример с реальными числами. Умножим матрицы:
Операция транспонирования матрицы
Транспонирование матрицы – это операция, когда соответствующие строки и столбцы меняются местами. Например, транспонируем матрицу A из первого примера:
Определитель матрицы
Определитель, о же детерминант – одно из основных понятий линейной алгебры. Когда-то люди придумали линейные уравнения, а за ними пришлось выдумать и определитель. В итоге, разбираться со всем этим предстоит вам, так что, последний рывок!
Определитель – это численная характеристика квадратной матрицы, которая нужна для решения многих задач.
Чтобы посчитать определитель самой простой квадратной матрицы, нужно вычислить разность произведений элементов главной и побочной диагоналей.
Определитель матрицы первого порядка, то есть состоящей из одного элемента, равен этому элементу.
А если матрица три на три? Тут уже посложнее, но справиться можно.
Для такой матрицы значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.
К счастью, вычислять определители матриц больших размеров на практике приходится редко.
Здесь мы рассмотрели основные операции над матрицами. Конечно, в реальной жизни можно ни разу так и не встретить даже намека на матричную систему уравнений или же наоборот — столкнуться с гораздо более сложными случаями, когда придется действительно поломать голову. Именно для таких случаев и существует профессиональный студенческий сервис . Обращайтесь за помощью, получайте качественное и подробное решение, наслаждайтесь успехами в учебе и свободным временем.
Пусть имеется квадратная матрица n-го порядка
Матрица А -1 называется обратной матрицей
по отношению к матрице А, если А*А -1 = Е, где Е — единичная матрица n-го порядка.
Единичная матрица
— такая квадратная матрица, у которой все элементы по главной диагонали, проходящей от левого верхнего угла к правому нижнему углу, — единицы, а остальные — нули, например:
Обратная матрица
может существовать только для квадратных матриц
т.е. для тех матриц, у которых число строк и столбцов совпадают.
Теорема условия существования обратной матрицы
Для того чтобы матрица имела обратную матрицу необходимо и достаточно, чтобы она была невырожденной.
Матрица А = (А1, А2,…А n) называется невырожденной
, если векторы-столбцы являются линейно независимыми. Число линейно независимых векторов-столбцов матрицы называется рангом матрицы . Поэтому можно сказать, что для того, чтобы существовала обратная матрица, необходимо и достаточно, чтобы ранг матрицы равнялся ее размерности, т.е. r = n.
Алгоритм нахождения обратной матрицы
- Записать в таблицу для решения систем уравнений методом Гаусса матрицу А и справа (на место правых частей уравнений) приписать к ней матрицу Е.
- Используя преобразования Жордана, привести матрицу А к матрице, состоящей из единичных столбцов; при этом необходимо одновременно преобразовать матрицу Е.
- Если необходимо, то переставить строки (уравнения) последней таблицы так, чтобы под матрицей А исходной таблицы получилась единичная матрица Е.
- Записать обратную матрицу А -1 , которая находится в последней таблице под матрицей Е исходной таблицы.
Пример 1
Для матрицы А найти обратную матрицу А -1
Решение: Записываем матрицу А и справа приписываем единичную матрицу Е. Используя преобразования Жордана, приводим матрицу А к единичной матрице Е. Вычисления приведены в таблице 31.1.
Проверим правильность вычислений умножением исходной матрицы А и обратной матрицы А -1 .
В результате умножения матриц получилась единичная матрица. Следовательно, вычисления произведены правильно.
Ответ:
Решение матричных уравнений
Матричные уравнения могут иметь вид:
АХ = В, ХА = В, АХВ = С,
где А,В,С — задаваемые матрицы, Х- искомая матрица.
Матричные уравнения решаются с помощью умножения уравнения на обратные матрицы.
Например, чтобы найти матрицу из уравнения , необходимо умножить это уравнение на слева.
Следовательно, чтобы найти решение уравнения , нужно найти обратную матрицу и умножить ее на матрицу , стоящие в правой части уравнения.
Аналогично решаются другие уравнения.
Пример 2
Решить уравнение АХ = В, если
Решение
: Так как обратная матрица равняется (см. пример 1)
Матричный метод в экономическом анализе
Наряду с другими в находят применение также матричные методы
. Эти методы базируются на линейной и векторно-матричной алгебре. Такие методы применяются для целей анализа сложных и многомерных экономических явлений. Чаще всего эти методы используются при необходимости сравнительной оценки функционирования организаций и их структурных подразделений.
В процессе применения матричных методов анализа можно выделить несколько этапов.
На первом этапе
осуществляется формирование системы экономических показателей и на ее основе составляется матрица исходных данных , которая представляет собой таблицу, в которой по ее отдельным строкам показываются номера систем (i = 1,2,….,n)
, а по вертикальным графам — номера показателей (j = 1,2,….,m)
.
На втором этапе
по каждой вертикальной графе выявляется наибольшее из имеющихся значений показателей, которое и принимается за единицу.
После этого все суммы, отраженные в данной графе делят на наибольшее значение и формируется матрица стандартизированных коэффициентов .
На третьем этапе
все составные части матрицы возводят в квадрат. Если они имеют различную значимость, то каждому показателю матрицы присваивается определенный весовой коэффициент k
. Величина последнего определяется экспертным путем.
На последнем, четвертом этапе
найденные величины рейтинговых оценок R j
группируются в порядке их увеличения или уменьшения.
Изложенные матричные методы следует использовать, например, при сравнительном анализе различных инвестиционных проектов, а также при оценке других экономических показателей деятельности организаций.
>> Матрицы
4.1.Матрицы. Операции над матрицами
Прямоугольной матрицей размера mxn называется совокупность mxn чисел, расположенных в виде прямоугольной таблицы, содержащей m строк и n столбцов. Мы будем записывать ее в виде
или сокращенно в виде A = (a i j) (i = ; j = ), числа a i j , называются ее элементами; первый индекс указывает на номер строки, второй — на номер столбца. A = (a i j) и B = (b i j) одинакового размера называются равными, если попарно равны их элементы, стоящие на одинаковых местах, то есть A = B, если a i j = b i j .
Матрица, состоящая из одной строки или одного столбца, называется соответственно -строкой или вектор-столбцом. Вектор-столбцы и вектор-строки называют просто векторами.
Матрица, состоящая из одного числа, отождествляется с этим числом. A размера mxn, все элементы которой равны нулю, называются нулевой и обозначается через 0. Элементы с одинаковыми индексами называют элементами главной диагонали. Если число строк равно числу столбцов, то есть m = n, то матрицу называют квадратной порядка n. Квадратные матрицы, у которых отличны от нуля лишь элементы главной диагонали, называются диагональными и записываются так:

Если все элементы a i i диагонали равны 1, то она называется единичной и обозначается буквой Е:

Квадратная матрица называется треугольной, если все элементы, стоящие выше (или ниже) главной диагонали, равны нулю. Транспонированием называется такое преобразование, при котором строки и столбцы меняются местами с сохранением их номеров. Обозначается транспонирование значком Т наверху.
Если в (4.1) переставим строки со столбцами, то получим

которая будет транспонированной по отношению к А. В частности, при транспонировании вектора-столбца получается вектор-строка и наоборот.
Произведением А на число b называется матрица, элементы которой получаются из соответствующих элементов А умножением на число b: b A = (b a i j).
Суммой А = (a i j) и B = (b i j) одного размера называется C = (c i j) того же размера, элементы которой определяются по формуле c i j = a i j + b i j .
Произведение АВ определяется в предположении, что число столбцов А равно числу строк В.
Произведением AB, где А = (a i j) и B = (b j k), где i = , j= , k= , заданных в определенном порядке АВ, называется С = (c i k), элементы которой определяются по следующему правилу:
c i k = a i 1 b 1 k + a i 2 b 2 k +… + a i m b m k = a i s b s k . (4.2)
Иначе говоря, элемент произведения AB определяются следующим образом: элемент i-й строки и k-го столбца С равен сумме произведений элементов i-й строки А на соответствующие элементы k-го столбца В.
Пример 2.1. Найти произведение AB и .
Решение. Имеем: А размера 2×3, В размера 3×3, тогда произведение АВ = С существует и элементы С равны
С 11 = 1×1 +2×2 + 1×3 = 8, с 21 = 3×1 + 1×2 + 0×3 = 5, с 12 = 1×2 + 2×0 + 1×5 = 7,
с 22 =3×2 + 1×0 + 0×5 = 6, с 13 = 1×3 + 2×1 + 1×4 = 9, с 23 = 3×3 + 1×1 + 0×4 = 10.
, а произведение BA не существует.
Пример 2.2. В таблице указано количество единиц продукции, отгружаемой ежедневно на молокозаводах 1 и 2 в магазины М 1 , М 2 и М 3 , причем доставка единицы продукции с каждого молокозавода в магазин М 1 стоит 50 ден. ед., в магазин М 2 — 70, а в М 3 — 130 ден. ед. Подсчитать ежедневные транспортные расходы каждого завода.
|
Молокозавод |
|||
Решение. Обозначим через А матрицу, данную нам в условии, а через
В — матрицу, характеризующую стоимость доставки единицы продукции в магазины, т.е.,
,
Тогда матрица затрат на перевозки будет иметь вид:

Итак, первый завод ежедневно тратит на перевозки 4750 ден. ед., второй — 3680 ден.ед.
Пример 2.3. Швейное предприятие производит зимние пальто, демисезонные пальто и плащи. Плановый выпуск за декаду характеризуется вектором X = (10, 15, 23). Используются ткани четырех типов Т 1 , Т 2 , Т 3 , Т 4 . В таблице приведены нормы расхода ткани (в метрах) на каждое изделие. Вектор С = (40, 35, 24, 16) задает стоимость метра ткани каждого типа, а вектор P = (5, 3, 2, 2) — стоимость перевозки метра ткани каждого вида.
|
Расход ткани |
||||
|
Зимнее пальто |
||||
|
Демисезонное пальто |
||||
1. Сколько метров ткани каждого типа потребуется для выполнения плана?
2. Найти стоимость ткани, расходуемой на пошив изделия каждого вида.
3. Определить стоимость всей ткани, необходимой для выполнения плана.
Решение. Обозначим через А матрицу, данную нам в условии, т. е.,

тогда для нахождения количества метров ткани, необходимой для выполнения плана, нужно вектор X умножить на матрицу А:
Стоимость ткани, расходуемой на пошив изделия каждого вида, найдем, перемножив матрицу А и вектор C T:

Стоимость всей ткани, необходимой для выполнения плана, определится по формуле:
Наконец, с учетом транспортных расходов вся сумма будет равна стоимости ткани, т. е. 9472 ден. ед., плюс величина
X А P T = 
Итак, X А C T + X А P T = 9472 + 1037 = 10509 (ден. ед).
Итак, сервисы по решению матриц онлайн:
Сервис работы с матрицами позволяет выполнить элементарные
преобразования матриц.
Если у Вас стоит задача выполнить более сложное преобразование,
то этим сервисом стоит пользоваться как конструктором.
Пример
. Даны матрицы A
и B
, надо найти
C
= A
-1 * B
+ B
T ,
- Вам стоит сначала найти
обратную матрицу
A1
= A
-1 , воспользовавшись
сервисом по нахождению обратной матрицы ; - Далее, после того, как нашли матрицу A1
выполним
умножение матриц
A2
= A1
* B
,
воспользовавшись
сервисом по умножению матриц ; - Выполним транспонирование матрицы
A3
= B
T
(сервис по нахождению транспонированной матрицы); - И последнее — найдем сумму матриц С
= A2
+ A3
(сервис по вычислению суммы матриц)
— и получаем ответ с самым подробным решением!;
Произведение матриц
Это он-лайн сервис в два шага
:
- Ввести первый сомножитель матрицу A
- Ввести второй сомножитель матрицу или вектор-столбец B
Умножение матрицы на вектор
Умножение матрицы на вектор можно найти, воспользовавшись сервисом
Умножение матриц
(Первым сомножителем будет данная матрица, вторым сомножителем будет столбец,
состоящий из элементов данного вектора)
Это он-лайн сервис в два шага
:
- Введите матрицу A
, для которой нужно найти обратную матрицу - Получите ответ с подробным решением по нахождению обратной матрицы
Определитель матрицы
Это он-лайн сервис в один шаг
:
- Введите матрицу A
, для которой нужно найти определитель матрицы
Транспонирование матрицы
Здесь Вы сможете отследить алгоритм транспонирования матрицы и научиться самому решать подобные задачи.
Это он-лайн сервис в один шаг
:
- Введите матрицу A
, которую надо транспонировать
Ранг матрицы
Это он-лайн сервис в один шаг
:
- Введите матрицу A
, для которой нужно выполнить нахождение ранга
Собственные значения матрицы и собственные вектора матрицы
Это он-лайн сервис в один шаг
:
- Введите матрицу A
, для которой нужно найти собственные вектора и собственные значения (собственные числа)
Возведение матрицы в степень
Это он-лайн сервис в два шага
:
- Введите матрицу A
, которую будете возводить в степень - Ввести целое число q
— степень
Линейные уравнения. Решение систем линейных уравнений матричным методом.
Матричный метод решения СЛАУ применяют к решению систем уравнений, у которых количество уравнений соответствует количеству неизвестных. Метод лучше применять для решения систем низкого порядка. Матричный метод решения систем линейных уравнений основывается на применении свойств умножения матриц.
Этот способ, другими словами метод обратной матрицы, называют так, так как решение сводится к обычному матричному уравнению, для решения которого нужно найти обратную матрицу.
Матричный метод решения СЛАУ с определителем, который больше или меньше нуля состоит в следующем:
Предположим, есть СЛУ (система линейных уравнений) с n неизвестными (над произвольным полем):
Значит, её легко перевести в матричную форму:
AX=B, где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно:
Умножим это матричное уравнение слева на A −1 — обратную матрицу к матрице A: A −1 (AX)=A −1 B.
Т.к. A −1 A=E, значит, X=A −1 B. Правая часть уравнения дает столбец решений начальной системы. Условием применимости матричного метода есть невырожденность матрицы A. Необходимым и достаточным условием этого есть неравенство нулю определителя матрицы A:
Для однородной системы линейных уравнений, т.е. если вектор B=0, выполняется обратное правило: у системы AX=0 есть нетривиальное (т.е. не равное нулю) решение лишь когда detA=0. Эта связь между решениями однородных и неоднородных систем линейных уравнений называется альтернатива Фредгольма.
Т.о., решение СЛАУ матричным методом производится по формуле 
Известно, что у квадратной матрицы А порядка n на n есть обратная матрица A −1 только в том случае, если ее определитель ненулевой. Таким образом, систему n линейных алгебраических уравнений с n неизвестными решаем матричным методом только в случае, если определитель основной матрицы системы не равен нулю.
Не взирая на то, что есть ограничения возможности применения такого метода и существуют сложности вычислений при больших значениях коэффициентов и систем высокого порядка, метод можно легко реализовать на ЭВМ.
Пример решения неоднородной СЛАУ.
Для начала проверим, не равен ли нулю определитель матрицы коэффициентов у неизвестных СЛАУ.
Далее вычисляем алгебраические дополнения для элементов матрицы, которая состоит из коэффициентов при неизвестных. Эти коэффициенты нужны будут для вычисления обратной матрицы.
Теперь находим союзную матрицу, транспонируем её и подставляем в формулу для определения обратной матрицы.
Подставляем переменные в формулу:
Теперь находим неизвестные, перемножая обратную матрицу и столбик свободных членов.
При переходе от обычного вида СЛАУ к матричной форме будьте внимательными с порядком неизвестных переменных в уравнениях системы. Например:
НЕЛЬЗЯ записать как:
Необходимо, для начала, упорядочить неизвестные переменные в кадом уравнении системы и только после этого переходить к матричной записи:
Кроме того, нужно быть внимательными с обозначением неизвестных переменных, вместо x1, x2, …, xn могут оказаться другие буквы. К примеру:
в матричной форме записываем так:
Матричным методом лучше решать системы линейных уравнений, в которых количество уравнений совпадает с числом неизвестных переменных и определитель основной матрицы системы не равен нулю. Когда в системе более 3-х уравнений, на нахождение обратной матрицы потребуется больше вычислительных усилий, поэтому, в этом случае целесообразно использовать для решения метод Гаусса.
Матрицы коэффициентов и правых частей уравнений
Системой m линейных уравнений с n неизвестными называется система вида
где aij и bi (i=1,…,m; b=1,…,n) – некоторые известные числа, а x1,…,xn – неизвестные. В обозначении коэффициентов aij первый индекс iобозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.
Коэффициенты при неизвестных будем записывать в виде матрицы 
Числа, стоящие в правых частях уравнений, b1,…,bm называются свободными членами.
Совокупность n чисел c1,…,cn называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c1,…,cn вместо соответствующих неизвестных x1,…,xn.
Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:
- Система может иметь единственное решение.
- Система может иметь бесконечное множество решений. Например,
. Решением этой системы является любая пара чисел, отличающихся знаком.
- И третий случай, когда система вообще не имеет решения. Например,
, если бы решение существовало, то x1 + x2 равнялось бы одновременно нулю и единице.
Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.
Рассмотрим способы нахождения решений системы.
МАТРИЧНЫЙ МЕТОД РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Матрицы дают возможность кратко записать систему линейных уравнений. Пусть дана система из 3-х уравнений с тремя неизвестными:
Рассмотрим матрицу системы 
т.е. в результате произведения мы получаем левые части уравнений данной системы. Тогда пользуясь определением равенства матриц данную систему можно записать в виде

Здесь матрицы A и B известны, а матрица X неизвестна. Её и нужно найти, т.к. её элементы являются решением данной системы. Это уравнение называют матричным уравнением.
Пусть определитель матрицы отличен от нуля |A| ≠ 0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу A -1 , обратную матрице A: 
Заметим, что поскольку обратную матрицу можно найти только для квадратных матриц, то матричным методом можно решать только те системы, в которых число уравнений совпадает с числом неизвестных. Однако, матричная запись системы возможна и в случае, когда число уравнений не равно числу неизвестных, тогда матрица A не будет квадратной и поэтому нельзя найти решение системы в виде X = A -1 B.
Примеры. Решить системы уравнений.

Найдем матрицу обратную матрице A.

Таким образом, x = 3, y = – 1.
Решите матричное уравнение: XA+B=C, где
Выразим искомую матрицу X из заданного уравнения.
Найдем матрицу А -1 .
Решите матричное уравнение AX+B=C, где
Из уравнения получаем 
Следовательно,
Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:
Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,
называется определителем системы.
Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов
Тогда можно доказать следующий результат.
Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём
Доказательство. Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A11 элемента a11, 2-ое уравнение – на A21 и 3-е – на A31:
Сложим эти уравнения:
Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца

Далее рассмотрим коэффициенты при x2:
Аналогично можно показать, что и 
Наконец несложно заметить, что
Таким образом, получаем равенство: 
Следовательно, 
Аналогично выводятся равенства 

Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.
Примеры. Решить систему уравнений

Решите систему уравнений при различных значениях параметра p:
Система имеет единственное решение, если Δ ≠ 0.


- При
- При p = 30 получаем систему уравнений
которая не имеет решений.
- При p = –30 система принимает вид
и, следовательно, имеет бесконечное множество решений x=y,y Î R.
Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.
Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:

Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x1. Для этого второе уравнение разделим на а21 и умножим на –а11, а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а31 и умножим на –а11, а затем сложим с первым. В результате исходная система примет вид:
Теперь из последнего уравнения исключим слагаемое, содержащее x2. Для этого третье уравнение разделим на 

Отсюда из последнего уравнения легко найти x3, затем из 2-го уравнения x2 и, наконец, из 1-го – x1.
При использовании метода Гаусса уравнения при необходимости можно менять местами.
Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:
и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.
К элементарным преобразованиям матрицы относятся следующие преобразования:
- перестановка строк или столбцов;
- умножение строки на число, отличное от нуля;
- прибавление к одной строке другие строки.
Примеры: Решить системы уравнений методом Гаусса.

Вернувшись к системе уравнений, будем иметь
Выпишем расширенную матрицу системы и сведем ее к треугольному виду.
Вернувшись к системе уравнений, несложно заметить, что третье уравнения системы будет ложным, а значит, система решений не имеет.
Разделим вторую строку матрицы на 2 и поменяем местами первый и третий столбики. Тогда первый столбец будет соответствовать коэффициентам при неизвестной z, а третий – при x.
Вернемся к системе уравнений.
Из третьего уравнения выразим одну неизвестную через другую и подставим в первое.
Таким образом, система имеет бесконечное множество решений.
VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Системы линейных уравнений
Обозначим через $ mathbb A_<> $ любое из множеств $ mathbb Q_<>, mathbb R_<> $ или $ mathbb C_<> $.
Примеры систем уравнений над $ mathbb R $.
Относительно числа $ m_<> $ уравнений не делается ни какого предположения: оно может быть меньше, больше или равно числу переменных $ n_<> $. Если $ m_<>>n $ то система называется переопределенной. Решением системы уравнений называется любой набор значений переменных $ x_1=alpha_<1>,dots, x_n = alpha_n $, обращающий каждое из уравнений в истинное равенство. Система называется совместной если она имеет хотя бы одно решение и несовместной в противном случае.
Можно доказать (см. результаты ☟ НИЖЕ ), что все возможности для произвольной системы ограничиваются следующими вариантами:
1. система совместна и имеет единственное решение;
2. cистема совместна и имеет бесконечное множество решений;
3. cистема несовместна.
При этом все решения будут находиться в том же множестве $ mathbb A_<> $, что и коэффициенты системы.
Матричная форма записи
Для системы линейных уравнений относительно переменных $ x_1,x_2,dots,x_n $ $$ left< begin a_<11>x_1 &+a_<12>x_2&+ ldots&+a_<1n>x_n &=b_1,\ a_<21>x_1 &+a_<22>x_2&+ ldots&+a_<2n>x_n &=b_2,\ dots & & & & dots \ a_x_1 &+a_x_2&+ ldots&+a_x_n &=b_m. end right. $$ матрицей системы называется матрица $$ A=left( begin a_ <11>& a_ <12>& dots & a_ <1n>\ a_ <21>& a_ <22>& dots & a_ <2n>\ dots &&& dots \ a_ & a_ & dots & a_ end right)_ ; $$ cтолбец $$ <mathcal B>= left( begin b_ <1>\ b_ <2>\ vdots \ b_ end right) $$ называется столбцом правых частей системы, а столбец $$ X= left( begin x_ <1>\ x_ <2>\ vdots \ x_ end right) $$ — столбцом неизвестных. Используя правило умножения матриц, систему можно записать в матричном виде: $$ AX= <mathcal B> . $$ Любое решение $ x_1=alpha_1,dots,x_n=alpha_n $ системы можно также записать в виде столбца: $$ X=left( begin alpha_1 \ vdots \ alpha_n end right) in mathbb A^n . $$ Матрица, составленная из всех коэффициентов системы уравнений: $$ [A mid mathcal B ]= left( begin a_ <11>& a_ <12>& dots & a_ <1n>& b_1 \ a_ <21>& a_ <22>& dots & a_ <2n>& b_2 \ dots &&& & dots \ a_ & a_ & dots & a_ & b_m end right)_ , $$ т.е. конкатенацией матрицы $ A_<> $ и столбца правых частей $ <mathcal B>_<> $ называется расширенной матрицей системы л.у.
Исключение переменных (метод Гаусса)
метода достаточно проста.
Пример. Решить систему уравнений $$ left< begin 2x_1&-3x_2&-x_3&=3 \ 4x_1&-3x_2&-5x_3&=6 \ 3x_1&+5x_2&+9x_3&=-8 end right. $$
Решение. Выразим из первого уравнения $ x_ <1>$ $$ x_1=frac<3> <2>x_2+frac<1> <2>x_3 + frac<3> <2>$$ и подставим в оставшиеся уравнения $$ 4 left(frac<3> <2>x_2+frac<1> <2>x_3 + frac<3><2>right) -3,x_2-5,x_3=6 <coloriff > 3x_2-3x_3 = 0 $$ $$ <coloriff > x_2-x_3=0 ; $$ $$ 3 left(frac<3> <2>x_2+frac<1> <2>x_3 + frac<3><2>right) +5x_2+9x_3=-8 <coloriff > frac<19> <2>x_2 +frac<21><2>x_3=-frac<25> <2>$$ $$ <coloriff > 19x_2 +21x_3=-25 . $$ Два получившихся уравнения не зависят от неизвестной $ x_ <1>$ — она оказалась исключенной из этих уравнений. Иными словами, мы получили новую подсистему уравнений $$ left< begin x_2&-x_3&=0 \ 19x_2&+21x_3&=-25, end right. $$ которой должны удовлетворять неизвестные $ x_ <2>$ и $ x_ <3>$. Продолжаем действовать по аналогии: выразим из первого уравнения $ x_ <2>$ через $ x_ <3>$: $$x_2=x_3 $$ и подставим во второе: $$ 40 x_3 =-25 iff x_3=-frac<5> <8> . $$ Итак, значение одной компоненты решения получено. Для нахождения оставшихся подставим значение $ x_ <3>$ в полученные по ходу решения соотношения: $$ x_2=x_3=-frac<5> <8> Rightarrow x_1=frac<3> <2>x_2+frac<1> <2>x_3 + frac<3><2>=frac<1> <4> . $$
Ответ. $ x_<1>=1/4, x_2=-5/8, x_3=-5/8 $.
Теперь осталось формализовать изложенную идею метода (сформулировав допустимые правила действия над уравнениями — те, что в принципе, очевидны из здравого смысла ), а также исследовать возможные последствия его применения к системам общего вида.
Исключение переменных
Элементарными преобразованиями системы л.у. называются преобразования следующих трех типов:
1. перестановка двух уравнений;
2. умножение обеих частей уравнения на любое отличное от нуля число;
3. прибавление к одному уравнению любого другого, умноженного на произвольное число: пара уравнений $$ begin a_x_1 +a_x_2+ ldots+a_x_n &=&b_j,\ a_x_1 +a_x_2+ ldots+a_x_n &=&b_k end $$ заменяется парой $$ begin (a_+ <colorlambda > a_) x_1 &+ (a_+ <colorlambda > a_) x_2 &+ ldots &+ (a_+ <colorlambda > a_) x_n &=&b_j + <colorlambda > b_k, , \ a_x_1 &+a_x_2&+ ldots &+a_x_n &=&b_k , . end $$
Теорема. Любое элементарное преобразование системы л.у. переводит эту систему в ей эквивалентную, т.е. имеющую то же множество решений, что и исходная.
Задача. С помощью элементарных преобразований привести систему л.у. к наиболее простому виду: такому, из которого легко было бы установить множество решений.
Предположим, что первое уравнение системы содержит явно неизвестную $ x_ <1>$, т.е. $ a_<11>^<> ne 0 $. Исключим эту неизвестную из всех оставшихся уравнений. С этой целью вычтем из второго уравнения первое, домноженное на $ a_<21>/a_<11>^<> $. Получим $$left(a_<22>— frac>> a_ <12>right)x_2 + dots + left(a_<2n>— frac>> a_ <1n>right)x_n = b_2 — frac>> b_1 , $$ Аналогичное преобразование — вычитание из третьего уравнения системы первого, умноженного на $ a_<31>/a_<11>^<> $, позволяет исключить $ x_ <1>$ из этого уравнения, т.е. заменить его на $$left(a_<32>— frac>> a_ <12>right)x_2 + dots + left(a_<3n>— frac>> a_ <1n>right)x_n = b_3 — frac>> b_1 . $$ Продолжаем процесс далее. В конечном итоге исключаем $ x_ <1>$ из всех уравнений кроме первого: $$ left< begin a_<11>x_1 &+a_<12>x_2&+ ldots&+a_<1n>x_n &=b_1,\ &a_<22>^<[1]>x_2&+ ldots&+a_<2n>^<[1]>x_n &=b_2^<[1]>,\ &dots & & & dots \ &a_^<[1]>x_2&+ ldots&+a_^<[1]>x_n &=b_m^<[1]>. end right. npu begin a_^ <[1]>&= & displaystyle a_ — fraca_<1k>>> ,\ b_j^ <[1]>&= & displaystyle b_j — fracb_1>> . end $$ Полученная система эквивалентна исходной системе, однако она имеет более простой вид: в ней выделилась подсиcтема $$ left< begin a_<22>^<[1]>x_2&+ ldots&+a_<2n>^<[1]>x_n &=b_2^<[1]>,\ dots & & & dots \ a_^<[1]>x_2&+ ldots&+a_^<[1]>x_n &=b_m^<[1]>, end right. $$ которая не зависит от переменной $ x_ <1>$. К этой новой подсистеме можно применить те же рассуждения, что и к исходной системе, поставив теперь целью исключение переменной $ x_ <2>$.
Понятно, что процесс исключения может быть продолжен и далее. Теперь посмотрим, где он может прерваться. Может так случиться, что очередная, $ ell_<> $-я подсистема имеет коэффициент $ a_<ell ell>^ <[ell-1]>$ равным нулю, что не позволит алгоритму идти дальше — т.е. исключить переменную $ x_<ell>^<> $ из оставшихся уравнений (в принципе, такое могло случиться уже на первом шаге, если бы коэффициент $ a_<11>^<> $ был бы равен нулю). Возможные варианты дальнейших действий:
1. если хотя бы один коэффициент при $ x_<ell>^<> $ в одном из оставшихся уравнений отличен от нуля: $ a_^<[ell-1]>ne 0^<> $, то это уравнение переставляется с $ ell_<> $-м;
2. если при всех $ jge ell^<> $ коэффициенты $ a_^ <[ell-1]>$ равны нулю, то переменная $ x_<ell>^<> $ не входит ни в одно оставшееся уравнение, и можно перейти к исключению переменной $ x_<ell+1>^<> $.
Поскольку число переменных конечно, то алгоритм исключения должен завершиться за конечное число шагов. Чем он может завершиться? Окончательная система должна иметь вид: $$ left< begin a_<11>x_1 +&a_<12>x_2&+ ldots& +a_<1 <mathfrak r>>x_<mathfrak r>& +a_ <1 ,<mathfrak r>+1>x_<<mathfrak r>+1>&+ ldots + & a_<1n>x_n &=b_1,\ &a_<22>^<[1]>x_2&+ ldots& +a_<2 <mathfrak r>>^ <[1]>x_<mathfrak r>& +a_<2 ,<mathfrak r>+1>^ <[1]>x_<<mathfrak r>+1>&+ ldots + & a_<2n>^ <[1]>x_n &=b_2^<[1]>,\ & & ddots & & & & & dots \ & & & a_ <<mathfrak r><mathfrak r>>^<[<mathfrak r>-1]>x_ <mathfrak r>& + a_ <<mathfrak r>, <mathfrak r>+1>^<[<mathfrak r>-1]>x_<<mathfrak r>+1>& + ldots + & a_ <<mathfrak r>,n>^<[<mathfrak r>-1]>x_n &=b_<mathfrak r>^<[<mathfrak r>-1]>, \ & & & & & & 0 &=b_<<mathfrak r>+1>^<[<mathfrak r>-1]>, \ & & & & & & dots & \ & & & & & & 0 &=b_^<[<mathfrak r>-1]>, \ end right. $$ при $ <mathfrak r>le n_<> $. Заметим, что все коэффициенты этой системы будут принадлежать тому же множеству, что и коэффициенты исходной системы.
Предположение . Мы будем считать, что каждое из первых $ <mathfrak r>_<> $ уравнений системы содержит в своей левой части хотя бы одну переменную с ненулевым коэффициентом.
Процесс получения системы такого вида из исходной системы уравнений называется прямым ходом метода Гаусса.
Исторический комментарий о Гауссе ☞ ЗДЕСЬ.
Установление множества решений
Теорема. Если хотя бы одно из чисел $ b_<<mathfrak r>+1>^<[<mathfrak r>-1]>,dots , b_^<[<mathfrak r>-1]> $ отлично от нуля, то исходная система линейных уравнений будет несовместной.
Для простоты мы будем иллюстрировать наши рассуждения на системах л.у. над $ mathbb R_<> $, в этом же множестве искать решения. Каждое из преобразований метода Гаусса будем обозначать $ to_<> $.
Пример. Решить систему л.у.
$$ left< begin x_1&+x_2&-3, x_3 =& -1 \ 2,x_1&+x_2&-2, x_3 =& 1 \ x_1&+x_2&+ x_3 =& 3 \ x_1&+2,x_2&-3, x_3 =& 1. end right. $$
Решение. $$ to left< begin x_1&+x_2&-3, x_3 =& -1 \ &-x_2&+4, x_3 =& 3 \ &&4, x_3 =& 4 \ &x_2&=& 2 end right. to left< begin x_1&+x_2&-3, x_3 =& -1 \ &-x_2&+4, x_3 =& 3 \ &&4, x_3 =& 4 \ &&4, x_3=& 5 end right. to $$ $$ to left< begin x_1&+x_2&-3, x_3 =& -1 \ &-x_2&+4, x_3 =& 3 \ &&4, x_3 =& 4 \ &&0=& 1 end right. $$ Последнее равенство абсолютно противоречиво.
Ответ. Система несовместна.
Пусть теперь $ b_<<mathfrak r>+1>^<[<mathfrak r>-1]>=0,<>dots, b_^<[<mathfrak r>-1]>=0 $. Возможны два случая: $ <mathfrak r>=n_<> $ и $ <mathfrak r>предположения , имеем $ a_^ <[n-1]>ne 0 $. Но тогда, поскольку система является конечной стадией прямого хода метода Гаусса, то и все коэффициенты $ a_^<[n-2]>, dots, a_<22>^<[1]>, a_ <11>$ должны быть отличны от нуля — в противном случае метод Гаусса не остановился бы на системе такого вида; он называется треугольным: 
Теорема. Если прямой ход метода Гаусса заканчивается треугольной системой, т.е. $ mathfrak r = n_<> $ и $ b_<<mathfrak r>+1>^<[<mathfrak r>-1]>=0,<>dots, b_^<[<mathfrak r>-1]>=0 $, то исходная система линейных уравнений имеет единственное решение.
Пример. Решить систему л.у.
$$ left< begin x_1&+3,x_2&+ x_3 =&5 \ 2,x_1&+x_2&+ x_3 =& 2 \ x_1&+x_2&+ 5,x_3 =& -7 \ 2,x_1&+3,x_2&-3, x_3 =& 14. end right. $$
Ответ. $ x_1=1,, x_<2>=2,, x_3=-2 $ .
Исследуем теперь случай $ <mathfrak r>1) : 
Теорема. Если прямой ход метода Гаусса заканчивается трапециевидной системой, т.е. $ mathfrak r 2) матрицы $ A_<> $ (третьего порядка). Понятие определителя распространяется и на квадратные матрицы бóльших порядков; образно говоря, определитель — это функция элементов матрицы, отвечающая за единственность решения системы уравнений.
Дальнейший матричный анализ метода Гаусса ☞ ЗДЕСЬ.
Формулы Крамера
Рассмотрим систему линейных уравнений с квадратной матрицей $ A_<> $, т.е. такую, у которой число уравнений совпадает с числом неизвестных.
Теорема. Cистема
$$ left<begin a_<11>x_1 +a_<12>x_2+ldots+a_<1n>x_n &=&b_1\ a_<21>x_1 +a_<22>x_2+ldots+a_<2n>x_n &=&b_2\ ldots& & ldots \ a_x_1 +a_x_2+ldots+a_x_n &=&b_n endright. $$ имеет единственное решение тогда и только тогда, когда определитель матрицы этой системы отличен от нуля: $$ left| begin a_ <11>& a_ <12>& dots & a_ <1n>\ a_ <21>& a_ <22>& dots & a_ <2n>\ dots &&& dots \ a_ & a_ & dots & a_ end right| ne 0 . $$ В этом случае решение можно вычислить по формулами Крамера 3) : $$ x_k =frac<det left[ A_<[1]>|dots|A_<[k-1]>|<mathcal B>|A_<[k+1]>|dots|A_ <[n]>right]> <det A>quad npu quad kin < 1,dots,n > . $$ Для получения значения $ x_ $ в числитель ставится определитель, получающийся из $ det A_<> $ заменой его $ k_<> $-го столбца на столбец правых частей ( здесь $ <> | $ означает конкатенацию).
Доказательство ☞ ЗДЕСЬ
Пример. Решить систему уравнений
$$ left<begin 2x_1& +3x_2&+11x_3&+5x_4 &=& color2,\ x_1& +x_2&+5x_3&+2x_4 &=& color1 ,\ 2x_1& +x_2&+3x_3&+2x_4 &=&color<-3>,\ x_1& +x_2&+3x_3&+4x_4 &=&color<-3>. endright. $$
Решение. $$ x_1=frac<left|begin color2 & 3&11&5 \ color1 & 1&5&2 \ color<-3>& 1&3&2 \ color <-3>& 1&3&4 endright|> <left|begin 2& 3&11&5 \ 1& 1&5&2 \ 2& 1&3&2 \ 1& 1&3&4 endright|>=frac<-28><14>=-2, x_2=frac<left|begin 2& color2&11&5 \ 1& color1&5&2 \ 2& color<-3>&3&2 \ 1& color<-3>&3&4 endright|> <left|begin 2& 3&11&5 \ 1& 1&5&2 \ 2& 1&3&2 \ 1& 1&3&4 endright|>=frac<0><14>=0, dots $$ Найдите оставшиеся компоненты решения. ♦
Решение системы линейных уравнений с квадратной матрицей $ A_<> $ является непрерывной функцией коэффициентов этой системы при условии, что $ det A_<> ne 0 $.
Кроме того, формулы Крамера начинают конкурировать по вычислительной эффективности с методом Гаусса в случае систем, зависящих от параметра. Подробнее ☞ ЗДЕСЬ.
Еще один способ решения системы основан на построении обратной матрицы: $$ AX= <mathcal B>quad Rightarrow quad X=A^<-1> <mathcal B> . $$ Этот способ малоэффективен при фиксированных числовых $ A_<> $ и $ <mathcal B>_<> $.
Найти достаточное условие существования общего решения систем уравнений:
$$ A_1 X = <mathcal B>_1 quad u quad A_2 Y = <mathcal B>_2 , $$ при квадратных матрицах $ A_1 $ и $ A_2 $ одинакового порядка.
Теорема Кронекера-Капелли
Матрица, получающаяся конкатенацией матрицы $ A_<> $ и столбца правых частей $ <mathcal B>_<> $ $$ [ A| <mathcal B>] = left( begin a_ <11>& a_ <12>& dots & a_ <1n>& b_1 \ a_ <21>& a_ <22>& dots & a_ <2n>& b_2 \ dots &&& & dots \ a_ & a_ & dots & a_ & b_m end right)_ $$ называется расширенной матрицей системы линейных уравнений $ AX= <mathcal B>$.
Теорема [Кронекер, Капелли]. Система $ AX= <mathcal B>$ совместна тогда и только тогда, когда ранг матрицы этой системы совпадает с рангом ее расширенной матрицы:
$$ operatorname, A = operatorname, [ A| <mathcal B>] . $$ При выполнении этого условия, система имеет единственное решение, если число неизвестных $ n_<> $ совпадает с общим значением ранга $ mathfrak r_<> $, и бесконечное множество решений, если $ n_<> $ больше этого значения.
Доказательство необходимости. Пусть существует решение $ x_1=alpha_1,dots,x_n=alpha_n $ системы, тогда $$alpha_1 A_<[1]>+dots+alpha_n A_<[n]>= <mathcal B> ,$$ т.е. столбец $ <mathcal B>$ линейно выражается через столбцы $ A_<[1]>,dots,A_ <[n]>$. Но тогда $$ operatorname ,dots,A_<[n]>>=operatorname ,dots,A_<[n]>,<mathcal B>> .$$ Следовательно $ operatorname, A = operatorname, [ A| <mathcal B>] $.
Доказательство достаточности проводится в следующем пункте. ♦
Пример. Исследовать совместность системы уравнений
Решение. В этом примере число уравнений совпадает с числом неизвестных. Это обстоятельство несколько облегчает рассуждения. Обратимся к замечанию из предыдущего пункта: система л.у. с числом уравнений, совпадающем с числом неизвестных, как правило, совместна. Тогда попробуем установить условия, обеспечивающие противоположное свойство — несовместность. Оно, фактически, единственно: за все отвечает определитель системы $ det A_<> $. Если он отличен от нуля — система совместна. $$det A = left| begin<color<lambda>> &1&1&1 \ 1&<color<lambda>>&1&1 \ 1&1&<color<lambda>>&1 \ 1&1&1&<color<lambda>> end right|= left| begin (<color<lambda>>-1) &(1-<color<lambda>>)&0&0 \ 0&(<color<lambda>>-1)&(1-<color<lambda>>)&0 \ 0&0&(<color<lambda>>-1)&(1-<color<lambda>>) \ 1&1&1&<color<lambda>> end right| =(<color<lambda>>-1)^3 left| begin 1 &-1&0&0 \ 0&1&-1&0 \ 0&0&1&-1 \ 1&1&1&<color<lambda>> end right|= $$ $ =(<color<lambda>>-1)^3(<color<lambda>>+3) $. По теореме Крамера при $ <color<lambda>>ne 1 $ и при $ <color<lambda>>ne -3 $ решение системы единственно: $$x_1=x_2=x_3=x_4=1/(<color<lambda>>+3) .$$
Осталось исследовать критические случаи: $ <color<lambda>>=1_<> $ и $ <color<lambda>>= -3 $: определитель системы обращается в нуль, но система может оказаться совместной. Придется вычислять ранги, но, к счастью, уже числовых матриц (а не зависящих от параметра, как исходная!). При $ <color<lambda>>= 1_<> $ имеем $$ operatorname left( begin 1 &1&1&1 \ 1&1&1&1 \ 1&1&1&1 \ 1&1&1&1 end right)= operatorname left( begin 1&1&1&1&1 \ 1&1&1&1&1 \ 1&1&1&1&1 \ 1&1&1&1&1 end right)=1 , $$ и система совместна. Она эквивалентна единственному уравнению $$x_1+x_2+x_3+x_4=1 ,$$ которое имеет бесконечно много решений.
При $ <color<lambda>>= -3 $: $$ operatorname left( begin -3 &1&1&1 \ 1&-3&1&1 \ 1&1&-3&1 \ 1&1&1&-3 end right)=3,quad operatorname left( begin -3 &1&1&1&1 \ 1&-3&1&1&1 \ 1&1&-3&1&1 \ 1&1&1&-3&1 end right)=4 $$ и система несовместна.
Ответ. Система несовместна при $ <color<lambda>> = -3 $; она имеет бесконечное множество решений при $ <color<lambda>> = 1_<> $ и единственное решение при $ <color<lambda>> notin <-3,1>$.
Система однородных уравнений
$$ left< begin a_<11>x_1 &+a_<12>x_2&+ ldots&+a_<1n>x_n &=0,\ a_<21>x_1 &+a_<22>x_2&+ ldots&+a_<2n>x_n &=0,\ dots & & & dots & \ a_x_1 &+a_x_2&+ ldots&+a_x_n &=0 end right. $$ всегда совместна: она имеет тривиальное решение $ x_1=0,dots,x_n=0 $. Для того, чтобы у нее существовало еще и нетривиальное решение необходимо и достаточно, чтобы определитель ее матрицы был равен нулю.
Пример. Найти условие, при котором три точки плоскости с координатами $ (x_1,y_1), (x_2,y_2) $ и $ (x_3,y_<3>) $ лежат на одной прямой.
Решение. Будем искать уравнение прямой в виде $ ax+by+c=0 $ при неопределенных коэффициентах $ a,b,c_<> $. Если точки лежат на прямой, то получаем для определения этих коэффициентов систему линейных уравнений: $$ left< begin ax_1+by_1+c & =0\ ax_2+by_2+c & =0\ ax_3+by_3+c & =0 end right. $$ Получившаяся система является однородной, условие существования у нее нетривиального решения (т.е. набора $ (a,b,c)_<> $ при хотя бы одном из чисел отличном от нуля): $$ left|begin x_1 & y_1 & 1 \ x_2 & y_2 & 1 \ x_3 & y_3 & 1 end right|=0 . $$ ♦
Доказать, что для совместности системы
$$ left< begin a_<11>x_1+a_<12>x_2+a_<13>x_3 &=& b_1 \ a_<21>x_1+a_<22>x_2+a_<23>x_3 &=& b_2 \ a_<31>x_1+a_<32>x_2+a_<33>x_3 &=& b_3 \ a_<41>x_1+a_<42>x_2+a_<43>x_3 &=& b_4 end right. $$ необходимо, чтобы было выполнено условие $$ left| begin a_<11>&a_<12>& a_ <13>& b_1 \ a_<21>&a_<22>& a_ <23>& b_2 \ a_<31>&a_<32>& a_ <33>& b_3 \ a_<41>&a_<42>& a_ <43>& b_4 end right|=0 quad . $$ Является ли это условие достаточным для совместности?
An elementary treatise on determinants
в следующей формулировке.
Теорема. Для того чтобы система $ n_<> $ неоднородных уравнений была совместна, необходимо и достаточно, чтобы порядок наибольшего отличного от нуля минора был одинаков в расширенной и нерасширенной матрице системы.
Додсон — один из самых знаменитых математиков мира. Назовите его псевдоним.
Ответ ☞ ЗДЕСЬ
Общее решение
Пусть выполнено условие теоремы Кронекера-Капелли: $ operatorname (A)=operatorname[Amid mathcal B ] =mathfrak $. По определению ранга матрицы, в матрице $ A $ существует минор порядка $ mathfrak $, отличный от нуля; этот же минор останется и минором расширенной матрицы $ [ Amid mathcal B ] $. Пусть, для определенности, ненулевой минор находится в левом верхнем углу матрицы 4) : $$ Delta = Aleft( begin 1 & 2 & dots & mathfrak \ 1 & 2 & dots & mathfrak end right) = left| begin a_ <11>& a_ <12>& dots & a_<1mathfrak> \ a_ <21>& a_ <22>& dots & a_<2mathfrak> \ dots &&& dots \ a_<mathfrak1> & a_<mathfrak2> & dots & a_ <mathfrakmathfrak> end right| ne 0 . $$ Тогда первые $ mathfrak $ строк матрицы $ A $ линейно независимы, а остальные будут линейно выражаться через них. Это же утверждение будет справедливо и для строк матрицы $ [Amid mathcal B] $. Умножая первые $ mathfrak $ уравнений системы на соответствующие числа и складывая их, получим любое оставшееся уравнение. Таким образом, система уравнений может быть заменена эквивалентной ей системой из первых $ mathfrak $ уравнений: $$ left< begin a_<11>x_1+dots+a_<1mathfrak>x_<mathfrak>&+a_<1,mathfrak+1>x_<mathfrak+1>+ dots +a_<1n>x_n&=&b_1, \ dots & & & dots \ a_<mathfrak1>x_1+dots+a_<mathfrakmathfrak>x_<mathfrak>& +a_<mathfrak,mathfrak+1>x_<mathfrak+1>+dots +a_<mathfrakn>x_n&=&b_mathfrak end right. quad iff quad A^ <prime>X=<mathcal B>^ <prime>$$ Если $ mathfrak=n $, то матрица $ A^ <prime>$ квадратная. По предположению $ det A^ <prime>ne 0 $. По теореме Крамера решение такой системы единственно.
Пусть теперь $ mathfrak произвольных фиксированных значениях $ x_<mathfrak+1>,dots,x_n $: $$ x_j=frac< left| begin a_ <11>& dots &a_ <1,j-1>&left[ b_1-(a_<1,mathfrak+1>x_<mathfrak+1>+dots +a_<1n>x_n) right] &a_<1,j+1>& dots &a_<1mathfrak> \ dots &&&dots&&& dots \ a_<mathfrak1> & dots &a_<mathfrak,j-1> & left[ b_<mathfrak>- (a_<mathfrak,mathfrak+1>x_<mathfrak+1>+dots +a_<mathfrakn>x_n) right] &a_<mathfrak,j+1>& dots &a_<mathfrakmathfrak> end right| > <Delta>$$ $$ mbox <при> jin <1,dots, mathfrak> . $$ Таким образом, в этом случае система имеет бесконечное множество решений. Используя свойство линейности определителя по столбцу (см. свойство 5 ☞ ЗДЕСЬ ), формулы можно переписать в виде $$ x_j=beta_j + gamma_+1>x_<mathfrak+1>+dots+gamma_x_n npu jin <1,dots, mathfrak> . $$ Здесь $$ beta_j =frac<1> <Delta>left| begin a_ <11>& dots &a_ <1,j-1>& b_1 &a_<1,j+1>& dots &a_<1mathfrak> \ vdots &&&vdots&&& vdots \ a_<mathfrak1> & dots &a_<mathfrak,j-1> & b_<mathfrak> &a_<mathfrak,j+1>& dots &a_<mathfrakmathfrak> end right|, , $$ $$ gamma_ = -frac<1> <Delta>left| begin a_ <11>& dots &a_ <1,j-1>& a_ <1k>&a_<1,j+1>& dots &a_<1mathfrak> \ vdots &&&vdots&&& vdots \ a_<mathfrak1> & dots &a_<mathfrak,j-1> & a_<mathfrakk> &a_<mathfrak,j+1>& dots &a_<mathfrakmathfrak> end right| . $$ Эти формулы называются общим решением системы $ A X=mathcal B $. Участвующие в них переменные $ x_<mathfrak+1>,dots,x_n $ называются основными (или свободными), а $ x_1,dots,x_<mathfrak> $ — зависимыми. Решение, получающееся из общего решения фиксированием значений основных переменных, называется частным решением системы уравнений.
Пример. Исследовать совместность и найти общее решение системы уравнений:
Решение проведем двумя способами, соответствующими двум способам вычисления ранга матрицы. Вычисляем сначала ранг матрицы $ A $ по методу окаймляющих миноров: $$ |2| ne 0,quad left| begin 2 & 1 \ 6 & 2 end right| ne 0, quad left| begin 2 & 1 & 2 \ 6 & 2 & 4 \ 4 & 1 & 1 end right|=2 ne 0 , $$ а все миноры, окаймляющие последний, равны нулю. Итак, $ operatorname (A) =3 $. Для нахождения ранга расширенной матрицы $ [Amid mathcal B] $ достаточно проверить окаймление найденного ненулевого минора третьего порядка с помощью элементов взятых из столбца правых частей. Имеется всего один такой минор, и он равен нулю. Следовательно $ operatorname[ Amid mathcal B ] =3 $, система совместна, и имеет бесконечное множество решений.
Ненулевой минор третьего порядка (базисный минор) находится в первой, второй и четвертых строках, что означает линейную независимость соответствующих уравнений. Третье уравнение линейно зависит от остальных, и может быть отброшено. Далее, указанный базисный минор образован коэффициентами при $ x_1,x_3 $ и $ x_4 $. Следовательно оставшиеся уравнения могут быть разрешены относительно этих переменных, т.е. они — зависимые, а $ x_2 $ и $ x_5 $ — основные. Использование формулы дает общее решение $$ begin x_1&=&frac<left| begin 2 & 1 & 2 \ 3 & 2 & 4 \ 1 & 1 & 1 end right|> <displaystyle 2>-x_2frac<left| begin -1 & 1 & 2 \ -3 & 2 & 4 \ -2 & 1 & 1 end right|> <displaystyle 2>-x_5frac<left| begin 3 & 1 & 2 \ 5 & 2 & 4 \ 2 & 1 & 1 end right|> <displaystyle 2>=-frac<1><2>+frac<1><2>x_2+frac<1><2>x_5, \ & & \ x_3&=&frac<left| begin 2 & 2 & 2 \ 6 & 3 & 4 \ 4 & 1 & 1 end right|> <displaystyle 2>-x_2frac<left| begin 2 & -1 & 2 \ 6 & -3 & 4 \ 4 & -2 & 1 end right|> <displaystyle 2>-x_5frac<left| begin 2 & 3 & 2 \ 6 & 5 & 4 \ 4 & 2 & 1 end right|><displaystyle 2>=3-4x_5, \ & & \ x_4 &=&frac<left| begin 2 & 1 & 2 \ 6 & 2 & 3 \ 4 & 1 & 1 end right|> <displaystyle 2>-x_2frac<left| begin 2 & 1 & -1 \ 6 & 2 & -3 \ 4 & 1 & -2 end right|> <displaystyle 2>-x_5frac<left| begin 2 & 1 & 3 \ 6 & 2 & 5 \ 4 & 1 & 2 end right|> <displaystyle 2>= 0. end $$ Решим теперь ту же задачу, воспользовавшись методом Гаусса исключения переменных в системе линейных уравнений: $$ left< begin 2x_1&-x_2&+x_3&+2x_4&+3x_5&=&2, \ &&x_3&+2x_4&+4x_5&=&3, \ &&&x_4&&=&0 end right. $$ Используя обратный ход метода Гаусса, снова приходим к полученным формулам.
Ответ. Общее решение системы: $ x_1=1/2 (x_2+x_5-1), x_3=3-4,x_5, x_4=0 $.
Проанализируем теперь полученные общие формулы для общего решения. В этих формулах $ beta_j $ представляет решение системы, получаемое при $ x_<mathfrak+1>=0,dots,x_n=0 $. Величины же коэффициентов $ gamma_ $ вовсе не зависят от правых частей системы и будут одинаковыми при любых значениях $ b_1,dots,b_m $. В частности, если $ b_1=0,dots,b_m=0 $, то в формулах величины $ beta_j $ обращаются в нуль и эти формулы превращаются в $$ x_j=gamma_+1>x_<mathfrak+1>+dots+gamma_x_n npu jin <1,dots, mathfrak> . $$
Вывод. Формула общего решения системы $ A X=mathcal B $: $$ x_j=beta_j + gamma_+1>x_<mathfrak+1>+dots+gamma_x_n npu jin <1,dots, mathfrak> $$ состоит из двух частей: слагаемые, не содержащие свободных переменных, определяют частное решение неоднородной системы: $$ x_1= beta_1,dots, x_<mathfrak>= beta_<mathfrak>,x_<mathfrak+1>=0,dots,x_n=0 ; $$ оставшиеся после их отбрасывания формулы задают общее решение системы $ AX=mathbb O $. Этот результат обобщается в следующей теореме.
Теорема. Общее решение системы уравнений $ A X=mathcal B $ представимо в виде суммы какого-то частного решения этой системы и общего решения соответствующей однородной системы $ A X=mathbb O $.
Доказательство тривиально если система $ A X=mathcal B $ имеет единственное решение. Если же решений бесконечно много, то выбрав какое-то одно частное $ X=X_1 $ мы получаем, что любое другое частное решение $ X=X_2 $ должно быть связано с первым соотношением $$ A(X_2-X_1)=mathbb O , $$ т.е. разность частных решений неоднородной системы обязательно является решением однородной системы уравнений $ AX=mathbb O $. ♦
Теперь посмотрим как можно описать общее решение однородной системы.
Система однородных уравнений
Система линейных уравнений называется однородной, если все коэффициенты правых частей равны нулю: $$ left< begin a_<11>x_1 &+a_<12>x_2&+ ldots&+a_<1n>x_n &=0,\ a_<21>x_1 &+a_<22>x_2&+ ldots&+a_<2n>x_n &=0,\ dots & & & dots & \ a_x_1 &+a_x_2&+ ldots&+a_x_n &=0. end right. $$ или, в матричном виде: $$ A_X=<mathbb O>_ $$
Задача ставится о поиске нетривиального решения. Оно не всегда существует. Так, к примеру, если матрица $ A_<> $ системы — квадратная и имеет ненулевой определитель, то, согласно теореме Крамера, нетривиальных решений у однородной системы нет. Теорема Кронекера-Капелли утверждает, что условие $ det (A_<>) = 0 $ является и достаточным для существования нетривиального решения.
Теорема 1. Для того, чтобы система однородных уравнений с квадратной матрицей $ A_<> $ имела нетривиальное решение необходимо и достаточно, чтобы $ det (A_<>) = 0 $.
Для произвольной (не обязательно квадратной) матрицы $ A_<> $ имеет место следующий общий результат.
Теорема 2. Если $ operatorname (A)=mathfrak r 5) $ A_^<> $.
Теорема 3. Множество решений системы однородных уравнений образует линейное подпространство пространства $ mathbb A^ $. Размерность этого подпространства равна $ n-mathfrak r $, а фундаментальная система решений образует его базис.
Пусть матрица системы $ AX=mathbb O $ квадратная и
$$ operatorname (A) =n_<>-1 , .$$ Доказать, что если ненулевой минор матрицы порядка $ n_<>-1 $ соответствует какому-нибудь элементу $ j_<> $-й строки, то система алгебраических дополнений к элементам $ a_,dots,a_^<> $ этой строки составляет ФСР для $ AX=mathbb O_<> $. Например, для системы $$ left< begin a_<11>x_1 +a_<12>x_2+a_<13>x_3&=0,\ a_<21>x_1 +a_<22>x_2+a_<23>x_3&=0 end right. $$ ФСР состоит из решения $$ x_1=left| begin a_ <12>& a_ <13>\ a_ <22>& a_ <23>end right| , x_2=-left| begin a_ <11>& a_ <13>\ a_ <21>& a_ <23>end right| , x_3=left| begin a_ <11>& a_ <12>\ a_ <21>& a_ <22>end right| , $$ если только хотя бы один из миноров отличен от нуля.
Теперь обсудим способы нахождения ФСР.
1. Первый из них получается из общего метода решения системы линейных уравнений, рассмотренного в предыдущем пункте. Так же, как и в том пункте, сделаем упрощающее обозначения предположение, что зависимыми переменными являются первые $ x_<1>,dots,x_ <mathfrak r>$, т.е. общее решение задается формулами $$ x_j=gamma_+1>x_<mathfrak+1>+dots+gamma_x_n npu jin <1,dots, mathfrak> . $$ Иными словами, вектор столбец $$ X=left(begin gamma_<1,mathfrak+1>x_<mathfrak+1>+dots+gamma_<1n>x_n \ gamma_<2,mathfrak+1>x_<mathfrak+1>+dots+gamma_<2n>x_n \ vdots \ gamma_<mathfrak,mathfrak+1>x_<mathfrak+1>+dots+gamma_<mathfrakn>x_n \ x_<mathfrak+1> \ x_<mathfrak+2> \ vdots \ x_ endright) $$ будет решением однородной системы при любых наборах значений основных переменных $ x_<mathfrak+1>,dots,x_ $. Представим этот вектор в виде суммы векторов: $$ =x_<mathfrak+1> underbrace< left(begin gamma_<1,mathfrak+1> \ gamma_<2,mathfrak+1> \ vdots \ gamma_<mathfrak,mathfrak+1> \ 1 \ 0 \ vdots \ 0 endright)>_ + x_<mathfrak+2> underbrace<left(begin gamma_<1,mathfrak+2> \ gamma_<2,mathfrak+2> \ vdots \ gamma_<mathfrak,mathfrak+2> \ 0 \ 1 \ vdots \ 0 endright)>_+dots+ x_ underbrace<left(begin gamma_ <1n>\ gamma_ <2n>\ vdots \ gamma_<mathfrakn> \ 0 \ 0 \ vdots \ 1 endright)>_> . $$ Таким образом, любое решение однородной системы представимо в виде линейной комбинации $ n_<>— mathfrak r $ фиксированных решений. Именно эти решения и можно взять в качестве ФСР — их линейная независимость очевидна (единицы в нижних частях каждого вектора $ X_ $ расположены на разных местах, и ни какая линейная комбинация столбцов $ < X_1,dots,X_> $ не сможет обратить их одновременно в нуль).
Оформим этот способ построения ФСР в теорему:
Теорема 4. Если система уравнений $ AX=mathbb O $ имеет структуру матрицы $ A_<> $ вида:
$$ A = left[ E_ <mathfrak r>mid P_ <mathfrak r times (n-mathfrak r)>right] , $$ то ее ФСР состоит из столбцов матрицы $$ left[ begin — P^ <top>\ hline E_ end right] . $$
Пример. Найти ФСР для системы уравнений
Решение. Приводим систему к трапециевидному виду: $$ left< begin x_1-&x_2+&x_3-&x_4=&0, \ &&x_3+&4x_4=&0 end right. $$ В качестве зависимых переменных можно взять, например, $ x_ <1>$ и $ x_ <3>$. $$ begin x_1 & x_3 & x_2 & x_4 \ hline 1 & 0 & 1 & 0 \ 5 & -4 & 0 & 1 end $$
2. Этот способ напоминает вычисление обратной матрицы методом приписывания единичной матрицы. Транспонируем матрицу $ A_<> $ системы и припишем к ней справа единичную матрицу порядка $ n_<> $: $$ left[ A^ <top>| E_n right] = left(begin a_ <11>& a_ <21>& dots & a_ & 1 & 0 & 0 & dots & 0 \ a_ <12>& a_ <22>& dots & a_ & 0 & 1 & 0 & dots & 0 \ a_ <13>& a_ <23>& dots & a_ & 0 & 0 & 1 & dots & 0 \ vdots & & & vdots & vdots & & & ddots & vdots \ a_ <1n>& a_ <2n>& dots & a_ & 0 & 0 & 0 & dots & 1 end right) ; $$ здесь $ <> |_<> <> $ означает конкатенацию. Получившуюся матрицу элементарными преобразованиями строк приводим к форме: $$ left( begin hat A & K \ mathbb O & L end right) = left(begin color <star>& * & * & dots & * & * & * & * & * & * & * & dots & * \ 0 & color <star>& * & dots & * & * & * & * & * & * & * & dots & * \ 0 & 0 & color <star>& dots & * & * & * & * & * & * & * & dots & * \ vdots & & & ddots & & vdots & & & vdots & & & & vdots \ 0 & 0 & dots & & 0 & color <star>& * & * & * & * & * & dots & * \ hline 0 & 0 & dots & 0 & 0 & 0 & 0 & 0 & Box & Box & Box & dots & Box \ vdots & & & & & vdots & & & vdots & & & & vdots \ 0 & 0 & dots & 0 & 0 & 0 & 0 & 0 & Box & Box & Box & dots & Box end right) begin left.begin \ \ \ \ \ endright> mathfrak r \ left. begin \ \ \ endright> n — mathfrak r end . $$ Элементы трапециевидной матрицы $ hat A $, обозначенные $ color <star>$, могут быть равны нулю, но $ operatorname(hat A)= mathfrak r_<> $. В этом случае строки матрицы $ L_<> $, образовавшейся в правом нижнем углу (ее элементы обозначены $ Box $), составляют ФСР для системы $ AX=mathbb O $.
Пример. Найти ФСР для системы уравнений
$$ left< begin x_1 &+2,x_2&+ x_3&+3,x_4&-x_5&+2,x_6=&0,\ -3x_1 &-x_2&+ 2,x_3&-4,x_4&+x_5&-x_6=&0,\ x_1 &+x_2&+ 3,x_3&+2,x_4&+x_5&+3,x_6=&0,\ -8,x_1 &-7,x_2&+ 4,x_3&-15,x_4&+6,x_5&-5,x_6=&0,\ 6x_1 &+5,x_2& +5,x_3&+11,x_4 &&+9,x_6=&0. end right. $$ Решение. Преобразуем матрицу $ left[ A^ <top>| E_6 right] $
$$ left(begin 1 & -3 & 1 & -8 & 6 & 1 \ 2 & -1 & 1 & -7 & 5 & & 1 \ 1 & 2 & 3 & 4 & 5 & & & 1 \ 3 & -4 & 2 & -15 & 11 &&&& 1 \ -1 & 1 & 1 & 6 & 0 &&&&& 1 \ 2 & -1 & 3 & -5 & 9 &&&&&& 1 end right)_ <6times 11>$$ к трапециевидной форме с помощью элементарных преобразований строк: $$ rightarrow left(begin 1 & -3 & 1 & -8 & 6 & 1 \ 0 & 5 & -1 & 9 & -7 &-2 & 1 \ 0 & 5 & 2 & 12 & -1 &-1 &0 & 1 \ 0 & 5 & -1 & 9 & -7 &-3&0&0& 1 \ 0 & -2 & 2 & -2 & 6 &1&0&0&0& 1 \ 0 & 5 & 1 & 11 & -3 &-2&0&0&0&0& 1 end right)rightarrow $$ $$ rightarrow left(begin 1 & -3 & 1 & -8 & 6 & 1 \ 0 & 5 & -1 & 9 & -7 &-2 & 1 \ 0 & 0 & 3 & 3 & 6 &1 &-1 & 1 \ 0 & 0 & 0 & 0 & 0 &-1&-1&0& 1 \ 0 & 0 & 8/5 & 8/5 & 16/5 &1/5&2/5&0&0& 1 \ 0 & 0 & 2 & 2 & 4 &0&-1&0&0&0& 1 end right)rightarrow $$ $$ rightarrow left(begin 1 & -3 & 1 & -8 & 6 & 1 \ 0 & 5 & -1 & 9 & -7 &-2 & 1 \ 0 & 0 & 3 & 3 & 6 &1 &-1 & 1 \ 0 & 0 & 0 & 0 & 0 &-1&-1&0& 1 \ 0 & 0 & 0 & 0 & 0 &-1/3&14/15&-8/15&0& 1 \ 0 & 0 & 0 & 0 & 0 &-2/3&-1/3&-2/3&0& 0 & 1 end right) $$
3. Еще один способ построения ФСР основан на теореме Гамильтона-Кэли.
Теорема. Пусть матрица системы $ AX=mathbb O $ квадратная и $ operatorname (A) = <mathfrak r>$. Тогда характеристический полином матрицы $ A_<> $ имеет вид:
Пример. Найти ФСР для системы уравнений
Решение. Здесь $$ A= left( begin 1 & 1 & -1 & -1 \ 2 & 3 & 1 & -2 \ 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 end right), quad det (A-lambda E) = lambda^2(lambda^2-4lambda+1), $$ $$ A^2-4A+E= left( begin 0 & 0 & 4 & 1 \ 0 & 0 & -3 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1 end right) $$
Блок-схемы зависимости множества решений системы уравнений $ AX= mathcal B $ от комбинации чисел $ n, mathfrak r $ ☞ ЗДЕСЬ.
Геометрическая интерпретация
Геометрический смысл введенных определений поясним на примере $ mathbb R^ <3>$. Уравнение $$ a_1x_1+a_2x_2+a_3x_3=b $$ — при фиксированных вещественных коэффициентах $ a_1,a_2,a_3 $ (хотя бы один из них считаем отличным от нуля) и $ b_<> $ — задает плоскость. Если, к примеру, $ a_1ne 0 $, то из уравнения получаем выражение для $ x_ <1>$ как функции $ x_2,x_3 $: $$ x_1=frac-fracx_2-fracx_3 . $$ В этом представлении переменные $ x_ <2>$ и $ x_ <3>$ могут принимать любые вещественные значения независимо друг от друга, а вот переменная $ x_ <1>$ полностью определяется заданием $ x_ <2>$ и $ x_ <3>$. С одной стороны, последняя формула определяет общее решения системы линейных уравнений (которая в нашем частном случае состоит из одного-единственного уравнения); переменные $ x_ <2>$ и $ x_ <3>$ выбраны основными, а $ x_ <1>$ оказывается зависимой. Строго говоря, координаты любой точки плоскости можно представить формулами $$x_1=frac-fract-fracu, x_2=t, x_3=u quad npu quad \subset mathbb R , $$ которые называются параметрическим представлением плоскости. Таким образом, получили геометрическую интерпретацию общего решения системы уравнений. Идем далее: представим последние формулы в векторной форме: $$ left( begin x_1 \ x_2 \ x_3 end right)= left( begin b/a_1- t, a_2/a_1- u, a_3/a_1 \ t \ u end right)= left( begin b/a_1\ 0 \ 0 end right)+ t left( begin -a_2/a_1\ 1 \ 0 end right) + u left( begin -a_3/a_1\ 0 \ 1 end right) . $$ Какой геометрический смысл имеет каждое из слагаемых? Первое слагаемое $$ X_0=left( begin b/a_1\ 0 \ 0 end right) $$ получается при задании $ t=0,u=0_<> $ в общем решении. Это — частное решение нашего уравнения и определяет точку, через которую проходит плоскость. Два оставшихся столбца $$ X_1=left( begin -a_2/a_1\ 1 \ 0 end right) quad u quad X_2=left( begin -a_3/a_1\ 0 \ 1 end right) $$ не задают решения нашего уравнения — если только $ bne 0_<> $. Но оба удовлетворяют однородному уравнению $$ a_1x_1+a_2x_2+a_3x_3=0 , $$ Последнее также определяет плоскость — параллельную исходной и проходящую через начало координат. Первая плоскость получается из второй сдвигом (параллельным переносом) на вектор $ vec $: и этот факт составляет геометрическую интерпретацию теоремы, сформулированной в конце ☞ ПУНКТА:
Теорема. Общее решение системы уравнений $ A X=mathcal B $ представимо в виде суммы какого-то частного решения этой системы и общего решения соответствующей однородной системы $ A X=mathbb O $.

Теперь рассмотрим систему из двух уравнений: $$ left<begin a_<11>x_1 +a_<12>x_2+a_<13>x_3 &=&b_1,\ a_<21>x_1 +a_<22>x_2+a_<23>x_3 &=&b_2. endright. $$ Ее можно интерпретировать как пересечение двух плоскостей в $ mathbb R^ <3>$. Здесь уже возможны варианты: пересечение может оказаться как пустым так и непустым. От чего это зависит? — В соответствии с теоремой Кронекера-Капелли, надо сравнить два числа $$ operatorname left( begin a_ <11>& a_ <12>& a_ <13>\ a_ <21>& a_ <22>& a_ <23>end right) quad u quad operatorname left( begin a_ <11>& a_ <12>& a_ <13>& b_1 \ a_ <21>& a_ <22>& a_ <23>& b_2 end right) . $$ Очевидно, ни одно из них не может быть большим $ 2_<> $. Если оба равны $ 2_<> $ и этот факт обеспечен, например, условием $$ left| begin a_ <11>& a_ <12>\ a_ <21>& a_ <22>end right| ne 0, $$ то решения системы определяют прямую в пространстве. Действительно, при таком условии систему можно разрешить относительно неизвестных $ x_ <1>$ и $ x_ <2>$ и представить общее решение в виде: $$ x_1= frac<left|begin b_1 & a_ <12>\ b_2 & a_ <22>end right|><left|begin a_ <11>& a_ <12>\ a_ <21>& a_ <22>end right|>+ frac<left|begin a_ <12>& a_ <13>\ a_ <21>& a_ <23>end right|><left|begin a_ <11>& a_ <12>\ a_ <21>& a_ <22>end right|>x_3 , quad x_2= frac<left|begin a_ <11>& b_ <1>\ a_ <12>& b_ <2>end right|><left|begin a_ <11>& a_ <12>\ a_ <21>& a_ <22>end right|>- frac<left|begin a_ <11>& a_ <13>\ a_ <21>& a_ <23>end right|><left|begin a_ <11>& a_ <12>\ a_ <21>& a_ <22>end right|>x_3 . $$ В этих формулах переменная $ x_ <3>$ принимает любое значение, а значения переменных $ x_ <1>$ и $ x_ <2>$ линейно выражаются через $ x_ <3>$. Общее решение фактически задает прямую в параметрическом виде: координаты произвольной ее точки определяются формулами $$ left( begin x_1 \ x_2 \ x_3 end right)=X_0+tX_1 , $$ где вектор $$ quad X_0 = left(frac<left|begin a_ <11>& b_ <1>\ a_ <12>& b_ <2>end right|><left|begin a_ <11>& a_ <12>\ a_ <21>& a_ <22>end right|> , frac<left|begin a_ <11>& b_ <1>\ a_ <12>& b_ <2>end right|><left|begin a_ <11>& a_ <12>\ a_ <21>& a_ <22>end right|>, 0right)^ <top>$$ задает координаты точки, лежащей на прямой (т.е. принадлежащей пересечению плоскостей), а вектор $$ X_1= left(frac<left|begin a_ <12>& a_ <13>\ a_ <21>& a_ <23>end right|><left|begin a_ <11>& a_ <12>\ a_ <21>& a_ <22>end right|>, — frac<left|begin a_ <11>& a_ <13>\ a_ <21>& a_ <23>end right|><left|begin a_ <11>& a_ <12>\ a_ <21>& a_ <22>end right|>, 1 right)^ <top>$$ является направляющим для прямой. С тем же успехом мы могли бы взять в качестве направляющего вектор, получающийся растяжением $ X_ <1>$: $$ tilde X_1 = left(left|begin a_ <12>& a_ <13>\ a_ <21>& a_ <23>end right|, — left|begin a_ <11>& a_ <13>\ a_ <21>& a_ <23>end right|, left|begin a_ <11>& a_ <12>\ a_ <21>& a_ <22>end right| right)^ <top> . $$ 
Мы рассмотрели пока только случай пересекающихся плоскостей в пространстве. Его можно считать общим, т.е. случаем «как правило»: две случайным образом выбранные плоскости в $ mathbb R^ <3>$ пересекаться будут. Исследуем теперь исключительный случай — параллельности плоскостей. Исключительность этого случая может быть проверена и аналитикой. Для несовместности системы из двух уравнений необходимо, чтобы ранг ее матрицы $$ left( begin a_ <11>& a_ <12>& a_ <13>\ a_ <21>& a_ <22>& a_ <23>end right) $$ оказался меньшим $ 2_<> $. Это равносильно тому, что все миноры второго порядка этой матрицы обращаются в нуль: $$ left| begin a_ <11>& a_ <12>\ a_ <21>& a_ <22>end right|=0, left| begin a_ <12>& a_ <13>\ a_ <22>& a_ <23>end right| =0, left| begin a_ <11>& a_ <13>\ a_ <21>& a_ <23>end right|=0 . $$ Эти условия можно переписать в виде $$ frac>>=frac>>=frac>> ; $$ и, если обозначить общую величину последний отношений через $ tau_<> $, то получаем: $$ (a_<11>,a_<12>,a_<13>)=tau (a_<21>,a_<22>,a_<23>) . $$ Если вспомнить, что каждый из этих наборов коэффициентов задает вектор $ vec> $ в $ mathbb R^ <3>$, перпендикулярный соответствующей плоскости, то, в самом деле, плоскости, определяемые уравнениями, оказываются параллельными. Пересекаться они, как правило, не будут: для пересечения необходимо, чтобы расширенная матрица системы $$ left( begin a_ <11>& a_ <12>& a_ <13>& b_1 \ a_ <21>& a_ <22>& a_ <23>& b_2 end right) $$ имела ранг меньший $ 2_<> $. Это возможно только при условии когда коэффициенты правых частей удовлетворяют соотношению $$ b_1 = tau b_2 $$ при величине $ tau_<> $ определенной выше. При выполнении этого условия второе уравнение получается из первого домножением на $ tau_<> $ и соответствующие плоскости попросту совпадают.
Перейдем теперь к системе из трех уравнений: $$ left< begin a_<11>x_1 +&a_<12>x_2+&a_<13>x_3=&b_1, \ a_<21>x_1 +&a_<22>x_2+&a_<23>x_3=&b_2, \ a_<31>x_1 +&a_<32>x_2+&a_<33>x_3=&b_3. end right. $$ Вариантов взаимного расположения трех плоскостей в $ mathbb R^ <3>$ уже значительно больше. Какой из них будет самым распространенным, то есть случаем «как правило»? Геометрически ответ очевиден: если пересечение двух плоскостей определяет, как правило, прямую, то эта прямая пересекается с третьей плоскостью, как правило, в одной-единственной точке. И алгебра подтверждает геометрию: в комментарии к теореме Крамера говорится, что система, число уравнений которой совпадает с числом неизвестных, как правило, имеет единственное решение. Условие для этого случая «как правило» дается той же теоремой Крамера: $$ left| begin a_ <11>& a_ <12>& a_<13>\ a_ <21>& a_ <22>& a_ <23>\ a_ <31>& a_ <32>& a_ <33>end right| ne 0 . $$
Теорема Кронекера-Капелли в этом случае не нужна — нет, она остается справедливой! — но проверка условия на ранги матриц тривиальна: они оба равны $ 3_<> $. Если же указанный определитель обращается в нуль, то этот факт эквивалентен тому, что три строки определителя линейно зависимы. Например, возможно, что строка $ (a_<31>,a_<32>, a_<33>) $ может быть представлена в виде линейной комбинации первых двух строк. Вспомним геометрический смысл этих строк: они задают координаты векторов, перпендикулярных соответствующим плоскостям. Если система уравнений $$ left<begin a_<11>x_1 +a_<12>x_2+a_<13>x_3 &=&b_1,\ a_<21>x_1 +a_<22>x_2+a_<23>x_3 &=&b_2 endright. $$ определяет прямую в $ mathbb R^ <3>$, то оба вектора $ vec> $ и $ vec> $ при $ A^<[1]>= (a_<11>,a_<12>, a_<13>) $ и $ A^<[2]>= (a_<21>,a_<22>, a_<23>) $ перпендикулярны этой прямой; любая их комбинация также перпендикулярна этой прямой, а, следовательно, плоскость $$ a_<31>x_1 +a_<32>x_2+a_<33>x_3 =b_3 $$ будет ей параллельна.
Статья не закончена!
Ортогональность
Геометрические соображения из предыдущего пункта могут быть обобщены на случай когда размерности рассматриваемых пространств увеличиваются, и мы говорим о точках и векторах многомерных пространств. В последующих пунктах нам потребуются понятия линейной оболочки, линейного пространства, размерности, базиса и координат применительно к векторам-столбцам или векторам-строкам. Их можно найти ☞ ЗДЕСЬ.
Задача решения системы линейных уравнений $$ left< begin 3x_1&+4x_2&-x_3&=2, \ x_1&-2x_2&+3x_3&=1 end right. $$ может быть рассмотрена с двух точек зрения. С одной стороны, переписав систему в виде $$ x_1left(begin 3 \ 1 end right)+ x_2left(begin 4 \ -2 end right)+ x_3left(begin -1 \ 3 end right)= left(begin 2 \ 1 end right) , $$ можно говорить о поиске линейной комбинации столбцов $$ left(begin 3 \ 1 end right), left(begin 4 \ -2 end right), left(begin -1 \ 3 end right) $$ равной заданному столбцу $$ left(begin 2 \ 1 end right) . $$ В случае произвольной системы, записанной в матричном виде $$ A_X=mathcal B_ $$ совместность системы интерпретировать в смысле принадлежности столбца $ mathcal B $ линейной оболочке столбцов $ A_<[1]>,dots,A_ <[n]>$: $$ mathcal B=x_1 A_<[1]>+dots+x_nA_ <[n]>quad iff quad mathcal B in mathcal L (A_<[1]>,dots,A_<[n]>) . $$ В случае положительного ответа числа $ x_<1>,dots,x_n $ интерпретируются как координаты столбца $ mathcal B $ в системе столбцов 11) $ ,dots,A_<[n]>> $.
С другой стороны, к той же задаче решения системы уравнений, в предыдущем ПУНКТЕ мы подошли с другой стороны. Первое из уравнений системы $$ 3,x_1+4,x_2-x_3=2 $$ можно интерпретировать так: скалярное произведение векторов $ vec<<mathbf OA>^<[1]>> $ и $ vec<<mathbf OX>> $ равно фиксированному числу $ 2_<> $. Здесь вектора рассматриваются в пространстве строк $ mathbb R_<>^ <3>$; считается, что каждый вектор имеет начало в начале координат $ mathbf O=[0,0,0] $, а конец — в точке с координатами $ [3,4,-1] $ или, соответственно, $ [x_1,x_2,x_3] $. Если скалярное произведение векторов обозначать скобками $ langle <> mbox < >rangle $, то систему уравнений можно переписать в виде $$ langle vec<<mathbf OA>^<[1]>> , vec<<mathbf OX>> rangle=2, langle vec<<mathbf OA>^<[2]>> , vec<<mathbf OX>> rangle=1 quad npu quad A^ <[1]>= [3,4,-1], A^<[2]>=[1,-2,3] $$ — строках матрицы $ A_<> $. И задачу решения такой системы понимать в смысле: найти координаты всех векторов-строк $ [x_1,x_2,x_3] $ которые обеспечат нам заданные значения скалярных произведений с двумя фиксированными векторами.
Геометрическая интерпретация еще более упрощается если рассмотреть случай однородной системы уравнений. Так, решить систему уравнений $$ left< begin 3x_1&+4x_2&-x_3&=0, \ x_1&-2x_2&+3x_3&=0 end right. $$ означает подобрать вектор $ vec<<mathbf OX>> $ перпендикулярный (ортогональный) одновременно обоим векторам $ vec<<mathbf OA>^<[1]>> $ и $ vec<<mathbf OA>^<[2]>> $. Очевидно, что таких векторов в $ mathbb R^ <3>$ бесконечно много — найдя хотя бы один такой вектор $ vec<<mathbf OX>> $, другие получим его растяжением: $ alpha cdot vec<<mathbf OX>> $ остается перпендикулярным векторам $ vec<<mathbf OA>^<[1]>> $ и $ vec<<mathbf OA>^<[2]>> $ при $ forall alpha in mathbb R $.
Все эти геометрические соображения обобщаются в произвольное пространство $ mathbb R_<>^ $ строк или столбцов, состоящих из $ n_<> $ вещественных чисел (компонент). Для этого приходится обобщать понятие скалярного произведения. В общем случае оно вводится аксиоматически (и, более того, в одном и том же множестве может быть определено разными способами, см. ☞ ЕВКЛИДОВО ПРОСТРАНСТВО ). Мы сейчас не будем залезать так глубоко в эту аксиоматику, а просто определим скалярное произведение двух строк $ X=[x_1,x_2,dots,x_n] $ и $ Y=[y_1,y_2,dots,y_n] $ формулой $$ langle X,Y rangle=x_1y_1+x_2y_2+dots+x_ny_n $$ и продекларируем без обоснований, что все привычные нам по случаям $ mathbb R^ <2>$ и $ mathbb R^ <3>$ свойства скалярного произведения будут выполнены.
В терминах скалярного произведения, задачу решения системы линейных уравнений можно переформулировать как поиск строки $ X=[x_1,x_2,dots,x_n] $, ортогональной всем строкам матрицы $ A_<> $: $$ langle A^<[1]>,X rangle=0, langle A^<[2]>,X rangle=0,dots, langle A^<[m]>,X rangle=0 . $$ Множество таких строк образует линейное подпространство пространства $ mathbb R_<>^ $, это подпространство является ортогональным дополнением линейной оболочки $ mathcal L ( A^<[1]>, A^<[2]>,dots, A^ <[m]>) $ в пространстве $ mathbb R_<>^ $. Это подпространство называется нуль-пространством матрицы или ядром матрицы $ A_<> $ и обозначается 12) $ <mathcal K>er (A) $. Фундаментальная система решений системы $ AX=mathbb O $ составляет базис этого подпространства. Для произвольного линейного пространства количество векторов его базиса называется размерностью пространства и обозначается $ operatorname $. Во введенных обозначениях теорема из ☞ ПУНКТА переформулируется так:
Теорема. $ operatorname left( <mathcal K>er (A) right)=n- mathfrak r $, где $ n_<> $ — количество столбцов матрицы $ A_<> $, а $ mathfrak r=operatorname (A) $ — ее ранг.
источники:
http://toehelp.ru/theory/math/lecture14/lecture14.html
http://vmath.ru/vf5/algebra2/linearsystems

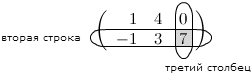
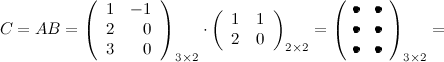
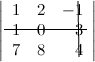



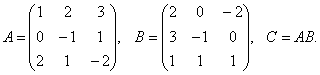
































 . Решением этой системы является любая пара чисел, отличающихся знаком.
. Решением этой системы является любая пара чисел, отличающихся знаком. , если бы решение существовало, то x1 + x2 равнялось бы одновременно нулю и единице.
, если бы решение существовало, то x1 + x2 равнялось бы одновременно нулю и единице.





















 которая не имеет решений.
которая не имеет решений. и, следовательно, имеет бесконечное множество решений x=y,y Î R.
и, следовательно, имеет бесконечное множество решений x=y,y Î R.









