Not to be confused with eclipse.
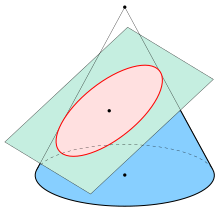
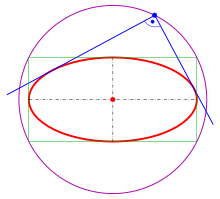
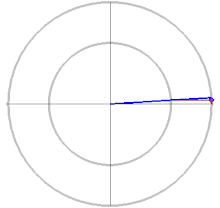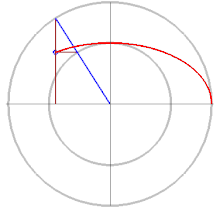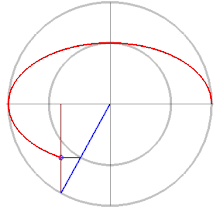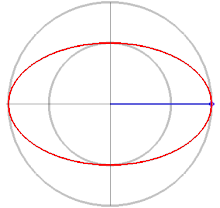
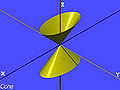
An ellipse (red) obtained as the intersection of a cone with an inclined plane.
Ellipses: examples with increasing eccentricity
In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity 


An ellipse has a simple algebraic solution for its area, but only approximations for its perimeter (also known as circumference), for which integration is required to obtain an exact solution.
Analytically, the equation of a standard ellipse centered at the origin with width 

Assuming 


Ellipses are the closed type of conic section: a plane curve tracing the intersection of a cone with a plane (see figure). Ellipses have many similarities with the other two forms of conic sections, parabolas and hyperbolas, both of which are open and unbounded. An angled cross section of a cylinder is also an ellipse.
An ellipse may also be defined in terms of one focal point and a line outside the ellipse called the directrix: for all points on the ellipse, the ratio between the distance to the focus and the distance to the directrix is a constant. This constant ratio is the above-mentioned eccentricity:
Ellipses are common in physics, astronomy and engineering. For example, the orbit of each planet in the Solar System is approximately an ellipse with the Sun at one focus point (more precisely, the focus is the barycenter of the Sun–planet pair). The same is true for moons orbiting planets and all other systems of two astronomical bodies. The shapes of planets and stars are often well described by ellipsoids. A circle viewed from a side angle looks like an ellipse: that is, the ellipse is the image of a circle under parallel or perspective projection. The ellipse is also the simplest Lissajous figure formed when the horizontal and vertical motions are sinusoids with the same frequency: a similar effect leads to elliptical polarization of light in optics.
The name, ἔλλειψις (élleipsis, «omission»), was given by Apollonius of Perga in his Conics.
Definition as locus of points[edit]
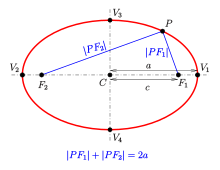
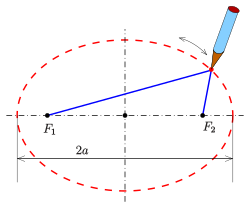
Ellipse: definition by sum of distances to foci
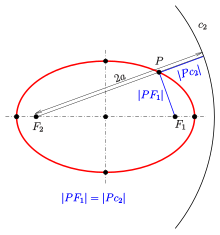
Ellipse: definition by focus and circular directrix
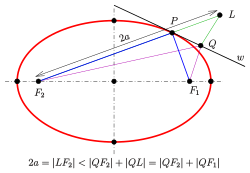
An ellipse can be defined geometrically as a set or locus of points in the Euclidean plane:
- Given two fixed points
called the foci and a distance
which is greater than the distance between the foci, the ellipse is the set of points
such that the sum of the distances
is equal to
:
The midpoint 




The case 
The equation 
- If
is the circle with center
and radius
, then the distance of a point
to the circle
equals the distance to the focus
:


Using Dandelin spheres, one can prove that any section of a cone with a plane is an ellipse, assuming the plane does not contain the apex and has slope less than that of the lines on the cone.
In Cartesian coordinates[edit]
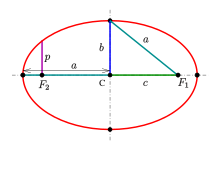
Shape parameters:
- a: semi-major axis,
- b: semi-minor axis,
- c: linear eccentricity,
- p: semi-latus rectum (usually
).
Standard equation[edit]
The standard form of an ellipse in Cartesian coordinates assumes that the origin is the center of the ellipse, the x-axis is the major axis, and:
- the foci are the points
,
- the major points are
.
For an arbitrary point 




Removing the radicals by suitable squarings and using 
or, solved for y:
The width and height parameters 




It follows from the equation that the ellipse is symmetric with respect to the coordinate axes and hence with respect to the origin.
Parameters[edit]
Principal axes[edit]
Throughout this article, the semi-major and semi-minor axes are denoted 


In principle, the canonical ellipse equation 





Linear eccentricity[edit]
This is the distance from the center to a focus: 
Eccentricity[edit]
The eccentricity can be expressed as:
assuming 

Semi-latus rectum[edit]
The length of the chord through one focus, perpendicular to the major axis, is called the latus rectum. One half of it is the semi-latus rectum 
[4]
The semi-latus rectum 
Tangent[edit]
An arbitrary line 


A vector parametric equation of the tangent is:
with
Proof:
Let 




There are then cases:
Then line
and the ellipse have only point
in common, and
is a tangent. The tangent direction has perpendicular vector
, so the tangent line has equation
for some
. Because
is on the tangent and the ellipse, one obtains
.
Then line
has a second point in common with the ellipse, and is a secant.
Using (1) one finds that 

If 



Shifted ellipse[edit]
If the standard ellipse is shifted to have center 
The axes are still parallel to the x- and y-axes.
General ellipse[edit]
In analytic geometry, the ellipse is defined as a quadric: the set of points 
provided 
To distinguish the degenerate cases from the non-degenerate case, let ∆ be the determinant
Then the ellipse is a non-degenerate real ellipse if and only if C∆ < 0. If C∆ > 0, we have an imaginary ellipse, and if ∆ = 0, we have a point ellipse.[7]: p.63
The general equation’s coefficients can be obtained from known semi-major axis 



These expressions can be derived from the canonical equation
by an affine transformation of the coordinates 
Conversely, the canonical form parameters can be obtained from the general form coefficients by the equations:[citation needed]
Parametric representation[edit]
The construction of points based on the parametric equation and the interpretation of parameter t, which is due to de la Hire
Ellipse points calculated by the rational representation with equal spaced parameters (
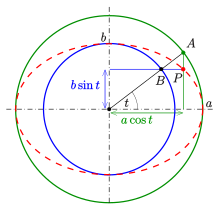
Standard parametric representation[edit]
Using trigonometric functions, a parametric representation of the standard ellipse 
The parameter t (called the eccentric anomaly in astronomy) is not the angle of 
Rational representation[edit]
With the substitution 
and the rational parametric equation of an ellipse
which covers any point of the ellipse 

For ![{displaystyle uin [0,,1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c61b780db9ac550dd283876e16abe9c2cccdf8c3)


Alternately, if the parameter ![{displaystyle [u:v]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/297de5a93c52f13ef84add1d79d693fcda686176)

Then ![{textstyle [1:0]mapsto (-a,,0).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0da12e69b8138a30dcb6cfbeeb95bd63b890f2db)
Rational representations of conic sections are commonly used in computer-aided design (see Bezier curve).
Tangent slope as parameter[edit]
A parametric representation, which uses the slope 
can be obtained from the derivative of the standard representation 
With help of trigonometric formulae one obtains:
Replacing 

Here 



The equation of the tangent at point 



This description of the tangents of an ellipse is an essential tool for the determination of the orthoptic of an ellipse. The orthoptic article contains another proof, without differential calculus and trigonometric formulae.
General ellipse[edit]
Ellipse as an affine image of the unit circle
Another definition of an ellipse uses affine transformations:
- Any ellipse is an affine image of the unit circle with equation
.
- Parametric representation
An affine transformation of the Euclidean plane has the form 






Here 

- Vertices
The four vertices of the ellipse are 

(If 


At a vertex parameter 
Expanding and applying the identities 

- Area
From Apollonios theorem (see below) one obtains:
The area of an ellipse 
- Semiaxes
With the abbreviations

Solving this nonlinear system for 
- Implicit representation
Solving the parametric representation for 

.
Conversely: If the equation
with
of an ellipse centered at the origin is given, then the two vectors
point to two conjugate points and the tools developed above are applicable.
Example: For the ellipse with equation 
.
Whirls: nested, scaled and rotated ellipses. The spiral is not drawn: we see it as the locus of points where the ellipses are especially close to each other.
- Rotated Standard ellipse
For 

- Ellipse in space
The definition of an ellipse in this section gives a parametric representation of an arbitrary ellipse, even in space, if one allows 
Polar forms[edit]
Polar form relative to center[edit]
Polar coordinates centered at the center.
In polar coordinates, with the origin at the center of the ellipse and with the angular coordinate 
where 
Polar form relative to focus[edit]
Polar coordinates centered at focus.
If instead we use polar coordinates with the origin at one focus, with the angular coordinate 
where the sign in the denominator is negative if the reference direction 
In the slightly more general case of an ellipse with one focus at the origin and the other focus at angular coordinate 
The angle 

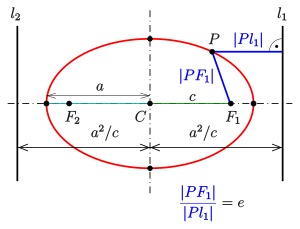
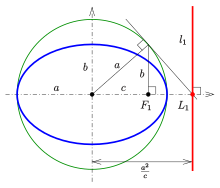
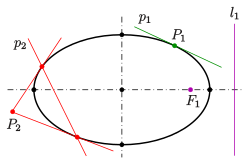
Eccentricity and the directrix property[edit]
Ellipse: directrix property
Each of the two lines parallel to the minor axis, and at a distance of 
- For an arbitrary point
of the ellipse, the quotient of the distance to one focus and to the corresponding directrix (see diagram) is equal to the eccentricity:
The proof for the pair 


The second case is proven analogously.
The converse is also true and can be used to define an ellipse (in a manner similar to the definition of a parabola):
- For any point
(focus), any line
(directrix) not through
, and any real number
with
the ellipse is the locus of points for which the quotient of the distances to the point and to the line is
that is:
The extension to 
(The choice 

Pencil of conics with a common vertex and common semi-latus rectum
- Proof
Let 

The directrix 



and
The substitution 
This is the equation of an ellipse (


If 


which is the equation of an ellipse with center 
the major/minor semi axis 
Construction of a directrix
- Construction of a directrix
Because of 







- General ellipse
If the focus is 

(The right side of the equation uses the Hesse normal form of a line to calculate the distance 
Focus-to-focus reflection property[edit]
Ellipse: the tangent bisects the supplementary angle of the angle between the lines to the foci.
Rays from one focus reflect off the ellipse to pass through the other focus.
An ellipse possesses the following property:
- The normal at a point
bisects the angle between the lines
.
- Proof
Because the tangent is perpendicular to the normal, the statement is true for the tangent and the supplementary angle of the angle between the lines to the foci (see diagram), too.
Let 














From the diagram and the triangle inequality one recognizes that 






- Application
The rays from one focus are reflected by the ellipse to the second focus. This property has optical and acoustic applications similar to the reflective property of a parabola (see whispering gallery).
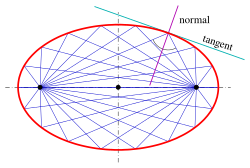
Conjugate diameters[edit]
Definition of conjugate diameters[edit]
Orthogonal diameters of a circle with a square of tangents, midpoints of parallel chords and an affine image, which is an ellipse with conjugate diameters, a parallelogram of tangents and midpoints of chords.
A circle has the following property:
- The midpoints of parallel chords lie on a diameter.
An affine transformation preserves parallelism and midpoints of line segments, so this property is true for any ellipse. (Note that the parallel chords and the diameter are no longer orthogonal.)
- Definition
Two diameters 


From the diagram one finds:
- Two diameters
of an ellipse are conjugate whenever the tangents at
and
are parallel to
.
Conjugate diameters in an ellipse generalize orthogonal diameters in a circle.
In the parametric equation for a general ellipse given above,
any pair of points 

For the common parametric representation 

(signs: (+,+) or (-,-) )
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response («Math extension cannot connect to Restbase.») from server «http://localhost:6011/en.wikipedia.org/v1/»:): {displaystyle (x_2,y_2)=({color{red}{mp}} asin t,pm bcos t)quad }
(signs: (-,+) or (+,-) ) - are conjugate and
In case of a circle the last equation collapses to 
Theorem of Apollonios on conjugate diameters[edit]
For the alternative area formula
For an ellipse with semi-axes 
- Let
and
be halves of two conjugate diameters (see diagram) then
.
- The triangle
with sides
(see diagram) has the constant area
, which can be expressed by
, too.
is the altitude of point
and
the angle between the half diameters. Hence the area of the ellipse (see section metric properties) can be written as
.
- The parallelogram of tangents adjacent to the given conjugate diameters has the
- Proof
Let the ellipse be in the canonical form with parametric equation
.
The two points 

The area of the triangle generated by 
and from the diagram it can be seen that the area of the parallelogram is 8 times that of 
Orthogonal tangents[edit]
Ellipse with its orthoptic
For the ellipse 

This circle is called orthoptic or director circle of the ellipse (not to be confused with the circular directrix defined above).
Drawing ellipses[edit]
Central projection of circles (gate)
Ellipses appear in descriptive geometry as images (parallel or central projection) of circles. There exist various tools to draw an ellipse. Computers provide the fastest and most accurate method for drawing an ellipse. However, technical tools (ellipsographs) to draw an ellipse without a computer exist. The principle of ellipsographs were known to Greek mathematicians such as Archimedes and Proklos.
If there is no ellipsograph available, one can draw an ellipse using an approximation by the four osculating circles at the vertices.
For any method described below, knowledge of the axes and the semi-axes is necessary (or equivalently: the foci and the semi-major axis).
If this presumption is not fulfilled one has to know at least two conjugate diameters. With help of Rytz’s construction the axes and semi-axes can be retrieved.
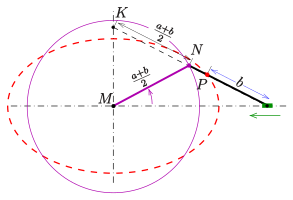
de La Hire’s point construction[edit]
The following construction of single points of an ellipse is due to de La Hire.[11] It is based on the standard parametric representation 
- Draw the two circles centered at the center of the ellipse with radii
and the axes of the ellipse.
- Draw a line through the center, which intersects the two circles at point
and
, respectively.
- Draw a line through
that is parallel to the minor axis and a line through
that is parallel to the major axis. These lines meet at an ellipse point (see diagram).
- Repeat steps (2) and (3) with different lines through the center.
-
de La Hire’s method
-
Animation of the method
Ellipse: gardener’s method
Pins-and-string method[edit]
The characterization of an ellipse as the locus of points so that sum of the distances to the foci is constant leads to a method of drawing one using two drawing pins, a length of string, and a pencil. In this method, pins are pushed into the paper at two points, which become the ellipse’s foci. A string is tied at each end to the two pins; its length after tying is 
A similar method for drawing confocal ellipses with a closed string is due to the Irish bishop Charles Graves.
Paper strip methods[edit]
The two following methods rely on the parametric representation (see section parametric representation, above):
This representation can be modeled technically by two simple methods. In both cases center, the axes and semi axes 
- Method 1
The first method starts with
- a strip of paper of length
.
The point, where the semi axes meet is marked by 




A technical realization of the motion of the paper strip can be achieved by a Tusi couple (see animation). The device is able to draw any ellipse with a fixed sum 
-
Ellipse construction: paper strip method 1
-
Ellipses with Tusi couple. Two examples: red and cyan.
A variation of the paper strip method 1 uses the observation that the midpoint 






-
Variation of the paper strip method 1
-
Animation of the variation of the paper strip method 1
Ellipse construction: paper strip method 2
- Method 2
The second method starts with
- a strip of paper of length
.
One marks the point, which divides the strip into two substrips of length 



This method is the base for several ellipsographs (see section below).
Similar to the variation of the paper strip method 1 a variation of the paper strip method 2 can be established (see diagram) by cutting the part between the axes into halves.
-
-
Variation of the paper strip method 2
Most ellipsograph drafting instruments are based on the second paperstrip method.
Approximation of an ellipse with osculating circles
Approximation by osculating circles[edit]
From Metric properties below, one obtains:
The diagram shows an easy way to find the centers of curvature 


- mark the auxiliary point
and draw the line segment
- draw the line through
, which is perpendicular to the line
- the intersection points of this line with the axes are the centers of the osculating circles.
(proof: simple calculation.)
The centers for the remaining vertices are found by symmetry.
With help of a French curve one draws a curve, which has smooth contact to the osculating circles.
Steiner generation[edit]
Ellipse: Steiner generation
Ellipse: Steiner generation
The following method to construct single points of an ellipse relies on the Steiner generation of a conic section:
- Given two pencils
of lines at two points
(all lines containing
and
, respectively) and a projective but not perspective mapping
of
onto
, then the intersection points of corresponding lines form a non-degenerate projective conic section.
For the generation of points of the ellipse 













Steiner generation can also be defined for hyperbolas and parabolas. It is sometimes called a parallelogram method because one can use other points rather than the vertices, which starts with a parallelogram instead of a rectangle.
As hypotrochoid[edit]
An ellipse (in red) as a special case of the hypotrochoid with R = 2r
The ellipse is a special case of the hypotrochoid when 


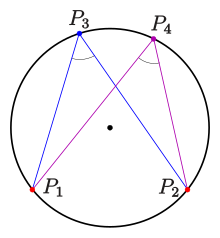
Inscribed angles and three-point form[edit]
Circles[edit]
Circle: inscribed angle theorem
A circle with equation 


- For four points
(see diagram) the following statement is true:
- The four points are on a circle if and only if the angles at
and
are equal.
Usually one measures inscribed angles by a degree or radian θ, but here the following measurement is more convenient:
- In order to measure the angle between two lines with equations
one uses the quotient:
Inscribed angle theorem for circles[edit]
For four points 
- The four points are on a circle, if and only if the angles at
and
are equal. In terms of the angle measurement above, this means:
At first the measure is available only for chords not parallel to the y-axis, but the final formula works for any chord.
Three-point form of circle equation[edit]
- As a consequence, one obtains an equation for the circle determined by three non-colinear points
:
For example, for 
, which can be rearranged to
Using vectors, dot products and determinants this formula can be arranged more clearly, letting 
The center of the circle 
The radius is the distance between any of the three points and the center.
Ellipses[edit]
This section, we consider the family of ellipses defined by equations 

and to write the ellipse equation as:
where q is fixed and 


Inscribed angle theorem for an ellipse
Like a circle, such an ellipse is determined by three points not on a line.
For this family of ellipses, one introduces the following q-analog angle measure, which is not a function of the usual angle measure θ:[13][14]
- In order to measure an angle between two lines with equations
one uses the quotient:
Inscribed angle theorem for ellipses[edit]
- Given four points
, no three of them on a line (see diagram).
- The four points are on an ellipse with equation
if and only if the angles at
and
are equal in the sense of the measurement above—that is, if
At first the measure is available only for chords which are not parallel to the y-axis. But the final formula works for any chord. The proof follows from a straightforward calculation. For the direction of proof given that the points are on an ellipse, one can assume that the center of the ellipse is the origin.
Three-point form of ellipse equation[edit]
- A consequence, one obtains an equation for the ellipse determined by three non-colinear points
:
For example, for 

and after conversion
Analogously to the circle case, the equation can be written more clearly using vectors:
where 

Pole-polar relation[edit]
Ellipse: pole-polar relation
Any ellipse can be described in a suitable coordinate system by an equation 



- point
is mapped onto the line
, not through the center of the ellipse.
This relation between points and lines is a bijection.
The inverse function maps
Such a relation between points and lines generated by a conic is called pole-polar relation or polarity. The pole is the point; the polar the line.
By calculation one can confirm the following properties of the pole-polar relation of the ellipse:
- The intersection point of two polars is the pole of the line through their poles.
- The foci
and
, respectively, and the directrices
and
, respectively, belong to pairs of pole and polar. Because they are even polar pairs with respect to the circle
, the directrices can be constructed by compass and straightedge (see Inversive geometry).
Pole-polar relations exist for hyperbolas and parabolas as well.
Metric properties[edit]
All metric properties given below refer to an ellipse with equation
-
(1)
except for the section on the area enclosed by a tilted ellipse, where the generalized form of Eq.(1) will be given.
Area[edit]
The area 
-
(2)
where 









![{displaystyle xin [-a,a],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb19e5015712fa6f6c57d3f334266c73d7782434)

![[-a,a]](https://wikimedia.org/api/rest_v1/media/math/render/svg/50ccbcece37f9ec0a4c6d396be3a143a0b76d5c1)
The second integral is the area of a circle of radius 

An ellipse defined implicitly by 

The area can also be expressed in terms of eccentricity and the length of the semi-major axis as 
The area enclosed by a tilted ellipse is 
So far we have dealt with erect ellipses, whose major and minor axes are parallel to the 

-
(3)
where 



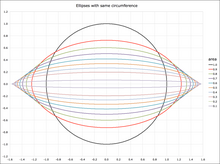
Circumference[edit]
Ellipses with same circumference
The circumference 
where again 


which is in general not an elementary function.
The circumference of the ellipse may be evaluated in terms of 
The exact infinite series is:
where 



Srinivasa Ramanujan gave two close approximations for the circumference in §16 of «Modular Equations and Approximations to 
and
where 


Arc length[edit]
More generally, the arc length of a portion of the circumference, as a function of the angle subtended (or x coordinates of any two points on the upper half of the ellipse), is given by an incomplete elliptic integral. The upper half of an ellipse is parameterized by
Then the arc length 


This is equivalent to
where 

Some lower and upper bounds on the circumference of the canonical ellipse 

Here the upper bound 

Curvature[edit]
The curvature is given by
radius of curvature at point 
Radius of curvature at the two vertices 
Radius of curvature at the two co-vertices 
In triangle geometry[edit]
Ellipses appear in triangle geometry as
- Steiner ellipse: ellipse through the vertices of the triangle with center at the centroid,
- inellipses: ellipses which touch the sides of a triangle. Special cases are the Steiner inellipse and the Mandart inellipse.
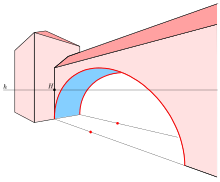
As plane sections of quadrics[edit]
Ellipses appear as plane sections of the following quadrics:
- Ellipsoid
- Elliptic cone
- Elliptic cylinder
- Hyperboloid of one sheet
- Hyperboloid of two sheets
-
Ellipsoid
-
Elliptic cone
-
Elliptic cylinder
-
Hyperboloid of one sheet
-
Hyperboloid of two sheets
Applications[edit]
Physics[edit]
Elliptical reflectors and acoustics[edit]
Wave pattern of a little droplet dropped into mercury in one focus of the ellipse
If the water’s surface is disturbed at one focus of an elliptical water tank, the circular waves of that disturbance, after reflecting off the walls, converge simultaneously to a single point: the second focus. This is a consequence of the total travel length being the same along any wall-bouncing path between the two foci.
Similarly, if a light source is placed at one focus of an elliptic mirror, all light rays on the plane of the ellipse are reflected to the second focus. Since no other smooth curve has such a property, it can be used as an alternative definition of an ellipse. (In the special case of a circle with a source at its center all light would be reflected back to the center.) If the ellipse is rotated along its major axis to produce an ellipsoidal mirror (specifically, a prolate spheroid), this property holds for all rays out of the source. Alternatively, a cylindrical mirror with elliptical cross-section can be used to focus light from a linear fluorescent lamp along a line of the paper; such mirrors are used in some document scanners.
Sound waves are reflected in a similar way, so in a large elliptical room a person standing at one focus can hear a person standing at the other focus remarkably well. The effect is even more evident under a vaulted roof shaped as a section of a prolate spheroid. Such a room is called a whisper chamber. The same effect can be demonstrated with two reflectors shaped like the end caps of such a spheroid, placed facing each other at the proper distance. Examples are the National Statuary Hall at the United States Capitol (where John Quincy Adams is said to have used this property for eavesdropping on political matters); the Mormon Tabernacle at Temple Square in Salt Lake City, Utah; at an exhibit on sound at the Museum of Science and Industry in Chicago; in front of the University of Illinois at Urbana–Champaign Foellinger Auditorium; and also at a side chamber of the Palace of Charles V, in the Alhambra.
Planetary orbits[edit]
In the 17th century, Johannes Kepler discovered that the orbits along which the planets travel around the Sun are ellipses with the Sun [approximately] at one focus, in his first law of planetary motion. Later, Isaac Newton explained this as a corollary of his law of universal gravitation.
More generally, in the gravitational two-body problem, if the two bodies are bound to each other (that is, the total energy is negative), their orbits are similar ellipses with the common barycenter being one of the foci of each ellipse. The other focus of either ellipse has no known physical significance. The orbit of either body in the reference frame of the other is also an ellipse, with the other body at the same focus.
Keplerian elliptical orbits are the result of any radially directed attraction force whose strength is inversely proportional to the square of the distance. Thus, in principle, the motion of two oppositely charged particles in empty space would also be an ellipse. (However, this conclusion ignores losses due to electromagnetic radiation and quantum effects, which become significant when the particles are moving at high speed.)
For elliptical orbits, useful relations involving the eccentricity 
where
Also, in terms of 




.
Harmonic oscillators[edit]
The general solution for a harmonic oscillator in two or more dimensions is also an ellipse. Such is the case, for instance, of a long pendulum that is free to move in two dimensions; of a mass attached to a fixed point by a perfectly elastic spring; or of any object that moves under influence of an attractive force that is directly proportional to its distance from a fixed attractor. Unlike Keplerian orbits, however, these «harmonic orbits» have the center of attraction at the geometric center of the ellipse, and have fairly simple equations of motion.
Phase visualization[edit]
In electronics, the relative phase of two sinusoidal signals can be compared by feeding them to the vertical and horizontal inputs of an oscilloscope. If the Lissajous figure display is an ellipse, rather than a straight line, the two signals are out of phase.
Elliptical gears[edit]
Two non-circular gears with the same elliptical outline, each pivoting around one focus and positioned at the proper angle, turn smoothly while maintaining contact at all times. Alternatively, they can be connected by a link chain or timing belt, or in the case of a bicycle the main chainring may be elliptical, or an ovoid similar to an ellipse in form. Such elliptical gears may be used in mechanical equipment to produce variable angular speed or torque from a constant rotation of the driving axle, or in the case of a bicycle to allow a varying crank rotation speed with inversely varying mechanical advantage.
Elliptical bicycle gears make it easier for the chain to slide off the cog when changing gears.[21]
An example gear application would be a device that winds thread onto a conical bobbin on a spinning machine. The bobbin would need to wind faster when the thread is near the apex than when it is near the base.[22]
Optics[edit]
- In a material that is optically anisotropic (birefringent), the refractive index depends on the direction of the light. The dependency can be described by an index ellipsoid. (If the material is optically isotropic, this ellipsoid is a sphere.)
- In lamp-pumped solid-state lasers, elliptical cylinder-shaped reflectors have been used to direct light from the pump lamp (coaxial with one ellipse focal axis) to the active medium rod (coaxial with the second focal axis).[23]
- In laser-plasma produced EUV light sources used in microchip lithography, EUV light is generated by plasma positioned in the primary focus of an ellipsoid mirror and is collected in the secondary focus at the input of the lithography machine.[24]
Statistics and finance[edit]
In statistics, a bivariate random vector 
Computer graphics[edit]
Drawing an ellipse as a graphics primitive is common in standard display libraries, such as the MacIntosh QuickDraw API, and Direct2D on Windows. Jack Bresenham at IBM is most famous for the invention of 2D drawing primitives, including line and circle drawing, using only fast integer operations such as addition and branch on carry bit. M. L. V. Pitteway extended Bresenham’s algorithm for lines to conics in 1967.[27] Another efficient generalization to draw ellipses was invented in 1984 by Jerry Van Aken.[28]
In 1970 Danny Cohen presented at the «Computer Graphics 1970» conference in England a linear algorithm for drawing ellipses and circles. In 1971, L. B. Smith published similar algorithms for all conic sections and proved them to have good properties.[29] These algorithms need only a few multiplications and additions to calculate each vector.
It is beneficial to use a parametric formulation in computer graphics because the density of points is greatest where there is the most curvature. Thus, the change in slope between each successive point is small, reducing the apparent «jaggedness» of the approximation.
- Drawing with Bézier paths
Composite Bézier curves may also be used to draw an ellipse to sufficient accuracy, since any ellipse may be construed as an affine transformation of a circle. The spline methods used to draw a circle may be used to draw an ellipse, since the constituent Bézier curves behave appropriately under such transformations.
Optimization theory[edit]
It is sometimes useful to find the minimum bounding ellipse on a set of points. The ellipsoid method is quite useful for solving this problem.
See also[edit]
- Cartesian oval, a generalization of the ellipse
- Circumconic and inconic
- Distance of closest approach of ellipses
- Ellipse fitting
- Elliptic coordinates, an orthogonal coordinate system based on families of ellipses and hyperbolae
- Elliptic partial differential equation
- Elliptical distribution, in statistics
- Elliptical dome
- Geodesics on an ellipsoid
- Great ellipse
- Kepler’s laws of planetary motion
- n-ellipse, a generalization of the ellipse for n foci
- Oval
- Spheroid, the ellipsoid obtained by rotating an ellipse about its major or minor axis
- Stadium (geometry), a two-dimensional geometric shape constructed of a rectangle with semicircles at a pair of opposite sides
- Steiner circumellipse, the unique ellipse circumscribing a triangle and sharing its centroid
- Superellipse, a generalization of an ellipse that can look more rectangular or more «pointy»
- True, eccentric, and mean anomaly
Notes[edit]
- ^ Apostol, Tom M.; Mnatsakanian, Mamikon A. (2012), New Horizons in Geometry, The Dolciani Mathematical Expositions #47, The Mathematical Association of America, p. 251, ISBN 978-0-88385-354-2
- ^ The German term for this circle is Leitkreis which can be translated as «Director circle», but that term has a different meaning in the English literature (see Director circle).
- ^ «Ellipse — from Wolfram MathWorld». Mathworld.wolfram.com. 2020-09-10. Retrieved 2020-09-10.
- ^ Protter & Morrey (1970, pp. 304, APP-28)
- ^ Larson, Ron; Hostetler, Robert P.; Falvo, David C. (2006). «Chapter 10». Precalculus with Limits. Cengage Learning. p. 767. ISBN 978-0-618-66089-6.
- ^ Young, Cynthia Y. (2010). «Chapter 9». Precalculus. John Wiley and Sons. p. 831. ISBN 978-0-471-75684-2.
- ^ a b Lawrence, J. Dennis, A Catalog of Special Plane Curves, Dover Publ., 1972.
- ^ K. Strubecker: Vorlesungen über Darstellende Geometrie, GÖTTINGEN,
VANDENHOECK & RUPRECHT, 1967, p. 26 - ^ Bronstein&Semendjajew: Taschenbuch der Mathematik, Verlag Harri Deutsch, 1979, ISBN 3871444928, p. 274.
- ^ Encyclopedia of Mathematics, Springer, URL: http://encyclopediaofmath.org/index.php?title=Apollonius_theorem&oldid=17516 .
- ^ K. Strubecker: Vorlesungen über Darstellende Geometrie. Vandenhoeck & Ruprecht, Göttingen 1967, S. 26.
- ^ J. van Mannen: Seventeenth century instruments for drawing conic sections. In: The Mathematical Gazette. Vol. 76, 1992, p. 222–230.
- ^ E. Hartmann: Lecture Note ‘Planar Circle Geometries’, an Introduction to Möbius-, Laguerre- and Minkowski Planes, p. 55
- ^ W. Benz, Vorlesungen über Geomerie der Algebren, Springer (1973)
- ^ Archimedes. (1897). The works of Archimedes. Heath, Thomas Little, Sir, 1861-1940. Mineola, N.Y.: Dover Publications. p. 115. ISBN 0-486-42084-1. OCLC 48876646.
- ^ Carlson, B. C. (2010), «Elliptic Integrals», in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
- ^ Ivory, J. (1798). «A new series for the rectification of the ellipsis». Transactions of the Royal Society of Edinburgh. 4 (2): 177–190. doi:10.1017/s0080456800030817. S2CID 251572677.
- ^ Bessel, F. W. (2010). «The calculation of longitude and latitude from geodesic measurements (1825)». Astron. Nachr. 331 (8): 852–861. arXiv:0908.1824. Bibcode:2010AN….331..852K. doi:10.1002/asna.201011352. S2CID 118760590. Englisch translation of Bessel, F. W. (1825). «Über die Berechnung der geographischen Längen und Breiten aus geodätischen Vermesssungen». Astron. Nachr. 4 (16): 241–254. arXiv:0908.1823. Bibcode:1825AN……4..241B. doi:10.1002/asna.18260041601. S2CID 118630614.
- ^ Ramanujan, Srinivasa (1914). «Modular Equations and Approximations to π». Quart. J. Pure App. Math. 45: 350–372. ISBN 9780821820766.
- ^ Jameson, G.J.O. (2014). «Inequalities for the perimeter of an ellipse». Mathematical Gazette. 98 (542): 227–234. doi:10.1017/S002555720000125X. S2CID 125063457.
- ^ David Drew.
«Elliptical Gears».
[1] - ^ Grant, George B. (1906). A treatise on gear wheels. Philadelphia Gear Works. p. 72.
- ^ Encyclopedia of Laser Physics and Technology — lamp-pumped lasers, arc lamps, flash lamps, high-power, Nd:YAG laser
- ^ «Cymer — EUV Plasma Chamber Detail Category Home Page». Archived from the original on 2013-05-17. Retrieved 2013-06-20.
- ^ Chamberlain, G. (February 1983). «A characterization of the distributions that imply mean—Variance utility functions». Journal of Economic Theory. 29 (1): 185–201. doi:10.1016/0022-0531(83)90129-1.
- ^ Owen, J.; Rabinovitch, R. (June 1983). «On the class of elliptical distributions and their applications to the theory of portfolio choice». Journal of Finance. 38 (3): 745–752. doi:10.1111/j.1540-6261.1983.tb02499.x. JSTOR 2328079.
- ^ Pitteway, M.L.V. (1967). «Algorithm for drawing ellipses or hyperbolae with a digital plotter». The Computer Journal. 10 (3): 282–9. doi:10.1093/comjnl/10.3.282.
- ^ Van Aken, J.R. (September 1984). «An Efficient Ellipse-Drawing Algorithm». IEEE Computer Graphics and Applications. 4 (9): 24–35. doi:10.1109/MCG.1984.275994. S2CID 18995215.
- ^ Smith, L.B. (1971). «Drawing ellipses, hyperbolae or parabolae with a fixed number of points». The Computer Journal. 14 (1): 81–86. doi:10.1093/comjnl/14.1.81.
References[edit]
- Besant, W.H. (1907). «Chapter III. The Ellipse». Conic Sections. London: George Bell and Sons. p. 50.
- Coxeter, H.S.M. (1969). Introduction to Geometry (2nd ed.). New York: Wiley. pp. 115–9.
- Meserve, Bruce E. (1983) [1959], Fundamental Concepts of Geometry, Dover Publications, ISBN 978-0-486-63415-9
- Miller, Charles D.; Lial, Margaret L.; Schneider, David I. (1990). Fundamentals of College Algebra (3rd ed.). Scott Foresman/Little. p. 381. ISBN 978-0-673-38638-0.
- Protter, Murray H.; Morrey, Charles B. Jr. (1970), College Calculus with Analytic Geometry (2nd ed.), Reading: Addison-Wesley, LCCN 76087042
External links[edit]
(схема 21)
Эллипсом называется
геометрическое место точек плоскости, сумма расстояний от каждой из которых до
двух данных точек этой плоскости, называемых
фокусами, есть величина постоянная, равная 2a.
Обозначим фокусы через F1 и F2,
расстояние между ними через 2c, а сумму расстояний от произвольной точки эллипса до
фокусов – через 2a. По определению 2a>2c, то есть a>c .
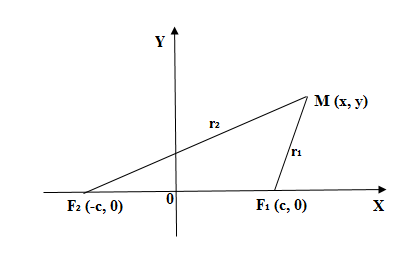
Выберем систему координат
так, чтобы
фокусы F1 и F2
лежали на оси 0x, а начало координат совпадало с серединой отрезка F1F2. Тогда фокусы имют координаты: F1(–c;0) и F2(c;0). Пусть M(x;y) –
произвольная точка эллипса (текущая точка). Тогда по определению эллипса можно записать
По сути, мы получили уравнение эллипса. Упростим его с помощью ряда несложных математических преобразований:
Так как, a>c, то a2–c2>0, то можно обозначить a2–c2=b2. Тогда
последнее уравнение имеет вид:

Это
уравнение равносильно первоначальному. Оно называется каноническим уравнением
эллипса – кривой
второго порядка.
Установим форму эллипса, пользуясь его каноническим
уравнением.
1. Уравнение (2.17) содержит x и y
только в четных степенях, поэтому
если точка (x;y)
принадлежит эллипсу, то
ему также принадлежат
точки (–x;y), (x;–y), (–x;–y). Отсюда: эллипс симметричен относительно осей 0x и 0y, а также
относительно точки O(0;0), которую называют центром эллипса.
2. Найдем точки пересечения эллипса с осями координат.
Положив y=0, найдем точки A1(a;0) и A2(–a;0), в которых ось 0x пересекает эллипс. Положив в уравнении
(2.17) x=0, находим точки пересечения эллипса с осью 0y: B1(0;b) и B2(0;–b). Точки A1, A2, B1, B2 называются вершинами эллипса. Отрезки А1А2,
В1В2, а также
их длины 2a и 2b – соответственно большая и малая оси эллипса (рис. 2.4).
3. Из уравнения (2.17) следует, что каждое слагаемое в
левой части не превосходит единицы,
т.е.:

Следовательно, все точки эллипса лежат внутри
прямоугольника, ограниченного прямыми x= ± a
и y= ± b.
4. В уравнении (2.17) левая часть – сумма
неотрицательных слагаемых, т.е. при возрастании одного слагаемого другое будет
уменьшаться, если |x| возрастает, |y|
уменьшается и наоборот.
Из сказанного следует, что эллипс имеет форму
овальной замкнутой кривой. Форма эллипса зависит от отношения
(2.17) принимает вид: x2+y2=a2. Отношение 

0<ε<1, так как 0<c<a.
Отсюда видно, что чем меньше эксцентриситет эллипса,
тем будет менее эллипс сплющенным; при ε=0 эллипс
превращается в окружность.
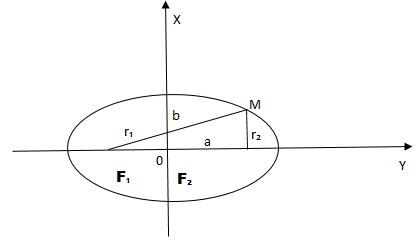
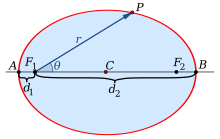
Пусть M(x;y) – произвольная точка эллипса с фокусами F1 и F2. Длины
отрезков |MF1|=r1 и |MF2|=r2 – фокальные
радиусы точки M, r1+r2=2a. Имеют место формулы: r1=a+εx и r2=a – εx.
Прямые 
эллипса.
Если r – расстояние от произвольной точки до какого–нибудь фокуса,
d –
расстояние от этой же точки до соответствующей этому фокусу директрисы (рис. 2.5), то отношение
постоянная, равная эксцентриситету эллипса: 
Из равенства a2–c2=b2
следует, что a>b. Если же
наоборот, то уравнение (2.17) определяет эллипс, большая ось которого 2b лежит на
оси 0y, а малая ось 2a – на оси 0x. Фокусы такого
эллипса находятся в точках F1(0;c) и F2(0;–c), где 
Пример 2.5. Составить уравнение линии, для каждой точки
которой отношение расстояний от нее до
точки A(3;0) и до прямой x=12, равно числу ε=0,5. Полученное
уравнение привести к простейшему виду.
Решение. Пусть M(x;y) – текущая (произвольная) точка искомого
геометрического множества точек. Опустим перпендикуляр MB на прямую
. Тогда точка B(12;y). По условию задачи

По формуле расстояния
двумя точками получаем:
Отсюда
Полученное уравнение представляет собой эллипс вида 
Определим фокусы эллипса F1(–c;0) и F2(c;0). Для эллипса справедливо равенство b2=a2–c2,
откуда c2=a2–b2 =9 и c=3. То есть,
F1(–3;0) и F1(3;0)–
фокусы эллипса (точки F2 и A совпадают).
Эксцентриситет эллипса
Примечание. Если эллипс (окружность) вращать вокруг одной из его
осей, то описываемая им поверхность будет эллипсоидом вращения (сферой)
Пример 2.6. В геодезии используется система географических координат,
основанная на понятии геоида. Геоид – поверхность Земли,
ограниченная уровенной поверхностью, продолженной под континенты. Поверхность
геоида отличается от физической поверхности Земли, на которой резко выражены
горы и океанические впадины.
Тело, поверхность которого более всего соответствует
поверхности геоида, имеет определенные размеры и ориентирована соответственно в
теле Земли, называется референц–эллипсоидом. В нашей стране с 1946 года для всех
геодезических работ принят референц–эллипсоид Красовского с
параметрами a=6 378 245 м, b=6 356 863 м, α=1: 298,3.
Линия, проходящая вертикально через центр эллипсоида
является полярной осью. Линия, проходящая через центр эллипсоида,
перпендикулярно к полярной оси, – экваториальной осью. При пересечении
поверхности эллипсоида плоскостью, проходящей через его центр, перпендикулярно
к полярной оси, образуется окружность, называемая экватором. Окружность,
полученная от пересечения поверхности эллипсоида плоскостью, параллельной
плоскости экватора, называется параллелью. Линия пересечения
поверхности эллипсоида с плоскостью, проходящей через заданную точку и полярную
ось, называется меридианом данной точки. Положение точки на земной поверхности
определяется пересечением параллели и меридиана, проходящих через нее. Угол φ между плоскостью экватора и отвесной
линией называется географической широтой. Для определения долгот
точек один из меридианов (Гринвичский) принимают за начальный или нулевой. Угол
λ, составленный плоскостью меридиана,
проходящего через данную точку, и плоскостью начального меридиана, называется
географической долготой
Гипербола – геометрическое место точек плоскости, модуль разности расстояний от
каждой из которых до двух данных точек этой плоскости – фокусов, есть величина
постоянная, равная 2a.
Обозначим фокусы через
F1 и F2, расстояние между ними через 2c, а модуль
разности расстояний от каждой точки
гиперболы до фокусов через 2a. По определению 2a<2c, то есть a<c.
Выберем систему координат x0y так, чтобы фокусы F1 и F2 лежали на оси 0x, а начало координат совпало с серединой отрезка F1F2. Тогда фокусы будут иметь координаты F1(c;0) и F2(–c;0). На этой основе выведем уравнение гиперболы. Пусть M(x;y) – ее произвольная точка. Тогда по определению |MF1–MF2|=2a, то есть

где
b2=a2–c2.
Гипербола – линия 2–го порядка.
Установим форму гиперболы, исходя из ее канонического
уравнения.
1. Уравнение (2.18) содержит x и y только в
четных степенях. Следовательно, гипербола симметрична относительно осей координат
0x и 0y, и относительно точки O(0;0) – центра гиперболы.
2. Найдем точки пересечения гиперболы с осями координат. Положив в
уравнении (2.18) y=0, находим две точки пересечения гиперболы с осью 0x: A1(a;0) и A2(–a;0).
Положив в (2.18) x=0, получаем y2= – b2,
чего быть не может. Т.е. гипербола ось 0y не пересекает.
Точки A1(a;0) и A2(–a;0) – вершины гиперболы, а отрезок |A1A2|=2a – действительная ось. Отрезок |B1B2|=2b,
соединяющий точки B1(0;b) и B2(0;–b) – мнимая ось (рис. 2.6). Прямоугольник
со сторонами 2a и 2b – основной
прямоугольник гиперболы.
3. Из уравнения (2.18) следует, что уменьшаемое 
от прямой x=a (правая
ветвь гиперболы) и слева от прямой x=–a (левая
ветвь) (рис. 2.6).
4. Из уравнения (2.18) гиперболы видно, что
когда |x| возрастает, то |y| также
возрастает. Это
следует из того, что разность 
сохраняет значение, равноe единице. Следовательно, гипербола имеет форму,
состоящую из двух неограниченных ветвей.
Прямая L называется асимптотой некоторой неограниченной кривой, если расстояние d от точки M этой кривой до прямой L стремится к нулю при неограниченном
удалении точки M вдоль кривой
от начала координат.
Покажем, что гипербола 

данные прямые и гипербола (2.18) симметричны относительно координатных
осей, то достаточно рассмотреть только точки, расположенные в первой четверти.
Возьмем на прямой 
ту же абсциссу, что и точка M(x;y) на гиперболе 
Очевидно: так как числитель есть величина постоянная, а знаменатель дроби увеличивается с возравстанием переменной х, то длина отрезка |MN| стремится
к нулю. Так как |MN| больше
расстояния d от точки M до прямой L, то d стремится к нулю тем более (и подавно). Следовательно, прямые

асимптоты гиперболы (рис. 2.7).
Построение гиперболы начинают с нанесения ее основного прямоугольника на координатную плоскость. Далее проводят диагонали этого прямоугольника, которые являются асимптотами гиперболы, затем отмечают ее вершины, фокусы и строят ветви гиперболы.
Эксцентриситет гиперболы –
отношение расстояния между фокусами к величине её действительной оси,
обозначается ε: 
как у гиперболы c>a, то
эксцентриситет ее больше единицы. Эксцентриситет характеризует форму гиперболы. Так как 
эксцентриситет гиперболы, тем меньше отношение 
значит, тем более вытянут ее основной прямоугольник.
Эксцентриситет
равносторонней гиперболы равен 

,
для точек
правой ветви гиперболы имеют вид: r1=εx+a, r2=εx–a; для точек
левой ветви: r1=–(εx+a), r2=–(εx–a).
Прямые
гиперболы. Тот факт, что для гиперболы ε>1, то 
левая – между центром и левой вершиной. Директрисы
гиперболы имеют тоже свойство 
Уравнение 
на рисунке 2.7 пунктиром).
Значит, гиперболы

имеют общие
асимптоты. Такие гиперболы называются сопряженными.
Примечание. Если у кривой 2–го порядка смещен центр в некоторую
точку O’(x0;y0), то она
называется нецентральной кривой. Уравнение такой кривой имеет вид:
Примечание. При вращении гиперболы вокруг ее действительной оси
образуется двуполостный гиперболоид, вокруг ее мнимой оси – однополостный гиперболоид
Подробно данные уравнения рассмотрены в теме:
«Исследование общего уравнения 2–ой степени» (смотри схему 10), частными
случаями которого являются данные формулы.
Вопросы
для самопроверки
Эллипс – это замкнутая плоская кривая, сумма расстояний от каждой точки до двух точек равняется постоянной величине.
Что такое эллипс и фокусное расстояние
Эллипс – это множество точек плоскости, сумма расстояний которых от двух заданных точек, что называются фокусами, есть постоянная величина и равна .
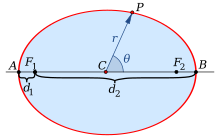
Обозначим фокусы эллипса и
. Допустим, что расстояние
=
– фокусное расстояние.
Рис. 1
– фокусы .
;
,
– половина расстояния между фокусами;
– большая полуось;
– малая полуось.
Теорема:
Фокусное расстояние и полуоси связаны соотношением:
Если точка находится на пересечении эллипса с вертикальной осью,
(теорема Пифагора). Если же точка
находится на пересечении его с горизонтальной осью,
. Так как по определению сумма
– постоянная величина, то приравнивая получается:
.
Уравнение эллипса
Уравнение элиппса бывает двух видов:
- Каноническое уравнение эллипса.
- Параметрическое уравнение эллипса.
Сначала рассмотрим каноническое уравнение эллипса:
Уравнение описывает эллипс в декартовой системе координат. Если центр эллипсa в начале системы координат, а большая ось лежит на абсциссе, то эллипс описывается уравнением:
Если центр эллипсa смещен в точку с координатами
тогда уравнение:
Чтобы получить каноническое уравнение эллипса, разместим и
на оси
симметричной к началу координат. Тогда у фокусов будут такие координаты
и
(см. рис. 2).
Пусть – произвольная точка эллипса. Обозначим через
и
– расстояние от точки
к фокусам. Согласно с определением эллипса:
(1)
Рис. 2
Подставим в (1) ,
и освободимся от иррациональности, подняв обе части к квадрату, получим:
(подносим к квадрату обе части): ,
Обозначим: , получаем каноническое уравнение эллипса:
(2)
Отметим, что по известному свойству треугольника (сумма двух сторон больше третьей) из у нас получается
. Так как
, тогда
, и поэтому
.
Для построения эллипса обратим внимание, что если точка принадлежит эллипсу, то есть удовлетворяет уравнение (2), тогда точки
тоже удовлетворяют это уравнение: из
.
Точки – расположены симметрично относительно осей координат. Значит, эллипс – фигура, симметричная относительно координатных осей. Поэтому достаточно построить график в первой четверти, а тогда симметрично продолжить его.
Из уравнения (2) находим , для первой четверти
.
Если , тогда
. Если же
, тогда
. Точки
и
, а также симметричные с ними
,
– вершины эллипса, точка
– центр эллипса,
=
большая ось,
– малая ось эллипса.
Если первой четверти, тогда из
получается, что при возрастании
от
к
значение
падает от
к
. (рис. 3)
Параметрическое уравнение выглядит так:
Основные свойства эллипса
Рассмотрим основные свойства эллипса, которые необходимы для решения многих задач.
1. Угол между касательной к эллипсу и фокальным радиусом равен углу между касательной и фокальным радиусом
.
2. Уравнение касательной к эллипсу в точке с координатами
:
.
3. Если эллипс пересекается двумя параллельными прямыми, то отрезок, который соединяет середины отрезков образовавшихся при пересечении прямых и эллипса, всегда проходит через середину (центр) эллипсa. (При помощи данного свойства можно построить эллипс при помощи циркуля и линейка, а также найти центр эллипса).
4. Эволюта эллипсa – это астероида, которая растянута вдоль короткой оси.
5. Если вписать эллипс с фокусами и
у треугольника
, тогда выполняется соотношение:
=
Эксцентриситет эллипса
Эксентриситет эллипса – это величина отношения межфокусного расстояния к большей оси и после сокращения на обозначается
Значения эксентриситета характеризует степень “сплющенность” эллипса. Если , тогда
– получается круг. Если же
, тогда
– эллипс превращается в отрезок. В некоторых случаях
. Для фокальных радиусов приведём без доказательства такие формулы:
Рис. 3
Эллипс можно построить механическим способом. Из канонического уравнения нужно найти полуоси и
, тогда вычислим
– полуфокусное расстояние.
Строим фокусы и
на расстоянии один от другого
Концы не растянутой нити длиной
закрепляем в точках
и
. Натягивая остриём карандаша нитку, водим остриём по плоскости таким образом, чтобы нитка скользила по острию. Карандаш при этом опишет полуось. Оттягивая нить в противоположную сторону, начертим вторую половину эллипса.
Примеры решения задач
Задача
Задан эллипс уравнением и точки
. Необходимо:
- убедиться, что точки
и
лежат на эллипсе;
- найти полуоси эллипса и координаты его фокусов;
- найти расстояние от точки
к фокусам;
- убедиться, что сумма этих расстояний равна длине большой оси;
- найти эксентриситет эллипса.
Решение
1. Подставим координаты точки
в левую часть уравнения эллипса:
– точка
лежит на эллипсе. Аналогично для
:
точка
лежит на эллипсе.
2. С канонического и данного уравнения
эллипса выходит:
Из равенства
получается:
– полуфокусное расстояние. Координаты фокусов
и
.
3. Найдём фокальные радиусы точки :
4. Найдём сумму , что отвечает определению эллипса.
5. Эксцентриситет находится по формуле .
Задача
Найти оси, вершины и фокусы эллипса
Решение
Сведём обычное уравнение к каноническому:
,
. Вершины эллипса в точках
,
,
,
. Строим вершины на координатных осях и соединяем плавной линией (см. рис. 2). Так как в данном случае
больше, чем
, то эллипс, который вытянут вдоль оси
, находим полуфокусное расстояние
.
Фокусы в точках и
. (см. рис. 3)
Рис. 4
Найти оси, вершины и фокусы эллипса или
. Построить эллипс.
Сравнивая последнее уравнение с уравнением (2), у нас получается:
,
. Откуда находим оси эллипса:
,
и координаты вершин:
,
,
,
. Дальше из формулы:
. Значит, фокусами эллипса есть точки:
и
. Для построения эллипса отложим на осях
и
вершины
соответственно соединим их плавной линией, (см. задачу 1).
Замечание! Если в каноническом уравнении большей полуосью будет
, тогда фокусы эллипса будут расположены на оси
и тогда
.
Эллипсом называется множество точек
плоскости, сумма расстояний от которых
до двух данных точек
и
этой плоскости, называемых фокусами,
есть величина постоянная, равная
,
,
большая, чем расстояние между фокусами
.
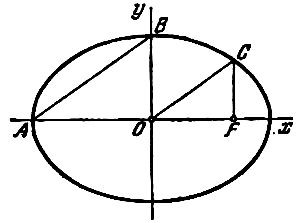
Е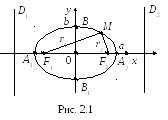
оси координат расположены по отношению
к эллипсу так, как на рис. 2.1, а фокусы
эллипса находятся на оси
на равных расстояниях от начала координат
в точках
и
,
то получится простейшее (каноническое)
уравнение эллипса:
,
(2.2)
где
– большая,
– малая полуось эллипса, причем
,
и
(
– половина расстояния между фокусами)
связаны соотношением
.
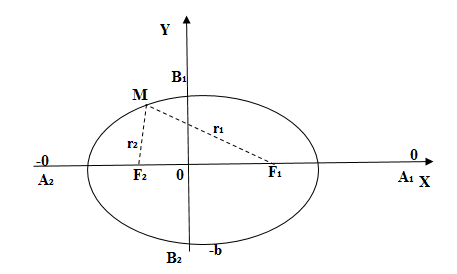
Точки
,
.
,
называются вершинами эллипса, оси
симметрии
и
– главными осями, а центр симметрии 0 –
центром эллипса.
Векторы
и
называются фокальными радиус—векторами,
а числа
и
– фокальными радиусами точки
,
принадлежащей эллипсу (в силу определения
эллипса для любой его точки
).
В частном случае
фокусы
и
совпадают с центром, а каноническое
уравнение имеет вид
,
или
,
т. е. описывает окружность радиуса
с центром в начале координат.
Форма эллипса (мера его сжатия)
характеризуется его эксцентриситетом
(;
при
эллипс является окружностью, а т. к.
,
то
).
Прямые
и
,
перпендикулярные главной оси и проходящие
на расстоянии
от центра, называются директрисами
эллипса.
Фокальные радиусы-векторы выражаются
через абсциссу точки эллипса по формулам
и
.
Если центр эллипса с полуосями
и
смещен в точку
,
то его каноническое уравнение имеет
вид
.
(2.3)
Примеры
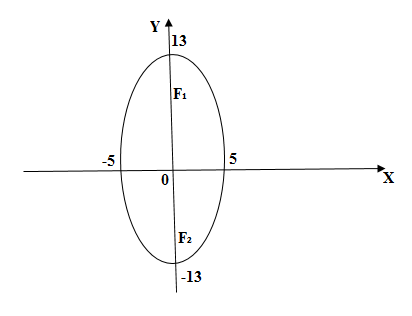
1. Какую линию определяет уравнение
?
Разделим данное уравнение почленно на
12:
.
Сравнивая полученное уравнение с
уравнением (2.2), заключаем, что оно
определяет эллипс с полуосями
,
.
Найдем фокусы этого эллипса. Так как
,
то
,
.
Следовательно, фокусы эллипса находятся
в точках
,
.
2. Даны координаты точек
,
и радиус окружности
,
центр которой находится в начале
координат. Требуется:
а) составить каноническое уравнение
эллипса, проходящего через данные точки
и
;
б) найти полуоси, фокусы и эксцентриситет
этого эллипса;
в) найти все точки пересечения эллипса
с данной окружностью;
г) построить эллипс и окружность.
Решение.
а) Пусть
– искомое уравнения эллипса. Этому
уравнению должны удовлетворять координаты
данных точек. Следовательно, подставляя
координаты точек, получим
Отсюда находим
,
.
Итак, уравнение эллипса имеет вид
.
б)
,
– соответственно большая и малая полуоси
эллипса. Для эллипса
,
значит
,
откуда
.
Следовательно,
,
– соответственно левый и правый фокусы
эллипса. Эксцентриситет эллипса
.
в) Найдем точки пересечения эллипса с
данной окружностью. Уравнение окружности
.
Решая систему уравнений
получим
,
,
.
Но
,
значит
,
откуда
.
Итак, существуют две точки пересечения
эллипса и окружности
и
.
г) Построить эллипс и окружность.
3. Большая ось эллипса равна 12, а
директрисами его служат прямые
.
Найти уравнение эллипса и его
эксцентриситет.
Решение. По условию
.
Из уравнений директрис
и формулы
находим
.
Тогда
.
Следовательно, искомое уравнение эллипса
есть
,
а эксцентриситет его
.
4. Эллипс касается оси
в точке
и пересекает ось
в точках
и
.
Зная, что оси эллипса параллельны осям
координат, составить его уравнение.
Решение. Будем искать уравнение
эллипса в виде (2.3). Так как эллипс касается
оси
,
то
.
Далее,
,
т. к. прямая
параллельна оси
и отсекает на оси
отрезок
.
Следовательно, уравнение эллипса имеет
вид
.
Полуось
.
В таком случае получим
– уравнение эллипса. Найдем
.
Так как
лежит на эллипсе, то ее координаты
удовлетворяют его уравнению, т. е.
.
Итак, искомое уравнение эллипса
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
фокусы которого лежат на оси абсцисс симметрично
относительно начала координат, зная, кроме того,
что:
и 2;
равна 10, а расстояние между фокусами 2c=8;
24, а расстояние между фокусами 2c=10;
его фокусами 2c=6 и эксцентриситет e=3/5.
равна 20, а эксцентриситет e=3/5.
10, а эксцентриситет e=12/13;
его директрисами равно 5 и расстояние между
фокусами 2c=4;
равна 8, а расстояние между директрисами равно 16;
6, а расстояние между директрисами равно 13;
его директрисами равно 32 и e=1/2.
уравнение эллипса, фокусы которого лежат на оси
ординат симметрично начала координат, зная,
кроме того, что:
соответственно 7 и 2;
равна 10, а расстояние между фокусами 2c=8;
его фокусами 2c=24 и эксцентриситет e=12/13.
16, а эксцентриситет e=3/5.
его фокусами 2c=6 и расстояние между директрисами
равно 50/3;
его директрисами равно 32/3 и эксцентриситет e=3/4.
каждого из следующих эллипсов:
эксцентриситет, уравнения директрис.
четырехугольника, две вершины которого лежат в
фокусах эллипса
совпадают с концами его малой оси.
эксцентриситет, уравнения директрис.
четырехугольника, две вершины которого лежат в
фокусах эллипса
концами его малой оси.
расстояние от фокуса F(c; 0) эллипса
односторонней с этим фокусом директрисы.
циркулем, построить фокусы эллипса
что изображены оси координат и задана масштабная
единица).
–3.
из точек A1(-2; 3), A2(2; -2), A3(2;
-4), A4(-1; 3), A5(-4; -3), A6(3; -1), A7(3;
-2), A8(2; 1), A9(0; 15), A10(0; -16) лежат на эллипсе
внутри и какие вне его.
линии опеределяются следующими уравнениями.
Изобразить эти линии на чертеже.
эллипса e=2/3, фокальный радиус точки М эллипса
равен 10. Вычислить расстояние от точки М до
односторонней с этим фокусом директрисы.
эллипса e=2/5, расстояние от точки эллипса до
директрисы равно 20. Вычислить расстояние от
точки М до фокуса, односторонней с этой
директрисой.
уравнения прямых, на которых лежат фокальные
радиусы точки М1.
459
точка M1(-4; 2,4) лежит
на эллипсе
М1.
эллипса e=1/3, центр его совпадает с началом
координат, один из фокусов (-2; 0). Вычислить
расстояние от точки М1 эллипса с абсциссой, равной 2, до
директрисы, односторонней с данным фокусом.
эллипса e=1/2, центр его совпадает с началом
координат, одна из директрис дана уравнением x=16.
Вычислить расстояние от точки M1
эллипса с абсциссой, равной –4, до
фокуса, одностороннего с данной директрисой.
эллипса
правого фокуса равно 14.
эллипса
левого фокуса равно 2,5.
большой оси. Определить расстояния от точек
пересечения этого перпендикуляра с эллипсом до
фокусов.
уравнения эллипса, фокусы которого расположены
на оси абсцисс симметрично относительно начала
координат, если даны:
и его малая полуось b=3;
-2) эллипса и его большая полуось
a=4;
М2(
и его эксцентриситет e=2/3;
-5/3) эллипса и его эксцентриситет
e=2/3;
12) эллипса и расстояние r1=20
от нее до левого фокуса.
и расстояние между его директрисами, равное 10.
эксцентриситет e эллипса, если:
из фокусов под углом 600;
фокусами виден и вершин малой оси под прямым
углом;
директрисами в три раза больше расстояния между
фокусами;
перпендикуляра, опущенного из центра эллипса на
его директрису, делится вершиной эллипса
пополам.
эллипса проведен перпендикуляр к его большой оси
(см. рис.). Определить, при каком значении
эксцентриситета эллипса отрезки
параллельны.
уравнение эллипса с полуосями a, b и центром C(x0, y0), если
известно, что оси симметрии эллипса параллельны
осям координат.
абсцисс в точке А(3; 0) и оси ординат в точке В(0; -4).
Составить уравнение этого эллипса, зная, что его
оси симметрии параллельны координатным осям.
является центром эллипса, касающегося обеих
координатных осей. Составить уравнение этого
эллипса, зная, что его оси симметрии параллельны
координатным осям.
каждое из следующих уравнений определяет эллипс,
и найти координаты его центра С, полуоси,
эксцентриситет и уравнения директрис:
линии определяются следующими уравнениями.
Изобразить эти линии на чертеже.
уравнение эллипса, зная, что:
равна 26 и фокусы суть F1(-10; 0), F2(14;0);
473.2
2 и фокусы суть F1(-1; -1), F2(1;
1);
473.3
эксцентриситет e=
473.4
расстояние между директрисами равно
474
эксцентриситет
фокус F (-4; 1) и уравнение соответствующей
директрисы
уравнение эллипса, если известны его
эксцентриситет e=1/2, фокус F(-4; 1) и уравнение
соответствующей директрисы
на эллипсе, фокус которого F(-1; -4), а
соответствующая директриса дана уравнением
уравнение эллипса, если известны его
эксцентриситет e=1/2, фокус F(3; 0) и уравнение
соответствующей директрисы
-1) лежит на эллипсе, фокус
которого F(1; 0), а соответствующая директриса дана
уравнением
-1) является концом малой оси
эллипса, фокусы которого лежат на прямой
уравнение этого эллипса, зная его эксцентриситет
e=
пересечения прямой
пересечения прямой
пересечения прямой
расположена прямая относительно эллипса:
пересекает ли, касается или проходит вне его,
если прямая и эллипс заданы следующими
уравнениями:
каких начениях m прямая
эллипса.
при котором прямая
уравнение касательной к эллипсу
точке M1(x1; y1).
касательные к эллипсу
в концах одного и того же диаметра, параллельны.
(Диаметром эллипса называется его хорда,
проходящая через его центр).
уравнения касательных к эллипсу
прямой
уравнения касательных к эллипсу
к прямой
прямой
ближайшую к прямой
этой прямой.
проведены касательные к эллипсу
их уравнения.
проведены касательные к эллипсу
уравнение хорды, соединяющей точки касания.
проведены касательные к эллипсу
расстояние d от точки Р до хорды эллипса,
соединяющей точки касания.
через точку А(4; -1) и касается прямой
уравнение этого эллипса при условии, что его оси
совпадают с осями координат.
уравнение эллипса, касающегося двух прямых
условии, что его ося совпадают с осями координат.
произведение расстояний от центра эллипса до
точки пересечения любой его касательной с
фокальной осью и до основания перпендикуляра,
опущенного из точки касания на фокульную ось,
если величина постоянная, равная квадрату
большой полуоси эллипса.
произвдение расстояний от фокусов до любой
касательной к эллипсу равно квадрату малой
полуоси.
эллипса, фокусы которого находятся в точках F1(-3;
0), F2(3; 0). Составить
уравнение этого эллипса.
уравнение эллипса, фокусы которого расположены
на оси абсцисс симметрично относительно начала
координат, если известны уравнение касательной к
эллипсу
прямая, касающаяся эллипса в некоторой точке М,
составляет равные углы с фокальными радиусами F1M, F2M и проходит
вне угла F1MF2.
эллипса
Ox направлен луч света. Известно, что
до эллипса, луч на него отразился. Составить
уравнение прямой, на которой лежит отраженный
луч.
пересечения эллипсов
эллипсы
в четырех точках, лежающих на окружности с
центром в начале координат, определить радиус R
этой окружности.
полуоси эллипса, полученного проектированием на
плоскость
плоскости
полуось которого равна 6, является проекцией
окружности радиуса R=12. Опредилть угол
эллипс и окружность.
круглого цилиндра является окружность радиуса
R=8. Определить полуоси эллипса, полученного в
сечении этого цилиндра плоскостью, наклоненной к
его оси под уголом
круглого цилиндра является окружность радиуса R=
цилиндра нужно его пересечь плоскостью, чтобы в
сечении получить эллипс с большой полуосью a=2.
сжатием (или равномерным растяжением) плоскости
к оси абсцисс называется такое преобразование
точек плоскости, при котором произвольная точка
M(x; y) перемещается в точку M’(x’; y’) (рис.1 ) так, что
x’=x, y’=qy, где q>0 – постоянная, называемая
коэффициентом равномерного сжатия. Аналогично
рпи помощи уравнения x’=qx, y’=y определяется
равномерное сжатия плоскости к оси Oy (рис. 2).
Определить, в какую линию преобразуется
окружность
равномерного сжатия плоскости к оси абсцисс q=4/5.
равномерного сжатия плоскости к оси Oy равен 3/4.
Определить уравнение линии, в которую при таком
сжатии преобразуется эллипс
линии, в которую преобразуется эллипс
равномерных сжатиях плоскости к координатным
осям, если коэффициенты равномерного сжатия
плоскости к осям Ox и Oy равны соответственно 4/3 и
6/7.
коэффициент q равномерного сжатия плоскости к
оси Ox, при котором эллипс
в эллипс
коэффициент q равномерного сжатия плоскости к
оси Oy, при котором эллипс
в эллипс
коэффициенты q1, q2 двух последовательных равномерных
сжатий плоскости к осям Ox и Oy, при которых
эллипс






























![{displaystyle {begin{aligned}A&=a^{2}sin ^{2}theta +b^{2}cos ^{2}theta \[3mu]B&=2left(b^{2}-a^{2}right)sin theta cos theta \[3mu]C&=a^{2}cos ^{2}theta +b^{2}sin ^{2}theta \[3mu]D&=-2Ax_{circ }-By_{circ }\[3mu]E&=-Bx_{circ }-2Cy_{circ }\[3mu]F&=Ax_{circ }^{2}+Bx_{circ }y_{circ }+Cy_{circ }^{2}-a^{2}b^{2}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0229cbcba4d890d8b7ee7c0bec065a95a2b91229)


![{displaystyle {begin{aligned}a,b&={frac {-{sqrt {2{big (}AE^{2}+CD^{2}-BDE+(B^{2}-4AC)F{big )}{big (}(A+C)pm {sqrt {(A-C)^{2}+B^{2}}}{big )}}}}{B^{2}-4AC}}\x_{circ }&={frac {2CD-BE}{B^{2}-4AC}}\[5mu]y_{circ }&={frac {2AE-BD}{B^{2}-4AC}}\[5mu]theta &={begin{cases}operatorname {arccot} {dfrac {C-A-{sqrt {(A-C)^{2}+B^{2}}}}{B}}&{text{for }}Bneq 0\[5mu]0&{text{for }}B=0, A<C\[10mu]90^{circ }&{text{for }}B=0, A>C\end{cases}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c099e609531d008740862f621a7295d5015a2f9d)



![{displaystyle {begin{aligned}x(u)&=a{frac {1-u^{2}}{1+u^{2}}}\[10mu]y(u)&=b{frac {2u}{1+u^{2}}}end{aligned}};,quad -infty <u<infty ;,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c86f5ffc504dac624df3b6ce483c47521615fd18)
![{displaystyle [u:v]mapsto left(a{frac {v^{2}-u^{2}}{v^{2}+u^{2}}},b{frac {2uv}{v^{2}+u^{2}}}right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa1c21205522d70966ce62b8e324b19ec4c90f41)













































































































![{displaystyle {begin{aligned}C&=2pi aleft[{1-left({frac {1}{2}}right)^{2}e^{2}-left({frac {1cdot 3}{2cdot 4}}right)^{2}{frac {e^{4}}{3}}-left({frac {1cdot 3cdot 5}{2cdot 4cdot 6}}right)^{2}{frac {e^{6}}{5}}-cdots }right]\&=2pi aleft[1-sum _{n=1}^{infty }left({frac {(2n-1)!!}{(2n)!!}}right)^{2}{frac {e^{2n}}{2n-1}}right]\&=-2pi asum _{n=0}^{infty }left({frac {(2n-1)!!}{(2n)!!}}right)^{2}{frac {e^{2n}}{2n-1}},end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e202a234c19a28620ecf9c6d260eb21b1bd7aa0)
![{displaystyle {begin{aligned}C&=pi (a+b)sum _{n=0}^{infty }left({frac {(2n-3)!!}{2^{n}n!}}right)^{2}h^{n}\&=pi (a+b)left[1+{frac {h}{4}}+sum _{n=2}^{infty }left({frac {(2n-3)!!}{2^{n}n!}}right)^{2}h^{n}right]\&=pi (a+b)left[1+sum _{n=1}^{infty }left({frac {(2n-1)!!}{2^{n}n!}}right)^{2}{frac {h^{n}}{(2n-1)^{2}}}right].end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d29d8f31216e5d32400e99b04e75e242d987893)
![{displaystyle Capprox pi {biggl [}3(a+b)-{sqrt {(3a+b)(a+3b)}}{biggr ]}=pi {biggl [}3(a+b)-{sqrt {10ab+3left(a^{2}+b^{2}right)}}{biggr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86c8a7234c16af19a7338faafe61b4cf9a333f80)



![{displaystyle s=b left[;Eleft(z;{Biggl |};1-{frac {a^{2}}{b^{2}}}right);right]_{z = arccos {frac {x_{2}}{a}}}^{arccos {frac {x_{1}}{a}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7338c6c7bf9cc8e20da6c7da90eecd93f540416)










![{displaystyle {begin{aligned}a&={frac {r_{a}+r_{p}}{2}}\[2pt]b&={sqrt {r_{a}r_{p}}}\[2pt]ell &={frac {2}{{frac {1}{r_{a}}}+{frac {1}{r_{p}}}}}={frac {2r_{a}r_{p}}{r_{a}+r_{p}}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08835a73be73e7094f529d4eff42804930898271)