Пределы со степенями: показательная, степенная и показательно-степенная функции
Пределы со степенями бывают различных видов в зависимости от положения неизвестной $x$ в пределе. Рассмотрим примеры решений для следующих ситуаций:
- Показательная функция
$$limlimits_{xto a} a^{f(x)} = a^{limlimits_{xto a} f(x)} $$ - Степенная функция
$$ limlimits_{xto a} (f(x))^a = bigg(limlimits_{xto a} f(x) bigg)^a $$ - Показательно-степенная функция
$$limlimits_{xto a} bigg(f(x)bigg)^{g(x)} = limlimits_{xto a} frac{ln(f(x))}{frac{1}{g(x)}} $$
| Пример 1 |
| Найти предел показательной функции $limlimits_{xto 2} 2^{frac{x^2-4}{x-2}}$ |
| Решение |
|
Подставив точку $x=2$ в предел получим неопределенность $2^{big(frac{0}{0}big)}$. Итак, перенесем знак предела в показатель и попробуем его вычислить путем разложения числителя по формуле разности квадратов $a^2-b^2 = (a-b)(a+b)$. $$limlimits_{xto 2} 2^{frac{x^2-4}{x-2}} = 2^{limlimits_{xto 2} frac{(x-2)(x+2)}{x-2}} = $$ Сокращаем числитель со знаменателем на $x-2$ и вычисляем предел степени. $$ =2^{limlimits_{xto 2} (x+2)} = 2^{2+2} = 2^4 = 16 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$limlimits_{xto 2} 2^{frac{x^2-4}{x-2}} = 16$$ |
| Пример 2 |
| Решить предел степенной функции $limlimits_{xto 0} bigg(frac{sin x^2}{1-cos x}bigg)^3$ |
| Решение |
|
Внесем знак предела внутрь скобок, а степень останется при этом снаружи. $$limlimits_{xto 0} bigg(frac{sin x^2}{1-cos x}bigg)^3 = bigg(limlimits_{xto 0} frac{sin x^2}{1-cos x}bigg)^3 = $$ При подстановке точки $x=0$ в предел получаем неопределенность $frac{0}{0}$. Для её устранения воспользуемся таблицей эквивалентностей пределов. $$sin x^2 sim x^2$$ $$ 1-cos x sim frac{x^2}{2}$$ Подставляем эквивалентные функции в предел и сокращаем $x$. $$ = bigg(limlimits_{xto 0} frac{x^2}{frac{x^2}{2}}bigg)^3 = bigg(limlimits_{xto 0} frac{2x^2}{x^2} bigg)^3 = 2^3 = 8$$ |
| Ответ |
| $$limlimits_{xto 0} bigg(frac{sin x^2}{1-cos x}bigg)^3 = 8$$ |
| Пример 3 |
| Вычислить предел показательно-степенной функции $limlimits_{xto 0} (tg x)^{sin x} $ |
| Решение |
|
Если подставим $x=0$, то получим предел ноль в степени ноль $(0^0)$. Превратим это в другую неопределенность $(frac{infty}{infty})$ с помощью третьей формулы. $$limlimits_{xto 0} (tg x)^{sin x} = limlimits_{xto 0} frac{ln (tg ;x)}{frac{1}{sin x}} = frac{infty}{infty} = $$ Используем правило Лопиталя для продолжения решения. По нему, как известно, предел отношения функций равен пределу отношения производных от этих функций. $$ = limlimits_{xto 0} frac{(ln (tg ;x))’}{(frac{1}{sin x})’} = limlimits_{xto 0} frac{frac{frac{1}{cos^2 x}}{tg ;x}}{-frac{cos x}{sin^2 x}} = $$ Преобразуем числитель в нормальный вид с помощью формулы $tg ; x = frac{sin x}{cos x}$ и выполняем все необходимые сокращения. $$ = limlimits_{xto 0} frac{frac{1}{sin x cos x}}{-frac{cos x}{sin^2 x}} = -limlimits_{xto 0} frac{sin x}{cos^2 x} = $$ Теперь подставляя точку $x=0$ возможно получить окончательный ответ. $$ = — frac{sin 0}{cos^2 x} = -frac{0}{1} = 0 $$ |
| Ответ |
| $$limlimits_{xto 0} (tg x)^{sin x} = 0$$ |
Вычисление пределов степенно-показательных функций
Пусть функции
и
заданы на множестве
и функция
на нем положительна. Функция
называется степенно
— показательной.
Предположим, что
– точка сгущения множества
и существуют конечные пределы
,
,
где
.
Нужно найти
.
Воспользовавшись
тождествами
,
запишем исходное выражение в виде
.
В силу теоремы 6.1
получим
.
При заданных
значениях пределов будем иметь
.
Из проведенного
рассуждения видно, что предположение
о существовании конечных пределов
и
можно отбросить. Действительно, для
нахождения предела выражения
достаточно знать предел произведения
(конечный или бесконечный).
1) Пусть
.
Тогда
.
2) Если
,
то
.
3) Если
,
то
.
Заметим, что
произведение
может оказаться неопределенностью типа
.
Тогда и исходное выражение
представляет собой неопределенность.
Перечислим возникающие здесь
неопределенности.
1) Если
,
то вычисление предела
приводит к неопределенности типа
.
2) Если
,
то вычисление предела
приводит к неопределенности типа
.
3) Если
,
то вычисление предела
приводит к неопределенности типа
.
Во всех указанных
случаях (,
,
)
можно раскрыть неопределенность
в показателе степени, преобразуя ее к
типу
и используя соответствующие эквивалентные
бесконечно малые.
Замечание 8.3.
Приведенные выше рассуждения справедливы
и для вычисления предела степенно-показательной
функции в бесконечно удаленной точке:
.
Пример 8.2.
Вычислить
.
Решение.
Здесь
,
,
поэтому имеем неопределенность типа
.
Преобразуем выражение под знаком
предела:
.
В показателе
степени имеем неопределенность типа
.
Заменой
при
на эквивалентную бесконечно малую
раскрываем ее:
.
Таким образом,
.
Замечание 8.4.
Аналогично доказывается равенство
.
Пределы
,
образуют две формы
одного и того же равенства, которое
также является замечательным
пределом
и часто служат определением числа
.
Задачи к §8
Задача
1. Вычислить

Решение.
Здесь имеем
неопределенность типа
.
Преобразуем числитель дроби к форме
произведения:

Затем
заменим бесконечно малую в точке
функцию
эквивалентной бесконечно малой
.
Тогда
получим
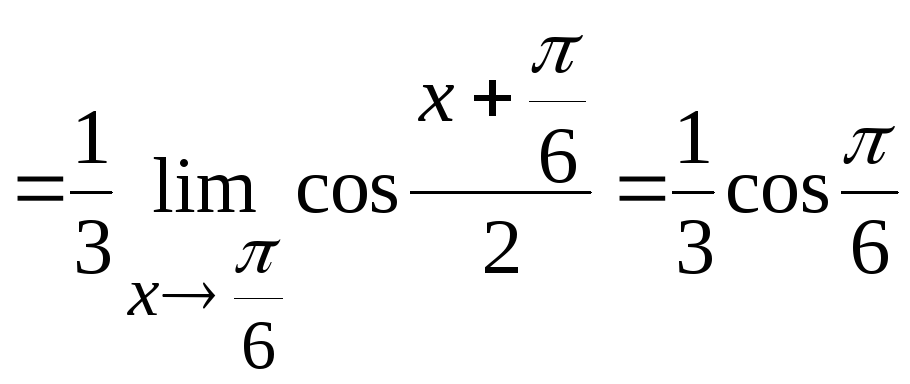
Ответ:
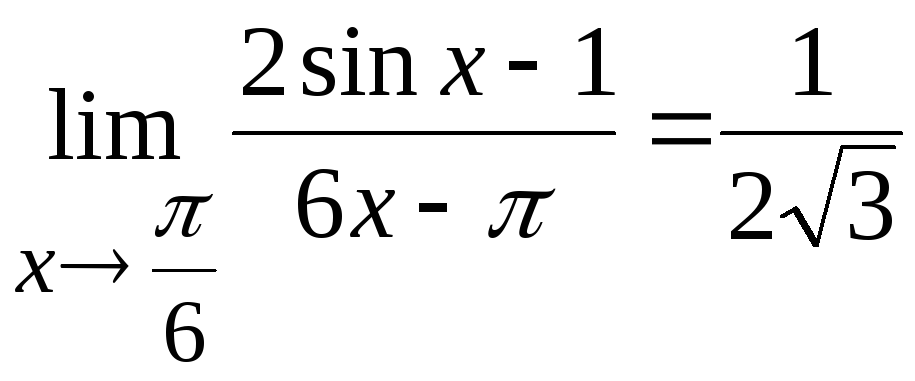
Задача
2. Вычислить
.
Решение.
Здесь возникает неопределенность типа
.
Преобразуем знаменатель, воспользовавшись
свойствами логарифмической функции, и
выделим в аргументе логарифма слагаемое,
равное 1:
.
Заменим
бесконечно малую в точке
функцию
эквивалентной бесконечно малой
.
Числитель разложим на множители:
.
Тогда
получим:

Ответ:
.
Задача
3. Вычислить
.
Решение.
Здесь возникает неопределенность типа
.
Представим числитель в виде:
.
Затем
заменим его эквивалентной бесконечно
малой в точке
функцией
.
Функцию
в точке
тоже заменим на эквивалентную бесконечно
малую
.
Тогда
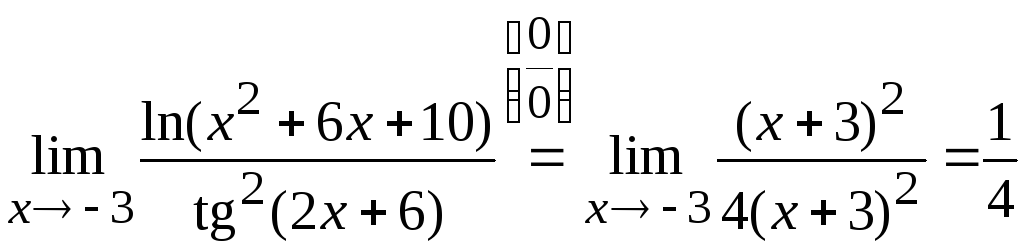
Ответ:
.
Задача
4. Вычислить
.
Решение.
Здесь возникает неопределенность типа
.
Представим числитель в виде:
.
Затем
заменим его эквивалентной бесконечно
малой в точке
функцией
.
Преобразуем
знаменатель:
и
заменим его на эквивалентную бесконечно
малую
.
Тогда получим
.
Ответ:
.
Задача
5. Вычислить
.
Решение.
Здесь возникает неопределенность типа
.
Числитель
можно заменить эквивалентной бесконечно
малой
.
Чтобы
воспользоваться соотношением (8.4),
преобразуем знаменатель:
и
заменим его эквивалентной бесконечно
малой
.
Тогда
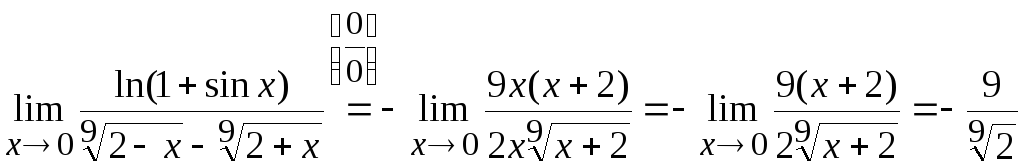
Ответ:
.
Задача
6. Вычислить
.
Решение.
Здесь имеем неопределенность типа
.
Чтобы применить к выражению
соотношение (8.3), представим его в виде:
,
и
заменим бесконечно малую функцию
эквивалентной бесконечно малой
.
Знаменатель же представим в виде:
и,
используя соотношения (8.2) и (8.8), заменим
его эквивалентной бесконечно малой
.
Учитывая проведенные выкладки и
соотношение (8.4), получим:
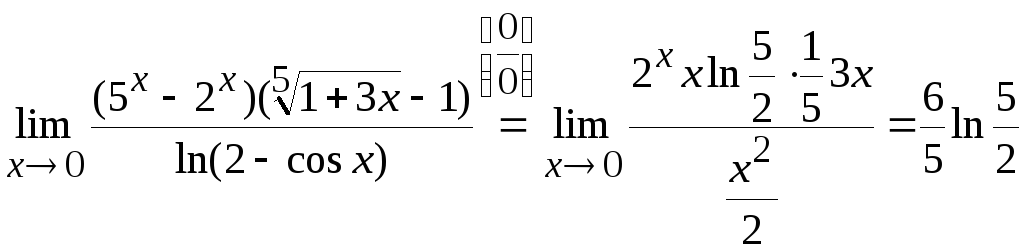
Ответ:
.
Задача
7. Вычислить
.
Решение.
Здесь имеем неопределенность типа
.
Используя ряд приемов, примененных в
задачах 1–7, получим
.
Ответ:
.
Задача
8. Вычислить
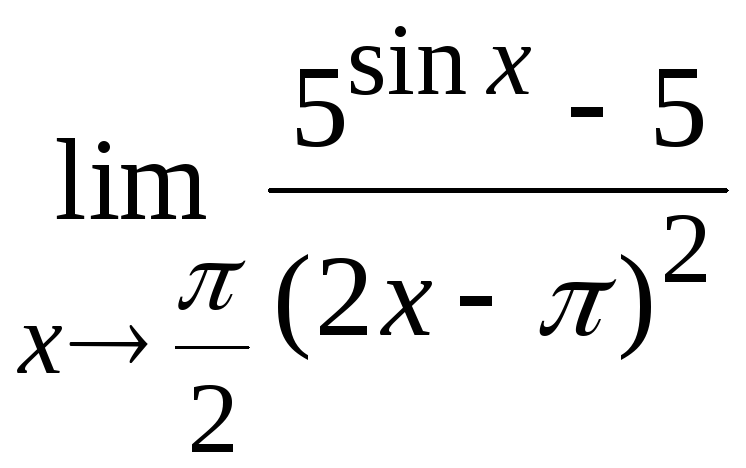
Решение.
Здесь имеем неопределенность типа
.
Используя ряд приемов, примененных в
задачах 1–7 и формулы приведения для
тригонометрических функций, получим
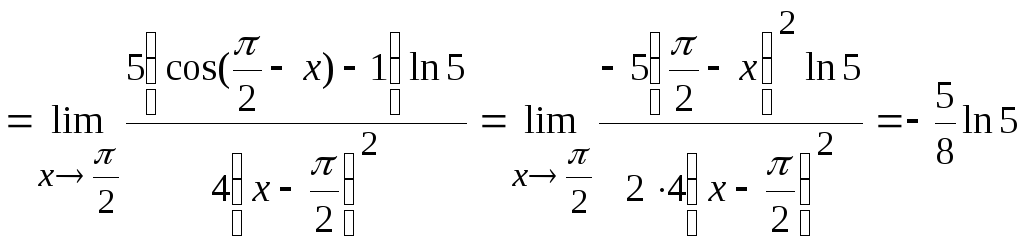
Ответ:
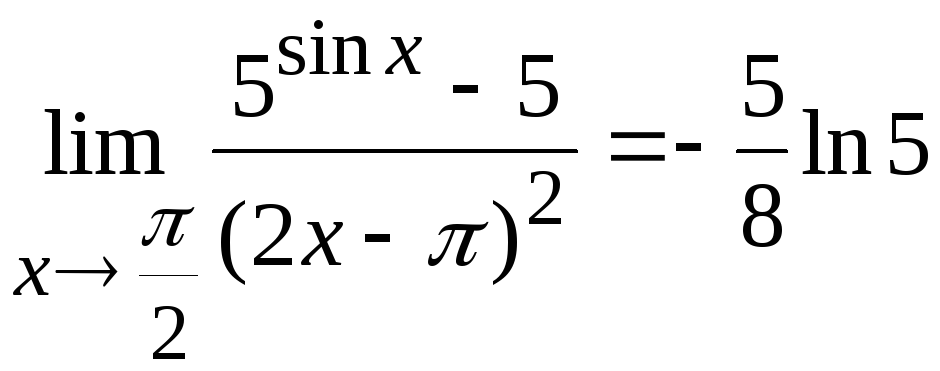
Задача
9. Вычислить
.
Решение.
Здесь имеем неопределенность типа
.
Чтобы применить к числителю соотношение
(8.2), преобразуем его следующим образом:
.
Теперь
числитель согласно соотношению (8.2)
можно заменить эквивалентной бесконечно
малой
.
Преобразуем
знаменатель
.
Заменяем,
используя соотношение (8.1),
эквивалентной бесконечно малой
.
Тогда

Ответ:
.
Задача
10. Вычислить
.
Решение.
Здесь имеем неопределенность типа
.
Используя приемы, описанные выше, получим
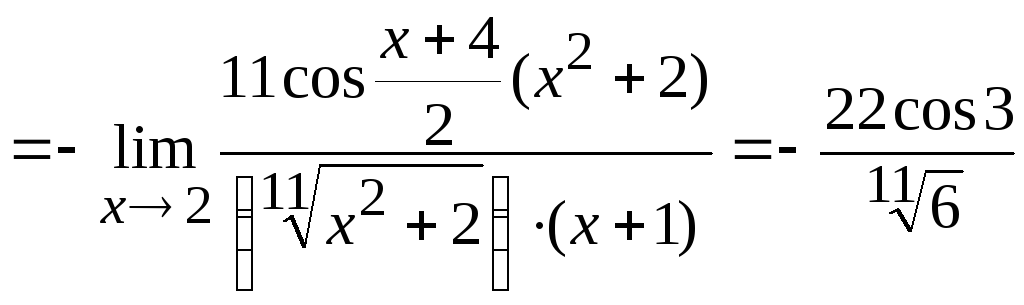
.
Ответ:
.
Задача
11. Вычислить

Решение.
Здесь имеем неопределенность типа
.
Используя теоремы 6.2 и 6.1, получим
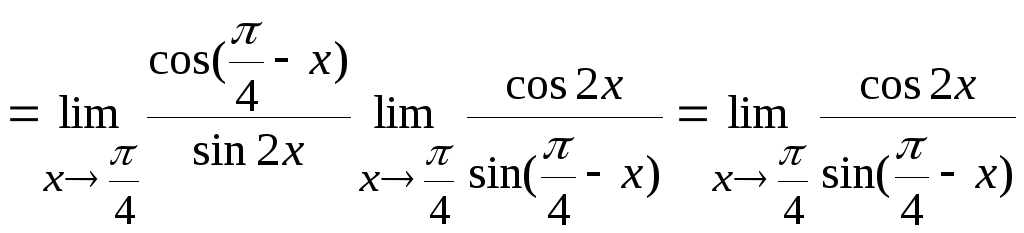
Получили
неопределенность типа
.
Преобразуем выражение с помощью формул
приведения, затем переходим к эквивалентным
бесконечно малым. В итоге получим
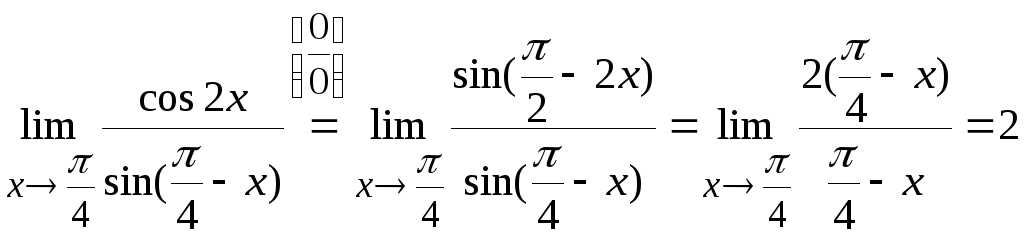
Ответ:
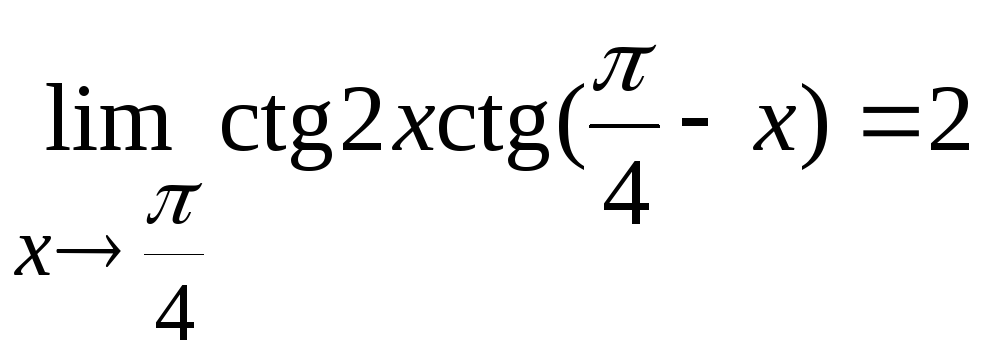
Задача
12. Вычислить
.
Решение.
Здесь имеем неопределенность типа
.
Выделим
в основании степени:
.
Заметим,
что
при
.
Справедлива
цепочка равенств

Заменяя
логарифм эквивалентной бесконечно
малой согласно соотношению (8.2) и используя
замечание 6.4 для раскрытия неопределенности,
получим
.
Ответ:
.
Задача
134.
Вычислить
.
Решение.
Здесь имеем неопределенность типа
.
Введем переменную
.
Если
,
то
.
.
Выделим
в основании степени:
,
тогда
.
Заметим,
что
при
.
Заменим функцию
эквивалентной бесконечно малой
,
будем иметь
.
Используя
теорему 7.3, окончательно получим
.
Ответ:
.
Задача
14. Вычислить
.
Решение.
Здесь возникает неопределенность типа
.
Поскольку
,
вычислим
сначала
.
Мы имеем дело с неопределенностью типа
.
Воспользовавшись
последовательно соотношениями (8.2) и
(8.1), будем иметь
.
Ответ:
.
Задача
15. Вычислить
.
Решение.
Здесь возникает неопределенность типа
.
Воспользуемся формулой
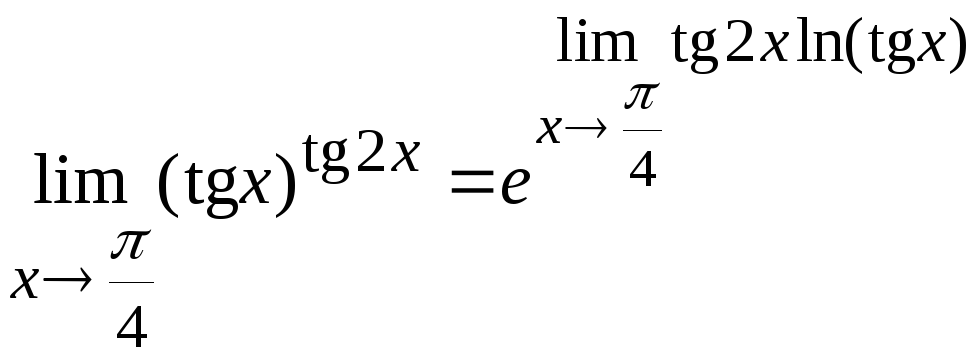
Вычислим
предел, стоящий в показателе степени.
Для этого требуется раскрыть
неопределенность типа
.
Преобразуем ее в неопределенность типа
и воспользуемся эквивалентностью
бесконечно малых:

Ответ:
.
Задача
16. Вычислить
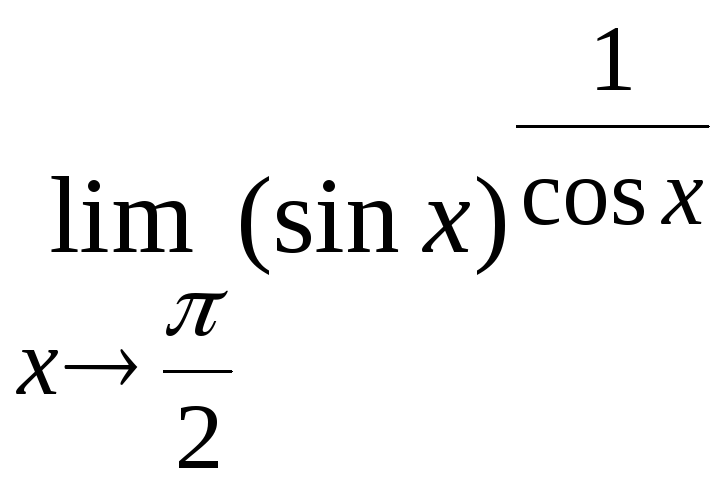
Решение.
Здесь возникает неопределенность типа
.
Преобразуем исходное предельное
выражение
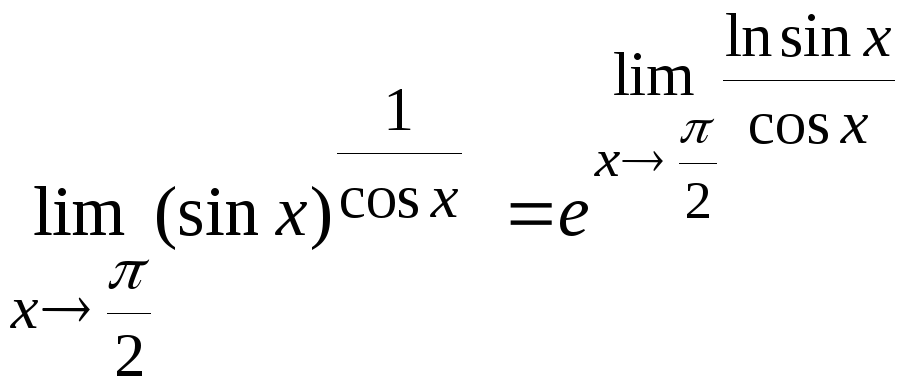
Вычислим
предел, стоящий в показателе степени.
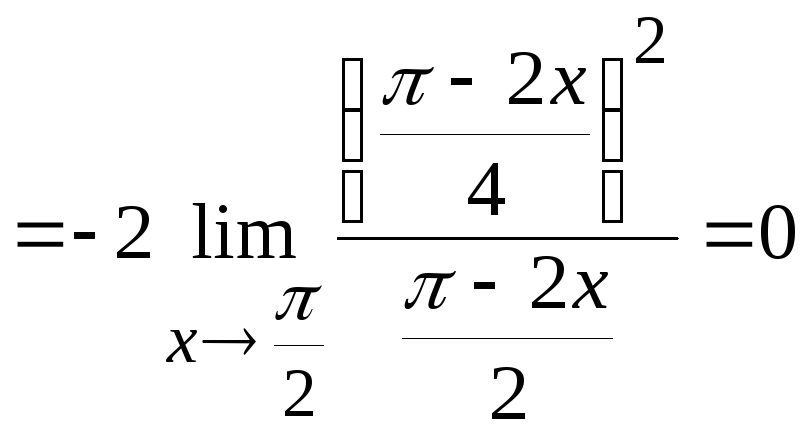
Ответ:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
2
Лекция 7. «Первый замечательный предел».
Предел функции в точке. Основные теоремы о пределах Первый замечательный предел
к.п.н., преподаватель высшей категории Никитин М.Е. Раменское, 2021
Предел функции
- Предел функции в точке
- Односторонние пределы
- Предел функции при x стремящемся к бесконечности
- Основные теоремы о пределах
- Вычисление пределов
- Раскрытие неопределенностей
- Первый замечательный предел
Предел функции в точке
Пусть функция y = f(x) определена в некоторой окрестности точки x 0 , кроме, быть может самой точки x 0 .
Число А называют пределом функции в точке x 0 (или при ), если для любого положительного
ε найдется такое положительное число δ , что для всех х из δ – окрестности точки x 0 справедливо неравенство:
Предел функции в точке
ε окрестность точки А
y
А
0
х 0
х
δ окрестность точки x 0
Геометрический смысл предела: для всех х из δ – окрестности точки x 0 точки графика функции лежат внутри полосы, шириной 2 ε , ограниченной прямыми: у = А + ε , у = А — ε .
0 найдется такое δ 0 , что для всех справедливо неравенство: Предел слева записывают так: «
Односторонние пределы
В определении предела функции
предполагается, что x стремится к x 0 любым способом: оставаясь меньше, чем x 0 (слева от x 0 ), большим, чем x 0 (справа от x 0 ), или колеблясь около точки x 0 .
Бывают случаи, когда способ приближения аргумента x к x 0 существенно влияет на значение предела, поэтому вводят понятия односторонних пределов.
Число А 1 называют пределом функции слева в точке x 0 , если для любого ε 0 найдется такое δ 0 , что для всех справедливо неравенство:
Предел слева записывают так:
Односторонние пределы
Число А 2 называют
пределом функции справа в точке x 0 , если
Предел справа записывают так:
Пределы функции слева и справа называют односторонними пределами .
y
y
А 2
А 1 =А 2 =А
А 1
Очевидно, если существует
0
0
х
х
х 0
х 0
то существуют и оба односторонних предела, причем А = А 1 = А 2
M или при x — M точки графика функции лежат внутри полосы шириной 2 ε , ограниченной прямыми: у = А + ε , у = А — ε . А 0 х М «
Предел функции при x стремящемся к бесконечности
Пусть функция y = f(x) определена в промежутке .
Число А называют пределом функции при , если
y
Геометрический смысл этого определения таков:
существует такое число М , что при х M или при x — M точки графика функции лежат внутри полосы шириной 2 ε , ограниченной прямыми:
у = А + ε , у = А — ε .
А
0
х
М
Основные теоремы о пределах
Рассмотрим теоремы, которые облегчают нахождение пределов функций.
Формулировка теорем, когда или аналогичны, поэтому будем пользоваться обозначением: .
Предел суммы (разности) двух функций равен сумме (разности) пределов:
Предел произведения двух функций равен произведению пределов:
Постоянный множитель можно выносить за знак предела:
Основные теоремы о пределах
Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя не равен нулю:
Предел степени с натуральным показателем равен той же степени предела:
Предел показательно – степенной функции:
x 0 , то существует соответственно ее левый предел: или ее правый предел: «
Основные теоремы о пределах
Если между соответствующими значениями трех функций
при этом:
выполняются неравенства:
тогда:
Если функция f(x) монотонна и ограничена при
x x 0 или при
x x 0 , то существует соответственно ее левый предел:
или ее правый предел:
Вычисление пределов
Вычисление предела:
начинают с подстановки предельного значения x 0 в функцию f(x) .
Если при этом получается конечное число, то предел равен этому числу.
Если при подстановки предельного значения x 0 в функцию f(x) получаются выражения вида:
то предел будет равен:
Вычисление пределов
Часто при подстановке предельного значения x 0 в функцию f(x) получаются выражения следующих видов:
Эти выражения называются неопределенности , а вычисление пределов в этом случае называется раскрытие неопределенности.
Раскрытие неопределенностей
Раскрытие неопределенности
Если f(x) – дробно – рациональная функция, необходимо разложить на множители числитель и знаменатель дроби
Если f(x) – иррациональная дробь, необходимо умножить числитель и знаменатель дроби на выражение, сопряженное числителю.
Раскрытие неопределенностей
Раскрытие неопределенности
Если f(x) – дробно – рациональная функция или иррациональная дробь необходимо разделить числитель и знаменатель дроби на x в старшей степени
Раскрытие неопределенностей
Раскрытие неопределенности
Умножим и разделим функцию на сопряженное выражение.
Первый замечательный предел
Функция
не определена при x = 0 .
Найдем предел этой функции при
С
М
x
Обозначим:
S 1 — площадь треугольника OMA ,
S 2 — площадь сектора OM А,
S 3 — площадь треугольника O СА,
В
А
О
Из рисунка видно, что S 1 2 3
Первый замечательный предел
С
М
x
В
А
О
Первый замечательный предел
Формула справедлива также при x 0
Следствия:
Первый замечательный предел
Пределы — предварительный расчет
Все ресурсы для предварительного расчета
12 диагностических тестов
380 практических тестов
Вопрос дня
Карточки
Learn by Concept
← Предыдущая 1 2 3 Следующая →
Precalculus Help »
Вводный расчет »
Пределы
При каком значении функция разрывна,
?
Возможные ответы:
Отверстия нет
Правильный ответ:
Пояснение:
Чтобы найти разрыв, нужно посмотреть, где знаменатель функции равен нулю.
нам нужно установить знаменатель равным нулю и решить для:
Когда , что не определено.
Следовательно, здесь функция разрывна.
Сообщить об ошибке
Что такое
?
Возможные ответы:
Предел не существует
Правильный ответ:
6
Объяснение:
Означает найти предел функции при приближении слева. Мы видим, что это вертикальная асимптота, поэтому нам нужно смотреть на числа, очень близкие к нулю в левой части. Значение продолжает уменьшаться слева от нуля, при этом значение снижается еще больше по мере приближения к . Таким образом, предел составляет 9 0005
Сообщить об ошибке
Что такое
?
Возможные ответы:
Предел не существует
Правильный ответ:
6
Пояснение:
Сначала нам нужно упростить функцию, мы можем сделать это, разложив числитель и знаменатель на множители.
Если мы подставим 3 в упрощенную функцию, то получим:
Сообщить об ошибке
Что такое
?
Возможные ответы:
Правильный ответ:
Объяснение:
замены для получения следующего:
Отчет о ошибке
Оцените следующее:
Возможные ответы:
Правильный ответ:
Объяснение:
При оценке пределов на бесконечности следует помнить три правила:
- Если степень старшего показателя в числителе равна степени старшего показателя в знаменателе, то предел равен отношение коэффициента при старшем показателе в числителе к коэффициенту при старшем показателе в знаменателе.
Обязательно включите знаки.
- Если степень старшего показателя в числителе меньше степени старшего показателя в знаменателе, предел = 0,
- Если степень наибольшего показателя в числителе больше степени наибольшего показателя в знаменателе, разделите наибольшую степень в числителе на наибольшую степень в знаменателе и подставьте бесконечность. Вы либо замените положительную, либо отрицательную бесконечность в зависимости от того, какие вопросы просят вас оценить предел.
В этом случае степень в числителе больше, чем в знаменателе (правило №3). Значит, нужно разделить высшие силы и оценить.
Оценка как x:
Ответ: лимит =
Отчет о ошибке
Оценка следующего:
Возможные ответы:
. Правильный: 9005
000
000
000
000
000
000
000
000
000
000
000
000
000
000
000
000
000
000
000
000
000
000
000
000
000
000
000
000
000
0009000
000 .
Объяснение:
При оценке пределов на бесконечности следует помнить три правила:
- Если степень старшего показателя в числителе равна степени старшего показателя в знаменателе, то предел равен отношению коэффициента при старшем показателе в числителе над коэффициентом при старшем показателе в знаменателе. Обязательно включите знаки.
- Если степень старшего показателя в числителе меньше, чем степень старшего показателя в знаменателе, предел = 0,
- Если степень наибольшего показателя в числителе больше степени наибольшего показателя в знаменателе, разделите наибольшую степень в числителе на наибольшую степень в знаменателе и подставьте бесконечность. Вы либо замените положительную, либо отрицательную бесконечность в зависимости от того, какие вопросы просят вас оценить предел.
В этом случае и числитель, и знаменатель имеют наивысшую степень показателя степени 4 (правило №1). Следовательно, вам нужно сравнить соотношение коэффициентов.
Ответ: limit =
Сообщить об ошибке
Что такое,
?
Возможные ответы:
Правильный ответ:
Объяснение:
Конечное поведение функции соответствует наивысшим степеням как в числителе, так и в знаменателе. Следовательно, чтобы найти предел, нам нужно смотреть только на термин: так как это высшие степени в числителе и демонинаторе.
Теперь берем
.
Таким образом, предел нашей исходной функции также .
Сообщить об ошибке
Оцените предел ниже:
Возможные ответы:
Правильный ответ:
6
Объяснение:
будет приближаться при приближении , поэтому будет иметь тип, как показано ниже:
Итак, мы можем применить правило L’Hospital:
С момента:
Отсюда:
.
Объяснение:
Когда x=3/2, наш знаменатель равен нулю, поэтому мы не можем просто подставить 3/2, чтобы получить предел. Если мы посмотрим на числитель, когда x = 3/2, мы обнаружим, что он также равен нулю, поэтому наш числитель можно разложить на множители. Мы видим, что наш предел можно переписать как:
затем мы можем исключить 2x-3 из числителя и знаменателя, оставив нам:
и мы можем просто подставить 3/2 в этот предел, чтобы получить
примечание: наша функция не непрерывна при x=3/2, но предел существует.
Сообщить об ошибке
Решить следующее ограничение:
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту задачу, нам нужно расширить член в числителе
, когда мы это сделаем, мы получим
вторая степень х слагаемых отменяется, и мы получим
теперь мы можем сократить наши h в числителе и знаменателя, чтобы получить
, тогда мы можем просто подставить 0 вместо h, и мы получим наш ответ0003
12 диагностических тестов
380 практических тестов
Вопрос дня
Карточки
Learn by Concept
Ограничение по времени на получение степеней решение в поисках проблемы
«Похоже, оно предназначено для выявления вечного студента, который просто получает степень за степенью.
«Большая восьмерка» в своем представлении на консультации по проекту руководящих принципов для права на обучение студентов заявляет, что она обеспокоена тем, что законодательство может иметь разрушительные последствия для предложения медицинских стажеров. Большое количество студентов-медиков получают трехлетнюю степень бакалавра в смежной области, такой как естественные науки, прежде чем перейти на четырехлетнюю субсидируемую государством аспирантуру.
Вики Томсон, исполнительный директор Go8, сказала, что уже существует нехватка врачей, 30% которых прошли обучение за границей.
«Нам также необходимо тщательно рассмотреть последствия семилетнего ограничения для студентов, испытывающих затруднения в учебе, особенно из фондовых групп, а также взаимодействие этой меры с ограничением по Программе займов на высшее образование и правилом 50-процентного проходного балла. .
Однако представитель отдела образования сообщил, что более длительные степени, длящиеся шесть и более лет, будут учитываться в руководящих принципах SLE.
Учащиеся, не сдавшие более 50% предметов, потеряют право на обучение. В настоящее время студенты могут получить максимум 108 232 доллара США в виде ссуды на оплату обучения, широко известной как HECS, или 155 448 долларов США для тех, кто изучает медицину, стоматологию или ветеринарию, более известную как HECS.
Реклама
Г-жа Томсон также сказала, что Go8 настаивает на том, чтобы правило 50-процентного проходного балла было отложено до 2023 года на том основании, что нынешние учащиеся 11 и 12 классов пережили бурный и нестабильный период пандемии, и есть раннее свидетельствуют о том, что показатели успеваемости уже снижаются среди первокурсников.
«Например, в Сиднейском университете мы наблюдаем более высокий уровень отказов в 2021 году, чем в 2020 году или в предыдущие годы, особенно в таких дисциплинах, как наука со значительными практическими компонентами.
, учитывая перерыв в их обучении», — говорится в сообщении.
Студенты Мельбурнского университета и Университета Западной Австралии также ощутят право на обучение. Оба имеют модель, в которой студенты проходят обширную трехлетнюю программу бакалавриата, а затем специализируются на двухлетней профессиональной магистерской программе.
Представитель Мельбурнского университета сказал, что ограничение по времени «возложит больше ответственности на студентов, которые проходят более продолжительные учебные программы, поскольку у них фактически меньше гибкости, чем у студентов, которые изучают более короткие курсы».
Представитель отдела образования сказал, что право на обучение студентов было разработано, чтобы «поощрить студентов получать дипломы и поступать на работу».
Он добавил, что учащимся может быть повторно зачислено их право при некоторых обстоятельствах, в том числе, если события выйдут из-под их контроля.
При вычислении пределов от показательно-степенной функции пользуются либо формулой 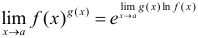
Пример №1.
Вычислить 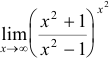
Решение:
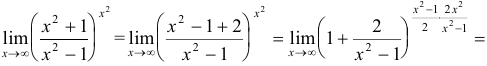
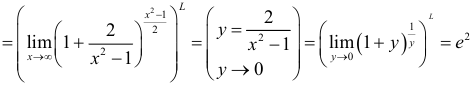
Пример №1.
Вычислить 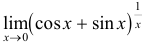
Решение:
Заметим, что 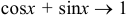
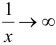
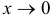
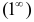
так как
Пример №2.
Вычислить 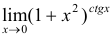
Решение:
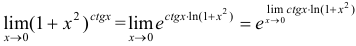
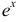
Следовательно, 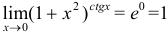
Пример №3.
Вычислить 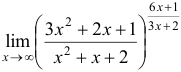
Решение:
Так как 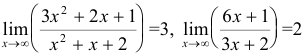
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
Если при нахождении предела получаем число в степени бесконечность, то для отличных от нуля и единицы значений такое выражение не является неопределенностью и вычисляется непосредственно.Поскольку показательная функция
при а>1 возрастает, то для таких а
При 0<а<1 показательная функция убывает, поэтому в этом случае ее значение на бесконечности стремится к нулю :
Соответственно, применение второго замечательного предела здесь не требуется. Используем следующее свойство пределов:
при условии, что эти пределы существуют.
Рассмотрим примеры, в которых нужно найти число в степени бесконечность.
Найти пределы функций:
1)
Получили неопределенность бесконечность на бесконечность в степени бесконечность.
Найдем пределы основания и показателя степени. (Как находить предел бесконечность на бесконечность, уже рассматривали ранее. Делим и числитель, и знаменатель на старшую степень икса, в данном случае — на x.)
Таким образом, приходим к выводу, что
2) Вычислить предел функции:
Рассуждаем аналогично. При нахождении предела основания степени делим многочлены в числителе и знаменателе на старшую степень икса, то есть на x²:



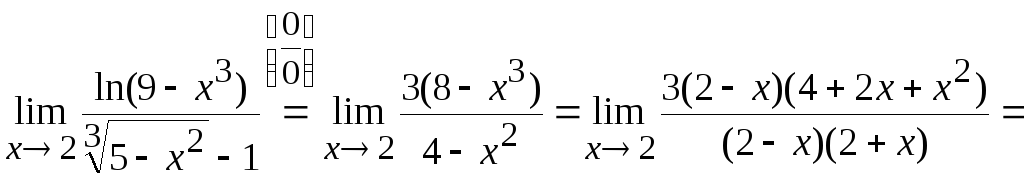
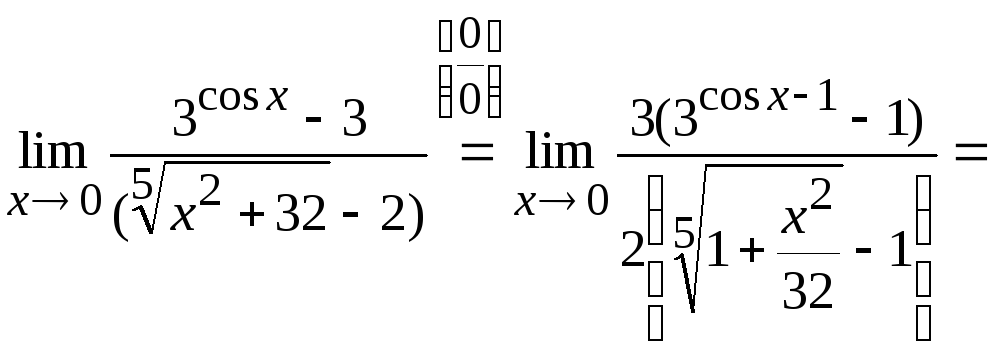
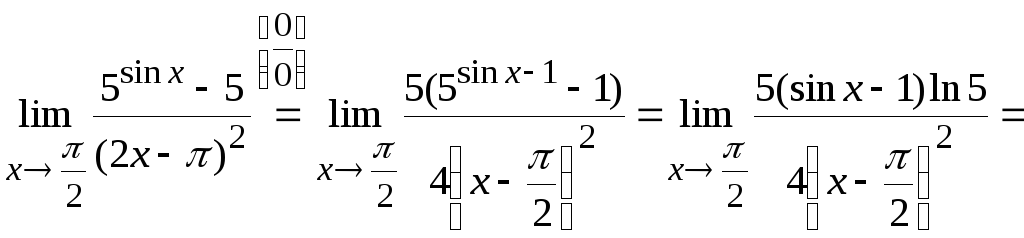




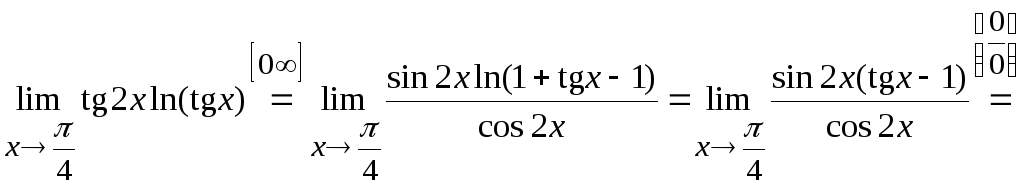
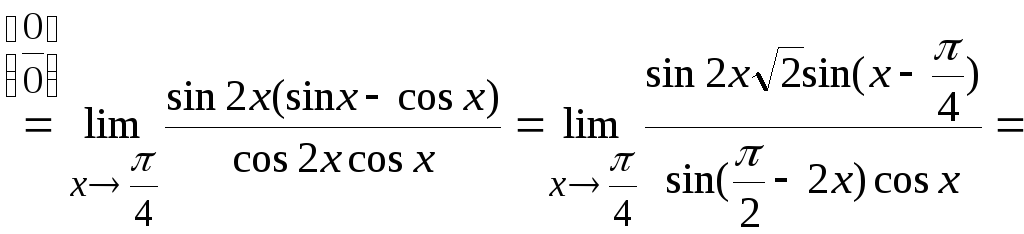


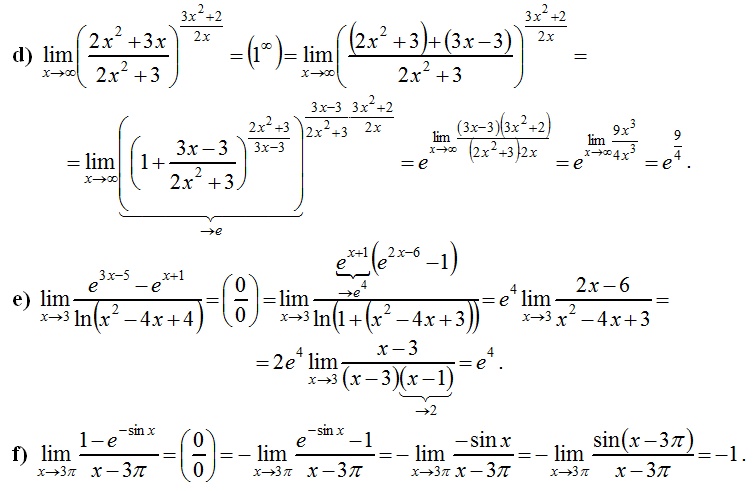 Обязательно включите знаки.
Обязательно включите знаки. 
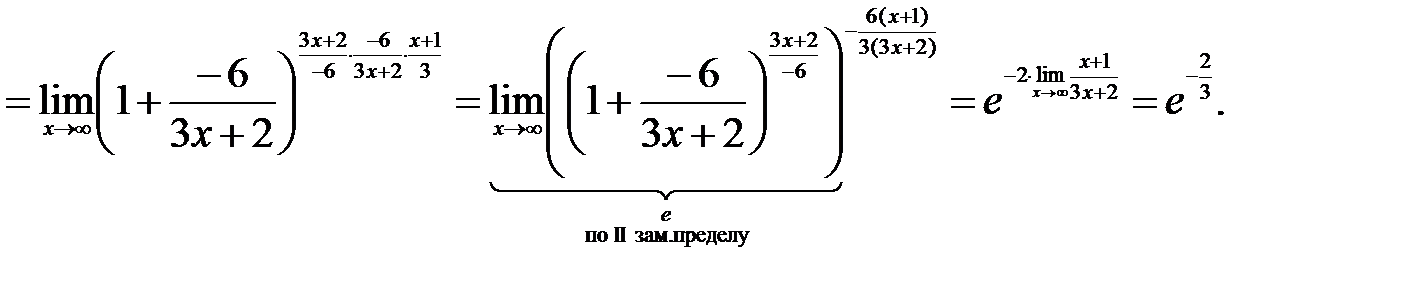

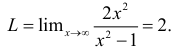
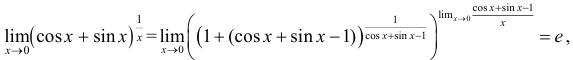
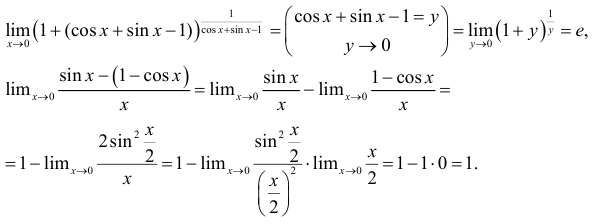
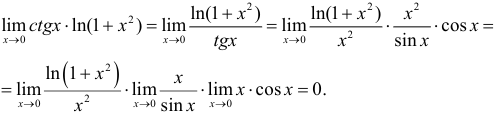
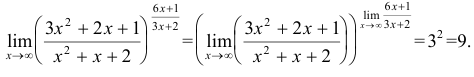

![Rendered by QuickLaTeX.com [ = mathop {lim }limits_{x to infty } {left[ {frac{{3 - frac{7}{{{x^2}}}}}{{2 + frac{5}{{{x^2}}}}}} right]^{mathop {lim }limits_{x to infty } (4{x^2} - 1)}} = {left[ {frac{3}{2}} right]^infty } = infty .]](https://www.matematika.uznateshe.ru/wp-content/ql-cache/quicklatex.com-55824751de531de0dbada0116615fa7f_l3.png)