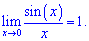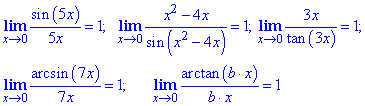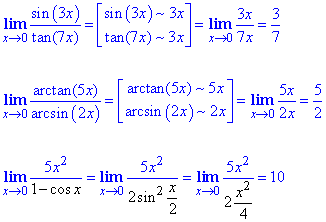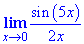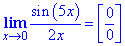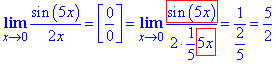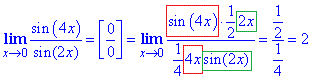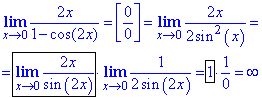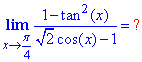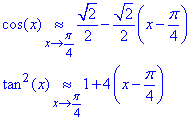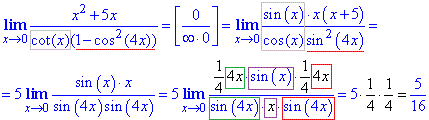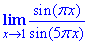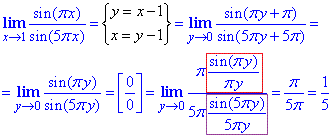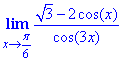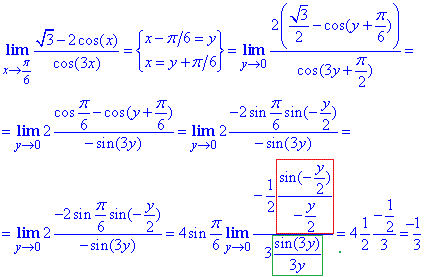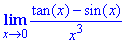Как найти предел для синуса - Исправление недочетов и поиск решений вместе с Examum.ru

Пределы с тригонометрическими функциями

Существует множество различных пределов тригонометрических функций. На помощь могут прийти основные методы вычисления:

Первый замечательный предел и его следствие с тангенсом $$limlimits_{xto 0} frac{sin x}{x} = 1, qquad limlimits_{xto 0} frac{tg x}{x} = 1$$
Тригонометрические преобразования и формулы
Таблица бесконечно малых эквивалентных функций
Правило Лопиталя

Рассмотрим примеры подробного решения тригонометрических пределов для разбора каждого способа. Стоит отметить, что все методы можно комбинировать в одной задаче между собой для ускорения процесса вычисления.

Пример 1

Решить предел с тригонометрическими функциями с помощью первого замечательного предела $limlimits_{xto 0} frac{tg 2x}{sin3x}$

Решение

Подставляя $x=0$ в предел получаем неопределенность $(frac{0}{0})$. Сделаем преобразования в числителе и знаменателе таким образом, чтобы появился замечательный предел.

$$ tg 2x = frac{tg 2x}{2x} cdot 2x $$ $$ sin 3x = frac{sin 3x}{3x} cdot 3x $$

Подставляем получившиеся преобразования, чтобы применить формулу первого замечательного предела.

$$ limlimits_{xto 0} frac{frac{tg 2x}{2x} cdot 2x}{frac{sin 3x}{3x} cdot 3x} = limlimits_{xto 0} frac{1 cdot 2x}{1 cdot 3x} = $$

Теперь остается только сократить $x$ и записать ответ.

$$ = frac{2x}{3x} = frac{2}{3} $$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$limlimits_{xto 0} frac{tg 2x}{sin3x} = frac{2}{3}$$

Пример 2

Вычислить предел с помощью тригонометрического преобразования $limlimits_{xto 0} frac{sqrt{4+x}-2}{1-cos 3x}$

Решение

Обратим внимание на корень в числителе. От него нужно избавиться путём умножения и деления на сопряженное к нему число (отличающееся знаком между слагаемыми).

$$limlimits_{xto 0} frac{(sqrt{4+x}-2)(sqrt{4+x}+2)}{(1-cos 3x)(sqrt{4+x}+2)} = $$

Теперь с помощью формулы разности квадратов $(a-b)(a+b)=a^2 — b^2$ упростим числитель.

$$ = limlimits_{xto 0} frac{4+x-4}{(1-cos 3x)(sqrt{4+x}+2)} = limlimits_{xto 0} frac{x}{(1-cos 3x)(sqrt{4+x}+2)} $$

В этой задаче не обойтись без тригонометрической формулы $1-cos x = 2sin^2 frac{x}{2}$. Выполним по ней преобразование выражение в знаменателе.

$$1-cos 3x = 2sin^2 frac{3x}{2}$$

$$ = limlimits_{xto 0} frac{x}{2sin^2 frac{3x}{2} (sqrt{4+x}+2)} = $$

Видим, что в знаменателе появился синус, а это значит, что можно избавиться от него с помощью первого замечательного предела. Как в предыдущем примере одновременно умножаем и делим на аргумент синуса.

$$ sin^2 frac{3x}{2} = (sin frac{3x}{2})^2 = (frac{sin frac{3x}{2}}{frac{3x}{2}} cdot frac{3x}{2})^2 $$

Подставляем преобразование синуса, чтобы применить замечательный предел.

$$ = limlimits_{xto 0} frac{x}{2(frac{sin frac{3x}{2}}{frac{3x}{2}} cdot frac{3x}{2})^2 (sqrt{4+x}+2)} = limlimits_{xto 0} frac{x}{frac{9x^2}{2}(sqrt{4+x}+2)} = $$

Выносим константу перед пределом и сокращаем $x$ в числителе и знаменателе.

$$ = frac{2}{9} limlimits_{xto 0} frac{1}{x(sqrt{4+x}+2)} = frac{2}{9} cdot (frac{1}{0}) = infty $$

Ответ

$$limlimits_{xto 0} frac{sqrt{4+x}-2}{1-cos 3x} = infty$$

Пример 3

Найти предел с помощью логарифмирования $limlimits_{xto 0} (tg x)^{sin x} $

Решение

Подставляя $x=0$ получаем неопределенность (0^0). Под пределом показательно-степенная функция, поэтому нужно воспользоваться логарифмированием и свести к неопределенности $(frac{infty}{infty})$, чтобы затем воспользоваться правилом Лопиталя.

$$limlimits_{xto 0} e^{sin x ln(tg x)} = limlimits_{xto 0} e^{frac{ln(tg x)}{frac{1}{sin x}}} = e^frac{infty}{infty} = $$

Берем производные числителя и знаменателя дроби, стоящей в показателе экспоненты.

$$ bigg(frac{ln(tg x)}{frac{1}{sin x}}bigg)’ = frac{frac{frac{1}{cos^2 x}}{tg x}}{-frac{cos x}{sin^2 x}} = frac{frac{1}{sin x cos x}}{-frac{cos x}{sin^2 x}} = -frac{sin x}{cos^2 x}$$

Подставляем полученное выражение под знак предела и применяем свойство предела для показательной функции.

$$ = limlimits_{xto 0} e^{ -frac{sin x}{cos^2 x}} = e^{-limlimits_{xto 0} frac{sin x}{cos^2 x} } = $$

Теперь, подставляя $x=0$ в предел, вычисляем окончательный ответ.

$$ = e^{-frac{0}{1}} = e^0 = 1 $$

Ответ

$$limlimits_{xto 0} (tg x)^{sin x} = 1$$

Пример 4

Взять предел путем замены на бесконечно малые эквивалентные функции $limlimits_{xto 0} frac{xarcsin 3x}{1-cos 2x}$

Решение

Итак, в пределе неопределенность ноль делить на ноль. Выполним замены на эквивалентные функции.

$$ arcsin 3x sim 3x $$ $$1-cos 2x sim 2x^2 $$

Подставляем в предел и получаем готовый ответ.

$$limlimits_{xto 0} frac{xarcsin 3x}{1-cos 2x} = limlimits_{xto 0} frac{xcdot 3x}{2x^2} = limlimits_{xto 0} frac{3x^2}{2x^2} = frac{3}{2} $$

Ответ

$$limlimits_{xto 0} frac{xarcsin 3x}{1-cos 2x} = frac{3}{2}$$

Источник

Простое объяснение принципов решения пределов тригонометрических функций и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.

Алгоритм решения пределов тригонометрических функций

Для тригонометрических функций существует много разных пределов, но как правило, все они вычисляются, опираясь на первый замечательный предел и его следствия.

Первый замечательный предел выглядит следующим образом:

$[lim_{xrightarrow 0}frac{sinx}{x}=1]$

Следствия первого замечательного предела

Главным следствием первого замечательного предела считают:

$[lim_{xrightarrow 0}frac{tgx}{x}=1]$

Также следствиями являются:

$[lim_{xrightarrow 0}frac{1 - cosx}{x^2}=1]$

$[lim_{xrightarrow 0}frac{arcsinx}{x}=1]$

$[lim_{xrightarrow 0}frac{arctgx}{x}=1]$

Нужна помощь в написании работы?

Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.

Подробнее

Примеры решения пределов тригонометрических функций

Задание

Найти предел функции:

$[lim_{xrightarrow 0}frac{sin(10x)}{3x}=]$

Решение

Заменим значение х на число, к которому стремится функция:

$[lim_{xrightarrow 0}frac{sin(10x)}{3x}=begin{bmatrix}0\0end{bmatrix}=?]$

Так как мы пришли на неопределённость вида 0/0, преобразуем синус так, чтобы он стал вида первого замечательного предела:

$[lim_{xrightarrow 0}frac{frac{sin(10x)}{10x}cdot 10x}{3x}=lim_{xrightarrow 0}frac{frac{sin(10x)}{10x}cdot 10}{3}]$

Мы знаем, что первый замечательный предел равен единице, следовательно

$[lim_{xrightarrow 0}frac{sin(10x)}{10x}=1]$

Таким образом найдём предел функции:

$[lim_{xrightarrow 0}frac{frac{sin(10x)}{10x}cdot 10}{3}=frac{1cdot 10}{3}=frac{10}{3}]$

Задание

Найти предел функции:

$[lim_{xrightarrow 0}frac{3x^2-5x}{sin3x}=]$

Решение

При замене х на число, к которому он стремится, снова получаем неопределённость

$[lim_{xrightarrow 0}frac{3x^2-5x}{sin3x}=begin{bmatrix}frac{0}{0}end{bmatrix}]$

Данную задачу можно решить, применив правило Лопиталя.

Найдём производные числителя и знаменателя функции и решим задачу:

$[lim_{xrightarrow 0}frac{6x-5}{3cos3x}=frac{0-5}{3cdot 1}=-frac{5}{3}]$

Задание

Найти предел функции:

$[lim_{xrightarrow 0}frac{1-cos2x}{4x^2}]$

Решение

При подстановке нуля получим неопределённость типа 0/0:

$[lim_{xrightarrow 0}frac{1-cos2x}{4x^2}=frac{1-1}{0}=frac{0}{0}]$

Воспользуемся свойством

$[frac{1-cost}{2}=sin^2left(frac{t}{2} right)]$

Преобразуем функцию и упростим её:

$[lim_{xrightarrow 0}frac{1-cos2x}{4x^2}=lim_{xrightarrow 0}frac{frac{2cdot (1-cos2x)}{2}}{4x^2}=lim_{xrightarrow 0}frac{2sin^2x}{4x^2}=lim_{xrightarrow 0}frac{sin^2x}{2x^2}]$

Вынесем константу ½ за лимит и, пользуюсь свойством первого замечательного предела, найдём передел данной функции:

$[lim_{xrightarrow 0}frac{sin^2x}{2x^2}=frac{1}{2}lim_{xrightarrow 0}left(frac{sinx}{x} right)^2=frac{1}{2}cdot 1^2=frac{1}{2}cdot 1=frac{1}{2}]$

Задание

Найти предел функции:

$[lim_{xrightarrow 0}frac{sin7x}{x^2+pi x}=]$

Решение

Если заменить x на число, придём к неопределённости 0/0:

$[lim_{xrightarrow 0}frac{sin7x}{x^2+pi x}=left[ frac{0}{0}right]]$

Для решения данного примера применим правило Лопиталя и заменим х на число в производных:

$[lim_{xrightarrow 0}frac{7cos7x}{2x+pi}=left[ frac{7cos0}{2 cdot0 + pi } =frac{7cdot 1}{pi }right]=frac{7}{pi}]$

Задание

Вычислить предел функции:

$[lim_{xrightarrow 0}frac{cosx-cos5x}{2x^2}=]$

Решение

Для решения данного примера воспользуемся свойством разности косинусов:

$[cosalpha -cosbeta =-2cdot sinfrac{alpha +beta }{2}cdot sinfrac{alpha -beta }{2}]$

и получим

$[lim_{xrightarrow 0}frac{-2cdot sin3xcdot sin2x}{2x^2}=]$

Вынесем минус за лимит, дабы не потерять и продолжим решение. Для решения задачи приведём функцию к виду первого замечательного предела. Для этого нужно разделить дробь на множители и добавить в знаменатель коэффициент, равный коэффициенту в числителе. А потом упростим выражение:

$[-lim_{xrightarrow 0}frac{sin3x}{x}cdot frac{sin2x}{x}=-lim_{xrightarrow 0}frac{sin3x}{frac{3x}{3}}cdot frac{sin2x}{frac{2x}{2}}=-lim_{xrightarrow 0}frac{3sin3x}{3x}cdot frac{2sin2x}{2x}=]$

Снова вынесем константы за лимит и получим вид первого замечательного предела, с помощью которого приходим к искомому решению:

$[-6lim_{xrightarrow 0}frac{sin3x}{3x}cdot frac{sin2x}{2x}=-6cdot 1cdot 1=-6]$

Задание

Вычислить предел функции:

$[lim_{xrightarrow 0}frac{sinx-tgx}{x^3}=]$

Решение

При подстановке х снова получаем неопределённость

$[lim_{xrightarrow 0}frac{sinx-tgx}{x^3}=left[ frac{0}{0} right]]$

Значит будем искать передел путём приведения к виду первого замечательного предела.

Представим тангенс в виде частного синуса х и косинуса х

$[lim_{xrightarrow 0}frac{sinx-tgx}{x^3}=lim_{xrightarrow 0}frac{sinx-frac{sinx}{cosx}}{x^3}=lim_{xrightarrow 0}frac{sinx(1-frac{1}{cosx})}{x^3}=]$

Приведём к общему знаменателю и разделим выражение на множители следующим образом:

$[lim_{xrightarrow 0}frac{sinx(1-frac{1}{cosx})}{x^3}=lim_{xrightarrow 0}frac{sinx}{x}cdot lim_{xrightarrow 0}frac{1-frac{1}{cosx}}{x^2}]$

Мы видим первый замечательный предел, а значит, можем упростить до:

$[lim_{xrightarrow 0}frac{sinx}{x}=1]$

Далее снова приведём числитель к общему знаменателю:

$[lim_{xrightarrow 0}frac{1-frac{1}{cosx}}{x^2}=lim_{xrightarrow 0}frac{frac{cosx-1}{cosx}}{x^2}=lim_{xrightarrow 0}frac{cosx-1}{x^2cdot cosx}=]$

Вновь разделим на множители и подставим значение х во второй косинус:

$[lim_{xrightarrow 0}frac{cosx-1}{x^2}cdot lim_{xrightarrow 0}frac{1}{cosx}=lim_{xrightarrow 0}frac{cosx-1}{x^2}cdot 1=]$

Таким образом нам остаётся разобраться с первым числителем. Поменяем местами 1 и косинус и вынесем минус за лимит.

Далее воспользуемся формулой понижения степени и найдём решение:

$[-lim_{xrightarrow 0}frac{1-cosx}{x^2}=-lim_{xrightarrow 0}frac{2sin^2frac{x}{2}}{x^2}=-lim_{xrightarrow 0}2cdot left( frac{sinfrac{x}{2}}{x}right)^2=-2lim_{xrightarrow 0}left( frac{sinfrac{x}{2}}{frac{2x}{2}}right)^2=-frac{1}{2}cdot 1^2=-frac{1}{2}]$

Задание

Вычислить предел функции:

$[lim_{xrightarrow 0}frac{sin3x}{tg2x}]$

Решение

При простом вычислении получаем неопределённость

$[lim_{xrightarrow 0}frac{sin3x}{tg2x}=left[frac{0}{0} right ]]$

Следовательно, будем вычислять предел, опираясь на правило первого замечательного предела. Приведём тангенс к виду частного синуса и косинуса:

$[lim_{xrightarrow 0}frac{sin3x}{tg2x}=lim_{xrightarrow 0}frac{sin3x}{frac{sin2x}{cos2x}}=lim_{xrightarrow 0}frac{sin3x cdot cos2x}{sin2x}=]$

Разделим пример на множители.

Приведём синусы к виду первого замечательного предела и получим ответ:

$[lim_{xrightarrow 0}frac{sin3x}{sin2x}cdot lim_{xrightarrow 0}cos2x=lim_{xrightarrow 0}frac{frac{3xcdot sin3x}{3x}}{frac{2xcdot sin2x}{2x}}cdot 1=lim_{xrightarrow 0}frac{3x}{2x}cdot frac{frac{sin3x}{3x}}{frac{sin2x}{2x}}=frac{3}{2}cdotfrac{1}{1}=frac{3}{2}]$

Задание

Найти предел функции:

$[lim_{xrightarrow 0}frac{sin^2x-tg^2x}{x^4}=]$

Решение

При подставлении числа на место х приходим к неопределённости типа 0/0:

$[lim_{xrightarrow 0}frac{sin^2x-tg^2x}{x^4}=left[frac{0}{0} right ]]$

Преобразуем tg, приведем выражение к общему знаменателю cos x, вынесем общий множитель – sin x за скобку:

$[lim_{xrightarrow 0}frac{sin^2x-tg^2x}{x^4}=lim_{xrightarrow 0}frac{sin^2x-frac{sin^2x}{cos^2x}}{x^4}=lim_{xrightarrow 0}frac{frac{sin^2xcdot cos^2x-sin^2x}{cos^2x}}{x^4}=]$

$[= lim_{xrightarrow 0}frac{frac{-sin^2x(1-cos^2x)}{cos^2x}}{x^4}=]$

Используя следствие из первого замечательного предела, преобразим выражение и избавимся от тангенса.

Затем вновь приведем функцию к следствию первого замечательного предела и найдем ответ:

$[lim_{xrightarrow 0}frac{-tg^2x}{x^2}cdot frac{frac{1-cos^2x}{cos^2x}}{x^2}=lim_{xrightarrow 0}- left(frac{tgx}{x} right)^2cdot frac{frac{sin^2x}{cos^2x}}{x^2}=]$

$[= lim_{xrightarrow 0} left(-1^2 cdot frac{tg^2x}{x^2} right)=lim_{xrightarrow 0}left(-left(frac{tgx}{x} right)^2 right)=lim_{xrightarrow 0}left(-left(1 right )^2 right )=-1]$

Задание

Найти предел функции:

$[lim_{xrightarrow 0} left(1-x right) cdot tgfrac{pi x}{2}]$

Решение

При подстановке числа видим неопределённость.

$[lim_{xrightarrow 0} left(1-x right) cdot tgfrac{pi x}{2}=left[ 0 cdot infty right ]]$

Следовательно, искать предел будем, опираясь на правило первого замечательного предела. Для этого заменим переменную, которая будет стремиться к нулю:

Подставим в функцию:

$[lim_{trightarrow 0}tcdot tgfrac{pileft(1-t right)}{2}=lim_{trightarrow 0}t cdot tg left(frac{pi}{2}-frac{pi t}{2} right)=]$

Опираясь на свойства тригонометрии, заменим тангенс.

$[lim_{trightarrow 0}t cdot tg left(frac{pi}{2}-frac{pi t}{2} right)=lim_{trightarrow 0}t cdot ctg left(frac{pi t}{2} right)=lim_{trightarrow 0}frac{t cdot cos left(frac{pi t}{2} right )}{sin left(frac{pi t}{2} right )}=]$

Зная, что предел косинуса нуля = 1, преобразуем пример и приведём к виду первого замечательного предела.

Найдём ответ.

$[lim_{trightarrow 0}frac{t cdot cos left(frac{pi t}{2} right )}{sin left(frac{pi t}{2} right )}=lim_{trightarrow 0}frac{t cdot 1 cdot frac{pi}{2} cdot frac{2}{pi}}{sin left(frac{pi t}{2} right )}=frac{2}{pi}lim_{trightarrow 0}left(frac{sinleft(frac{pi t}{2} right )}{frac{pi t}{2}} right )^{-1}=frac{2}{pi} cdot left(1 right )^{-1}=frac{2}{pi}]$

Задание

Вычислить предел функции:

$[lim_{trightarrow 0}frac{arcsin3x}{2x}=]$

Решение

Здесь так же получим неопределённость:

$[lim_{trightarrow 0}frac{arcsin3x}{2x}=left[frac{0}{0} right ]]$

Значит, введём новую переменную t:

$[x=frac{1}{3}sint]$

Подставим получившиеся значения в пример и найдём предел:

$[lim_{trightarrow 0}frac{t}{2 cdot sin3x}=lim_{trightarrow 0}frac{t}{2 cdot frac{1}{3}sint}=frac{3}{2}lim_{trightarrow 0}left( frac{sint}{t}right )^{-1}=frac{3}{2}]$

Источник

Синус ⚠️ бесконечности: чему равен предел, доказательство
- Что такое Синус (sin) бесконечности
- Предел тригонометрической функции
- Результат решения уравнения
- Поиск по содержимому
§ 2. Односторонние пределы функции
- § 3. Предел отношения синуса к своей дуге
- § 4. Число e
исчисление — пределы функций синуса и косинуса
- - Зарегистрируйтесь или войдите в систему
  - Опубликовать как гость
  - Опубликовать как гость
Вопрос Видео: Нахождение пределов, связанных с тригонометрическими функциями
- - Стенограмма видео

Синус ⚠️ бесконечности: чему равен предел, доказательство

Содержание:

Что такое Синус (sin) бесконечности
Предел тригонометрической функции
Требование к выполнению тригонометрического тождества
Результат решения уравнения

Содержание

Что такое Синус (sin) бесконечности
Предел тригонометрической функции
Требование к выполнению тригонометрического тождества
Результат решения уравнения

Что такое Синус (sin) бесконечности

Примечание

Предел синуса на бесконечность не поддается определению.

Известно, что sin(x) имеет любое значение в пределах [-1, 1]. Когда указывается, что x стремится к бесконечности, это означает, что x увеличивается. Изобразив это графически, мы увидим колеблющийся ряд, где (-1leqslant xleqslant1).

(x mapsto ∞ \) не приближается к какому-либо фиксированному значению y.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Колеблющиеся значения синуса означают, что для каждого действительного числа R существуют числа x, y⩾R, такие что sin (x) = 1 и что sin (y) = -1.

Предел тригонометрической функции

Неопределенность предела синуса на бесконечности доказывается через тригонометрическую функцию. Допустим, что существует некий предел выражения:

(lim_{nrightarrowinfty}sinleft(nright))

Этот предел предполагает, что выражение стремится к какой-то конечной величине на бесконечности. 2n=1

)

Результат решения уравнения

Исходя из вышеописанного, если (lim_{nrightarrowinfty}sinleft(nright)) существует, то будет применимо условие (lim;sinleft(nright)=0)

Но тогда cos(n) должен стремиться к нулю, а sin(n) к единице. Подобное заключение не соответствует здравому смыслу. Следовательно, доказано, что для синуса предел на бесконечности не определяется.

Насколько полезной была для вас статья?

Рейтинг: 3.00 (Голосов: 4)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

§ 2. Односторонние пределы функции

Пусть а
и А
— конечные числа.

Определение.
Число А
называют правым
пределом
функции
при
и пишут:
или
,
если для любого, сколь угодно малого,
числа
можно указать число
такое, что как только
и
,
так сейчас же
(т. е. для всех
оказывается
;
здесь
— правая полуокрестность точки а).

Определение.
Число А
называют левым
пределом
функции
при
и пишут:
или
,
если для любого, сколь угодно малого,
числа
можно указать число
такое, что как только
и
,
так сейчас же
(т. е. для всех
оказывается
;
здесь
— левая полуокрестность точки

а).

Замечание 1.
Справедливы утверждения:

1) если у функции
при
существует предел А
в обычном смысле, т. е. двусторонний, то
существуют оба односторонних предела:
и
,
причем оба они равны А;

2) если у функции
при
существуют оба односторонних предела:
и
и оба они равны числу А,
то у
при
существует двусторонний предел, равный
указанным односторонним пределам, т.
е. числу А.

В качестве упражнения
утверждения 1) и 2) предлагается доказать
самостоятельно.

Замечание 2.
В определении односторонних пределов
функции
при
число А
предполагалось конечным. Отметим, что

А
может быть и числом несобственным:
или
.

§ 3. Предел отношения синуса к своей дуге

Установим, что

.
(1)

► Так как
,
то
,
если эти пределы существуют.Поэтому,
чтобы установить (1), достаточно доказать,
что существует и равен 1 хотя бы один
односторонний предел функции
при
,
например, правый, т. е. достаточно
доказать, что

.
(2)

Так как мы станем
устанавливать справедливость соотношения
(2), то можно рассматривать лишь значения
,
удовлетворяющие неравенству:
.
В круге радиуса
рассмотрим угол
,
радианная мера которого
;
хорду
и касательную
к окружности в точке А
(см. рис. 3.1). Имеем очевидные неравенства:
площадь
< площади сектора
< площади
(при этом мы пользуемся теми сведениями
о площадях элементарных фигур, которые
известны из школьного курса), или

откуда

.
(3)

Рис. 3.1.
К выводу формулы (1)

Разделим каждый из членов
неравенства (3) на
().
Получим

Вычитая из 1 каждый
из членов последнего неравенства, будем
иметь

.
(4)

Но
(в силу(3)). Следовательно, вместо
неравенства (4) будем иметь

.
(5)

Возьмем
— любое, сколь угодно малое (можно
считать, что
).
Ясно, что если положить
(),
то для всех
,
удовлетворяющих неравенству
,
будет

ибо если
,
то
.
Значит,
,
если
.
Последнее означает, что
.
Видим, что соотношение (2)
установлено, а значит, доказано и
соотношение (1). ◄

§ 4. Число e

Определение.
Числом е называется предел переменной

при
натуральном, стремящемся к бесконечности.

Чтобы оправдать
это определение, надо установить, что
у переменной
существует конечный предел при
.
Мы установим, что
существует, конечный, если покажем, что
переменная
— возрастающая и ограниченная сверху.

► 1.
Покажем, что переменная
— возрастающая.

Применяя формулу
бинома Ньютона,
-й
член последовательности
можно написать в виде

или

.
(2)

Аналогично, для
-го
члена последовательности
находим

.
(3)

Заметим, что правая
часть соотношения (2) имеет
слагаемых, а правая часть (3) имеет
слагаемых.

Сравнивая
и
,
видим, что первые слагаемые в правых
частях (2) и (30 одинаковы, второе, третье
и т д.
-е
слагаемое у
больше, чем у
,
ибо

Кроме того, в
составе
имеется еще
-е
слагаемое, которого в составе
нет и которое является числом положительным.
Значит
,
для любого
,
и, следовательно, переменная
— возрастающая.

2.
Покажем теперь, что переменная
ограничена сверху. Для этого снова
воспользуемся формулой (2). Заменим все
разности, стоящие в скобках в правой
части этой формулы, на единицы, отчего
правая часть увеличится (ведь каждая
такая разность меньше единицы). Получим

Но

Поэтому и подавно

Так как

то получаем
,
для любого
,
т. е. переменная
ограничена сверху.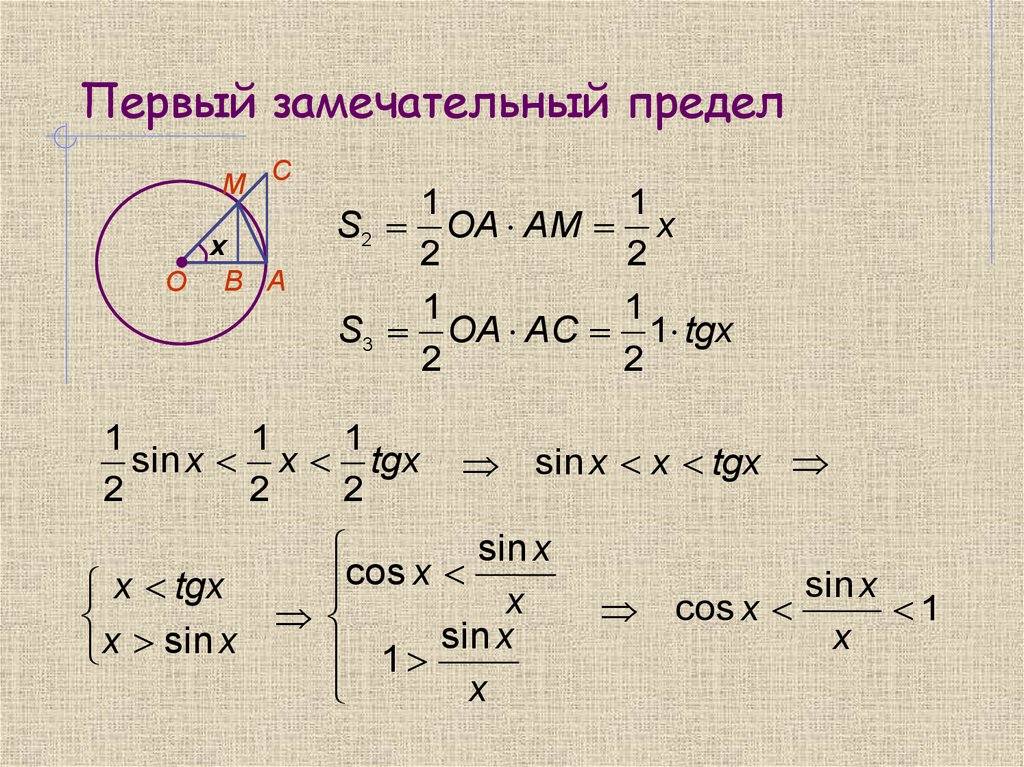 (Из формулы (2) видно,
что
и, следовательно,
при всех
.)

Итак, показано,
что переменная
монотонно
возрастает и ограничена сверху. Поэтому
существует конечный
,
величина которого заключена между
числами 2 и 3. Этот предел обозначается
буквой

e.
◄

Число е
играет большую роль в математическом
анализе и его приложениях. Доказано,
что е
— число иррациональное. Имеются приемы,
позволяющие вычислить любое число
знаков в его представлении бесконечной
десятичной дробью. При этом установлено,
что

е
= 2,718281828459045… .

Рассмотрим теперь
переменную
,
где
— положительные числа, большие 2 (
— не обязательно целые).

Справедливо
утверждение:
если
,
то

► 1.
Рассмотрим сначала случай, когда все
значения переменной
являются целыми положительными числами.
Возьмем
— любое, сколь угодно малое.

Мы знаем, что
.
Значит, взятому
отвечает номер
такой, что для всех
будет

По условию
.
Поэтому можно утверждать, что, начиная
с некоторого места, т. е. при
()
будет:
.
У нас, по предположению, все значения
переменной
— целые положительные числа. Поэтому
при всех
будет иметь место неравенство

А это означает,
что
.

Отметим, что даже
в рассмотренном случае переменная
не обязательно монотонно возрастающая.

2.
Пусть теперь значения переменной
— положительные числа, большие 2, не
обязательно целые.

Пусть
(
— наибольшее натуральное число,
удовлетворяющее неравенству:
).
Ясно, что
;
,
если
.
Имеем

А тогда

(4)

Имеем

;

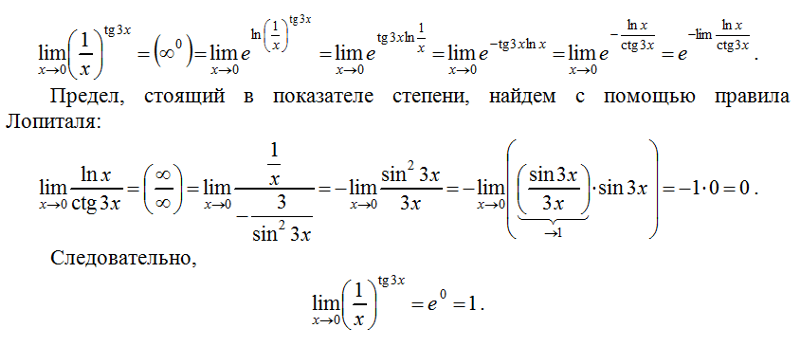
А тогда из (4), по
теореме о сжатой переменной, находим

Подчеркнем еще
раз, что здесь переменная
— любая стремящаяся к
.
(
может и не быть монотонной). ◄

исчисление — пределы функций синуса и косинуса

$begingroup$

Недавно я прошел тест, в котором мне дали эти два предела для оценки:
$lim_limits{h to 0}frac{sin(x+h)-sin{(x)}}{h}$ и $lim_limits{h to 0}frac{ cos(x+h)-cos{(x)}}{h}.$ Я использовал формулы сложения синуса и косинуса и нашел значение каждого предела по отдельности, в конечном итоге сократив $sin xcdot frac1h$ и $ cos xcdot frac1h$, потому что я узнал, что мы можем оценивать пределы по частям. В результате я получил два ответа $cos x $ и $-sin x$. Однако мой учитель пометил это неправильно, сказав, что мы не можем отменить $sin{x}cdotfrac1h$ или $cos{x}cdotfrac1h$, потому что этих ограничений не существует. Может кто-нибудь объяснить, почему это не работает? Я подумал, что мы можем отменить эти ограничения, поскольку мы никогда не смотрим на $0,$ только около $0,$ при оценке этих двух лимитов.

Синус: $$frac{sin(x+h)-sin(x)}h=frac{sin(x)cos(h)+sin(h)cos(x)} h-frac{sin(x)}h$$

$$=sin(x)frac1h+cos(x)-sin(x)frac1h=cos(x)$$

Косинус : $ $ frac { cos (x + h) — cos (x)} h = frac { cos (x) cos (h) — sin (x) sin (h)} h- cos(x)frac1h$$

$$=cos(x)frac1h-sin(x)cdot1-cos(x)frac1h=-sin(x)$$

Примечание: I мне разрешено принять $lim_limits{xto 0} frac{sin(h)}h=1,lim_limits{xto 0} frac{cos(h)-1}h =0.$

исчисление
пределы
тригонометрия

$endgroup$

$begingroup$

Это стандартный способ нахождения производных для $sin x$ и $cos x$ по определению.

Ваш путь был неверным, так как при $hto 0$ у нас есть $sin x/h not to 0$, чтобы правильно действовать для первого, у нас есть

$$sin(x+h) -sin{(x)}=sin xcos h+sin hcos x-sin x$$ 92}=frac12 подразумевает lim_{h to 0}frac{1-cos h}{h}=0$

$lim_{h to 0}frac{sin h}{h}=1$

Для другого мы можем действовать аналогичным образом.

$endgroup$

$begingroup$

Вы неправильно разбили пределы. Это можно сделать только тогда, когда существуют индивидуальные ограничения. $color{red}{lim_limits{h to 0} frac{sin x}{h}}$ и $color{red}{lim_limits{h to 0}frac{ cos x}{h}}$ НЕ существует.

Вот как правильно решить первое ограничение.

$$lim_{h to 0}frac{sin(x+h)-sin x}{h}$$

$$= lim_{h to 0}frac{color {синий}{sin xcos h}+cos xsin hcolor{blue}{-sin x}}{h}$$

$$= lim_{h to 0}frac { color {синий} { sin x ( cos h-1)} + cos x sin h} {h} $ $

$ $ = lim_ {h to 0} frac { sin x ( cos h-1)} {h} + lim_ {h to 0} frac { cos x sin h} {h} $ $

$ $ = sin x cdot lim_ {h до 0}frac{cos h-1}{h}+cos xcdotlim_{h to 0}frac{sin h}{h}$$

Используя $lim_limits{h to 0} frac{sin h}{h} = 1$ и $lim_limits{h to 0}frac{cos h-1}{h } = 0$, вы получите

$$= sin xcdot 0 + cos xcdot 1 = cos x$$

Обратите внимание, как существуют отдельные пределы. Следовательно, процедура правильная. Можете ли вы использовать тот же способ для решения второго предела?

$endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Вопрос Видео: Нахождение пределов, связанных с тригонометрическими функциями

Стенограмма видео

Найдите предел, когда 𝑥 приближается к нулю четырех 𝑥 в квадрате, деленного на квадрат греха пяти 𝑥.

Мы видим, что вопрос заключается в том, чтобы оценить предел, когда 𝑥 приближается к нулю частного двух функций. В данном случае это частное полиномиальной функции и квадрат тригонометрической функции. Первое, о чем мы должны подумать, когда нас просят оценить такое ограничение, как это, разрешено ли нам использовать прямую замену?

И в этом случае мы можем попытаться вычислить это с помощью прямой подстановки, так как мы можем вычислять многочлены и квадраты тригонометрических функций с помощью прямой подстановки. Подставляя 𝑥 равно нулю, мы получаем четыре раза ноль в квадрате, деленный на квадрат греха пяти раз ноль. И если мы вычислим это выражение, то получим неопределенную форму деления ноль на ноль. И это не значит, что мы не можем оценить этот предел.

Это говорит нам о том, что мы не можем определить значение этого предела, используя этот метод. Поэтому нам нужно придумать другой способ попытаться оценить этот предел. Например, мы могли бы попробовать переписать этот предел в терминах пределов, которые мы знаем, как оценивать. Например, мы знаем стандартный результат тригонометрического предела, что предел, когда 𝑥 приближается к нулю, для греха 𝑥, деленного на 𝑥, равен единице. И это похоже на ограничение, данное нам в вопросе.

Однако в этом случае у нас есть 𝑥 в числителе и функция синуса в знаменателе. К счастью, мы знаем результат о пределах, который позволит нам взять обратную функцию внутри нашего предела. Мы знаем, что если предел при приближении 𝑥 к 𝑎 некоторой функции 𝑓 от 𝑥 равен 𝐿, то предел при приближении 𝑥 к 𝑎 обратной величины 𝑓 от 𝑥 равен единице, деленной на 𝐿. И, конечно же, при условии, что значение 𝐿 не равно нулю.

Мы хотим применить это к нашему стандартному результату тригонометрического предела: предел, когда 𝑥 приближается к нулю, деления 𝑥 на 𝑥 равен единице. Итак, мы установим 𝑓 из 𝑥 как грех 𝑥, деленный на 𝑥, а 𝐿 равным единице. Поскольку значение 𝐿 не равно нулю, мы можем использовать тот факт, что предел обратной величины равен обратной величине предела. Это говорит нам, что предел, когда 𝑥 приближается к нулю обратной величины греха 𝑥, деленной на 𝑥, равен обратной единице.

Конечно, величина, обратная единице, равна единице. И мы можем взять обратную величину греха 𝑥, деленную на 𝑥, чтобы получить 𝑥, деленную на грех 𝑥. Итак, мы показали, что предел, когда 𝑥 приближается к нулю 𝑥, деленному на грех 𝑥, равен единице.

Давайте посмотрим, как мы можем использовать это, чтобы оценить предел, заданный нам в вопросе. Во-первых, мы возьмем постоянную четверку за пределы нашего предела. Далее мы замечаем, что берем частное двух квадратов. Таким образом, используя наши законы показателей, мы можем вместо этого возвести в квадрат все частное. Теперь мы можем переписать это, используя правило мощности для пределов. Это говорит нам о том, что для положительного целого числа 𝑛 предел, когда 𝑥 приближается к 𝑎 из 𝑔 из 𝑥 в 𝑛-й степени, равен пределу, когда 𝑥 приближается к 𝑎 из 𝑔 из 𝑥, возведенному в 𝑛-ю степень. Другими словами, предел мощности равен мощности предела. Это дает нам четыре, умноженные на квадрат предела, поскольку 𝑥 приближается к нулю 𝑥, деленного на грех пяти 𝑥.

Теперь мы хотим оценить этот предел, используя предел, который мы придумали ранее. Однако мы видим, что берем в знаменателе грех в пять 𝑥. Предел, к которому мы пришли, имеет только грех 𝑥 в знаменателе. Мы обойдем это, заменив все значения 𝑥 в этом правиле ограничения на пять 𝑥. Таким образом, это дает нам предел, когда пять 𝑥 приближаются к нулю из пяти 𝑥, разделенных на грех пяти 𝑥, равно единице.

В этот момент мы должны быть осторожны, так как теперь у нас есть предел, когда пять 𝑥 приближаются к нулю, а 𝑥 приближаются к нулю. Однако если пять 𝑥 все ближе и ближе к нулю, то 𝑥 становится все меньше и меньше. На самом деле 𝑥 все ближе и ближе к нулю. Таким образом, мы можем просто переписать этот предел, поскольку 𝑥 приближается к нулю.

Далее мы можем взять постоянную пятерку за пределы нашего предела.

Источник

Определение первого замечательного предела: предел отношения синуса к аргументу, когда он стремится к нулю равен единице

Последствия первого замечательного предела

Стоит отметить, что не все пределы, содержащие тригонометрические функции следует сразу сводить к первому замечательному пределу. Все зависит, как входит функция, и можно ли свести под нужную формулу. Плюс тригонометрические функции, когда те стремятся к нулю всегда можно заменить эквивалентными бесконечно малыми выражениями, но это уже другая техника вычисления пределов.
что стремится к нулю. Об этом Вы должны помнить и только в таких случаях сводить вычисления под правило первого замечательного предела. Важно чтобы переменная в тригонометрической функции стремилась к нулю, например:

В следующих пределах все аргументы тригонометрических функций стремятся к нулю.

У Вас возникнет вопрос, Почему так? А потому что выражение x³+3x^2+1 не стремится к нулю, когда переменная x стремится к нулю.
Попробуйте самостоятельно найти предложенный предел, а мы в конце статьи сверим ответы.

что есть правильно, целесообразно и оправдано в плане времени затраченного на расчеты.
Но сейчас у нас задача, научить Вас решать задачи на первый предел, поэтому переходим к подготовленных ответов.

Примеры на первый замечательный предел

Пример 1 Найти лимит

Вычисления: Если видите в пределе синус, то из этого не всегда следует о необходимости сводить к первому замечательному пределу.
Сначала подставим 0 в выражение под знаком лимита (делаем это в голове не записывая в тетрадь, или можете записать какую особенность получили):

Итак, имеем особенность типа 0/0, ее можно указать при разборе, все зависит от Вуза и требований к оформлению ответов. Дробь под знаком предела похож на первый замечательный предел, но это не он.
Для сведения под формулу первого замечательного предела необходимо в искусственный способ в знаменателе получить такое же выражение, которое имеем под синусом.

Обведенное выражение у нас равно первому пределу, все остальные — множитель при ней.
Аналогично получите если заменить синус эквивалентным бесконечно малым значением sin(5x)~5x.
Ответ: 5/2.

Пример 2 Вычислить предел дроби

Вычисления: Числитель и знаменатель умножили на переменную, а далее искусственно ввели множители которые фигурируют как аргументы синусов. Таким образом получили две замечательные пределы и множители, которые в конце упростили.
Ответ: 5/2.

Пример 3 Найти предел

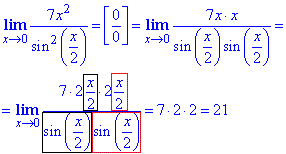
Вычисления: Здесь искусственно возвели выражение в числителе под аргумент синуса и выразили первый замечательный предел, после этого вычисления упростились до умножения трех чисел.
Ответ:21.

Пример 4 Найти предел

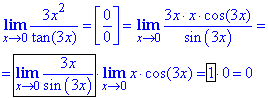
Вычисления: Простая подстановка показывает, что имеем неопределенность вида 0/0, которую нужно раскрыть. Распишем в знаменателе tan(3x) по тригонометрической формуле tan(3x)=sin(3x)/cos(3x), а в числителе выделим множитель 3x. Таким образом получим первый важный предел умноженный на предел от x•cos(3x), который равен нулю.
Здесь не пришлось искать дополнительные множители, однако раскрытие неопределенности показало, что можно получить в результате как нуль, так и бесконечность, если бы имели обратное выражение.
Ответ:0.

Пример 5 Вычислить предел

Вычисления: Неопределенность типа 0/0 раскрываем путем выделения первого замечательного предела, только на этот раз выражение, что остается во втором пределе стремится к бесконечности при переменной стремящейся к нулю.
Здесь использовали тригонометрическую формулу
1-cos(2x)=2sin²(x).
Ответ: ∞.

Бывают примеры когда применение эквивалентных бесконечно малых величин является более эффективным в плане простоты вычислений, чем возведение под первый предел.

Пример 6 Найти предел

Вычисления: Легко убедиться, что числитель и знаменатель стремятся к нулю. Для нахождения предела используем разложение функций cos(x), tan²(x) по степеням при x→π/4.

Подставим полученные значения в предел

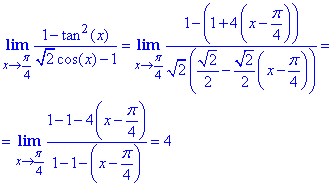
Ответ:4.

Пример 7 Найти предел

Вычисления: Здесь сot(х) расписали по формуле ctg(x)=cos(x)/sin(x). Далее упростили слагаемые, которые не вносят вклада в предел. И напоследок в числителе и знаменателе ввели множители, которые позволили в одном примере выделить три замечательных предела. Все остальные константы после умножения дали значение предела.
Ответ: 5/16.

Пример 8 Найти предел функции

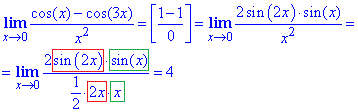
Вычисление: Получили несколько иную неопределенность от рассмотренных ранее, которую раскрыли с помощью тригонометрической формулы

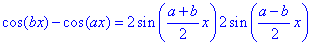
В результате получили произведение двух первых важных пределов.
Ответ: 4.

Пример 9 Вычислить лимит

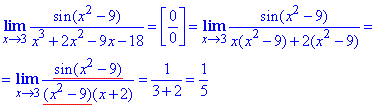
Вычисление Раскрыть неопределенность типа 0/0 удалось благодаря выделению в знаменателе множителя, который фигурирует в качестве аргумента синуса в числителе дроби. Здесь можно было выполнить замену переменных y = x-3 , что вы можете проверить самостоятельно и подобным образом свести решение к первому важному пределу.
Ответ: 1/5.

Пример 10 Вычислить предел функции

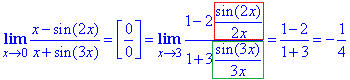
Вычисление Подстановка 0 показывает, что у нас неопределенность 0/ 0, которую необходимо раскрыть. Чтобы свести дробь под первую особую границу в числителе и знаменателе выносим аргумент и добиваемся, чтобы дроби, содержащий синусы имели в знаменателе одинаковые аргументы как в синусах.
Ответ: — 1/4.

Пример 11 Вычислить предел

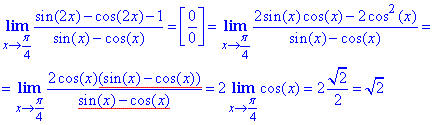
Здесь использовали тригонометрические формулы синуса двойного угла sin(2x)=2sin(x)cos(x) и зависимость 1+cos(2x)=2cos2(x)
Ответ: √2.

Пример 12 Вычислить предел

Решение: Первый замечательный предел здесь применять напрямую нельзя, поскольку аргументы πx, 5πx не стремятся к нулю при x→1. Поэтому необходимо выполнить замену переменных x-1=y, тогда при x→1 переменная y→0, что и необходимо для применения 1 замечательного предела. Далее учли периодичность тригонометрических функций и искусственно ввели нужные множители

Ответ: 1/5.

Пример 13 Вычислить предел

Решение: Вводим замену переменных x-π/6=y, далее расписав функции используем тригонометрическую форму представления разности косинусов через произведение соответствующих синусов. Остальные вычислений заключается в выделении первого важного предела

Ответ: -1/3.

Пример 14 Найти лимит функции

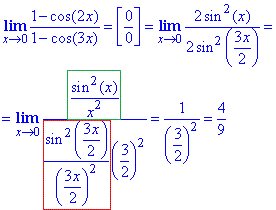
Решение: Поскольку, взятые отдельно пределы числителя 1-cos(2x) и знаменателя 1-cos(3x) стремятся к нулю когда x стремится к нулю, то имеем особенность типа нуль разделить на нуль. Раскроем неопределенность посредством сведения к первому замечательному пределу. Для этого используем следующие тригонометрические формулы, чтоб, перейти от косинусов к синусам
1-cos(2x)=2sin²(x);
1-cos(3x)=2sin²(3x/2).
С учетом формул выше, вычислим предел функции

Ответ: 4/9.

Пример 15 Найти лимит функции

Решение: Подстановка в уме аргумента равного нулю в числитель и знаменатель дает особенность типа нуль разделить на нуль 0/0. Для раскрыияь неопределенности распишем тангенс, а дальше с помощью тригонометрических формул заменим 1-cos(x)=2sin2(x/2). Далее искусственным введением необходимого множителя сведём под правило первого замечательного предела.

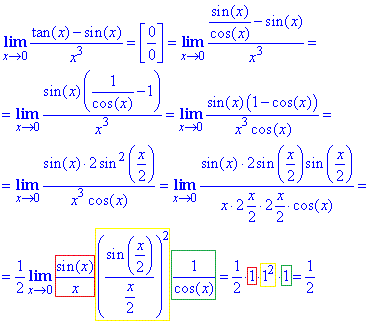
Ответ: 1/2.

При вычислениях Вам часто приходится использовать различные тригонометрические формулы, которые позволяют перейти к синусам. Мы для Вас их сгруппировали, можете скопировать, распечатать и использовать в обучении.

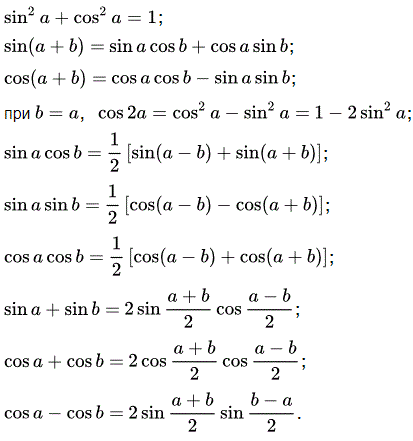
И в начале мы говорили что предел 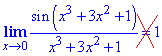подобный первому пределу, но не равен 1, потому что аргумент не стремится к нулю. Если подставить нуль в числитель и знаменатель, то получим limit=sin(1). Если Вы к этому пришли самостоятельно, и можете решать приведённые примеры без помощи, то практикумы и экзамены сдадите на отлично.
На этом решение примеров на первую важную границу не заканчивается, больше готовых ответов Вы можете найти на соседних страницах сайта.

Источник

Первый замечательный предел

Первым замечательным пределом именуют следующее равенство:

$$
begin{equation}
lim_{alphato{0}}frac{sinalpha}{alpha}=1
end{equation}
$$

Так как при $alphato{0}$ имеем $sinalphato{0}$, то говорят, что первый замечательный предел раскрывает неопределённость вида $frac{0}{0}$. Вообще говоря, в формуле (1) вместо переменной $alpha$ под знаком синуса и в знаменателе может быть расположено любое выражение, – лишь бы выполнялись два условия:

Выражения под знаком синуса и в знаменателе одновременно стремятся к нулю, т.е. присутствует неопределенность вида $frac{0}{0}$.
Выражения под знаком синуса и в знаменателе совпадают.

Часто используются также следствия из первого замечательного предела:

$$
begin{equation}
lim_{alphato{0}}frac{tgalpha}{alpha}=1
end{equation}
$$

$$
begin{equation}
lim_{alphato{0}}frac{arcsinalpha}{alpha}=1
end{equation}
$$

$$
begin{equation}
lim_{alphato{0}}frac{arctgalpha}{alpha}=1
end{equation}
$$

На данной странице решены одиннадцать примеров. Пример №1 посвящен доказательству формул (2)-(4). Примеры №2, №3, №4 и №5 содержат решения с подробными комментариями. Примеры №6-10 содержат решения практически без комментариев, ибо подробные пояснения были даны в предыдущих примерах. При решении используются некоторые тригонометрические формулы, которые можно найти тут.

Замечу, что наличие тригонометрических функций вкупе с неопределённостью $frac {0} {0}$ ещё не означает обязательное применение первого замечательного предела. Иногда бывает достаточно простых тригонометрических преобразований, – например, см. пример №11.

Пример №1

Доказать, что $lim_{alphato{0}}frac{tgalpha}{alpha}=1$,
$lim_{alphato{0}}frac{arcsinalpha}{alpha}=1$,
$lim_{alphato{0}}frac{arctgalpha}{alpha}=1$.

Решение

а) Так как $tgalpha=frac{sinalpha}{cosalpha}$, то:

$$
lim_{alphato{0}}frac{tg{alpha}}{alpha}=left|frac{0}{0}right|
=lim_{alphato{0}}frac{sin{alpha}}{alphacos{alpha}}
$$

Так как $lim_{alphato{0}}cos{0}=1$ и $lim_{alphato{0}}frac{sinalpha}{alpha}=1$, то:

$$
lim_{alphato{0}}frac{sin{alpha}}{alphacos{alpha}}
=frac{displaystylelim_{alphato{0}}frac{sin{alpha}}{alpha}}{displaystylelim_{alphato{0}}cos{alpha}}
=frac{1}{1}
=1.
$$

Формула доказана. Более строгое доказательство (с обоснованием равенства $lim_{alphato{0}}cosalpha=1$) можно посмотреть в решебнике Демидовича (№474.1).

б) Сделаем замену $alpha=sin{y}$. Поскольку $sin{0}=0$, то из условия $alphato{0}$ имеем $yto{0}$. Кроме того, существует окрестность нуля, в которой $arcsinalpha=arcsin(sin{y})=y$, поэтому:

$$
lim_{alphato{0}}frac{arcsinalpha}{alpha}=left|frac{0}{0}right|
=lim_{yto{0}}frac{y}{sin{y}}
=lim_{yto{0}}frac{1}{frac{sin{y}}{y}}
=frac{1}{displaystylelim_{yto{0}}frac{sin{y}}{y}}
=frac{1}{1}
=1.
$$

Равенство $lim_{alphato{0}}frac{arcsinalpha}{alpha}=1$ доказано.

в) Сделаем замену $alpha=tg{y}$. Поскольку $tg{0}=0$, то условия $alphato{0}$ и $yto{0}$ эквивалентны. Кроме того, существует окрестность нуля, в которой $arctgalpha=arctgtg{y})=y$, поэтому, опираясь на результаты пункта а), будем иметь:

$$
lim_{alphato{0}}frac{arctgalpha}{alpha}=left|frac{0}{0}right|
=lim_{yto{0}}frac{y}{tg{y}}
=lim_{yto{0}}frac{1}{frac{tg{y}}{y}}
=frac{1}{displaystylelim_{yto{0}}frac{tg{y}}{y}}
=frac{1}{1}
=1.
$$

Равенство $lim_{alphato{0}}frac{arctgalpha}{alpha}=1$ доказано.

Равенства а), б), в) часто используются наряду с первым замечательным пределом.

Пример №2

Вычислить предел $lim_{xto{2}}frac{sinleft(frac{x^2-4}{x+7}right)}{frac{x^2-4}{x+7}}$.

Решение

Так как $lim_{xto{2}}frac{x^2-4}{x+7}=frac{2^2-4}{2+7}=0$ и $lim_{xto{2}}sinleft(frac{x^2-4}{x+7}right)=sin{0}=0$, т.е. и числитель и знаменатель дроби одновременно стремятся к нулю, то здесь мы имеем дело с неопределенностью вида $frac{0}{0}$, т.е. первое условие выполнено. Кроме того, видно, что выражения под знаком синуса и в знаменателе совпадают (т.е. выполнено и второе условие):

Итак, оба условия, перечисленные в начале страницы, выполнены. Из этого следует, что применима формула (1), т.е. $lim_{xto{2}} frac{sinleft(frac{x^2-4}{x+7}right)}{frac{x^2-4}{x+7}}=1$.

Ответ: $lim_{xto{2}}frac{sinleft(frac{x^2-4}{x+7}right)}{frac{x^2-4}{x+7}}=1$.

Пример №3

Найти $lim_{xto{0}}frac{sin{9x}}{x}$.

Решение

Так как $lim_{xto{0}}sin{9x}=0$ и $lim_{xto{0}}x=0$, то мы имеем дело с неопределенностью вида $frac{0}{0}$, т.е. первое условие выполнено. Однако выражения под знаком синуса и в знаменателе не совпадают. Здесь требуется подогнать выражение в знаменателе под нужную форму. Нам необходимо, чтобы в знаменателе расположилось выражение $9x$, – тогда второе условие станет истинным. По сути, нам не хватает множителя $9$ в знаменателе, который не так уж сложно ввести, – просто домножить выражение в знаменателе на $9$. Естественно, что для компенсации домножения на $9$ придётся тут же на $9$ и разделить:

$$
lim_{xto{0}}frac{sin{9x}}{x}=left|frac{0}{0}right|
=lim_{xto{0}}frac{sin{9x}}{9xcdotfrac{1}{9}}
=9lim_{xto{0}}frac{sin{9x}}{9x}
$$

Теперь выражения в знаменателе и под знаком синуса совпали. Оба условия для предела $lim_{xto{0}}frac{sin{9x}}{9x}$ выполнены. Следовательно, $lim_{xto{0}}frac{sin{9x}}{9x}=1$. А это значит, что:

$$
9lim_{xto{0}}frac{sin{9x}}{9x}=9cdot{1}=9.
$$

Ответ: $lim_{xto{0}}frac{sin{9x}}{x}=9$.

Пример №4

Найти $lim_{xto{0}}frac{sin{5x}}{tg{8x}}$.

Решение

Так как $lim_{xto{0}}sin{5x}=0$ и $lim_{xto{0}}tg{8x}=0$, то здесь мы имеем дело с неопределенностью вида $frac{0}{0}$. Однако форма первого замечательного предела нарушена. Числитель, содержащий $sin{5x}$, требует наличия в знаменателе $5x$. В этой ситуации проще всего разделить числитель на $5x$, – и тут же на $5x$ домножить. Кроме того, проделаем аналогичную операцию и со знаменателем, домножив и разделив $tg{8x}$ на $8x$:

$$lim_{xto{0}}frac{sin{5x}}{tg{8x}}=left|frac{0}{0}right|
=lim_{xto{0}}frac{frac{sin{5x}}{5x}cdot{5x}}{frac{tg{8x}}{8x}cdot{8x}}$$

Сокращая на $x$ и вынося константу $frac{5}{8}$ за знак предела, получим:

$$
lim_{xto{0}}frac{frac{sin{5x}}{5x}cdot{5x}}{frac{tg{8x}}{8x}cdot{8x}}
=frac{5}{8}cdotlim_{xto{0}}frac{frac{sin{5x}}{5x}}{frac{tg{8x}}{8x}}
$$

Обратите внимание, что $lim_{xto{0}}frac{sin{5x}}{5x}$ полностью удовлетворяет требованиям для первого замечательного предела. Для отыскания $lim_{xto{0}}frac{tg{8x}}{8x}$ применима формула (2):

$$
frac{5}{8}cdotlim_{xto{0}}frac{frac{sin{5x}}{5x}}{frac{tg{8x}}{8x}}
=frac{5}{8}cdotfrac{displaystylelim_{xto{0}}frac{sin{5x}}{5x}}{displaystylelim_{xto{0}}frac{tg{8x}}{8x}}
=frac{5}{8}cdotfrac{1}{1}
=frac{5}{8}.
$$

Ответ: $lim_{xto{0}}frac{sin{5x}}{tg{8x}}=frac{5}{8}$.

Пример №5

Найти $lim_{xto{0}}frac{cos{5x}-cos^3{5x}}{x^2}$.

Решение

Так как $lim_{xto{0}}(cos{5x}-cos^3{5x})=1-1=0$ (напомню, что $cos{0}=1$) и $lim_{xto{0}}x^2=0$, то мы имеем дело с неопределённостью вида $frac{0}{0}$. Однако чтобы применить первый замечательный предел следует избавиться от косинуса в числителе, перейдя к синусам (дабы потом применить формулу (1)) или тангенсам (чтобы потом применить формулу (2)). Сделать это можно таким преобразованием:

$$cos{5x}-cos^3{5x}=cos{5x}cdotleft(1-cos^2{5x}right)$$

Так как $sin^2{5x}=1-cos^2{5x}$ (см. тригонометрические формулы), то:

$$cos{5x}-cos^3{5x}=cos{5x}cdotleft(1-cos^2{5x}right)=cos{5x}cdotsin^2{5x}.$$

Вернемся к пределу:

$$
lim_{xto{0}}frac{cos{5x}-cos^3{5x}}{x^2}=left|frac{0}{0}right|
=lim_{xto{0}}frac{cos{5x}cdotsin^2{5x}}{x^2}
=lim_{xto{0}}left(cos{5x}cdotfrac{sin^2{5x}}{x^2}right)
$$

Дробь $frac{sin^2{5x}}{x^2}$ уже близка к той форме, что требуется для первого замечательного предела. Немного поработаем с дробью $frac{sin^2{5x}}{x^2}$, подгоняя её под первый замечательный предел (учтите, что выражения в числителе и под синусом должны совпасть):

$$frac{sin^2{5x}}{x^2}=frac{sin^2{5x}}{25x^2cdotfrac{1}{25}}=25cdotfrac{sin^2{5x}}{25x^2}=25cdotleft(frac{sin{5x}}{5x}right)^2$$

Вернемся к рассматриваемому пределу:

$$
lim_{xto{0}}left(cos{5x}cdotfrac{sin^2{5x}}{x^2}right)
=lim_{xto{0}}left(25cos{5x}cdotleft(frac{sin{5x}}{5x}right)^2right)=\
=25cdotlim_{xto{0}}cos{5x}cdotlim_{xto{0}}left(frac{sin{5x}}{5x}right)^2
=25cdot{1}cdot{1^2}
=25.
$$

Ответ: $lim_{xto{0}}frac{cos{5x}-cos^3{5x}}{x^2}=25$.

Пример №6

Найти предел $lim_{xto{0}}frac{1-cos{6x}}{1-cos{2x}}$.

Решение

Так как $lim_{xto{0}}(1-cos{6x})=0$ и $lim_{xto{0}}(1-cos{2x})=0$, то мы имеем дело с неопределенностью $frac{0}{0}$. Раскроем ее с помощью первого замечательного предела. Для этого перейдем от косинусов к синусам. Так как $1-cos{2alpha}=2sin^2{alpha}$, то:

$$1-cos{6x}=2sin^2{3x};;1-cos{2x}=2sin^2{x}.$$

Переходя в заданном пределе к синусам, будем иметь:

$$
lim_{xto{0}}frac{1-cos{6x}}{1-cos{2x}}=left|frac{0}{0}right|
=lim_{xto{0}}frac{2sin^2{3x}}{2sin^2{x}}
=lim_{xto{0}}frac{sin^2{3x}}{sin^2{x}}=\

=lim_{xto{0}}frac{frac{sin^2{3x}}{(3x)^2}cdot(3x)^2}{frac{sin^2{x}}{x^2}cdot{x^2}}
=lim_{xto{0}}frac{left(frac{sin{3x}}{3x}right)^2cdot{9x^2}}{left(frac{sin{x}}{x}right)^2cdot{x^2}}
=9cdotfrac{displaystylelim_{xto{0}}left(frac{sin{3x}}{3x}right)^2}{displaystylelim_{xto{0}}left(frac{sin{x}}{x}right)^2}
=9cdotfrac{1^2}{1^2}
=9.
$$

Ответ: $lim_{xto{0}}frac{1-cos{6x}}{1-cos{2x}}=9$.

Пример №7

Вычислить предел $lim_{xto{0}}frac{cos(alpha{x})-cos(beta{x})}{x^2}$ при условии $alphaneqbeta$.

Решение

Подробные пояснения были даны ранее, здесь же просто отметим, что вновь наличествует неопределенность $frac{0}{0}$. Перейдем от косинусов к синусам, используя формулу

$$cosalpha-cosbeta=-2sinfrac{alpha+beta}{2}cdotsinfrac{alpha-beta}{2}.$$

Используя указанную формулу, получим:

$$
lim_{xto{0}}frac{cos(alpha{x})-cos(beta{x})}{x^2}=left|frac{0}{0}right|
=lim_{xto{0}}frac{-2sinfrac{alpha{x}+beta{x}}{2}cdotsinfrac{alpha{x}-beta{x}}{2}}{x^2}=\
=-2cdotlim_{xto{0}}frac{sinleft(xcdotfrac{alpha+beta}{2}right)cdotsinleft(xcdotfrac{alpha-beta}{2}right)}{x^2}

=-2cdotlim_{xto{0}}left(frac{sinleft(xcdotfrac{alpha+beta}{2}right)}{x}cdotfrac{sinleft(xcdotfrac{alpha-beta}{2}right)}{x}right)=\
=-2cdotlim_{xto{0}}left(frac{sinleft(xcdotfrac{alpha+beta}{2}right)}{xcdotfrac{alpha+beta}{2}}cdotfrac{alpha+beta}{2}cdotfrac{sinleft(xcdotfrac{alpha-beta}{2}right)}{xcdotfrac{alpha-beta}{2}}cdotfrac{alpha-beta}{2}right)=\

=-frac{(alpha+beta)cdot(alpha-beta)}{2}lim_{xto{0}}frac{sinleft(xcdotfrac{alpha+beta}{2}right)}{xcdotfrac{alpha+beta}{2}}cdotlim_{xto{0}}frac{sinleft(xcdotfrac{alpha-beta}{2}right)}{xcdotfrac{alpha-beta}{2}}
=-frac{alpha^2-beta^2}{2}cdot{1}cdot{1}
=frac{beta^2-alpha^2}{2}.
$$

Ответ: $lim_{xto{0}}frac{cos(alpha{x})-cos(beta{x})}{x^2}=frac{beta^2-alpha^2}{2}$.

Пример №8

Найти предел $lim_{xto{0}}frac{tg{x}-sin{x}}{x^3}$.

Решение

Так как $lim_{xto{0}}(tg{x}-sin{x})=0$ (напомню, что $sin{0}=tg{0}=0$) и $lim_{xto{0}}x^3=0$, то здесь мы имеем дело с неопределенностью вида $frac{0}{0}$. Раскроем её следующим образом:

$$
lim_{xto{0}}frac{tg{x}-sin{x}}{x^3}=left|frac{0}{0}right|
=lim_{xto{0}}frac{frac{sin{x}}{cos{x}}-sin{x}}{x^3}
=lim_{xto{0}}frac{sin{x}cdotleft(frac{1}{cos{x}}-1right)}{x^3}
=lim_{xto{0}}frac{sin{x}cdotleft(1-cos{x}right)}{x^3cdotcos{x}}=\

=lim_{xto{0}}frac{sin{x}cdot{2}sin^2frac{x}{2}}{x^3cdotcos{x}}
=frac{1}{2}cdotlim_{xto{0}}left(frac{sin{x}}{x}cdotleft(frac{sinfrac{x}{2}}{frac{x}{2}}right)^2cdotfrac{1}{cos{x}}right)
=frac{1}{2}cdot{1}cdot{1^2}cdot{1}
=frac{1}{2}.
$$

Аналогичную задачу можно посмотреть в решебнике Демидовича (№475)

Ответ: $lim_{xto{0}}frac{tg{x}-sin{x}}{x^3}=frac{1}{2}$.

Пример №9

Найти предел $lim_{xto{3}}frac{1-cos(x-3)}{(x-3)tgfrac{x-3}{2}}$.

Решение

Так как $lim_{xto{3}}(1-cos(x-3))=0$ и $lim_{xto{3}}(x-3)tgfrac{x-3}{2}=0$, то наличествует неопределенность вида $frac{0}{0}$. Перед тем, как переходить к её раскрытию, удобно сделать замену переменной таким образом, чтобы новая переменная устремилась к нулю (обратите внимание, что в формулах (1)-(4) переменная $alpha to 0$). Проще всего ввести переменную $t=x-3$. Однако ради удобства дальнейших преобразований (эту выгоду можно заметить по ходу приведённого ниже решения) стоит сделать такую замену: $t=frac{x-3}{2}$. Отмечу, что обе замены применимы в данном случае, просто вторая замена позволит поменьше работать с дробями. Так как $xto{3}$, то $tto{0}$.

$$
lim_{xto{3}}frac{1-cos(x-3)}{(x-3)tgfrac{x-3}{2}}=left|frac{0}{0}right|
=left|begin{aligned}&t=frac{x-3}{2};\&tto{0}end{aligned}right|
=lim_{tto{0}}frac{1-cos{2t}}{2tcdottg{t}}
=lim_{tto{0}}frac{2sin^2t}{2tcdottg{t}}
=lim_{tto{0}}frac{sin^2t}{tcdottg{t}}=\
=lim_{tto{0}}frac{sin^2t}{tcdotfrac{sin{t}}{cos{t}}}
=lim_{tto{0}}frac{sin{t}cos{t}}{t}
=lim_{tto{0}}left(frac{sin{t}}{t}cdotcos{t}right)
=lim_{tto{0}}frac{sin{t}}{t}cdotlim_{tto{0}}cos{t}
=1cdot{1}
=1.
$$

Ответ: $lim_{xto{3}}frac{1-cos(x-3)}{(x-3)tgfrac{x-3}{2}}=1$.

Пример №10

Найти предел $lim_{xtofrac{pi}{2}}frac{1-sin{x}}{left(frac{pi}{2}-xright)^2}$.

Решение

Вновь мы имеем дело с неопределенностью $frac{0}{0}$. Перед тем, как переходить к ее раскрытию, удобно сделать замену переменной таким образом, чтобы новая переменная устремилась к нулю (обратите внимание, что в формулах (1)-(4) переменная $alphato{0}$). Проще всего ввести переменную $t=frac{pi}{2}-x$. Так как $xtofrac{pi}{2}$, то $tto{0}$:

$$
lim_{xtofrac{pi}{2}}frac{1-sin{x}}{left(frac{pi}{2}-xright)^2}
=left|frac{0}{0}right|
=left|begin{aligned}&t=frac{pi}{2}-x;\&tto{0}end{aligned}right|
=lim_{tto{0}}frac{1-sinleft(frac{pi}{2}-tright)}{t^2}
=lim_{tto{0}}frac{1-cos{t}}{t^2}=\
=lim_{tto{0}}frac{2sin^2frac{t}{2}}{t^2}

=2lim_{tto{0}}frac{sin^2frac{t}{2}}{t^2}
=2lim_{tto{0}}frac{sin^2frac{t}{2}}{frac{t^2}{4}cdot{4}}
=frac{1}{2}cdotlim_{tto{0}}left(frac{sinfrac{t}{2}}{frac{t}{2}}right)^2
=frac{1}{2}cdot{1^2}
=frac{1}{2}.
$$

Ответ: $lim_{xtofrac{pi}{2}}frac{1-sin{x}}{left(frac{pi}{2}-xright)^2}=frac{1}{2}$.

Пример №11

Найти пределы $lim_{xtofrac{pi}{2}}frac{1-sin{x}}{cos^2x}$, $lim_{xtofrac{2pi}{3}}frac{tg{x}+sqrt{3}}{2cos{x}+1}$.

Решение

В данном случае нам не придётся использовать первый замечательный предел. Обратите внимание: как в первом, так и во втором пределах присутствуют только тригонометрические функции и числа. Зачастую в примерах такого рода удаётся упростить выражение, расположенное под знаком предела. При этом после упомянутого упрощения и сокращения некоторых сомножителей неопределённость исчезает. Я привёл данный пример лишь с одной целью: показать, что наличие тригонометрических функций под знаком предела вовсе не обязательно означает применение первого замечательного предела.

Так как $lim_{xtofrac{pi}{2}}(1-sin{x})=0$ (напомню, что $sinfrac{pi}{2}=1$) и $lim_{xtofrac{pi}{2}}cos^2x=0$ (напомню, что $cosfrac{pi}{2}=0$), то мы имеем дело с неопределенностью вида $frac{0}{0}$. Однако это вовсе не означает, что нам потребуется использовать первый замечательный предел. Для раскрытия неопределенности достаточно учесть, что $cos^2x=1-sin^2x$:

$$
lim_{xtofrac{pi}{2}}frac{1-sin{x}}{cos^2x}
=left|frac{0}{0}right|
=lim_{xtofrac{pi}{2}}frac{1-sin{x}}{1-sin^2x}
=lim_{xtofrac{pi}{2}}frac{1-sin{x}}{(1-sin{x})(1+sin{x})}
=lim_{xtofrac{pi}{2}}frac{1}{1+sin{x}}
=frac{1}{1+1}
=frac{1}{2}.
$$

Аналогичный способ решения есть и в решебнике Демидовича (№475). Что же касается второго предела, то как и в предыдущих примерах этого раздела, мы имеем неопределённость вида $frac{0}{0}$. Отчего она возникает? Она возникает потому, что $tgfrac{2pi}{3}=-sqrt{3}$ и $2cosfrac{2pi}{3}=-1$. Используем эти значения с целью преобразования выражений в числителе и в знаменателе. Цель наших действий: записать сумму в числителе и знаменателе в виде произведения. Кстати сказать, зачастую в пределах аналогичного вида удобна замена переменной, сделанная с таким расчётом, чтобы новая переменная устремилась к нулю (см., например, примеры №9 или №10 на этой странице). Однако в данном примере в замене смысла нет, хотя при желании замену переменной $t=x-frac{2pi}{3}$ несложно осуществить.

$$
lim_{xtofrac{2pi}{3}}frac{tg{x}+sqrt{3}}{2cos{x}+1}
=lim_{xtofrac{2pi}{3}}frac{tg{x}+sqrt{3}}{2cdotleft(cos{x}+frac{1}{2}right)}
=lim_{xtofrac{2pi}{3}}frac{tg{x}-tgfrac{2pi}{3}}{2cdotleft(cos{x}-cosfrac{2pi}{3}right)}=\

=lim_{xtofrac{2pi}{3}}frac{frac{sinleft(x-frac{2pi}{3}right)}{cos{x}cosfrac{2pi}{3}}}{-4sinfrac{x+frac{2pi}{3}}{2}sinfrac{x-frac{2pi}{3}}{2}}
=lim_{xtofrac{2pi}{3}}frac{sinleft(x-frac{2pi}{3}right)}{-4sinfrac{x+frac{2pi}{3}}{2}sinfrac{x-frac{2pi}{3}}{2}cos{x}cosfrac{2pi}{3}}=\

=lim_{xtofrac{2pi}{3}}frac{2sinfrac{x-frac{2pi}{3}}{2}cosfrac{x-frac{2pi}{3}}{2}}{-4sinfrac{x+frac{2pi}{3}}{2}sinfrac{x-frac{2pi}{3}}{2}cos{x}cosfrac{2pi}{3}}
=lim_{xtofrac{2pi}{3}}frac{cosfrac{x-frac{2pi}{3}}{2}}{-2sinfrac{x+frac{2pi}{3}}{2}cos{x}cosfrac{2pi}{3}}=\

=frac{1}{-2cdotfrac{sqrt{3}}{2}cdotleft(-frac{1}{2}right)cdotleft(-frac{1}{2}right)}
=-frac{4}{sqrt{3}}.
$$

Как видите, нам не пришлось применять первый замечательный предел. Конечно, при желании это можно сделать (см. примечание ниже), но необходимости в этом нет.

Каким будет решение с использованием первого замечательного предела? показатьскрыть

Ответ: $lim_{xtofrac{pi}{2}}frac{1-sin{x}}{cos^2x}=frac{1}{2}$, $lim_{xtofrac{2pi}{3}}frac{tg{x}+sqrt{3}}{2cos{x}+1}=-frac{4}{sqrt{3}}$.

Источник