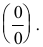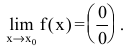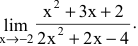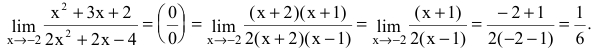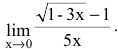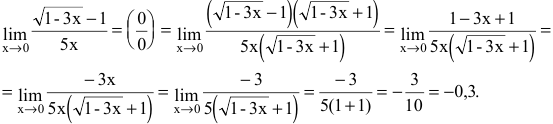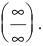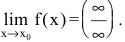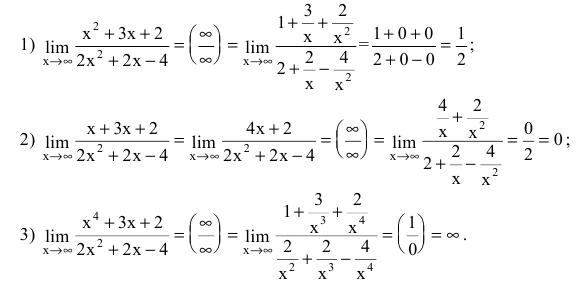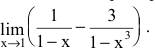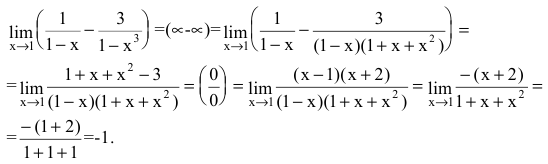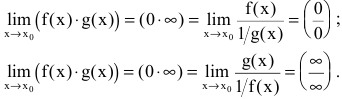Второй замечательный предел
Обычно второй замечательный предел записывают в такой форме:
$$
begin{equation}
lim_{xtoinfty}left(1+frac{1}{x}right)^x=e
end{equation}
$$
Число $e$, указанное в правой части равенства (1), является иррациональным. Приближённое значение этого числа таково: $eapprox{2{,}718281828459045}$. Если сделать замену $t=frac{1}{x}$, то формулу (1) можно переписать в следующем виде:
$$
begin{equation}
lim_{tto{0}}biggl(1+tbiggr)^{frac{1}{t}}=e
end{equation}
$$
Как и для первого замечательного предела, неважно, какое выражение стоит вместо переменной $x$ в формуле (1) или вместо переменной $t$ в формуле (2). Главное – выполнение двух условий:
- Основание степени (т.е. выражение в скобках формул (1) и (2)) должно стремиться к единице;
- Показатель степени (т.е. $x$ в формуле (1) или $frac{1}{t}$ в формуле (2)) должен стремиться к бесконечности.
Говорят, что второй замечательный предел раскрывает неопределенность $1^infty$. Заметьте, что в формуле (1) мы не уточняем, о какой именно бесконечности ($+infty$ или $-infty$) идёт речь. В любом из этих случаев формула (1) верна. В формуле (2) переменная $t$ может стремиться к нулю как слева, так и справа.
Отмечу, что есть также несколько полезных следствий из второго замечательного предела. Примеры на использование второго замечательного предела, равно как и следствий из него, очень популярны у составителей стандартных типовых расчётов и контрольных работ.
Пример №1
Вычислить предел $lim_{xtoinfty}left(frac{3x+1}{3x-5}right )^{4x+7}$.
Решение
Сразу отметим, что основание степени (т.е. $frac{3x+1}{3x-5}$) стремится к единице:
$$
lim_{xtoinfty}frac{3x+1}{3x-5}=left|frac{infty}{infty}right|
=lim_{xtoinfty}frac{3+frac{1}{x}}{3-frac{5}{x}}
=frac{3+0}{3-0}
=1.
$$
При этом показатель степени (выражение $4x+7$) стремится к бесконечности, т.е. $lim_{xtoinfty}(4x+7)=infty$.
Основание степени стремится к единице, показатель степени – к бесконечности, т.е. мы имеем дело с неопределенностью $1^infty$. Применим формулу (1) для раскрытия этой неопределённости. В основании степени формулы (1) расположено выражение $1+frac{1}{x}$, а в рассматриваемом нами примере основание степени таково: $frac{3x+1}{3x-5}$. Посему первым действием станет формальная подгонка выражения $frac{3x+1}{3x-5}$ под вид $1+frac{1}{x}$. Для начала прибавим и вычтем единицу:
$$
lim_{xtoinfty}left(frac{3x+1}{3x-5}right )^{4x+7}
=|1^infty|
=lim_{xtoinfty}left(1+frac{3x+1}{3x-5}-1right)^{4x+7}
$$
Следует учесть, что просто так добавить единицу нельзя. Если мы вынуждены добавить единицу, то её же нужно и вычесть, дабы не изменять значения всего выражения. Для продолжения решения учтём, что
$$
frac{3x+1}{3x-5}-1
=frac{3x+1}{3x-5}-frac{3x-5}{3x-5}
=frac{3x+1-3x+5}{3x-5}
=frac{6}{3x-5}.
$$
Так как $frac{3x+1}{3x-5}-1=frac{6}{3x-5}$, то:
$$
lim_{xtoinfty}left(1+ frac{3x+1}{3x-5}-1right)^{4x+7}
=lim_{xtoinfty}left(1+frac{6}{3x-5}right )^{4x+7}
$$
Продолжим «подгонку». В выражении $1+frac{1}{x}$ формулы (1) в числителе дроби находится 1, а в нашем выражении $1+frac{6}{3x-5}$ в числителе находится $6$. Чтобы получить $1$ в числителе, опустим $6$ в знаменатель с помощью следующего преобразования:
$$
1+frac{6}{3x-5}
=1+frac{1}{frac{3x-5}{6}}
$$
Таким образом,
$$
lim_{xtoinfty}left(1+frac{6}{3x-5}right )^{4x+7}
=lim_{xtoinfty}left(1+frac{1}{frac{3x-5}{6}}right )^{4x+7}
$$
Итак, основание степени, т.е. $1+frac{1}{frac{3x-5}{6}}$, подогнано под вид $1+frac{1}{x}$, который требуется в формуле (1). Теперь начнём работать с показателем степени. Заметьте, что в формуле (1) выражения, стоящие в показатели степени и в знаменателе, одинаковы:
Значит, и в нашем примере показатель степени и знаменатель нужно привести к одинаковой форме. Чтобы получить в показателе степени выражение $frac{3x-5}{6}$, просто домножим показатель степени на эту дробь. Естественно, что для компенсации такого домножения, придется тут же домножить на обратную дробь, т.е. на $frac{6}{3x-5}$. Итак, имеем:
$$
lim_{xtoinfty}left(1+frac{1}{frac{3x-5}{6}}right )^{4x+7}
=lim_{xtoinfty}left(1+frac{1}{frac{3x-5}{6}}right )^{frac{3x-5}{6}cdotfrac{6}{3x-5}cdot(4x+7)}
=lim_{xtoinfty}left(left(1+frac{1}{frac{3x-5}{6}}right)^{frac{3x-5}{6}}right)^{frac{6cdot(4x+7)}{3x-5}}
$$
Отдельно рассмотрим предел дроби $frac{6cdot(4x+7)}{3x-5}$, расположенной в степени:
$$
lim_{xtoinfty}frac{6cdot(4x+7)}{3x-5}
=left|frac{infty}{infty}right|
=lim_{xtoinfty}frac{6cdotleft(4+frac{7}{x}right)}{3-frac{5}{x}}
=6cdotfrac{4}{3}
=8.
$$
Согласно формуле (1) имеем $lim_{xtoinfty}left(1+frac{1}{frac{3x-5}{6}}right )^{frac{3x-5}{6}}=e$. Кроме того, $lim_{xtoinfty}frac{6cdot(4x+7)}{3x-5}=8$, поэтому возвращаясь к исходному пределу, получим:
$$
lim_{xtoinfty}left(left(1+frac{1}{frac{3x-5}{6}}right )^{frac{3x-5}{6}}right)^{frac{6cdot(4x+7)}{3x-5}}
=e^8.
$$
Полное решение без промежуточных пояснений будет иметь такой вид:
$$
lim_{xtoinfty}left(frac{3x+1}{3x-5}right )^{4x+7}=left|1^inftyright|
=lim_{xtoinfty}left(1+frac{3x+1}{3x-5}-1right)^{4x+7}
=lim_{xtoinfty}left(1+frac{6}{3x-5}right)^{4x+7}=\
=lim_{xtoinfty}left(1+frac{1}{frac{3x-5}{6}}right)^{4x+7}
=lim_{xtoinfty}left(1+frac{1}{frac{3x-5}{6}}right )^{frac{3x-5}{6}cdotfrac{6}{3x-5}cdot(4x+7)}
=lim_{xtoinfty}left(left(1+frac{1}{frac{3x-5}{6}}right)^{frac{3x-5}{6}}right)^{frac{6cdot(4x+7)}{3x-5}}
=e^8.
$$
Кстати сказать, вовсе не обязательно использовать первую формулу. Если учесть, что $frac{6}{3x-5}to{0}$ при $xtoinfty$, то применяя формулу (2), получим:
$$
lim_{xtoinfty}left(frac{3x+1}{3x-5}right )^{4x+7}=left|1^inftyright|
=lim_{xtoinfty}left(1+frac{3x+1}{3x-5}-1right)^{4x+7}
=lim_{xtoinfty}left(1+frac{6}{3x-5}right)^{4x+7}=\
=lim_{xtoinfty}left(1+frac{6}{3x-5}right)^{frac{3x-5}{6}cdotfrac{6}{3x-5}cdot(4x+7)}
=lim_{xtoinfty}left(left(1+frac{6}{3x-5}right)^{frac{3x-5}{6}}right)^{frac{6cdot(4x+7)}{3x-5}}
=e^8.
$$
Ответ: $lim_{xtoinfty}left(frac{3x+1}{3x-5}right)^{4x+7}=e^8$.
Пример №2
Найти предел $lim_{xto{1}}biggl(7-6xbiggr)^{frac{x}{3x-3}}$.
Решение
Выражение, стоящее в основании степени, т.е. $7-6x$, стремится к единице при условии $xto{1}$, т.е. $lim_{xto{1}}(7-6x)=7-6cdot1=1$. Для показателя степени, т.е. $frac{x}{3x-3}$, получаем: $lim_{xto{1}}frac{x}{3x-3}=infty$. Итак, здесь мы имеем дело с неопределенностью вида $1^infty$, которую раскроем с помощью второго замечательного предела.
Для начала отметим, что в формуле (1) переменная $x$ стремится к бесконечности, в формуле (2) переменная $t$ стремится к нулю. В нашем случае $xto{1}$, поэтому имеет смысл ввести новую переменную, чтобы она стремилась или к нулю (тогда применим формулу (2)), или к бесконечности (тогда применим формулу (1)). Введение новой переменной, вообще говоря, не является обязательным, это будет сделано просто для удобства решения. Проще всего новую переменную $y$ ввести так: $y=x-1$. Так как $xto{1}$, то ${x-1}to{0}$, т.е. $yto{0}$. Подставляя $x=y+1$ в рассматриваемый пример, и учитывая $yto{0}$, получим:
$$
lim_{xto{1}}biggl(7-6xbiggr )^{frac{x}{3x-3}}
=left|begin{aligned}&y=x-1;;x=y+1\&yto{0}end{aligned}right|=\
=lim_{yto{0}}biggl(7-6cdot(y+1)biggr)^{frac{y+1}{3cdot(y+1)-3}}
=lim_{yto{0}}biggl(1-6ybiggr)^frac{y+1}{3y}
=lim_{yto 0}biggl(1+(-6y)biggr)^frac{y+1}{3y}
$$
Применим формулу (2). Выражение в основании степени в формуле (2), т.е. $1+t$, соответствует форме выражения в основании степени нашего примера, т.е. $1+(-6y)$ (выражение $-6y$ играет роль $t$). Формула (2) предполагает, что показатель степени будет иметь вид $frac{1}{t}$, т.е. в нашем случае в показателе степени следует получить $frac{1}{-6y}$. Домножим показатель степени на выражение $frac{1}{-6y}$. Для компенсации такого домножения нужно домножить показатель степени на обратную дробь, т.е. на выражение $frac{-6y}{1}=-6y$:
$$
lim_{yto{0}}biggl(1-6ybiggr)^frac{y+1}{3y}=lim_{yto{0}}biggl(1+(-6y)biggr)^{frac{1}{-6y}cdot(-6y)cdotfrac{y+1}{3y}}
=lim_{yto{0}}left(biggl(1+(-6y)biggr)^{frac{1}{-6y}}right)^{-2(y+1)}
$$
Так как $lim_{yto{0}}biggl(1+(-6y)biggr)^{frac{1}{-6y}}=e$ и $lim_{yto{0}}(-2(y+1))=-2$, то получим:
$$
lim_{yto{0}}left(biggl(1+(-6y)biggr)^{frac{1}{-6y}}right)^{-2(y+1)}
=e^{-2}
=frac{1}{e^2}.
$$
Полное решение без пояснений таково:
$$
lim_{xto{1}}biggl(7-6xbiggr)^{frac{x}{3x-3}}
=left|begin{aligned}&y=x-1;;x=y+1\&yto{0}end{aligned}right|
=lim_{yto{0}}biggl(7-6cdot(y+1)biggr)^{frac{y+1}{3cdot(y+1)-3}}=\
=lim_{yto{0}}biggl(1-6ybiggr)^frac{y+1}{3y}
=lim_{yto{0}}biggl(1+(-6y)biggr)^{frac{1}{-6y}cdot(-6y)cdotfrac{y+1}{3y}}
=lim_{yto{0}}left(biggl(1+(-6y)biggr)^{frac{1}{-6y}}right)^{-2(y+1)}
=e^{-2}
=frac{1}{e^2}.
$$
Ответ: $lim_{xto{1}}biggl(7-6xbiggr)^{frac{x}{3x-3}}=frac{1}{e^2}$.
Пример №3
Найти предел $lim_{xto{0}}biggl(cos{2x}biggr)^{frac{1}{sin^2{3x}}}$.
Решение
Так как $lim_{xto{0}}(cos{2x})=1$ и $lim_{xto{0}}frac{1}{sin^2{3x}}=infty$ (напомню, что $sin{u}to{0}$ при $uto{0}$), то мы имеем дело с неопределённостью вида $1^infty$. Преобразования, аналогичные рассмотренным в примерах №1 и №2, укажем без подробных пояснений, ибо они были даны ранее:
$$
lim_{xto{0}}biggl(cos{2x}biggr)^{frac{1}{sin^2{3x}}}
=|1^infty|
=lim_{xto{0}}biggl(1+cos{2x}-1biggr)^{frac{1}{sin^2{3x}}}
$$
Так как $sin^2x=frac{1-cos{2x}}{2}$, то $cos{2x}-1=-2sin^2x$, поэтому:
$$
lim_{xto{0}}biggl(1+cos{2x}-1biggr)^{frac{1}{sin^2{3x}}}
=lim_{xto{0}}biggl(1+left(-2sin^2xright)biggr)^{frac{1}{-2sin^2x}cdot(-2sin^2x)cdotfrac{1}{sin^2 3x}}=\
=lim_{xto{0}}left(biggl(1+left(-2sin^2xright)biggr)^{frac{1}{-2sin^2x}}right)^{frac{-2sin^2{x}}{sin^2{3x}}}
=e^{-frac{2}{9}}.
$$
Здесь мы учли, что $lim_{xto{0}}frac{sin^2{x}}{sin^2{3x}}=frac{1}{9}$. Подробное описание того, как находить этот предел, дано в соответствующей теме.
Ответ: $lim_{xto{0}}biggl(cos{2x}biggr)^{frac{1}{sin^2{3x}}}=e^{-frac{2}{9}}$.
Пример №4
Найти предел $lim_{xto+infty}xleft(ln(x+1)-ln{x}right)$.
Решение
Так как при $x>0$ имеем $ln(x+1)-ln{x}=lnleft(frac{x+1}{x}right)$, то:
$$
lim_{xto+infty}xleft(ln(x+1)-ln{x}right)
=lim_{xto+infty}left(xcdotlnleft(frac{x+1}{x}right)right)
$$
Раскладывая дробь $frac{x+1}{x}$ на сумму дробей $frac{x+1}{x}=1+frac{1}{x}$ получим:
$$
lim_{xto+infty}left(xcdotlnleft(frac{x+1}{x}right)right)
=lim_{xto+infty}left(xcdotlnleft(1+frac{1}{x}right)right)
=lim_{xto+infty}left(lnleft(frac{x+1}{x}right)^xright)
=ln{e}
=1.
$$
Ответ: $lim_{xto+infty}xleft(ln(x+1)-ln{x}right)=1$.
Пример №5
Найти предел $lim_{xto{2}}biggl(3x-5biggr)^{frac{2x}{x^2-4}}$.
Решение
Так как $lim_{xto{2}}(3x-5)=6-5=1$ и $lim_{xto{2}}frac{2x}{x^2-4}=infty$, то мы имеем дело с неопределенностью вида $1^infty$. Подробные пояснения даны в примере №2, здесь же ограничимся кратким решением. Сделав замену $t=x-2$, получим:
$$
lim_{xto{2}}biggl(3x-5biggr)^{frac{2x}{x^2-4}}
=left|begin{aligned}&t=x-2;;x=t+2\&tto{0}end{aligned}right|
=lim_{tto{0}}biggl(1+3tbiggr)^{frac{2t+4}{t^2+4t}}=\
=lim_{tto{0}}biggl(1+3tbiggr)^{frac{1}{3t}cdot 3tcdotfrac{2t+4}{t^2+4t}}
=lim_{tto{0}}left(biggl(1+3tbiggr)^{frac{1}{3t}}right)^{frac{6cdot(t+2)}{t+4}}
=e^3.
$$
Можно решить данный пример и по-иному, используя замену: $t=frac{1}{x-2}$. Разумеется, ответ будет тем же:
$$
lim_{xto{2}}biggl(3x-5biggr)^{frac{2x}{x^2-4}}
=left|begin{aligned}&t=frac{1}{x-2};;x=frac{2t+1}{t}\&ttoinftyend{aligned}right|
=lim_{ttoinfty}left(1+frac{3}{t}right)^{tcdotfrac{4t+2}{4t+1}}=\
=lim_{ttoinfty}left(1+frac{1}{frac{t}{3}}right)^{frac{t}{3}cdotfrac{3}{t}cdotfrac{tcdot(4t+2)}{4t+1}}
=lim_{ttoinfty}left(left(1+frac{1}{frac{t}{3}}right)^{frac{t}{3}}right)^{frac{6cdot(2t+1)}{4t+1}}
=e^3.
$$
Ответ: $lim_{xto{2}}biggl(3x-5biggr)^{frac{2x}{x^2-4}}=e^3$.
Пример №6
Найти предел $lim_{xtoinfty}left(frac{2x^2+3}{2x^2-4}right)^{3x} $.
Решение
Выясним, к чему стремится выражение $frac{2x^2+3}{2x^2-4}$ при условии $xtoinfty$:
$$
lim_{xtoinfty}frac{2x^2+3}{2x^2-4}
=left|frac{infty}{infty}right|
=lim_{xtoinfty}frac{2+frac{3}{x^2}}{2-frac{4}{x^2}}
=frac{2+0}{2-0}=1.
$$
Таким образом, в заданном пределе мы имеем дело с неопределенностью вида $1^infty$, которую раскроем с помощью второго замечательного предела:
$$
lim_{xtoinfty}left(frac{2x^2+3}{2x^2-4}right)^{3x}
=|1^infty|
=lim_{xtoinfty}left(1+frac{2x^2+3}{2x^2-4}-1right)^{3x}=\
=lim_{xtoinfty}left(1+frac{7}{2x^2-4}right)^{3x}
=lim_{xtoinfty}left(1+frac{1}{frac{2x^2-4}{7}}right)^{3x}=\
=lim_{xtoinfty}left(1+frac{1}{frac{2x^2-4}{7}}right)^{frac{2x^2-4}{7}cdotfrac{7}{2x^2-4}cdot 3x}
=lim_{xtoinfty}left(left(1+frac{1}{frac{2x^2-4}{7}}right)^{frac{2x^2-4}{7}}right)^{frac{21x}{2x^2-4}}
=e^0
=1.
$$
Ответ: $lim_{xtoinfty}left(frac{2x^2+3}{2x^2-4}right)^{3x}=1$.
Второй замечательный предел
Данная статья: «Второй замечательный предел» посвящена раскрытию в пределах неопределенностей вида:
$ bigg[frac{infty}{infty}bigg]^infty $ и $ [1]^infty $.
Так же такие неопределенности можно раскрывать с помощью логарифмирования показательно-степенной функции, но это уже другой метод решения, о котором будет освещено в другой статье.
Формула и следствия
Формула второго замечательного предела записывается следующим образом: $$ lim_{x to infty} bigg (1+frac{1}{x}bigg)^x = e, text{ где } e approx 2.718 $$
Из формулы вытекают следствия, которые очень удобно применять для решения примеров с пределами: $$ lim_{x to infty} bigg (1 + frac{k}{x} bigg)^x = e^k, text{ где } k in mathbb{R} $$ $$ lim_{x to infty} bigg (1 + frac{1}{f(x)} bigg)^{f(x)} = e $$ $$ lim_{x to 0} bigg (1 + x bigg)^frac{1}{x} = e $$
Стоить заметить, что второй замечательный предел можно применять не всегда к показательно-степенной функции, а только в случаях когда основание стремится к единице. Для этого сначала в уме вычисляют предел основания, а затем уже делают выводы. Всё это будет рассмотрено в примерах решений.
Примеры решений
Рассмотрим примеры решений с использованием прямой формулы и её следствий. Так же разберем случаи, при которых формула не нужна. Достаточно записать только готовый ответ.
| Пример 1 |
| Найти предел $ lim_{xtoinfty} bigg( frac{x+4}{x+3} bigg)^{x+3} $ |
| Решение |
|
Подставим бесконечность в предел и посмотрим на неопределенность: $$ lim_{xtoinfty} bigg( frac{x+4}{x+3} bigg)^{x+3} = bigg(frac{infty}{infty}bigg)^infty $$ Найдем предел основания: $$ lim_{xtoinfty} frac{x+4}{x+3}= lim_{xtoinfty} frac{x(1+frac{4}{x})}{x(1+frac{3}{x})} = 1 $$ Получили основание равное единице, а это значит уже можно применить второй замечательный предел. Для этого подгоним основание функции под формулу путем вычитания и прибавления единицы: $$ lim_{xtoinfty} bigg( 1 + frac{x+4}{x+3} — 1 bigg)^{x+3} = lim_{xtoinfty} bigg( 1 + frac{1}{x+3} bigg)^{x+3} = $$ Смотрим на второе следствие и записываем ответ: $$ lim_{xtoinfty} bigg( 1 + frac{1}{x+3} bigg)^{x+3} = e $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ lim_{xtoinfty} bigg( 1 + frac{1}{x+3} bigg)^{x+3} = e $$ |
| Пример 2 |
| Определить предел $ lim_{xtoinfty} bigg (1+frac{1}{x^3}bigg)^{x^2} $ |
| Решение |
|
Замечаем, что основание степени стремится к единице $ 1+frac{1}{x^3} to 1 $, при $ xtoinfty $, а показатель $ x^2 to infty $. Поэтому можно применить второе следствие. Но сперва, разберемся с показателем и приведем его в нужный вид — сделаем равным знаменателю основания. Для этого умножим его на $ x $ и разделим на него же. Получаем: $$ lim_{xtoinfty} bigg (1+frac{1}{x^3}bigg)^{x^2 cdot frac{x}{x}} = lim_{xtoinfty} bigg (1+frac{1}{x^3}bigg)^{frac{x^3}{x}} = $$ Уже теперь применяем формулу и получаем: $$ lim_{xtoinfty}e^ frac{1}{x} = e^{lim_{xtoinfty} frac{1}{x}} = e^0 = 1 $$ |
| Ответ |
| $$ lim_{xtoinfty} bigg (1+frac{1}{x^3}bigg)^{x^2} = 1 $$ |
| Пример 3 |
| Вычислить предел $ lim_{xto 1} (6-5x)^frac{x}{x-1} $ |
| Решение |
|
Получаем неопределенность $ 1^infty $. Для её раскрытия воспользуемся вторым замечательным пределом. Но у нас $ xto 1 $. Как быть? Выполняем замену $ y = x-1 $, тогда $ yto 0 $, при $ x to 1 $. Из замены следует, что $ x = y + 1 $. $$ lim_{xto 1} (6-5x)^frac{x}{x-1} = lim_{yto 0} (6-5(y+1))^frac{y+1}{y} = 1^infty = $$ $$ = lim_{yto 0} (1-5y)^frac{y+1}{y} = lim_{yto 0} (1+(-5y))^frac{(y+1)cdot (-5)}{-5cdot y} = $$ $$ = lim_{yto 0} e^{-5cdot (y+1)} = e^{-5} $$ |
| Ответ |
| $$ lim_{xto 1} (6-5x)^frac{x}{x-1} = e^{-5} $$ |
| Пример 4 |
| Решить предел $ lim_{xto infty} bigg (frac{3x^2+4}{3x^2-2} bigg) ^{3x} $ |
| Решение |
|
Находим предел основания и видим, что $ lim_{xtoinfty} frac{3x^2+4}{3x^2-2} = 1 $, значит можно применить второй замечательный предел. Стандартно по плану прибавляем и вычитаем единицу из основания степени: $$ lim_{xto infty} bigg (1+frac{3x^2+4}{3x^2-2}-1 bigg) ^{3x} = lim_{xto infty} bigg (1+frac{6}{3x^2-2} bigg) ^{3x} = $$ Подгоняем дробь под формулу 2-го замеч. предела: $$ = lim_{xto infty} bigg (1+frac{1}{frac{3x^2-2}{6}} bigg) ^{3x} = $$ Теперь подгоняем степень. В степени должна быть дробь равная знаменателю основания $ frac{3x^2-2}{6} $. Для этого умножим и разделим степень на неё, и продолжим решать: $$ = lim_{xto infty} bigg (1+frac{1}{frac{3x^2-2}{6}} bigg) ^{frac{3x^2-2}{6} cdot frac{6}{3x^2-2}cdot 3x} = lim_{xto infty} e^{frac{18x}{3x^2-2}} = $$ Предел, расположенный в степени при $ e $ равен: $ lim_{xto infty} frac{18x}{3x^2-2} = 0 $. Поэтому продолжая решение имеем: $$ = e^0 = 1 $$ |
| Ответ |
| $$ lim_{xto infty} bigg (frac{3x^2+4}{3x^2-2} bigg) ^{3x} = 1 $$ |
Разберем случаи, когда задача похожа на второй замечательный предел, но решается без него.
| Пример 5 |
| Найти $ lim_{xtoinfty} bigg ( frac{x+3}{3x+4} bigg )^{x+1} $ |
| Решение |
|
Начинаем с проверки равен ли предел основания единице. Имеем: $$ lim_{xtoinfty} frac{x+3}{3x+4} = frac{1}{3} $$ А это значит, что формулировка второго замечательного предела не соответствует данной задаче, так как $ frac{1}{3}ne 1 $ Продолжаем вычисление предела: $$ lim_{xtoinfty} bigg ( frac{x+3}{3x+4} bigg )^{x+1} = bigg (frac{1}{3} bigg ) ^infty = 0 $$ |
| Ответ |
| $$ lim_{xtoinfty} bigg ( frac{x+3}{3x+4} bigg )^{x+1} = 0 $$ |
| Пример 6 |
| Найти $ lim_{xtoinfty} bigg ( frac{3x+4}{x+3} bigg )^{x-5} $ |
| Решение |
|
Начинаем с проверки равен ли предел основания единице. Имеем: $$ lim_{xtoinfty} frac{3x+4}{x+3} = 3 $$ А это значит, что формулировка второго замечательного предела не соответствует данной задаче, так как $ 3 ne 1 $ Продолжаем вычисление предела: $$ lim_{xtoinfty} bigg ( frac{3x+4}{x+3} bigg )^{x-5} = 3^infty = infty $$ |
| Ответ |
| $$ lim_{xtoinfty} bigg ( frac{3x+4}{x+3} bigg )^{x-5} =infty $$ |
В статье: «Второй замечательный предел: примеры решений» была разобрана формула, её следствия и приведены частые типы задач по этой теме.
Преподаватель который помогает студентам и школьникам в учёбе.
Раскрытие неопределенностей — определение и вычисление с примерами решения
Раскрытие неопределенностей вида 
Пусть 
Если f(x) — рациональная дробь, то числитель и знаменатель дроби раскладывают на множители.
Пример №1
Вычислить предел 
Решение:
Числитель и знаменатель дроби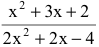 
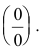
при х=-2 обращаются в нуль. Имеем неопределенность вида
Для ее раскрытия разложим числитель и знаменатель дроби на множители, а затем применим теоремы о пределах частного, суммы и произведения:
Если f(x) — дробь, содержащая иррациональные выражения, то выделение множителей вида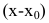 
достигается переводом иррациональностей в числитель или знаменатель.
Пример №2
Вычислить предел 
Решение:
Имеем неопределенность вида 
Избавимся от иррациональности в числителе, умножив и разделив дробь на сопряженное к числителю выражение 
Получим:
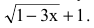
В остальных случаях для раскрытия неопределенности вида 
используют первый замечательный предел или эквивалентные бесконечно малые функции.
Раскрытие неопределенностей вида 
Пусть 
Если f(x) — рациональная дробь или дробь, содержащая иррациональности, то числитель и знаменатель делят на х в старшей степени.
Пример №3
Вычислить предел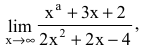 
если 1) а=2; 2) а=1; 3) а=4.
Решение:
Числитель и знаменатель дроби конечного предела не имеют. Имеем неопределенность вида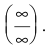 
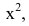
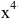
Для ее раскрытия разделим числитель и знаменатель дроби на высшую степень х (в первом и втором случаях на 
во третьем — на 
), а затем воспользуемся теоремами о пределах функций:
Вывод. Предел рациональной дроби на бесконечности равен отношению коэффициентов при старших степенях, если эти степени совпадают, нулю — если показатель степени числителя меньше показателя степени знаменателя и бесконечности в противном случае.
Замечание. Для раскрытия неопределенностей вида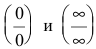 
используют также правило Лопиталя.
- Заказать решение задач по высшей математике
Раскрытие неопределенностей вида 
Неопределенное выражение вида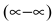 
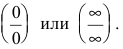
преобразуется к неопределенности вида 
Методику раскрытия такой неопределенности покажем на примерах.
Пример №4
Вычислить предел 
Решение:
Имеем неопределенность вида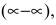 
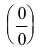
которая преобразуется к неопределенности вида 
приведением функции к общему знаменателю:
Пример №5
Вычислить предел последовательности 
Решение:
Для раскрытия неопределенности вида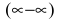 
умножим и разделим выражение в скобках на сопряженное:
Получили неопределенность вида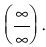 
Раскроем ее, разделив все члены полученного выражения на n:
Раскрытие неопределенностей вида 
Неопределенное выражение вида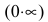 
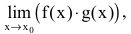
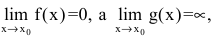
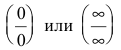
получается при нахождении пределов вида 
где 
и сводится к неопределенности вида 
следующим образом:
Замечание. При вычислении пределов показательно-степенных функций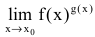 
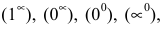
могут получиться неопределенности вида 
для раскрытия которых используют второй замечательный предел или правило Лопиталя.
- Дробно-рациональные уравнения
- Дробно-рациональные неравенства
- Прогрессии в математике — арифметическая, геометрическая
- Единичная окружность — в тригонометрии
- Рациональная дробь
- Функция в математике
- Наибольшее и наименьшее значения функции
- Вычисления в Mathematica с примерами
6.1.1. Вычисление предела дробно — рациональной функции при 
Пусть 
и 
– многочлены соответственно степеней 
и 
.
Выражение 
при может не представлять собой неопределённости или быть отношением двух бесконечно малых. При вычислении 
могут представляться следующие случаи.
А. Выражение не представляет собой неопределённости, если 
— не является корнем знаменателя, то есть 
. В этом случае используют теорему об арифметических действиях над функциями, имеющими предел в точке:
Б. Не представляет никакого труда вычисление предела и в случае, если – корень знаменателя, но не является корнем числителя, то есть 
, 
. В этом случае отношение При является бесконечно большой функцией, поэтому 
.
В. Если же является и корнем числителя и корнем знаменателя: 
, , то выражение При представляет собой неопределённость типа 
. В этом случае в числителе и в знаменателе можно выделить общий множитель наибольшей степени 
и сократить на него. Выделить такой множитель можно либо с помощью деления многочленов на 
«в столбик», либо путём группировки слагаемых. После сокращения на приходим либо к случаю А, либо к случаю Б.
Пример 1. Вычислить 
.
Решение. Число 
не является корнем знаменателя: 
(случай А), поэтому
.
Пример 2. Вычислить 
Решение. Здесь ситуация такая же: число 2 не является корнем знаменателя (хотя и является корнем числителя).
Пример 3. Вычислить 
Решение. В данном случае число 
является корнем знаменателя, но не является корнем числителя (случай Б)
Пример 4. Вычислить 
Решение. В этом случае 
является корнем и числителя, и знаменателя, а значит выражение представляет собой неопределённость . В знаменателе следует выделить множетель 
. Возможно этот множитель будет входить в некоторой степени (если корни кратные). В числителе выделить такой множитель несложно:
Для того чтобы выделить такой множитель в знаменателе удобно разделить знаменатель на “в столбик”. Такое деление возможно без остатка по следствию из теоремы Безу. Действительно:
Теперь знаменатель можно представить как произведение:
Окончательно: 
6.1.2 Вычисление предела дробно – рациональной функции при 
Пусть при дробно-рациональная функция представляет собой неопределённость типа 
. Тогда при вычислении 
полезно учитывать, что при
Поэтому
Пример 6.
;
Пример 7.
;
Пример 8.
.
Если многочлены в числителе и знаменателе не представлены в стандартном виде, нужно внимательно отнестись к определению старшей степени. Например, выражение 
является многочленом третьей, а не четвёртой степени.
| < Предыдущая | Следующая > |
|---|
Предел показательно степенной функции, примеры нахождения
В процессе нахождения предела показательно-степенной функции типа lim x → x 0 ( f ( x ) ) g ( x ) часто работаем с такими степенными неопределенностями, как 1 ∞ , 0 0 , ∞ 0 .
Для их раскрытия необходимо задействовать логарифмирование a = e ln ( a ) , свойство логарифма a · ln ( b ) = ln ( b a ) и применение его предела заданной непрерывной функции, причем ее знак разрешено менять местами.
Для этого производятся преобразования вида:
lim x → x 0 ( f ( x ) ) g ( x ) = e ln lim x → x 0 f ( x ) ) g ( x ) = e lim x → x 0 ( ln ( f ( x ) ) g ( x ) = e lim x → x 0 ( g ( x ) ln ( f ( x ) ) ) = = e lim x → x 0 ln ( f ( x ) ) 1 g ( x )
Отсюда видно, что задание приводится к нахождению предела заданной функции вида e lim x → x 0 ln ( f ( x ) ) 1 g ( x ) = ∞ ∞ или 0 0 .
Данный случай рассматривает методы:
- непосредственного вычисления;
- использования правила Лопиталя;
- с заменой эквивалентных бесконечно малых функций;
- применение первого замечательного предела.
Для того, чтобы неопределенность была раскрыта, необходимо применять второй замечательный предел, при наличии 1 ∞ .
Рассмотрим теорию на элементарных примерах заданий.
Найти предел заданной функции lim x → 0 ( x 3 + 2 x + 1 ) 3 2 x 3 + x .
Для решения необходимо произвести подстановку. Получаем :
lim x → 0 ( x 3 + 2 x + 1 ) 3 2 ( x 3 + x ) = ( 0 3 + 2 · 0 + 1 ) 3 2 ( 0 3 + 0 ) = 1 ∞
Получение единицы в степени бесконечность называют неопределенностью, значит, необходимо решить другим методом.
Следует произвести преобразования данного предела. Получаем:
lim x → 0 ( x 3 + 2 x + 1 ) 3 2 ( x 3 + x ) = e ln lim x → 0 ( x 3 + 2 x + 1 ) 3 2 ( x 3 + x ) = = e lim x → 0 ln ( x 3 + 2 x + 1 ) 3 2 ( x 3 + x ) = e lim x → 0 3 ln ( x 3 + 2 x + 1 ) 2 ( x 3 + x )
Видим, что преобразование сводится к пределу вида lim x → 0 3 ln ( x 3 + 2 x + 1 ) 2 ( x 3 + x ) .
lim x → 0 3 ln ( x 3 + 2 x + 1 2 ( x 3 + x ) = 0 0 = 3 2 lim x → 0 ln ( x 3 + 2 x + 1 ) x 3 + x = = 3 2 lim x → 0 x 3 + 2 x x 3 + x = 3 2 lim x → 0 x 2 + 2 x 2 + 1 = 3 2 · 0 2 + 2 0 2 + 1 = 3
Данные преобразования были выполнены при помощи применения замены логарифма на эквивалентную бесконечно малую функцию.
Тогда исходный предел принимает вид lim x → 0 ( x 2 + 2 x + 1 ) 3 2 ( x 3 + x ) = e 3 .
Вычисление данного предела возможно с применением второго замечательного предела. Тогда получаем:
lim x → 0 ( x 2 + 2 x + 1 ) 3 2 ( x 3 + x ) = lim x → 0 ( 1 + ( x 3 + 2 x ) 1 x 3 + 2 x ( x 3 + 2 x ) 3 2 ( x 3 + x ) = = lim x → 0 ( 1 + ( x 3 + 2 x ) ) 1 x 3 + 2 x 3 ( x 3 + 2 x ) 2 ( x 3 + x ) = lim x → 0 1 + ( x 3 + 2 x ) ) 1 x 3 + 2 x 3 ( x 2 + 2 ) 2 ( x 2 + 1 ) = = lim x → 0 ( 1 + ( x 3 + 2 x ) 1 x 3 + 2 x 3 = e 3
Найти и вычислить предел lim x → π 2 ( t g x ) 2 c o s x
Если произведем подстановку, в результате получим ответ в виде бесконечности в степени ноль, а это является знаком, что необходимо применить другой метод для преобразования. Получаем:
lim x → π 2 ( t g x ) 2 c o s x = ∞ 0 = e ln lim x → π 2 ( t g x ) 2 cos x = = e 2 lim x → π 2 ( t g x ) 2 cos x = e lim x → π 2 ( 2 cos x · ln · ( t g x ) ) = = e 2 lim x → π 2 ln ( t g x ) 1 cos x
Отсюда видно, что решение сводится к переделу lim x → π 2 ln ( t g x ) 1 cos x = ∞ ∞ .
Для дальнейшего преобразования применим правило Лопиталя, так как получили неопределенность в виде частного бесконечностей. Видим, что
lim x → π 2 ln ( t g x ) 1 cos x = ∞ ∞ = lim x → π 2 = ln ( t g x ) ‘ 1 cos ( x ) ‘ = = lim x → π 2 1 t g ( x ) · 1 cos 2 ( x ) sin ( x ) cos 2 ( x ) = lim x → π 2 cos ( x ) sin 2 ( x ) = cos π 2 sin 2 π 2 = 0 1 2 = 0
Отсюда следует, что пределом показательно-степенной функции является результат, полученный при вычислении. Имеем вы предел вида lim x → π 2 ( t g x ) 2 cos x = e 2 · 0 = e 0 = 1 .
Второй замечательный предел
Обычно второй замечательный предел записывают в такой форме:
Число $e$, указанное в правой части равенства (1), является иррациональным. Приближённое значение этого числа таково: $eapprox718281828459045>$. Если сделать замену $t=frac$, то формулу (1) можно переписать в следующем виде:
Как и для первого замечательного предела, неважно, какое выражение стоит вместо переменной $x$ в формуле (1) или вместо переменной $t$ в формуле (2). Главное – выполнение двух условий:
- Основание степени (т.е. выражение в скобках формул (1) и (2)) должно стремиться к единице;
- Показатель степени (т.е. $x$ в формуле (1) или $frac$ в формуле (2)) должен стремиться к бесконечности.
Говорят, что второй замечательный предел раскрывает неопределенность $1^infty$. Заметьте, что в формуле (1) мы не уточняем, о какой именно бесконечности ($+infty$ или $-infty$) идёт речь. В любом из этих случаев формула (1) верна. В формуле (2) переменная $t$ может стремиться к нулю как слева, так и справа.
Отмечу, что есть также несколько полезных следствий из второго замечательного предела. Примеры на использование второго замечательного предела, равно как и следствий из него, очень популярны у составителей стандартных типовых расчётов и контрольных работ.
Сразу отметим, что основание степени (т.е. $frac$) стремится к единице:
При этом показатель степени (выражение $4x+7$) стремится к бесконечности, т.е. $lim_(4x+7)=infty$.
Основание степени стремится к единице, показатель степени – к бесконечности, т.е. мы имеем дело с неопределенностью $1^infty$. Применим формулу (1) для раскрытия этой неопределённости. В основании степени формулы (1) расположено выражение $1+frac$, а в рассматриваемом нами примере основание степени таково: $frac$. Посему первым действием станет формальная подгонка выражения $frac$ под вид $1+frac$. Для начала прибавим и вычтем единицу:
Следует учесть, что просто так добавить единицу нельзя. Если мы вынуждены добавить единицу, то её же нужно и вычесть, дабы не изменять значения всего выражения. Для продолжения решения учтём, что
Продолжим «подгонку». В выражении $1+frac$ формулы (1) в числителе дроби находится 1, а в нашем выражении $1+frac$ в числителе находится $6$. Чтобы получить $1$ в числителе, опустим $6$ в знаменатель с помощью следующего преобразования:
Итак, основание степени, т.е. $1+frac>$, подогнано под вид $1+frac$, который требуется в формуле (1). Теперь начнём работать с показателем степени. Заметьте, что в формуле (1) выражения, стоящие в показатели степени и в знаменателе, одинаковы:
Значит, и в нашем примере показатель степени и знаменатель нужно привести к одинаковой форме. Чтобы получить в показателе степени выражение $frac$, просто домножим показатель степени на эту дробь. Естественно, что для компенсации такого домножения, придется тут же домножить на обратную дробь, т.е. на $frac$. Итак, имеем:
Отдельно рассмотрим предел дроби $frac$, расположенной в степени:
Согласно формуле (1) имеем $lim_left(1+frac>right )^>=e$. Кроме того, $lim_frac=8$, поэтому возвращаясь к исходному пределу, получим:
Полное решение без промежуточных пояснений будет иметь такой вид:
Кстати сказать, вовсе не обязательно использовать первую формулу. Если учесть, что $fracto$ при $xtoinfty$, то применяя формулу (2), получим:
Выражение, стоящее в основании степени, т.е. $7-6x$, стремится к единице при условии $xto$, т.е. $lim_>(7-6x)=7-6cdot1=1$. Для показателя степени, т.е. $frac$, получаем: $lim_>frac=infty$. Итак, здесь мы имеем дело с неопределенностью вида $1^infty$, которую раскроем с помощью второго замечательного предела.
Для начала отметим, что в формуле (1) переменная $x$ стремится к бесконечности, в формуле (2) переменная $t$ стремится к нулю. В нашем случае $xto$, поэтому имеет смысл ввести новую переменную, чтобы она стремилась или к нулю (тогда применим формулу (2)), или к бесконечности (тогда применим формулу (1)). Введение новой переменной, вообще говоря, не является обязательным, это будет сделано просто для удобства решения. Проще всего новую переменную $y$ ввести так: $y=x-1$. Так как $xto$, то $to$, т.е. $yto$. Подставляя $x=y+1$ в рассматриваемый пример, и учитывая $yto$, получим:
Применим формулу (2). Выражение в основании степени в формуле (2), т.е. $1+t$, соответствует форме выражения в основании степени нашего примера, т.е. $1+(-6y)$ (выражение $-6y$ играет роль $t$). Формула (2) предполагает, что показатель степени будет иметь вид $frac$, т.е. в нашем случае в показателе степени следует получить $frac$. Домножим показатель степени на выражение $frac$. Для компенсации такого домножения нужно домножить показатель степени на обратную дробь, т.е. на выражение $frac=-6y$:
Полное решение без пояснений таково:
Так как $lim_>(cos)=1$ и $lim_>frac>=infty$ (напомню, что $sinto$ при $uto$), то мы имеем дело с неопределённостью вида $1^infty$. Преобразования, аналогичные рассмотренным в примерах №1 и №2, укажем без подробных пояснений, ибо они были даны ранее:
Так как $sin^2x=frac>$, то $cos-1=-2sin^2x$, поэтому:
Здесь мы учли, что $lim_>frac>>=frac$. Подробное описание того, как находить этот предел, дано в соответствующей теме.
Так как при $x>0$ имеем $ln(x+1)-ln=lnleft(fracright)$, то:
Раскладывая дробь $frac$ на сумму дробей $frac=1+frac$ получим:
Так как $lim_>(3x-5)=6-5=1$ и $lim_>frac=infty$, то мы имеем дело с неопределенностью вида $1^infty$. Подробные пояснения даны в примере №2, здесь же ограничимся кратким решением. Сделав замену $t=x-2$, получим:
Можно решить данный пример и по-иному, используя замену: $t=frac$. Разумеется, ответ будет тем же:
Выясним, к чему стремится выражение $frac$ при условии $xtoinfty$:
Таким образом, в заданном пределе мы имеем дело с неопределенностью вида $1^infty$, которую раскроем с помощью второго замечательного предела:
Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).
Замечательные пределы: Первый и второй замечательный предел.
Понятие замечательных пределов используется на просторах бывшего Советского Союза для обозначения хорошо известных математических тождеств со взятием предела. Замечательны они потому, что они уже доказаны великими математиками и нам нам остается лишь пользоваться ими для удобства нахождения пределов. Из них наиболее известны первый и второй замечательные пределы. Дальнейшее чтение статье будет намного интереснее, если вы уже знакомы с понятием пределов. Если для вас lim , это то что новое, то рекомендуем к прочтению статью «Пределы. Понятие пределов. Вычисление пределов.»
Теперь со спокойной душой переходим к рассмотрению замечательных пределов.
Первый замечательный предел имеет вид 
.
Вместо переменной х могут присутствовать различные функции, главное, чтобы они стремились к 0.
Необходимо вычислить предел 
Как видно, данный предел очень похож на первый замечательный, но это не совсем так. Вообще, если Вы замечаете в пределе sin, то надо сразу задуматься о том, возможно ли применение первого замечательного предела.
Согласно нашему правилу №1 подставим вместо х ноль:
Получаем неопределенность 
.
Теперь попробуем самостоятельно организовать первый замечательный предел. Для этого проведем нехитрую комбинацию:
Таким образом мы организовываем числитель и знаменатель так, чтобы выделить 7х. Вот уже и проявился знакомый замечательный предел. Желательно при решении выделять его:
Подставим решение первого замечательного примера и получаем:
Как видите – все очень просто.
Второй замечательный предел имеет вид 
, где e = 2,718281828… – это иррациональное число.
Вместо переменной х могут присутствовать различные функции, главное, чтобы они стремились к 
.
Необходимо вычислить предел 
Здесь мы видим наличие степени под знаком предела, значит возможно применение второго замечательного предела.
Как всегда воспользуемся правилом №1 – подставим вместо х:
Видно, что при х 
основание степени 
, а показатель – 4x > , т.е. получаем неопределенность вида 
:
Воспользуемся вторым замечательным пределом для раскрытия нашей неопределенности, но сначала надо его организовать. Как видно – надо добиться присутствия в показателе, для чего возведем основание в степень 3х, и одновременно в степень 1/3x, чтобы выражение не менялось:
Не забываем выделять наш замечательный предел:
Дальше знак предела перемещаем в показатель:
Вот такие действительно замечательные пределы!
Если у вас остались какие то вопросы по первому и второму замечательным пределам, то смело задавайте их в комментариях.
Всем по возможности ответим.
Также вы можете позаниматься с педагогом по этой теме.
Мы рады предложить вам услуги подбора квалифицированного репетитора в вашем городе. Наши партнеры оперативно подберут для вас хорошего преподавателя на выгодных для вас условиях.