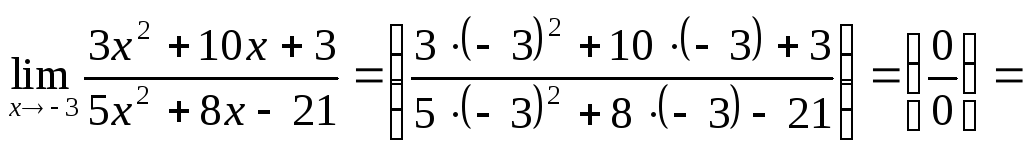Как найти предел дробной функции

6.1.1. Вычисление предела дробно — рациональной функции при

Пусть и – многочлены соответственно степеней и .

Выражение при может не представлять собой неопределённости или быть отношением двух бесконечно малых. При вычислении могут представляться следующие случаи.

А. Выражение не представляет собой неопределённости, если — не является корнем знаменателя, то есть . В этом случае используют теорему об арифметических действиях над функциями, имеющими предел в точке:

Б. Не представляет никакого труда вычисление предела и в случае, если – корень знаменателя, но не является корнем числителя, то есть , . В этом случае отношение При является бесконечно большой функцией, поэтому .

В. Если же является и корнем числителя и корнем знаменателя: , , то выражение При представляет собой неопределённость типа . В этом случае в числителе и в знаменателе можно выделить общий множитель наибольшей степени и сократить на него. Выделить такой множитель можно либо с помощью деления многочленов на «в столбик», либо путём группировки слагаемых. После сокращения на приходим либо к случаю А, либо к случаю Б.

Пример 1. Вычислить .

Решение. Число не является корнем знаменателя: (случай А), поэтому

.

Пример 2. Вычислить

Решение. Здесь ситуация такая же: число 2 не является корнем знаменателя (хотя и является корнем числителя).

Пример 3. Вычислить

Решение. В данном случае число является корнем знаменателя, но не является корнем числителя (случай Б)

Пример 4. Вычислить

Решение. В этом случае является корнем и числителя, и знаменателя, а значит выражение представляет собой неопределённость . В знаменателе следует выделить множетель . Возможно этот множитель будет входить в некоторой степени (если корни кратные). В числителе выделить такой множитель несложно:

Для того чтобы выделить такой множитель в знаменателе удобно разделить знаменатель на “в столбик”. Такое деление возможно без остатка по следствию из теоремы Безу. Действительно:

Теперь знаменатель можно представить как произведение:

Окончательно:

6.1.2 Вычисление предела дробно – рациональной функции при

Пусть при дробно-рациональная функция представляет собой неопределённость типа . Тогда при вычислении полезно учитывать, что при

Поэтому

Пример 6.

;

Пример 7.

;

Пример 8.

.

Если многочлены в числителе и знаменателе не представлены в стандартном виде, нужно внимательно отнестись к определению старшей степени. Например, выражение является многочленом третьей, а не четвёртой степени.

< Предыдущая		Следующая >

Пределы дробно-рациональных функций с квадратичными выражениями

В случае
неопределённости
следует разложить квадратичное выражение
на множители. Для этого можно

а)
воспользоваться тождеством
,
гдеи– корни уравнения,
найденные по формуле;

б)
учесть, что, когда
,
то– один из корней, и другой кореньможно найти по теореме Виета, например,
из равенства,
где;

в)
применить равенство
,
где
.

Пример 7.

(решили уравнения
ии применили 1-й способ).

Пример 8.

.

В уравнении
свободный коэффициент –10 разделили на
коэффициент, стоящий перед(число 4). Результат разделили на известный
корень 2. Получили 2-й корень.

Затем в уравнении
нашли 2-й корень из условия,
где 2 – известный корень, а 6 – свободный
коэффициент (Теорема Виета).

Пример 9.

.

Скобка
получена как,
а остальные найдены 3-м способом.

ПР6. Раскройте
неопределённость
,
разложив дробь на множители:

1) а)
; б); в);
г);

2) а)
; б); в);
г);

3) а)
; б); в);
г);

4) а)
; б); в);
г).

Пример 10.

.

Предел дробно-рациональной функции в бесконечности

Пусть дана функция
(см. стр. 16) и надо найти.
Оказывается, прився дробь ведёт себя так, как отношение
старших степеней:

.

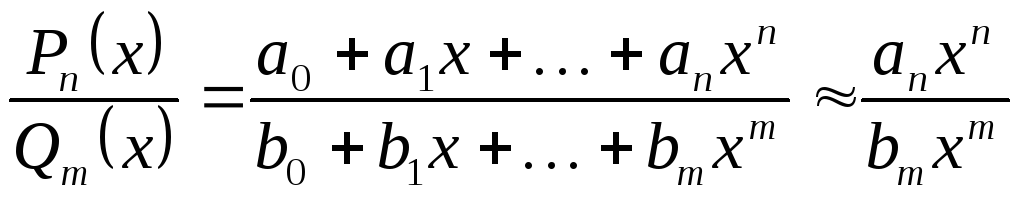
Тогда
.
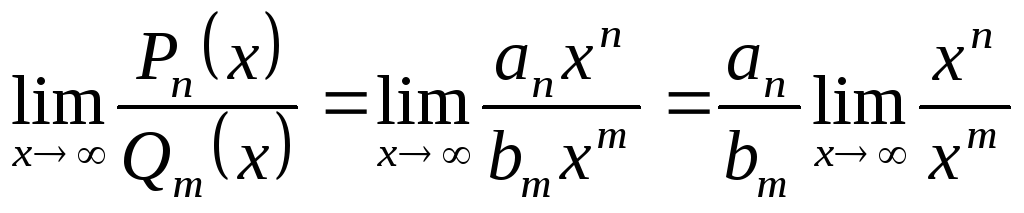
Обозначим.
Возможны 3 случая:

1)
,
тогда,
где

();

2)
,
тогда,
где

();

3)
,
тогда.

Таким образом,
предел равен

а) бесконечности,
если степень числителя больше, чем
степень знаменателя;

б) 0 в противоположном
случае;

в) отношению
старших коэффициентов, если степени
равны.

ПР7.
Найдите пределы

1) а)
; б); в); г); д);

2) а)
; б); в); г);
д);

3) а)
; б); в); г);
д);

ПР8.
Найдите пределы

1) а)
; б); в);

2) а)
; б); в);

3) а)
; б); в).

Пример 11. Оставив
в числителе и в знаменателе старшие
степени, находим

а)
;

б)
;

в)
.

Пример 12.
Оставив старшие степени, видим, что

а)
;

б)
;

в)
.

Обратите внимание,
что знак бесконечности (если таковая
получается) в ответе не указывается.
Тем не менее, если обе старшие степени
– чётные (или если обе нечётные), очевидно,
их отношение всегда положительно, что
можно учесть.

ПР9. Найдите
пределы функций
в точках,,,,,
а также при.

.

Пределы иррациональных функций

Если функция
содержит корень, подставляем, как обычно,
предельную точку. Сложности связаны с
неопределённостью
,
когда приходится умножать числитель и
знаменатель насопряжённое
выражение.

Выражения сопряжены
относительно
разности квадратов,
если их произведение превращается в
разность квадратов по формуле
.

Примеры сопряжённых выражений

а)
сопряжено с,
при этом;

б)
сопряжено с,
и тогда;

в)
сопряжено с,
поскольку

,

причём под корнем
всё остаётся без изменений;

г)
сопряжено с:

.

ПР10. Найдите
пределы иррациональных функций простой
подстановкой:

1) а)
; б); в); г);

2) а)
; б); в); г);

3) а)
; б); в); г);

4) а)
; б); в); г).

Пример 13.
Подставив указанные точки, находим
значения

а)
;

б)

.

ПР11. Раскройте
неопределённость
,
умножив числитель и знаменатель дроби
на подходящее сопряжённое выражение и
сократив одинаковые скобки:

1) а)
; б); в); г);

2) а)
; б); в); г);

3) а)
; б); в); г);

4) а)
; б); в);

г)
; д); е).

Пример 14.

.

Пример 15.

.

Пример 16.

.

ПР12. Умножьте
числитель и знаменатель на выражение,
сопряжённое к числителю, а затем – на
выражение, сопряжённое к знаменателю.
Сократив скобки, раскройте неопределённость
:

1) а)
; б); в); г);

2) а)
; б); в); г);

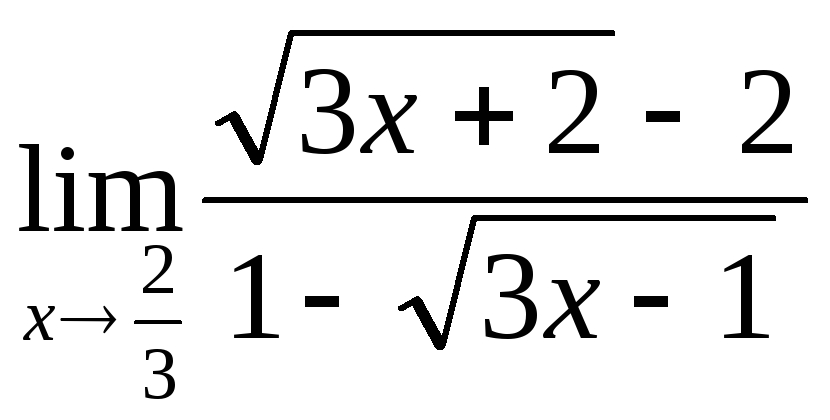
3) а)
; б); в);

4) а)
; б); в).

Пример 17.
Умножим, чтобы получить разность
квадратов:

.

Пример 18.
Так же, как в примере 17,

.

Иррациональные
пределы при
в случае неопределённостинаходят подобно рациональным, при помощи
старших степеней, а в случае неопределённостисводят её кпри помощи сопряжённого выражения.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Вопросы для самопроверки

Раскрытие неопределенностей от дробно-рациональных функций

Дробно-рациональной функцией (рациональной дробью) называется отношение двух многочленов вида:

, (3.3)

где – степень многочлена числителя, – степень многочлена знаменателя.

Предел от дробно-рациональной функции при может приводить к математической неопределенности или при к неопределенности . Рассмотрим подробнее методы раскрытия этих неопределенностей.

1. Для раскрытия неопределенности от многочленов, стоящих в числителе и знаменателе дробно-рациональной функции, выносят за скобки переменную в наибольшей степени: , где .

Возможны три случая формулы (3.3):

а) при предел равен отношению коэффициентов, стоящих при наибольших степенях переменной;

б) при предел всегда равен ;

в) при предел всегда равен нулю.

Пример 3.1. Вычислить предел функции .

Решение.

Пример 3.2. Вычислить предел функции .

Решение.

Пример 3.3. Вычислить предел функции .

Решение. .

2. В случае, когда предел от дробно-рациональной функции

приводит к математической неопределенности при , можно сделать вывод о том, что число является корнем многочленов числителя и знаменателя, то есть , . Учитывая кратность корня каждого из многочленов, последние можно разложить на множители следующим образом:

= , где s – кратность корня числителя; k — кратность корня знаменателя. Возможны три случая:

а) при предел = . (3.4)

б) при предел всегда равен ;

в) при предел всегда равен нулю.

Пример 3.4. Вычислить предел функции .

Решение. В данном случае имеем неопределенность . Для ее устранения числитель и знаменатель приравняем к нулю и найдем корни полученных квадратных уравнений. Разложим трехчлены, стоящие в числителе и знаменателе дроби на линейные множители, получим:

3. Неопределенность возникает не только при вычислении пределов от дробно-рациональных функций, но и от иррациональных выражений.

Пример 3.5. Вычислить предел функции

.

Решение. В этом случае числитель и знаменатель дроби домножаем на сопряженное выражение с целью получения разности квадратов:

Замечание. При наличии кубических корней у функции, стоящей под знаком предела, производят домножение на неполный квадрат суммы (разности) с целью применения формулы разности кубов.

4. При вычислении пределов от тригонометрических функций часто приходят к так называемому первому замечательному пределу:

. (3.5)

Пример 3.6. Вычислить предел функции .

Решение. , так как

5. Математическая неопределенность устраняется при помощи второго замечательного предела, имеющего две формы записи:

или (3.6)

(3.7)

Пример 3.7. Вычислить предел функции .

Решение.

Вопросы для самопроверки.

1.  Какая функция называется дробно-рациональной?

2.  К каким математическим неопределенностям может приводить предел от дробно-рациональной и иррациональной функции?

3.  Как раскрыть математическую неопределенность при ?

4.  Как раскрыть математическую неопределенность при ?

5.  Какие математические неопределенности раскрываются с помощью первого и второго замечательных пределов?

Пределы дробно-рациональных функций — пределы дробных выражений, в которых и числитель, и знаменатель являются многочленами с рациональными коэффициентами.

Приёмы нахождения пределов:[править]

Раскрытие неопределённости типа [∞/∞]:[править]

1)

2)

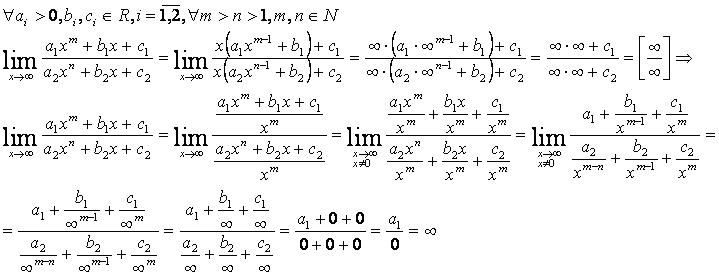
3)

Раскрытие неопределённости типа [0/0]:[править]

Другие пределы:[править]

• первый замечательный предел;
• второй замечательный предел;
• пределы функций с корнями.

Литература[править]

• Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970.

Ссылки[править]

• Участник:Logic-samara