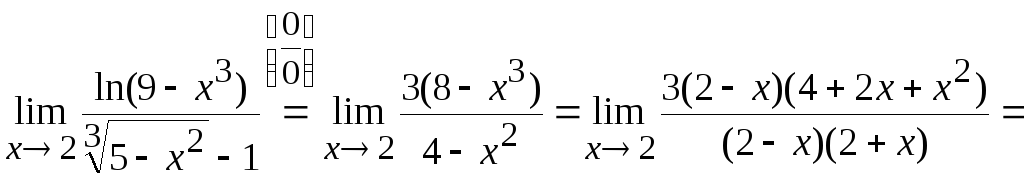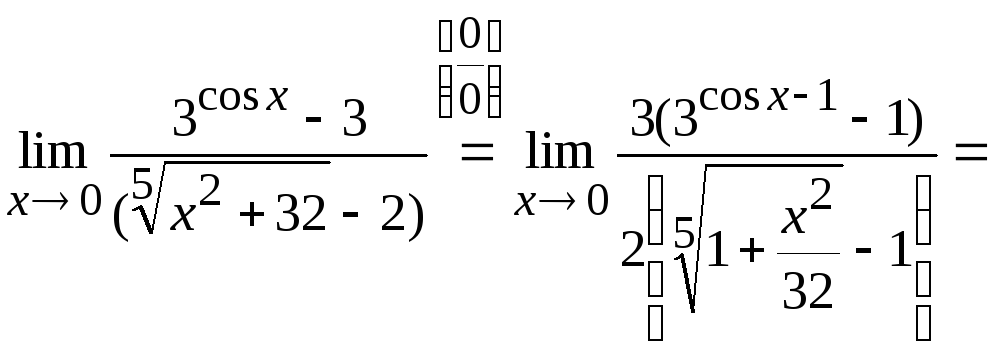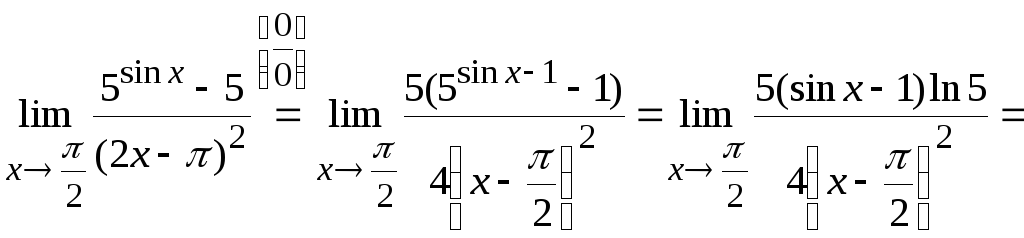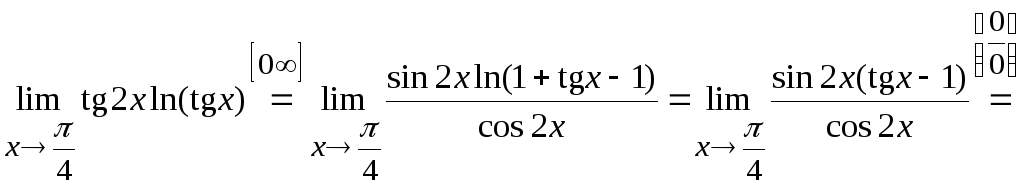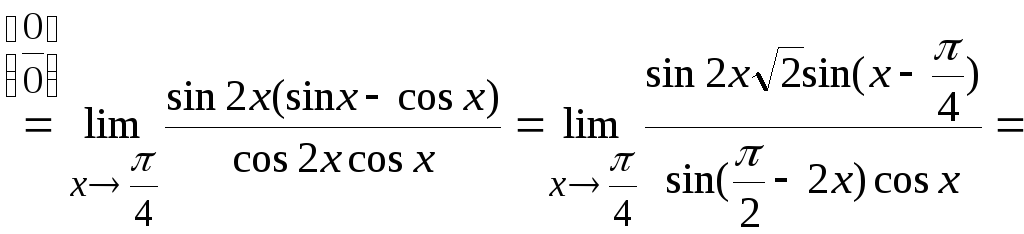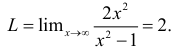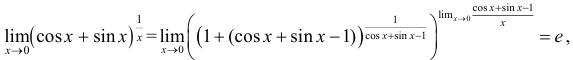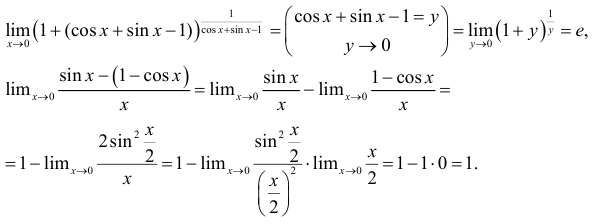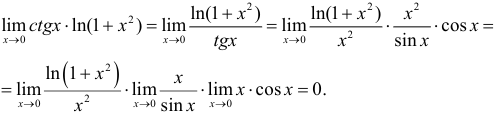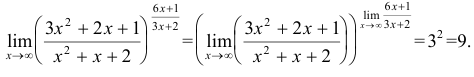Пределы со степенями: показательная, степенная и показательно-степенная функции
Пределы со степенями бывают различных видов в зависимости от положения неизвестной $x$ в пределе. Рассмотрим примеры решений для следующих ситуаций:
- Показательная функция
$$limlimits_{xto a} a^{f(x)} = a^{limlimits_{xto a} f(x)} $$ - Степенная функция
$$ limlimits_{xto a} (f(x))^a = bigg(limlimits_{xto a} f(x) bigg)^a $$ - Показательно-степенная функция
$$limlimits_{xto a} bigg(f(x)bigg)^{g(x)} = limlimits_{xto a} frac{ln(f(x))}{frac{1}{g(x)}} $$
| Пример 1 |
| Найти предел показательной функции $limlimits_{xto 2} 2^{frac{x^2-4}{x-2}}$ |
| Решение |
|
Подставив точку $x=2$ в предел получим неопределенность $2^{big(frac{0}{0}big)}$. Итак, перенесем знак предела в показатель и попробуем его вычислить путем разложения числителя по формуле разности квадратов $a^2-b^2 = (a-b)(a+b)$. $$limlimits_{xto 2} 2^{frac{x^2-4}{x-2}} = 2^{limlimits_{xto 2} frac{(x-2)(x+2)}{x-2}} = $$ Сокращаем числитель со знаменателем на $x-2$ и вычисляем предел степени. $$ =2^{limlimits_{xto 2} (x+2)} = 2^{2+2} = 2^4 = 16 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$limlimits_{xto 2} 2^{frac{x^2-4}{x-2}} = 16$$ |
| Пример 2 |
| Решить предел степенной функции $limlimits_{xto 0} bigg(frac{sin x^2}{1-cos x}bigg)^3$ |
| Решение |
|
Внесем знак предела внутрь скобок, а степень останется при этом снаружи. $$limlimits_{xto 0} bigg(frac{sin x^2}{1-cos x}bigg)^3 = bigg(limlimits_{xto 0} frac{sin x^2}{1-cos x}bigg)^3 = $$ При подстановке точки $x=0$ в предел получаем неопределенность $frac{0}{0}$. Для её устранения воспользуемся таблицей эквивалентностей пределов. $$sin x^2 sim x^2$$ $$ 1-cos x sim frac{x^2}{2}$$ Подставляем эквивалентные функции в предел и сокращаем $x$. $$ = bigg(limlimits_{xto 0} frac{x^2}{frac{x^2}{2}}bigg)^3 = bigg(limlimits_{xto 0} frac{2x^2}{x^2} bigg)^3 = 2^3 = 8$$ |
| Ответ |
| $$limlimits_{xto 0} bigg(frac{sin x^2}{1-cos x}bigg)^3 = 8$$ |
| Пример 3 |
| Вычислить предел показательно-степенной функции $limlimits_{xto 0} (tg x)^{sin x} $ |
| Решение |
|
Если подставим $x=0$, то получим предел ноль в степени ноль $(0^0)$. Превратим это в другую неопределенность $(frac{infty}{infty})$ с помощью третьей формулы. $$limlimits_{xto 0} (tg x)^{sin x} = limlimits_{xto 0} frac{ln (tg ;x)}{frac{1}{sin x}} = frac{infty}{infty} = $$ Используем правило Лопиталя для продолжения решения. По нему, как известно, предел отношения функций равен пределу отношения производных от этих функций. $$ = limlimits_{xto 0} frac{(ln (tg ;x))’}{(frac{1}{sin x})’} = limlimits_{xto 0} frac{frac{frac{1}{cos^2 x}}{tg ;x}}{-frac{cos x}{sin^2 x}} = $$ Преобразуем числитель в нормальный вид с помощью формулы $tg ; x = frac{sin x}{cos x}$ и выполняем все необходимые сокращения. $$ = limlimits_{xto 0} frac{frac{1}{sin x cos x}}{-frac{cos x}{sin^2 x}} = -limlimits_{xto 0} frac{sin x}{cos^2 x} = $$ Теперь подставляя точку $x=0$ возможно получить окончательный ответ. $$ = — frac{sin 0}{cos^2 x} = -frac{0}{1} = 0 $$ |
| Ответ |
| $$limlimits_{xto 0} (tg x)^{sin x} = 0$$ |
Вычисление пределов степенно-показательных функций
Пусть функции
и
заданы на множестве
и функция
на нем положительна. Функция
называется степенно
— показательной.
Предположим, что
– точка сгущения множества
и существуют конечные пределы
,
,
где
.
Нужно найти
.
Воспользовавшись
тождествами
,
запишем исходное выражение в виде
.
В силу теоремы 6.1
получим
.
При заданных
значениях пределов будем иметь
.
Из проведенного
рассуждения видно, что предположение
о существовании конечных пределов
и
можно отбросить. Действительно, для
нахождения предела выражения
достаточно знать предел произведения
(конечный или бесконечный).
1) Пусть
.
Тогда
.
2) Если
,
то
.
3) Если
,
то
.
Заметим, что
произведение
может оказаться неопределенностью типа
.
Тогда и исходное выражение
представляет собой неопределенность.
Перечислим возникающие здесь
неопределенности.
1) Если
,
то вычисление предела
приводит к неопределенности типа
.
2) Если
,
то вычисление предела
приводит к неопределенности типа
.
3) Если
,
то вычисление предела
приводит к неопределенности типа
.
Во всех указанных
случаях (,
,
)
можно раскрыть неопределенность
в показателе степени, преобразуя ее к
типу
и используя соответствующие эквивалентные
бесконечно малые.
Замечание 8.3.
Приведенные выше рассуждения справедливы
и для вычисления предела степенно-показательной
функции в бесконечно удаленной точке:
.
Пример 8.2.
Вычислить
.
Решение.
Здесь
,
,
поэтому имеем неопределенность типа
.
Преобразуем выражение под знаком
предела:
.
В показателе
степени имеем неопределенность типа
.
Заменой
при
на эквивалентную бесконечно малую
раскрываем ее:
.
Таким образом,
.
Замечание 8.4.
Аналогично доказывается равенство
.
Пределы
,
образуют две формы
одного и того же равенства, которое
также является замечательным
пределом
и часто служат определением числа
.
Задачи к §8
Задача
1. Вычислить

Решение.
Здесь имеем
неопределенность типа
.
Преобразуем числитель дроби к форме
произведения:

Затем
заменим бесконечно малую в точке
функцию
эквивалентной бесконечно малой
.
Тогда
получим
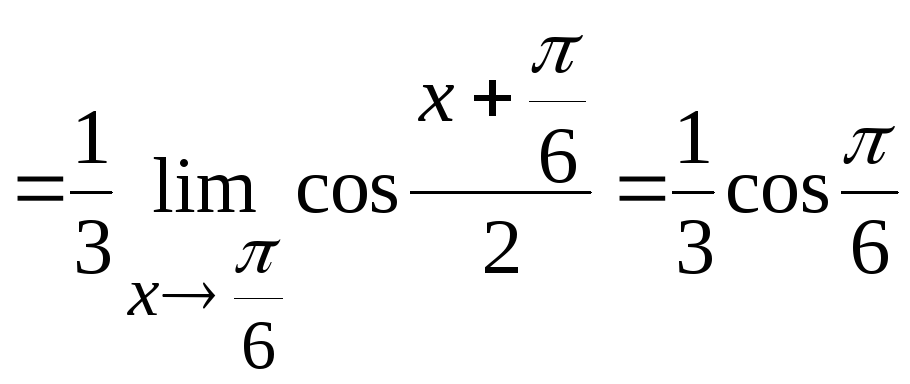
Ответ:
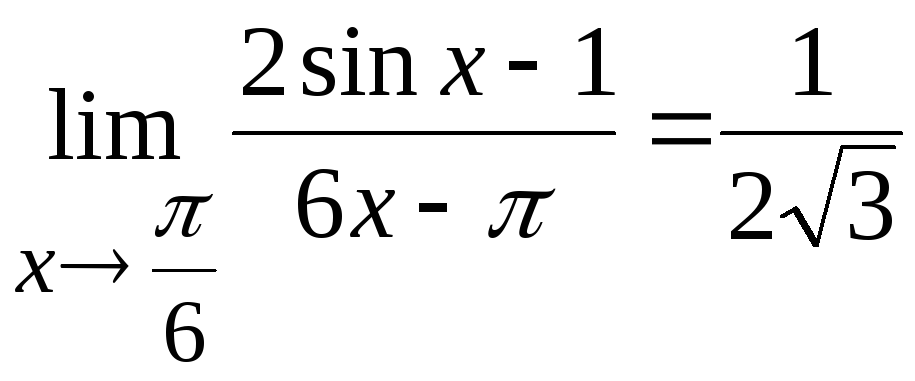
Задача
2. Вычислить
.
Решение.
Здесь возникает неопределенность типа
.
Преобразуем знаменатель, воспользовавшись
свойствами логарифмической функции, и
выделим в аргументе логарифма слагаемое,
равное 1:
.
Заменим
бесконечно малую в точке
функцию
эквивалентной бесконечно малой
.
Числитель разложим на множители:
.
Тогда
получим:

Ответ:
.
Задача
3. Вычислить
.
Решение.
Здесь возникает неопределенность типа
.
Представим числитель в виде:
.
Затем
заменим его эквивалентной бесконечно
малой в точке
функцией
.
Функцию
в точке
тоже заменим на эквивалентную бесконечно
малую
.
Тогда
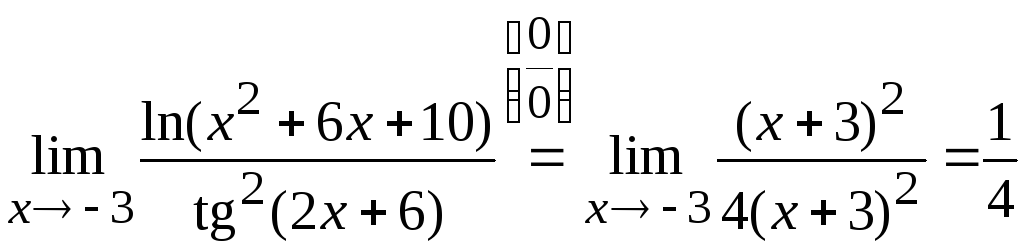
Ответ:
.
Задача
4. Вычислить
.
Решение.
Здесь возникает неопределенность типа
.
Представим числитель в виде:
.
Затем
заменим его эквивалентной бесконечно
малой в точке
функцией
.
Преобразуем
знаменатель:
и
заменим его на эквивалентную бесконечно
малую
.
Тогда получим
.
Ответ:
.
Задача
5. Вычислить
.
Решение.
Здесь возникает неопределенность типа
.
Числитель
можно заменить эквивалентной бесконечно
малой
.
Чтобы
воспользоваться соотношением (8.4),
преобразуем знаменатель:
и
заменим его эквивалентной бесконечно
малой
.
Тогда
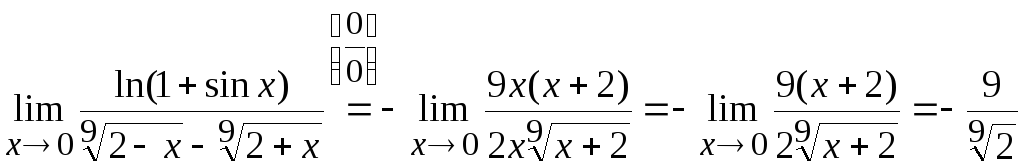
Ответ:
.
Задача
6. Вычислить
.
Решение.
Здесь имеем неопределенность типа
.
Чтобы применить к выражению
соотношение (8.3), представим его в виде:
,
и
заменим бесконечно малую функцию
эквивалентной бесконечно малой
.
Знаменатель же представим в виде:
и,
используя соотношения (8.2) и (8.8), заменим
его эквивалентной бесконечно малой
.
Учитывая проведенные выкладки и
соотношение (8.4), получим:
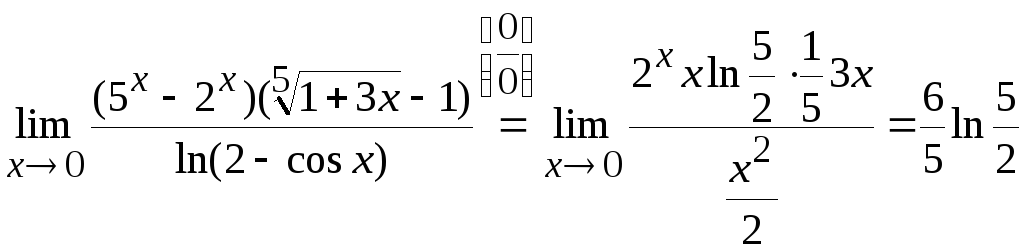
Ответ:
.
Задача
7. Вычислить
.
Решение.
Здесь имеем неопределенность типа
.
Используя ряд приемов, примененных в
задачах 1–7, получим
.
Ответ:
.
Задача
8. Вычислить
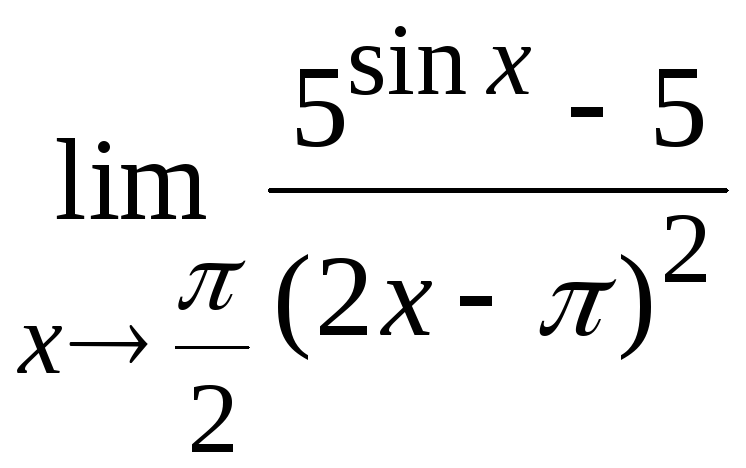
Решение.
Здесь имеем неопределенность типа
.
Используя ряд приемов, примененных в
задачах 1–7 и формулы приведения для
тригонометрических функций, получим
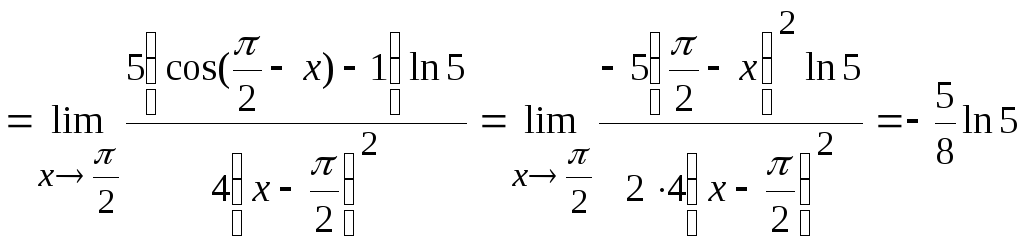
Ответ:
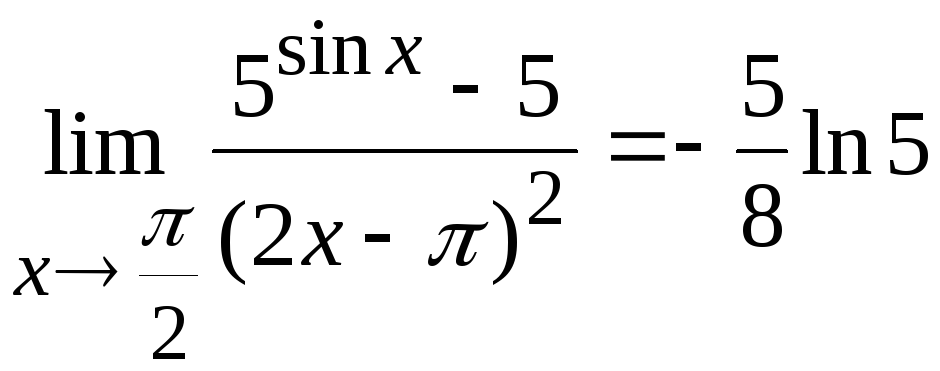
Задача
9. Вычислить
.
Решение.
Здесь имеем неопределенность типа
.
Чтобы применить к числителю соотношение
(8.2), преобразуем его следующим образом:
.
Теперь
числитель согласно соотношению (8.2)
можно заменить эквивалентной бесконечно
малой
.
Преобразуем
знаменатель
.
Заменяем,
используя соотношение (8.1),
эквивалентной бесконечно малой
.
Тогда

Ответ:
.
Задача
10. Вычислить
.
Решение.
Здесь имеем неопределенность типа
.
Используя приемы, описанные выше, получим
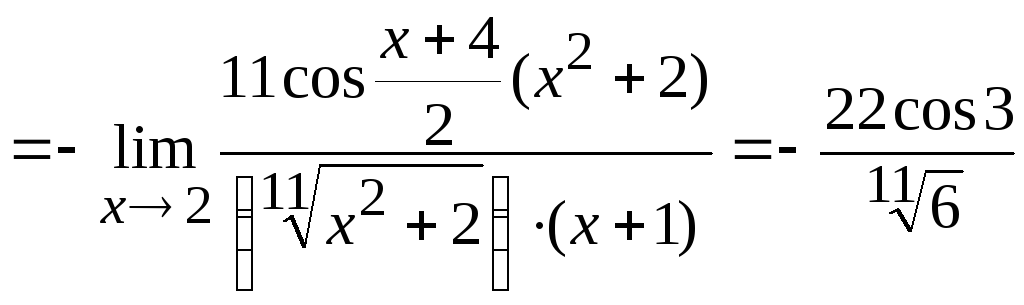
.
Ответ:
.
Задача
11. Вычислить

Решение.
Здесь имеем неопределенность типа
.
Используя теоремы 6.2 и 6.1, получим
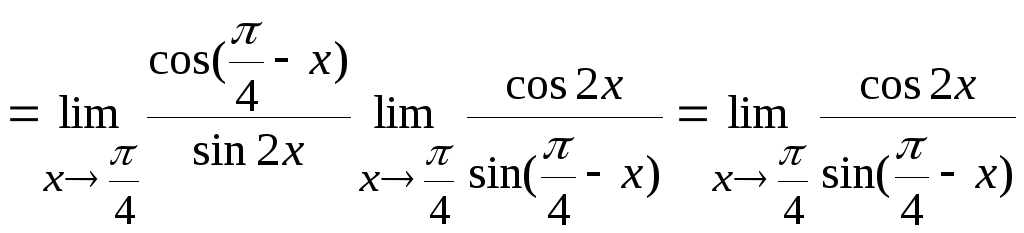
Получили
неопределенность типа
.
Преобразуем выражение с помощью формул
приведения, затем переходим к эквивалентным
бесконечно малым. В итоге получим
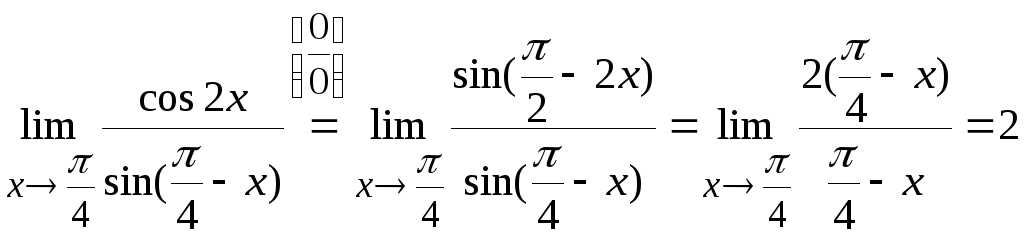
Ответ:
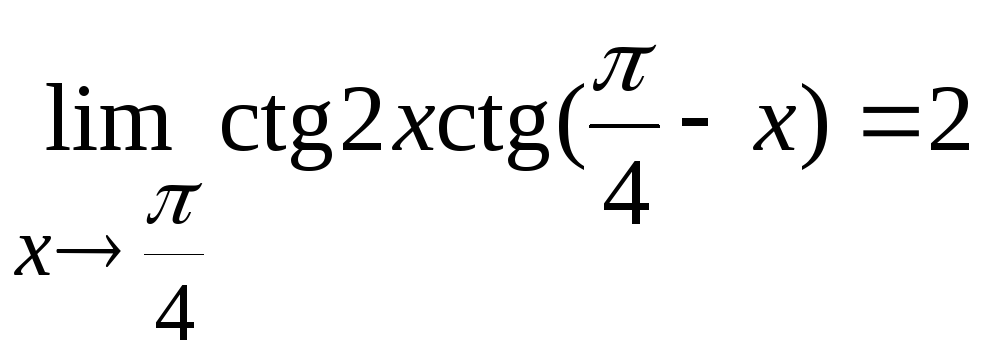
Задача
12. Вычислить
.
Решение.
Здесь имеем неопределенность типа
.
Выделим
в основании степени:
.
Заметим,
что
при
.
Справедлива
цепочка равенств

Заменяя
логарифм эквивалентной бесконечно
малой согласно соотношению (8.2) и используя
замечание 6.4 для раскрытия неопределенности,
получим
.
Ответ:
.
Задача
134.
Вычислить
.
Решение.
Здесь имеем неопределенность типа
.
Введем переменную
.
Если
,
то
.
.
Выделим
в основании степени:
,
тогда
.
Заметим,
что
при
.
Заменим функцию
эквивалентной бесконечно малой
,
будем иметь
.
Используя
теорему 7.3, окончательно получим
.
Ответ:
.
Задача
14. Вычислить
.
Решение.
Здесь возникает неопределенность типа
.
Поскольку
,
вычислим
сначала
.
Мы имеем дело с неопределенностью типа
.
Воспользовавшись
последовательно соотношениями (8.2) и
(8.1), будем иметь
.
Ответ:
.
Задача
15. Вычислить
.
Решение.
Здесь возникает неопределенность типа
.
Воспользуемся формулой
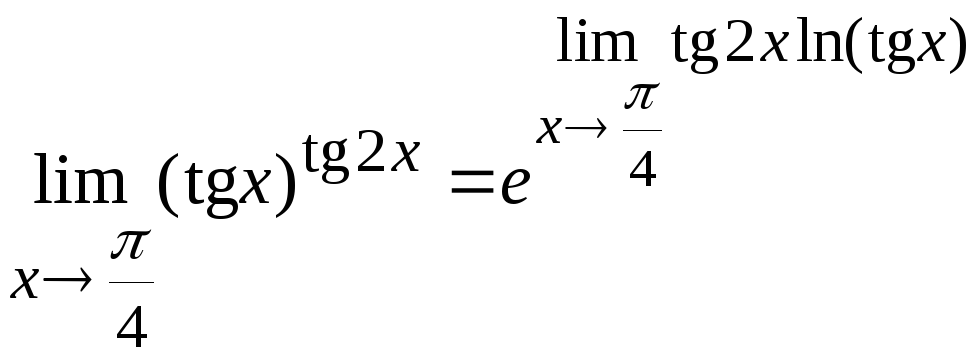
Вычислим
предел, стоящий в показателе степени.
Для этого требуется раскрыть
неопределенность типа
.
Преобразуем ее в неопределенность типа
и воспользуемся эквивалентностью
бесконечно малых:

Ответ:
.
Задача
16. Вычислить
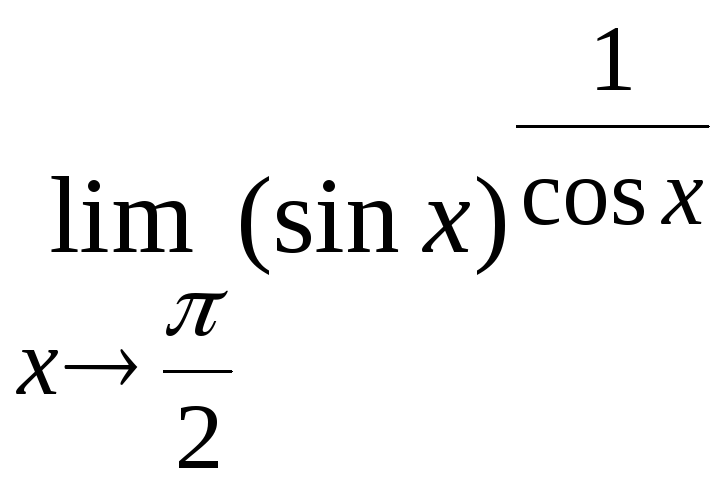
Решение.
Здесь возникает неопределенность типа
.
Преобразуем исходное предельное
выражение
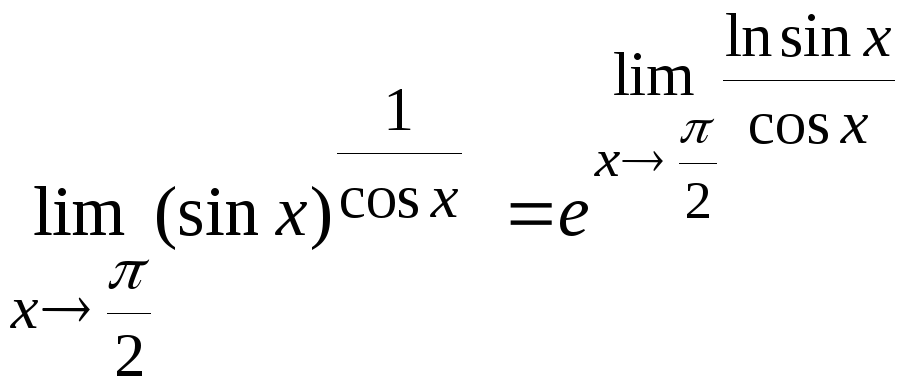
Вычислим
предел, стоящий в показателе степени.
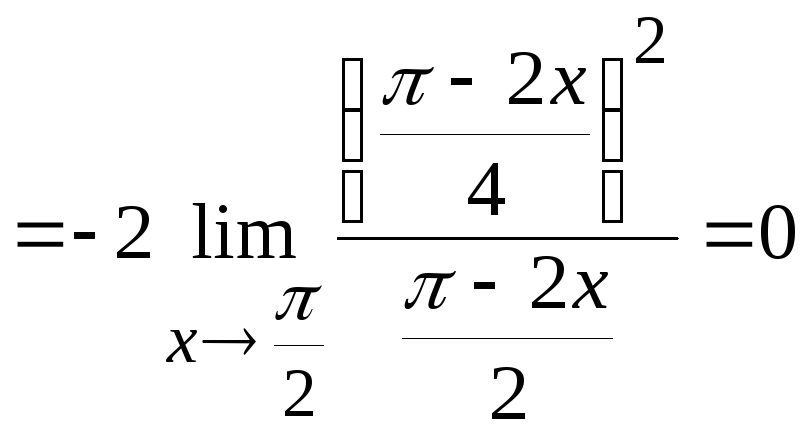
Ответ:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Итак, ты ученик первого курса технического вуза, а единственное, что ты можешь сказать, глядя на эту хуйню, — это «ебись оно конем»? Тогда этот гайд для тебя.
Урок математики. Учительница говорит:
— Сегодня мы будем брать интегралы.
Вовочка спрашивает:
— А как это в жизни пригодится?
— Ты ебало-то завали.
Рассмотрим простейший пример:
Все очень просто. Видишь как икс стремится к трем? То-то же. Просто подставь в дробь значение икс равное трем. В числителе получается 10, а в знаменателе 5. Делим и получаем ответ 2. Понял в чем дело? Просто подставляем в предел вместо икса то, к чему стремится этот самый икс. И все.
Но такое на контрольной тебе никогда не дадут. Рассмотрим пример посложнее.
Подставляем бесконечность вместо икса и включаем мозг: логично предположить, что бесконечность это очень много, а когда мы делим небольшое число на очень большое, то получаем очень маленький ответ. А когда мы делим любое число на бесконечно большое, то получаем 0. Запомнил? Молодец, даже у Эйнштейна это только с третьего раза получилось.
Ну а что, если икс стремится к нулю? На ноль делить же нельзя? Это правда, только мы подставляем не 0, а число бесконечно стремящееся к нулю. Логика подсказывает, что в таком случае в ответе получится бесконечность. Понял? Если нет, спроси свою маму или бабушку.
А теперь глядь сюды:
Что у нас тут получается? Бесконечность в числителе и бесконечность в знаменателе? Неопределенность какая-то. Именно с неопределенностями разных типов тебе придется сразится на контрольной. В данном случае у нас неопределенность вида ВОСЬМЕРКА НА БОКУ РАЗДЕЛИТЬ НА ВОСЬМЕРКУ НА БОКУ. Решить данную блевоту можно вынеся старшую степень за скобки. Ну мы же не такие, правда? Лови лайфхак: когда у нас Х стремится к бесконечности и в пределе отношение многочлена на многочлен, то ответом является отношение коэффициентов при старших степенях. То есть нам нужно взять циферку перед икс в кубе из числителя и разделить его на циферку перед икс в кубе в знаменателе. Ответ получается в уме — 1/2. Да, ты можешь выкрикнуть ответ с места еще до того, как пример будет дописан на доске. Учителя такое очень любят, рекомендую.
Подобную хуету можно применить для поебени посложнее:
Решается абсолютно аналогично. Видишь хрень под корнем? Мысленно убери х+1 и извлеки корень. Выходит, что старшая степень 2. У нас получается так, что в числителе старшая степень и под корнем прячется и вне корня тоже есть. В общем, мне лень дальше писать, ответ 4/3. Кто не понял, тот лох.
Если старшие степени не совпадают, то ответом будет либо ноль либо бесконечность (зависит от вашего настроения).
Заикнувшимся про правило Лопиталя напомню, что за него на контрольной могут и выебать.
Теперь посмотрим на неопределенность иного типа:
Подставляем значение икса в предел и получаем неопределенность вида 0/0. Хуйня какая-то. Но только до тех пор, пока ты не догадаешься разложить числитель на множители. Находим корни в уме за пять лет (отсылка на предыдущий пост, охуеть!) и раскладываем поеботу по следующей формуле: (циферка ПЕРЕД ИКСОМ В квадрате)×(ИКС МИНУС первый корень)×(ИКС МИНУС второй корень). Эту формулу знает даже Невский.
Корни получились 5/2 и -1.
Теперь просто подставляем -1 и получаем ответ -7.
Внимательно глядим на новое спецзадание. Тут нас ждет неопределенность нового типа — бесконечность минус бесконечность. Домножем этот понос на такой же понос, только со знаком плюс вместо минуса. Ну раз мы домножили выражение на что-то, то на это самое что-то нужно и разделить, чтобы выражение не изменилось. В числителе применим формулу из продвинутого курса высшей математики:
Получилось вот что:
А дальше вспоминай пример номер 3 (это там, где мне было лень все расписывать и я выдал сразу ответ) и действуй аналогично. Ответ (2) находится в уме настолько быстро, что как-то неловко об этом писать.
Закрепим материал заданием, которым пытают Гитлера в аду:
Видишь классическую неопределенность вида 0/0? Значит нужно разложить на множители. Должно получиться что-то вроде (х-1)*(………) и в числителе и в знаменателе. Далее х-1 сократится и все будет хорошо. Есть один секретный способ, но я тебе его не покажу, поэтому будет раскладывать на множители делением в столбик. Ахтунг! Далее идет шок контент. Я предупредил.
В общем, в процессе деления столбиком ты увидишь, что в ответе вырисовывается ряд из степеней от большей к нулю. В конце у нас остается остаток в самом низу рисунка. Это полный квадрат выражения х-1. То есть при делении его на х-1 мы получим х-1. В знаменателе будет тоже самое, только ряд степеней начнется с 49. На множитель (х-1) мы сократили и числитель и знаменатель в предыдущем абзаце, если кто забыл. Теперь подставляем х=1 и получаем 98/48 или 49/24.
Вот и все. Полученных знаний тебе хватит, чтобы получить на контрольной твердую 2, а учительница если и будет тебя бить, то не сильно.
Напоследок дам универсальный способ. Если ты не можешь найти ответ, то он находится
При вычислении пределов от показательно-степенной функции пользуются либо формулой 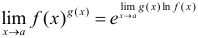
Пример №1.
Вычислить 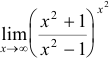
Решение:
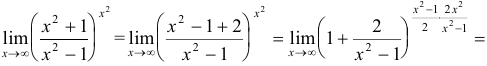
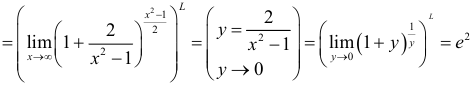
Пример №1.
Вычислить 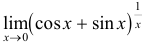
Решение:
Заметим, что 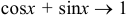
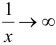
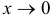
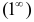
так как
Пример №2.
Вычислить 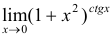
Решение:
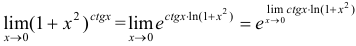
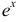
Следовательно, 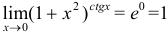
Пример №3.
Вычислить 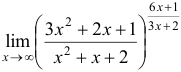
Решение:
Так как 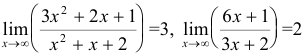
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
2
Как считать пределы со степенями
Предел показательно степенной функции, примеры нахождения
В процессе нахождения предела показательно-степенной функции типа lim x → x 0 ( f ( x ) ) g ( x ) часто работаем с такими степенными неопределенностями, как 1 ∞ , 0 0 , ∞ 0 .
Для их раскрытия необходимо задействовать логарифмирование a = e ln ( a ) , свойство логарифма a · ln ( b ) = ln ( b a ) и применение его предела заданной непрерывной функции, причем ее знак разрешено менять местами.
Для этого производятся преобразования вида:
lim x → x 0 ( f ( x ) ) g ( x ) = e ln lim x → x 0 f ( x ) ) g ( x ) = e lim x → x 0 ( ln ( f ( x ) ) g ( x ) = e lim x → x 0 ( g ( x ) ln ( f ( x ) ) ) = = e lim x → x 0 ln ( f ( x ) ) 1 g ( x )
Отсюда видно, что задание приводится к нахождению предела заданной функции вида e lim x → x 0 ln ( f ( x ) ) 1 g ( x ) = ∞ ∞ или 0 0 .
Данный случай рассматривает методы:
- непосредственного вычисления;
- использования правила Лопиталя;
- с заменой эквивалентных бесконечно малых функций;
- применение первого замечательного предела.
Для того, чтобы неопределенность была раскрыта, необходимо применять второй замечательный предел, при наличии 1 ∞ .
Рассмотрим теорию на элементарных примерах заданий.
Найти предел заданной функции lim x → 0 ( x 3 + 2 x + 1 ) 3 2 x 3 + x .
Для решения необходимо произвести подстановку. Получаем :
lim x → 0 ( x 3 + 2 x + 1 ) 3 2 ( x 3 + x ) = ( 0 3 + 2 · 0 + 1 ) 3 2 ( 0 3 + 0 ) = 1 ∞
Получение единицы в степени бесконечность называют неопределенностью, значит, необходимо решить другим методом.
Следует произвести преобразования данного предела. Получаем:
lim x → 0 ( x 3 + 2 x + 1 ) 3 2 ( x 3 + x ) = e ln lim x → 0 ( x 3 + 2 x + 1 ) 3 2 ( x 3 + x ) = = e lim x → 0 ln ( x 3 + 2 x + 1 ) 3 2 ( x 3 + x ) = e lim x → 0 3 ln ( x 3 + 2 x + 1 ) 2 ( x 3 + x )
Видим, что преобразование сводится к пределу вида lim x → 0 3 ln ( x 3 + 2 x + 1 ) 2 ( x 3 + x ) .
lim x → 0 3 ln ( x 3 + 2 x + 1 2 ( x 3 + x ) = 0 0 = 3 2 lim x → 0 ln ( x 3 + 2 x + 1 ) x 3 + x = = 3 2 lim x → 0 x 3 + 2 x x 3 + x = 3 2 lim x → 0 x 2 + 2 x 2 + 1 = 3 2 · 0 2 + 2 0 2 + 1 = 3
Данные преобразования были выполнены при помощи применения замены логарифма на эквивалентную бесконечно малую функцию.
Тогда исходный предел принимает вид lim x → 0 ( x 2 + 2 x + 1 ) 3 2 ( x 3 + x ) = e 3 .
Вычисление данного предела возможно с применением второго замечательного предела. Тогда получаем:
lim x → 0 ( x 2 + 2 x + 1 ) 3 2 ( x 3 + x ) = lim x → 0 ( 1 + ( x 3 + 2 x ) 1 x 3 + 2 x ( x 3 + 2 x ) 3 2 ( x 3 + x ) = = lim x → 0 ( 1 + ( x 3 + 2 x ) ) 1 x 3 + 2 x 3 ( x 3 + 2 x ) 2 ( x 3 + x ) = lim x → 0 1 + ( x 3 + 2 x ) ) 1 x 3 + 2 x 3 ( x 2 + 2 ) 2 ( x 2 + 1 ) = = lim x → 0 ( 1 + ( x 3 + 2 x ) 1 x 3 + 2 x 3 = e 3
Найти и вычислить предел lim x → π 2 ( t g x ) 2 c o s x
Если произведем подстановку, в результате получим ответ в виде бесконечности в степени ноль, а это является знаком, что необходимо применить другой метод для преобразования. Получаем:
lim x → π 2 ( t g x ) 2 c o s x = ∞ 0 = e ln lim x → π 2 ( t g x ) 2 cos x = = e 2 lim x → π 2 ( t g x ) 2 cos x = e lim x → π 2 ( 2 cos x · ln · ( t g x ) ) = = e 2 lim x → π 2 ln ( t g x ) 1 cos x
Отсюда видно, что решение сводится к переделу lim x → π 2 ln ( t g x ) 1 cos x = ∞ ∞ .
Для дальнейшего преобразования применим правило Лопиталя, так как получили неопределенность в виде частного бесконечностей. Видим, что
lim x → π 2 ln ( t g x ) 1 cos x = ∞ ∞ = lim x → π 2 = ln ( t g x ) ‘ 1 cos ( x ) ‘ = = lim x → π 2 1 t g ( x ) · 1 cos 2 ( x ) sin ( x ) cos 2 ( x ) = lim x → π 2 cos ( x ) sin 2 ( x ) = cos π 2 sin 2 π 2 = 0 1 2 = 0
Отсюда следует, что пределом показательно-степенной функции является результат, полученный при вычислении. Имеем вы предел вида lim x → π 2 ( t g x ) 2 cos x = e 2 · 0 = e 0 = 1 .
Второй замечательный предел
Обычно второй замечательный предел записывают в такой форме:
Число $e$, указанное в правой части равенства (1), является иррациональным. Приближённое значение этого числа таково: $eapprox718281828459045>$. Если сделать замену $t=frac$, то формулу (1) можно переписать в следующем виде:
Как и для первого замечательного предела, неважно, какое выражение стоит вместо переменной $x$ в формуле (1) или вместо переменной $t$ в формуле (2).
Следует учесть, что просто так добавить единицу нельзя. Если мы вынуждены добавить единицу, то её же нужно и вычесть, дабы не изменять значения всего выражения. Для продолжения решения учтём, что
Продолжим «подгонку». В выражении $1+frac$ формулы (1) в числителе дроби находится 1, а в нашем выражении $1+frac$ в числителе находится $6$. Чтобы получить $1$ в числителе, опустим $6$ в знаменатель с помощью следующего преобразования:
Итак, основание степени, т.е. $1+frac>$, подогнано под вид $1+frac$, который требуется в формуле (1). Теперь начнём работать с показателем степени. Заметьте, что в формуле (1) выражения, стоящие в показатели степени и в знаменателе, одинаковы:
Значит, и в нашем примере показатель степени и знаменатель нужно привести к одинаковой форме.
Для начала отметим, что в формуле (1) переменная $x$ стремится к бесконечности, в формуле (2) переменная $t$ стремится к нулю. В нашем случае $xto$, поэтому имеет смысл ввести новую переменную, чтобы она стремилась или к нулю (тогда применим формулу (2)), или к бесконечности (тогда применим формулу (1)). Введение новой переменной, вообще говоря, не является обязательным, это будет сделано просто для удобства решения. Проще всего новую переменную $y$ ввести так: $y=x-1$. Так как $xto$, то $to$, т.е. $yto$. Подставляя $x=y+1$ в рассматриваемый пример, и учитывая $yto$, получим:
Применим формулу (2). Выражение в основании степени в формуле (2), т.е. $1+t$, соответствует форме выражения в основании степени нашего примера, т.е. $1+(-6y)$ (выражение $-6y$ играет роль $t$). Формула (2) предполагает, что показатель степени будет иметь вид $frac$, т.е. в нашем случае в показателе степени следует получить $frac$.
Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).
Замечательные пределы: Первый и второй замечательный предел.
Понятие замечательных пределов используется на просторах бывшего Советского Союза для обозначения хорошо известных математических тождеств со взятием предела. Замечательны они потому, что они уже доказаны великими математиками и нам нам остается лишь пользоваться ими для удобства нахождения пределов. Из них наиболее известны первый и второй замечательные пределы. Дальнейшее чтение статье будет намного интереснее, если вы уже знакомы с понятием пределов. Если для вас lim , это то что новое, то рекомендуем к прочтению статью «Пределы. Понятие пределов. Вычисление пределов.»
Теперь со спокойной душой переходим к рассмотрению замечательных пределов.
Первый замечательный предел имеет вид .
Вместо переменной х могут присутствовать различные функции, главное, чтобы они стремились к 0.
Необходимо вычислить предел
Как видно, данный предел очень похож на первый замечательный, но это не совсем так. Вообще, если Вы замечаете в пределе sin, то надо сразу задуматься о том, возможно ли применение первого замечательного предела.
Согласно нашему правилу №1 подставим вместо х ноль:
Получаем неопределенность .
Теперь попробуем самостоятельно организовать первый замечательный предел. Для этого проведем нехитрую комбинацию:
Таким образом мы организовываем числитель и знаменатель так, чтобы выделить 7х. Вот уже и проявился знакомый замечательный предел. Желательно при решении выделять его:
Подставим решение первого замечательного примера и получаем:
Как видите – все очень просто.
Второй замечательный предел имеет вид , где e = 2,718281828… – это иррациональное число.
Вместо переменной х могут присутствовать различные функции, главное, чтобы они стремились к .
Необходимо вычислить предел
Здесь мы видим наличие степени под знаком предела, значит возможно применение второго замечательного предела.
Как всегда воспользуемся правилом №1 – подставим вместо х:
Видно, что при х основание степени , а показатель – 4x > , т.е. получаем неопределенность вида :
Воспользуемся вторым замечательным пределом для раскрытия нашей неопределенности, но сначала надо его организовать. Как видно – надо добиться присутствия в показателе, для чего возведем основание в степень 3х, и одновременно в степень 1/3x, чтобы выражение не менялось:
Не забываем выделять наш замечательный предел:
Дальше знак предела перемещаем в показатель:
Вот такие действительно замечательные пределы!
Если у вас остались какие то вопросы по первому и второму замечательным пределам, то смело задавайте их в комментариях.
Всем по возможности ответим.
Также вы можете позаниматься с педагогом по этой теме.
Мы рады предложить вам услуги подбора квалифицированного репетитора в вашем городе. Наши партнеры оперативно подберут для вас хорошего преподавателя на выгодных для вас условиях.
Limits — Лимиты в бесконечности
Что самое большое вы когда-либо видели? Самый большой в мире мяч из резинок? Может океан? На самом деле, солнце довольно большое (преуменьшение), и мы видим это каждый день. Но тогда мы могли бы сказать, что небо покрывает почти всю вселенную.
Кажется, это трудно превзойти. Однако даже это ничтожно по сравнению с некоторыми ограничениями, ведь они могут доходить до бесконечности. Мы говорим о x , поскольку оно становится очень, очень большим или очень, очень маленьким. Эта идея известна как конечное поведение функции, и именно это помогут нам описать эти пределы на бесконечности.
По большей части эти ограничения делятся на три категории. Вместо того, чтобы тратить ваше и наше время, мы просто покажем вам каждую из них в примере задачи.
Пример задачи
Оценка .
Еще раз привет. Давно не виделись. Но посмотрите на этот предел; x не приближается к какому-то числу, оно просто будет продолжаться и продолжаться вечно. Есть несколько способов взглянуть на это. Давайте еще раз посмотрим на его график:
Обратите внимание, что происходит, когда x становится все больше и больше. Значения и все ближе и ближе к нулю. Это означает:
Еще один способ подумать об этом — рассмотреть, что происходит, когда мы подставляем действительно большие значения вместо x . Что, если бы мы использовали, например, 1000? В итоге мы получим долю . Это очень мало, то есть близко к нулю. И дальше будет только меньше. Следовательно:
Наши ответы совпадают. Ура. Мы ненавидим, когда наши ответы противоречат друг другу.
Есть третий способ найти пределы на бесконечности, и он еще более полезен. Всякий раз, когда нас просят оценить предел дроби, мы должны посмотреть и сравнить степень числителя и знаменателя. Как судьи на конкурсе помпадур, мы хотим знать, кто из них больше.
Для , больший член стоит в знаменателе. Это означает, что по мере того, как все большие и большие числа подставляются вместо x знаменатель растет быстрее, чем числитель. Хорошо, это плохой пример, потому что числитель постоянен, но вы поняли идею. Функция имеет тяжелое дно, что заставляет ее опускаться до нуля на бесконечности.
Пример задачи
Оценка .
На этот раз мы перейдем сразу к проверке степени (хотя подстановка цифр тоже всегда работает). Если числитель больше (например, x 3 больше, чем x в этом случае), функция устремится к бесконечности как x становится большим. Это означает, что:
Функция будет перемещаться вверх и вправо, вечно достигая звезд.
Этот результат вполне логичен, потому что числитель станет просто огромным, а знаменатель будет довольно большим, но не до смешного. Очень точно, мы знаем.
Пример задачи
Оценка .
Теперь этот предел немного отличается от того, что мы видели в предыдущих разделах. У вас может возникнуть соблазн упростить, разделить и сделать что-то подобное. Боритесь с искушением, не поддавайтесь. Подумайте о чем-нибудь другом, например, о животных, играющих музыку. Вместо этого мы будем умножать вещи, но только немного.
Да, вы правильно прочитали; «Кому какое дело» и «не имеет значения» теперь стали официальным сленгом Shmoop limit. Все, что нам нужно для оценки этого предела, — это члены с наибольшим показателем степени.
На этот раз степень та же, 2. Теперь у нас на руках гонка ноздря в ноздрю. Это будет фотофиниш — э-э, финиш — и все сводится к ведущему коэффициенту.
У нас есть 2 в числителе (от 2 x 2 ) и 1 внизу (от x 2 ).
Не верите? Посмотрите график здесь. Прямо на y = 2 есть горизонтальная асимптота, которая идеально согласуется с тем, что мы только что нашли.
Пример задачи
Оценка .
Степень числителя больше степени знаменателя. Ответ: ∞, верно? Проблема: сделано, верно? Не так быстро.
У нас есть предел, поскольку x на этот раз приближается к минус бесконечности. Мы не можем просто бросить эту сумасшедшую восьмерку и двигаться дальше. Вместо этого мы вынуждены учитывать знак нашего окончательного ответа.
Квадрат чего угодно будет положительным, даже такого сверхотрицательного, как -∞, поэтому числитель будет положительным. Знаменатель, однако, будет отрицательным, если вы подставите отрицательные числа для x .
Мы должны следить за знаками наших ответов.
Пример задачи
Оценка .
Беглый взгляд может показать, что эта функция имеет x больше x 2 , и поэтому предел равен нулю. Извините, но проблема еще более странная, потому что с нашим самым большим сроком происходят странные вещи. Здесь наибольший член в знаменателе имеет квадратный корень. Это означает, что самый большой заказ больше нельзя считать равным 2, на самом деле это:
( x 2 ) 1/2 = x 2/2 = x
Внезапно числитель и знаменатель имеют один и тот же порядок. Просто будьте осторожны с этим квадратным корнем. Края острые.
Да, мы тоже должны извлечь квадратный корень из 9. Это дает нам предел 1, поскольку x приближается к бесконечной пустоте в правой части графика.
Пример задачи
Оценить .
Итак, последняя проблема, а эта проблема триггера. Мы не можем посмотреть на степень функции, поэтому наш предыдущий метод не сработает. Вместо этого попробуйте изобразить график синуса.
Может быть, вы говорите себе: «Как будет работать этот предел? Когда x стремится к бесконечности, синус делает это (вы двигаете рукой волнообразно перед собой) во веки веков».
Это движение руки описывает поведение синуса как x становится бесконечно большим. Он идет назад и к четвертому между 1 и -1 снова, и снова, и снова. Так что на самом деле это не приближается к какой-либо ценности.
Иногда просто нет предела. Функция не приближается к одному значению, но и не увеличивается или уменьшается без конца. Почему ты не можешь просто принять решение, синус?
Резюме
- Если градус в верхней части дроби меньше, чем градус в нижней части, он приближается к нулю.
- Однако, если степень больше вверху, то функция стремится к бесконечности.
- При равенстве степеней сравниваем старшие коэффициенты. Их отношение является горизонтальной асимптотой, к которой приближается функция.
- Обратите внимание на знак вашего ответа, особенно когда используется -∞.
- Превратите любые радикалы в дробные степени, упростите и только потом сравнивайте степени.
- Некоторые функции, например триггерные, не приближаются ни к чему на бесконечности.
Предельный срок для получения степени
последние новости
- Центр социальных инноваций USC Sol Price, исследование арендной платы округа Лос-Анджелес, упомянутое 4 октября 2022 г. профессор Мотт Смит процитировал последние законопроекты о жилищном строительстве 30 сентября 2022 г.
- Гинзбург дал интервью об агентстве медицинского обслуживания президента Байдена и использовании вызывающего споры лекарства от болезни Альцгеймера 30 сентября 2022 г.
больше новостей
последние видео
больше видео
Аспиранты должны получить степень в течение определенного количества лет. Хотя конкретных сроков для получения степени бакалавра нет, студенты должны учитывать, что факультеты меняют свои основные требования в соответствии с развитием своих областей. Ниже указаны сроки, необходимые для получения степени аспирантами, а также обязанности, которых должны придерживаться студенты бакалавриата:
» Аспиранты
» Студенты бакалавриата
» Прекращенные программы на получение степени
Аспиранты
Срок для получения степени магистра составляет пять лет. Срок для получения степени доктора философии. и DPA составляет восемь лет. Срок для завершения DPDS составляет шесть лет. Для студентов, которые получили соответствующую степень магистра в течение пяти лет до поступления в докторантуру, срок для получения степени доктора философии. или DPA составляет шесть лет.
Академическая единица может предоставить продление до одного года за один раз максимум на два года.
Процесс запроса продления срока
Процесс запроса продления времени состоит из следующих шагов:
- Студенты подают ходатайство USC Price Master’s Petition (PDF, для студентов магистратуры) или USC Price Doctoral Petition (PDF, для докторантов) студентов) соответствующему консультанту по обслуживанию студентов. Учащиеся должны указать, почему они не смогли получить степень в течение требуемого периода времени, и включить реалистичный график того, когда они ожидают получить степень. Они должны включать срок, в течение которого они ожидают получить степень.
- Студенты, запрашивающие продление срока обучения более чем на семь лет (студенты магистратуры) или 10 лет (студенты докторантуры), также должны заполнить Общее ходатайство об аспирантуре (PDF).
- Советник по работе со студентами направляет петицию директору соответствующей степени.
- Советник по работе со студентами письменно информирует студента о принятом решении.
Для получения дополнительной информации посетите страницу аспирантов в разделе «Требования к выпускным» каталога USC. Для получения дополнительной информации о ценах USC перейдите на страницу «Докторские степени» в разделе «Цены USC» каталога USC.
Студенты бакалавриата
Хотя конкретных сроков для получения степени бакалавра не существует, с течением времени многие факультеты меняют свои основные требования в соответствии с развитием отрасли и факультетов. Иногда требования к общему образованию меняются или программа на получение степени прекращается. Таким образом, студентам бакалавриата, которые не получают степени в течение шести лет подряд с первого семестра, в котором они завершили какую-либо курсовую работу USC, может быть отказано в продолжении выполнения их предварительных, основных и второстепенных требований, как указано выше.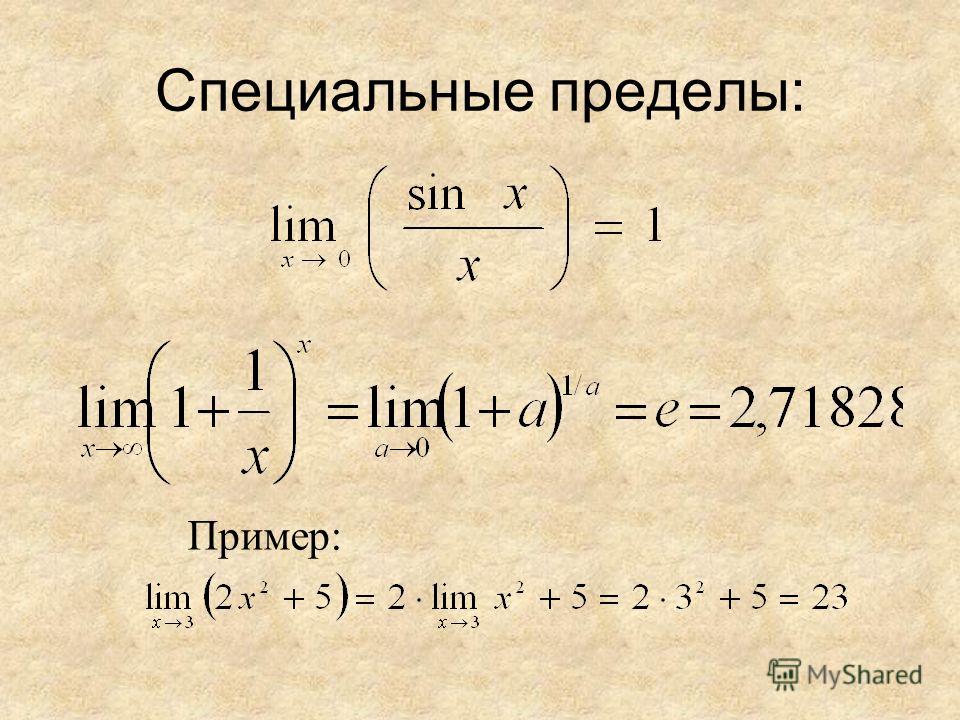
Студенты, не получившие степень в течение 10 лет подряд с начала семестра их первой завершенной курсовой работы USC, не будут автоматически допущены к выполнению требований общего образования. (Этот срок включает в себя семестры, в течение которых учащиеся не зачислены.) Управление общего образования принимает решение о том, каким общеобразовательным требованиям должен следовать каждый учащийся, и сообщает об этом решении учащемуся в письменной форме.
Для получения дополнительной информации перейдите на страницу «Студенты бакалавриата» в разделе «Требования к выпускным» каталога USC.
Прекращенные программы на получение степени
Студентам, обучающимся по программам на получение степени, которые университет прекращает, будет разрешено завершить программы на получение степени или второстепенные программы в течение определенного срока, определяемого на момент прекращения.
Дополнительную информацию см. в разделе «Требования к получению диплома» каталога USC.
Запрос на продление максимального срока: докторская степень
Перейти к основному содержанию
-
Календарь
- Академический календарь
- Убрать/добавить дедлайны
- Время регистрации
- График финансовой помощи
- Время выпускных экзаменов
-
Регистрация
-
Зарегистрироваться на занятия
- Поиск классов
- Зарегистрироваться на занятие
- Время регистрации
- Зарегистрируйтесь в нескольких кампусах UMN
- Разрешение класса
- Списки ожидания
- Классный временной конфликт
- Требования к курсу
- Двойная карьера
-
Изменить регистрацию
- Бросить курс
- Обмен или будущий обмен классами
- Изменить основу оценки
- Консультирование
- Правила регистрации
- Без степени
- Образовательная программа для пенсионеров
-
Зарегистрироваться на занятия
-
Академики
-
Бакалавриат
- АПАС
-
Обзор требований к библиотеке
- Требования к гуманитарному образованию
-
Требования к образованию до осени 2010 г.
-
Бакалавриат