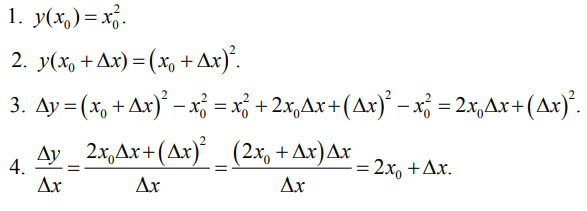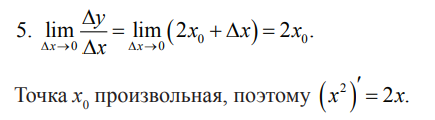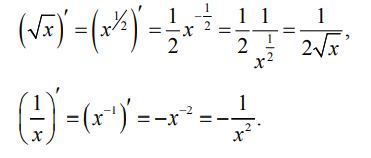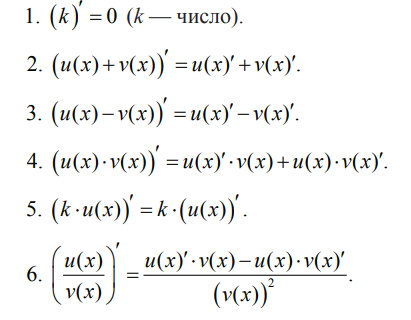Как найти предел квадратного уравнения

Вычисление пределов. Пределы с неопределенностью

Прежде чем рассказать о вычислении пределов с неопределенностью, хочется верить, что у вас уже есть понимание того, что такое предел и как вычислить элементарные пределы. Если такого понимания нет, то сначала прочитайте статью «Пределы. Понятие пределов. Вычисление пределов».
Теперь перейдем к рассмотрению пределов с неопределенностью.

Существует группа пределов, когда x , а функция представляет собой дробь, подставив в которую значение х = получим неопределенность вида .

Необходимо вычислить предел

Воспользуемся нашим правилом №1 и подставим в функцию. Как видно мы получаем неопределенность .

В числителе находим х в старшей степени, которая в нашем случае = 2:

То же самое проделаем со знаменателем:

Здесь также старшая степень = 2.

Далее надо из двух найденных степеней выбрать самую старшую. В нашем случае степень числителя и знаменателя совпадают и =2.

Итак, для раскрытия неопределенности нам потребуется разделить числитель и знаменатель на х в старшей степени, т.е. на x 2 :

Существуют также пределы с другой неопределенностью — вида . Отличие от предыдущего случая лишь в том, что х стремится уже не к , а к конечному числу.

Необходимо вычислить предел .

Снова воспользуемся правилом №1 и подставим в место х число -1:

Мы получили неопределенность , для раскрытия которой необходимо разложить числитель и знаменатель на множители, для чего в свою очередь обычно решается квадратное уравнение или используются формулы сокращенного умножения.

В нашем случае решаем уравнение:

.

Если корень не извлекается целый вероятней всего D вычислен неправильно.

Теперь находим корни уравнения:

В знаменателе у нас х + 1, что итак является простейшим множителем.

Тогда наш предел примет вид:

х + 1 красиво сокращается:

Теперь подставим вместо х значение -1 в функцию и получаем:

Рассмотрим основные положения, применяемые при решении различного рода задач с пределами:

Предел суммы 2-х или более функций равен сумме пределов этих функций:

Предел постоянной величины равен самой постоянной величине:

За знак предела можно выносить постоянный коэффициент:

Предел произведения 2-х и более функций равен произведению пределов этих функций ( последние должны существовать):

Предел отношения 2-х функций равен отношению пределов этих функций (в том случае, если предел знаменателя 0:

Степень функции, находящейся под знаком предела, применима к самому пределу этой функции (степень должна быть действительным числом):

На этом с вычислением пределов с неопределенностью всё. Еще в статье «Замечательные пределы: Первый и второй замечательный предел» мы отдельно рассматриваем интересную группу пределов. Статья вставит еще один блок для решения большинства пределов, встречающихся не просторах обучения.
Если у вас появились какие то вопросы по вычислению пределов с неопределенностью, то задавайте их в комментариях. Будем рады ответить.

Заметка: Если не хватает времени на учебу, вы можете заказать контрольную работу (http://forstuds.ru/kontrolnaya-rabota-na-zakaz), учтите правда наличие знаний по теме у вас после этого.

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

Вот с фразы «Воспользуемся нашим правилом №1» поподробнее пожалуйста. У вас есть отдельный список таких правил? Хочу себе сделать как бы карманный мини справочник, чтобы всегда был под рукой.

Я так и не понял как вы числитель разложили, будто колоду карт раскидали и все)

Что такое предел функции

В данной публикации мы рассмотрим одно из главных понятий математического анализа – предел функции: его определение, а также различные способы решения с практическими примерами.

Определение предела функции

Предел функции – величина, к которой стремится значение данной функции при стремлении ее аргумента к предельной для области определения точке.

Запись предела:

• предел обозначается значком lim;
• под ним добавляется, к какому значению стремится аргумент (переменная) функции. Обычно, это x , но не обязательно, например: “ x →1″;

Таким образом, финальная запись предела выглядит выглядит так (в нашем случае):

Читается как “предел функции при икс, стремящемся к единице”.

x →1 – это значит, что “икс” последовательно принимает значения, которые бесконечно приближаются к единице, но никогда с ней не совпадут (ее не достигнут).

Решение пределов

С заданным числом

Давайте решим рассмотренный выше предел. Для этого просто подставляем единицу в функцию (т.к. x →1):

Таким образом, чтобы решить предел, сперва пробуем просто подставить заданное число в функцию под ним (если икс стремится к конкретному числу).

С бесконечностью

В данному случае аргумент функции бесконечно возрастает, то есть “икс” стремится к бесконечности (∞). Например:

Если x →∞, то заданная функция стремится к минус бесконечности (-∞), т.к.:

• 3 – 1 = 2
• 3 – 10 = -7
• 3 – 100 = -97
• 3 – 1000 – 997 и т.д.

Другой более сложный пример

Для того, чтобы решить этот предел, также, просто увеличиваем значения x и смотрим на “поведение” функции при этом.

Таким образом при “икс”, стремящемся к бесконечности, функция неограниченно растет.

С неопределенностью (икс стремится к бесконечности)

В данном случае речь идет про пределы, когда функция – это дробь, числитель и знаменатель которой представляют собой многочлены. При этом “икс” стремится к бесконечности.

Пример: давайте вычислим предел ниже.

Выражения и в числителе, и а знаменателе стремятся к бесконечности. Можно предположить, что в таком случае решение будет таким:

Однако не все так просто. Чтобы решить предел нам нужно сделать следующее:

1. Находим x в старшей степени для числителя (в нашем случае – это два).

2. Аналогичным образом определяем x в старшей степени для знаменателя (тоже равняется двум).

3. Теперь делим и числитель, и знаменатель на x в старшей степени. В нашем случае в обоих случаях – во второй, но если бы они были разные, следовало бы взять наибольшую степень.

4. В получившемся результате все дроби стремятся к нулю, следовательно ответ равен 1/2.

С неопределенностью (икс стремится к конкретному числу)

И в числителе, и в знаменателе представлены многочлены, однако, “икс” стремится к конкретному числу, а не к бесконечности.

В данном случае условно закрываем глаза на то, что в знаменателе стоит ноль.

Пример: Найдем предел функции ниже.

1. Для начала подставим в функцию число 1, к которому стремится “икс”. Получаем неопределенность рассматриваемого нами вида.

2. Далее раскладываем числитель и знаменатель на множители. Для этого можно воспользоваться формулами сокращенного умножения, если они подходят, или решить квадратное уравнение.

В нашем случаем корнями выражения в числителе () являются числа 1 и 1,5. Следовательно его можно представить в виде: .

Знаменатель () изначально является простым.

3. Получаем вот такой видоизмененный предел:

4. Дробь можно сократить на ():

5. Остается только подставить число 1 в выражение, получившееся под пределом:

Предел по-шагам

Результат

Примеры пределов

• Пределы от рациональных дробей на бесконечности
• Пределы от рациональных дробей в конечной точке
• Пределы от дроби в нуле
• Первый замечательный предел
• Второй замечательный предел
• Пределы с квадратными корнями
• Правило Лопиталя

Указанные выше примеры содержат также:

• квадратные корни sqrt(x),
  кубические корни cbrt(x)
• тригонометрические функции:
  синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x)
• показательные функции и экспоненты exp(x)
• обратные тригонометрические функции:
  арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс actan(x)
• натуральные логарифмы ln(x),
  десятичные логарифмы log(x)
• гиперболические функции:
  гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x)
• обратные гиперболические функции:
  asinh(x), acosh(x), atanh(x), actanh(x)
• число Пи pi
• комплексное число i

Правила ввода

Можно делать следующие операции

2*x — умножение 3/x — деление x^3 — возведение в степень x + 7 — сложение x — 6 — вычитание Действительные числа вводить в виде 7.5, не 7,5

Чтобы увидеть подробное решение,
помогите рассказать об этом сайте:

Теория пределов – раздел математического анализа. Наряду с системами линейных уравнений и диффурами пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.

В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Понятие предела в математике

Первый вопрос: что это вообще за предел и предел чего? Можно говорить о пределах числовых последовательностей и функций. Нас интересует понятие предела функции , так как именно с ними чаще всего сталкиваются студенты. Но сначала — самое общее определение предела:

Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a, то a – предел этой величины.

Для определенной в некотором интервале функции f(x)=y пределом называется такое число A, к которому стремится функция при х, стремящемся к определенной точке а. Точка а принадлежит интервалу, на котором определена функция.

Звучит громоздко, но записывается очень просто:

Lim — от английского limit — предел.

Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.

Приведем конкретный пример. Задача — найти предел.

Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:

Кстати, если Вас интересуют базовые операции над матрицами, читайте отдельную статью на эту тему.

В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:

Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.

Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х. Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность. Что делать в таких случаях? Прибегать к хитростям!

Неопределенности в пределах

Неопределенность вида бесконечность/бесконечность

Пусть есть предел:

Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?

Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:

Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Еще один вид неопределенностей: 0/0

В таких случаях рекомендуется раскладывать числитель и знаменатель на множители. Но давайте посмотрим на конкретный пример. Нужно вычислить предел:

Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:

Сократим и получим:

Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.

Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:

Правило Лопиталя в пределах

Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?

Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.

Наглядно правило Лопиталя выглядит так:

Важный момент: предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.

А теперь – реальный пример:

Налицо типичная неопределенность 0/0. Возьмем производные от числителя и знаменателя:

Вуаля, неопределенность устранена быстро и элегантно.

Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос «как решать пределы в высшей математике». Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.

МАТЕМАТИЧЕСКИЙ АНАЛИЗ.
Пределы
функций. Производная функции

Продолжим рассматривать примеры вычисления пределов последовательностей.
4. Найти предел последовательности

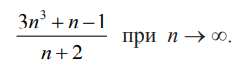
Наибольшая степень в числителе и знаменателе — третья, поэтому поделим числитель и знаменатель на n³. Получим

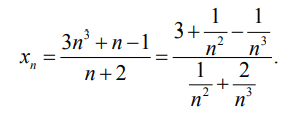
Воспользоваться теоремой 4 для вычисления предела отношения двух последовательностей невозможно, так как предел последовательности

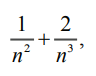
стоящей в знаменателе, равен 0.
Рассмотрим последовательность

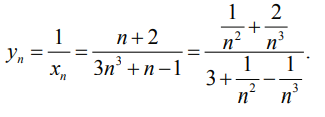
Предел этой последовательности равен 0:

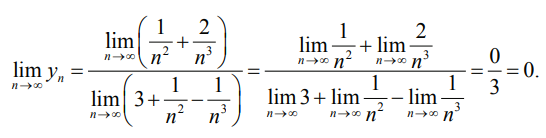
Так как последовательность y_n — бесконечно малая, то

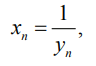
согласно теореме 1, бесконечно большая последовательность. Таким образом,

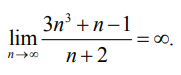
Правило. Если у общего члена последовательности степень числителя больше степени знаменателя, то последовательность
бесконечно большая.

Пределы функций

Рассмотрим функцию y = 2x + 1. Фиксируем точку x₀ = 0. Пусть x_n — некоторая последовательность, сходящаяся к x₀ при n,
стремящемся к ∞. Рассмотрим, например, последовательность

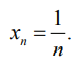
Она сходится к 0

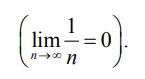
Подставив в функцию вместо x x_n, получим новую последовательность

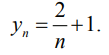
Нас интересует, как ведет себя эта последовательность. Последовательность y_n сходится к 1 при N, стремящемся к ∞(lim_n→∞ y_n= 1).

Рассмотрим, как геометрически изображается связь между
последовательностями x_n и y_n (рис. 30).

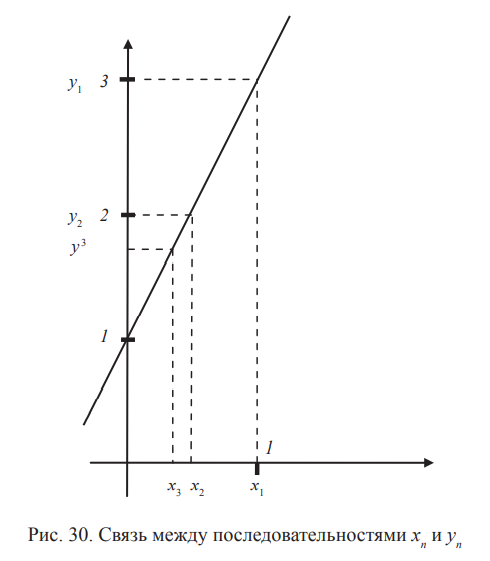
Нас интересует, как ведет себя последовательность y_n, если последовательность x_n сходится к x₀.

Определение предела функции

Определение. Число a называется пределом функции y(x) при x, стремящемся к x₀,
если для любой последовательности x_n, удовлетворяющей условиям: x_n принадлежит области определения X функции y(x), x_n ≠ x₀
и lim_n→∞ x_n = x₀,

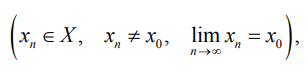
соответствующая последовательность y_n = y(x_n) сходится к a. Это записывают так:

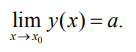
Теоремы о предельном переходе при выполнении арифметических операций над функциями

Пусть на множестве X рассматриваются функции y(x) и z(x).
Пусть x₀ ∈ X и lim_n→∞ y(x) = a, lim_n→∞ z(x) = b. Тогда:

Теорема 1. Предел суммы (разности, произведения) двух функций при x, стремящемся к x₀, равен сумме
(разности, произведению) пределов этих функций, т. е.

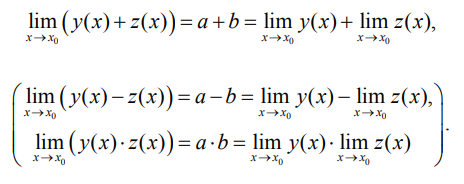
Теорема 2. Пусть b ≠ 0. Тогда

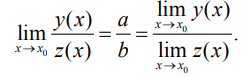
Примеры вычисления пределов функций

1. Найдем

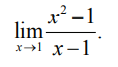
Если мы попытаемся воспользоваться теоремой 2, то увидим, что при x, стремящемся к 1, числитель и знаменатель дроби стремятся
к 0. Такая ситуация называется неопределенностью «ноль на ноль»
(

0
/
0

)
Пока теоремой 2 воспользоваться нельзя. Заметим, что
в числителе стоит разность квадратов. Используя формулу

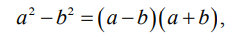
получим

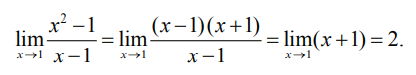
2. Найдем

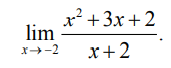
Попытаемся использовать теорему 2. Найдем предел числителя:

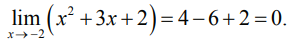
Найдем предел знаменателя:

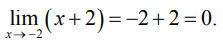
Имеем неопределенность типа «ноль на ноль».
В числителе дроби стоит квадратный трехчлен. Разложим его
на множители. Для этого найдем корни квадратного уравнения

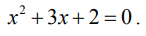
Они равны x₁ = -1, x₂ = -2.
Напомним, что для квадратного уравнения

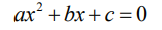
корни x_1,2 находятся по формуле

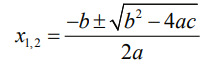
и разложение на множители записывается так:

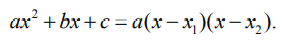
Возвращаясь к нашему примеру, получим

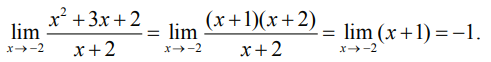
Предел функции при x, стремящемся к бесконечности (x→∞), вычисляется так же, как для последовательности.

Производная функции

Приращение функции

Приращение функции, обозначаемое через Δ_y, показывает, на
сколько значение функции в точке x₀ + Δ_x отличается от значения функции в точке x₀(рис. 31).

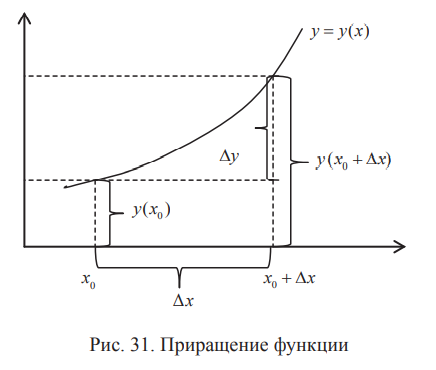
Приращение аргумента — Δ_x, приращение функции — Δy = y(x₀ + Δx) — y(x₀)

Производная

Определение. Производной y′(x₀) функции y(x) в точке x₀
называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:

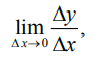
если этот предел существует. Итак,

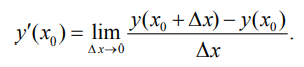
Схема вычисления производной

1. Вычислить y(x₀).
2. Вычислить y(x₀+ Δx).
3. Найти приращение функции Δy = y(x₀ + ∆x) — y(x₀).
4. Найти отношение

Δy
/
∆x

5.  Найти предел отношения при ∆x →0, т. е. производную y′(x₀).

Найдем по определению производную функции y = x².

Физический смысл производной

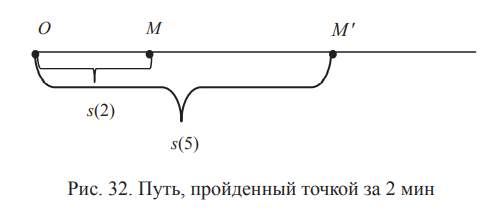
Пусть независимая переменная t — это время. Рассматриваемая функция s(t) — путь,
пройденный точкой M от начальной точки O за время t (если t измеряется, например, в минутах, то s(3) — путь, пройденный точкой M от начальной точки O за
3 мин, s(5) — путь, пройденный точкой M от начальной точки O за 5 мин).
Тогда s(t + Δt) — путь, пройденный точкой M от начальной точки O за время t + Δt.
На рис. 32 путь MM′ пройден за 2 мин и равен s(3) − s(5)

На рис. 33 путь MM′ пройден за Δt мин и равен

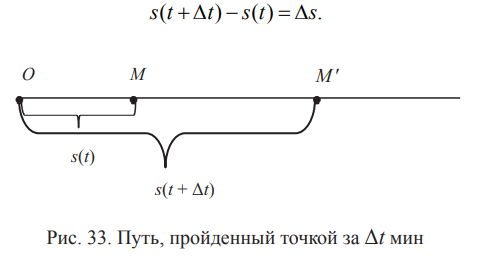
Средняя скорость ν на заданном отрезке пути определяется как отношение пути ко времени, за которое этот путь пройден.
Средняя скорость ν на отрезке MM′ на рис. 32 равна

s(5) — s(3)
/
2

на рис. 33 —

Δs
/
Δt

Если Δt → 0, то M′ → M и lim_Δt→0

Δs
/
Δt

= s‘(t)— это
мгновенная скорость в точке M Итак, производная пути по времени при t = t₀
— это мгновенная скорость движения точки M в моментem t₀.
Таким образом, y′(x₀) — это скорость изменения функции y(x)
в точке x₀.

Таблица производных

Примеры использования формулы 1 из таблицы производных

Свойства производной

В данной публикации мы рассмотрим одно из главных понятий математического анализа – предел функции: его определение, а также различные способы решения с практическими примерами.

Определение предела функции

Предел функции – величина, к которой стремится значение данной функции при стремлении ее аргумента к предельной для области определения точке.

Запись предела:

• предел обозначается значком lim;
• под ним добавляется, к какому значению стремится аргумент (переменная) функции. Обычно, это x, но не обязательно, например: “x→1″;
• затем справа дописывается сама функция, например:
  

Таким образом, финальная запись предела выглядит выглядит так (в нашем случае):

Читается как “предел функции при икс, стремящемся к единице”.

x→1 – это значит, что “икс” последовательно принимает значения, которые бесконечно приближаются к единице, но никогда с ней не совпадут (ее не достигнут).

Решение пределов

С заданным числом

Давайте решим рассмотренный выше предел. Для этого просто подставляем единицу в функцию (т.к. x→1):

Таким образом, чтобы решить предел, сперва пробуем просто подставить заданное число в функцию под ним (если икс стремится к конкретному числу).

С бесконечностью

В данному случае аргумент функции бесконечно возрастает, то есть “икс” стремится к бесконечности (∞). Например:

Если x→∞, то заданная функция стремится к минус бесконечности (-∞), т.к.:

• 3 – 1 = 2
• 3 – 10 = -7
• 3 – 100 = -97
• 3 – 1000 – 997 и т.д.

Другой более сложный пример

Для того, чтобы решить этот предел, также, просто увеличиваем значения x и смотрим на “поведение” функции при этом.

• При x = 1, y = 1² + 3 · 1 – 6 = -2
• При x = 10, y = 10² + 3 · 10 – 6 = 124
• При x = 100, y = 100² + 3 · 100 – 6 = 10294

Таким образом при “икс”, стремящемся к бесконечности, функция x² + 3x – 6 неограниченно растет.

С неопределенностью (икс стремится к бесконечности)

В данном случае речь идет про пределы, когда функция – это дробь, числитель и знаменатель которой представляют собой многочлены. При этом “икс” стремится к бесконечности.

Пример: давайте вычислим предел ниже.

Решение

Выражения и в числителе, и а знаменателе стремятся к бесконечности. Можно предположить, что в таком случае решение будет таким:

Однако не все так просто. Чтобы решить предел нам нужно сделать следующее:

1. Находим x в старшей степени для числителя (в нашем случае – это два).

2. Аналогичным образом определяем x в старшей степени для знаменателя (тоже равняется двум).

3. Теперь делим и числитель, и знаменатель на x в старшей степени. В нашем случае в обоих случаях – во второй, но если бы они были разные, следовало бы взять наибольшую степень.

4. В получившемся результате все дроби стремятся к нулю, следовательно ответ равен 1/2.

С неопределенностью (икс стремится к конкретному числу)

И в числителе, и в знаменателе представлены многочлены, однако, “икс” стремится к конкретному числу, а не к бесконечности.

В данном случае условно закрываем глаза на то, что в знаменателе стоит ноль.

Пример: Найдем предел функции ниже.

Решение

1. Для начала подставим в функцию число 1, к которому стремится “икс”. Получаем неопределенность рассматриваемого нами вида.

2. Далее раскладываем числитель и знаменатель на множители. Для этого можно воспользоваться формулами сокращенного умножения, если они подходят, или решить квадратное уравнение.

В нашем случаем корнями выражения в числителе (2x² – 5x + 3 = 0) являются числа 1 и 1,5. Следовательно его можно представить в виде: 2(x-1)(x-1,5).

Знаменатель (x – 1) изначально является простым.

3. Получаем вот такой видоизмененный предел:

4. Дробь можно сократить на (x – 1):

5. Остается только подставить число 1 в выражение, получившееся под пределом: