Вычисление пределов функций y
= f(x),
значение которых в точке при х = х0
определено f(x)
= А не вызывает затруднений:
Затруднения возникают, когда в точке х
= х0 при вычислении значения
функции получаем неопределенности вида
В этом случае для вычисления пределов
нужно преобразовать исходную функцию,
чтобы неопределенность исчезла, либо
в результате преобразования привести
исходную функцию к первому или второму
замечательному пределу.
Пример 1.
Вычислить
при
Решение. Так
как
определена
в точке
,
то предел функции в точке
равен значению функции в этой точке, т.
е.
;
Пример 2.
Вычислить
при
Решение. В
точке
функция также определена. Тогда получим:
.
Пример 3.
Вычислить
при
.
Решение. При
получили неопределенность
.
Для решения разложим числитель и
знаменатель на множители, сократим
дробь:
;
;
;
.
;
;
;
;
После сокращения дроби опять в предел
подставляем
и вычисляем предел.
Пример 4.
Найти предел:
Решение.
.
Избавимся от
иррациональности в знаменателе, умножив
и разделив дробь на выражение
,
сопряженное знаменателю, и применим
формулу
.
Выделим множитель
и сократим на него дробь.
Примечание.
Аналогично
избавляются от иррациональности в
числителе.
Пример 5.
Вычислить предел:
Решение. При непосредственной
подставке х = –1 получаем неопределенность
.
Для ее исключения проведем преобразование
функции:
При х = –1 знаменатель обращаться в
ноль за счет сомножителя х + 1. разделим
числитель на этот сомножитель:
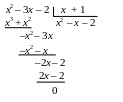
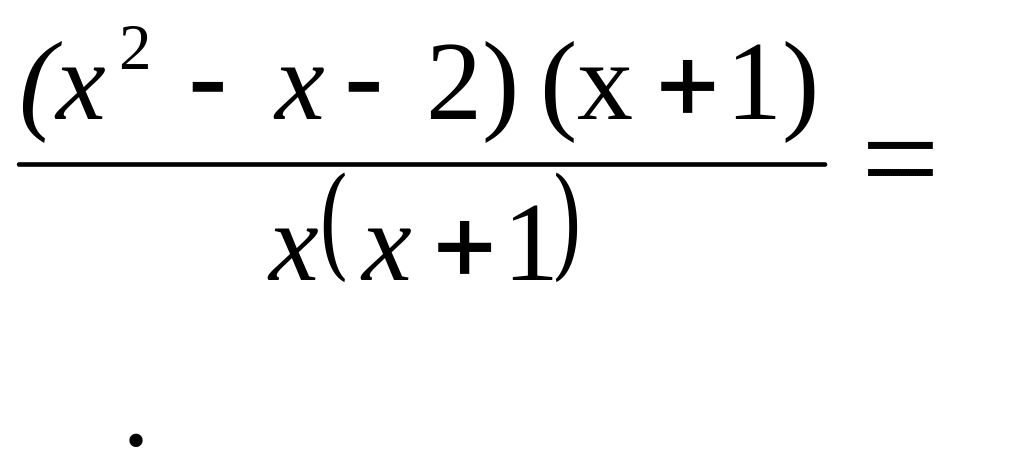
В результате предел преобразуется к
виду:
Пример 6.
Вычислить предел:
Решение. При непосредственной
подставке х = –2 получаем неопределенность
.
Для устранения неопределенности разложим
числитель и знаменатель на сомножители.
Так как и числитель, и знаменатель при
х = 2 обращаются в ноль, то они содержат
общий сомножитель х – 2. найдем
вторые сомножители числителя и
знаменателя:
|
|
|
В результате разложения на сомножители
числителя и знаменателя предел
преобразуется к виду:
При подстановке х = 2 опять получаем
неопределенность
.
Еще раз разделим числитель и знаменатель
на х – 2 и в результате получим:
Пример 7.
Вычислить предел:
Решение. При непосредственной
подстановке х = 0 получаем
неопределенность
.
Для ее устранения умножим числитель и
знаменатель дроби на выражение,
сопряженное числителю, на
В результате мы избавимся от иррациональности
в числителе:
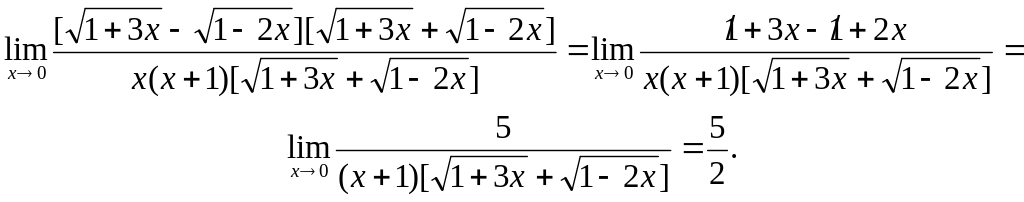
Соседние файлы в папке Предел и непрерывность
- #
- #
- #
- #
- #
- #
- #
- #
Рассмотрим примеры, в которых, чтобы найти пределы функций, надо раскрыть неопределенность вида 0 на 0.
Примеры для самопроверки:
Показать решение
Как решать пределы для чайников?
Для тех, кто хочет научиться находить пределы в данной статье мы расскажем об этом. Не будем углубляться в теорию, обычно её дают на лекциях преподаватели. Так что «скучная теория» должна быть у Вас законспектирована в тетрадках. Если этого нет, то почитать можно учебники взятые в библиотеке учебного заведения или на других интернет-ресурсах.
Итак, понятие предела достаточно важно в изучении курса высшей математики, особенно когда вы столкнетесь с интегральным исчислением и поймёте связь между пределом и интегралом. В текущем материале будут рассмотрены простые примеры, а также способы их решения.
Примеры решений
| Пример 1 |
| Вычислить а) $ lim_{x to 0} frac{1}{x} $; б)$ lim_{x to infty} frac{1}{x} $ |
| Решение |
|
а) $$ lim limits_{x to 0} frac{1}{x} = infty $$ б)$$ lim_{x to infty} frac{1}{x} = 0 $$ Нам часто присылают эти пределы с просьбой помочь решить. Мы решили их выделить отдельным примером и пояснить, что данные пределы необходимо просто запомнить, как правило. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ text{a)} lim limits_{x to 0} frac{1}{x} = infty text{ б)}lim limits_{x to infty} frac{1}{x} = 0 $$ |
| Пример 2 |
| $$ lim limits_{x to 1} frac{x^2 + 2x + 1}{x + 1} $$ |
| Решение |
|
Внимание «чайникам» $$ lim limits_{x to 1} frac{x^2+2 cdot x+1}{x+1}=frac{1^2+2 cdot 1+1}{1+1} = $$ $$ = frac{4}{2}=2 $$ Как видим в итоге у нас вычислился предел, результатом стала двойка. Хорошо, когда так получается, но бывает так, что результатом становятся неопределенности. Попробуем разобраться с ними — это не так страшно как кажется |
| Ответ |
| $$ lim limits_{x to 1} frac{x^2 + 2x + 1}{x + 1} = 2 $$ |
Что делать с неопределенностью вида: $ bigg [frac{0}{0} bigg ] $
| Пример 3 |
| Решить $ lim limits_{x to -1} frac{x^2-1}{x+1} $ |
| Решение |
|
Как всегда начинаем с подстановки значения $ x $ в выражение, стоящее под знаком предела. $$ lim limits_{x to -1} frac{x^2-1}{x+1} = frac{(-1)^2-1}{-1+1}=frac{0}{0} $$ Что теперь дальше? Что же должно получиться в итоге? Так как это неопределенность, то это ещё не ответ и продолжаем вычисление. Так как в числители у нас многочлен, то разложим его на множители, помощью знакомой всем формулы ещё со школьной скамьи $$ a^2-b^2=(a-b)(a+b) $$. Вспомнили? Отлично! Теперь вперед и с песней применять её Получаем, что числитель $ x^2-1=(x-1)(x+1) $ Продолжаем решать учитывая вышеприведенное преобразование: $$ lim limits_{x to -1}frac{x^2-1}{x+1} = lim limits_{x to -1}frac{(x-1)(x+1)}{x+1} = $$ $$ = lim limits_{x to -1}(x-1)=-1-1=-2 $$ |
| Ответ |
| $$ lim limits_{x to -1} frac{x^2-1}{x+1} = -2 $$ |
| Пример 4 |
| $$ lim limits_{x to 2}frac{x^2-4}{x^2-4x+4} $$ |
| Решение |
|
$$ lim limits_{x to 2}frac{x^2-4}{x^2-4x+4} = frac{0}{0} = $$ $$ = lim limits_{x to 2}frac{(x-2)(x+2)}{(x-2)^2} = $$ $$ = lim limits_{x to 2}frac{x+2}{x-2} = frac{2+2}{2-2} = frac{4}{0} = infty $$ Бесконечность получилась в результате — это следует из примера 1. Когда число делится на 0 под знаком предела, то получается бесконечность. |
| Ответ |
| $$ lim limits_{x to 2}frac{x^2-4}{x^2-4x+4} = infty $$ |
Устремим предел в последних двух примерах к бесконечности и рассмотрим неопределенность: $ bigg [frac{infty}{infty} bigg ] $
| Пример 5 |
| Вычислить $ lim limits_{x to infty} frac{x^2-1}{x+1} $ |
| Решение |
|
$ lim limits_{x to infty} frac{x^2-1}{x+1} = frac{infty}{infty} $ Что же делать? Как быть? Не стоит паниковать, потому что невозможное — возможно. Нужно вынести за скобки и в числителе и в знаменателе икс, а потом его сократить. После этого предел попытаться вычислить. Пробуем… $$ lim limits_{x to infty} frac{x^2-1}{x+1} =lim limits_{x to infty} frac{x^2(1-frac{1}{x^2})}{x(1+frac{1}{x})} = $$ $$ = lim limits_{x to infty} frac{x(1-frac{1}{x^2})}{(1+frac{1}{x})} = $$ Используя определение из примера 2 и подставляя в место х бесконечность получаем: $$ = frac{infty(1-frac{1}{infty})}{(1+frac{1}{infty})} = frac{infty cdot 1}{1+0} = frac{infty}{1} = infty $$ |
| Ответ |
| $$ lim limits_{x to infty} frac{x^2-1}{x+1} = infty $$ |
| Пример 6 |
| $$ lim limits_{x to infty}frac{x^2-4}{x^2-4x+4} $$ |
| Решение |
|
$$ lim limits_{x to infty}frac{x^2-4}{x^2-4x+4} = frac{infty}{infty} $$ Чтобы устранить такую неопределенность нужно вынести за скобки икс в числителе и в знаменателе, далее их сократить. В полученное выражение подставить икс равное бесконечности. Пробуем… $$ lim limits_{x to infty}frac{x^2-4}{x^2-4x+4} = frac{infty}{infty} = $$ $$ lim limits_{x to infty}frac{x^2(1-frac{4}{x^2})}{x^2(1-frac{4}{x}+frac{4}{x^2})} = $$ $$ lim limits_{x to infty}frac{1-frac{4}{x^2}}{1-frac{4}{x}+frac{4}{x^2}} = frac{1}{1} = 1 $$ |
| Ответ |
| $$ lim limits_{x to infty}frac{x^2-4}{x^2-4x+4} = 1 $$ |
Алгоритм вычисления лимитов
Итак, давайте кратко подведем итог разобранным примерам и составим алгоритм решения пределов:
- Подставить точку х в выражение, следующее после знака предела. Если получается определенное число, либо бесконечность, то предел решен полностью. В противном случае имеем неопределенность: «ноль делить на ноль» или «бесконечность делить на бесконечность» и переходим к следующим пунктам инструкции.
- Чтобы устранить неопределенность «ноль делить на ноль» нужно разложить числитель и знаменатель на множители. Сократить подобные. Подставить точку х в выражение, стоящее под знаком предела.
- Если неопределенность «бесконечность делить на бесконечность», тогда выносим и в числителе, и в знаменателе x наибольшей степени. Сокращаем иксы. Подставляем значения икса из под предела в оставшееся выражение.
В этой статье Вы ознакомились с основами решения пределов, часто используемых в курсе Математического анализа. Конечно же это не все типы задач, предлагающихся экзаменаторами, а только простейшие пределы. В следующих статьях поговорим о других типах заданий, но сперва необходимо усвоить этот урок, чтобы двигаться далее. Обсудим, что делать, если есть корни, степени, изучим бесконечно малые эквивалентные функции, замечательные пределы, правило Лопиталя.
Если у Вас не получается самостоятельно решить пределы, то не паникуйте. Мы всегда рады помочь!

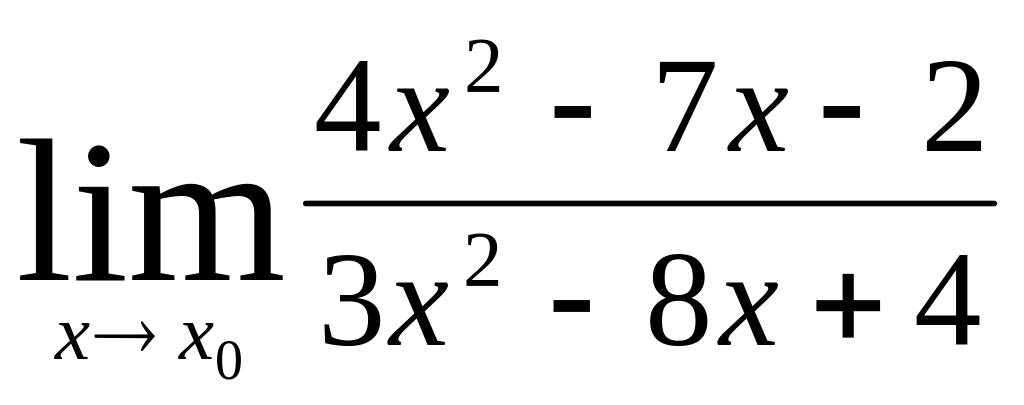
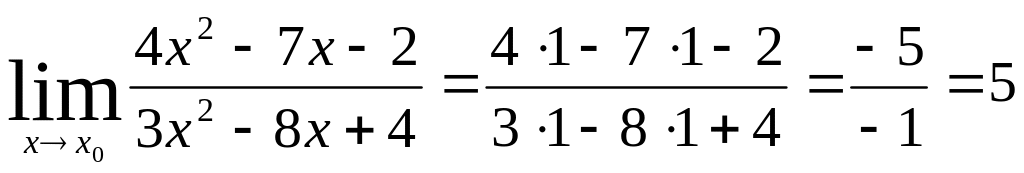
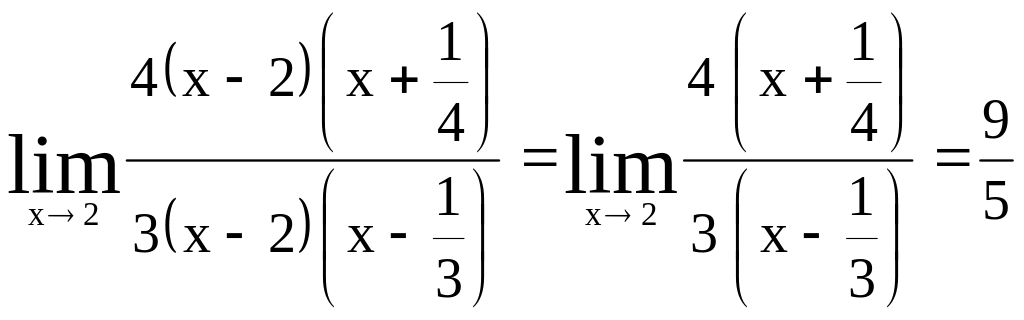
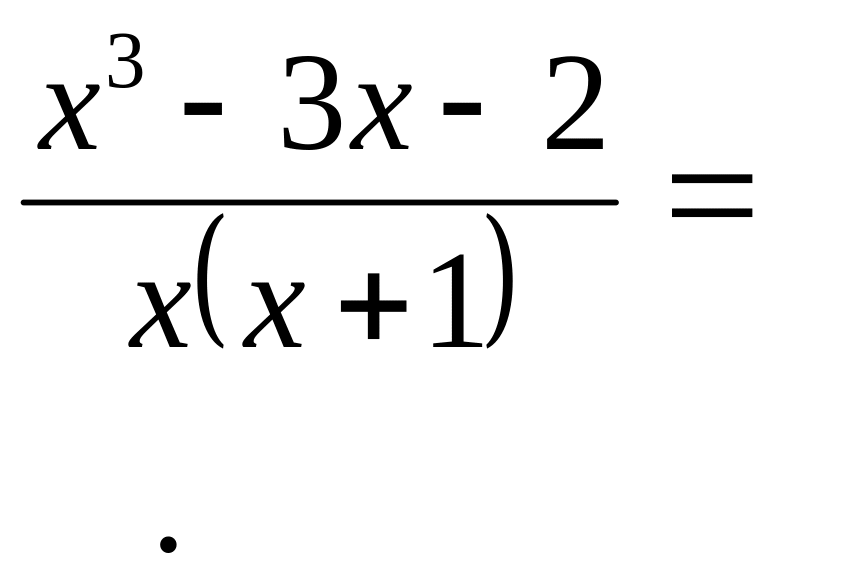
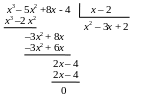
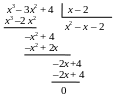
 Чтобы вычислить предел любого типа и вида нужно подставить значение x, указанное под пределом, в функцию, стоящую под знаком предела. Давайте попробуем это сделать:
Чтобы вычислить предел любого типа и вида нужно подставить значение x, указанное под пределом, в функцию, стоящую под знаком предела. Давайте попробуем это сделать: