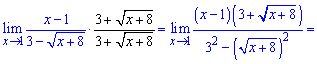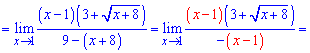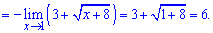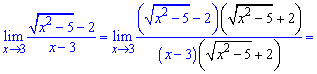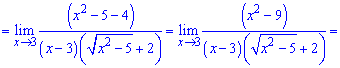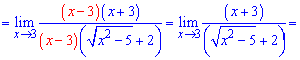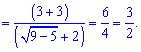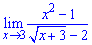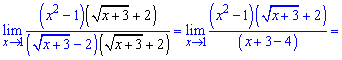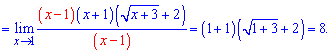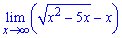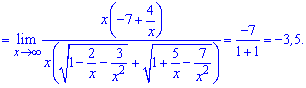Пределы с корнями: примеры решений
Среди задач на решение пределов попадаются пределы с корнями. В результате подстановки значения $ x $ в функцию получаются неопределенности трёх видов:
- $ bigg [frac{0}{0} bigg ] $
- $ bigg [frac{infty}{infty} bigg ] $
- $ bigg [infty-infty bigg ] $
Перед тем, как приступить к решению определите тип своей задачи
Тип 1 $ bigg [frac{0}{0} bigg ] $
Для того, чтобы раскрывать такие неопределенности необходимо домножить числитель и знаменатель дроби на сопряженное к выражению содержащему корень.
| Пример 1 |
| Найти предел с корнем $$ lim limits_{x to 4} frac{x-4}{4-sqrt{x+12}} $$ |
| Решение |
|
Подставляем $ x to 4 $ в подпределельную функцию: $$ lim limits_{x to 4} frac{x-4}{4-sqrt{x+12}} = frac{0}{0} = $$ Получаем неопределенность $ [frac{0}{0}] $. Домножим числитель и знаменатель на выражение сопряженное к нему, так как он содержит корень: $ 4+sqrt{x+12} $ $$ = lim limits_{x to 4} frac{(x-4)(4+sqrt{x+12})}{(4-sqrt{x+12})(4+sqrt{x+12})} = $$ Используя формулу разности квадратов $ (a-b)(a+b) = a^2-b^2 $ приведем предел к следующему виду: $$ = lim limits_{x to 4} frac{(x-4)(4+sqrt{x+12})}{16-(x+12)} = $$ Раскрываем скобки в знаменателе и упрощаем его: $$ = lim limits_{x to 4} frac{(x-4)(4+sqrt{x+12})}{4-x} = $$ Сокращам функцию в пределе на $ x-4 $, имеем: $$ = -lim limits_{x to 4} (4+sqrt{x+12}) = -(4+sqrt{4+12}) = -8 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ lim limits_{x to 4} frac{x-4}{4-sqrt{x+12}} = -8 $$ |
Тип 2 $ bigg [frac{infty}{infty} bigg ] $
Пределы с корнем такого типа, когда $ x to infty $ вычислять нужно по-другому в отличии от предыдущего случая. Необходимо определить старшие степени выражений числителя и знаменателя. Затем вынести самую старшую из двух степеней за скобки и сократить.
| Пример 2 |
| Решить предел с корнем $$ lim limits_{x to infty} frac{x^2+5x+2}{sqrt{x+6}} $$ |
| Решение |
|
Вставляем $ x to infty $ в предел и получаем $ [frac{infty}{infty}] $. Определяем, что в числителе старшая степень это $ x^2 $, а в знаменателе $ sqrt{x} $. Выносим их за скобки: $$ lim limits_{x to infty} frac{x^2(1+frac{5x}{x^2}+frac{2}{x^2})}{x^2(sqrt{frac{x}{x^4}+frac{6}{x^4})}} = $$ Теперь выполняем сокращение: $$ = lim limits_{x to infty} frac{1+frac{5x}{x^2}+frac{2}{x^2}}{sqrt{frac{1}{x^3}+frac{6}{x^4}}} = $$ Снова подставляем $ x to infty $ в предел, имеем: $$ = frac{1 + 0 + 0}{ sqrt{0 + 0}} = lbrack frac{1}{0} rbrack = infty $$ |
| Ответ |
| $$ lim limits_{x to infty} frac{x^2+5x+2}{sqrt{x+6}} = infty $$ |
Тип 3 $ bigg [infty-infty bigg ] $
Этот вид пределов часто попадается в дополнительных заданиях на экзамене. Ведь часто студенты не правильно вычисляют пределы такого типа. Как решать пределы с корнями данного вида? Всё просто. Необходимо умножить и разделить функцию, стоящую в пределе, на выражение сопряженное к ней.
| Пример 3 |
| Вычислить предел корня $$ lim limits_{x to infty} sqrt{x^2-3x}-x $$ |
| Решение |
|
При $ x to infty $ в пределе видим: $$ lim limits_{x to infty} sqrt{x^2-3x}-x = [infty — infty] = $$ После домножения и разделения на сопряженное имеем предел: $$ lim limits_{x to infty} frac{(sqrt{x^2-3x}-x)(sqrt{x^2-3x}+x)}{sqrt{x^2-3x}+x} = $$ Упростим числитель, используя формулу разности квадратов: $ (a-b)(a+b)=a^2-b^2 $ $$ = lim limits_{x to infty} frac{(x^2-3x)-x^2}{sqrt{x^2-3x}+x} = $$ После раскрытия скобок и упрощения получаем: $$ lim limits_{x to infty} frac{-3x}{sqrt{x^2-3x}+x} = $$ Далее выносим $ x $ за скобки и сокращаем: $$ = lim limits_{x to infty} frac{-3x}{x(sqrt{1-frac{3}{x}}+1)} = lim limits_{x to infty} frac{-3}{sqrt{1-frac{3}{x}}+1} = $$ Снова подставляем $ x to infty $ в предел и вычисляем его: $$ = frac{-3}{sqrt{1-0}+1} = -frac{3}{2} $$ |
| Ответ |
| $$ lim limits_{x to infty} sqrt{x^2-3x}-x = -frac{3}{2} $$ |
Простое объяснение принципов решения пределов с корнями и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.
Основные свойства пределов с корнями
Для нахождения предела функции необходимо подставить в предел вместо Х то значение переменной, к которому стремится Х.
Нужна помощь в написании работы?

Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.
Подробнее
Примеры решений пределов с корнями
Задание
Найти предел
Решение
Мы имеем неопределенность вида
Первый шаг – разделить числитель и знаменатель на ”х” в высшей степени. Старшая степень для числителя в данном случае равна двум.
Со знаменателем немного сложнее. Так как у нас корень, обращаем внимание только на самое ”старшее” слагаемое –
Число (4) – это константа, его тоже отбрасываем. Находим корень
Так как числитель и знаменатель оказываются одного порядка роста, предел равен конечному числу, отличному от нуля.
Видим, что функции эквивалентны на бесконечности.
Оформляем решение:
Ответ: 1
Задание
Найти предел с корнем
Решение
Подставляем
в подпредельную функцию:
Получаем неопределенность
Домножаем числитель и знаменатель на выражение, сопряженное к нему –
так как он содержит корень.
Далее, пользуясь формулой разности квадратов
и раскрывая скобки, упрощаем предел. Последний шаг – сокращение функции на
Ответ: -8
Задание
Решить предел с корнем
Решение
Подставляем
в предел и получаем неопределённость вида
Как и в предыдущих примерах, находим старшую степень для числителя и знаменателя, и выносим её за скобки.
И опять подставляем
в предел и решаем:
Ответ:
Задание
Вычислить предел корня:
Решение
Аналогично предыдущим примерам, подставляем
в предел и видим:
Находим сопряженное, в данном случае это
Как и в примере №2, пользуясь формулой разности квадратов
и раскрывая скобки, упрощаем предел:
Раскрываем скобки и упрощаем. Затем выносим х за скобки и сокращаем:
Как и в начале, подставляем в предел, получаем:
Ответ:
Задание
Вычислить предел функции
Решение
Если подставить х=1, видно, что и числитель, и знаменатель обращаются в ноль. Получаем неопределенность вида
Как и в предыдущих примерах, первым шагом находим сопряжённое –
и домножаем на него числитель и знаменатель.
Применяем правило разности квадратов
и преобразовываем предел:
Сокращаем числитель и знаменатель на (x-1) и приходим к конечному ответу:
Ответ: 6
Задание
Вычислить предел:
Решение:
Первый шаг – подставить в предел выражение
и убедиться, что выходит неопределённость вида
Шаг второй – раскрываем нашу неопределенность путём умножения числителя и знаменателя на сопряжённое выражение, в данном случае –
Далее, пользуясь формулой разности квадратов раскладываем числитель:
Подставляем х=3 в предел и вычисляем:
Ответ:
Задание
Вычислить предел
Решение
Как и в предыдущих заданиях, подставляем
и убеждаемся, что имеем дело с неопределённостью вида
Порядок действий стандартный. Избавляемся от иррациональности в знаменателе с помощью домножения числителя и знаменателя на сопряженное выражение. В данном примере сопряжённое выражение имеет вид –
Перемножаем знаменатель и сокращаем в числителе и знаменателе
Подставляем, как и ранее, х=3 и находим ответ:
Ответ: 17,8
Задание
Определить предел функции
Решение
Смотрим на функцию, подставляем
мы имеем дело с неопределённостью вида:
Начинаем работать с функциями, содержащими корень. Умножаем числитель и знаменатель на сопряжённое выражение и упрощаем предел:
После преобразований получаем ответ:
Ответ: -2
Задание
Решить предел
Решение:
Подставляя
в выражение лимита, подтверждаем догадки, что перед нами неопределённость вида
Как и раньше, первый шаг – избавиться от иррациональности с помощью домножения числителя и знаменателя на соответствующее сопряженное выражение.
Раскрываем скобки и сокращаем выражения на
Неопределённости
больше нет и ничего нам не мешает вычислить пример:
Ответ:
Задание
Вычислить предел
Решение
Оба лимита числителя и знаменателя равны нулю, значит опять неопределённость вида
Находим сопряжённое к числителю и знаменателю число:
Домножаем на полученное выражение числитель и знаменатель, раскрываем скобки и упрощаем:
Раскладываем числитель и знаменатель:
Вычисляем предел:
Ответ:
Содержание:
- Примеры с решением
- Раскрытие неопределенностей вида
При вычислении предела 



(это объясняется непрерывностью элементарной функции на своей области определения)
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Примеры с решением
Пример 1:
Вычислить:
a)
б)
в) 
Решение:
а)
б) 
в) 
Правило сохраняет силу, если 


неограниченно возрастает, функция
стремится к нулю (это ясно из графика функции).
Возможно вам будут полезны данные страницы:
Пример 2:
Найти:
а)
б)
в) 
Решение:
а)
б)
в) 
Пример 3:
Найти
Решение:
При подстановке в значение функции 

Что считать ответом в этом случае?
При вычислении подобных пределов пользуются одним из следующих правил (в приводимых ниже формулах с означает число):
Приведенные формулы следуют из соображений здравого смысла. Например, первая из приведенных формул по существу утверждает, что если одна из функций становится очень большой и положительной, а другая ограничена, то сумма их становится очень большой и положительной.
Те же соображения приводят и к формальному доказательству: надо только вместо «очень больших» значений говорить о «больших любого заданного числа».
Применим эти правила для вычисления пределов, которые были оставлены без вычисления:
Соображениями здравого смысла руководствуются и при вычислении пределов от функций при 

Пример 4:
Вычислить:
а)
б)
в) 
Решение:
а) При 




Этот же ответ получается при применении последнего из приведенных выше правил
б)
в)
Приведенные рассуждения не являются строгими. Однако они вполне достаточны для приложений и интуитивно понятны . Как уже было отмечено ранее, выражение 

Выражение 
Пример 5:
Найти:
а) 
б)
в) 
Решение:
а)
б) 
в)
Имеются случаи, не охватываемые правилами из предыдущего параграфа. Не существует «общей формулы» для выражения 










Как для случая неопределенности вида 


Пример 6:
Найти
Решение:
Непосредственной подстановкой вместо аргумента его предельного значения вычислить предел нельзя, поскольку получается неопределенность вида
Разложим числитель и знаменатель на множители, чтобы сократить дробь на общий множитель, стремящийся к нулю. Нужно иметь в виду, что здесь не производится сокращение на нуль, что недопустимо. По определению предела функции аргумент 


Пример 7:
Найти
Решение:
Пределы числителя и знаменателя при 
Разложим квадратный трехчлен в числителе на линейные множители по формуле 



Пример 8:
Найти 
Решение:

Пример 9:
Найти 
Решение:
Пределы числителя и знаменателя при 



Пример 10:
Найти
Решение:
Когда 


Перейдя к пределу, получим
В предыдущих примерах неопределенность вида 

называемому 300 лет назад первым замечательным пределом. Доказательство равенства 
Заметим, что выражение 



Пример 11:
Найти 
Решение:
Пример 12:
Найти 
Решение:
Пример 13:
Найти
Решение:
При 




Пример 14:
Найти
Решение:
При непосредственной подстановке символа 




(при 

Пример 14:
Наити
Решение:
Вообще, предел отношения полиномов при 
Пример 15:
Найти 
Решение:
Пример 16:
Найти 
Решение:
В подобных примерах полезно иметь в виду, что функция 






Неопределенности вида 



Покажем на примерах, как находятся такие пределы.
Пример 17:
Найти 
Решение:
Произведем вычитание дробей, получим
Пример 18:
Найти
Решение:




Пример 19:
Найти
Решение:

(сделали замену 
Пример 20:
Найти 
Ответ: 
Раскрытие неопределенностей вида
Рассмотрим последовательность 
Может показаться, что неограниченное возрастание показателя степени 







Обозначением числа 

Функция 







или короче
Этот предел часто используется в математике для раскрытия неопределенности 
Пример 21:
Найти пределы:
а)
б)
Решение:
а) 

б) 
Пример 22:
Найти пределы
а)
б)
Решение:
а) При 



тогда 
б)
Число 





Неопределенности вида 



Лекции:
- Уравнение касательной. Угловой коэффициент
- Вычислить криволинейный интеграл
- Перпендикулярность плоскостей
- Решение задач на нахождение пределов
- Предел функции двух переменных в точке
- Решение дифференциальных уравнений
- Дифференциальные уравнения первого порядка. Понятие о методе Рунге—Кутта
- Усеченный конус. Поверхность усеченного конус
- Функция Лагранжа
- Признак Даламбера. Признак Коши. Критерий Коши сходимости ряда
Можно ли извлечь квадратный корень из предела.
Содержание
- Какой самый простой способ найти предел
- Как упростить пределы на бесконечности
- Как решить предел шаг за шагом
- Что означает утверждение, что lim N → ∞ an ∞
- Что такое правило корня для пределов
- Каковы 3 правила пределов
- Какой самый простой способ найти предел
- Как решать пределы до бесконечности с помощью радикалов
- Можете ли вы взять квадратный корень из предела
- Как найти предел уравнения с квадратным корнем
Рекомендую! Узнайте больше на странице: Как мы можем помочь бедным семьям в 2023.
Какой самый простой способ найти предел
Как найти предел квадрата.
Рекомендую! Узнайте в посту: Что вы получаете, когда набираете 99 очков в 2K22 в 2023?.
Как упростить пределы на бесконечности
Как решать пределы на бесконечности с помощью радикалов.
Рекомендую! Узнайте в посту: Будет ли Duolingo добавлять маратхи в 2023?.
Как решить предел шаг за шагом
Как найти предел уравнения с квадратным корнем.
Рекомендую! Узнайте здесь: Как приготовить чай из свежего гриба индюшиного хвоста в 2023.
Что означает утверждение, что lim N → ∞ an ∞
Как решать пределы на бесконечности с радикалами «Это читается как «предел f от x по мере приближения x к c равен L». Limn→0an=8 lim n → 0 a n = 8 означает, что члены an приближаются к 8 по мере того, как n становится большим. Вариант (iii) является ответом. Пример: limx→0=1x=∞ lim x → 0 = 1 x = ∞ означает, что член 1/x приближается к ∞ большому значению по мере того, как n становится все меньше и меньше. «.
Рекомендую! Прочитайте на странице: Какие игры входят в топ-5 в 2023.
Что такое правило корня для пределов
Можно ли извлечь квадратный корень из предела Закон корней для пределов гласит, что предел n-го корня функции равен n-му корню из предела функции. .
Каковы 3 правила пределов
Как найти предел квадрата Предел произведения равен произведению пределов. Предел квантора равен квантору пределов. Предел постоянной функции равен константе. .
Какой самый простой способ найти предел
Как найти предел квадрата.
Как решать пределы до бесконечности с помощью радикалов
Как решать пределы с помощью квадратных корней.
Можете ли вы взять квадратный корень из предела
Как решать пределы с квадратными корнями.
Как найти предел уравнения с квадратным корнем
Как решать пределы с квадратными корнями.
Все права защищены. Несанкционированное копирование, полностью или частично, строго запрещено.
Среди примеров пределов функции часто встречаются функции с корнями, которые не всегда понятно как раскрывать. Проще когда есть пример границе с корневой функцией вида
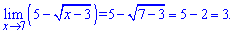
Решение подобных пределов просто и понятно каждому.
Трудности возникают если есть следующие примеры функций с корнями.
Пример 1. Вычислить предел функции
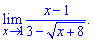
При прямой подстановке точки x = 1 видно что и числитель и знаменатель функции
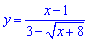
превращаются в ноль, то есть имеем неопределенность вида 0/0.
Для раскрытия неопределенности следует умножить выражение, содержащее корень на сопряженное к нему и применить правило разности квадратов. Для заданного примера преобразования будут следующими
Предел функции с корнями равен 6. Без приведенного правила ее трудно было бы найти.
Рассмотрим подобные примеры вычисления границы с данным правилом
Пример 2. Найти предел функции
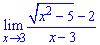
Убеждаемся что при подстановке x = 3 получаем неопределенность вида 0/0.
Ее раскрываем умножением числителя и знаменателя на сопряженное к числителю.
Далее числитель раскладываем согласно правилу разности квадратов
Вот так просто нашли предел функции с корнями.
Пример 3. Определить предел функции
Видим, что имеем неопределенность вида 0/0.
Избавляемся ирациональносьти в знаменателе
Предел функции равна 8.
Теперь рассмотрим другой тип примеров, когда переменная в переделе стремится к бесконечности.
Пример 4. Вычислить предел функции
Много из Вас не знают как найти предел функции. Ниже будет раскрыта методика вычислений.
Имемем предел типа бесконечность минус бесконечность. Умножаем и делим на сопряженный множитель и используем правило разности квадратов
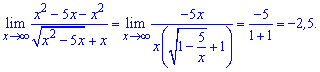
Границ функции равна -2,5.
Вычисление подобных пределов фактически сводится к раскрытию иррациональности , а затем подстановке переменной
Пример 5. Найти предел функции
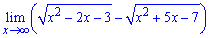
Предел эквивалентен — бесконечность минус бесконечность
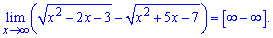
Умножим и разделим на сопряженное выражение и выполним упрощение
Пример 6. Чему равен предел функции?
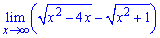
Имеем неопределенность вида бесконечность минус бесконечность
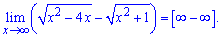
Выполняем преобразования с корневыми функциями
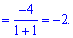
предел функции равен -2.
Хорошо ознакомьтесь с методикой раскрытия неопределенностей, алгоритм достаточно прост и поможем найти сложную границу функции.







 стремится к нулю (это ясно из графика функции).
стремится к нулю (это ясно из графика функции).