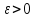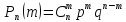Этот раздел, разумеется, не претендует на то, чтобы заменить собой учебник по теории вероятностей и математической статистике, и мы не будем вспоминать здесь все используемые в эконометрике факты из этих наук. Однако последующие разделы учебника будут восприниматься легче, если перед непосредственным знакомством с ними освежить в памяти некоторые ключевые результаты, касающиеся асимптотической теории.
Сходимость по вероятности. Рассмотрим последовательность случайных величин (X_1,X_2,{dots},X_n,{dots})
Если для любого (varepsilon >0) вероятность события (left|X_n-aright|>varepsilon ) стремится к нулю при (nrightarrow infty ), то говорят, что число (a) — это предел по вероятности для последовательности (X_1,X_2,{dots},X_n,{dots})
Для предела по вероятности обычно используют обозначение (mathbf{X}_{mathbf{n}}overset{mathbf{text{p}}}{rightarrow}mathbf{a}) или (mathbf{text{plim}}mathbf{ }mathbf{X}_{mathbf{n}}mathbf{=}mathbf{a}.) Также в этом случае говорят, что последовательность сходится по вероятности к числу (mathbf{a}).
Состоятельность. Оценка параметра называется состоятельной, если её предел по вероятности равен истинному значению оцениваемого параметра: (widehat {beta }text{ }underset{rightarrow }{text{ }text{ }text{ }text{ }ptext{ }text{ }text{ }text{ }}text{ }beta ).
Говоря проще, если оценка параметра состоятельна, то всё, что вам нужно, чтобы узнать его истинное значение, — собрать достаточно большую выборку. Поэтому эконометристы очень любят состоятельные оценки в сочетании с большими массивами данных.
Достаточное условие состоятельности. Если оценка параметра является несмещенной (или асимптотически несмещенной), и ее дисперсия стремится к нулю при (nrightarrow infty ), то эта оценка состоятельна.
Пример 6.1. Регрессия на константу
Рассмотрим модель регрессии на константу:
begin{equation*} y_i=theta +varepsilon _i,i=1,2{dots}mathit{n.} end{equation*}
Пусть для неё выполнены все предпосылки классической линейной модели множественной регрессии. Докажите, что МНК-оценка параметра (theta ) является состоятельной.
Решение:
МНК-оценка параметра (theta ) может быть вычислена по формуле: (widehat {theta }=overline y) (см. задание 9 из главы 2).
Она является несмещенной:
begin{equation*} Eleft(widehat {theta }right)=Eleft(frac{sum _{i=1}^ny_i} nright)=Eleft(frac{sum _{i=1}^nleft(theta +varepsilon _iright)} nright)=frac{mathit{ntheta }+sum _{i=1}^nEleft(varepsilon _iright)} n=mathit{theta .} end{equation*}
Её дисперсия равна:
begin{equation*} mathit{var}left(widehat {theta }right)=mathit{var}left(frac{sum _{i=1}^n(theta +varepsilon _itext{ })} nright)= end{equation*}
begin{equation*} =mathit{var}left(theta +frac{sum _{i=1}^nvarepsilon _i} nright)=text{ }frac{mathit{var}left(sum _{i=1}^nvarepsilon _iright)}{n^2}=frac{nast sigma ^2}{n^2}=frac{sigma ^2} n. end{equation*}
Таким образом, МНК-оценка коэффициента является несмещенной, а при (nrightarrow infty ) ее дисперсия стремится к нулю. Поэтому выполнено достаточное условие состоятельности.
Закон больших чисел в форме Чебышёва. Если (Y_1,Y_2,{dots},Y_n{dots}) — независимые и одинаково распределенные случайные величины, причем (E(Y_i)=mu ,) (mathit{var}left(Y_iright)< infty ,) то (overline Yunderset{rightarrow }{text{ }text{ }text{ }text{ }ptext{ }text{ }text{ }text{ }}mu ).
Иными словами, для последовательности независимых и одинаково распределенных величин с конечной дисперсией среднее значение будет состоятельной оценкой математического ожидания.
Неравенство Коши — Буняковского. Это неравенство является достаточно общим результатом, однако нам в рамках этой главы будет достаточно его частного случая для математических ожиданий:
Пусть (xi ) и (eta ) — случайные величины, для которых определены конечные вторые моменты распределения. Тогда
(E|xi*eta| leq sqrt{Eleft( xi^{2} right)*Eleft( eta^{2} right)})
Замечание. Не удивляйтесь тому, что в англоязычной эконометрической литературе вы такого названия неравенства не встретите. Там этот результат принято называть неравенством Коши — Шварца (the Cauchy-Schwarz inequality).
Сходимость по распределению. Последовательность случайных величин (X_1,X_2,{dots},X_n,{dots}) сходится по распределению к случайной величине (xi ), если
begin{equation*} lim _{nrightarrow infty }Pleft{X_n<xright}=Pleft{xi <xright} end{equation*}
для всех точек, где функция (Fleft(xright)=Pleft{xi <xright}) непрерывна.
Обозначение сходимости по распределению: (X_nunderset{rightarrow }{text{ }text{ }text{ }text{ }dtext{ }text{ }text{ }text{ }}xi ).
Обратите внимание на важное отличие сходимости по вероятности от сходимости по распределению. В первом случае речь идёт о том, что последовательность сходится к некоторой (неслучайной) константе, а во втором — к случайной величине.
Сходимость по распределению главным образом понадобится нам для использования центральной предельной теоремы.
Центральная предельная теорема (ЦПТ). Если (Y_1,{dots},Y_n,{dots}) — независимые и одинаково распределенные случайные величины, причём (E(Y?_i)=mu ,text{ }text{ }text{ }text{ }text{ }text{ }mathit{var}left(Y_iright)=sigma ^2< infty ,) то
begin{equation*} frac{sqrt nleft(overline Y-mu right)}{sigma }underset{rightarrow }{text{ }text{ }text{ }text{ }dtext{ }text{ }text{ }text{ }}Nleft(0,1right)(6.1). end{equation*}
Выражение (6.1) иногда записывают в одном из эквивалентных вариантов.
Во-первых, напомним (см. пример 6.1), что (text{var}left( overline{Y} right) = frac{sigma^{2}}{n}). Тогда, обозначив (text{var}left( overline{Y} right) = sigma_{overline{Y}}^{2}), можно переписать (6.1) вот так:
(frac{ left( overline{Y} — mu right)}{sigma_{overline{Y}}}overset{text{d}}{rightarrow}N(0,1).)
В этом случае говорят, что распределение (overline Y) является асимптотически нормальным с математическим ожиданием (mu ) и дисперсией (frac{sigma ^2} n).
Во-вторых, если случайную величину (frac{sqrt nleft(overline Y-mu right)}{sigma }) домножить на коэффициент (sigma ), то её дисперсия увеличится в (sigma ^2) раз (по свойству дисперсии). Следовательно, выражение (6.1) эквивалентно следующему утверждению:
begin{equation*} sqrt nleft(overline Y-mu right)underset{rightarrow }{text{ }text{ }text{ }text{ }dtext{ }text{ }text{ }text{ }}Nleft(0,sigma ^2right). end{equation*}
Центральная предельная теорема даёт уверенность в том, что при указанных предпосылках и достаточно большой выборке среднее значение будет иметь приблизительно нормальное распределение. Причем для этого не требуется, чтобы отдельные случайные величины (Y_1,{dots},Y_n{dots}) сами имели нормальное распределение. Они могут быть распределены как угодно, лишь бы имели конечную дисперсию.
Для эконометристов этот результат важен, так как во многих ситуациях гарантирует асимптотическую нормальность оценок коэффициентов, что позволяет легко тестировать гипотезы и вообще упрощает работу, так как свойства нормального распределения изучены очень хорошо.
Теорема Слуцкого (теорема Манна — Вальда).
Если
- (X_nunderset{rightarrow }{text{ }text{ }text{ }text{ }ptext{ }text{ }text{ }text{ }}a) (то есть последовательность случайных величин (X_1,X_2,{dots},X_n,{dots}) сходится по вероятности к константе (a)),
- функция (g(x)) непрерывна в точке (a) и некоторой её окрестности,
то (g(X?_n)text{ }underset{rightarrow }{text{ }text{ }text{ }text{ }ptext{ }text{ }text{ }text{ }}g(a)).
Пример 6.2. Регрессия на константу (продолжение)
Вернемся к нашему примеру 6.1. Вычислите предел по вероятности для (widehat {theta }^2.)
Решение:
Так как (gleft(xright)=x^2) — это непрерывная функция, и (widehat {theta }=overline yunderset{rightarrow }{text{ }ptext{ }text{ }}theta ), то по только что сформулированной теореме получаем, что (widehat {theta }^2underset{rightarrow }{text{ }text{ }text{ }text{ }ptext{ }text{ }text{ }text{ }}theta ^2.)
Замечание 1. Эта теорема верна и в случае, когда (X_n) — это случайный вектор, и (a) — это вектор констант.
Замечание 2. Эта теорема называется теоремой Слуцкого только в русскоязычной традиции. Если обратиться к англоязычным учебникам по статистике и эконометрике, то там она называется теоремой Манна — Вальда (Mann–Wald theorem) или даже теоремой о непрерывном отображении (continuous mapping theorem). А теоремой Слуцкого там называется вот такой результат:
Теорема Слуцкого. Если
- (X_nunderset{rightarrow }{text{ }text{ }text{ }text{ }ptext{ }text{ }text{ }text{ }}a) (то есть последовательность случайных величин (X_1,X_2,{dots},X_n,{dots}) сходится по вероятности к константе (a)),
- (Y_nunderset{rightarrow }{text{ }text{ }text{ }text{ }dtext{ }text{ }text{ }text{ }}xi ) (то есть последовательность случайных величин (Y_1,Y_2,{dots},Y_n,{dots}) сходится по распределению к случайной величине (xi )),
то
begin{equation*} X_n+Y_nunderset{rightarrow }{dtext{ }}a+xi , end{equation*}
begin{equation*} X_nast Y_nunderset{rightarrow }{d}aast xi , end{equation*}
begin{equation*} frac{Y_n}{X_n}underset{rightarrow }{d}frac{xi } a, end{equation*}
Для последнего соотношения также требуется, чтобы случайная величина (X_n) не равнялась нулю с единичной вероятностью.
Обратите внимание: чтобы указанные соотношения выполнялись, каждый из пределов в отдельности должен существовать.
Обе сформулированные теоремы пригодятся нам в дальнейшем. Для определенности в контексте доказательств в данной главе договоримся, что, когда мы ссылаемся на теорему Слуцкого, мы подразумеваем последний из двух вариантов.
Аннотация: Сходимость «почти наверное». Сходимость по вероятности.
Свойства этих сходимостей. Неравенство Маркова. Неравенство Чебышёва.
Обобщенное неравенство Чебышёва. Законы больших чисел
Сходимости «почти наверное» и «по
вероятности»
Напомним, что случайная величина есть (измеримая)
функция из некоторого непустого множества 
Последовательность случайных величин 
тем самым последовательность
функций, определенных на одном и том же множестве 
Существуют разные виды сходимости последовательности
функций. Давать определение любой сходимости мы будем,
опираясь на сходимость числовых
последовательностей, как на уже известное основное понятие.
В частности, при каждом новом
мы имеем новую числовую последовательность
Поэтому можно говорить
о сходимости последовательности значений функций в данной точке 
В теории вероятностей можно не обращать внимание на неприятности, происходящие
с нулевой вероятностью. Поэтому вместо сходимости
«всюду» принято рассматривать сходимость «почти
всюду», или «почти наверное».
Определение 42.
Говорят, что последовательность 
почти наверное к случайной величине 
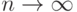
и пишут: 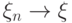
если 
Иначе говоря, если 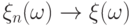
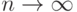
всех 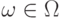
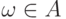

вероятность.
Заметим сразу: определение сходимости «почти наверное»
требует знания того, как устроены
отображения 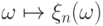
вероятностей, как правило, известны не сами случайные величины, а
лишь их распределения.
Можем ли мы, обладая только информацией о распределениях,
говорить о какой-либо сходимости последовательности случайных
величин 

Можно, скажем, потребовать, чтобы вероятность тех
элементарных исходов 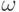
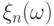
в » 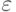

уменьшалась до нуля
с ростом 
сходимостью «по мере», а в теории вероятностей —
сходимостью «по вероятности».
Определение 42.
Говорят, что последовательность случайных величин
сходится
по вероятности к случайной величине 
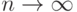
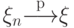
Пример 70.
Рассмотрим последовательность 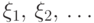
все величины имеют разные распределения: величина
принимает значения 
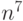
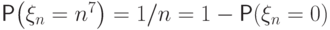
Докажем, что эта последовательность сходится по вероятности к нулю.
Зафиксируем произвольное 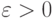
всех 
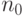
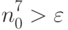
верно равенство 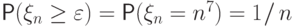
Поэтому
Итак, случайные величины 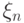
могут принимать все большие и большие значения,
но со все меньшей и меньшей вероятностью.
Например, последовательность 
вероятностном пространстве
так:
положим 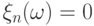
и 
![omegain(1-1mspace{1mu}/,n,,1]](https://intuit.ru/sites/default/files/tex_cache/87c8f28d6ba46a95d46887b66f2c8f27.png)
Заметим, что сходимость по вероятности имеет место совершенно независимо
от того, как именно заданы случайные величины на 
поскольку
определяется лишь их распределениями.
Замечание
Иное дело — сходимость «почти наверное».
Если, скажем, задать случайные величины как указано выше,
то сходимость «почти наверное» будет иметь место.
Действительно,
для всякого 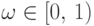
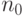
![omega in [0, 1-1/n_0]](https://intuit.ru/sites/default/files/tex_cache/ac522c00717511a4c73f57c9b991b7d8.png)
для всех 
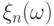
Можно попробовать задать случайные величины 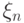
![[0,,1]](https://intuit.ru/sites/default/files/tex_cache/3c677f273d5640cb290c4e4ac717fbc7.png)
иначе, чтобы не было сходимости почти наверное. Для этого нужно заставить
отрезок длины 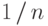

«бегать» по
отрезку ![[0,,1]](https://intuit.ru/sites/default/files/tex_cache/3c677f273d5640cb290c4e4ac717fbc7.png)
попадала внутрь этого
отрезка бесконечное число раз, и, тем самым, для любого
существовала подпоследовательность 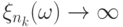
Сходимость по вероятности не обязательно сопровождается сходимостью
математических ожиданий или моментов других порядков:
из 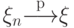
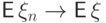
Действительно,
в примере 70 имеет место
сходимость 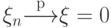
но 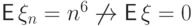
последовательность 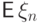
А если вместо значения 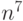

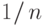
то получим 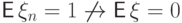
предел у
последовательности математических ожиданий конечен.
Если же 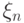


из примера 70, то 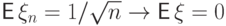
сходиться ко второму моменту 
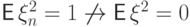
Однако сходимость математических ожиданий и других моментов сходящихся
последовательностей
бывает чрезвычайно важна в различных задачах статистики.
Существуют условия, при выполнении которых сходимость по вероятности
влечет сходимость математических ожиданий 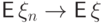
Сформулируем без доказательства следующее утверждение.
Это
сходимость последовательности случайных
величин Х 1, Х 2, . . ., Х n, . . ., заданных на
нек-ром вероятностном пространстве
следующим
образом:

для любого
P
5.4 Закон больших числе в форме Чебышёва
Пусть
последовательность Х 1, Х 2, . . ., Х n, . .
случайных величин удовлетворяет закону
больших чисел, если для любого
Иными
словами, выполнение закона больших
чисел отражает предельную устойчивость
средних арифметических случайных
величин: при большом числе испытаний
они практически перестают быть случайными
и совпадают со ссвоими средними
значениями.
Последовательность
Х 1, Х 2, . . ., Х n, . . удовлетворяет закону
больших чисел тогда и только тогда,
когда среднее арифметическое случайных
величин X1-m1
Х2-m2,
. . ., Хn-mn
сходятся по вероятности к нулю при
5.5 Закон больших чисел в форме Бернулли (схема Бернулли)
Пусть
производится последовательность
независимых испытаний, в результате
каждого из которых может наступить или
не наступить событие А, причем вероятность
наступления этого события одна и та же
при каждом испытании и равна р. Если
событие А фактически произошло m раз в
n испытаниях, то отношение m/n называют,
как мы знаем, частотой появления события
А. Частота есть случайная величина,
причем вероятность того, что частота
принимает значение m/n, выражается по
формуле Бернулли
Закон
больших чисел в форме Бернулли состоит
в следующем: с вероятностью, сколь угодно
близкой к единице, можно утверждать,
что при достаточно большом числе опытов
частота появления события А как угодно
мало отличается от его вероятности, т.
е.

словами, при неограниченном увеличении
числа n опытов частота m/n события А
сходится по вероятности к Р(А).
5.6 Центральная предельная теорема (формулировка, пример применения для решения задач)
Закон
распределения суммы независимых
случайных величин Xi(i=1,2,…,n)
приближается
к нормальному закону распределения при
неограниченном увеличении n, если
выполняются следующие условия:
1)
все величины имеют конечные математические
ожидания и дисперсии:
2)
ни одна из величин по значению резко не
отличается от остальных:
5.7 Центральная предельная теорема в случае схемы Бернулли (теорема Муавра-Лапласа).
Если
вероятность p наступления события A в
каждом испытании
постоянна
и отлична от нуля и единицы, а число
независимых испытаний
достаточно
велико, то вероятность можно вычислять
по приближённой
формуле:

точнее, чем больше n)
Глава 1. Случайные события
1.
Случайные события: элементарные,
достоверные, невозможные, несовместные,
совместные, равновозможные.
Попарно-несовместные, образующие полную
группу. Пространство элементарных
событий. Случай.
2.
Сумма, произведение, разность, отрицание.
Теоретико-множественная трактовка.
Диаграммы Эйлера-Венна. Алгебра событий.
Понятие сигма-алгебры.
3.
Частота события. Свойство статистической
устойчивости. Статистическое определение
вероятности.
4.
Классическое определение вероятности
события. Непосредственное вычисление
вероятностей.
5.
Комбинаторика: правило умножения и
сложения. Основные схемы: с возвращением,
без возвращения. Понятия размещения,
сочетания, перестановки.
6.
Геометрическое определение вероятности.
7.
Аксиоматическое определение вероятности.
Свойства вероятностей.
8.
Вероятностное пространство.
9.
Условная вероятность.
10.
Вероятность произведения событий.
11.
Независимость событий.
12.
Вероятность суммы событий.
13.
Формула полной вероятности.
14.
Формула Байеса.
15.
Понятие простой однородной цепи Маркова.
16.
Независимые испытания. Схема Бернулли.
Формула Бернулли. Многоугольник
распределения вероятностей.
17.
Предельные теоремы в схеме Бернулли:
формула Пуассона, локальная и интегральная
теоремы Муавра-Лапласа.
18.
Схема Бернулли. Наивероятнейшее число.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задачи и разборы экзамена ШАД. Часть вторая — с визуальными приёмами
Время на прочтение
10 мин
Количество просмотров 4.4K
Набор в ШАД продолжается, а тем временем мы с Егором Хайруллиным Mikari разобрали ещё несколько задач из письменного экзамена 2019 года (первая часть — здесь). Сначала пробуйте свои силы и постарайтесь решить задачи самостоятельно — например, номер 8 вообще не содержит формул, к решению можно прийти простыми рассуждениями и рисованием на листочке.
Задача 5. Предел и вероятности
Найдите предел:
Видеоразбор
Текстовый разбор
Прежде всего необходимо понять физический смысл этого выражения. Когда мы видим одну пятую в каких-то степенях, к тому же перемножающуюся друг с другом и умножающуюся на биномиальный коэффициент, то сразу начинаем думать об испытаниях Бернулли. В частности, об испытаниях Бернулли с вероятностью успеха одна пятая.
Выражения в скобках с такими степенями похожи на вероятность того, что в первые n раз нам повезло, а в следующие k-n раз нам не везло. Умножение на биномиальный коэффициент намекает, что n раз были успешными. Однако у нас используется не С из k по n, а C из k-1 по n-1:
Запишем выражение по-другому, чтобы и в степенях использовались не k и n, а k-1 и n-1:
Часть выражения до умножения на одну пятую в конце — это вероятность того, что среди k-1 испытаний ровно n-1 успешны. Биномиальный коэффициент отвечает за выбор тех n-1 позиций, которые среди k-1 испытаний оказались успешны. C учётом этого стоящая в конце одна пятая означает, что на k-м испытании будет успех. Получается, выражение целиком означает, что на k-м испытании достигается n-й по счёту успех.
Вспомним, что в искомом пределе только что записанное нами выражение стоит под знаком суммы:
Вместе с суммой выражение равняется вероятности того, что n-й успех случился где-то между n-м и 5n-м испытанием. Так как раньше n-го испытания успех произойти не мог, то сумму
можно охарактеризовать как вероятность того, что n-й успех случился не позже 5n-го испытания.
Ищем пределы вероятности
Итак, мы поняли физический вероятностный смысл того, что стоит под знаком предела. Постараемся понять, как считать предел.
Введём независимые одинаково распределённые случайные величины:
каждая из которых распределена как номер первого успеха в серии испытаний Бернулли с вероятностью p = ⅕. Тогда номер n-го успеха равняется сумме этих величин.
А поскольку ранее мы охарактеризовали сумму
как вероятность, что n-й успех случился не позже 5n-го испытания, то
Мы свели исходное выражение к более понятным вероятностным сущностям.
Вспоминаем предельные теоремы
Итак, в наших рассуждениях появилась вероятность неравенства с суммой, причём нам надо найти её предел при n → ∞. Это повод вспомнить одну из предельных теорем. Можно вспомнить закон больших чисел, но он никак не характеризует вероятности.
Вспомним центральную предельную теорему (ЦПТ). Она говорит о том, как распределено некоторое выражение, в котором участвует сумма. Если точнее, ЦПТ говорит, что:
где имеется в виду сходимость по распределению. В числителе стоит разность суммы и математического ожидания любой из наших случайных величин, умноженного на n. В знаменателе — корень из дисперсии, умноженной на n; cправа — нормальное распределение с параметрами 0 и 1.
Взглянем одновременно на выражение из левой части ЦПТ и на неравенство, предел вероятности которого нам нужно найти:
Приведём неравенство справа к виду, похожему на выражение слева.
Мы имеем право добавить знаменатель в неравенство, если он положителен:
Равняется ли матожидание пяти? Мы можем вспомнить или догадаться, что да, матожидание номера первого успеха в серии испытаний Бернулли с вероятностью успеха ⅕ — это 5. Действительно, в среднем при вероятности ⅕ нам будет везти на каждой 5-й попытке.
То есть можно выразить искомый предел как
Выражение, стоящее слева в неравенстве, согласно ЦПТ стремится к нормальному распределению с параметрами 0 и 1. Следовательно:
Ответ: ½
Задача 6. Размерности
Для квадратичной вещественной матрицы A размера n x n и вектора v ∈ ℝⁿ положим:
Пусть матрица A такова, что dim W(A, v) = n для любого v ≠ 0. Какова максимально возможная размерность U(A)?
Видеоразбор
Текстовый разбор
Перед нами страшноватая на вид задача по линейной алгебре. Постараемся лучше понять её условие.
Свойства W
Обратим внимание на W. Это довольно интересное подпространство. Оно инвариантно относительно A: если линейную комбинацию векторов v, Av, A²v и так далее умножить на A, то останется линейная комбинация таких векторов. А раз любое инвариантное содержащее v подпространство содержит и все Аᵏv, то получается, что W — это минимальное содержащее v подпространство.
И мы знаем из условия, что это минимальное инвариантное подпространство, содержащее любой ненулевой вектор из нашего пространства, имеет размерность n. Следовательно, любое ненулевое инвариантное подпространство тоже имеет размерность n — другими словами, совпадает с ℝⁿ.
Проще говоря, у линейного оператора А есть лишь два инвариантных подпространства — нулевое и ℝⁿ.
Что нам известно об инвариантных подпространствах над ℝ?
Теорема.
Над ℝ всякий линейный оператор имеет инвариантное подпространство размерности 1 или 2.
То есть наше подпространство W — это либо ℝ, либо ℝ².
В условии спрашивается, какой может быть максимально возможная размерность U(A).
В случае W = ℝ матрица имеет размерность 1×1, то есть состоит из одного числа, а линейный оператор является умножением на это число. Условие, что все матрицы в U должны коммутировать с A (XA = AX), всегда выполняется, поскольку все числа коммутируют друг с другом. Следовательно, U(A) — подпространство размерности 1.
Случай ℝ²
Но что если W совпадает с ℝ², в котором нет инвариантных подпространств размерности 1?
Вспомним, что такое инвариантное подпространство размерности 1. Это прямая, которая под действием линейного оператора переходит в саму себя — то есть её направляющий вектор умножается на число. Другими словами, это линейная оболочка некоторого собственного вектора: <w>.
И наоборот, если есть собственный вектор, то порождённая им прямая — это инвариантное подпространство размерности 1.
В нашем ℝ² нет инвариантных подпространств размерности 1, то есть нет собственных векторов. Другими словами, характеристический многочлен матрицы не имеет корней над полем действительных чисел, а имеет два сопряжённых комплексных корня — z и z̅:
Над полем комплексных чисел ℂ матрица A диагонализуется c числами z и z̅ на диагонали. Обозначим полученную матрицу как B:
Обозначим через Uℂ(B) пространство всех комплексных матриц 2×2, которые коммутируют с B. Нетрудно проверить, что каждая из матриц в Uℂ(B) будет диагональной:
Значит, размерность Uℂ(B) над пространством комплексных чисел будет равна двум:
Как от B перейти к A, а от ℂ — к ℝ?
Переход от B к A
Предположим, матрица Y коммутирует с B:
Вспомним, что B получается из A заменой базиса, то есть:
Умножим и правую, и левую часть равенства слева на C, а справа — на С⁻¹:
То есть если матрица Y коммутирует с B, то матрица CYC⁻¹ коммутирует с A. Другими словами, линейное преобразование, переводящее Y в CYC⁻¹, осуществляет изоморфизм:
В частности, они имеют одинаковую размерность 2:
То есть если бы мы рассматривали A как комплексную матрицу, то пространство коммутирующих с ней комплексных матриц имело бы размерность 2.
Переход от ℂ к ℝ
Уравнение XA=AX можно считать однородной системой линейных уравнений на элементы матрицы X. Вспомним, что размерность пространства решений однородной системы уравнений, коэффициенты A которой заданы над ℝ, — одинаковое над ℂ и ℝ. Эта размерность зависит только от ранга матрицы системы, а при переходе от ℂ к ℝ ранг не меняется.
Таким образом:
Мы выяснили, что для случая W = ℝ размерность U равняется единице, для случая W = ℝ² — двойке. В условии спрашивалось, какой может быть максимально возможная размерность. Значит, ответ — 2.
Ответ: 2
Задача 7. Неравенство для производной
Вещественнозначная функция f определена на отрезке [a; b] (b – a ≥ 4) и дифференцируема на нём. Докажите, что найдётся точка x₀ ∈ (a; b), для которой
Видеоразбор
Текстовый разбор
Когда речь идёт о доказательстве существования x₀ на интервале и упоминается дифференцируемость, то вспоминается теорема Лагранжа о промежуточном значении и теорема о промежуточном значении непрерывной функции.
Вспомним также, что:
Если рассмотреть сложную функцию arctg f(x), то её производная в точке x₀ будет равна
Приведём неравенство из условия задачи к похожему виду, разделив его на 1 + f²(x₀). Это выражение не меньше единицы, поэтому в ноль не обращается.
Это можно переписать в таком виде:
И мы должны доказать, что существует точка x₀, в которой это неравенство выполняется — то есть арктангенс в этой точке не может круто идти вверх. Звучит правдоподобно, ведь арктангенс — в целом довольно пологая функция. Но давайте придумаем строгое доказательство.
Итак, раз мы имеем дело с производной, самое время применить теорему Лагранжа о промежуточном значении. Запишем ее в удобном нам виде:
Поскольку арктангенс лежит на интервале (-π/2, π/2), то левая часть равенства не может быть большой:
Следовательно:
Из условия мы знаем, что b – a ≥ 4. Значит,
Выбирая для них x₀ из теоремы Лагранжа, получаем:
что и требовалось доказать.
Задача 8. Рёбра в графе
Дан граф с 40 вершинами без петель и кратных рёбер. Известно, что среди любых 5 вершин найдётся одна, соединённая с четырьмя остальными. Каково минимально возможное число рёбер в этом графе?
Видеоразбор
Текстовый разбор
Поскольку в графе много вершин и рёбер, представить его визуально будет непросто, нас это запутает.
Поэтому мы применим трюк — инвертируем задачу: заменим каждое ребро на отсутствие ребра, а каждое отсутствие ребра — на ребро. Каким будет новое условие задачи?
Дан граф с 40 вершинами без петель и кратных рёбер. Известно, что среди любых 5 вершин найдётся одна, не соединённая с четырьмя остальными. Каково минимально возможное число «отсутствий» рёбер в этом графе?
Минимальное число «отсутствий» рёбер тривиально выражается через максимальное число рёбер. При таком условии рёбер в графе будет немного.
Разберём два случая.
Случай 1. В графе есть связная компонента хотя бы из трёх вершин — то есть между ними есть хотя бы два ребра
Ответим на два вопроса:
- Может ли ещё где-то в графе быть хотя бы одно ребро?
- Могут ли в графе быть ещё две вершины, соединённые с одной или с несколькими из первоначальных трёх?
Оба варианта исключены. Потому что среди этих пяти вершин нет ни одной, не соединённой с четырьмя другими — что противоречит условию задачи.
А какие варианты не исключены? Может существовать ещё только одна вершина, соединённая с одной или несколькими из первоначальных трёх:
То есть самый «насыщенный» рёбрами граф, который может получиться, — это граф K₄. Он состоит из четырёх вершин, каждая из которых соединена с тремя другими (всего шесть рёбер):
Итак, если в графе есть связная компонента хотя бы из трёх вершин, то рёбер в таком графе может быть не больше шести.
Случай 2. В графе нет связных компонент хотя бы из трёх вершин
Даже если в графе в принципе есть рёбра, они не могут иметь общих вершин:
Сколько тогда может быть рёбер? Не больше 20, потому что из условия известно, что в графе 40 вершин, а из них можно выбрать не больше 20 пар вершин, соединённых рёбрами.
Итак, в первом случае рёбер не больше шести, во втором — не больше 20. В инвертированной задаче требовалось найти максимальное число рёбер, поэтому ответ: 20.
Возврат к исходной задаче
Чтобы вернуться к исходной задаче, снова поменяем местами понятия «ребро» и «отсутствие ребра». Получается, что в таком графе не может быть более 20 отсутствующих рёбер.
Сколько вообще может быть рёбер в графе на n вершинах? n(n-1)/2, для нашего графа это 40 ⋅ 39/2 = 780.
Мы выяснили, что отсутствующих рёбер не более 20. В условии требуется найти минимальное число рёбер. Получается, что оно равняется 780 – 20 = 760.
Ответ: 760
Задача 9. Индекс ближайшего превосходящего элемента
В массиве A длины n для каждого i-го элемента найдите такой ближайший к нему j-й элемент, что j > i и aj ≥ 2aᵢ.
Видеоразбор
Текстовый разбор
Для начала придумаем решение в лоб — брутфорс, перебор или ещё какой-нибудь вариант: достаточно простой, но хоть как-нибудь решающий задачу.
Например, для элемента i переберём все элементы справа и найдём искомый результат. Какова будет временнáя сложность такого брутфорса? Для каждого из n элементов (в худшем случае) нужно будет совершить n действий, так что сложность такого решения составит О(n²). Это недостаточно хорошо.
Свойства структуры
Одно из требований к искомому элементу — он должен быть больше или равен заданному. Это повод вспомнить алгоритм бинарного поиска, который решает похожую задачу: находит в сортированном массиве первый элемент, больше или равный заданному. Сложность алгоритма — логарифмическая: O(log n).
Однако пока непонятно, как воспользоваться алгоритмом бинарного поиска. И если это сделать, возникнет другая проблема: для i мы найдём результат быстро, а для последующих шагов (в каждом случае i – 1) нам потребуется перестраивать заново структуру, поверх которой будет работать бинарный поиск. Такой процесс может оказаться медленным — мы каждый раз будем тратить линейное время от числа элементов. Важно, чтобы структуру не требовалось перестраивать.
Заметим, что структуры для i и i – 1 будут построены на похожем наборе элементов. Для i это все элементы, начиная с i + 1 до j включительно, а для i – 1 — те же самые элементы плюс элемент i. Тем самым структуру не нужно каждый раз перестраивать с нуля — достаточно научиться её перестраивать инкрементально. Запомним это.
Визуальное представление
Изобразим наш массив визуально, чтобы высота столбца соответствовала значению элемента. Некоторые элемента справа от i-го будут больше него, некоторые — меньше:
Будем двигаться вправо, поочерёдно рассматривая элементы. Числа < aᵢ нас заведомо не интересуют.
Предположим, один из элементов оказался ≥ aᵢ. Тогда он может оказаться ответом для выбранного i.
Посмотрим на следующие элементы. Если очередной элемент меньше того, который мы отметили, то он нам тоже не интересен (даже если при этом он ≥ aᵢ).
Если мы встретим элемент, больше или равный отмеченному ранее, то отметим и его тоже — теперь уже он будет для нас кандидатом на ответ. И так далее.
Возрастающая последовательность элементов, отмеченных синим цветом, — это сортированный массив, найти в котором нужный элемент можно уже упомянутым бинарным поиском.
Вернёмся к вопросу, как перестраивать такой массив при переходе от i к i – 1. Как мы уже выяснили, нужно уметь делать это инкрементально. Рассмотрим два случая.
1) aᵢ ≤ aᵢ₋₁
Если мы начинаем движение по массиву от i – 1, то первым же кандидатом на ответ будет i-й элемент — а все остальные кандидаты останутся прежними. Мы почти не потратим лишнего времени на перестроение — только добавим aᵢ.
2) aᵢ > aᵢ₋₁
В зависимости от значения aᵢ₋₁ первые несколько кандидатов могут перестать быть кандидатами:
В обоих случаях, получив массив кандидатов, мы выполним по нему бинарный поиск. Это и будет нашим решением. Оценим его сложность.
Оценка сложности и выбор способа хранения
Во-первых, узнаем, сколько памяти нам потребуется. Мы должны будем хранить элементы, отмеченные синим. Таких элементов не может быть больше, чем всего элементов в массиве — n. Значит, сложность по памяти — O(n).
Во-вторых, какова сложность по времени? Нам потребуется запускать два вида операций:
- Бинарный поиск для каждого i. Эту операцию мы осуществим не более чем n раз — для каждого элемента в массиве длины n. Сложность каждого бинарного поиска — O(log n), значит всего мы потратим O(n log n).
- Перестроение массива при переходе от i к i – 1. Здесь, как мы выяснили выше, потребуется либо добавить в массив один элемент, либо удалить из него некоторое число элементов. Возможно, их будет много — всё зависит от значения aᵢ₋₁. На то, чтобы их удалить, может потребоваться много времени.
Поэтому мы будем хранить «синие» элементы в обратном порядке — начиная с того, у которого в исходном массиве был самый большой индекс. Очевидно, этот же элемент будет самым большим и по своему значению. Тогда все добавления и удаления мы будем осуществлять в конце массива.
Каждая такая операция (добавление или удаление) выполняется за константу, а не за линейное время, как при работе с произвольным фрагментом массива. Общее число операций не превысит n, поэтому суммарная сложность перестроений массива будет равна О(n).
Итак, сложность всех операций первого вида (бинарных поисков) составит O(n log n), а всех операций второго вида (перестроений массива) — O(n). Значит, сложность решения целиком — O(n log n). Это нас вполне устраивает.
Решение
Для каждого i = n..1:
- Выполним бинарный поиск по массиву, который назовём массивом кандидатов. Будем искать элемент, больше либо равный 2aᵢ.
- Если aᵢ₋₁ ≤ aᵢ, то запишем aᵢ в конец массива кандидатов.
- Если aᵢ₋₁ > aᵢ и в массиве кандидатов есть элементы меньше, чем aᵢ₋₁, то удалим их из массива кандидатов.


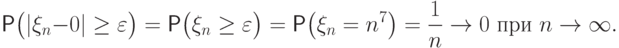
![langleOmega,,mathcal F,,Probrangle=
langle [0,,1],,mathfrak{B}([0,,1]),,lambdarangle](https://intuit.ru/sites/default/files/tex_cache/cf1718b0638c966e1deca0a6a72a5cdd.png)
![omegain[0,,1-1mspace{1mu}/,n]](https://intuit.ru/sites/default/files/tex_cache/87bcf7ba472726b656dda22c332c3d06.png)
![omegain[0,,1]](https://intuit.ru/sites/default/files/tex_cache/6267c165bba32251c965f3413a53ecac.png)