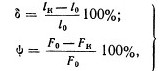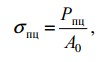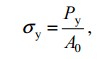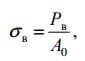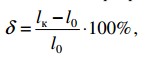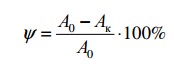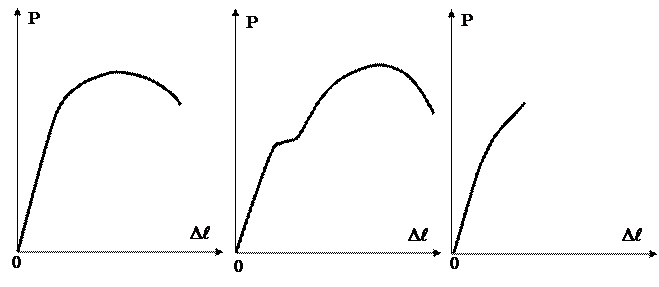5. Механические свойства металлов.
Механические
свойства определяют на специальных
образцах. В зависимости от условий
приложения нагрузки различают статические
и динамические испытания. При статических
испытаниях нагрузка прилагается медленно
и плавно возрастает. При динамических
— она прилагается с высокой скоростью.
Определение предела прочности, предела текучести, относительного удлинения и сужения.
Эти характеристики
определяются при испытаниях на растяжение,
это наиболее распространенный метод
определения свойств конструкционных
материалов. Пределы прочности и текучести
относят к прочностным свойствам, а
относительное удлинение и сужение
характеризуют пластичность материала.
Испытания
выполняются на разрывных машинах с
использованием специальных цилиндрических
образцов, которые растягивают до
разрушения.
В
процессе приложения нагрузки в образце
возникает напряжение
(s),
равное отношению приложенного усилия
(Р) к площади образца (F):
s
= Р/F
[МПа
или кгс/мм2].
Под действием приложенной нагрузки
возникает деформация
— изменение размеров образца.
Деформация
может быть упругой или пластической.
Упругая
деформация полностью снимается (исчезает)
после снятия нагрузки. Упругая деформация
не приводит к заметным изменениям в
структуре и свойствах материала.
Различают абсолютную и относительную
деформацию. Абсолютная
(Dl)
— изменение размера (длины при испытаниях
на растяжение), относительная (e)
— отношение абсолютной деформации к
первоначальной длине (l),
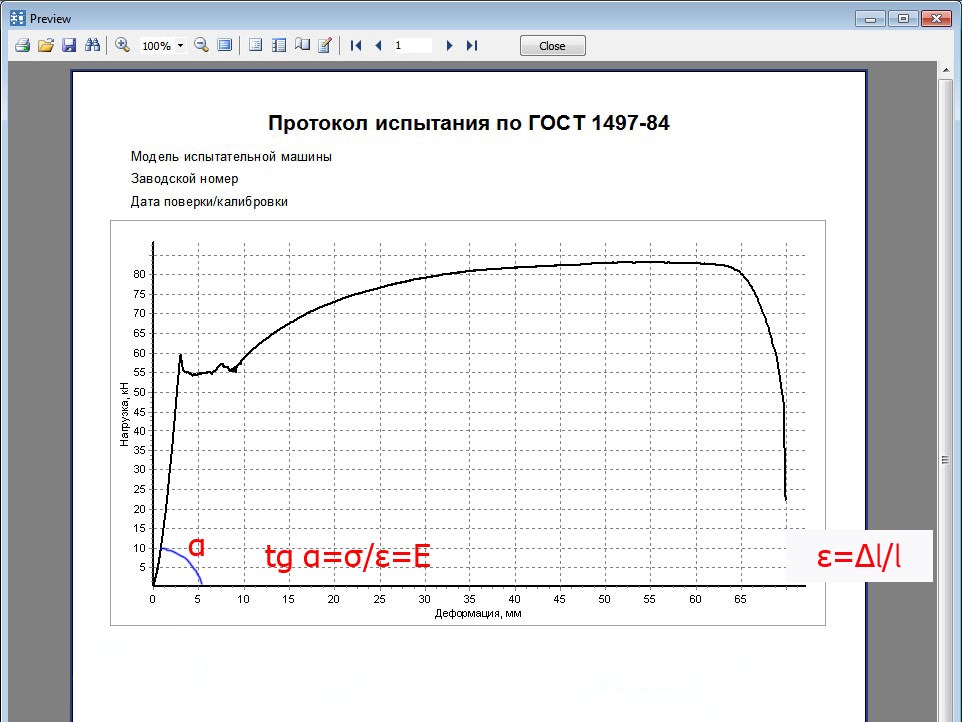
т.е. e=Dl/l.
Между напряжением
и величиной относительной упругой
деформации существует линейная
зависимость — закон Гука:
s=Е×e,
где Е — модуль упругости, свойство
материала характеризующее его жесткость,
т.е. способность сопротивляться упругим
деформациям.
Пластическая
деформация
не исчезает после снятия нагрузки
(согните алюминиевую проволоку, после
того как нагрузка снята, проволока не
разгибается — она пластически
деформирована).
При
испытаниях на растяжение строится
диаграмма в координатах «относительное
удлинение e
— напряжение s»
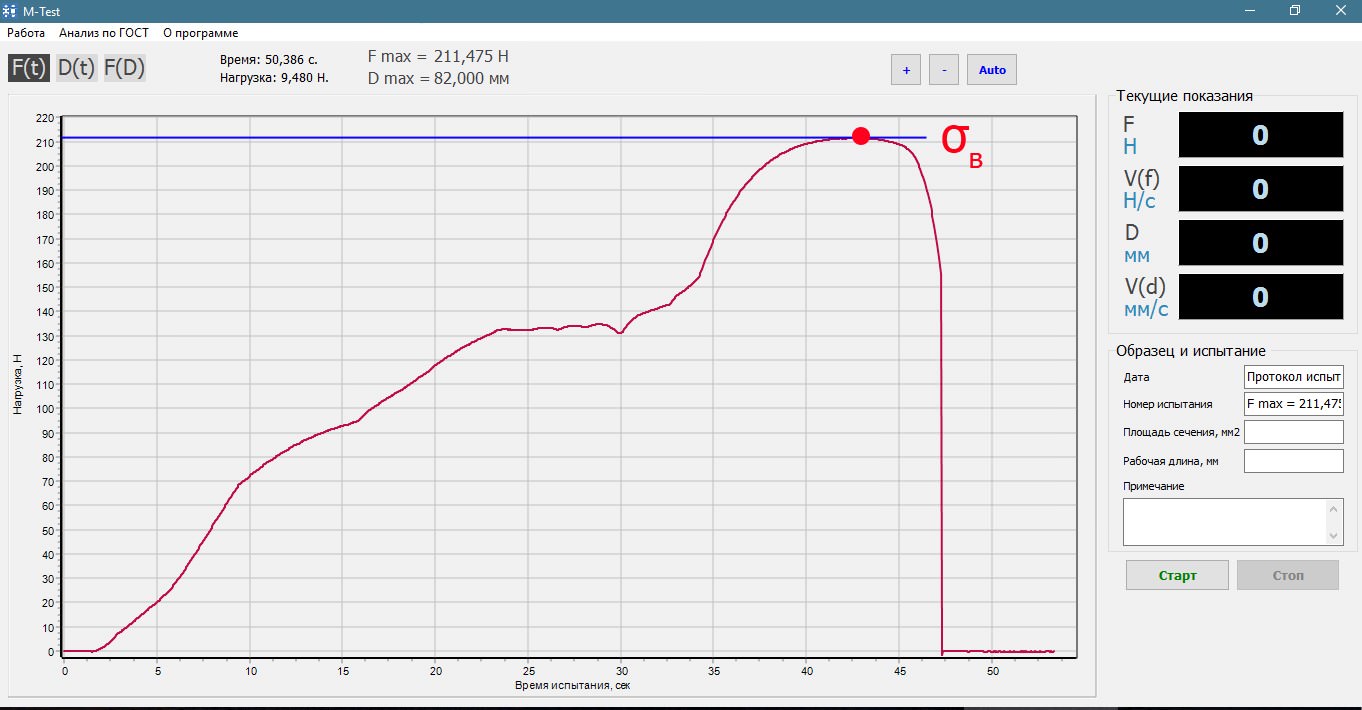
(рис. 5.1). При этом определяются: предел
прочности (sв)
— напряжение, при котором происходит
разрушение образца (максимальная точка
на кривой «s-e»);
предел
пропорциональности
— максимальное напряжение, при котором
отсутствует пластическая деформация.
Поскольку точное определение предела
пропорциональности затруднено в практике
определяется предел
текучести
sт
— напряжение, вызывающее остаточную
деформацию определенной величины,
например, s0,2
— напряжение при котором остаточная
деформация равна 0.2% от первоначальной
длины образца.
Перед
разрушением образец претерпевает
пластическую деформацию, он удлиняется,
также происходит уменьшение диаметра
— образуется «шейка». Относительное
удлинение
d=Dl/l
и относительное
сужение
Y=Fн-Fk/Fн
(здесь Fн
и Fk
— начальная до испытаний и конечная
минимальная площадь образца, т.е. площадь
шейки после разрушения) характеризуют
пластичность материала. Чем больше эти
характеристики, тем материал пластичнее.
Определение твердости
Твердость
характеризует сопротивление материала
большим пластическим деформациям.
Наиболее распространенные методы
определения твердости связаны с
внедрением специального тела —
индентора,
в испытуемый материал, с таким усилием,
чтобы в материале остался отпечаток
индентора. О величине твердости судят
по отпечатку.
Твердость наиболее
распространенный метод определения
свойств материала. Это объясняется
рядом причин: определения твердости
являются неразрушающим методом, т.к.
деталь после такого измерения может
быть использована по назначению;
испытания на твердость не требуют
высокой квалификации и, кроме того, зная
твердость, можно судить и о других
механических свойствах.
Метод
Бринелля.
В качестве
индентора используется стальной
закаленный шарик, который вдавливается
в испытуемый образец на специальном
прессе, в результате на поверхности
образца образуется отпечаток в виде
сферической лунки. Значения твердости
— это отношение приложенной нагрузки и
площади поверхности отпечатка. Они
вычисляются по формуле: НВ=2Р/D(D-(D2-d2)1/2).
Здесь НВ — обозначение твердости
(например, 200НВ); Р — прилагаемая нагрузка
[кгс];
D
и d
— диаметры шарика и отпечатка [мм].
На практике
пользуются таблицей, в которой указаны
значения твердости в зависимости от
диаметра отпечатка.
Метод
Бринелля не является универсальным. Он
не позволяет испытывать материалы с
твердостью более 450НВ, т.к. при этом может
деформироваться индентор — шарик, а
также образцы толщиной менее 1…2 мм
из-за их продавливания.
Между
твердостью по Бринеллю и пределом
прочности разных материалов соблюдается
следующие примерные соотношения: для
стали sв=НВ/3,
sт=НВ/6;
для алюминиевых сплавов; sв=0,362НВ;
для медных сплавов sв=0,26НВ.
Метод
Роквелла.
Принципиальное
отличие этого метода от рассмотренного
ранее в том, что твердость определяется
не площадью поверхности отпечатка
индентора, а глубиной его проникновения
в исследуемый образец.
В качестве индентора
используют алмазный конус — при испытаниях
твердых материалов и стальной закаленный
шарик — при испытаниях мягких материалов.
Нагрузка при использовании алмазного
конуса устанавливается 150 или 60 кгс в
зависимости от твердости материала —
большая для менее твердых материалов
(например, закаленные стали); меньшая
для материалов с очень высокой твердостью
(твердые сплавы, режущая керамика), чтобы
избежать скола алмазного конуса. Стальной
шарик вдавливают с нагрузкой 100 кгс.
Испытания
выполняются на специальном приборе,
имеющем две шкалы — черную и красную.
Черная шкала используется при испытаниях
алмазным конусом, красная — стальным
закаленным шариком. Обозначения
твердости: НRC
— алмазный конус, нагрузка 150кгс (64НRC),
HRA
— алмазный конус, нагрузка 60кгс (90HRA),
HRB
— шарик, нагрузка 100 кгс (120HRB).
Значения
твердости в единицах HRC
примерно в 10 раз меньше, чем в единицах
НВ. Т.е. твердость 30 HRC
примерно соответствует 300НВ. Между
значениями твердости по шкалам «С» и
«А» имеется следующая зависимость:
HRC=2HRA-102.
Метод
Виккерса.
Метод основан на вдавливании четырехгранной
алмазной пирамидки с углом между
противоположными гранями, равным 136°.
Твердость (она обозначается HV,
например,1000HV)
определяется отношением нагрузки и
площади поверхности отпечатка. Значения
твердости вычисляются по формуле:
HV=1,854
Р/d2,
где d
— среднее значение длины диагоналей
отпечатка.
Нагрузка может
изменяться в пределах от 1 до100 кгс.
Величина диагоналей определяется с
помощью специального микроскопа,
встроенного в прибор.
Определение
ударной вязкости.
Испытания
на ударную вязкость относятся к
динамическим методам. При определении
ударной вязкости используют призматические
образцы (10×10×55 мм)с надрезом, который
служит концентратором напряжений.
Используют U-
и V-образные
надрезы (рис. 5.2). В зависимости от формы
надреза ударная вязкость обозначается
КСU
или КСV.
Образец устанавливают на маятниковом
копре (рис. 5.3), так чтобы удар маятника
происходил против надреза, раскрывая
его. Маятник поднимают на высоту h1,
при падении он разрушает образец,
поднимаясь на высоту h2,
при этом h2<h1,
т.к. часть запасенной при подъеме работы
тратится на разрушение образца. Таким
образом, работа разрушения составит:
А=mg(h1-h2)
[кгс
м/см2 или КДж/м2].
Ее значения считываются со шкалы,
установленной на маятниковом копре.
Ударная
вязкость — это относительная работа
разрушения, т.е. работа, отнесенная к
площади (F)
образца до разрушения. Таким образом,
КСU(КСV)=A/F.
1. Предел прочности
Пределом прочности называют максимальное усилие растяжения, отнесенное к единице площади его первоначального сечения
σВ=P/F,Па
Другими словами, предел прочности есть условное максимальное напряжение, которое выдерживает материал при растяжении. Под «истинным пределом прочности»(или под действительным сопротивлением разрыву) понимается усилие в момент разрыва P, отнесенное к площади сечения.
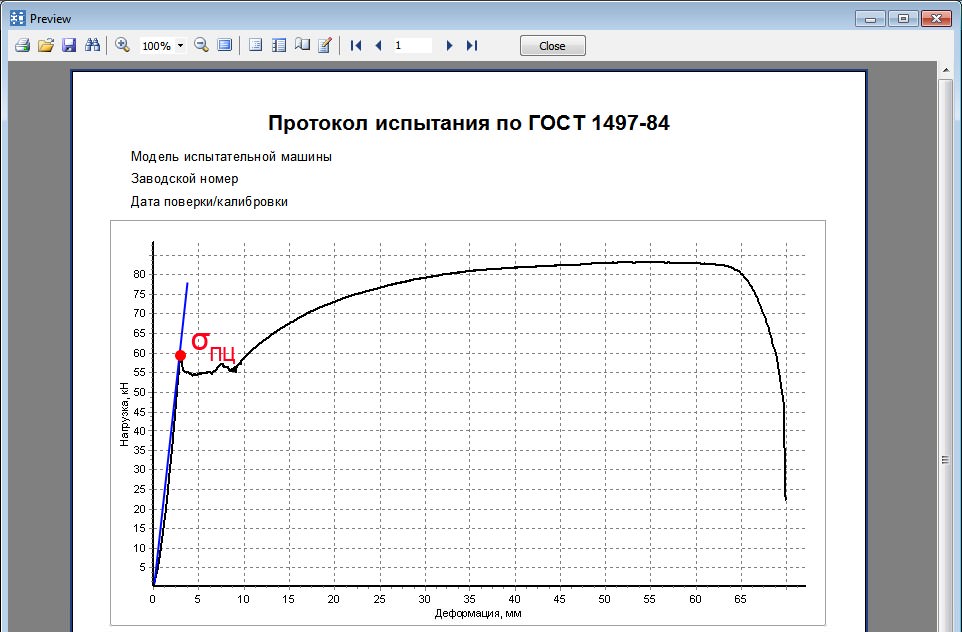
2. Предел пропорциональности и упругости
Под пределом пропорциональности σПЦ понимают наименьшее напряжение вызывающее в испытуемом материале отклонение от закона пропорциональности (или наибольшее напряжение от этого закона), а под пределом упругости σУП — наибольшее напряжение, ниже которого величина деформации является определенной функцией напряжения, независимо от возрастания или убывания последнего, то нет оснований предполагать идентичность этих двух величин.
3. Предел текучести
Пределом текучести σТ называется напряжение, при котором возникающая остаточная деформация образца распространяется равномерно по его рабочей части при временном постоянстве растягивающего усилия.
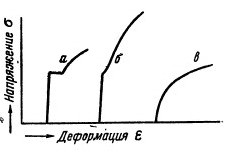
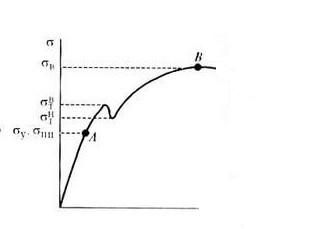
Практически в качестве предела текучести обычно принимается напряжение, при котором деформация образца возрастает, а стрелка динамометра разрывной машины либо останавливается, либо отходит назад. В этом случае на кривой «напряжение — деформация» образуется так называемая площадка текучести (кривая a), и тогда предел текучести называют явным или физическим.
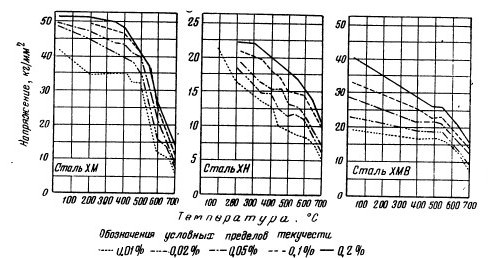
Типичные кривые растяжения (α — ε)
В некоторых случаях площадка текучести бывает неясно выражена (кривая б) или совершенно отсутствует (кривая в); такую форму кривых при нормальной температуре испытания имеют весьма пластичные металлы (например, медь). С повышением же температуре явным пределом текучести, форма кривой имеет вид, показанный на рисунке, в. Мягкая углеродистая сталь с содержанием 0,05% при 300°С дает кривую, соответствующую кривой б; другие, более теплоустойчивые стали сохраняют явный предел текучести до 400 и даже до 500°С; выше этих температур форма кривых растяжения аналогична кривой в.
Во всех случаях, когда отсутствует явный предел текучести, приходится прибегать к нахождению так называемых условных пределов текучести, основанных на определении напряжений, вызывающих заданную остаточную деформацию небольшой величины (в пределах 0,01—0,5%). Чаще всего на практике определяют условные пределы текучести, вызывающие остаточную деформацию, равную 0,1 или 0,2%.
Условные пределы текучести некоторых легированных сталей
Если условные пределы текучести при нормальной температуре мало различаются между собой, то при высоких температурах разница между условными пределами текучести, например 0,01 и 0,2% (после текучести), становится значительной.
4. Удлинение и поперечное сужение образца
Удлинение и поперечное сужение образца, испытанного при высокой температуре, являются показателями пластических свойств металла при данной температуре.
Удлинение δ и поперечное сужение ψ замеряются на охлажденных образцах и подсчитываются по общеизвестным формулам:
- где l0 — начальная длина расчетного участка образца;
- lk — конечная длина расчетного участка образца;
- F0 — начальная площадь поперечного сечения образца;
- Fk — конечная площадь поперечного сечения образца.
Наибольшее влияние на эти свойства оказывает время до разрыва или, что то же самое, скорость растяжения образца.
5. Модуль упругости
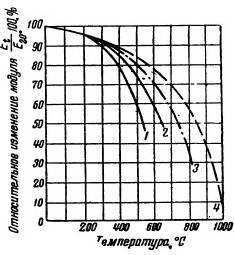
Модуль нормальной упругости E является важной физико-механической характеристикой металла. Знание величины модуля упругости стали для широкого диапазона температур необходимо не только при конструкторских расчетах деталей машин и аппаратуры, работающих при повышенных температурах, но и в ряде других случаев.
Относительное изменение модуля упругости E (в % от его значения при 20°) в зависимости от температуры для сталей: 1-нелегированной; 2-низколегированной; 3-среднелегированной; 4-высоколегированной
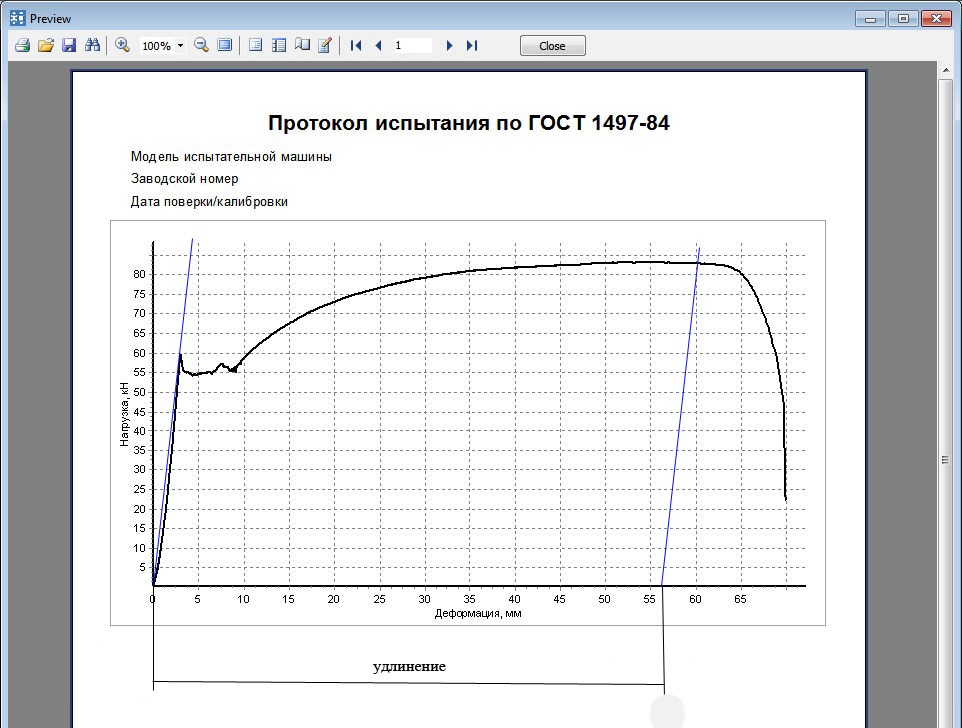
Испытание на растяжение металла заключаются в растяжении образца с построением графика зависимости удлинения образца (Δl) от прилагаемой нагрузки (P), с последующим перестроением этой диаграммы в диаграмму условных напряжений (σ — ε).
Вырезку заготовок для образцов проводят на металлорежущих станках, ножницах, штампах путем применения кислородной и анодно-механической резки и другими способами, предусматривая припуски на зону металла с измененными свойствами при нагреве и наклепе.
Места вырезки заготовок для образцов, количество их, направление продольной оси образцов по отношению к заготовке, величины припусков при вырезке должны быть указаны в нормативно-технической документации на правила отбора проб, заготовок и образцов или на металлопродукцию.
Образцы рекомендуется изготовлять на металлорежущих станках. При изготовлении образцов принимают меры (охлаждение, соответствующие режимы обработки), исключающие возможность изменения свойств металла при нагреве или наклепе, возникающих в результате механической обработки. Глубина резания при последнем проходе не должна превышать 0,3 мм.
Плоские образцы должны сохранять поверхностные слои проката, если не имеется иных указаний в нормативно-технической документации на правила отбора проб, заготовок и образцов или на металлопродукцию.
Для плоских образцов стрела прогиба на длине 200 мм не должна превышать 10% от толщины образца, но не более 4 мм. При наличии указаний в нормативно-технической документации на металлопродукцию допускается рихтовка или иной вид правки заготовок и образцов.
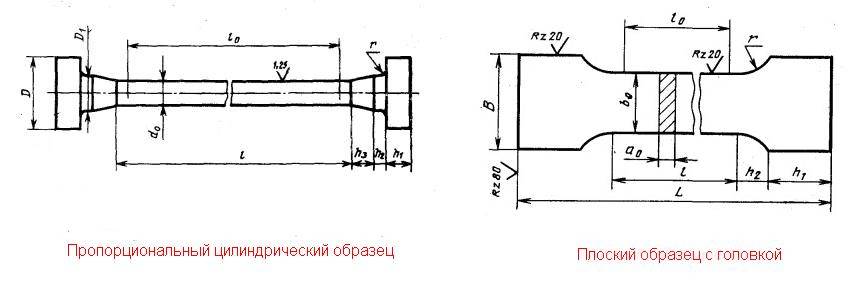
Для испытания на растяжение применяют пропорциональные цилиндрические или плоские образцы диаметром или толщиной в рабочей части 3,0 мм и более с начальной расчетной длиной или
. Применение коротких образцов предпочтительнее.
Литые образцы и образцы из хрупких материалов допускается изготовлять с начальной расчетной длиной .
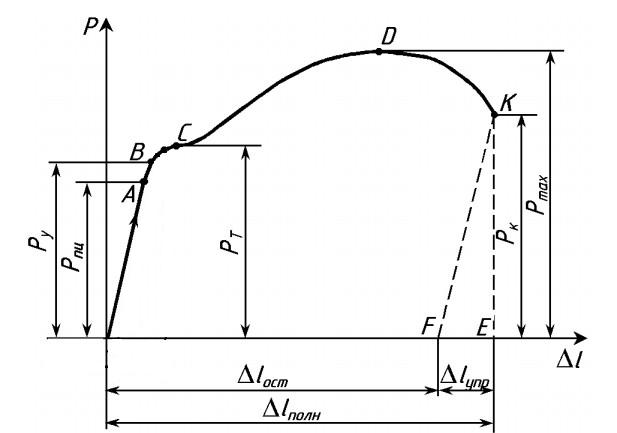
- Участок ОА — участок пропорциональности между нагрузкой Р и удлинением ∆l. Это участок, на котором сохраняется закон Гука. Данная пропорциональность была открыта Робертом Гуком в 1670 г. и в дальнейшем получила название закона Гука.
- Участок ОВ — участок упругой деформации. Т.е., если к образцу приложить нагрузку, не превышающую Ру, а потом разгрузить, то при разгрузке деформации образца будут уменьшаться по тому же закону, по которому они увеличивались при нагружении
Выше точки В диаграмма растяжения отходит от прямой — деформация начинает расти быстрее нагрузки, и диаграмма принимает криволинейный вид. При нагрузке, соответствующей Рт (точка С ), диаграмма переходит в горизонтальный участок. В этой стадии образец получает значительное остаточное удлинение практически без увеличения нагрузки. Получение такого участка на диаграмме растяжения объясняется свойством материала деформироваться при постоянной нагрузке. Это свойство называется текучестью материала, а участок диаграммы растяжения, параллельный оси абсцисс, называется площадкой текучести.
После появления площадки текучести, материал снова приобретает способность сопротивляться растяжению и диаграмма поднимается вверх. В точке D усилие достигает максимального значения Pmax. При достижении усилия Pmax на образце появляется резкое местное сужение — шейка. Уменьшение площади сечения шейки вызывает падение нагрузки и в момент, соответствующий точке K диаграммы, происходит разрыв образца.
Прилагаемая нагрузка для растяжения образца зависит от геометрии этого образца. Чем больше площадь сечения, тем более высокая нагрузка необходима для растяжения образца. По этой причине, получаемая машинная диаграмма не дает качественной оценки механических свойств материала. Чтобы исключить влияние геометрии образца, машинную диаграмму перестраивают в координатах σ − ε путем деления ординат P на первоначальную площадь сечения образца A0 и абсцисс ∆l на lо. Перестроенная таким образом диаграмма называется диаграммой условных напряжений. Уже по этой, новой диаграмме, определяют механические характеристики материала.
Определяются следующие механические характеристики:
Предел пропорциональности σпц – наибольшее напряжение, после которого нарушается справедливость закона Гука σ = Еε , где Е – модуль продольной упругости, или модуль упругости первого рода. При этом Е =σ/ε = tgα , т. е. модуль E это тангенс угла наклона прямолинейной части диаграммы к оси абсцисс
Предел упругости σу — условное напряжение, соответствующее появлению остаточных деформаций определенной заданной величины (0,05; 0,001; 0,003; 0,005%); допуск на остаточную деформацию указывается в индексе при σу
Предел текучести σт – напряжение, при котором происходит увеличение деформации без заметного увеличения растягивающей нагрузки
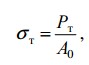
Предел прочности (временное сопротивление разрыву) σв – напряжение, соответствующее наибольшей нагрузке Pmax , предшествующей разрыву образца
Кроме характеристик прочности материала, при испытании на растяжение определяют также характеристики пластичности — относительное удлинение δ и относительное сужение ψ
где lо – первоначальная расчетная длина образца, а lк – конечная расчетная длина образца
Испытания на растяжение (ГОСТ 1497-84) широко применяют для определения механических свойств конструкционных сталей, цветных металлов и сплавов.
Стандарт устанавливает методы статических испытаний на растяжение для определения при температуре 20±15С пределов пропорциональности, упругости, текучести (условного и физического), временного сопротивления, относительного удлинения и относительного сужения после разрыва.
1. Изучить методику испытаний металлов и сплавов на растяжение.
2. Ознакомиться с конструкцией и работой разрывной машины.
3. Провести испытания на растяжение двух образцов из разных материалов, получить диаграммы растяжения.
4. Определить положение характерных точек, рассчитать параметры в характерных и промежуточных точках.
5. На основании выполненных расчетов построить диаграмму зависимости условных напряжений от степени деформации.
6. Определить основные механические характеристики материалов и дать заключение о свойствах испытанных материалов.
Содержание работы
Испытания на растяжение (ГОСТ 1497-84) широко применяют для определения механических свойств конструкционных сталей, цветных металлов и сплавов.
Стандарт устанавливает методы статических испытаний на растяжение для определения при температуре 20±15°С пределов пропорциональности, упругости, текучести (условного и физического), временного сопротивления, относительного удлинения и относительного сужения после разрыва.
При испытаниях на растяжение принимают следующие обозначения и определения:
— рабочая длина образца l (м, мм) — часть образца с постоянной площадью поперечного сечения между его головками или участками для захвата;
— начальная расчетная длина образца l0 (м, мм) — участок рабочей длины образца между нанесенными метками до испытания, на котором определяется удлинение;
— конечная расчетная длина образца lк (м, мм) — длина расчетной части образца после разрыва;
— начальный диаметр образца d0 (м, мм) — диаметр рабочей части цилиндрического образца до испытаний;
— диаметр образца после разрыва dк (м, мм) — минимальный диаметр рабочей части цилиндрического образца после разрыва;
— начальная площадь поперечного сечения образца F0 (м2, мм2) — площадь поперечного сечения рабочей части образца до испытаний;
— площадь поперечного сечения образца после разрыва Fк (м2, мм2) — минимальная площадь поперечного сечения рабочей части образца после разрыва;
— осевая растягивающая нагрузка P (Н, кгс) — нагрузка, действующая на образец в данный момент испытания;
— условное напряжение S (МПа, кгс/мм2) — напряжение, определяемое отношением нагрузки P к начальной площади поперечного сечения F0 образца;
— истинное нормальное напряжение S (МПа, кгс/мм2) — напряжение, определяемое отношением нагрузки P к действительной в данный момент испытания площади поперечного сечения F образца;
— абсолютное удлинение образца Dl (м, мм) — приращение начальной расчетной длины образца в любой момент испытания;
— предел пропорциональности sпц (МПа, кгс/мм2) — напряжение, при котором отступление от линейной зависимости между нагрузкой и удлинением достигает такой величины, что тангенс угла наклона, образованного касательной к кривой «нагрузка-удлинение» в точке Pпц с осью нагрузки, увеличивается на 50% от своего значения на упругом (линейном) участке;
— условный предел упругости S0,05 (МПа, кгс/мм2) — напряжение, после снятия которого остаточное удлинение достигает 0,05% длины участка рабочей части образца, равного базе измерения;
— модуль упругости E (МПа, кгс/мм2) — отношение приращения напряжения к соответствующему приращению деформации в пределах упругой деформации;
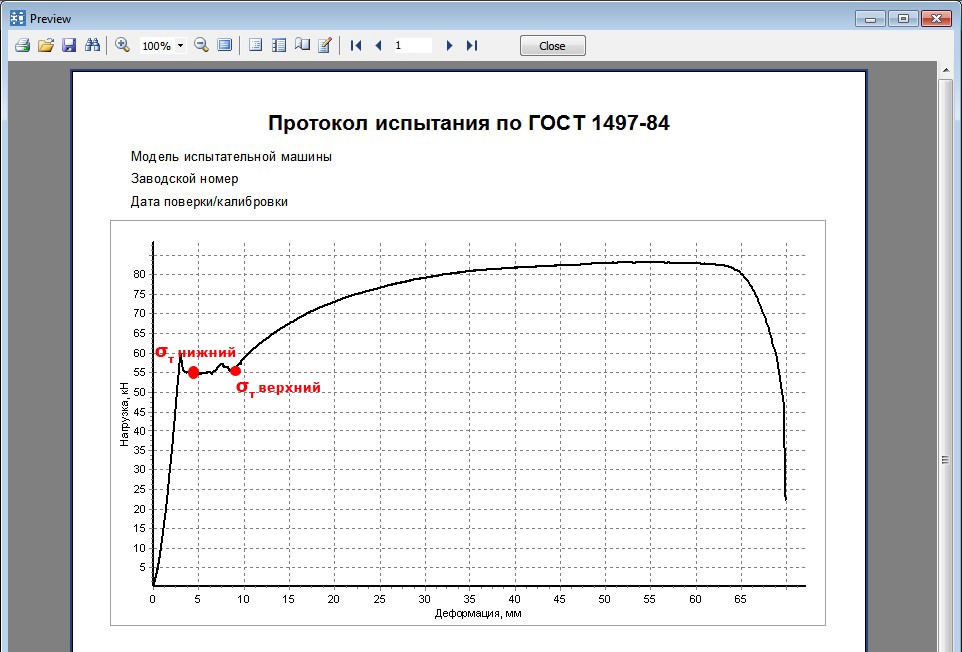
— предел текучести физический:
— нижний предел текучести Sт (МПа, кгс/мм2) — наименьшее напряжение, при котором образец деформируется без заметного увеличения растягивающей нагрузки;
— верхний предел текучести Sтв (МПа, кгс/мм2) — напряжение, соответствующее первому пику нагрузки, зарегистрированному до начала текучести рабочей части образца;
— предел текучести условный S0,2 (МПа, кгс/мм2) — напряжение, после снятия которого остаточное удлинение достигает 0,2% длины рабочего участка образца;
— временное сопротивление (предел прочности) Sв (МПа, кгс/мм2) — максимальное напряжение, которое выдерживает образец до разрушения;
— относительное равномерное удлинение dр (%) — отношение приращения длины участка в рабочей части образца до момента начала образования шейки (в т. в) для пластичных материалов или до разрыва в материалах, у которых шейка не образуется, к длине образца до испытания;
— относительное удлинение после разрыва d (%) — отношение приращения расчетной длины образца Dlк = (lк -l0) после разрушения к начальной расчетной длине l0;
— относительное сужение после разрыва y (%) — отношение разности начальной F0 и минимальной конечной Fкплощадей поперечного сечения образца после разрушения к начальной площади поперечного сечения образца F0;
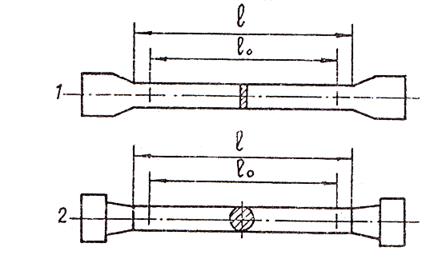
Для испытаний на растяжение применяют пропорциональные цилиндрические или плоские образцы (рис. 1.1) диаметром или толщиной в рабочей части 3 мм и более. Начальная расчетная длина цилиндрических образцов
l0 =5d0, l0 =10d0, а образцов квадратного или прямоугольного сечения —
l0 = 5,65 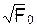
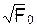
Образцы из тонких листов и лент толщиной от 0,5 до 3 мм изготавливают в соответствии с ГОСТ 11701-84.
Испытания проводят обычно на двух образцах.
Допускается применение непропорциональных образцов, для которых начальная расчетная длина l0устанавливается независимо от начальной площади поперечного сечения образца F0.
Типы и размеры пропорциональных цилиндрических и плоских образцов приведены в приложениях к ГОСТ 1497-84.
Рис. 1. Образцы для испытаний на растяжение: 1 — плоский; 2 — цилиндрический
Форма и размеры головок и переходных частей образцов определяются способом крепления образцов в захватах разрывной машины.
По ГОСТ 1497-84 определяют место вырезки, способ изготовления, качество поверхности, предельные отклонения по размерам образцов.
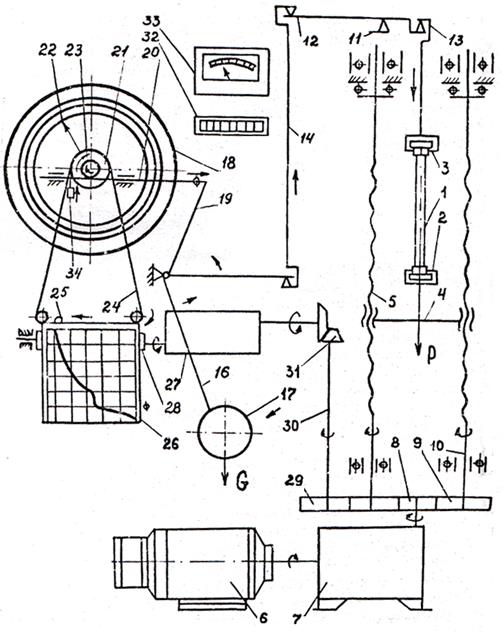
В качестве испытательных применяют разрывные и универсальные машины различных систем. Машина должна обеспечивать: надежное центрирование образца в захватах, плавность нагрузки, скорость перемещения подвижного захвата не более 0,1 мм/мин до предела текучести и не более 0,4 мм/мин за пределом текучести. Принципиальная схема разрывной машины Р-5 с рычажно-маятниковым силоизмерителем показана на рис. 2 (стрелками на схеме указаны движения элементов машины в процессе нагружения образца).
Испытываемый образец 1 помещают в захваты, один из которых (2) называется активным, а другой (3) — пассивным. Активный захват располагается на подвижной траверсе 4, в которой имеются застопоренные (не вращающиеся) гайки 5. Привод активного захвата (создание силы Р ) осуществляется электромеханическим путем: вращательное движение вала электродвигателя 6 через червячный редуктор 7 и шестерни 8 и 9 передается винтам 10; вращаясь в застопоренных гайках, винты заставляют траверсу перемещаться поступательно.
На опоре11 верхней неподвижной траверсы установлен рычаг 12 маятникового силоизмерителя, связанный с тягой 13 пассивного захвата 3. Через систему рычагов и тяг силоизмерителя 12 — 16 нагрузка Р, действующая на образец, уравновешивается силой G маятникового груза 17. Отклонение маятника от начального положения (когда Р = 0) фиксируется по отсчетному устройству 18 со шкалами, проградуированными по силе Р .
При отклонении маятника поводок 19, жестко соединенный с рычагами 15 и 16 маятника, перемещает зубчатую рейку 20, которая вращает шестерню 21, сидящую на одной оси с рабочей стрелкой 22 отсчетного устройства силоизмерителя. При перемещении рабочая стрелка ведет за собой контрольную стрелку, которая фиксирует максимальное усилие. На циферблате отсчетного устройства нанесены три шкалы (А, Б и В), соответствующие различным диапазонам нагрузок (машина может быть настроена на создание предельных нагрузок: 1000, 2500 и 5000 кгс соответственно).
На одной оси с шестерней и рабочей стрелкой указателя нагрузок установлен шкив 23, который с помощью гибкого тросика 24 перемещает перо 25 самописца.
Для записи диаграммы Р = f(Dl) используют специальную бумажную ленту 26 (ЛПГ 320, ГОСТ 7836-75) с величиной наименьших делений 1,6 мм.
Одно такое деление по оси ординат (сила Р) при наладке машины на предельную нагрузку 1000 кгс соответствует 5 кгс, на 2500 кгс — 12,5 кгс, на 5000 кгс — 25 кгс.
При растяжении образца перемещению активного захвата в 1 мм будет соответствовать перемещение ленты по оси абсцисс (абсолютная деформация Dl ) на 10, 50 или 100 мм.
Желаемый масштаб Dl (10:1, 50:1 или 100:1) обеспечивается настройкой масштабного преобразователя 27, который является настраиваемым редуктором, передающим вращение на барабан 28 лентопротяжного механизма от шестерни 29 через валик 30 и пару конических шестерен 31.
Одновременно деформация может контролироваться специальным счетчиком 32, одна единица показаний которого соответствует 0,2 мм перемещения подвижной траверсы 4.
Движение активного захвата без нагрузки может происходить с различной скоростью (от 1 до 100 мм/мин), которая контролируется прибором 33.
Рис. 2. Принципиальная схема разрывной машины
Показанный на схеме груз 34 служит для возврата в исходное положение (к нулю) рабочей стрелки 22 и пера 25 при снятии нагрузки.
На этой же машине, применяя специальное приспособление, можно испытывать металлы на сжатие и изгиб.
Диаграмма деформации при растяжении
Записывающее устройство разрывной машины графически изображает зависимость между действующей осевой нагрузкой и абсолютной деформацией образца.
На рис. 3 даны типичные диаграммы растяжения различных металлов. Первая диаграмма на рис. 3 свойственна большинству металлов и сплавов. Для малоуглеродистой отожженной стали и некоторых отожженных бронз характерна вторая диаграмма с площадкой текучести, которая приведена на рис. 3. Хрупкие металлы (чугун и др.) разрушаются при малых пластических деформациях (рис. 3, третья диаграмма).
Рис. 3. Диаграммы растяжения различных металлов
Характерные участки и точки диаграммы растяжения показаны на рис. 4.
Первый участок диаграммы 0P представляет собой прямую линию, т.е. между Р и Dl соблюдается закон Гука. Напряжение в точке Р есть предел пропорциональности 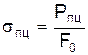
При дальнейшем увеличении силы прямолинейная зависимость нарушается.
Несколько выше точки Р находится точка «е». Напряжение в точке «е» есть предел упругости s0,05, который вычисляют по формуле
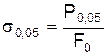
Предел упругости s0,05 , как и предел пропорциональности, определяется расчетным или графическим способом.
Точно так же определяется и модуль упругости Е, МПа (кгс/мм2):
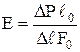
 |
Рис. 4. Характерные участки и точки диаграммы растяжения
За точкой «е» возникают заметные остаточные деформации, в точке S наблюдается переход к горизонтальной площадке S-S¢ (площадка текучести). Для участка S-S¢ характерен рост деформации без заметного увеличения нагрузки. Если обозначить величину нагрузки, соответствующую площадке текучести, через Рт, то напряжение в этой точке можно вычислить по формуле
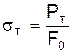
что и является физическим пределом текучести.
Следует отметить, что иногда (особенно это характерно для малоуглеродистой стали) на площадке текучести появляется «зуб» или низкочастотные колебания нагрузки. Это объясняется особенностями строения испытываемых материалов.
В этом случае предел текучести определяется по верхней точке амплитуды «зуба» («зубьев») и называется верхним пределом текучести (рис. 5).
Для материалов, не имеющих на диаграмме площадки текучести, определяют условный предел текучести
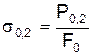
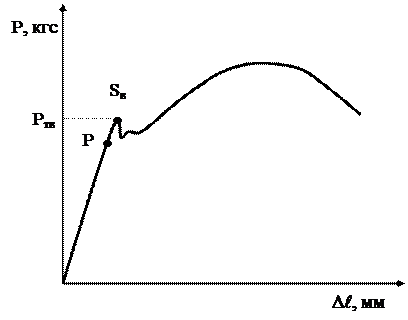 |
Рис. 5. Определение верхнего предела текучести
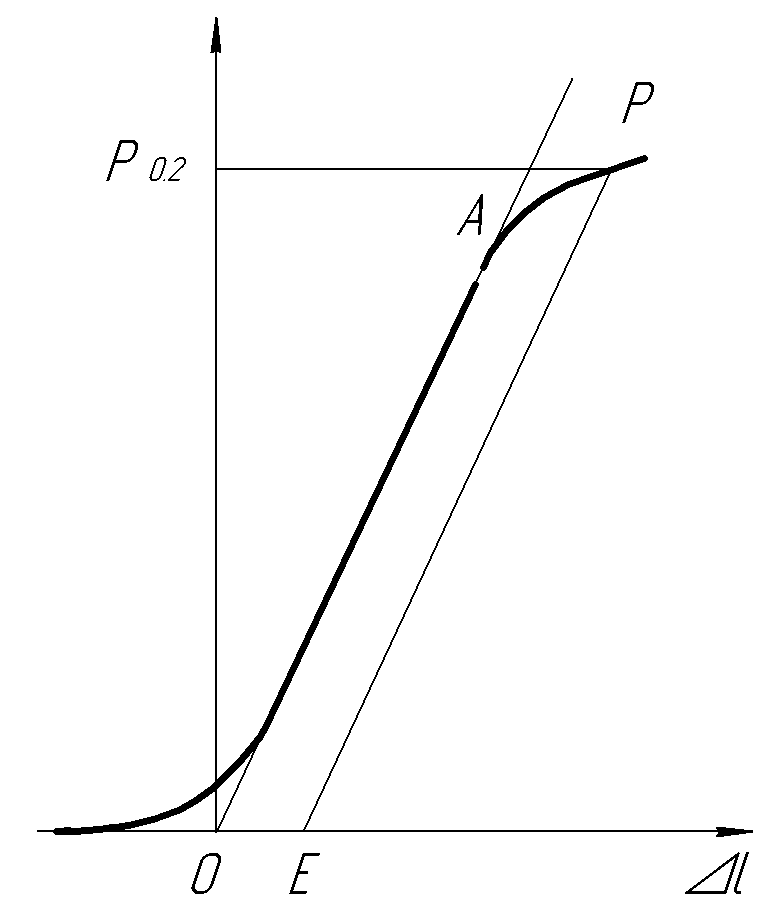
Для нахождения величины Р0,2 в масштабе диаграммы по оси абсцисс вправо от точки 0 (рис. 1.6) откладывают отрезок ОЕ, равный 0,002l0, что составляет 0,2% от l0, и из точки Е проводят прямую, параллельную прямой ОР, до пересечения с кривой растяжения в точке S . Ордината этой точки определяет нагрузку Р0,2.
За площадкой текучести происходит упрочнение материала, и сопротивление деформации увеличивается, поэтому наблюдается увеличение нагрузки на кривой растяжения. До точки «в» образец деформируется равномерно.
Наибольшая нагрузка, предшествующая разрушению образца, обозначается Рв = Рmax. Напряжение в точке «в» называется временным сопротивлением, или пределом прочности:
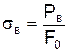
После точки «в», соответствующей максимальной силе Рв, происходит заметное местное сужение образца (образуется шейка). Если до этого образец имел цилиндрическую форму, то теперь растяжение образца сосредотачивается в области шейки. На участке в-к сечение образца быстро уменьшается, вследствие чего уменьшается растягивающая нагрузка. В точке «к» образец разрывается по наименьшему сечению шейки Fк.
Показателем пластичности материала является его абсолютное остаточное удлинение lост при разрыве (см. рис. 4, отрезок 0А1), так как упругая деформация (отрезок А1А2) исчезает после разрыва:
Dlост =lк — l0 . (1.6)
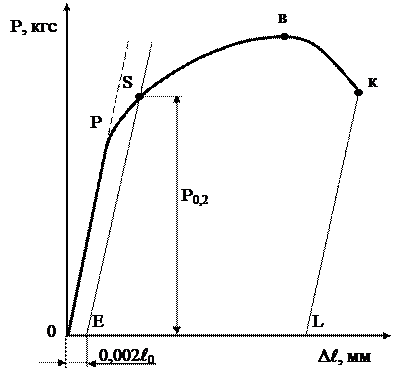 |
Рис. 6. Определение местоположения точки S, соответствующей условному пределу текучести
Размеры испытуемых образцов могут быть различными, поэтому характеристикой пластичности образца является не его абсолютное, а относительное остаточное удлинение после разрыва
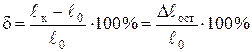
Другой характеристикой пластичности металла является относительное сужение Y после разрыва, выраженное в процентах:
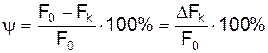
При определении sпц, s0,05, sт и sв соответствующую им нагрузку Р делим на начальную площадь поперечного сечения образца F0. Напряжения эти называются условными. Однако при растяжении образца площадь поперечного сечения уменьшается. Напряжения, определенные по отношению приложенной нагрузки к действительной площади поперечного сечения образца в момент приложения этой нагрузки, называются истинными напряжениями:
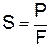
Диаграмма растяжения Р–Dl характеризует поведение образца из испытываемого материала с определенными геометрическими размерами. Чтобы исключить влияние размеров, диаграмму Р–Dl перестраивают в диаграмму s–e , где 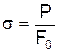
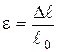
Как уже было сказано, для точного определения sпц, s0,05 и s0,2 используются специальные тензометры и электрические силоизмерители. С меньшей точностью эти характеристики можно определить, воспользовавшись машинными диаграммами и простейшим мерительным инструментом (линейка, штангенциркуль, микрометр).
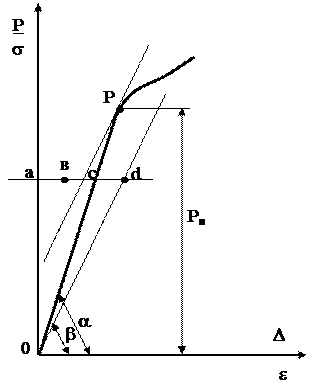 |
Рис. 7. Определение местоположения точки Р, соответствующей пределу пропорциональности
Графическое определение местоположения точки Р предела пропорциональности состоит в следующем (рис. 7).
Произвольной горизонтальной прямой пересекают кривую растяжения на линейном участке. Полученный отрезок ас делят на две равные части. Откладывают отрезок сd, который равен половине отрезка ас: ав=вс=сd. Из начала координат 0 проводят луч через точку d. Точку Р, соответствующую пределу пропорциональности, находят построением касательной к кривой растяжения, параллельной лучу 0d.
Значение предела упругости s0,05 принимается равным значению полученного предела пропорциональности sпц из-за незначительного различия между ними.
Численные значения механических характеристик позволяют оценить прочностные и пластические свойстве испытанного материала
Оценка прочности и пластичности
| Материал | sв | Уровень прочности | d ,% | Уровень пластичности | |
| кгс/мм2 | МПа | пластичности | |||
| Стали | 140-200 и более | 1400-2000 и более | высокопрочные | >40 | высоко- пластичные |
| 80-140 | 800-1400 | прочные | 20-40 | пластичные | |
| 20-80 | 200-800 | средней прочности | 10-20 | средней пластичности | |
| <20 | <200 | малопрочные | <10 | малопластичные | |
| Алюминиевые сплавы | >50 | >500 | высокопрочные | 25-35 | повышенной пластичности |
| 35-40 | 350-400 | нормальной прочности | 20-25 | пластичные | |
| <35 | <350 | малопрочные | <20 | малопластичные |
Оценка прочности и пластичности
| Материал | Sв | Уровень прочности | d ,% | Уровень пластичности | |
| кгс/мм2 | МПа | пластичности | |||
| Стали | 140-200 и более | 1400-2000
и более |
высокопрочные | >40 | высоко- пластичные |
| 80-140 | 800-1400 | прочные | 20-40 | пластичные | |
| 20-80 | 200-800 | средней прочности | 10-20 | средней пластичности | |
| <20 | <200 | малопрочные | <10 | малопластичные | |
| Алюминиевые сплавы | >50 | >500 | высокопрочные | 25-35 | повышенной пластичности |
| 35-40 | 350-400 | нормальной прочности | 20-25 | пластичные | |
| <35 | <350 | малопрочные | <20 | малопластичные |
При растяжении образца до разрушения графически фиксируют зависимости между приложенным усилием и удлинением образца, получая диаграммы деформации (рис. 8).
Рис. 8. Диаграмма деформации материала
Деформация образца при нагружении сначала является макроупругой, а затем постепенно и в разных зернах при неодинаковой нагрузке переходит в пластическую, происходящую путем сдвигов по дислокационному механизму. Накопление дислокаций в результате деформации ведет к упрочнению металла, но при значительной их плотности, особенно в отдельных участках, возникают очаги разрушения, приводящие в конечном счете к полному разрушению образца в целом.
При испытании на растяжение согласно ГОСТ 1497-84 определяют следующие характеристики:
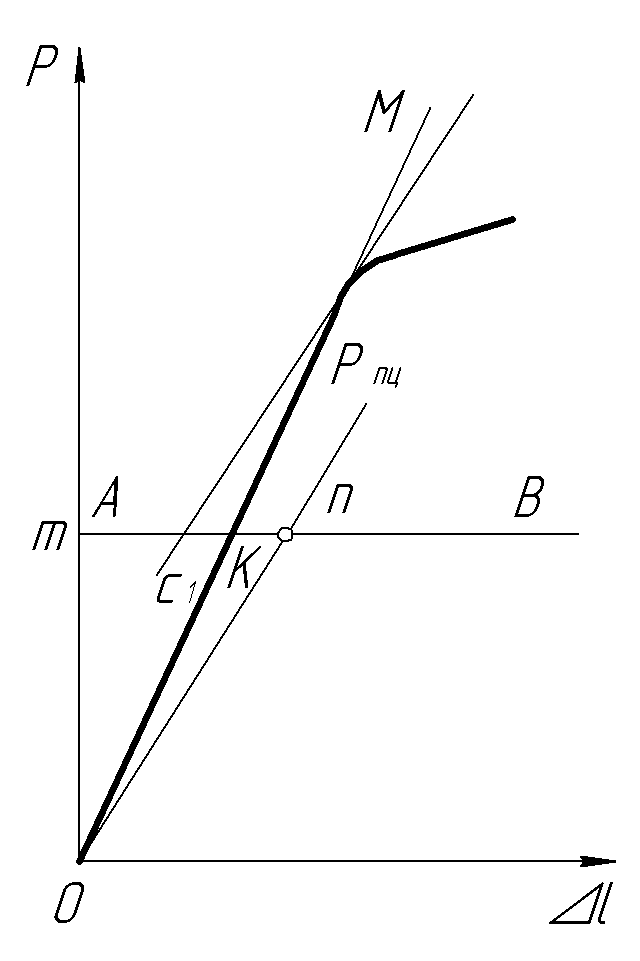
1. Предел пропорциональности σпц – отвечает напряжению, при котором отклонение от линейной зависимости между нагрузкой и удлинением достигает такой величины, что тангенс угла наклона, образованного касательной к кривой нагрузка-удлинение в точке Рпц с осью нагрузок увеличивается на 50 % от своего значения на упругом (линейном) участке. На рис. 4 показано определение предела пропорциональности графическим способом. В этом случае из начала координат диаграммы растяжения, записанной от электрического силоизмерителя и измерителя деформации, проводят прямую, совпадающую с начальным линейным участком этой диаграммы. Затем на произвольном уровне проводят прямую АВ,параллельную оси абсцисс, и на ней откладывают отрезок rn равный половине отрезка mr. Через точку п и начало координат проводят прямую On и параллельно ей – касательную CD к диаграмме растяжения. Точка касания определяет нагрузку Рпц в ньютонах, отвечающую пределу пропорциональности:
где Fo – начальное поперечное сечение образца.
Размеры пропорциональных цилиндрических образцов III типа и плоских образцов для испытания на растяжение приведены в табл. 1 и табл. 2 соответственно.
Таблица 1
Размеры пропорциональных цилиндрических образцов III типа, мм
|
Номер образца |
d0 |
l0=5d0 |
l=10d |
D |
h1 |
h2 |
r |
|
1 |
25 |
125 |
250 |
45 |
30 |
5 |
5 |
|
2 |
20 |
100 |
200 |
34 |
25 |
5 |
5 |
|
3 |
15 |
75 |
150 |
28 |
20 |
3 |
3 |
|
4 |
10 |
50 |
100 |
16 |
10 |
3 |
3 |
|
5 |
8 |
40 |
80 |
13 |
10 |
3 |
2 |
|
6 |
6 |
30 |
60 |
12 |
10 |
2,5 |
1,5 |
|
7 |
5 |
25 |
50 |
11 |
10 |
2,5 |
1,5 |
|
8 |
4 |
20 |
40 |
9 |
8 |
2,5 |
1,5 |
|
9 |
3 |
15 |
30 |
7 |
7 |
2,0 |
1,5 |
Таблица 2
Размеры пропорциональных плоских образцов, мм
|
Номер образца |
a0 |
b0 |
l0=5,65 |
l0=11,3 |
B |
h1 |
|
1 |
25 |
30 |
155 |
310 |
40 |
100 |
|
2 |
24 |
30 |
155 |
310 |
40 |
100 |
|
3 |
23 |
30 |
150 |
300 |
40 |
90 |
|
4 |
22 |
30 |
145 |
290 |
40 |
90 |
|
5 |
21 |
30 |
140 |
280 |
40 |
80 |
|
6 |
20 |
30 |
140 |
280 |
40 |
80 |
|
7 |
19 |
30 |
135 |
270 |
40 |
80 |
|
8 |
18 |
30 |
130 |
260 |
40 |
80 |
|
9 |
17 |
30 |
125 |
250 |
40 |
80 |
|
10 |
16 |
30 |
125 |
250 |
40 |
80 |
|
11 |
15 |
30 |
120 |
240 |
40 |
70 |
|
12 |
14 |
30 |
115 |
230 |
40 |
70 |
|
13 |
13 |
30 |
110 |
220 |
40 |
70 |
|
14 |
12 |
30 |
105 |
210 |
40 |
60 |
|
15 |
11 |
30 |
105 |
210 |
40 |
60 |
|
16 |
10 |
30 |
100 |
200 |
40 |
60 |
|
17 |
9 |
30 |
90 |
180 |
40 |
50 |
|
18 |
8 |
30 |
85 |
170 |
40 |
50 |
|
19 |
7 |
20 |
70 |
140 |
40 |
50 |
|
20 |
6 |
20 |
65 |
130 |
40 |
50 |
|
21 |
5 |
20 |
60 |
120 |
40 |
50 |
|
22 |
4 |
20 |
50 |
100 |
40 |
50 |
|
23 |
3 |
20 |
45 |
90 |
30 |
40 |
2. Предел упругости а0,05 – напряжение, при котором остаточное удлинение достигает 0,05 % длины участка рабочей части образца, равного базе тензометра. Определяют предел упругости расчетным (по разгрузке и нагрузке) и графическим способами. При использовании способа нагрузки с допуском на величину полного удлинения (упругого + остаточного) образец после установки на него тензометра нагружают равными ступенями до нагрузки, соответствующей напряжению 70-80 % от предполагаемого предела упругости σ0,05. Дальнейшее нагружение проводят более мелкими ступенями с выдержкой не более 7 с.
Вычисляют величину допуска на полное удлинение суммированием определенного среднего упругого удлинения и рассчитанного остаточного удлинения.
Определяют нагрузку Р0,05, соответствующую установленному допуску на полное удлинение образца. Для уточнения значения Р0,05 допускается применение метода линейной интерполяции.
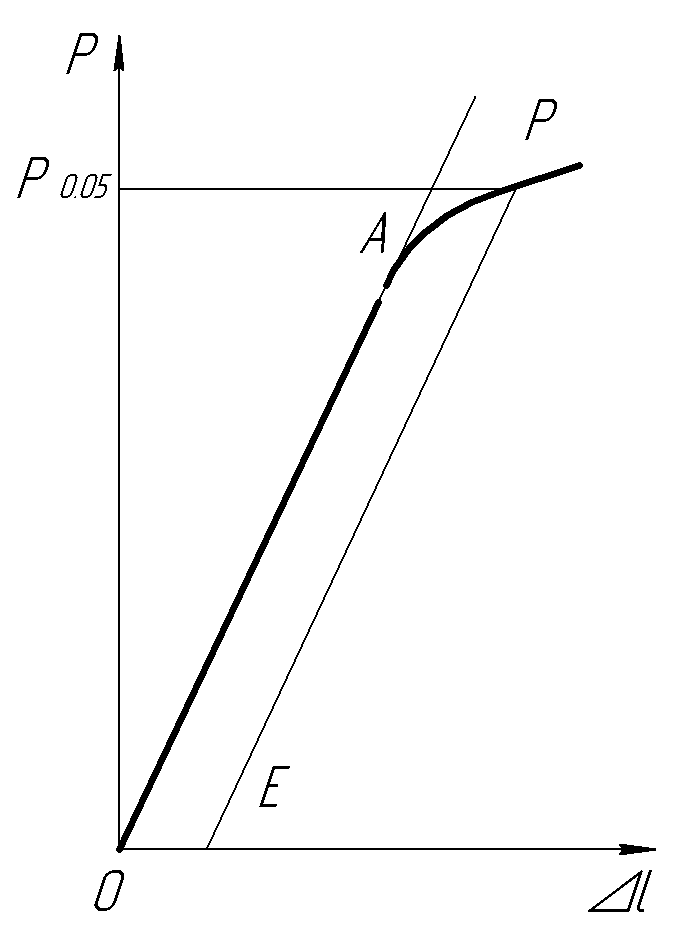
Графическим способом предел упругости σ0,05 определяют по начальному участку диаграммы растяжения, записанной от электрических силоизмерителя и измерителя деформации (рис. 9). Удлинение определяется на участке, равном базе измерителя деформации.
Для определения нагрузки Р0,05 вычисляют соответствующее остаточное удлинение с учетом базы измерителя деформации. Найденное значение увеличивают пропорционально масштабу диаграммы по оси абсцисс вправо от начала координат О. Из точки Е проводят прямую ЕР, параллельную прямой ОА. Точка пересечения Р с диаграммой растяжения определяет искомую нагрузку Р0,05. Масштаб по оси удлинения должен быть не менее 100 : 1 при базе измерителя деформации 50 мм и более и не менее 200 : 1 при базе измерителя менее 50 мм; по оси нагрузки 1 мм диаграммы должен соответствовать не более 10 МПа.
Предел упругости σ0,05 вычисляют по формуле, МПа:
.
Рис. 9. Схема определения предела пропорциональности σпц при растяжении
Рис. 10. Схема определения предела упругости σ0,05 при растяжении
3. Модуль упругости Е – отношение приращения напряжения к соответствующему приращению удлинения в пределах упругой деформации; модуль упругости определяют расчетным способом с помощью тензометров и графическим способом по начальному участку диаграммы растяжения, записанной от электрических силоизмерителя и измерителя деформации.
Модуль упругости вычисляют по формуле, МПа:
,
где – приращение нагрузки;
– среднее приращение удлинения;
– начальная расчетная длина образца;Fо – начальная площадь поперечного сечения.
4. Предел текучести физический (нижний предел текучести) – наименьшее напряжение, при котором образец деформируется без заметного увеличения растягивающей нагрузки.
Верхний предел текучести – напряжение, соответствующее верхнему пику нагрузки, зарегистрированному до начала текучести рабочей части образца.
Предел текучести (условный) – напряжение при котором остаточное удлинение достигает 0,2 % длины участка образца на его рабочей части, удлинение которого принимается в расчет при определении указанной характеристики. Упомянутые пределы текучести определяют по диаграмме растяжения, полученной на испытательной машине, если 1 мм диаграммы по оси нагрузок соответствует не более 10 МПа:
МПа
Соответствующие нагрузки Рт, Ртв, Ртн для различных видов диаграммы растяжения представлены на рис. 6.
Предел текучести условный определяют расчетным способом с применением тензометров так же, как и предел упругости
. Для определения
графическим методом сначала вычисляют величину остаточного удлинения с учетом установленного допуска исходя из рабочей длины образца. Найденное значение увеличивают пропорционально масштабу диаграммы растяжения и полученный отрезок длины откладывают по оси удлинения от точки О до точки Е (см. рис. 11). Из точки Е проводят прямую параллельно прямой ОА. Точка пересечения Р с диаграммой растяжения определяет нагрузку Р0,2, соответствующую условному пределу текучести
, МПа:
.
Рис. 11. Схема определения предела текучести при растяжении
Условный предел текучести определяют только при отсутствии на диаграмме растяжения площадки текучести.
5. Временное сопротивление (предел прочности) σв – напряжение, соответствующее наибольшей нагрузке Ртах, предшествующей разрыву образца. Временное сопротивление вычисляют по формуле, МПа:
6. Относительное удлинение (после разрыва) – одна из характеристик пластичности материалов, равная отношению приращения расчетной длины образца после разрушения к начальной расчетной длине
,%:
7. Относительное равномерное удлинение – отношение приращения длины участков в рабочей части образца после разрыва к длине до испытания, выраженное в процентах.
8. Относительное сужение после разрыва , как и относительное удлинение – характеристика пластичности материала и определяется как отношение разности Fo и минимальной Fк площади поперечного сечения образца после разрушения к начальной площади поперечного сечения Fo,выраженное в процентах.
Литература:
1. Конструкционное материаловедение/ Борисевич В.К., Виноградский А.Ф., Карпов Я.С., Самойлов В.Я., Семишов Н.И.: В 2 кн. Х.: Нац. аэрокосм. ун-т им. Н.Е. Жуковского «ХАИ», 2001. Кн. 1. Металлы и сплавы. 456 с.
2. Лахтин Ю.М., Леонтьева В.П. Материаловедение. М.: Машиностроение, 1990. 528 с.
3. Гуляев А.П. Металловедение. М.: Металлургия, 1977. 647 с.
4. Борисевич В.К., Виноградский А.Ф., Семишов Н.И. Конструкционное материаловедение. Х.: Харьк. авиац. ин-т, 1998. 404 с.
5. Лахтин Ю.М. Металловедение и термическая обработка металлов. М.: Металлургия, 1977. 407 с.
6. Мозберг Р.К. Материаловедение. Таллин: Валгус, 1976. 554 с.
7. Глазунов С.Г., Моисеев В.Н. Конструкционные титановые сплавы. М.: Металлургия, 1984. 367 с.
8. Сазоненко Н.Д., Горбань В.П., Каныгин С.Л. Свойства и применение нержавеющих, жаростойких и жаропрочных сталей и сплавов в авиадвигателестроении: Учеб. пособие. Х.: Харьк. авиац. ин-т, 1994. 30 с.
9. Свойства и применение сплавов алюминия, магния, бериллия в авиастроении: Учеб. пособие/ Горбань В.П., Рева Л.С., Сазоненко Н.Д., Кириченко Л.Р., Каныгин С.Л. Х. :Харьк. авиац. ин-т, 1994. 62 с.