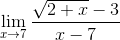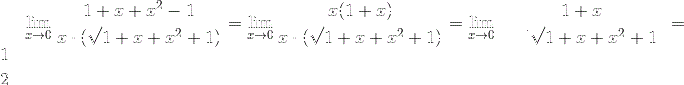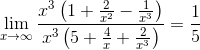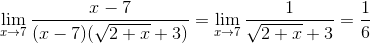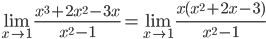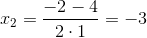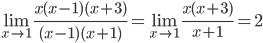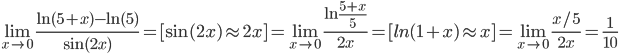Вычисление пределов, производной, касательной
Выберите задачу для решения.
Решение пределов
Найти производную
Уравнение касательной к графику функции
Решение пределов
Число A называется пределом функции y=f(x) в точке x0, если для любой последовательности точек из области определения функции, отличных от x0, сходящейся к точке x0(lim xn = x0), последовательность соответствующих значений функции сходится к числу A.
- Решение онлайн
- Видеоинструкция
- Оформление Word
- Также решают
Если выбрать вид предела, то подробное решение по шагам будет доступно в MS Word:
1. Не знаю
2. Пределы вида 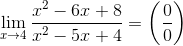
3. Вычислить предел, используя правило Лопиталя.
4. Пределы простейших иррациональности вида
5. Нахождение пределов, используя свойства первого замечательного предела ,
6. Нахождение пределов, используя свойства второго замечательного предела ,
,
Для нахождения предела слева
используйте знак -, справа
: +. Например, 0-, 1+
Примечание: число «пи» (π) записывается как pi, знак ∞ как infinity
Некоторые виды записи пределов
Например, найти предел 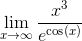
см. также нахождение пределов, используя свойства первого замечательного предела и второго замечательного предела.
Примеры.
Вычислить указанные пределы:
1. 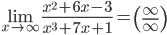
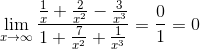
2. 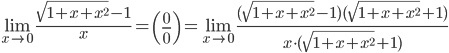
3. 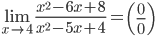
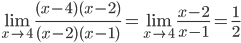
4. 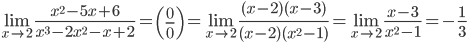
5. 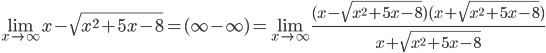
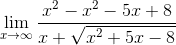
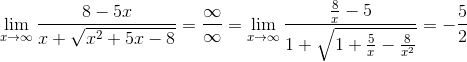
6. 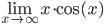
7. 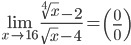
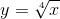
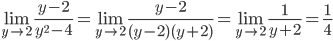
8. 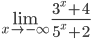
9. 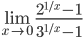
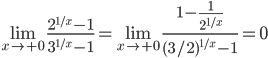
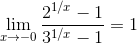
Следовательно, 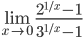
Найти пределы функции, не применяя правило Лопиталя.
а)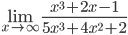
Ответ: 1/5
б) 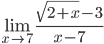
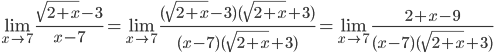
Ответ: 1/6
в) 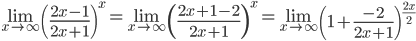
e-2/2 = e-1
Ответ: 1/e
г)
Так как числитель и знаменатель обратились в нуль при x=1, то 1 – корень обоих многочленов, а значит, каждый из них разлагается на множители, одним из которых будет (x-1).
Найдем корни первого многочлена: x2+2x-3=0
D=22-4•1•(-3)=16
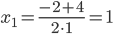
Найдем корни второго многочлена: x2-1=(x-1)(x+1)
Получаем:
Ответ: 2
д) 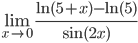
Ответ: 1/10
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
© 2011-2023 Довжик Михаил
Копирование материалов запрещено.
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Если Вы хотите связаться со мной, имеете вопросы, предложения или хотите помочь развивать сайт OnlineMSchool пишите мне support@onlinemschool.com
Что такое предел? Понятие предела
Все без исключения где-то в глубине души понимают, что такое предел, но как только слышат «предел функции» или «предел последовательности», то возникает легкая растерянность.
Не волнуйтесь, это всего лишь от незнаний! Через 3 минуты прочтения ниженаписанного, вы станете грамотнее.
Важно раз и навсегда понять, что имеют в виду, когда говорят о каких-то предельных положениях, значениях, ситуациях и вообще, когда по жизни прибегают к термину предела.
Взрослые люди это понимает интуитивно, а мы разберем на нескольких примерах.
Пример первый
Вспомним строки из песни группы «Чайф»: «… не доводи до предела, до предела не доводи …».
В данном случае по задумке автора предельная ситуацию в отношениях между людьми – это расставание.
Автор как бы предупреждает, что в результате последовательности конкретных действий мы придем к конкретному результату – расставанию.
Пример второй
Наверняка вы слышали фразу о предельно устойчивом положении предмета в пространстве.
Вы сами можете без труда смоделировать такую ситуацию с подручными вещами.
Например, слегка наклоните пластиковую бутылку и отпустите её. Она обратно встанет на днище.
Но есть такие предельные наклонные положения, за границами которых она просто упадет.
Опять же предельное положение в данном случае — это нечто конкретное. Важно это понимать.
Можно много приводить примеров использования термина предела: предел человеческих возможностей, предел прочности материала и так далее.
Ну а с беспределами так вообще каждый день сталкиваемся)))
Но сейчас нас интересуют предел последовательности и предел функции в математике.
Предел числовой последовательности в математике
Предел (числовой последовательности) — одно из основных понятий математического анализа. На понятии предельного перехода базируются сотни и сотни теорем, определяющие современную науку.
Сразу конкретный пример для наглядности.
Допустим есть бесконечная последовательность чисел, каждое из которых в два раза меньше предыдущего, начиная с единицы: 1, ½, ¼, …
Так вот предел числовой последовательности (если он существует) – это какое-то конкретное значение.
В процессе деления пополам каждое последующее значение последовательности неограниченно приближается к определенному числу.
Несложно догадаться, что это будет ноль.
Важно!
Когда мы говорим о существовании предела (предельного значения), это не значит, что какой-то член последовательности будет равен этому предельному значению. Он может лишь только стремиться к нему.
Из нашего примера это более чем понятно. Сколько бы раз мы не делили единицу на два, мы никогда не получим ноль. Будет лишь число в два раза меньше предыдущего, но никак не ноль!
Предел функции в математике
В математическом анализе безусловно самое важное – это понятие предела функции.
Не углубляясь в теорию, скажем следующее: предельное значение функции не всегда может принадлежать области значений самой функции.
При изменении аргумента, функция будет стремиться к какому-то значению, но может его не принять никогда.
Например, гипербола 1/x не имеет значения ноль ни в какой точке, но она неограниченно стремится к нулю при стремлении x к бесконечности.
Калькулятор пределов
Нашей целью не является дать вам какие-то теоретические знания, для этого есть куча умных толстых книжек.
Но мы предлагаем вам воспользоваться онлайн калькулятором пределов, с помощью которого сможете сравнить ваше решение с правильным ответом.
Помимо всего, калькулятор выдает пошаговое решение пределов, применяя зачастую правило Лопиталя с использованием дифференцирования числителя и знаменателя непрерывной в точке или на некотором отрезке функции.
Постоянная называется пределом функции
при , если для любого числа
существует число
такое, что при всех , удовлетворяющих условию
выполняется неравенство
Для того чтобы вычислить предел необходимо знать основные правила вычисления пределов или воспользоваться нашим онлайн калькулятором.
Наш онлайн калькулятор способен вычислить пределы для очень многих математических выражений, калькулятор также генерирует подробное решение задачи.