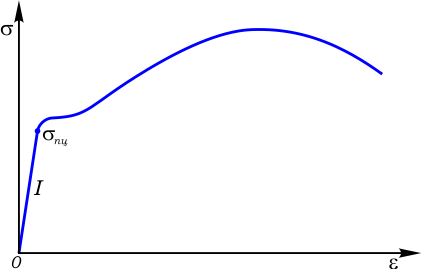
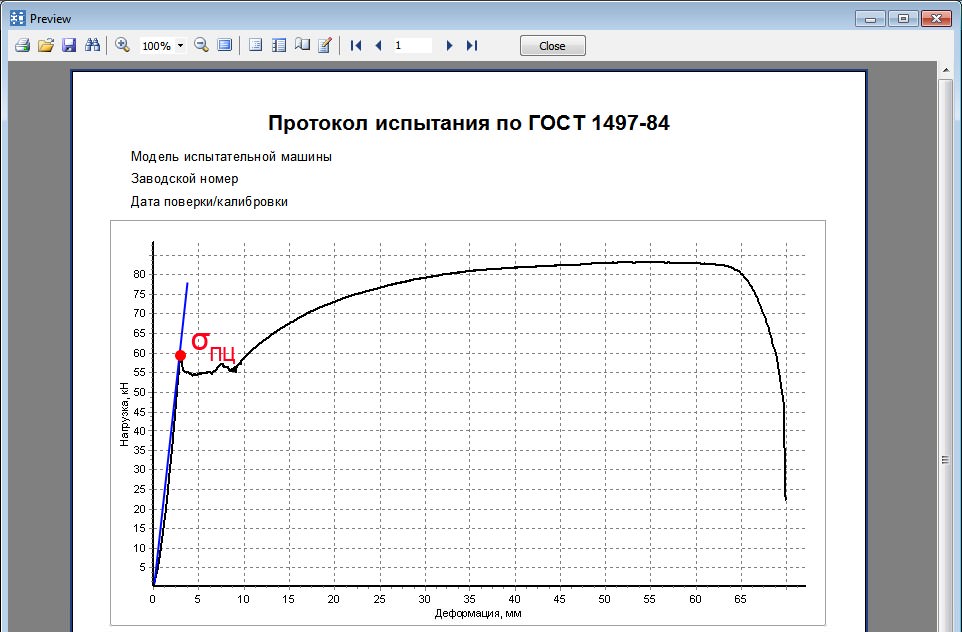
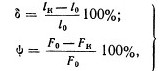Пределом пропорциональности называют значение напряжения, превышение которого приводит к отклонению от закона Гука.
Обозначение: σпц
Единица измерения: Паскаль [Па] либо кратные значения — мегапаскаль [МПа].
Это важная механическая характеристика материалов, определяется по ординате самой верхней точки начального прямолинейного участка диаграммы напряжений (рис. 1).
Рис. 1. Предел пропорциональности на диаграмме напряжений
Участок I диаграммы от точки O до σпц называется участком пропорциональности. На этом участке относительные деформации ε растут пропорционально нормальным напряжениям σ.
После прохождения предела пропорциональности, зависимость между напряжениями и деформациями меняется, и закон Гука становится неактуальным.
Все деформации в пределах участка пропорциональности являются упругими.
Предел текучести >
Предел прочности >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
1. Предел прочности
Пределом прочности называют максимальное усилие растяжения, отнесенное к единице площади его первоначального сечения
σВ=P/F,Па
Другими словами, предел прочности есть условное максимальное напряжение, которое выдерживает материал при растяжении. Под «истинным пределом прочности»(или под действительным сопротивлением разрыву) понимается усилие в момент разрыва P, отнесенное к площади сечения.
2. Предел пропорциональности и упругости
Под пределом пропорциональности σПЦ понимают наименьшее напряжение вызывающее в испытуемом материале отклонение от закона пропорциональности (или наибольшее напряжение от этого закона), а под пределом упругости σУП — наибольшее напряжение, ниже которого величина деформации является определенной функцией напряжения, независимо от возрастания или убывания последнего, то нет оснований предполагать идентичность этих двух величин.
3. Предел текучести
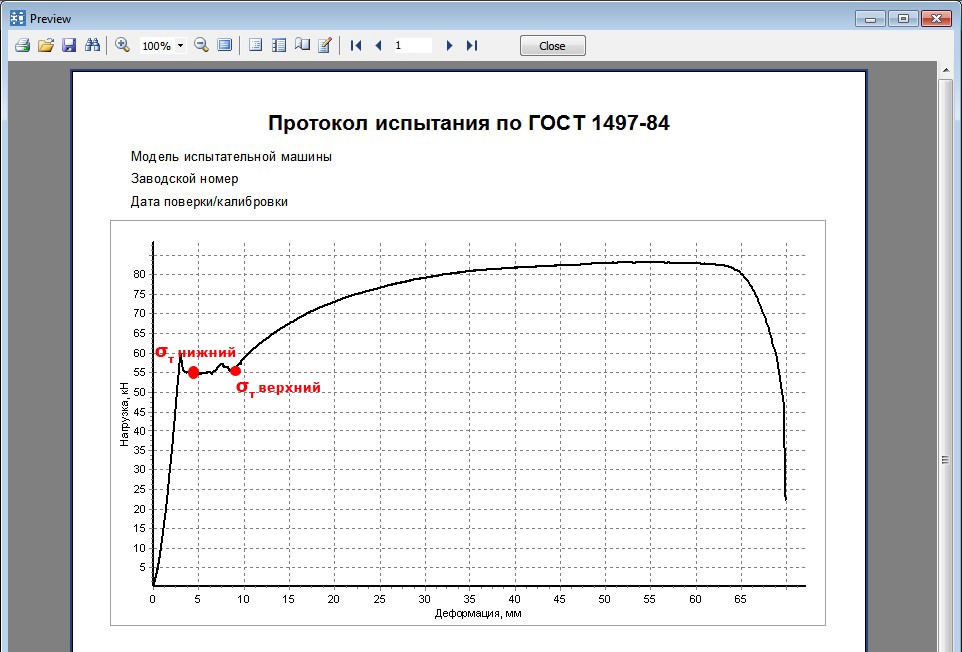
Пределом текучести σТ называется напряжение, при котором возникающая остаточная деформация образца распространяется равномерно по его рабочей части при временном постоянстве растягивающего усилия.
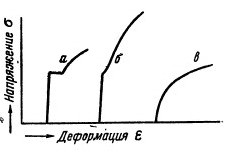
Практически в качестве предела текучести обычно принимается напряжение, при котором деформация образца возрастает, а стрелка динамометра разрывной машины либо останавливается, либо отходит назад. В этом случае на кривой «напряжение — деформация» образуется так называемая площадка текучести (кривая a), и тогда предел текучести называют явным или физическим.
Типичные кривые растяжения (α — ε)
В некоторых случаях площадка текучести бывает неясно выражена (кривая б) или совершенно отсутствует (кривая в); такую форму кривых при нормальной температуре испытания имеют весьма пластичные металлы (например, медь). С повышением же температуре явным пределом текучести, форма кривой имеет вид, показанный на рисунке, в. Мягкая углеродистая сталь с содержанием 0,05% при 300°С дает кривую, соответствующую кривой б; другие, более теплоустойчивые стали сохраняют явный предел текучести до 400 и даже до 500°С; выше этих температур форма кривых растяжения аналогична кривой в.
Во всех случаях, когда отсутствует явный предел текучести, приходится прибегать к нахождению так называемых условных пределов текучести, основанных на определении напряжений, вызывающих заданную остаточную деформацию небольшой величины (в пределах 0,01—0,5%). Чаще всего на практике определяют условные пределы текучести, вызывающие остаточную деформацию, равную 0,1 или 0,2%.
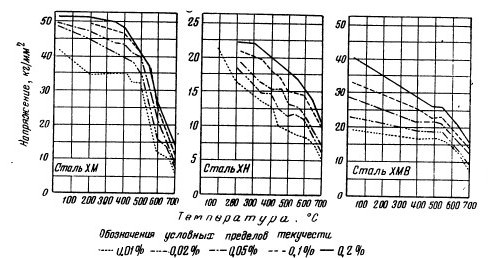
Условные пределы текучести некоторых легированных сталей
Если условные пределы текучести при нормальной температуре мало различаются между собой, то при высоких температурах разница между условными пределами текучести, например 0,01 и 0,2% (после текучести), становится значительной.
4. Удлинение и поперечное сужение образца
Удлинение и поперечное сужение образца, испытанного при высокой температуре, являются показателями пластических свойств металла при данной температуре.
Удлинение δ и поперечное сужение ψ замеряются на охлажденных образцах и подсчитываются по общеизвестным формулам:
- где l0 — начальная длина расчетного участка образца;
- lk — конечная длина расчетного участка образца;
- F0 — начальная площадь поперечного сечения образца;
- Fk — конечная площадь поперечного сечения образца.
Наибольшее влияние на эти свойства оказывает время до разрыва или, что то же самое, скорость растяжения образца.
5. Модуль упругости
Модуль нормальной упругости E является важной физико-механической характеристикой металла. Знание величины модуля упругости стали для широкого диапазона температур необходимо не только при конструкторских расчетах деталей машин и аппаратуры, работающих при повышенных температурах, но и в ряде других случаев.
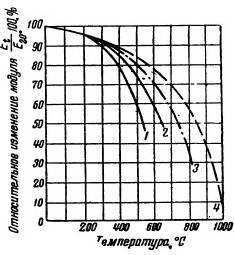
Относительное изменение модуля упругости E (в % от его значения при 20°) в зависимости от температуры для сталей: 1-нелегированной; 2-низколегированной; 3-среднелегированной; 4-высоколегированной
Работа № 1
ИСПЫТАНИЕ
МАЛОУГЛЕРОДИСТОЙ СТАЛИ
НА РАСТЯЖЕНИЕ
Цель работы
-
Ознакомиться со
стандартной методикой механических
испытаний конструкционных материалов
на одноосное растяжение. -
Провести испытание
малоуглеродистой стали на одноосное
растяжение и получить диаграмму
растяжения. -
Определить по
полученной диаграмме прочностные
характеристики материала образца:
предел пропорциональности, предел
текучести, предел прочности и напряжение
в момент разрыва. -
Определить
характеристики пластичности материала
образца: относительное удлинение и
относительное сужение при разрыве.
Краткие
теоретические сведения
Испытания на
одноосное статическое растяжение — это
наиболее распространенный вид испытаний
для определения механических свойств
металлов и сплавов. Статическим
называется такое нагружение материала,
когда внешняя нагрузка возрастает
настолько медленно, что силами инерции
в деформирующихся и перемещающихся
частях тела можно пренебречь. В противном
случае нагружение называется динамическим.
Методы испытаний
на растяжение стандартизированы.
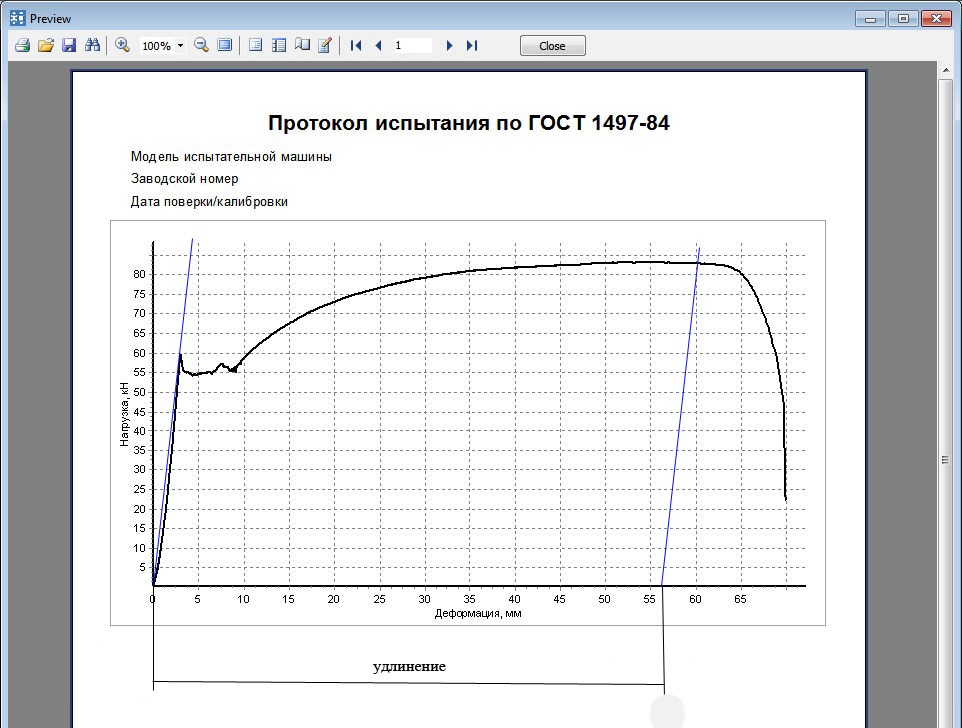
Испытания при
комнатной температуре регламентирует
ГОСТ 1497-84. В нем сформулированы определения
характеристик, устанавливаемых при
испытании, даны типовые формы и размеры
образцов, приведены основные требования
к испытательному оборудованию, описаны
методики проведения испытаний и обработки
полученных экспериментальных данных.
Образцы для
испытаний
Для испытаний на
растяжение часто используют образцы с
рабочей цилиндрической частью. На рис.1
показан такой стандартный образец.
Основные размеры
образца:
-
– рабочая
длина – часть образца, расположенная
между его головками (участками большего
диаметра, предназначенными для
закрепления образца в захватах
испытательной машины); -
– начальная
расчетная длина – участок рабочей
длины, на котором определяется
удлинение; -
– начальный
диаметр рабочей части.
Между размерами
образца установлены определенные
соотношения. Рабочая длина l должна
составлять от l0 + 0,5 d0 до
l0 + 2 d0 . Если А0 –
начальная площадь поперечного сечения
рабочей части образца (не обязательно
цилиндрического), то расчетная длина
(для коротких образцов) и
( для длинных ). Для цилиндрических
образцов эти условия превращаются в
соотношения:
(пятикратные) и
(десятикратные образцы) Диаметр рабочей
части образцов должен быть изготовлен
с точностью 0,04 мм.
Начальную расчетную длину на образце
отмечают неглубокими рисками.
В
данной лабораторной работе испытания
проводятся на машине УГ-20/2, развивающей
максимальное усилие в 200 кН. Машина
снабжена устройством, записывающим
диаграмму растяжения, т.е. график
зависимости между силой F и абсолютным
удлинением образца l.
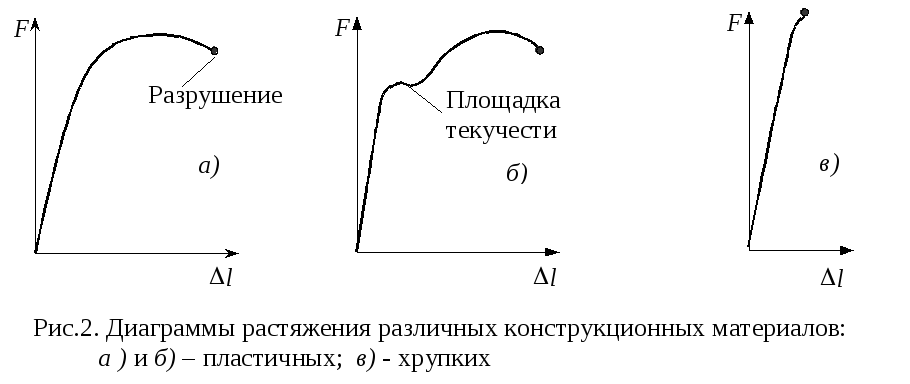
На рис.2 представлены
типичные диаграммы растяжения различных
материалов:
-
а)
для большинства пластичных
материалов с постепенным переходом
из упругой области в пластическую
(сталь 45, сталь 20Х); -
б) для некоторых
материалов (таких как малоуглеродистая
сталь Cт3пс), которые переходят из
упругой области в пластическую с явно
выраженной площадкой текучести; -
в) для хрупких
материалов (закаленные стали, твердые
сплавы).
На диаграмме
растяжения малоуглеродистой стали
(рис.3) нанесены характерные точки, по
ординатам которых рассчитывают
прочностные характеристики.
Предел
пропорциональности
По усилию
(т.А) определяют величину предела
пропорциональности
, (1)
напряжения, при
котором отступление от линейной
зависимости между нагрузкой и удлинением
достигает такой величины, что тангенс
угла, образованного касательной к кривой
“нагрузка – удлинение “ в точке А с
осью нагрузок, увеличивается на 50% от
своего значения на линейном участке
диаграммы. Приближенно величину
можно определить как ординату точки, в
которой начинается расхождение кривой
растяжения и продолжения линейного
участка OA.
Предел упругости
По усилию
(т.В) рассчитывают предел упругости
— напряжение, при
котором остаточное удлинение достигает
заданной величины, обычно равной 0,05%,
иногда меньше – до 0,005%. Соответствующие
этим значениям пределы упругости
обозначаются:
и т.д. Предел упругости – это напряжение,
при котором в материале образца
появляются первые признаки пластических
деформаций.
Предел текучести
Усилие
(т.С)
определяет величину физического предела
текучести
(2)
— напряжения, при
котором образец деформируется без
заметного увеличения растягивающей
нагрузки. Предел текучести устанавливает
границу между упругой и пластической
зонами деформирования. Для материалов,
не имеющих на диаграмме площадки
текучести, определяют условный предел
текучести
— напряжение, при котором остаточное
удлинение достигает 0,2% длины участка
образца на его рабочей части. Как видно,
эта характеристика отличается от предела
упругости только величиной допуска.
При дальнейшем
увеличении напряжения происходит
упрочнение металла и сопротивление
деформации растет. Поэтому за площадкой
текучести наблюдается подъем кривой
растяжения (участок упрочнения). На этом
участке диаграммы образец получает
значительные остаточные удлинения.
Чтобы убедиться в этом, прекращают
нагружение образца в некоторый момент
испытания (т.К). Полное удлинение
образца в данный момент определяется
отрезком ОН на оси абсцисс. Затем,
постепенно разгружая образец, замечают
уменьшение его длины, при этом процесс
разгрузки происходит вдоль прямой КМ,
параллельной первоначальному линейному
участку диаграммы ОА. Отрезок МН
представляет упругое удлинение, а
отрезок ОМ – остаточное (пластическое)
удлинение образца. Упругое удлинение
подчиняется закону Гука в любой стадии
деформирования. При повторном нагружении
на диаграмме этот процесс пойдет вдоль
этой же прямой МК, но в обратном
направлении, а после т. К он продолжится
вдоль единой кривой участка деформационного
упрочнения КD.
До точки D рабочая
часть образца остается цилиндрической,
а ее деформирование происходит равномерно
по всему объему. В т. D, соответствующей
наибольшему значению нагрузки
,
в какой-то части образца появляется
местное утонение – шейка.
Остановимся теперь
на физической сущности процесса
деформирования металлов и сплавов. Все
металлы и сплавы имеют кристаллическое
строение. Если деформация, вызванная
внешними силами, исчезает при прекращении
действия внешних сил и тело полностью
восстанавливает свои форму и размеры,
то какую деформацию называют упругой.
При упругой деформации величина смещения
атомов кристаллической решетки из
положения равновесия не превышает
расстояния между соседними атомами.
В металлах процесс
пластической деформации в основном
осуществляется за счет скольжения.
Скольжение представляет собой параллельное
смещение тонких слоев монокристалла
относительно смежных. В настоящее время
значительное распространение получила
теория, объясняющая процесс скольжения
перемещением в плоскости скольжения
отдельных несовершенств пространственной
решетки, так называемых дислокаций.
Дислокации в
большом количестве образуются и при
самом пластическом деформировании
металла. На рис.4 показана простейшая
схема образования пластической деформации
сдвига монокристалла за счет появления
и перемещения так называемой краевой
дислокации. Дефекты кристаллической
решётки являются не только точечными
(вакансии, лишние атомы), а также линейными,
это нарушения правильного строения
атомов на значительные расстояния в
одном направлении.
Реальный
металлический сплав представляет собой
поликристалл, состоящий из множества
хаотично ориентированных монокристаллов.
При пластическом деформировании в них
в разных направлениях (в различных
плоскостях скольжения) одновременно
перемещается огромное число дислокаций
(в отожжённом металле на 1 см2 108
дислокаций). Таким образом, пластические
деформации металлов происходят за счет
сдвиговых микродеформаций, вызванных
движением дислокаций. Следует отметить,
что металлическая связь является
наиболее слабой из всех химических
связей, что облегчает процесс перемещения
дислокаций. Все вышесказанное и объясняет
такое характерное свойство металлов
как пластичность.
Пластичность –
это способность материала воспринимать
значительные пластические деформации
без разрушения. Противоположное
свойство хрупкость – это способность
разрушаться при незначительных
пластических деформациях. При сдвиге
объем материала не меняется (изменяется
только его форма). Отсюда следует важный
вывод: при пластическом деформировании
металлов и сплавов их объем не изменяется.
Этот факт хорошо подтверждается
экспериментами.
Для перемещения
дислокаций необходимо совершать работу.
Это и есть та работа, которую нужно
затратить, чтобы пластически деформировать
образец. Таким образом, работа
пластического деформирования металлов
расходуется на перемещение дислокаций.
Она, в конечном счете, практически вся
превращается в тепловую энергию. Вот
почему при быстром пластическом
деформировании образец может сильно
разогреться.
Если дислокация
на своем пути встречает препятствие,
то для его преодоления нужно совершать
дополнительную работу пластического
деформирования. Такими препятствиями
для дислокации являются границы
микрокристаллов, различные включения
в кристаллической решетке, а также
другие дислокации. При пластическом
деформировании число дислокаций
(препятствий) растет, следовательно
растет и сопротивляемость металла
пластическому деформированию, этот
процесс называется упрочнение (наклёп),
в наклёпанном металле число дислокаций
1012 на 1 см2. Вот почему
практически все металлы и их сплавы на
диаграмме деформирования имеют участок
деформационного упрочнения. При
деформационном упрочнении пластичность
металла уменьшается, а хрупкость,
соответственно, растет. Одновременно
увеличивается и его твердость.
Предел прочности
Предел прочности
(часто называемый временным сопротивлением)
рассчитывается по формуле:
. (3)
При дальнейшем
растяжении образца деформируется только
область шейки, которая постепенно
утоняется, а для ее деформирования
необходимо прикладывать все меньшую и
меньшую силу. Этому процессу соответствует
ниспадающая часть диаграммы DE. В
точке Е происходит разрыв образца
в самом тонком месте шейки. Следует
отметить, что хотя сила на участке DE
и падает, но истинное напряжение в
самом тонком месте шейки образца растет.
Действительно, оно равно
, где А – площадь самого малого
поперечного сечения шейки, которая
уменьшается быстрее силы, что и приводит
к росту истинного напряжения.
Таким образом,
условное напряжение
отличается от истинного из-за различия
и А. Однако для
это
отличие пренебрежимо мало из-за малости
упругих деформаций. У хрупких материалов
также незначительно отличается от
истинного напряжения в момент разрыва
образца, т.к. их разрушение происходит
при малых деформациях. У пластичных
материалов
имеет условный характер, т.к. их разрушение
или начало шейкообразования происходят
при значительных пластических деформациях
и соответствующее истинное напряжение
заметно отличается от предела прочности.
Рассмотрим основные
показатели показателями пластичности
материала.
Относительное
удлинение образца после разрыва
— отношение приращения расчетной длины
образца
к начальной длине
,
выраженное в %:
(4)
Относительное
сужение образца после разрыва
— отношение разности начальной
и минимальной
(в
месте разрыва шейки) площадей поперечного
сечения к начальной
,
выраженное в %:
(5)
Для определения
измеряется минимальный диаметр шейки
в месте разрыва образца.
Испытательная
машина
Машина УГ-20/2
относится к классу универсальных
испытательных машин и позволяет проводить
испытания на растяжение, сжатие и изгиб,
с максимальным усилием в 20 т (200 кН). Ее
схема показана на рис.5.
Машина состоит из
двух агрегатов: собственно машины и
маятникового силоизмерительного
устройства. Основная машина представляет
собой две рамы – неподвижную 1 и подвижную
2.
Неподвижная рама
состоит из массивной плиты-основания,
в которой смонтирован червячный механизм
с приводом от электромотора и ходовой
винт для быстрого перемещения нижнего
захвата, двух вертикальных колон и
верхней поперечены. Сверху на ней
установлен силовой гидроцилиндр 3,
создающий необходимое усилие. Он несет
на себе подвижную раму 2, состоящую из
верхней поперечины, покоящейся поршне
гидроцилиндра, двух вертикальных штанг
и массивной нижней поперечины (траверсы).
Последняя снабжена следующими
приспособлениями для установки и
закрепления образцов: снизу – захват
для крепления образцов 4 при испытании
на разрыв; сверху – площадка для
установки образцов при испытании на
сжатие и две раздвижные опоры, на которые
устанавливаются изгибаемые образцы.
При испытаниях нижний захват не
перемещается.
Принцип работы
машины следующий: при помощи насоса 5 в
гидроцилиндр 3 нагнетается масло,
благодаря чему его поршень движется
вверх, а вместе с ним и подвижная рама
2 вместе с верхним захватом, в котором
закреплен конец растягиваемого образца.
Если образец установлен сверху траверсы,
то он нагружается сжимающей или изгибающей
нагрузкой.
Маятниковый
силоизмеритель предназначен для
измерения создаваемого в образце усилия.
Принцип его работы следующий. В этом
агрегате имеется свой небольшой
гидроцилиндр 6. Его камера соединена с
камерой силового гидроцилиндра 3 трубкой
гидропривода 7.
Таким образом,
давление создаваемое насосом в прессе
толкает вниз поршень гидроцилиндра 6 c
силой
.
Поскольку в двух цилиндрах давление
одинаково, то сила
пропорциональна растягивающей силе
.
Поршень толкает рамку 8, шарнирно
связанную с горизонтальным рычагом ВА
маятника 9. При этом маятник отклоняется
и его вес создает момент М относительно
шарнира А, который по условию
равновесия этого рычага должен
уравновесить момент от силы
:
.
При малых отклонениях маятника момент
М пропорционален горизонтальному
смещению маятника .

Зубчатая рейка 10
соединена с маятником и ее смещение
будет пропорционально .
Из всего вышесказанного
следует, что в данном маятниковом
механизме смещение рейки 10 будет
прямо пропорционально величине усилия
F. На рейке закреплен пишущий
инструмент. Рейка также вращает стрелку
силоизмерителя 11.
Тросик 12 соединяет
движущуюся траверсу с барабаном
самописца, следовательно, угол поворота
барабана пропорционален абсолютному
удлинению образца. Таким образом,
данный самописец в определенном масштабе
записывает диаграмму растяжения
испытываемого образца.
Меняя
массу груза маятника, изменяют коэффициент
пропорциональности между силой
и величиной смещения рейки. Тем самым
изменяют масштаб (шкалы) силоизмерительного
стрелочного устройства
и масштаб диаграммы растяжения по
силовой оси.
Порядок выполнения
работы:
-
Измерить
штангенциркулем с точностью
0,05 мм начальный диаметр
и расчетную длину
образца. Разметить расчетную длину
образца, нанеся риски на расстоянии
от головок образца (см. рис.1). -
Установить образец
в захваты испытательной машины УГ-20/2.
Произвести испытания до разрушения,
записав диаграмму растяжения.
Зафиксировать по шкале силоизмерителя
максимальное усилие
.
-
Измерить с
точностью 0,1 мм
конечные размеры образца – диаметр в
месте разрыва
и конечную расчетную длину
.
4. Обработать
диаграмму растяжения:
а) определить
масштаб диаграммы по усилию
,
где
— длина участка диаграммы, соответствующего
максимальному усилию;
б) определить
масштаб диаграммы по абсолютному
удлинению
,
где
— длина участка диаграммы, соответствующего
остаточному абсолютному удлинению
расчетной части образца. При определении
необходимо учитывать, что разгрузка
образца происходит по закону Гука
(рис.3);
в)Определить
характерные точки диаграммы. С учетом
масштаба определить
.
5. По формулам (1)
– (3) рассчитать характеристики
прочности материала:
.
6. По зависимостям
(4), (5) вычислить относительное
удлинение и сужение
образца при разрыве.
7. Определить
усилие в момент разрыва
и рассчитать
истинное напряжение
в шейке образца в момент разрыва
.
Сравнить предел прочности и истинное
напряжение при разрыве. Все экспериментальные
и расчетные данные занести в таблицу.
|
Экспериментальные и расчетные данные |
Значе- ния |
|
|
Материал |
||
|
Начальный диаметр |
||
|
Диаметр в месте |
||
|
Начальная |
||
|
Конечная расчетная |
||
|
Нагрузка при |
||
|
Максимальная |
||
|
Нагрузка при |
||
|
Нагрузка при |
||
|
Истинное |
||
|
Предел прочности сопротивление) |
||
|
Предел текучести |
||
|
Предел |
||
|
Относительное |
||
|
Относительное |
8. На основе
определенных характеристик прочности
и пластичности
построить условную диаграмму растяжения
в координатах “условное напряжение –
относительная деформация”. Для этого
вычисляется относительное удлинение
расчетной части образца
,
где
— размер диаграммы по оси
,
соответствующий текущей деформации.
Содержание отчета
-
Эскизы исходного
и разрушенного образцов с указанием
размеров. -
Диаграмма растяжения
в координатах ”F-l”
с отмеченными характерными точками. -
Расчеты параметров
и таблица с экспериментальными и
расчетными данными. -
Условная диаграмма
растяжения в координатах ”
— ” с указанием
характерных точек.
Контрольные
вопросы
-
Как определяется
расчетная длина образца? -
Какой вид имеют
типичные диаграммы растяжения различных
материалов? -
Что называется
пределом пропорциональности материала
и как он определяется? -
Что называется
пределом упругости материала и как он
определяется? -
Что называется
физическим и условным пределом текучести
и как они определяются? -
Какой участок на
диаграмме растяжения называется
участком упрочнения и почему? -
Как происходит
разгрузка пластически деформированного
образца и последующая его повторная
нагрузка? -
Что называется
пределом прочности (временным
сопротивлением) и как он определяется? -
Из каких частей
складывается текущее полное удлинение
образца? -
Как определяются
характеристики пластичности материала? -
Как вычисляются
масштабы диаграммы по осям F и l? -
В каких координатах
строится условная диаграмма растяжения? -
Как работает
испытательная машина УГ-20/2? -
Каков принцип
работы силоизмерительного механизма? -
Почему предел
прочности пластичных материалов может
существенно отличаться от истинного
напряжения в образце? -
Каков механизм
пластических деформаций в металлах? -
В чем заключается
причина деформационного упрочнения
металлов? -
Как при деформационном
упрочнении изменяются пластичность,
хрупкость и твердость металлов и их
сплавов? -
Каковы преимущества
и недостатки испытания на растяжение?
Соседние файлы в папке Все лабы по сопромату
- #
- #
- #
- #
- #
- #
- #
- #
Определяем предел пропорциональности
Работа добавлена на сайт samzan.net: 2016-03-13
Поможем написать учебную работу
Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой — мы готовы помочь.
Предоплата всего
от 25%
Подписываем
договор
7. Выполнение индивидуального задания
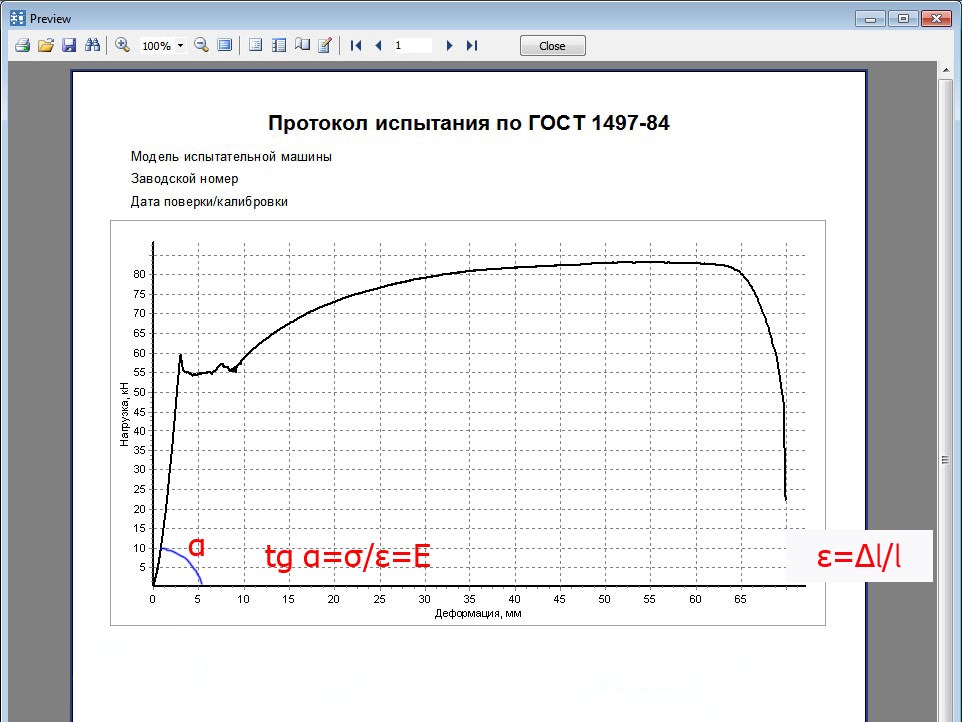
1. Определяем предел пропорциональности . Для этого проводим луч ОТ, начало которого совпадает с первым участком (зоной упругости) диаграммы растяжения. Точка А, начиная с которой диаграмма отклоняется от указанного луча, определяет предел пропорциональности:
.
2. Определяем – относительную продольную деформацию при пределе пропорциональности. Опустив перпендикуляр из точки А на ось , получаем точку S. Величина отрезка OS соответствует :
.
3. Поскольку на диаграмме имеется площадка текучести, то точка B, взятая на этой площадке, определяет величину предела текучести :
.
4. Определяем предел прочности , проводя горизонтальную прямую по касательной к точке С – наивысшей точке диаграммы до пересечения с осью :
.
5. Определяем напряжение при разрыве , проводя горизонтальную прямую из последней точки диаграммы (точки D) до пересечения с осью :
.
6. Выбираем произвольную точку К, расположенную в зоне упрочнения, т. е. на участке ВС диаграммы. Если в точке К прекратить нагружение образца и начать процесс разгрузки, то линия разгрузки имеет вид отрезка KL || ОА. После разгрузки образца (в точке L) относительная деформация полностью не исчезает. Она уменьшается на величину упругой части деформации. Отрезок OL характеризует величину остаточной (пластической) деформации , а отрезок LM – величину упругой деформации , полностью исчезающей после разгрузки образца. Точка М получена опусканием перпендикуляра из точки К на ось .
, ,
полная относительная продольная деформация:
.
7. Проводим из точки D диаграммы луч, параллельный начальному участку ОА, до пересечения с осью . Отрезок OW определяет относительное удлинение образца при разрыве:
.
Поскольку в рассматриваемом примере то материал считается пластичным.
8. Ответы на контрольные вопросы (по вариантам)
|
Вариант |
Номера вопросов |
|
1 |
2,9,18,27,36 |
|
2 |
1,8,17,26,35 |
|
3 |
3,10,19,28,34 |
|
4 |
4,11,20,29,33 |
|
5 |
5,14,25,31,36 |
|
6 |
6,12,21,29,30 |
|
7 |
7,15,24,31,32 |
|
8 |
8,16,22,25,31 |
|
9 |
9,17,20,30,33 |
|
10 |
2,19,26,31,36 |
|
11 |
3,18,22,27,30 |
|
12 |
1,14,24,27,34 |
|
Вариант |
Номер задания |
|
13 |
8,17,23,26,32 |
|
14 |
7,14,20,30,36 |
|
15 |
11,18,25,29,31 |
|
16 |
6,14,20,28,35 |
|
17 |
3,19,24,31,33 |
|
18 |
12,22,25,30,36 |
|
19 |
10,20,23,27,30 |
|
20 |
5,15,21,25,31 |
|
21 |
4,14,24,28,34 |
|
22 |
11,22,23,28,33 |
2)Сформулируйте правило знаков при центральном растяжении (сжатии).
Нормальная сила считается положительной при растяжении и направлена от рассматриваемого сечения и отрицательной при сжатии и направлена к рассматриваемому сечению.
9)Сформулируйте закон Гука. Границы применимости закона Гука.
Закон Гука при растяжении (сжатии). В пределах упругих деформаций (в пределах малых удлинений (укорочений)) относительная продольная деформация прямо пропорциональна нормальному напряжению:
.
18)Что такое предел пропорциональности?
– предел пропорциональности – наибольшее напряжение, до которого материал следует закону Гука. Эта величина определяется степенью отклонения кривой от прямой , т. е. тангенсом угла (), который составляет касательная к диаграмме с осью .
- Какие показатели пластичности вы знаете? Напишите формулы для их вычисления.
Пластичность – способность материала без разрушения получать большие остаточные деформации.
Две основные характеристики пластичности:
1) относительное удлинение образца при разрыве,
2) относительное сужение поперечного сечения образца при разрыве.
Относительное удлинение образца при разрыве – отношение абсолютного удлинения образца при разрыве к его первоначальной длине:
где – длина расчетной части образца до начала нагружения (первоначальная длина); – суммарная длина обоих участков расчетной части образца после разрыва.
Относительное сужение поперечного сечения образца при разрыве – отношение абсолютного уменьшения площади поперечного сечения образца при разрыве к его первоначальной площади:
27) Образец был нагружен до точки К, лежащей в зоне упрочнения диаграммы растяжения малоуглеродистой стали, а затем разгружен. Покажите, как пройдет линия разгрузки? Покажите на этой диаграмме упругие и пластические относительные продольные деформации?
Если в точке К, находящейся на участке ВС, прекратить нагружение образца и начать процесс разгрузки, то линия разгрузки имеет вид отрезка KL || ОА (рис. 11). После разгрузки образца (в точке L) относительная деформация полностью не исчезает. Она уменьшается на величину упругой части деформации. Отрезок OL характеризует величину остаточной (пластической) деформации , а отрезок LM – величину упругой деформации , полностью исчезающей после разгрузки образца. Точка М получена опусканием перпендикуляра из точки К на ось .
Рис. 11. Нагружение до точки К, находящейся в зоне упрочнения ВС, и последующая разгрузка до точки L
СПИСОК ЛИТЕРАТУРЫ
Буланов Э.А., Тарасов А.С., Зубарев А.А. Лабораторный практикум по курсу «Прикладная механика». Раздел «Сопротивление материалов». – М.: МГТУ им. А.Н. Косыгина, 2001. – 31 с.
Дарков А.В., Шпиро Г.С. Сопротивление материалов: Учеб. для техн. вузов. 5-е изд., перераб. и доп. – М.: Высш. шк., 1989. – 624 с.
Епифанов А.П., Морозов А.Н. Виртуальные лабораторные работы по сопротивлению материалов и прикладной механике. – Красноярск: КФ ИрГУПС, 2005. – 34 с.
Ицкович Г.М. Сопротивление материалов: Учеб. для техникумов. – 4-е изд., перераб. и доп. – М.: Высш. шк., 1970. – 488 с.
Карцов С.К. Журнал лабораторных работ по курсу «Сопротивление материалов». – М.: МАДИ (ГТУ), 2007. – 17 с.
Морозов А.Н. Лабораторный практикум по сопротивлению материалов и прикладной механике. – Красноярск: КФ ИрГУПС, 2003. – 82 с.
Сопротивление материалов. Под ред. А.Ф. Смирнова: Учеб. для вузов. – 3-е изд., перераб. и доп. – М.: Высш. шк., 1975. – 480 с.
Стёпин П.А. Сопротивление материалов: Учеб. для вузов. – 7-е изд. – М.: Высш. шк., 1983. – 303 с.
Феодосьев В.И. Сопротивление материалов: Учеб. для вузов. – 10-е изд., перераб. и доп. М.: Изд-во МГТУ им. Н. Э. Баумана, 2001. – 592 с.
Шинкин В.Н. Сопротивление материалов. Простые и сложные виды деформаций: Курс лекций. – М.: Издательский Дом МИСиС, 2008. – 307 с.