
§3. ВЕКТОРНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И ПОСЛЕДОВАТЕЛЬНОСТИ ТОЧЕК
3.1. Сходимость векторных последовательностей.
Определение. Если каждому натуральному числу k по некоторому правилу
отвечает n -мерный вектор xk , то говорят, что в пространстве Rn задана векторная последовательность (последовательность векторов) xk .
|
Примеры последовательности векторов: |
|||||||||||||||||||||||||||||
|
1) |
в R3 |
||||||||||||||||||||||||||||
|
1 |
0 |
0 |
1 |
0 |
0 |
||||||||||||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
||||||||||||||||||||||||
|
x |
0 |
, x |
1 |
, x |
0 |
, x |
0 |
, x |
1 |
, x |
0 |
,….; |
|||||||||||||||||
|
0 |
0 |
1 |
0 |
0 |
1 |
||||||||||||||||||||||||
|
2) |
в R2 |
||||||||||||||||||||||||||||
|
O |
|
x100 |
||
|
a |
||
|
x 2 |
||
|
x |
1 |
O |
Нас будет интересовать поведение членов последовательности при неограни-
ченном увеличении номера, то есть при k . Существуют два определения схо-
димости (предела) векторной последовательности, при этом оба подхода опираются на понятие предела числовой последовательности.
Первый подход использует координаты векторов и называется координатным.
Пусть в векторном пространстве выбран некоторый базис. Тогда каждый вектор по-
следовательности получает координатное представление xk (x1k , x2k ,…, xnk ) . С по-
следовательностью векторов xk естественно связывается n числовых последова-
тельностей x1k , x2k ,…, xnk . Эти последовательности называются координат-
ными последовательностями или, если выбирается стандартный базис, последова-
тельностями компонент. Обратите внимание на особенность обозначения. Если в числовой последовательности ak номер члена записывался нижним индексом, то в xik номер члена записывается верхним индексом, а нижний индекс – номер компоненты.
Определение 1. Вектор a (a1, a2 ,…, an ) называется пределом по коорди-
натам векторной последовательности xk , если каждая координатная последова-
тельность сходится к соответствующей координате вектора a .
|
lim xk a lim xk a , i 1, 2,.., n. |
|||
|
k |
k |
i |
i |
Также говорят, что векторная последовательность xk сходится к вектору a по
координатам (по компонентам).
Если векторная последовательность сходится, то все координатные последо-
вательности необходимо сходятся. Если хотя бы одна из координатных последова-
тельностей расходится, то и векторная последовательность расходится. В рассмот-
ренном выше примере векторная последовательность в R3 расходится.
Координаты вектора зависят от выбора базиса векторного пространства. По-
этому при переходе к другому базису координатные последовательности данной векторной последовательности могут изменяться. Необходимо показать, что сходи-
мость по координатам не зависит от выбора базиса пространства (если в каком-то базисе векторная последовательность сходится по координатам, то она сходится по координатам в любом базисе и к тому же самому вектору).
Второй тип сходимости векторных последовательностей использует понятие нормы вектора и называется сходимостью по норме.
Определение 2. Вектор a называется пределом по норме векторной последо-
вательности xk , если (числовая) последовательность 

стей стремится к нулю.

|
lim xk a lim |
xk a |
0 . |
||||||
|
k |
k |
|||||||
Преимущество второго определения сходимости в том, что оно не использует,
по крайней мере, явно понятия координат, и, следовательно, не зависит от выбора базиса пространства. Следующая теорема устанавливает эквивалентность сходимо-
сти по координатам и сходимости по норме в пространстве Rn . Следовательно, схо-
димость по координатам не зависит от выбора базиса пространства.
ТЕОРЕМА. Если векторная последовательность сходится по норме, то она сходится к тому же самому вектору и по координатам, и наоборот, если она сходит-
ся по координатам, то сходится и по норме.
Доказательство.
Ограничимся случаем ортонормированного базиса. Тогда норма вектора
a (a1, a2 ,…, an ) вычисляется формулой || a || 
Пусть последовательность xk сходится к вектору a по норме. Для каждого
номера i, 1 i n, имеет место очевидное неравенство
|
0 |
xk a |
(xk a )2 |
… (xk a )2 |
… (xk a )2 |
xk a |
. |
||||||||||||
|
i |
i |
1 |
1 |
i |
i |
n |
n |
|||||||||||
|
По предположению, lim |
0 . Из теоремы о сжатой переменной сле- |
|||||||||||||||||
|
xk a |
||||||||||||||||||
|
k |
||||||||||||||||||
|
0 . Следовательно, для всех i, 1 i n, выполняется равен- |
||||||||||||||||||
|
дует, что lim |
xk a |
|||||||||||||||||
|
k |
i |
i |
||||||||||||||||
|
ство lim xik ai , и последовательность xk сходится к вектору a по координатам. |
||
|
k |
||
|
Пусть теперь последовательность xk сходится к вектору a по координатам. |
||
|
Из равенства lim xik ai |
следует, что lim xik ai |
0 . Тогда lim xik ai 2 0 |
|
k |
k |
k |
(предел произведения равен произведению пределов). Предел суммы равен сумме
|
пределов, поэтому lim (xk a1 )2 … (xk an )2 |
lim |
xk a |
2 0. И оста- |
|||||||||||
|
k |
1 |
n |
k |
|||||||||||
|
ется проверить, что lim |
0 , и тогда последовательность xk сходится к |
|||||||||||||
|
xk a |
||||||||||||||
|
k |
||||||||||||||

вектору a по норме. И тут нас ожидает некоторое затруднение. Если бы было из-
вестно, что последовательность 

равен нулю. Мы же знаем только, что сходится последовательность квадратов


довательность квадратов может сходиться, а сама последовательность не иметь пре-
дела. Однако, если предел последовательности квадратов равен нулю, то и сама по-
следовательность стремится к нулю. Попробуйте доказать этот факт самостоятель-
но, используя определение предела числовой последовательности.
Достоинство координатного определения предела векторной последователь-
ности в том, с его помощью можно вычислять предел. Например,
|
k |
1 |
lim |
k |
1 |
||||||||||
|
k |
k |
1 |
||||||||||||
|
lim |
k |
. |
||||||||||||
|
k |
k |
0 |
||||||||||||
|
k |
lim |
|||||||||||||
|
k |
2 |
1 |
k |
2 |
1 |
|||||||||
|
k |
||||||||||||||
Перечислим свойства сходящихся векторных последовательностей. Пусть
|
lim xk x , lim yk y , |
– произвольное число. Тогда |
|
|
k |
k |
1. lim( xk ) x – при умножении сходящейся векторной последовательно-
k
сти на число ее предел умножается на это число.
2. lim(xk yk ) x y – предел суммы сходящихся векторных последова-
k
тельностей равен сумме их пределов.
|
3. lim |
xk , yk |
x, y – предел скалярного произведения сходящихся век- |
||
|
k |
торных последовательностей равен скалярному произведению их пределов.
4. Векторная последовательность xk сходится тогда и только тогда, когда для любого 0 существует такой номер N ( ), что для всех m, p N ( ) выпол-
няется неравенство 


ностей (члены сходящейся векторной последовательности неограниченно «сгуща-
ются» при достаточно больших номерах и наоборот, если члены последовательности неограниченно сгущаются, то она сходится).
5. Предел векторной последовательности единственный.
Перечисленные свойства следуют из аналогичных свойств числовых последо-
вательностей, примененных к координатным последовательностям.
3.2. Решение систем линейных уравнений методом итераций.
Рассмотрим систему из двух уравнений с двумя неизвестными.
|
1000001x1 |
1000x2 |
1001001 |
||||
|
1000x1 |
x2 |
1001 |
. |
|||
Определитель этой системы равен 1, и легко можно увидеть решение
x1 1, x2 1. Изменим «немного» правую часть второго уравнения, добавив к 1001
всего одну тысячную:
|
1000001x1 |
1000x2 |
1001001 |
||||||
|
x2 |
. |
|||||||
|
1000x1 |
1001,001 |
|||||||
|
Казалось бы, что решение должно измениться незначительно, так как правая |
||||||||
|
часть изменилась (по норме) на |
0,001 |
100% 0,0000001% |
||||||
|
(1001001)2 (1001)2 |
||||||||
(одну десятимиллионную процента). Решением новой системы является пара
x1 0, x2 1000,001. Первая компонента уменьшилась на 100%, а вторая вырос-
ла приблизительно на 100000% (!!!). А длина вектора решения увеличилась при-
близительно в 700 раз. Этот пример показывает, что небольшие по здравому смыслу ошибки (в частности, ошибки округления) могут приводить к катастрофическому изменению результатов расчета. Системы уравнений с таким свойством называют неустойчивыми или плохо обусловленными. С увеличением числа неизвестных и уравнений ситуация только усугубляется. По этой причине в реальных расчетах формулы Крамера (особенно) и метод Гаусса используются редко. Существует спе-
циальная наука, изучающая приближенные вычисления. Один из методов, применя-

емых при приближенных вычислениях, называется методом последовательных при-
ближений. Суть метода состоит в построении некоторой последовательности, кото-
рая сходится к решению задачи.
Сейчас мы рассмотрим пример решения системы линейных уравнений мето-
дом итераций (итерация – повторение некоторых действий). Результат каждой сле-
дующей итерации оказывается все ближе и ближе к точному решению системы уравнений (происходит последовательное приближение к точному решению). Рас-
сматриваемый метод годится для решения некоторых систем уравнений. Пусть дана система уравнений
|
10x1 |
2x2 |
5x3 |
3 |
||||
|
x1 |
5x2 |
2x3 |
4 . |
||||
|
2x |
4x |
10x |
4 |
||||
|
1 |
2 |
3 |
|
10 |
2 |
5 |
|||
|
1 |
5 |
2 |
имеет, так называемую, доминирую- |
||
|
Матрица этой системы |
|||||
|
2 |
4 |
10 |
|||
щую диагональ. А именно, модуль диагонального элемента больше суммы модулей остальных элементов строки. В частности, для второй строки имеем 5 1 2.
Разделим каждое уравнение на диагональный элемент матрицы. В результате полу-
чим приведенную форму системы:
|
x |
2 |
x |
5 |
x |
3 |
|||||||||||||||
|
1 |
10 |
2 |
10 |
3 |
10 |
|||||||||||||||
|
1 |
2 |
4 |
||||||||||||||||||
|
x1 |
x2 |
x3 |
. |
|||||||||||||||||
|
5 |
5 |
5 |
||||||||||||||||||
|
2 |
x1 |
4 |
x2 |
x3 |
4 |
|||||||||||||||
|
10 |
10 |
10 |
||||||||||||||||||
В матричной форме
Ax b .
|
1 |
2 |
5 |
|||||||||||||||||||
|
10 |
10 |
x |
3 |
||||||||||||||||||
|
1 |
2 |
1 |
1 |
||||||||||||||||||
|
1 |
x |
8 |
. |
||||||||||||||||||
|
5 |
5 |
2 |
10 |
||||||||||||||||||
|
4 |
|||||||||||||||||||||
|
2 |
4 |
x3 |
|||||||||||||||||||
|
1 |
|||||||||||||||||||||
|
10 |
10 |
||||||||||||||||||||
Обратите внимание, что теперь на главной диагонали матрицы приведенной системы стоят единицы (с плюсом). Запишем полученную систему в виде В результате равносильных преобразований
Ax b x Ax b x x b Ax x x b (A E)x
система уравнений принимает вид
x b (A E)x ,
здесь E – единичная матрица.
А теперь, глядя на полученное уравнение, напишем рекуррентную формулу,
задающую последовательность xk :
xk b ( A E)xk 1 .
Первый член такой последовательности (его удобно обозначить x0 ) должен быть задан отдельно. Нетрудно понять, что если последовательность xk сходится,
то ее предел является решением системы уравнений. Действительно, пусть
x* lim xk , тогда вектор x* удовлетворяет уравнению x* b ( A E)x* и, следо-
k
вательно, он удовлетворяет равносильному уравнению Ax* b .
Оказывается, что для матриц с доминирующей диагональю последователь-
ность xk сходится. Мы получаем возможность, выбрав произвольно вектор x0 ,
построить последовательность векторов, сходящуюся к решению системы уравне-
ний. Метод последовательных приближений, как правило, не дает точного решения задачи, но существуют методы, которые позволяют определить число итераций для

достижения заданной точности. Грубо говоря, решение получено, если результаты итераций перестают практически различаться. Здесь уместна аналогия с критерием Коши сходимости числовой последовательности – вблизи предела члены последова-
тельности неограниченно сгущаются, разность между ними становится меньше лю-
бого наперед заданного числа. Существенное достоинство метода итераций состоит в том, что если в процессе расчетов возникла случайная ошибка, то последующие вычисления все равно будут приближаться к решению задачи.
Сейчас мы построим для нашей системы уравнений несколько членов после-
довательности и посмотрим, как они приближаются к точному решению. Вам пред-
стоит выполнить аналогичную домашнюю работу. В качестве первого шага находим точное решение нашей системы (не имеет значения, каким методом это делать, са-
мый простой – угадать). В данном случае точное решение x* ( 1,1,1) . В качестве нулевого приближения возьмем нулевой вектор x0 o (0,0,0) . Подставляя x0 в
рекуррентную формулу, находим x1 b ( A E)x0 b ( A E)o b . На этом
«простые» вычисления заканчиваются.
Назовем вектором ошибки с номером k вектор k x* xk , а его норму 

Для нулевого шага имеем, 0 x* o x* ( 1,1,1) , 

Для первого шага
|
1 |
3 |
7 |
0,7 |
||||||||||||||||||||
|
1 |
* |
1 |
* |
1 |
1 |
||||||||||||||||||
|
x |
x |
x |
b |
1 |
8 |
2 |
0, 2 |
, |
|||||||||||||||
|
10 |
10 |
||||||||||||||||||||||
|
1 |
4 |
6 |
0,6 |
||||||||||||||||||||



Второй шаг. Найдем матрицу A E

|
1 |
2 |
5 |
0 |
2 |
5 |
|||||||||||||||||||||||||||||||
|
10 |
10 |
1 |
0 |
10 |
10 |
0 |
5 |
|||||||||||||||||||||||||||||
|
1 |
0 |
1 |
2 |
|||||||||||||||||||||||||||||||||
|
2 |
2 |
1 |
||||||||||||||||||||||||||||||||||
|
1 |
0 |
1 |
0 |
0 |
2 |
0 4 |
. |
|||||||||||||||||||||||||||||
|
5 |
5 |
5 |
5 |
10 |
||||||||||||||||||||||||||||||||
|
0 |
0 |
1 |
2 |
4 |
0 |
|||||||||||||||||||||||||||||||
|
2 |
4 |
2 |
4 |
|||||||||||||||||||||||||||||||||
|
1 |
0 |
|||||||||||||||||||||||||||||||||||
|
10 |
10 |
|||||||||||||||||||||||||||||||||||
|
10 |
10 |
Имеет смысл вынести общий множитель, чтобы работать с целыми числами.
Но нужно быть крайне внимательным, особенно, если диагональные элементы мат-
рицы различные.
|
Вычисляем следующее приближение x2 . |
||||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
0 |
2 5 |
3 |
|||||||||||||||||||||||||||||||||||||||||||||
|
2 |
1 |
1 |
1 |
1 |
||||||||||||||||||||||||||||||||||||||||||||
|
x |
b ( A E)x |
8 |
2 |
0 4 |
8 |
|||||||||||||||||||||||||||||||||||||||||||
|
10 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
10 |
4 |
10 |
2 |
4 0 |
4 |
|||||||||||||||||||||||||||||||||||||||||||
|
1 |
3 |
1 |
36 |
1 |
66 |
0,66 |
||||||||||||||||||||||||||||||||||||||||||
|
8 |
10 |
90 |
0,90 |
. |
||||||||||||||||||||||||||||||||||||||||||||
|
10 |
100 |
100 |
||||||||||||||||||||||||||||||||||||||||||||||
|
4 |
38 |
78 |
0,78 |
|||||||||||||||||||||||||||||||||||||||||||||
|
1 |
66 |
34 |
0,34 |
|||||||||||||||||||||||||||||||||||||||||||||
|
2 |
* |
2 |
1 |
1 |
||||||||||||||||||||||||||||||||||||||||||||
|
Ошибка |
x |
x |
1 |
90 |
10 |
0,10 |
. |
|||||||||||||||||||||||||||||||||||||||||
|
1 |
100 |
78 |
100 |
22 |
0, 22 |
|||||||||||||||||||||||||||||||||||||||||||
|
1 |
1 |
0,94 она |
||||||||||||||||||||||||||||||||||||||||||||||
|
Норма ошибки |
2 |
1740 0, 42 |
, по сравнению с |
|||||||||||||||||||||||||||||||||||||||||||||
|
100 |
||||||||||||||||||||||||||||||||||||||||||||||||
уменьшилась, приблизительно в два раза.
В домашнем задании делаются еще две итерации, в итоге будут получены первые 5 членов последовательности: x0 , x1, x2 , x3 , x4 . Для каждой итерации вы-
числяется вектор ошибки и норма ошибки.
3.3. Понятие о метрических пространствах.
Расстоянием d ( A, B)между двумя точками A и B прямой, плоскости, про-
странства называется длина соединяющего их отрезка. Отметим три свойства рас-

A(xA , yA , zA )
B(xB , yB , zB )
|
стояния: |
|
|
Д1. |
d ( A, B) 0 и d ( A, B) 0 только если A B (точки совпадают). |
|
Д2. |
d( A, B) d(B, A) (расстояние симметрично). |
|
Д3. |
d(A, B) d(B,C) d(A, B) (неравенство треугольника). |
Этими тремя свойствами определяют понятие расстояния в произвольном множестве. Именно, говорят, что в множестве определено расстояние d , если для любых его двух элементов x и y определено число d (x, y), и при этом выполня-
ются условия (аксиомы) Д1 – Д3. Множество, в котором определено расстояние,
называется метрическим пространством. Элементы метрического пространства обычно называют точками. Обычная прямая, плоскость, пространство – примеры метрических пространств. В частности, в прямоугольных координатах расстояние
между точками и вычисляется с помощью формулы
d ( A, B) 
Любое векторное пространство с нормой превращается в метрическое про-
странство, если в нем определить расстояние формулой d (x, y) 

Расстояние между векторами x и y равно норме их разности. При таком определе-
нии расстояния аксиомы выполняются автоматически, так как они совпадают с тре-
мя из четырех аксиом нормы. Рассматривая векторное пространство как метриче-
ское пространство, мы имеем право называть векторы точками. С этого момента векторное пространство Rn будем считать метрическим пространством. Вектор бу-
дем называть точкой, а координатами точки – координаты вектора. Вспомним, что стандартная (евклидова) норма в пространстве Rn определяется через скалярное
|
произведение, а именно, |
y x |
( y x, y x) . В частности, если выбран орто- |
||||
нормированный базис, то расстояние между двумя точками x (x1, x2 ,…, xn ) и y ( y1, y2 ,…, yn ) вычисляется с помощью формулы
Соседние файлы в папке Математика 2 семестр
- #
- #
- #
- #
- #
- #
- #
Вектор-функции
Предел и непрерывность вектор-функции.
Понятие вектор-функции.
Если каждому значению (tin E), где (Esubsetmathbb), поставлен в соответствие вектор (r(t)) трехмерного пространства, то говорят, что на множестве (E) задана векторная функция (r(t)) скалярного аргумента (t).
Пусть в пространстве фиксирована прямоугольная система координат (Oxyz). Тогда задание вектор-функции (r(t), tin E), означает задание координат (x(t), y(t), z(t)) вектора (r(t), tin E). Если (i,j,k) — единичные векторы координатных осей, то
$$
r(t)=x(t)i+y(t)j+z(t)k,qquad tin E,nonumber
$$
или
$$
r(t)=(x(t),y(t),z(t)).nonumber
$$
Если (z(t)=0) при всех (tin E), то вектор-функцию (r(t)) называют двумерной.
В случае, когда начало каждого из векторов (r(t)) совпадает с началом координат (рис. 21.1), эти векторы называют радиус-векторами, а множество их концов — годографом вектор-функции (r(t)), (tin E), который можно рассматривать как траекторию точки (M(t)) конца вектора (r(t)), если считать, что (t) — время.
Предел вектор-функции.
Вектор (a) называют пределом вектор-функции (r(t)) в точке (t_0) и пишут (displaystyle lim_>r(t)=a) или (r(t)rightarrow a) при (trightarrow t_0), если
$$
lim_> |r(t)-a|=0,label
$$
то есть длина вектора (r(t)-a) стремится к нулю при (trightarrow t_0).
Рис. 20.1
Если заданы (r(t)=(x(t),y(t),z(t))) и (a=(a_<1>,a_<2>,a_<3>)), то
$$
lim_>r(t)=alabel
$$
тогда и только тогда, когда
$$
x(t)rightarrow a_1, y(t)rightarrow a_2, z(t)rightarrow a_3quad при trightarrow t_0.label
$$
Поэтому, если (r(t)rightarrow a) при (trightarrow t_0), то есть выполняется условие eqref, то выполняется условие eqref.
Обратно: если выполняются условия eqref, то из равенства eqref следует, что выполнено условие eqref. (bullet)
При доказательстве свойств предела вектор-функции удобно использовать следующее очевидное утверждение: условие eqref выполняется в том и только том случае, когда
$$
r(t)=a+alpha(t),nonumber
$$
где (alpha(t)) — бесконечно малая вектор-функция, то есть
$$
alpha(t)rightarrow 0quad mbox <при> trightarrow t_<0>.nonumber
$$
Свойства пределов вектор-функций.
(circ) Это свойство следует из неравенства
$$
||r(t)|-|a|| leq |r(t)-a|.qquad bulletnonumber
$$
Если (r(t)rightarrow a) при (trightarrow t_<0>), а скалярная функция (f(t)) такова, что (f(t)rightarrow A) при (trightarrow t_<0>), то (f(t)r(t)rightarrow Aa) при (trightarrow t_<0>), то есть
$$
lim_f(t)r(t)=lim_>f(t)lim_r(t).label
$$
(circ) Из определений пределов скалярной функции и вектор-функции следует, что (r(t)=a+alpha(t), f(t)=A+beta(t)), где (alpha(t)) — бесконечно малая вектор-функция, (beta(t)) — бесконечно малая функция при (trightarrow t_0). Поэтому (f(t)r(t)=Aa+gamma(t)), где (gamma(t)=Aalpha(t)+beta(t)a+beta(t)alpha(t)) — бесконечно малая вектор-функция при (trightarrow t_0), откуда получаем равенство eqref. (bullet)
(circ) По условию (r_(t)=a_+alpha_), где (a_i(t)rightarrow 0) при (trightarrow t_<0> (i=1,2)). Поэтому (r_1(t)+r_2(t)=a_1+a_2+beta(t)), где (beta(t)=alpha_<1>(t)+alpha_2(t)rightarrow 0) при (trightarrow t_<0>), откуда следует eqref. Докажем формулу eqref. В силу свойств скалярного произведения
$$
(r_<1>(t),r_2(t))-(a_1,a_2)=(alpha_<1>(t),a_<2>)+(alpha_<2>(t),a_1)+(alpha_1(t),alpha_2(t)),nonumber
$$
причем в правой части этого равенства — бесконечно малая функция, так как (alpha_<1>(t),alpha_<2>(t)) — бесконечно малые вектор-функции и (|(p,q)| leq |p|cdot|q|) для любых векторов (p) и (q).
Аналогично доказывается формула eqref, в этом случае следует воспользоваться неравенством (|[p,q]| leq |p|cdot|q|). (bullet)
Непрерывность вектор-функции.
Вектор-функцию (r(t)) называют непрерывной при (t=t_<0>), если
$$
lim_>r(t)=r(t_0).label
$$
Непрерывность вектор-функции (r(t)=(x(t),y(t),z(t))) при (t=t_<0>) в силу эквивалентности условий eqref и eqref означает, что ее координаты (x(t),y(t),z(t)) непрерывны в точке (t_<0>).
Назовем вектор-функцию (Delta r=r((t_0+Delta t)-r(t_0)) приращением вектор-функции (r(t)) в точке (t_<0>). Тогда условие eqref означает, что
$$
Delta rrightarrow 0quad приquad Delta trightarrow 0.label
$$
Из определения непрерывности вектор-функции и свойств пределов векторных функций следует, что сумма, векторное и скалярное произведения вектор-функций (r_1(t)) и (r_2(t)) являются непрерывными функциями при (t=t_<0>), если вектор-функции (r_1(t)) и (r_2(t)) непрерывны в точке (t_<0>).
Производная и дифференциал вектор-функции.
Производная вектор-функции.
Если существует (displaystyle lim_<Delta trightarrow 0>frac<Delta r><Delta t>) где (Delta r=r(t_0+Delta t)-r(t_0)), то этот предел называют производной вектор-функции (r(t)) в точке (t_0) и обозначают (r'(t_0)) или (dot(t_0)).
Таким образом,
$$
r'(t_<0>)=lim_<Delta trightarrow 0>frac+Delta t)-r(t_<0>)><Delta t>.label
$$
Аналогично вводится понятие второй производной
$$
r″(t_<0>)=lim_<Delta trightarrow 0>frac+Delta t)-r'(t_<0>)><Delta t>nonumber
$$
и производной порядка (n > 2) вектор-функции. Заметим, что если (r(t)=(x(t),y(t),z(t))), то
$$
r'(t_<0>)=(x'(t_0),y'(t_0),z'(t_0))label
$$
Утверждение eqref следует из определения eqref и свойств пределов вектор-функций.
Аналогично, если существует (r″(t_<0>)), то
$$
r″(t_<0>)=(x″(t_0),y″(t_0),z″(t_0)).nonumber
$$
Из определения производной следует, что (Delta r=r'(t_0)Delta t+alpha(Delta t)Delta t), где (alpha(Delta t)rightarrow 0) при (Delta trightarrow 0), и потому (Delta rrightarrow 0) при (Delta trightarrow 0). Таким образом, выполняется условие eqref, то есть вектор-функция (r(t)), имеющая производную в точке (t_<0>), непрерывна при (t=t_<0>).
(circ) Формулы eqref-eqref справедливы в точке (t), если в этой точке соответствующие функции имеют производные. Ограничимся доказательством формулы eqref. Пусть (Delta r_) — приращение вектор-функции (r_k(t)), соответствующее приращению аргумента (Delta t), то есть (Delta r_k=r_k(t+Delta t)-r_k(t), k=1,2). Тогда, используя свойства скалярного произведения и свойства пределов вектор-функций, получаем
$$
begin
(r_<1>,r_<2>)’=displaystylelim_<Delta trightarrow 0>frac<(r_<1>(t+Delta t),r_<2>(t+Delta t))-(r_<1>(t),r_<2>(t))><Delta t>=\
=lim_<Delta trightarrow 0>left[left(r_<1>(t),frac<Delta r_<2>(t)><Delta t>right)+left(frac<Delta r_<1>(t)><Delta t>,r_2(t)right)+left(frac<Delta r_<1>(t)><Delta t>,Delta r_2(t)right)right]=\
=(r_1,r_2′)+(r_1′,r_2),
endnonumber
$$
так как (displaystyle frac<triangle mathrm_><triangle t>rightarrow r_‘(t)) при (Delta trightarrow 0 (i=1,2)) и (Delta r_2rightarrow 0) при (Delta trightarrow 0). (bullet)
Пусть существует (r'(t)) для всех (tin(alpha,beta)) и пусть (|r(t)|=C=const) для всех (tin(alpha,beta)).
Доказать, что ((r(t),r'(t))=0), то есть векторы (r(t)) и (r'(t)) ортогональны.
(triangle) Используя формулу (|r(t)|^2=(r(t),r(t))), правило дифференцирования скалярного произведения (формула eqref) и условие (|r(t)|=C), получаем ((r(t),r(t))’=2(r'(t),r(t))=0), так как (|r(t)|^<2>)’=(C^<2>)’=0). Итак,
$$
|r(t)|=CRightarrow (r(t),r'(t))=0.quadblacktrianglenonumber
$$
Дифференциал вектор-функции.
Вектор-функцию (r(t)), определенную в некоторой окрестности точки (t_<0>), называют дифференцируемой при (t=t_<0>), если ее приращение (Delta r=r(t_<0>+Delta t)-r(t_<0>)) в точке (t_<0>) представляется в виде
$$
Delta r=aDelta t+Delta talpha(Delta t),label
$$
где вектор (a) не зависит от (Delta t), (alpha(Delta t)rightarrow 0) при (Delta trightarrow 0).
Полагая (dt=Delta t), запишем равенство eqref в виде
$$
dr=r’dt,nonumber
$$
где опущено обозначение аргумента функции (r’). Отсюда получаем
$$
r’=frac
$$
Замена переменного.
Если функция (t=t(s)) дифференцируема при (s=s_<0>, t(s_<0>)=t_<0>), а вектор-функция (r(t)) дифференцируема в точке (t_<0>), то вектор-функция (rho(s)=r(t(s))) дифференцируема в точке (s_<0>), а производная этой функции выражается формулой
$$
rho’ (s_0)=r_s'(t(s_0))=r_'(t_<0>)t_‘(s_<0>),label
$$
где индекс указывает, по какому переменному производится дифференцирование.
(circ) Функция (alpha(Delta(t))) в формуле eqref не определена при (Delta t=0). Доопределим ее при (Delta t=0), полагая (alpha(0)=0).
Так как (t=t(s)) — функция, дифференцируемая при (s=s_0), то (Delta t=t(s_<0>+Delta s)-t(s_<0>)rightarrow 0) при (Delta srightarrow 0). Разделив обе части равенства eqref на (Delta sneq 0), получим
$$
frac<Delta r><Delta s>=r'(t_0)frac<Delta t><Delta s>+alpha(Delta t)frac<Delta t><Delta s>.label
$$
Правая часть eqref имеет при (Delta srightarrow 0) предел, равный (r'(t_0)t'(s_0)), так как (Delta trightarrow 0) при (Delta srightarrow 0) и (alpha(Delta t)rightarrow 0) при (Delta trightarrow 0). Следовательно, существует предел в левом части eqref, и справедливо равенство eqref. Формулу eqref запишем кратко в виде равенства
$$
r_’=r_’t_’,label
$$
выражающего правило дифференцирования вектор-функции при замене переменного. (bullet)
Теорема Лагранжа и локальная формула Тейлора для вектор-функции.
Формула Лагранжа, то есть формула
$$
r(beta)-r(alpha)=r'(xi)(beta-alpha),quad xiin(alpha,beta),label
$$
для вектор-функции, вообще говоря, неверна.
(circ) В самом деле, пусть формула eqref верна, и пусть (r(t)=(cos t,sin t)), тогда (r'(t)=(-sin t,cos t), |r'(t)|=1). Полагая (alpha=0,beta=2pi), получим из равенства eqref (0=r(2pi)-r(0)=r'(xi)2pi), что невозможно, так как (|r'(xi)|=1). (bullet)
Если вектор-функция (r(t)) непрерывна на отрезке ([alpha,beta]) и дифференцируема на интервале ((alpha,beta)), то
$$
existsxiin(alpha,beta): |r(beta)-r(alpha)|leq|r'(xi)|(beta-alpha).label
$$
(circ) Рассмотрим скалярную функцию
$$
varphi(t)=(r(beta)-r(alpha),r(t)).nonumber
$$
эта функция непрерывна на отрезке ([alpha,beta]), так как вектор-функция (r(t)) непрерывна на этом отрезке. Кроме этого, функция (varphi(t)) дифференцируема на интервале ((alpha,beta)), так как функция (r(t)) дифференцируема этом интервале, причем в силу правила дифференцирования скалярного произведения
$$
varphi'(t)=(r(beta)-r(alpha),r'(t)).nonumber
$$
По теореме Лагранжа
$$
existsxiin(alpha,beta): varphi(beta)-varphi(alpha)=varphi'(xi)(beta-alpha)label
$$
Преобразуем левую часть неравенства eqref:
$$
begin
varphi(beta)-varphi(alpha)=(r(beta)-r(alpha),r(beta))-(r(beta)-r(alpha),r(alpha))=\
=(r(beta)-r(alpha),r(beta)-r(alpha))=|r(beta)-r(alpha)|^2
endnonumber
$$
Тогда равенство eqref примет вид
$$
|r(beta)-r(alpha)|^<2>=(r(beta)-r(alpha),r'(xi))(beta-alpha).label
$$
Если (r(beta)=r(alpha)), то неравенство eqref справедливо при любом (xiin in(alpha,beta)). Если (r(beta)neq r(alpha)), то (|r(beta)-r(alpha)| > 0). Тогда, используя неравенство (|(a,b)|leq|a|cdot|b|), из формулы eqref получим
$$
|r(beta)-r(alpha)|^<2>leq|r(beta)-r(alpha)|cdot |r'(xi)|(beta-alpha),nonumber
$$
откуда, разделив обе части неравенства на (|r(beta)-r(alpha)| > 0), получим неравенство eqref. (bullet)
Для вектор-функции (r(t)) справедлива локальная формула Тейлора
$$
r(t)=sum_^frac(t_<0>)>(t-t_<0>)^+varepsilon(t-t_<0>),label
$$
где (varepsilon(t-t_0)=o((t-t_<0>)^)) — вектор-функция такая, что (varepsilon(t-t_0)=(t-t_<0>)^varepsilon_<1>(t-t_<0>)), где (varepsilon_<1>(t-t_<0>)rightarrow 0) при (trightarrow t_<0>).Эта формула справедлива в предположении, что существует (r^<(n)>(t_0)). Для доказательства формулы eqref достаточно воспользоваться локальной формулой Тейлора для компонент вектор-функции (r(t)).
Переменные векторы. Вектор-функции и их дифференцирование


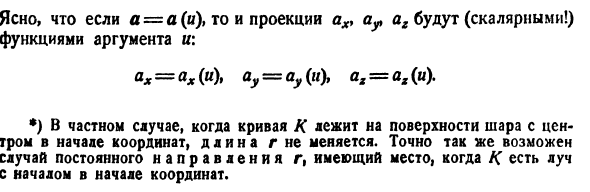



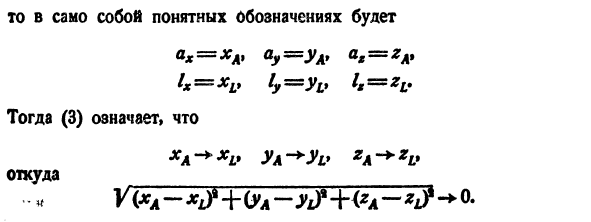

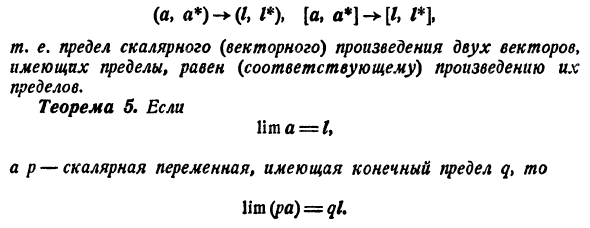





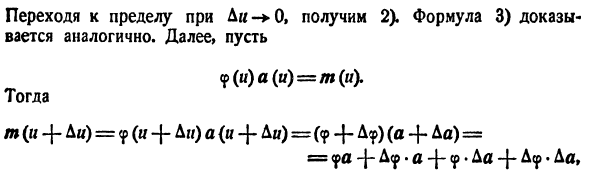


Переменные векторы. Вектор-функции и их дифференцирование
- Переменный вектор. Векторные функции и их различие № 1. Переменный вектор. Функция вектора Годограф. Представьте себе точку M (x, y, z) t, движущуюся в пространстве вдоль определенной кривой K (рис. 293). Выберите единицу времени и первый момент. И любой момент времени характеризуется числом т.
Непрерывность векторной функции. Их дифференциация № 3. Непрерывность векторной функции. Различать их. Дай мне а = а (и) Функция вектора и скалярного аргумента. Как и в случае обыкновенных дифференциальных вычислений, если бесконечно малое приращение аргумента соответствует бесконечно малому приращению функции, a (n) называется непрерывным. lirn [a (u + Lee) -a (//)] = 0. (7) к- * 0 Равенство (7) также может быть описано в следующем формате: lim a (u — — di) = a (u). Где u0, a, —
Поэтому гл. II, свойство непрерывности вектор-функции означает, что предел (и u0) этой функции равен значению из предела аргумента. Далее поясняется операция дифференцирования непрерывной вектор-функции. Дай мне а = а (и) -Такую функцию. Давайте сделаем пять вещей: 1) Исправьте значение аргумента и найдите соответствующее значение функции a (s). 2) Дайте аргументу приращение A и найдите новое значение функции a (u — <- Au); 3) Найдите приращение Da = a (u + A «)
a (u). .v да (s + Dy) -a (s) 4) Настройте отношение -m— = —1-! -r1, -;
б) (s) и обозначается одним из символов. , T, h da a, a ‘(s), g. Нахождение ‘(u) называется производной функции a (u). *) Конечно, этого может и не быть.
Поверните A на ноль и ищите пределы *) lim * Джим Ли 0 Ли Аа 0 Ли Это ограничение называется производной функции a Людмила Фирмаль
Легко найти геометрический смысл производной a ‘(u). Для этого представим годограф векторной функции. Если (см. Рисунок 295) a (u) -OM, a (n-dY) = ON, тогда A a = LSH Отношение-вектор в том же направлении А Ды]> 0 для ММ, Di 0 и о = МП, Вы можете видеть, что вектор MP направлен на годограф по секущей линии.
Если Да -О (из-за непрерывности вектор-функции), точка N стремится соответствовать точке М. Поэтому предельное положение вектора MP направлено на годограф по касательной MQ. Однако эта предельная позиция n является производной от o ‘(u). Следовательно, производная вектор-функции направлена по касательной к годографу этой функции. Пример. Переместить точку М в пространстве, r = r (t)
Векторное уравнение для этого движения. Годограф радиус-вектора r (0 — траектория точки М. Производная / (t) называется скоростью точки М. Следовательно, скорость точки — это вектор, который касается траектории этой точки. Этот вектор является направлением движения. И характеризуем скорость: r ‘(0 — предел длины вектора г (/ + ac-g (0 ат Учитывая ясность,Однако (рис. 296) DO-g (01 — длина кода MN, Включает в себя минимальную дугу MN точечной траектории. Как вы знаете, эти коды и дуги эквивалентны друг другу Поэтому друзья if’wi-lim, x, 1 w / a rW / r (t + AtJ
- Другими словами, длина вектора скорости является пределом отношения пути, по которому течет ток через бесконечно короткие промежутки времени. 296.Время этого периода Gap. Это скалярное значение — скорость точки. Направление вектора / (t) указывает направление движения. № 4. Формулы и правила дифференцирования векторных функций. Правила дифференцирования векторных функций полностью аналогичны правилам обыкновенных дифференциальных вычислений.
Они использованы в следующей таблице. a = a (u), b = b (u) -: векторная функция скалярного аргумента и вектор c-константы? (O) -скалярная функция и k-константа, v-скалярный аргумент, связанный с выражением q = u (m>): 1) ду * 6) рфа-дурь 2) d (a — — b) du da | du 1 db du * 7) rfu и i
. -A * + e du db du ‘8) rf (ffl) du 4) dfoa) du rfa. du * 9) d [ab] du б) д (ка) __ ду ■ к да • * ду ’10) да дв ‘да ду ду дв’ Формула 1) понятна. Положите s-a — — b, чтобы доказать 2). Тогда s + bs = (a — — Да) + отсюда D $ = Да + Db и AL, AB Я Ли 1 Ли
Когда вы достигнете предела Di 0, вы получите 2). Формула 3) тоже доказана. Дальше давайте
0, *) получается уравнение 4). Формулы 5) и 6) являются частными случаями 4). Уравнение 7) доказывается так же, как 4). Частные случаи 
Пусть ax, ay> ar — проекция вектор-функции a = a (n). тогда a = axi — — ay] — — атака. Используя уравнения 2) и 6) da_dax. , День da2- «Du
du J ^ Ifa Da Da Однако, когда вектор разлагается на векторы единичных координат, коэффициент единичного вектора i является проекцией разрешимого вектора на ось * Ox. так дакс н да du — iip * du 9
То есть проекция векторной производной на ось равна производной этой проекции на эту ось. Людмила Фирмаль
Пример. r = r (0 — радиус-вектор движущейся точки) М (х, у, z). Введите u =. Как вы уже знаете, v это скорость Точка М. Как сказано, vx = ^
-t. Но Tx = х. о Следовательно, проекция векторов на другие оси одинакова. Вот так дз дт *
То есть спроецированная скорость движущейся точки (на оси координат) равна производной соответствующей координаты по времени. Например, если точка движется как x = 8t * -1, = = z = tz + 1, vx = 16 /, r> y = 4, vz = 3Отс Выше называется «скорость движения®» и равна г / — = Y * 2LY * — — 1 () -) — 9/4 В момент времени t = 1, y = 16,8. *) Поскольку предполагается, что функция a (s) непрерывна, litnAa = 6 для Ли 0.
Равен длине временного интервала, отделяющего этот момент от первого момента. В этом случае знак присваивается номеру t. Или это зависит от того, следует ли момент интереса или предшествует первому моменту. Радиус-вектор r = OM в каждый конкретный момент t имеет определенную длину и направление. Однако их длина и направление со временем изменятся *). Итак, здесь мы имеем дело с переменными векторами. Как правило, переменные векторы — это векторы, которые различаются по длине или направлению.
Однако мы рассматриваем постоянные векторы как частный случай переменных (аналогично использованию констант в скалярном анализе). Скалярный анализ различал индивидуальные постоянные значения при работе с переменными. Фактически, переменная задача состояла из задачи этого набора значений. Аналогичным образом определим переменную вектор а Вы определите набор постоянных векторов — индивидуальное значение. В процессе изменения a принимает одно из этих значений. Если a является переменным вектором, его проекция ayt ax также является (скалярной!) Переменной. Установка вектора a эквивалентна установке переменных ay и av.
Если a принимает одно из своих значений, ay ay1 также принимает соответствующее постоянное значение. Очень важным примером переменного вектора является скалярная функция-вектор аргумента. Они говорят, что переменная vector a является векторной функцией скалярных аргументов, и каждое значение связано с определенным значением a. В этом случае они пишут а = а (к). г » И м Рисунок 293.
Если a = a (u), проекционный топор и ar ag являются (скалярными!) Аргументными функциями, ax = ax (u), y = a y (u), ax = ax (u). *) Длина r не изменяется, если кривая K находится на поверхности шара с центром в начале координат. Точно так же, если K — луч, происхождение которого является источником, это может быть в определенном направлении r.
Пример вектор-функции показан для радиус-вектора r = OM в точке M перемещения, описанной выше. Здесь, поскольку аргумент — время U, g = g (0- (1) Это уравнение называется векторным уравнением движения для точки М. Поскольку координаты точки M (x, y, r) являются проекциями ее радиус-вектора r, уравнение (1) можно заменить тремя скалярными уравнениями движения. x = x (t), y = y (f), z = z (t). Например, равенство x = Py y = 7t + 2, z = s nt Движение точки происходит. Их можно заменить одним векторным уравнением r = t4 — — (7t-2) / + sin tk.
Годограф определенного вектора переменных — это геометрическое положение конечных точек всех значений, если каждое значение откладывается от общей начальной точки. Годограф вектор-функции a (u) представляет собой (как правило, пространственную) кривую. Если все значения a (u) установлены на что-то отличное от источника, уравнение x = ax (u), y = ay (u), z = az (u) Представляет параметрическое уравнение вышеуказанной линии. Если вектор a (u) постоянен, годограф — это линия на поверхности шара.
Постоянный векторный годограф — это точка. Годограф радиус-вектора r = OM движущейся точки M является ее точкой. n ° 2. Векторное ограничение. Рассмотрим переменный вектор a, который изменяется в соответствии с законом *).Определение 1. Переменный вектор a называется бесконечно малым, если он имеет тенденцию быть нулевым по длине. Определение 2. Постоянный вектор I называется пределом переменного вектора a.
Разница между ними — бесконечно малый вектор. •) Например, a является векторной функцией скалярного аргумента a = a (s) и имеет определенные ограничения. Или, в более простом случае, пронумерованная последовательность постоянных значений alt at) atl …
Запишите с любой формулой Лима = /, а- + Л (Рис. 294) Приведите векторы / и a к общему началу координат 0 и приведите их в соответствие с началом координат. Далее разность I-a представлена вектором AL. Если длина этого вектора стремится к нулю, точка A стремится соответствовать точке L, поэтому X A XV Однако, в конце концов (поскольку 0 соответствует началу координат), xA и xL являются проекциями векторов a и / на ось Ox. Таким образом, предыдущие отношения Я, — * / *.
Эта ситуация аналогична проекции векторов на другие оси. 80М это правда Рисунок 294. Теорема 1. Связь (2) (3) 1g lim a = 1 Это предполагает тройные отношения. 1G a9 Покажем, что обратное также верно в соответствии с теоремой 2. (3) — (2). Фактически, переместите векторы a и / к общему началу координат 0. Это совпадает с происхождением. В то же время конечными точками векторов a и I являются точки A и ξ. a = OAt 1 = O b
В понятной нотации * «= * # Ay = ul ‘*» = * # (3) чк
+ ги Откуда Y (XA- + (YA-Y0 * + (* A- * jf- * ° — и Последнее соотношение можно записать как AL — + 0, Это означает, что по определению 2 (2) верно. Таким образом, векторное соотношение (2) эквивалентно скалярному отношению тройка (3). Эта эквивалентность позволяет легко переносить наиболее важные свойства скалярных переменных в вектор.
Например, теорема 3I верна. а * л * т (4) тогда a + a * a-a * -> l-l * t (5) м. е. Предел суммы (разности) ограниченных векторов равен сумме пределов (разности). Конечно, это из (4) * * *! * ….. AJ-WJ. тогда i * -faj + ^ -f>> / j, -f l> 9 + + (6) Для простоты Если a — — a * = b, 1 + 1 * = m, (6) можно переписать в следующем формате bx-> tx% by —► tu, bg- * mt> По теореме 2 Lim 6 = / I Это эквивалентно первому соотношению (5). Второе доказывается аналогично. Подобные рассуждения доказывают еще две теоремы. Теорема 4. С (4)
(A, a *) — * (/, / *), [a, a *) -> — [/, / *], / я. д. Предел скалярного (векторного) произведения двух векторов с ограничениями равен (соответствующему) произведению этих ограничений. Теорема б. если И это = /, l p скалярная переменная с конечными ограничениями q> then lim (pa) = 0 /.





















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
http://lfirmal.com/peremennye-vektory-vektor-funkcii-i-ih-differencirovanie/
Предел последовательности. Предел функции
В этом параграфе мы обобщим понятие предела числовой последовательности и сформулируем понятие предела последовательности точек евклидова пространства 
Договоримся впредь называть координатами точки 

Определение 2.9. Точка 







Как и для предела числовой последовательности будем в этом случае писать:
Чтобы подчеркнуть зависимость указанного 


Таким образом, понятие предела векторной последовательности по существу ничем не отличается от понятия предела числовой последовательности, но вместо модуля разности (расстояния между точками числовой прямой) фигурирует расстояние между точками (векторами) пространства .
С каждой последовательностью 



Рекомендуемые материалы
Положим 


Теорема 2.2 . Точка 




Доказательство. Пусть 




Но 
Следовательно,

и для каждого

Обратно, пусть для каждого 
Тогда для любого 








Значит,

Так как 

Теорема доказана.
Совершенно аналогично скалярному случаю строится и понятие предела функции.
Определение 2.10. Точка 








Обозначение: 
Опять-таки, желая подчеркнуть зависимость 


Несмотря на то, что в векторном случае понятие предела функции внешне ничем не отличается от такового в «одномерном анализе», здесь возникают более сложные и тонкие ситуации при вычислении пределов и при рассмотрении вопроса об их существовании.
Все хорошо помнят из одномерного анализа первого семестра понятие одностороннего предела функции в точке. Образно рассуждая, аргумент может приближаться к некоторой точке как слева, так и справа, в зависимости от чего предел функции в данной точке может меняться (левый и правый пределы в точке соответственно). В векторном случае «способов приближения» к точке у аргумента неизмеримо больше, и мы должны формализовать возникающую тут более общую и более сложную ситуацию зависимости предела от «траектории приближения» аргумента к заданной точке.
С этой целью введем понятие предела по множеству.
Определение 2.11. Точка 









Обозначение: 
Таким образом, в определении 2.11, в существенном отличии от определения 2.10, накладывается ограничение на «траекторию приближения» аргумента к заданной точке: аргумент должен не только попасть в 


Рис. 2.7
Нетрудно понять, что предел функции в точке существует тогда и только тогда, когда в этой точке существует предел данной функции по любому множеству (или, что равносильно, предел в точке не зависит от «траектории приближения» аргумента к этой точке).
Другая трактовка предела функции в точке состоит в понимании его как предела по множеству, совпадающему со всем пространством.
Рассмотрим некоторые примеры.
1) Зададим функцию 
Выясним, существует ли предел этой функции в точке 
Имеем:
Это значит, что в заданной точке функция имеет предел, равный нулю, по множествам: 1) точек оси абсцисс (

Но рассмотрим теперь предел по множеству точек какой-нибудь прямой 

Имеем:
Полученный результат показывает, что значение предела функции в рассматриваемой точке зависит от выбираемого множества: по разным лучам, пересекающимся в начале координат, мы имеем разные значения предела. Следовательно, предел данной функции в данной точке не существует.
2) Функция определена формулой:
Полагая 



Таким образом, при приближении к началу координат по любой прямой предел существует и равен нулю.
Но пусть теперь 
Бесплатная лекция: «МАСЛОУ Абрахам Хоралд» также доступна.
Это значит, что при приближении к заданной точке по параболе предел функции в точке зависит от параметра параболы. Тогда и предел функции в данной точке не существует.
Общий вывод таков: существование предела функции в точке по некоторому множеству (и даже по различным множествам) не гарантирует существование предела в точке. Это совершенно аналогично тому, что в одномерном анализе существование односторонних пределов не означает существование предела.
Замечание. Иногда определение предела функции в точке дается через проколотую окрестность точки, т.е. принимается, что
Если используется такое определение предела, то предел функции в точке может существовать, когда значение функции в точке определено, но не равно значению предела функции в этой точке. Если же рассматривается определение 2.10, то такая ситуация не может иметь места. А именно, предел функции в точке в смысле определения 2.10 может существовать, если значение функции в точке не определено, или значение функции в точке определено и равно значению предела (непрерывность). Заметим, что написанное выше определение предела (через проколотую окрестность) можно рассматривать как определение предела по множеству 
Вектор-функции
разделов
от теории до практики
примеров
Примеры решения задач
видео
Примеры решения задач
-
Предел и непрерывность вектор-функции.
Начать изучение
-
Понятие вектор-функции.
Начать изучение
-
Предел вектор-функции.
Начать изучение
-
Свойства пределов вектор-функций.
Начать изучение
-
Непрерывность вектор-функции.
Начать изучение
-
Производная и дифференциал вектор-функции.
Начать изучение
-
Производная вектор-функции.
Начать изучение
-
Дифференциал вектор-функции.
Начать изучение
-
Замена переменного.
Начать изучение
-
Теорема Лагранжа и локальная формула Тейлора для вектор-функции.
Начать изучение
Предел и непрерывность вектор-функции.
Понятие вектор-функции.
Если каждому значению (tin E), где (Esubsetmathbb{R}), поставлен в соответствие вектор (r(t)) трехмерного пространства, то говорят, что на множестве (E) задана векторная функция (r(t)) скалярного аргумента (t).
Пусть в пространстве фиксирована прямоугольная система координат (Oxyz). Тогда задание вектор-функции (r(t), tin E), означает задание координат (x(t), y(t), z(t)) вектора (r(t), tin E). Если (i,j,k) — единичные векторы координатных осей, то
$$
r(t)=x(t)i+y(t)j+z(t)k,qquad tin E,nonumber
$$
или
$$
r(t)=(x(t),y(t),z(t)).nonumber
$$
Если (z(t)=0) при всех (tin E), то вектор-функцию (r(t)) называют двумерной.
В случае, когда начало каждого из векторов (r(t)) совпадает с началом координат (рис. 21.1), эти векторы называют радиус-векторами, а множество их концов — годографом вектор-функции (r(t)), (tin E), который можно рассматривать как траекторию точки (M(t)) конца вектора (r(t)), если считать, что (t) — время.
Предел вектор-функции.
Вектор (a) называют пределом вектор-функции (r(t)) в точке (t_0) и пишут (displaystyle lim_{trightarrow t_{0}}r(t)=a) или (r(t)rightarrow a) при (trightarrow t_0), если
$$
lim_{trightarrow t_{0}} |r(t)-a|=0,label{ref1}
$$
то есть длина вектора (r(t)-a) стремится к нулю при (trightarrow t_0).
Утверждение 1.
Если заданы (r(t)=(x(t),y(t),z(t))) и (a=(a_{1},a_{2},a_{3})), то
$$
lim_{trightarrow t_{0}}r(t)=alabel{ref2}
$$
тогда и только тогда, когда
$$
x(t)rightarrow a_1, y(t)rightarrow a_2, z(t)rightarrow a_3quad при trightarrow t_0.label{ref3}
$$
Доказательство.
В самом деле, из неравенства
$$
|r(t)-a|=sqrt{(x(t)-a_1)^2+(y(t)-a_{2})^{2}+(z(t)-a_{3})^{2}}label{ref4}
$$
следует, что
$$
|x(t)-a_1| leq |r(t)-a|,quad|y(t)-a_2| leq |r(t)-a|,quad |z(t)-a_{3}| leq |r(t)-a|.nonumber
$$
Поэтому, если (r(t)rightarrow a) при (trightarrow t_0), то есть выполняется условие eqref{ref1}, то выполняется условие eqref{ref3}.
Обратно: если выполняются условия eqref{ref3}, то из равенства eqref{ref4} следует, что выполнено условие eqref{ref1}. (bullet)
При доказательстве свойств предела вектор-функции удобно использовать следующее очевидное утверждение: условие eqref{ref2} выполняется в том и только том случае, когда
$$
r(t)=a+alpha(t),nonumber
$$
где (alpha(t)) — бесконечно малая вектор-функция, то есть
$$
alpha(t)rightarrow 0quad mbox{при} trightarrow t_{0}.nonumber
$$
Свойства пределов вектор-функций.
Свойство 1.
Если (displaystyle lim_{trightarrow t_{0}}=a), то (displaystyle lim_{trightarrow t_{0}}|r(t)|=|a|).
Доказательство.
(circ) Это свойство следует из неравенства
$$
||r(t)|-|a|| leq |r(t)-a|.qquad bulletnonumber
$$
Свойство 2.
Если (r(t)rightarrow a) при (trightarrow t_{0}), а скалярная функция (f(t)) такова, что (f(t)rightarrow A) при (trightarrow t_{0}), то (f(t)r(t)rightarrow Aa) при (trightarrow t_{0}), то есть
$$
lim_{trightarrow t_0}f(t)r(t)=lim_{trightarrow t_{0}}f(t)lim_{trightarrow t_0}r(t).label{ref5}
$$
Доказательство.
(circ) Из определений пределов скалярной функции и вектор-функции следует, что (r(t)=a+alpha(t), f(t)=A+beta(t)), где (alpha(t)) — бесконечно малая вектор-функция, (beta(t)) — бесконечно малая функция при (trightarrow t_0). Поэтому (f(t)r(t)=Aa+gamma(t)), где (gamma(t)=Aalpha(t)+beta(t)a+beta(t)alpha(t)) — бесконечно малая вектор-функция при (trightarrow t_0), откуда получаем равенство eqref{ref5}. (bullet)
Свойство 3.
Если (r_1(t)rightarrow a_1, r_2(t)rightarrow a_2) при (trightarrow t_{0}), то (r_1+r_2rightarrow a_1+a_2, (r_1,r_2)rightarrow (a_1,a_2), [r_{1},r_2]rightarrow [a_1,a_2]) при (trightarrow t_{0}), то есть
$$
lim_{trightarrow t_{0}}(r_1(t)+r_2(t))=lim_{trightarrow t_{0}}r_1(t)+lim_{trightarrow t_{0}}r_2(t),label{ref6}
$$
$$
lim_{trightarrow t_{0}}(r_1(t),r_2(t))=left(lim_{trightarrow t_{0}}r_1(t),lim_{trightarrow t_{0}}r_2(t)right),label{ref7}
$$
$$
lim_{trightarrow t_{0}}[r_1(t),r_2(t)]=left[lim_{trightarrow t_{0}}r_1(t),lim_{trightarrow t_{0}}r_2(t)right].label{ref8}
$$
Доказательство.
(circ) По условию (r_{i}(t)=a_{i}+alpha_{i}), где (a_i(t)rightarrow 0) при (trightarrow t_{0} (i=1,2)). Поэтому (r_1(t)+r_2(t)=a_1+a_2+beta(t)), где (beta(t)=alpha_{1}(t)+alpha_2(t)rightarrow 0) при (trightarrow t_{0}), откуда следует eqref{ref6}. Докажем формулу eqref{ref7}. В силу свойств скалярного произведения
$$
(r_{1}(t),r_2(t))-(a_1,a_2)=(alpha_{1}(t),a_{2})+(alpha_{2}(t),a_1)+(alpha_1(t),alpha_2(t)),nonumber
$$
причем в правой части этого равенства — бесконечно малая функция, так как (alpha_{1}(t),alpha_{2}(t)) — бесконечно малые вектор-функции и (|(p,q)| leq |p|cdot|q|) для любых векторов (p) и (q).
Аналогично доказывается формула eqref{ref8}, в этом случае следует воспользоваться неравенством (|[p,q]| leq |p|cdot|q|). (bullet)
Непрерывность вектор-функции.
Вектор-функцию (r(t)) называют непрерывной при (t=t_{0}), если
$$
lim_{trightarrow t_{0}}r(t)=r(t_0).label{ref9}
$$
Непрерывность вектор-функции (r(t)=(x(t),y(t),z(t))) при (t=t_{0}) в силу эквивалентности условий eqref{ref2} и eqref{ref3} означает, что ее координаты (x(t),y(t),z(t)) непрерывны в точке (t_{0}).
Назовем вектор-функцию (Delta r=r((t_0+Delta t)-r(t_0)) приращением вектор-функции (r(t)) в точке (t_{0}). Тогда условие eqref{ref9} означает, что
$$
Delta rrightarrow 0quad приquad Delta trightarrow 0.label{ref10}
$$
Из определения непрерывности вектор-функции и свойств пределов векторных функций следует, что сумма, векторное и скалярное произведения вектор-функций (r_1(t)) и (r_2(t)) являются непрерывными функциями при (t=t_{0}), если вектор-функции (r_1(t)) и (r_2(t)) непрерывны в точке (t_{0}).
Производная и дифференциал вектор-функции.
Производная вектор-функции.
Если существует (displaystyle lim_{Delta trightarrow 0}frac{Delta r}{Delta t}) где (Delta r=r(t_0+Delta t)-r(t_0)), то этот предел называют производной вектор-функции (r(t)) в точке (t_0) и обозначают (r'(t_0)) или (dot{r}(t_0)).
Таким образом,
$$
r'(t_{0})=lim_{Delta trightarrow 0}frac{r(t_{0}+Delta t)-r(t_{0})}{Delta t}.label{ref11}
$$
Аналогично вводится понятие второй производной
$$
r″(t_{0})=lim_{Delta trightarrow 0}frac{r'(t_{0}+Delta t)-r'(t_{0})}{Delta t}nonumber
$$
и производной порядка (n > 2) вектор-функции. Заметим, что если (r(t)=(x(t),y(t),z(t))), то
$$
r'(t_{0})=(x'(t_0),y'(t_0),z'(t_0))label{ref12}
$$
Утверждение eqref{ref12} следует из определения eqref{ref11} и свойств пределов вектор-функций.
Аналогично, если существует (r″(t_{0})), то
$$
r″(t_{0})=(x″(t_0),y″(t_0),z″(t_0)).nonumber
$$
Из определения производной следует, что (Delta r=r'(t_0)Delta t+alpha(Delta t)Delta t), где (alpha(Delta t)rightarrow 0) при (Delta trightarrow 0), и потому (Delta rrightarrow 0) при (Delta trightarrow 0). Таким образом, выполняется условие eqref{ref10}, то есть вектор-функция (r(t)), имеющая производную в точке (t_{0}), непрерывна при (t=t_{0}).
Утверждение 2.
Справедливы следующие правила дифференцирования вектор-функций:
$$
(r_{1}+r_{2})’=r_{1}’+r_{2}’,label{ref13}
$$
$$
(fr)=f’r+fr’,label{ref14}
$$
$$
(r_1,r_2)’=(r_1′,r_2)+(r_1,r_2′),label{ref15}
$$
$$
[r_1,r_2]’=[r_1′,r_2]+[r_1,r_2′].label{ref16}
$$
Доказательство
(circ) Формулы eqref{ref13}-eqref{ref16} справедливы в точке (t), если в этой точке соответствующие функции имеют производные. Ограничимся доказательством формулы eqref{ref15}. Пусть (Delta r_{k}) — приращение вектор-функции (r_k(t)), соответствующее приращению аргумента (Delta t), то есть (Delta r_k=r_k(t+Delta t)-r_k(t), k=1,2). Тогда, используя свойства скалярного произведения и свойства пределов вектор-функций, получаем
$$
begin{array}{l}
(r_{1},r_{2})’=displaystylelim_{Delta trightarrow 0}frac{(r_{1}(t+Delta t),r_{2}(t+Delta t))-(r_{1}(t),r_{2}(t))}{Delta t}=\
=lim_{Delta trightarrow 0}left[left(r_{1}(t),frac{Delta r_{2}(t)}{Delta t}right)+left(frac{Delta r_{1}(t)}{Delta t},r_2(t)right)+left(frac{Delta r_{1}(t)}{Delta t},Delta r_2(t)right)right]=\
=(r_1,r_2′)+(r_1′,r_2),
end{array}nonumber
$$
так как (displaystyle frac{triangle mathrm{r}_{i}}{triangle t}rightarrow r_{i}'(t)) при (Delta trightarrow 0 (i=1,2)) и (Delta r_2rightarrow 0) при (Delta trightarrow 0). (bullet)
Пример 1.
Пусть существует (r'(t)) для всех (tin(alpha,beta)) и пусть (|r(t)|=C=const) для всех (tin(alpha,beta)).
Доказать, что ((r(t),r'(t))=0), то есть векторы (r(t)) и (r'(t)) ортогональны.
Решение.
(triangle) Используя формулу (|r(t)|^2=(r(t),r(t))), правило дифференцирования скалярного произведения (формула eqref{ref15}) и условие (|r(t)|=C), получаем ((r(t),r(t))’=2(r'(t),r(t))=0), так как (|r(t)|^{2})’=(C^{2})’=0). Итак,
$$
|r(t)|=CRightarrow (r(t),r'(t))=0.quadblacktrianglenonumber
$$
Дифференциал вектор-функции.
Вектор-функцию (r(t)), определенную в некоторой окрестности точки (t_{0}), называют дифференцируемой при (t=t_{0}), если ее приращение (Delta r=r(t_{0}+Delta t)-r(t_{0})) в точке (t_{0}) представляется в виде
$$
Delta r=aDelta t+Delta talpha(Delta t),label{ref17}
$$
где вектор (a) не зависит от (Delta t), (alpha(Delta t)rightarrow 0) при (Delta trightarrow 0).
В этом случае вектор (aDelta t) называют дифференциалом вектор-функции (r(t)) в точке (t_{0}) и обозначают (dr). Таким образом,
$$
dtextbf{r}=textbf{a}Delta t.nonumber
$$
Как и в случае скалярной функции, дифференцируемость вектор-функции (r(t)) в точке (t_{0}) равносильна существованию ее производной в точке (t_0), причем
$$
textbf{r}'(t_0)=textbf{a}.label{ref18}
$$
Следовательно,
$$
dr=r'(t_{0})Delta t.label{ref19}
$$
Если функция (r(t)) дифференцируема при (t=t_{0}), то, используя равенства eqref{ref17} и eqref{ref18}, получаем
$$
Delta r=r'(t_{0})Delta t+Delta t alpha(Delta t),label{ref20}
$$
где (alpha(Delta t)rightarrow 0) при (Delta trightarrow 0).
Полагая (dt=Delta t), запишем равенство eqref{ref19} в виде
$$
dr=r’dt,nonumber
$$
где опущено обозначение аргумента функции (r’). Отсюда получаем
$$
r’=frac{dr}{dt}.label{ref21} (21)
$$
Замена переменного.
Утверждение 3.
Если функция (t=t(s)) дифференцируема при (s=s_{0}, t(s_{0})=t_{0}), а вектор-функция (r(t)) дифференцируема в точке (t_{0}), то вектор-функция (rho(s)=r(t(s))) дифференцируема в точке (s_{0}), а производная этой функции выражается формулой
$$
rho’ (s_0)=r_s'(t(s_0))=r_{t}'(t_{0})t_{s}'(s_{0}),label{ref22}
$$
где индекс указывает, по какому переменному производится дифференцирование.
Доказательство.
(circ) Функция (alpha(Delta(t))) в формуле eqref{ref20} не определена при (Delta t=0). Доопределим ее при (Delta t=0), полагая (alpha(0)=0).
Так как (t=t(s)) — функция, дифференцируемая при (s=s_0), то (Delta t=t(s_{0}+Delta s)-t(s_{0})rightarrow 0) при (Delta srightarrow 0). Разделив обе части равенства eqref{ref20} на (Delta sneq 0), получим
$$
frac{Delta r}{Delta s}=r'(t_0)frac{Delta t}{Delta s}+alpha(Delta t)frac{Delta t}{Delta s}.label{ref23}
$$
Правая часть eqref{ref23} имеет при (Delta srightarrow 0) предел, равный (r'(t_0)t'(s_0)), так как (Delta trightarrow 0) при (Delta srightarrow 0) и (alpha(Delta t)rightarrow 0) при (Delta trightarrow 0). Следовательно, существует предел в левом части eqref{ref23}, и справедливо равенство eqref{ref22}. Формулу eqref{ref22} запишем кратко в виде равенства
$$
r_{s}’=r_{t}’t_{s}’,label{ref24}
$$
выражающего правило дифференцирования вектор-функции при замене переменного. (bullet)
Теорема Лагранжа и локальная формула Тейлора для вектор-функции.
Замечание 1.
Формула Лагранжа, то есть формула
$$
r(beta)-r(alpha)=r'(xi)(beta-alpha),quad xiin(alpha,beta),label{ref25}
$$
для вектор-функции, вообще говоря, неверна.
(circ) В самом деле, пусть формула eqref{ref25} верна, и пусть (r(t)=(cos t,sin t)), тогда (r'(t)=(-sin t,cos t), |r'(t)|=1). Полагая (alpha=0,beta=2pi), получим из равенства eqref{ref25} (0=r(2pi)-r(0)=r'(xi)2pi), что невозможно, так как (|r'(xi)|=1). (bullet)
Теорема Лагранжа.
(Для вектор-функций).
Если вектор-функция (r(t)) непрерывна на отрезке ([alpha,beta]) и дифференцируема на интервале ((alpha,beta)), то
$$
existsxiin(alpha,beta): |r(beta)-r(alpha)|leq|r'(xi)|(beta-alpha).label{ref26}
$$
Доказательство.
(circ) Рассмотрим скалярную функцию
$$
varphi(t)=(r(beta)-r(alpha),r(t)).nonumber
$$
эта функция непрерывна на отрезке ([alpha,beta]), так как вектор-функция (r(t)) непрерывна на этом отрезке. Кроме этого, функция (varphi(t)) дифференцируема на интервале ((alpha,beta)), так как функция (r(t)) дифференцируема этом интервале, причем в силу правила дифференцирования скалярного произведения
$$
varphi'(t)=(r(beta)-r(alpha),r'(t)).nonumber
$$
По теореме Лагранжа
$$
existsxiin(alpha,beta): varphi(beta)-varphi(alpha)=varphi'(xi)(beta-alpha)label{ref27}
$$
Преобразуем левую часть неравенства eqref{ref27}:
$$
begin{array}{l}
varphi(beta)-varphi(alpha)=(r(beta)-r(alpha),r(beta))-(r(beta)-r(alpha),r(alpha))=\
=(r(beta)-r(alpha),r(beta)-r(alpha))=|r(beta)-r(alpha)|^2
end{array}nonumber
$$
Тогда равенство eqref{ref27} примет вид
$$
|r(beta)-r(alpha)|^{2}=(r(beta)-r(alpha),r'(xi))(beta-alpha).label{ref28}
$$
Если (r(beta)=r(alpha)), то неравенство eqref{ref26} справедливо при любом (xiin in(alpha,beta)). Если (r(beta)neq r(alpha)), то (|r(beta)-r(alpha)| > 0). Тогда, используя неравенство (|(a,b)|leq|a|cdot|b|), из формулы eqref{ref28} получим
$$
|r(beta)-r(alpha)|^{2}leq|r(beta)-r(alpha)|cdot |r'(xi)|(beta-alpha),nonumber
$$
откуда, разделив обе части неравенства на (|r(beta)-r(alpha)| > 0), получим неравенство eqref{ref26}. (bullet)
Замечание 2.
Для вектор-функции (r(t)) справедлива локальная формула Тейлора
$$
r(t)=sum_{k=0}^{n}frac{r^{(k)}(t_{0})}{k!}(t-t_{0})^{k}+varepsilon(t-t_{0}),label{ref29}
$$
где (varepsilon(t-t_0)=o((t-t_{0})^{n})) — вектор-функция такая, что (varepsilon(t-t_0)=(t-t_{0})^{n}varepsilon_{1}(t-t_{0})), где (varepsilon_{1}(t-t_{0})rightarrow 0) при (trightarrow t_{0}).Эта формула справедлива в предположении, что существует (r^{(n)}(t_0)). Для доказательства формулы eqref{ref29} достаточно воспользоваться локальной формулой Тейлора для компонент вектор-функции (r(t)).
































