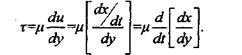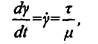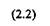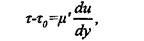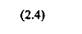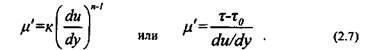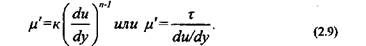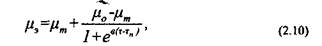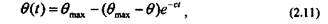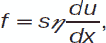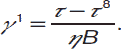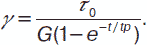Как найти предельное напряжение сдвига по бингаму

ПРЕДЕЛЬНОЕ НАПРЯЖЕНИЕ СДВИГА

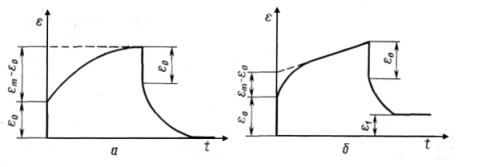
Реограммы пластично-вязких твердообразных материалов имеют сложный характер с несколькими характерными участка­ми (рис. 13.5).

С увеличением напряжения сдвига до точки 1 происходит только упругая деформация, слои друг относительно друга не пе­ремещаются, материал ведет себя как твердое тело, вязкость сис­темы бесконечно велика.

Величина θ_ст (статическое предельное напряжение сдвига) ха­рактеризует переход системы из состояния покоя в состояние медленного перемещения одного слоя относительно другого (ползучесть) без заметного разрушения структуры. Деформация становится высокоэластичной, вязкость принимает максималь­ное значение (η_max) и называется пластической или шведовской.

Величина θ_ст, или более распространенное на практике обоз­начение θ₀ — предельное напряжение сдвига неразрушенной структуры, является одной из основных реологических характе­ристик пластично-вязких материалов. Под предельным на­пряжением сдвига понимают напряжение, по достижении которого материал начинает необратимо деформироваться (течь).

Рис. 13.5. Реологические кривые для твердообразных систем:

а — зависимость градиента скорости

логарифма эффективной вязкости

0—1 — зона упругих деформаций;

2—3 — начало зоны лавинного

3—4— зона лавинного разрушения структуры (течение с наименьшей

5 и выше — зона ньютоновского течения с постоянной вязкостью

предельно разрушенной структуры

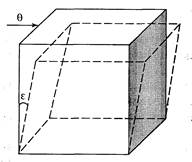
Для большей наглядности представим себе кубик (рис. 13.6), который нижним основанием приклеен к неподвижной плоско­сти, а к верхнему основанию приложено напряжение θ. В резуль­тате кубик превратится в ромбоэдр, так как его боковые стороны сдвинутся на угол ε. Этот угол называется углом сдвига. Он зави­сит от приложенного напряжения и свойств материала.

Рис. 13.6. Деформация сдвига

Если напряжения сдвига малы, то и углы невелики и исчеза­ют после того, как будут сняты напряжения, в этом случае тело проявляет упругие свойства. Если приложены большие напряже­ния, получаются большие углы ε, после снятия напряжений углы сдвига могут частично уменьшаться, но не до нуля, т. е. появятся остающиеся углы сдвига ε’. Напряжения, при которых они появ­ляются, называются пределом упругости и характеризуют пре­дельное напряжение сдвига.

Участок 2—3 (см. рис. 13.5) соответствует интенсивному (ла­винному) разрушению структуры в системе. Начало разрушения θ_т означает переход ползучести в течение с постоянно изменяю­щейся вязкостью, называемой эффективной вязкостью η_Эф.

Эффективная вязкость — это итоговая характеристика для данного напряжения сдвига, характеризующая равновесное со­стояние между процессами восстановления и разрушения струк­туры, а также ориентации частиц в направлении установившего­ся ламинарного потока жидкости.

Участок 3— 4 (прямая линия) отвечает течению системы с раз­рушенной структурой. Величина θ₀, отсекаемая на оси абсцисс продолжением прямолинейного участка, называется динамиче­ским или бингамовским предельным напряжением сдвига.

Величина θ_max соответствует практически полному разруше­нию структурных элементов. Вязкость системы принимает ми­нимально возможное значение.

Адгезия (от лат. adhesio — прилипание) — это сцепление раз­нородных тел, соприкасающихся своими поверхностями. Она относится к поверхностным свойствам пищевых продуктов, иг­рает важную роль в различных технологических процессах, где существует контакт между продуктом и поверхностью обрабаты­вающей машины, и, как правило, нежелательна.

На адгезию пищевых масс оказывают влияние свойства ис­пользуемого сырья и особенности технологии. Например, адге­зия дрожжевого теста зависит от способа приготовления (опарное, безопарное, сорт муки, количество дрожжей, добавки ПАВ и др.).

До настоящего времени природа адгезии полностью не выяс­нена и существует несколько теорий ее существования (адсорб­ционная, термодинамическая, диффузионная, электрическая, химическая и др.).

По адсорбционной теории адгезия связана с действи­ем межмолекулярных сил: физических — ван-дер-ваальсовых, ковалентно-ионных. При взаимодействии двух тел вследствие броуновского движения молекул и их перегруппировки на границе контакта устанавливается адсорбционное равно­весие.

Диффузионная теория, развиваемая С. С. Воюцким, объ­ясняет адгезию полимеров диффузией макромолекул в поры и трещины металлической поверхности, а также результатом диф­фузии в аморфный слой гидроксида, образующегося на поверх­ности металла.

Согласно электрической теории Б. В. Дерягина и Н. А. Кротовой адгезия объясняется контактной электризацией на границе разнородных тел, т. е. возникновением в зоне контак­та своеобразного электрического молекулярного конденсатора, обусловленного двойным электрическим слоем.

Химическая теория связывает явление адгезии с хи­мической активностью контактирующих тел. В месте контакта происходит химическое взаимодействие контактирующих ма­териалов, в результате которого на поверхности металла образу­ются мономолекулярный слой продуктов реакции взаимодей­ствия.

Таким образом, хотя механизм адгезии недостаточно изучен и не существует единой теории этого процесса, каждая из вышеприведенных теорий определенным образом объясняет явление адгезии.

С понятием адгезии тесно связано понятие когезии. Когезия означает связи внутри данного тела. Соотношение адгезии и когезии в значительной степени определяет условие после удале­ния структурированных пищевых масс (тесто, фарши и др.) при нарушении их контакта с твердой поверхностью.

В большинстве случаев силы адгезии превышают силы коге­зии и отрыв от поверхности субстрата происходит полностью или частично в объеме адгезива. В этом случае отрываемая по­верхность полностью или частично оказывается покрыта адгезивом, а вид отрыва называют когезионным или смешанным. Например, для мучного теста это означает прилипание части теста к внутренней поверхности различных емкостей, к деталям технологического оборудования. Повышенная по сравнению с когезией адгезия теста приводит к потерям пищевого сырья и снижению производительности оборудования.

На величину адгезии оказывают влияние различные факторы: влажность продукта, площадь, давление и продолжительность контакта с поверхностью, вид поверхности, скорость отрыва и др.

Источник

Неньютоновские жидкости

Течение некоторых жидкостей (коллоидных растворов, нефтей с большим содержанием асфальтенов и парафинов, растворы полимеров и т.д.) не подчи­няются закону Ньютона. Такие жидкости в реологии принято называть ненью­тоновскимиили аномальными.

Закон Ньютона обычно нарушается при течении коллоидных растворов с удлиненными частицами дисперсной фазы, способными деформироваться в поле напряжений и структурированных систем. Такие коллоидные системы обладают определенными механическими свойствами — пластичностью, упругостью, прочностью и вязкостью. Эти свойства в большинстве случаев связаны с обра­зованием структуры в жидкости, и поэтому их часто называют структурно —механическими или реологическими свойствами.

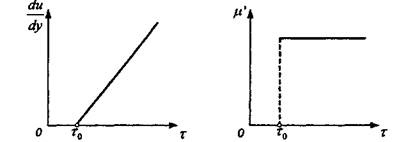
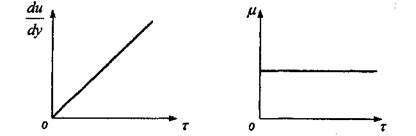
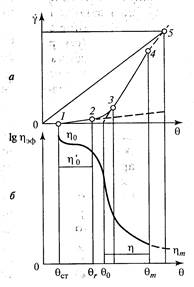
Основы реологии коллоидных растворов впервые изучены Ф.Н.Шведовым, Бингамом и Грином. В 1889 году Ф.Н. Шведов, позже в 1916 году Бингам уста­новили, что течение системы с пространственной структурой начинается лишь тогда, когда напряжение сдвига т превышает определенное критическое значе­ние х₀ (рис. 2.3), необходимое для разрушения в жидкости структурной сетки. Такое течение было названо пластическим, а критическое напряжение сдвига —пределом текучести или предельным напряжением сдвига.

Рис. 2.3. Линия консистентности и зависимость пластической вязкости ju’ от напряжения сдвига гдля пластических жидкостей

где ц ‘ — пластическая вязкость системы.

Систему, течение которой подчиняется такой идеализированной схеме, в реологии называют телом Бингама или бингановскими пластиками. Они опи­сываются следующим реологическим уравнением Бингама — Шведова:

Вязкость истинных растворов зависит от природы жидкости, температуры и давления.

Жидкости, течение которых подчиняется закону вязкого течения Ньютона, названы ньютоновскими.

Но dx/dy представляет собой сдвиг слоев у (деформацию). Отсюда следует выражение для градиента скорости сдвига:

Формуле (2.1) можно придать другой вид (см. рис. 2.1):

то есть у ньютоновских жидкостей скорость сдвига у пропорциональна касательному напряжению сдвига г и обратно пропорциональна динамической вязкости fi. Зависимость между г и у, очевидно, является прямой линией, про­ходящей через начало координат.

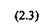
Таким образом, истинные или молекулярные растворы являются ньютонов­скими жидкостями. Примерами таких жидкостей, кроме воды, могут служить жидкие индивидуальные углеводороды с числом атомов углерода до 17 (спирт, бензол и т.д.).

Следует заметить, что закон Ньютона справедлив лишь при установившем­ся ламинарном течении истинной жидкости.

Вязкость жидкости определяется более точно, если имеется график зави­симости между напряжением сдвига т и градиентом скорости dx/dy — линия консистентное/пи. Линия консистентности ньютоновской жидкости представ­ляет собой прямую линию, исходящую из начала координат (рис. 2.2). Это ука­зывает на то, что истинные жидкости текут при сколь угодно малых напряжени­ях сдвига.

Рис. 2.2. Линия консистентности и зависимость динамической вязкости // от напряжения сдвига г для ньютоновских жидкостей

Параметры, с помощью которых можно описывать течение веществ, назы­ваются реологическими параметрами.

Таким образом, единственным реологическим параметром, характеризую­щим течение ньютоновской жидкости, является динамическая вязкость.

В смешанной системе единиц напряжение сдвига т измеряется в дин/см 2 (1 дин/см 2 =0,1 Н/м 2 ). Единица измерения динамической вязкости в честь фран­цузского ученого Пуазейля, впервые изучившего движение жидкостей в капил­лярах, названа Пуазом (1сП=1мПас).

2.2. Неньютоновские жидкости

Течение некоторых жидкостей (коллоидных растворов, нефтей с большим содержанием асфальтенов и парафинов, растворы полимеров и т.д.) не подчи­няются закону Ньютона. Такие жидкости в реологии принято называть ненью­тоновскимиили аномальными.

Закон Ньютона обычно нарушается при течении коллоидных растворов с удлиненными частицами дисперсной фазы, способными деформироваться в поле напряжений и структурированных систем. Такие коллоидные системы обладают определенными механическими свойствами — пластичностью, упругостью, прочностью и вязкостью. Эти свойства в большинстве случаев связаны с обра­зованием структуры в жидкости, и поэтому их часто называют структурно -механическими или реологическими свойствами.

Основы реологии коллоидных растворов впервые изучены Ф.Н.Шведовым, Бингамом и Грином. В 1889 году Ф.Н. Шведов, позже в 1916 году Бингам уста­новили, что течение системы с пространственной структурой начинается лишь тогда, когда напряжение сдвига х превышает определенное критическое значе­ние т₀ (рис. 2.3), необходимое для разрушения в жидкости структурной сетки. Такое течение было названо пластическим, а критическое напряжение сдвига —пределом текучести или предельным напряжением сдвига.

Рис. 2.3. Линия консистентности и зависимость пластической вязкости fx от напряжения сдвига г для пластических жидкостей

где /л ‘ — пластическая вязкость системы.

Систему, течение которой подчиняется такой идеализированной схеме, в реологии называют телом Бингама или бингановскими пластиками. Они опи­сываются следующим реологическим уравнением Бингама — Шведова:

Линия консистентности бингамова тела выражается прямой линией, отсе­кающей отрезок на оси абсцисс, равный т₀ от начала координат (рис. 2.3).

Для ньютоновских жидкостей предельное напряжение сдвига равно нулю, и уравнение (2.4) переходит в закон Ньютона, а пластическая вязкость — и истин­ную вязкость. Из уравнения (2.4) следует: система до т₀ упруго деформируется, после этого течет с постоянной пластической вязкостью

В области упругой деформации вязкость бингамовского пластика чрезвы­чайно высокая. Здесь упруго деформируется структурный «каркас» из частиц дисперсной фазы. При превышении т₀, согласно уравнению Бингама — Шведова, структурная сетка мгновенно разрушается и вязкость системы принимает посто­янное значение.

Примером систем, хорошо подчиняющихся уравнению (2.4), могут служить нефти с высоким содержанием парафинов при температурах ниже температуры кристаллизации.

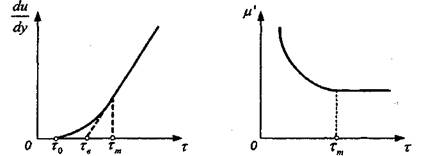
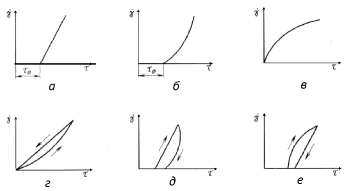
Однако у многих реальных структурированных коллоидных систем линия консистентности оказывается не прямой, а кривой, отсекающей на оси напряже­ний сдвига некоторый отрезок (рис. 2.4). В этом случае при достижении предела текучести структура разрушается не сразу, а постепенно, по мере увеличения скорости сдвига — упругопластические жидкости.

Рис. 2.4. Линия консистентности и зависимость кажущейся вязкости ju’ от напряжения сдвига т щя упругопластических жидкостей

Для характеристики механических свойств структуры в этом случае вводят три параметра: минимальный предел текучести (статическое напряжение сдвига), соответствующий началу течения жидкости х₀ предел текучести по Бингаму (динамическое напряжение сдвига по Бингаму) т_а максимальный предел текучести (напряжение сдвига предельного разрушения структуры), при котором кривая переходит в прямую линию т_т (рис. 2.4). Значение т_т равно напряжению, при котором структура в жидкости полностью разрушается.

Математическая модель упругопластической жидкости выражается сле­дующей степенной зависимостью:

где к — мера консистентности жидкости (с увеличением вязкости жидкости мера консистентности растет); п — степень неньютоновского поведения системы. Значение п всегда меньше единицы. Чем больше п отличается от единицы, тем сильнее проявляются неньютоновские свойства жидкости.

Кажущаяся вязкость системы определяется из соотношения

В качестве примера упругопластической жидкости можно указать на мас­ляную краску, буровые растворы, высокопарафинистую дегазированную нефть с температурой ниже температуры насыщения парафином. Например, линии кон­систентности такой формы (рис. 2.4) обнаружены у некоторых нефтей месторо­ждений Азербайджана, Узбекистана и Казахстана.

На практике наличие статического напряжения сдвига у жидкости часто иг­рает положительную роль. Так, толщина слоя краски, оставшейся после нанесе­ния на вертикальную поверхность определяется величиной т₀. Следовательно, изменяя значение т₀, можно регулировать расход краски на покраску.

При бурении скважин процесс проходки часто прерывается. Применение качественных буровых растворов позволяет удерживать во взвешенном состоя­нии часть шлама выбуренной породы и тем самым предотвращать прихват буро­вого инструмента. При этом регулирование количества и размеров частиц удер­живаемого в буровом растворе шлама достигается подбором параметра т₀.

То же самое наблюдается и при течении растворов высокомолекулярных соединений с гибкими, свернутыми в клубок макромолекулами, например у водных растворов полимеров. Здесь снижение вязкости обусловлено распрямле­нием молекул и ориентацией в направлении потока. Система ведет себя при те­чении как жидкость, в которой взвешены частицы, способные ориентироваться или деформироваться.

Во всех этих случаях речь идет о кажущейся или эффективной вязкости, так как истинная вязкость жидкости от скорости течения не зависит.

Механические свойства псевдопластической (вязкопластической) жид­кости характеризуются двумя параметрами: динамическим напряжением сдви­га по Бингаму т_в и напряжением сдвига предельного разрушения структуры или ориентирования частиц в потоке т_т (рис. 2.5).

Реологическое уравнение у таких систем выражают в виде степенной зави­симости

Рис. 2.5. Линия консистентное™ и зависимость кажущейся вязкости р.’ от напряжения сдвига г для вязкопластических жидкостей

Кажущаяся вязкость вязкопластической жидкости выражается следующим образом:

Здесь и в предыдущем случае необходимо иметь в виду, что для реальной жидкости п является переменным и зависящим от скорости сдвига. Поэтому при решении практических задач значение п следует определять в ограниченном пределе скоростей сдвига. Кроме того, неудобство использования степенного закона обусловлено зависимостью размерности меры консистентности от пока­зателя степени.

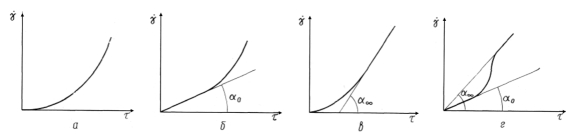
В настоящее время для увеличения нефтеотдачи пластов, при воздействии на призабойную зону скважин и проведении изоляционных работ применяются растворы полимеров. В некоторых условиях в пористой среде они проявляют свойства дилатантных жидкостей. Термин «дилатанткая» можно применять для тех жидкостей, кажущаяся вязкость которых с увеличением скорости сдвига повышается (рис. 2.6).

Рис. 2.6. Линия консистентности и зависимость кажущейся вязкости

m’ от напряжения сдвига г для дилатантных жидкостей

Такой тип течения был впервые обнаружен Рейнольдсом в суспензиях при большом содержании твердой фазы и крахмальных клейстерах. Рейнольде при объяснении дилатантных свойств суспензии высказывает предположение о том, что в состоянии покоя твердые частицы имеют наиболее плотную упаковку, а пространство между частицами заполнено жидкостью. При течении суспензии с небольшой скоростью жидкость служит смазкой, уменьшающей трение между частицами, и напряжения сдвига невелики. При больших скоростях сдвига плот­ная упаковка частиц нарушается, увеличивается объем суспензии и уже при но­вой структуре жидкости ее недостаточно для смазки трущихся друг о друга час­тиц. Действующие напряжения сдвига при этом увеличивается значительно бы­стрее, чем скорости сдвига.

Для описания реологического поведения дилатантной жидкости также при­меняют степенной закон, но с показателем степени больше единицы.

23. Аномалии вязкости нефти

Исследованиями установлено, что асфальтеносодержащие пластовые и де­газированные нефти при температурах выше температуры насыщения парафи­ном являются аномально вязкими. Линии консистентности этих нефтей по форме аналогичны полным реологическим кривым С. Оствальда (рис. 2.7).

Рис. 2.7. Линия консистентности и зависимость эффективной вязкости m ’ ,

от напряжения сдвига для аномально вязких нефтей

По классификации акад. П.А. Ребиндера кривые консистентности такой формы характерны для жидкообразных структурированных коллоидных систем. Структурная сетка образована в них мицеллами асфальтенов и относится к типу коагуляционных структур. Как правило, начальная температура в пласте выше температуры насыщения нефти парафином, поэтому асфальтеносодержащие нефти следует считать аномально вязкими.

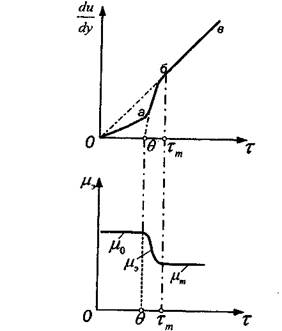
Рассмотрим более подробно форму линии течения таких нефтей и сущность процессов, происходящих на каждом характерном участке кривой консистент­ности. На кривой консистентности (рис. 2.7) можно выделить два линейных уча­стка, различающихся углом наклона к оси напряжения сдвига.

Участок (0-а) находится в начале кривой консистентности — в области ма­лых напряжений и скоростей сдвига. Угол наклона кривой на этом участке не­большой, течение нефти в этой области происходит практически без разрушения структуры, поэтому ее вязкость наибольшая. Продолжение участка (0-а) прохо­дит через начало координат.

По П.А. Ребиндеру в этой области разрушение структуры сопровождается полным тиксотропным ее восстановлением, и система движется с практически не разрушенной структурой, т.е. наблюдается явление ползучести. Вязкость нефти постоянна и названа наибольшей предельной вязкостью практически не разрушенной структуры д>.

Конечный участок линии консистентности (б-в) расположен правее напряжения сдвига предельного разрушения структуры (НСПРС) т_т до об­ласти турбулентного течения. Продолжение реологической линии этого участка проходит через начало координат. Вязкость нефти в этой области постоянная и наименьшая. Она названа наименьшей вязкостью предельно разрушенной структуры /^.

При выполнении практических расчетов можно принять, что при превыше­нии предельного динамического напряжения сдвига (ПДНС) в эффективная вязкость /4 начинает уменьшаться и при действующих напряжениях сдвига, превышающих т_т, достигает наименьшей величины д>- В этой области (а

б) эф­фективная или структурная вязкость соответствует равновесному состоянию процессов разрушения и восстановления структуры, протекающих одновремен­но в установившемся ламинарном потоке. От точки «а» до точки перегиба кри­вой (а-б) превалирует процесс восстановления структуры, а в дальнейшем от то­чки перегиба до «б» — процесс разрушения пространственной структурной сетки.

Из изложенного следует, что вязкость нефти зависит от напряжений и ско­ростей сдвига. Такая зависимость в реологии названа аномалией вязкости. В частности, у неньютоновских жидкостей, кроме дилатантных, кажущаяся или эффективная вязкость уменьшается с ростом действующих напряжений сдвига т.

Для аномально вязких нефтей связь между эффективной вязкостью и на­пряжением сдвига выражается следующей формулой:

где Т„ — некоторое напряжение сдвига, соответствующее началу сильного разрушения структуры. Оно находится из экспериментальной зависимости

J4 по величине М_э = t*_m + ° ‘_ m , т.е. по величине эффективной вяз­кости, соответствующей условию Т = Т„;

Ь — коэффициент, характеризующий скорость разрушения структуры в системе. Для нахождения этого коэффициента используется любая точка экспе­риментальной кривой /и, = Дт), лежащей в диапазоне напряжений сдвига от т„ до т_т. Коэффициент Ъ находится из формулы (2.10) по значениям х и jx, в этой экспериментальной точке и найденной ранее величине т_п.

К аномально вязким системам следует отнести фильтрующиеся без переры­ва нефти с температурой, превышающей температуру насыщения парафином. После появления в объеме нефти кристалликов парафина до температуры, близ­кой к температуре массовой кристаллизации, аномалии вязкости значительно усиливаются. При этом у нефтей с содержанием парафинов до 6% масс, при не­прерывном движении наблюдается линия типа С. Оствальда. Эти выводы осно­ваны на результатах многолетних исследований пластовых нефтей месторожде­ний Башкирии, Татарии, Западного Казахстана и Коми.

Нефть, содержащая асфальтены и парафины, относится к тиксотропным системам. Такие системы способны к изотермическому восстановлению струк­туры, разрушенной при механическом воздействии. В процессе теплового дви­жения частицы дисперсной фазы принимают такое взаимное расположение, при котором система обладает минимумом энергии и становится термодинамически более устойчивой. В частности, в состоянии покоя структура упрочняется на­столько, что при возобновлении течения вязкости при тех же скоростях сдвига будет выше, чем до перерыва в движении.

Тиксотропные свойства нефти ведут к усилению структурно- механических свойств. Например, с увеличением продолжительности покоя предельное дина­мическое напряжение сдвига (ПДНС) растет. Зависимость этого параметра от времени покоя записывается в виде

где в — ПДНС нефти в условиях непрерывного движения; #_тах — максималь­ное значение ПДНС нефти, находившейся в покое более 35 часов; t- время по­коя; с =0,42 — коэффициент, зависящий от свойств нефти.

Следует учесть, что наиболее быстро ПДНС увеличивается в течение 10 ча­сов после прекращения движения. В дальнейшем прочность структуры увеличи­вается незначительно. Рост ПДНС прекращается после 35 часов покоя нефти. Зависимость между &> T m,a для нефтей со сверханомалией вязкости — введением дополни­тельно еще одного параметра Т^.

Источник

Ньютоновскими
называются жидкости, движение которых
подчиняется закону внутреннего трения
Ньютона. Вязкость
этих жидкостей остается
постоянной
при данных температуре и давлении.

В отличие от них
вязкость
неньютоновских
жидкостей
не постоянна,
а изменяется в зависимости от скорости
сдвига, его продолжительности.

В технологии
строительных материалов к таким жидкостям
относятся цементные шламы, растворы,
бетонные смеси, растворы полимеров,
лакокрасочные материалы и др.

Неньютоновские
жидкости делят на три класса.

К первому классу
относятся вязкие
(стационарные)
жидкости, для которых функция P
= f(dw/dx)
не зависит от длительности действия
сил сдвига.

К этому классу
относятся следующие жидкости:

• Бингамовские;

• Псевдопластические;

• Дилатантные.

Течение бингамовской
жидкости (
реологическая модель, которой приведена
на рис. 9) начинается только после
приложения напряжения сдвига Р₀
≥ Р,
которое необходимо для разрушения
структуры, образовавшейся в данной
системе.

Рис. 9. Модель
вязкопластичного тела Бингама

Такое течение
называется пластическим,
а критическое (т.е. предельное) напряжение
сдвига Р₀
– пределом
текучести.

При напряжениях,
меньших Р₀,
бингамовские жидкости ведут себя, как
твердые тела, а при напряжениях, больших
Р₀
– как ньютоновские жидкости, т.е.
зависимость P
= f(dw/dx)
является линейной. Считается, что
структура тела Бингама под действием
предельного напряжения сдвига мгновенно
и полностью разрушается, в результате
чего тело Бингама превращается в
жидкость, при снижении напряжения
структура восстанавливается и тело
возвращается к твердому состоянию.

Уравнение кривой
течения бингамовской жидкости называется
уравнением
Шведова-Бингама:

(26)

где η_пл
– пластическая вязкость (коэффициент
жесткости).

Для большинства
структурированных систем зависимость
P
= f(dw/dx)
выражается
не прямой, а представляет кривую (рис.
10).

Рис. 10. Кривая
течения бингамовской жидкости

Различают два
предельных напряжения сдвига:

• нижний предел
  текучести Р_к
  – статическое предельное напряжение
  сдвига, величина которого соответствует
  началу остаточной деформации (отрезок
  ОА, т.А – предел
  упругости);

• динамическое
  предельное напряжение сдвига Р_о
  = Р_дин
  , соответствующее уравнению Шведова-Бингама.

Кривую течения
структурированной системы можно условно
разделить на 4 области, характеризующие
состояние системы в процессе нагружения.

Область А-А₁
– практически прямая линия, в которой
пластическое течение системы происходит
без заметного разрушения структуры при
наибольшей
пластической вязкости (шведовской),
имеющей постоянное значение:

(27)

Нарушение структуры
в этой области столь незначительно, что
успевает восстановиться в процессе
течения.

Область А₁-А₂
–область пластического течения с
постоянным разрушением структуры.
Пластическая вязкость резко падает,
вследствие чего скорость течения быстро
увеличивается.

Область А₂-А₃
– область предельно разрушенной
структуры, выше которой течение происходит
с наименьшей
пластической вязкостью (бингамовской):

(28)

Переход к этой
области характеризуется динамическим
предельным напряжением сдвига Р₀.
Дальнейшее увеличение напряжений
системы завершается разрывом сплошности
структуры, характеризующейся пределом
прочности Р_max.

К псевдопластическим
жидкостям
относятся суспензии с ассиметричными
или волокнистыми частицами твердой
фазы, а также растворы многих
высокополимеров, целлюлозы.

Псевдопластические
жидкости начинают течь уже при самых
малых значениях напряжения сдвига.
Течение этих жидкостей характеризуется
тем, что их
вязкость зависит от градиента скорости.
Поэтому для псевдопластических жидкостей
говорят о кажущейся
вязкости,
которая представляет
собой отношение напряжения сдвига к
градиенту скорости.

С увеличением
скорости сдвига кажущаяся вязкость
этих жидкостей уменьшается.

Для таких жидкостей
в соответствии с уравнением Оствальда
напряжение сдвига определяется
соотношением:

(29)

где K
и m
– постоянные коэффициенты (m
< 1)

Коэффициент К
зависит от консистенции жидкости и
увеличивается с ростом вязкости.
Коэффициент m
характеризует степень неньютоновского
поведения жидкости, и чем больше m,
тем ближе жидкость по характеру течения
к ньютоновской.

При бесконечно
большом градиенте скорости кривая
течения постоянна и переходит в прямую
с предельным значением кажущейся
вязкости, равным бесконечности (рис.
11).

Рис. 11. Кривые
течения псевдопластической 1 и дилатантной
2 жидкостей

К дилатантным
жидкостям
относятся суспензии с большим содержанием
твердой фазы. В таких жидкостях,
находящихся в состоянии покоя, жидкость
удерживается в прослойках между
частицами. При небольших скоростях
деформации она служит смазкой.

Эти жидкости
характеризуются возрастанием кажущейся
вязкости с увеличением градиента
скорости.

Течение этих
жидкостей также описывается уравнением
Оствальда, но при m
> 1.

Ко второму классу
относятся неньютоновские жидкости,
характеристики которых зависят от
времени (нестационарные
жидкости).

Эти жидкости
характеризуются тем, что их
кажущаяся вязкость зависит не только
от скорости сдвига, но и от продолжительности
действия сдвигового усилия.

Если жидкость
деформируется с постоянной скоростью,
то напряжение сдвига во времени может
нарастать или убывать. В зависимости
от этого различают два вида жидкости:

• тиксотропные;

• реопектические.

В тиксотропных
жидкостях
с увеличением
продолжительности воздействия постоянного
напряжения сдвига структура разрушается
и текучесть возрастает
(рис. 12).

Рис. 12. Кривые
течения тиксотропных а и реопектических
жидкостей б.

После снятия
напряжения структура может самопроизвольно
восстанавливаться, т.е. тиксотропия
является обратимым процессом.

К тиксотропным
жидкостям относятся многие краски,
строительные растворы, бетонные смеси,
керамические массы. Именно благодаря
тиксотропным свойствам краски легко
удерживаются на вертикальной стене, не
стекая.

Реопектические
жидкости
характеризуются ростом структурообразования
при увеличении скорости сдвига и
продолжительности воздействия напряжения
сдвига (рис. 12).

К таким жидкостям
относятся многие коллоидные растворы,
суспензия гипса в воде.

Установлено, что
при больших скоростях сдвига у этих
жидкостей наблюдается не образование,
а разрушение структуры.

К третьему классу
относятся вязкоупругие или максвелловские
жидкости.

Эти жидкости текут
под действием напряжения сдвига, но
после снятия напряжения они частично
восстанавливают свою структуру. Таким
образом, эти жидкости обладают двойным
свойством: вязким течением по закону
Ньютона и упругим восстановлением формы
по закону Гука.

По классификации
П.А. Ребиндера жидкости по пластично-вязким
свойствам делятся
на:

• нормально-вязкие
  (ньютоновские);

• аномально-вязкие
  (псевдопластические, дилатантные,
  реопектические и тиксотропные);

• пластичные
  (бингамовские).

Первые две системы
П.А. Ребиндер объединяет в одну группу
– жидкообразные
системы, а
последнюю называет твердообразной
системой.

Изменение вязкости
в зависимости от напряжения сдвига для
жидкообразных
систем
представлено на рис. 13.

Рис. 13. Кривая
течения жидкообразной системы

Для них при
напряжениях, меньших Р₁,
вязкость
имеет наибольшую величину, равную
ньютоновской вязкости практически не
разрушенной структуры.
При напряжениях, свыше Р₁,
вязкость уменьшается до предельного
значения η_min.

Изменение вязкости
в зависимости от напряжения сдвига для
твердообразных систем представлено на
рис. 14.

Рис. 14. Кривая
течения твердообразной системы

При напряжениях
сдвига, меньших P_min,
максимальная вязкость η₀
(ньютоновская вязкость) не разрушенной
структуры бесконечно велика. При этом
происходит деформация структурной
сетки без разрушения или с тиксотропным
восстановлением структуры в потоке
(область I).

При дальнейшем
повышении напряжения сдвига до Р_т
проявляется наибольшая пластическая
вязкость η^*_max.
Здесь появляются разрывы сплошности
(области II
и II^’).

При повышении
напряжения сдвига в области постоянного
разрушения структуры (до Р₂)
пластическая вязкость постоянно
уменьшается до η^*_min.
Имеет место распад структуры на агрегаты,
размер которых уменьшается, а число
увеличивается в процессе сдвиговой
деформации (область III).

Дальнейшее течение
осуществляется с вязкостью предельно
разрушенной структуры.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

ПРОДОЛЖЕНИЕ ЛЕКЦИИ № 6

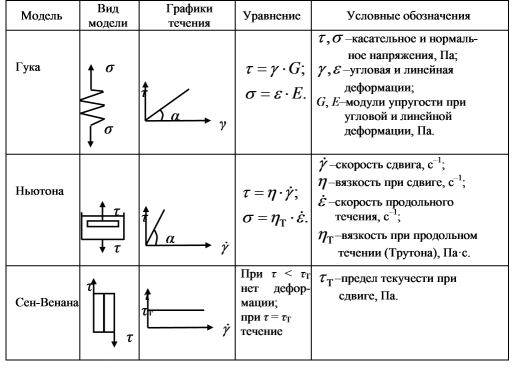
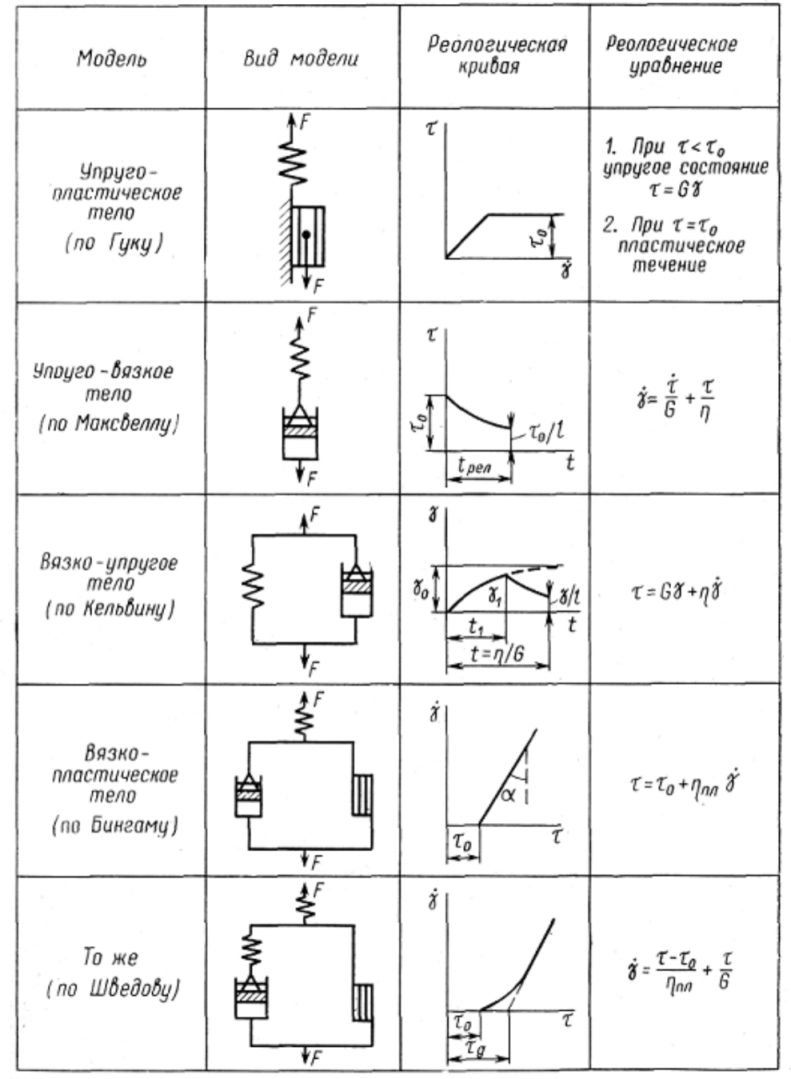
Реологические модели и уравнения течения пищевых масс

Рассмотрим основные модели и виды течения пищевых масс. При этом необходимо указать, что точные математические законо­мерности получены только для ньютоновского течения. Для всех неньютоновских течений выведены лишь приближенные формулы.

Известны три промежуточные модели идеализированных мате­риалов (см. таблица 6.4): идеальноупругое тело (по Гуку), идеальнопластическое тело (по Сен-Венану), идеальновязкая жидкость (по Ньютону).

Идеальноупругое тело является системой, в которой энергия, затраченная на деформацию, накапливается в теле и мо­жет быть возвращена при разгрузке.

Идеальнопластическое тело может быть представле­но в виде элемента, лежащего на плоскости с постоянным по вели­чине трением, не зависящим от нормальной силы. Тело по Сен-Ве­нану не начнет двигаться до тех пор, пока напряжение сдвига не превысит некоторого критического значения — предельного напря­жения, после чего элемент может двигаться с любой скоростью.

Таблица 6.4. Реологические модели простых идеализированных тел

Идеальновязкая жидкость характеризуется тем, что в ней напряжения пропорциональны скорости деформации.

                                                                                     (6.2)

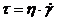
где h — коэффициент вязкости; 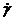   — скорость сдвига, с^–1.

Вязкое течение, происходит под действием любых сил, как бы малы они ни были, однако скорость деформации при уменьшении сил снижается, а при их исчезновении обращается в нуль.

Модели могут быть скомбинированы параллельно или последовательно из двух или трех элементов: пружины (тело по Гуку), поршня (тело по Ньютону) и двух прижатых плоскостных элементов (тело по Сен-Венану). Они.

Наиболее сложные модели отражают следующие тела: упруго-пластическое, упруго-вязкое (по Максвеллу), вязко-упругое (по Кельвину), вязко-пластическое (по Шведову-Бингаму) (рис. 6.1).

 Рис. 6.1. Реологические модели:

t — напряжение сдвига, Па; t₀ — предельное напряжение сдвига, Па; G — модуль сдвига, Па;   g — угловая деформация;   — скорость сдвига, с; h — вязкость, Па·с; h_пл — пластическая вязкость, Па·с.

Модель упруго-пластического тела получается при последова­тельном соединении упругого и пластического элементов.

Модель упруго-вязкого релаксирующего тела по Максвел­лу — это последовательно соединенные гуковский и ньютоновский элементы. Те­ло по Максвеллу ведет себя как упругое или как вязкое в зависимости от отношения времени релаксации к длительности эксперимента. Итак, если под дей­ствием мгновенного усилия пружина растягивается, а затем нагрузка сразу сни­мается, то поршень не успевает двигаться и система ведет себя как упругое тело. Однако, с другой стороны, если поддерживать растяжение пружины постоян­ным, она постепенно релаксирует, перемещая поршень вверх, и система ведет себя почти как ньютоновская жидкость.

Модель вязко-упругого тела по Кельвину — параллельное со­единение упругого и вязкого элементов. Под действием растягивающего усилия пружина удлиняется, а поршень будет двигаться в жидкости. Движение поршня связано с вязким сопротивлением жидкости, ввиду чего полное растяжение пру­жины наступает не сразу. Когда нагрузка устранена, пружина сжимается до пер­воначальной длины, но это требует времени вследствие вязкого сопротивления жидкости.

Модель тела по Кельвину отражает явление упругого последействия, которое представляет собой изменение упругой деформации во времени, когда она или постоянно нарастает до некоторого предела после приложения нагрузки, или постепенно уменьшается после ее снятия.

Модель вязко-пластического тела по Шведову—Бингаму характеризует материалы, которые в первом приближении можно рассматривать как тела по Сен-Венану. Они начинают течь, когда напряжение сдвига дости­гает предельного напряжения. Если нет вязкого сопротивления, то скорость те­чения материала станет сколь угодно большой. Во втором приближений такие материалы должны обладать еще вязкостью. Все это приводит к постулированию идеального тела, реологическое уравнение которого предложено Бингамом.

Модель тела по Шведову отличается от модели по Бингаму тем, что парал­лельно телу по Сен-Венану присоединено тело по Максвеллу, а параллельно те­лу по Бингаму — тело по Ньютону.

В технологии пищевых производств встречается много мате­риалов, которые не подчиняются закону Ньютона; вязкость их при заданных температуре и давлении не остается неизменной, а зави­сит от скорости деформации и других факторов, поэтому зависи­мость напряжения от скорости сдвига имеет нелинейный характер. Эти материалы получили название неныотоновских веществ (ано­мальных). Одно и то же вещество в зависимости от концентрации может проявлять различные виды течения.

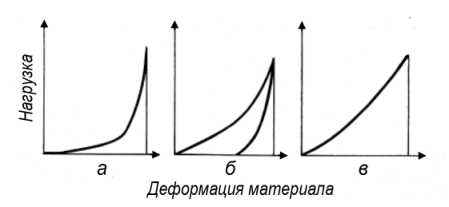
Рассмотрим наиболее типичные виды кривых течения псевдо­пластического материала (рис. 6.2).

Рис. 6.2. Кривые течения псевдопластических материалов.

Уравнение Оствальда (степенной закон) описывает кривую, представленную на рис. 6.2, а,

 при п < 1.                                                                          (6.3)

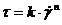
Уравнение (6.2) является эмпирическим, имеющим два пара­метра: константу k, зависящую от природы материала и геометри­ческих размеров измерительной аппаратуры, и константу n, явля­ющуюся индексом течения.

При 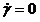, следовательно при α₀ = 0 (α — угол наклона каса­тельной к кривой), вязкость становится бесконечно большой. Од­нако практически находят конечное значение этой вязкости. При n = 1 степенной закон сводится к выражению Ньютона.

Степенной закон получил широкое распространение для описа­ния вязкости различных неньютоновских пищевых материалов: томатных паст, сахарных сиропов, абрикосового пюре, хлебопекар­ного теста, конфетных масс, крахмальных суспензий, майонеза, мыла и некоторых других.

На рис. 6.2, б приведена кривая (реограмма), которая может быть описана уравнением Штейгера,

 при с > 0,                                                                          (6.4)

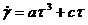
где а, с — эмпирические коэффициенты.

Уравнение (6.3) действительно также и при 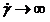, при этом предельная начальная вязкость h₀=1/с.

На рис. 6.2, в и г приведены кривые течения псевдопластиков, отличающихся аномалией при малых (в) или высоких (г) скоро­стях сдвига.

Дисперсные системы при напряжениях, меньших предельного, ведут себя как твердые тела и упруго деформируются, при напря­жении, превышающем предельное, становятся пластичными. Раз­личают несколько видов пластического течения (рис. 6.3).

Идеальнопластическое — течение, начинающееся после достижения предельного напряжения, когда наблюдается пропор­циональность между скоростью и напряжением сдвига. Для ха­рактеристик этого вида течения Бингам предложил уравнение (рис. 6.3, а)

,                                                                                 (6.5)

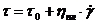
где t₀ — предельное напряжение сдвига, Па;  h_пл — пластическая вязкость, Па·с.

Примером систем, довольно близко следующих уравнению Бингама, могут служить маргарин, шоколадные смеси, зубная паста, жидкие мыла и моющие средства, сырково-творожные и конфет­ные массы.

Рис. 6.3. Кривые течения пластических материалов:

а — тело по Бингаму; б — тело по Балкли-Гершелю; в — дилатантные материалы; г — тиксотропные материалы; д — антитиксотропные материалы; е — реопексные материалы.

Кривые течения некоторых пищевых материалов описываются уравнением Балкли-Гершеля (рис. 6.3, б) (например, масса для конфет «Русский узор»),

 n < 1.                                                                             (6.6)

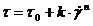
Пластическое течение, при котором не наблюдается пропорцио­нальной зависимости между скоростью сдвига и напряжением, называется неидеально-пластическим.

При достижении пре­дела текучести структура разрушается не сразу, а постепенно, по мере увеличения градиента скорости.

Кассон предложил  для подобного рода  течения следующее уравнение:

,                                                                            (6.7)

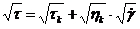
где t_К — предельное напряжение по Кассону, Па; h_К — пластическая вязкость по Кассону, Па·с.

Уравнение (6.6) было применено при описании течения рас­плавленного шоколада, сливочного масла, вафельного теста и сгу­щенного молока.

Дилатантное течение характерно для веществ, у кото­рых с увеличением скорости сдвига возрастает вязкость (рис. 6.3, в). Это течение описывается уравнением (6.5) при n >1. При очень высоких напряжениях вязкость может стать бесконечно большой, что приведет к разрушению вещества. Примером дилатантных ма­териалов могут служить сгущенное молоко, полимерный клей для сигарет, некоторые растворы сахара, крахмала и т. п.

На рис. 6.3, г, д и е приведены кривые течения соответственно тиксотропных, антитиксотропных и реопексных материалов.

Материал считается тиксотропным, когда вязкость его яв­ляется функцией времени, причем предполагается, что структура после определенного времени покоя возвращается к первоначаль­ному состоянию. Время тиксотропного разрушения, так же как и восстановления, для различных структур изменяется в очень ши­роких пределах. Тиксотропия может быть определена по реограмме при получении кривой гистерезиса.

Материалы, состояние течения которых во времени является противоположным тому, какое дают тиксотропные системы, назы­вают антитиксотропными.

Вещества, структура которых во времени упрочняется, облада­ют свойствами реопексии.

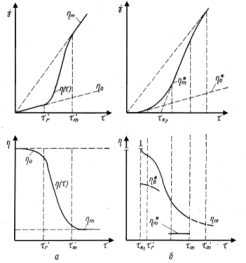
Высокомолекулярные системы разделяют на две группы: жидкообразные и твердообразные с постепенным переходом между ни­ми (рис. 6.4).

Если истинновязкие жидкости характеризуются по­стоянным значением вязкости, то структурированные жидкости определяются зависимостью эффективной вязкости от действую­щего напряжения и двумя областями напряжений с постоянным значением вязкости: наибольшей предельной вязкостью h₀ практи­чески неразрушенной структуры и наименьшей вязкостью h_т пре­дельно разрушенной структуры, где h_т остается постоянной. Твердообразность тела выражается тем резче, чем значительнее раз­ность между h₀ и h_т. Переходными между h₀ и h_т являются значения эффективной переменной вязкости, убывающей с ростом напряжения (или градиента скорости).

Рис. 6.4. Зависимость скорости сдвига и вязкости от напряжения для жидкообразных (а) и твердообразных (б) систем.

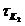
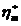
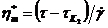
Для практических расчетов при больших градиентах скорости могут быть введены величины: условный динамический предел те­кучести  и наименьшая пластическая вязкость  по Бингаму, если на кривой течения имеется достаточно широкий участок, практически линейный и соответствующий наиболее крутому на­клону к оси абсцисс. Если вязкость, вычисленная для этого уча­стка,

,                                                                                   (6.8)

окажется значительно меньше h₀, то кривая течения аппроксими­руется прямой Бингама.

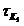
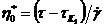
Для области несколько выше условного статического предела текучести  при наличии линейного участка кривой течения мо­жет быть введена величина наибольшей пластической вязкости (по Шведову)

                                                                                      (6.9)

Истиннопластические тела характеризуются наличием истин­ного предела текучести, совпадающего с пределом упругости, т.е. таким предельным напряжением сдвига, ниже которого экспери­ментально никакого течения не обнаруживается.

Для научного обоснования задач технологической обработки пищевых материалов большое значение имеет изучение процессов структурообразования систем. П. А. Ребиндер предложил разде­лить структуры на коагуляционные (тиксотропно-обратимые) и конденсационно-кристаллизационные (необратимо разрушаю­щиеся) .

Коагуляционные структуры возникают под действием связей и других нековалентных молекулярных сил сцепления кол­лоидных частиц, участвующих в интенсивном броуновском движе­нии, и более крупных частиц, находящихся в суспензии. Кинетика тиксотропного восстановления структуры вызывается интенсивным броуновским движением, в результате которого частицы сцепляются друг с другом и более крупными конгломератами по коагуляционным участкам или по местам наибольшего сближения поверхностей.

Конденсационно-кристал­лизационные структуры обра­зуются в результате срастания мелких кристаллов, образующихся в раство­рах, в пространственные системы или развития химических ковалентных свя­зей. Такие структуры весьма прочны и механически разрушаются необратимо.

Рис.  6.5.  Кривые кинетики де­формации.

Для определения упруго-пластич­но-вязких свойств дисперсных систем и растворов высокополимеров предло­жено экспериментальное определение семейства кривых деформации чистого сдвига e — время t, полученных при σ=const (рис. 6.5). При  испыта­ниях проводятся в области упругих об­ратимых деформаций (рис. 6.5, а), при 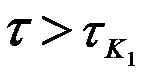, появляется остаточная деформация, которая после заверше­ния упругого последействия приводит к установившемуся течению (рис. 6.5, б).

Наиболее важным реологическим показателем свойств мате­риала является зависимость скорости деформации от напряжения. Для большинства пищевых масс эта зависимость имеет сложный характер. В этих случаях реологические свойства характеризуются кривой зависимости скорости деформации от напряжения, назы­ваемой кривой течения, или реограммой.

Объемная деформация пищевых масс

В тестоделителях для хлебопекарного теста, делительно-закаточных машинах для бараночных заготовок, макаронных прессах, прессах для отжима масла и соков, машинах для формования кон­фетных масс, грануляторах, машинах для таблетирования и т. п. обрабатываемые пищевые массы находятся в условиях всесторон­него сжатия. При этом происходит их уплотнение сначала в резуль­тате удаления воздуха или жидкости, а затем переориентации и более плотной упаковки частиц массы в основном благодаря пла­стической деформации.

При машинной обработке и формовании пищевых масс всегда одновременно происходят деформации сдвига и сжатия. Изучение «поведения» масс при объемной деформации дает возможность увязать конструкцию и прочность рабочих органов и кинематику машин с физико-механическими свойствами перерабатываемых масс.

При изучении объемной деформации материала под давлением в условиях всестороннего сжатия обычно решаются следующие задачи: распределение давления в объеме массы, сжимаемость материала под давлением, зависимость плотности массы от дав­ления, процессы релаксации напряжений и ползучести.

Исследование «поведения» макаронного теста в условиях все­стороннего сжатия показало, что давление в тесте распространяет­ся неодинаково: давление в осевом направлении превышает ра­диальное на 10-15%. В интервале изменения влажности от 28 до 33% стабилизация процесса всестороннего сжатия наступает при давлении 3 МПа. При испытании хлебопекарного теста было уста­новлено, что давление в тестовой массе при сжатии распределяет­ся также неравномерно и зависит от длительности приложения силы на нагнетателе. Превышение давления прессования над за­данным рабочим определяется размерами тестовой камеры техно­логической машины и физико-механическими свойствами теста.

При многократном нагружении хлебопекарного теста наиболь­шее увеличение плотности происходит после первого нагружения, при дальнейших нагружениях изменение плотности незначительно. Основные изменения плотности наблюдались при давлениях до 0,15-0,2 МПа. После пятикратного нагружения давлением 0,25 МПа плотность теста из муки I сорта влажностью 46,4% уве­личилась на 27,5%, теста влажностью 42,2% — на 21%, теста для украинского хлеба — на 18%. После разгрузки системы (при со­хранении получен-ной деформации) давление во времени медленно уменьшается.

Характерные кривые прессования для различных пищевых ма­териалов (макаронного и бараночного теста, пралиновых конфет­ных масс, чая, кофе и т.п.) приведены на рис. 6.6. По кривым вид­но, что до образования сплошной однородной структуры с мак­симальным уплотнением массы вначале происходит резкое изме­нение плотности от давления, а затем наблюдается незначительное повышение плотности при резком увеличении давления.

Практически различают трудно- и легкоуплотняемые материа­лы. Трудно-уплотняемыми являются такие, которые после длитель­ной зоны предвари-тельного уплотнения (без большой затраты энергии) незадолго до максимального уплотнения могут восприни­мать большие нагрузки без заметного уплотнения (рис. 6.6, а). Другие трудноуплотняемые материалы обладают большим упру­гим последействием (рис. 6.6, б). Диаграмма прессования легко­уплотняемых материалов (рис. 6.6, в) имеет короткую зону предуплотнения, нагрузка медленно возрастает на протяжении всего времени прессования.

От физико-механических свойств перерабатываемого материа­ла, его дисперсности и температуры, объема конечного спрессо­ванного продукта зависят: величина зоны предварительного уплот­нения, упругость массы, работа, затрачиваемая на изменение фор­мы, и скорость нагружения материала.

Рис. 6.6.  Кривые прессова­ния.

При определении зависимости плотности бараночного теста от давления было выяснено, что вначале происходит сжатие теста, имеющего большое количество газовых включений. При этом зави­симость имеет криволинейный характер. После уплотнения теста при давлении выше 0,8 МПа эта зависимость принимает линейный характер. Так как в рабочих цилиндрах делительно-закаточных ба­раночных машин при формовании тестовых заготовок давление превышает 0,8 МПа, то для практических расчетов представляет интерес линейная зависимость.

Количество получаемой жидкой фазы при прессовании маслич­ных материалов, плодов, ягод зависит от величины рабочего дав­ления, характера связи жидкости с материалом, содержания жид­кой фазы в исходном материале и остатке, температуры процесса, толщины прессуемого слоя и продолжительности процесса. Жид­кая фаза в прессуемых продуктах находится в свободном и связан­ном состоянии. Свободная жидкость легко отделяется от сухого вещества материала. Для отделения осмотической и адсорбционно связанной влаги требуется затрата значительной энергии, что происходит, например, при сушке.

Перед отжатием пищевые материалы подвергаются механиче­ской, термической, электрофизической обработке. Механическая обработка заключается в измельчении материала с целью разру­шения клеточных оболочек, препятствующих выходу жидкости из клеток. При тепловой и электрофизической обработке происходят более сложные процессы, но цель та же: подготовить сырье к наи­более полной отдаче жидкой фазы при прессовании.

Физическая сущность отжатая жидкой фазы при прессовании заключается в следующем. В начальный период прессования мате­риала его частицы сближаются и жидкость, находящаяся на по­верхности частиц, движется по каналам между частицами, а затем жидкость перемещается в слое пористого материала по капилля­рам переменного сечения и направления, т. е. осуществляется фильтрация жидкой фазы в слое.

Как было указано выше, отжатие массы материала при прессо­вании связано с фильтрацией, при которой отжимаемая жидкость должна проходить по сложной системе капилляров с переменным сечением. Следовательно, при прессовании происходит фильтрация, которую в общем виде можно описать законом Пуазейля

                                                                              (6.10)

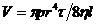
где V — объем жидкости, проходящей через канал за время t, м³; р — потеря напора в капилляре, Па; r — радиус капилляра, м; 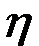  — динамическая вязкость жидкости, Па·с; l — длина капилляра, м.

Прессование — более сложный процесс, чем процесс фильтра­ции жидкости по капиллярам. Однако анализ уравнения Пуазейля позволяет сделать некоторые практические выводы. Из этого урав­нения следует, что при прессовании нерационально увеличивать толщину слоя и целесообразно повысить температуру массы. Бо­лее полному отжатию жидкости способствуют увеличение давле­ния и уменьшение вязкости жидкости. Но, с другой стороны, уве­личение давления уменьшает сечение капилляров, а следователь­но, и производительность прессов. Поэтому оптимальное рабочее давление при прессовании устанавливается опытным путем с уче­том свойств материала, количества и качества получаемой жидкой фазы.

Изменение объема теста зависит от сжимаемости газовых пу­зырьков и деформации структурной сетки, более компактной «упа­ковки» твердой дисперсной фазы в дисперсионной среде.

Существенное влияние на условия объемной деформации и те­чения пищевых масс при их прессовании, формовании и транс­портировании по трубам оказывают релаксация давления и ползу­честь материала. В пищевой промышленности эти явления изуче­ны для хлебного, макаронного и бараночного теста, различных конфетных масс, байхового чая и некоторых других продуктов.

Особый интерес релаксация представляет для циклических про­цессов формования (отсадка конфет, печенья, кремов), так как период релаксации несколько больше разности между временем кинематического цикла и временем выдавливания массы в реаль­ных отсадочных машинах. Это приводит к тому, что внутренние напряжения не успевают рассасываться в период между отсадками и масса, сохраняя упругое последействие, после остановки нагне­тательных органов продолжает выпрессовываться через отверстия матрицы, что препят-ствует образованию корпусов изделий задан­ной формы. При перекрывании отверстия в момент остановки нагнетателя остаточные напряжения в массе способствуют ее уп­лотнению и синерезису. Следовательно, при отсадке (особенно сбивных масс) необходимо принудительное снятие напряжений в массе в период между двумя отсадками.

Испытания различных вязко-пластических и псевдопластичес­ких пищевых масс (конфетных, макаронного (хлебного и бара­ночного теста и т. п.) показали, что с повышением давления все реологические характеристики возрастают. Например, при уве­личении давления от 0 до 49 кПа на пралиновые конфетные мас­сы вязкость увеличивается в 1,5-2,5 раза, а предельное напря­жение сдвига — в 2-3 раза. При повышении давления происходит уплотнение массы, причем график прессования пищевых материа­лов имеет нелинейный вид, что обусловливает и непостоянство влияния на структурно-механические свойства.

Опыты с бараночным тестом позволили установить, что с по­вышением избыточного давления от 0 до 2,45 МПа вязкость уве­личивается в 1,2-1,4 раза, а предельное напряжение сдвига — примерно в 3 раза. Для макаронного теста при изменении давле­ния от 3,5 до 9 МПа наблюдается увеличение вязкости примерно в 1,5-1,8 раза и предельного напряжения сдвига в 1,4-1,5 раза. Подводя итог влиянию давления на реологические свойства пищевых материалов, следует отметить, что давление влияет на качество го­товой продукции. Поэтому при расчете того или иного процесса нужно стремиться к тому, чтобы обработка пищевых материалов производилась при оптимальном давлении.

ПРОДОЛЖЕНИЕ СЛЕДУЕТ

111. Реологические свойства свободнодисперсных систем

Основными факторами, определяющими структуру и реологические свойства дисперсной системы, являются концентрация частиц φ (объемная доля) и потенциал парного взаимодействия частиц. Разбавленные агрегативно-устойчивые дисперсные системы, где частицы сохраняют полную свободу взаимного перемещения или определенная структура отсутствует, являются ньютоновскими, их вязкость вычисляется по уравнению Эйнштейна:

η = η₀(1 + αφ).

где η₀ – вязкость среды; α – коэффициент, равный 2,5 для сферических частиц при их свободном вращении в потоке.

Реологические свойства свободнодисперсных систем: вязкость, упругость, пластичность.

Создаваемое внешней силой F касательное напряжение т целиком идет на преодоление трения между слоями жидкости и пропорционально скорости сдвига – это закон Ньютона:

т = ηγ

Величина η = т/γ (вязкость) полностью характеризует реологические свойства жидкости в ламинарном режиме течения.

Вязкие тела отличаются от пластичных тем, что текут при любых напряжениях. Течение идеально вязких тел описывается уравнением Ньютона:

где f – сила вязкостного сопротивления; h – коэффициент трения; u – линейная скорость течения; х – координата, нормальная к потоку.

Более общим является выражение этого закона через деформацию сдвига. В упругом теле работа внешней силы т запасается в виде потенциальной энергии упругой деформации, а в вязкой среде она целиком превращается в теплоту. Часть энергии рассеивается, т. е. материал создает также и вязкое сопротивление деформированию. Такие материалы называются вязкоупругими. Важной реологической характеристикой вязкоупругой среды является время релаксации упругих деформаций (время восстановления формы). Кроме сил вязкого и упругого сопротивления деформированию, ряду материалов присуща способность оказывать сопротивление подобное силе внешнего (статического) трения. В дисперсных и полимерных материалах подобная сила возникает одновременно с вязким сопротивлением, общее сопротивление описывается уравнением:

т = т_с +ηγ.

Величина η* = (т – т_с) / γ называется пластической вязкостью, а материал – пластичным. Он полностью характеризуется двумя реологическими константами: т_с и η*. Величину т_с называют предельным напряжением сдвига (предел текучести). Поведение пластичного материала может быть описано законом Ньютона, где η – переменная величина, или законом Шведова-Бингама с двумя постоянными (т_с и η*). Вязкость, по Ньютону, учитывает все сопротивление, зависящее от скорости деформации. Пластическая вязкость учитывает только часть сопротивления.

Жидкости и пластично-вязкие тела, сила трения которых не подчиняется закону Ньютона, называются неньютоновскими (аномальными) жидкостями. Некоторые из них называются бингамовскими жидкостями. Пластичность является простейшим (в математическом отношении) проявлением неньютоновских свойств. Переход от ползучести к пластическому и далее ньютоновскому течению происходит постепенно. Чаще всего наибольший диапазон скоростей сдвига (от γ₁ до γ₂) приходится на участок пластического течения. Этим определяется практическое значение закона Шведова-Бингама и реологических констант η* и т_с.

112. Реологические свойства связнодисперсных систем. Уравнение Бингама

Основным методом реологии является рассмотрение механических веществ на определенных моделях, поведение которых может быть описано небольшим числом параметров, в простейших случаях реология может определяться только одним параметром.

Упругое поведение – процесс, который может характеризоваться пропорциональностью напряжений и деформаций, т. е. как бы линейной зависимостью между τ и γ. Эта зависимость выражается законом Гука:

τ = Gγ,

где G – модуль упругости Юнга.

Если изображать графически, то по закону Гука зависимость между напряжением сдвига и смещением может выражаться линейной зависимостью котангенс угла наклона к этой прямой будет являться модулем упругости Юнга.

При снятие нагрузки происходит немедленное восстановление первоначальных параметров тела, не происходит рассеивания энергии при процессах нагружения и разгрузки тела. Процесс упругого поведения может быть свойствен только твердым телам.

Природа этого явления может заключаться в обратимости малых деформаций. Модуль упругости может зависеть от характера взаимодействия в твердом теле и составляет очень большую величину. Тело может стремиться к восстановлению с тепловым движением, которое нарушает эту ориентацию.

Модуль упругости также зависит от температуры и может иметь небольшую величину. Упругая деформация для твердых тел может определяться, может происходить до определенного значения, выше которого происходит разрушение тела. Такой вид напряжения для хрупких тел характеризует прочность.

Вязкое поведение (или вязкое течение), которое может характеризоваться пропорциональностью напряжений и скоростью процессов деформации, называется законом Ньютона:

т = ηγ¹,

где t – напряжение сдвига; h – вязкость.

После прекращения воздействия напряжения сдвига прежняя форма тела уже не может восстановиться. Такое вязкое течение может сопровождаться рассеиванием энергии, т. е. той энергии, которая рассеивается в объеме тела. Вязкое течение связано с переносом массы при обмене местами между атомами или молекулами при их тепловом движении.

Приложенное потенциальное напряжение может снижать энергетический барьер перемещения частицы в одном направлении и увеличивать или уменьшать в другом. Можно предположить, что процесс вязкого течения является температурным активируемым процессом и вязкость будет зависеть от температуры экспоненциально.

Пластичность может представлять собой нелинейное поведение. При таком явлении отсутствует зависимость и пропорциональность между различными воздействиями, многими видами деформации. Пластичность является совокупностью как процессов дислокации, так и разрыва и перестройки связей между атомами. Пластичное тело после снятия напряжения сохраняет любую форму, которую ему придали в процессе.

Уравнение Бингама:

Скорость деформации, которая описывается уравнением Бингама, должна быть пропорциональна разности и действующего напряжения, и предельного напряжения сдвига. Причем уравнение основывается на комбинации двух простейших элементов реологии – параллельного соединения вязкого элемента и кулоновского элемента сухого трения.

113. Реологический метод исследования дисперсных систем. Основные понятия и идеальные законы реологии

Реология – комплекс знаний и понятий, формулирующий законы и правила, позволяющие определить поведения твердых и жидкообразных тел. Основным методом, который использует реология, является рассмотрение механических свойств материалов на определенных моделях, которые описываются небольшим числом параметров.

Упругая деформация описывается законом Гука:

τ = Gγ,

где t – напряжение сдвига; G – модуль сдвига (н/м²); γ – относительная деформация сдвига.

Природа упругости каждого тела заключается в обратимости малых деформаций, связей между атомами. Модуль упругости может определяться характером взаимодействий в твердом теле и практически не зависит от повышения температуры. Модуль упругости может рассматриваться как некая удвоенная величина упругой энергии, которая запасается единицей объема при единичной деформации. Упругая деформация тела может возникать до некоторого предельного значения, после которого происходит разрушение более хрупких тел.

Прочность – свойство материала сопротивляться внешним воздействиям под действием внешних напряжений.

Вязкость описывается законом Ньютона:

т = ηγ,

где h – вязкость (н/м²) – параметр, который характеризуется пропорциональным напряжением и скоростью деформации, может зависеть также от скорости сдвига.

Вязкость полимерных материалов может сопровождаться диссипацией энергии, т. е. состоянием когда вся выделяемая энергия может переходить в тепло. Вязкость – это процесс, термически активируемый, и вязкость имеет экспоненциальную зависимость от температуры.

Пластичность является нелинейным элементом, наблюдается отсутствие между воздействиями и различными деформациями. Пластичность материала будет определяться процессами разрыва и перестройки межатомных связей, для которых возможна дислокация.

Внутреннее напряжение – параллельное сочетание упругого элемента и трения сухого.

Деформация – относительное смещение во времени некоторых точек определяемой системы, при котором не происходит изменения сплошности материала.

Пластическая деформация – деформация, при которой не происходит разрушение материала.

Упругая деформация – деформация, при которой происходит полное восстановление тела после снятия определенной нагрузки.

Моделирование необходимо проводить с помощью реальных различных моделей тел. При использовании модельного подхода полная нагрузка приходится на каждый элемент, а соответственно, полная деформация системы или скорость деформации будет складываться из всех видов деформаций, действующих на тело, и скоростей всех элементов, заставляющих двигаться систему. Если рассматривать параллельное соединение элементов деформации и скорости, они будут одинаковы для всех элементов, а вся оставшаяся нагрузка системы будет складываться из нагрузок всех вместе взятых элементов. Если использовать правила последовательной и параллельной деформации, можно просто использовать различные реологические модели. Если расширять возможности характеристик количественных свойств для реальных тел, можно использовать несколько идеальных моделей. Было принято, что нет различия между реологическими свойствами жидкостей реальных, так же как и твердых тел. Это можно объяснить тем, что эти системы представляют собой конденсированные состояния вещества.

114. Реологические модели

Существуют три основных случая механического поведения:

1) упругость;

2) вязкость;

3) пластичность.

Комбинируя эти процессы и реологические модели процессов, можно получить более сложные модели, которые будут описывать реологические свойства самых различных систем.

Во всех случаях каждая комбинация будет рассматриваться в определенном режиме деформирования характерном для этого явления, в котором будут проявляться свойства моделей по сравнению со свойствами ее элементов.

1. Модель Максвелла – последовательное соединение упругости и вязкости. Последовательное соединение таких элементов может означать по третьему закону Ньютона, что на две составные части модели будут действовать одинаковые силы (напряжение сдвига τ), а деформации упругости (γ_G) и вязкости (γ_η) могут быть сложены:

γ = γ_G + γ?,

где g – общая деформация.

В этой модели возможно быстрое деформирование до определенного значения и сохранение ее на постоянном уровне. При больших значениях времени такой тип системы может быть близок по свойству к жидкости, но при приложении напряжения сдвига система может вести себя как упругое твердое тело.

2. Модель Кельвина – параллельное соединение упругости и вязкости. В такой модели деформации обоих элементов могут быть одинаковыми, а напряжения сдвига будут суммироваться. При постоянном воздействии напряжения модель Кельвина ведет себя иначе. Вязкий элемент не может позволить реализоваться немедленно деформации упругого элемента. Тогда общая деформация может постепенно развиваться во времени:

Это уравнение соответствует постепенно замедляющейся деформации. Снятие общего напряжения происходит за счет энергии, накопленной упругим элементом, здесь происходит процесс деформации эластического тела, и рассеивание энергии происходит на вязком элементе. Пример таких моделей: затухание колебаний, прежде всего механических в резине.

3. Ввод в систему нелинейного элемента. Получается модель, описывающая возникновение внутренних напряжений при параллельном сочетании упругого элемента и сухого трения. Если в системе приложенное напряжение превышает предел текучести, то возникает деформация, которая может быть обусловлена накоплением энергии упругого элемента.

4. Модель Бингама – параллельное соединение вязкого ньютоновского элемента и сухого кулоновского элемента трения. Так как элементы одинаковы, то и их деформации тоже будут одинаковыми, а напряжения будут складываться. Причем напряжение на кулоновском элементе не может превышать предельного значения напряжения сдвига.

Из этого следует вывод, что скорость деформации, которая описывается вязким элементом, должна быть пропорциональна разности действующего напряжения и предельного напряжения сдвига.

При усложнении реологических моделей усложняется математический аппарат описания деформаций, поэтому все виды напряжений стараются сводить к более простым моделям. Одним из методов облегчения таких задач служит использование т. н. электромеханических аналогий, т. е. получение реологических моделей с помощью электрических цепей.

115. Классификация дисперсных систем. Ньютоновские и неньютоновские жидкости. Псевдопластические, дилатантные жидкости и твердообразные тела

Известно, что существует много видов структурно-механических свойств, которые способны отражать все многообразие как природных, так и синтетических тел. Многие системы являются дисперсными фазами, которые, в свою очередь, имеют много различных комбинаций фаз, различающихся и природой, и агрегатным состоянием, и размером частиц. Структурно-механические свойства многих дисперсных систем являются непрерывными и бесконечными рядами, которые включают в себя как старые, так и возникающие новые при рассмотрении системы. Исследования в области структурно-механических свойств проводил П. А. Ребиндер, который предложил разделить вещества на конденсационно-кристаллизированные и коагуляционные структуры. Конденсационно-кристаллизированное образование структуры может происходить при непосредственном химическом взаимодействии как между частицами, так и при их срастании до образования жесткой структуры, имеющей большой объем. Если частицы, участвующие в процессе, являются аморфными, то структуры, которые образуются в дисперсных системах, принято называть конденсационными, если участвуют кристаллы, то полученные структуры являются кристализированными. Структуры конденсационно-кристализированного типа могут быть характерны для дисперсных систем связанного типа, т. е. систем, имеющих твердую дисперсную среду. Использование таких структур придает изделиям прочность, хрупкость, но они не восстанавливаются после разрушения. Коагуляционными могут являться те структуры, которые способны образовываться только при коагуляции. При образовании таких структур взаимодействие между структурами может осуществляться через все прослойки дисперсионной фазы, и являются вандерваальсовыми силами, использование таких структур не может приводить к устойчивости строения. Механические свойства таких структур определяются не только свойствами частиц, из которых состоит система, но также зависят от характера связей и прослоек между средами. Структуры коагуляционного типа имеют жидкую среду, для таких систем важным является восстановление системы после ее разрушения. В практическом использовании характерны как одни, так и другие материалы, которые позволяют обеспечивать регулировку состава и однородности материала, а в процессе технологии происходит регулирование процессов формирования.

Жидкообразные системы делятся на два вида:

1) ньютоновские;

2) неньютоновские.

Ньютоновскими называются системы, вязкость в которых не зависит от напряжения, возникающего при сдвиге, и может являться постоянной величиной. Эти жидкости делятся на два вида: стационарные (для таких систем реологические свойства не изменяются во времени), нестационарные, реологические характеристики которых определяются временными рамками.

Неньютоновскими называются системы, которым не свойствен закон Ньютона, и вязкость в таких системах зависит от напряжения сдвига.

Дилатантные жидкости – системы, у которых встречается большое количество твердой фазы, в них хаотическое движение молекул приводит к уменьшению вязкости из-за неупорядочивания. При увеличении нагрузки на такие системы плотная упаковка частиц может нарушаться, объем системы может увеличиться, что приведет к возрастанию вязкости в системе.

Псевдопластические жидкости – системы, для которых характерно снижение ньютоновской вязкости при увеличении скорости деформации всего сдвига.

116. Вязкость жидких агрегативно-устойчивых дисперсных систем

Основы этой теории были заложены А. Эйнштейном, который занимался изучением разбавленных суспензий. А. Эйнштейн изучал гидродинамические уравнения для всех твердых частиц, имеющих сферическую форму, которые могут приобретать дополнительное вращательное движение. Рассеяние, которое при этом происходило, являлось причиной возрастания вязкости. А. Эйнштейн вывел уравнение, которое связывает вязкость системы η и объемную долю дисперсной фазы φ:

η = η ₀(1+ 2,5φ).

При выводе уравнения было сделано предположение, что система может не сжиматься, нет скольжения между частицами и жидкостью. Опыты, которые много раз проводил А. Эйнштейн, подтвердили его предположения, он установил, что коэффициент, который стоит при параметре доли дисперсной фазы, зависит только от формы частиц.

Из теории А. Эйнштейна можно сделать выводы, что разбавленные и устойчивые системы являются ньютоновскими жидкостями, их вязкость линейно зависит от объемной доли дисперсной фазы и не зависит от дисперсности. Параметр 2,5, как правило, больше для некоторых частиц. Это объясняется тем, что вращение частицы несферической формы превышает объем самой частицы. У такой частицы большое сопротивление, что может увеличивать вязкость системы. Если происходят значительные отклонения от сферической формы, то система может превращаться в неньютоновскую жидкость, вязкость которой зависит от напряжения сдвига.

Уравнение Эйнштейна не учитывает наличия у частиц слоев поверхности (адсорбционных, сольватных). Увеличение вязкости может происходить из-за наличия таких слоев. Поверхностные слои не меняют форму частиц, их влияние учитывается при увеличении объемной доли фазы. Далее эту теорию дополнил Г. Штаудингер, который использовал ее для описания вязкости разбавленных растворов полимеров. Уравнение Штаудингера:

η_уд = KMc,

где К – константа, характеризующая полимер; М – масса полимера; с – массовая концентрация полимера.

Г. Штаудингер предположил, что при удлинении цепи полимера увеличивается ее объем вращения и увеличивается вязкость раствора при одной и той же концентрации. Вязкость по уравнению не зависит от концентрации раствора полимера и может быть пропорциональна его молекулярной массе. Уравнение, выведенное Г. Штаудингером, используется для определения молекулярной массы полимера. Это уравнение может быть справедливо только для растворов полимеров как с короткими, так и с жесткими цепями, при этом сохраняющими свою форму. Но наиболее частым используемым уравнением для определения массы полимера является уравнение Марка-Куна-Хаувинка:

{η} = KM^α,

где α является характеристикой, которая способна отражать форму и плотность макромолекулы, значения этой величины не превышают единицы.

Из уравнения следует, что чем выше напряжение в системе, тем в большей степени происходит разворачивание молекул полимеров и тем меньше становится их вязкость. Это обусловлено увеличением степени диссоциации полимерных материалов при разбавлении, что увеличивает рост заряда молекулы и увеличивает ее объем. В растворах любых полимеров межмолекулярное взаимодействие может приводить к резкому повышению вязкости системы, вместе с тем вязкость может определяться эффективным объемом частицы, который приходится на единицу массы полимера. Это справедливо для всех полимерных материалов, для которых можно определить вязкость системы.

117. Полная реологическая кривая дисперсных систем с коагуляционной структурой

Резко происходит изменение вязкости для связнодисперсных систем, имеющих коагуляционную структуру. При таком рассмотрении используют целый спектр значений между двумя крайними состояниями системы: с неразрушимой или полностью разрушенной системой. При рассмотрении приложенного напряжения сдвига реологические свойства таких систем изменяются в очень широких пределах вплоть до ньютоновских жидкостей. Такую зависимость реологических свойств от коагуляции можно представить в виде реологической кривой.

Реологическая кривая представляет собой зависимость предельной деформации от напряжения сдвига.

При исследовании релаксационных свойств было обнаружено, что при малых напряжениях сдвига происходит упругое воздействие, которое связано с взаимной ориентацией частиц, для них характерно тепловое движение. Высокие значения вязкости могут быть обусловлены перетеканием дисперсионной среды из ячеек, которые уменьшаются в размере, в соседние ячейки через узкие проходы и при скольжении частиц относительно друг друга.

При достижении некоторого значения предельного напряжения сдвига может наступать область медленного, но вязкопластичного течения или, как принято называть, ползучести.

1. На этом участке происходит сдвиг, который осуществляется при флуктуации и разрушается, но может восстановиться под действием приложенных извне напряжений. При этом все частицы объединяются в единую коагуляционную структуру, которая испытывает колебания относительно их положения в контактах.

2. На этом участке происходит ползучесть системы, которая может быть описана реологической моделью вязкопластического течения при малом предельном напряжении сдвига и достаточно высокой вязкости.

3. На третьем участке кривой образуется область течения энергично разрушаемой структуры. Этот участок может быть описан при использовании модели Бингама.

4. На этом этапе происходит проявление свойств ньютоновской жидкости, вязкость которой повышена. При дальнейшем увеличении напряжения может происходить отклонение от уравнения Ньютона, которое связано с явлением турбулентности.

Реологические свойства системы могут изменяться при воздействии вибрации. При анализе реологической кривой можно прийти к выводу, что даже очень сложное механическое поведение системы можно расчленить на несколько простых участков, которые будут определяться простой моделью.

Для достижения равновесия между процессами разрушения и восстановления контактов необходимо достаточно длинное деформирование системы при постоянной скорости, что не всегда возможно при проведении практических работ.

Но при этом разные по молекулярному механизму явления, такие как ползучесть и вязкопластическое течение, можно описывать одной и той же моделью, но с разными параметрами. Реологические характеристики дисперсных систем могут сильно изменяться при воздействии вибрационного поля.

Вибрация может приводить к разрушению контактов между частицами, что приводит к разжижению системы при очень низких напряжениях сдвига. Реологическая кривая в современной технике при использовании вибрационного воздействия позволяет видеть, как можно управлять разными свойствами дисперсных систем, таких как суспензии, различные пасты или порошки.

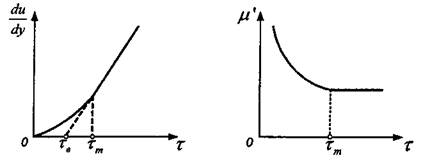
    Ф, Н. Шведов, основатель коллоидной механики, исследуя свойства структурированной жидкости в 1889 г., а затем Бингам в 1916 г. показали, что пластичные тела характеризуются в первом приближении двумя константами пределом текучести и так называемой пластической вязкостью, которая остается практически постоянной в некоторой области выше предела текучести, тогда как обычная эффективная вязкость в этой области резко падает с возрастанием напряжения сдвига. Постоянство пластической вязкости соответствует приближенной применимости двучленного уравнения Шведова Бингама для сопротивления пластичного потока  [c.177]

    Бннгамовские жидкости (кривая /). Течение бинга-мовской жидкости начинается только при достижении определенного напряжения сдвига Ху, называемого критическим напряжением сдвига (предел текучести). Покоящаяся бннгамовская жидкость имеет жесткую структуру, оказывающую сопротивление внешнему воздействию. При достижении напряжения, превышающего предел текучести, происходит разрушение структуры и последующее течение жидкости в соответствии с законом Ньютона. При напряжении сдвига меньше Ху структура снова восстанавливается. Поведение бингамовской жидкости описывается уравнением  [c.91]

    Ф. Н. Шведов, а затем и Бингам показали, что пластические тела характеризуются двумя константами пределом текучести и пластической вяз костью, которая остается практически постоянной в некоторой области выше предела текучести, тогда как в этой области обычная эффективная вязкость резко падает с возрастанием наиряжения сдвига [17, 97, 99]. [c.68]

    Второй случай более сложен. Сначала Ф. Н. Шведов, затем Бингам предположили, что течение системы с малопрочной пространственной структурой начнется лишь тогда, когда напряжение сдвига Р превысит какое-то определенное критическое значение 9, необходимое для разрушения структуры, т.е. когда начнет соблюдаться условие Р — 0 > 0. Такое течение Бингам называет пластическим, а критическое (предельное) напряжение сдвига б — пределом текучести, [c.328]

    Н. Ф. Шведов, основатель коллоидной механики, в 1889 г., а затем Бингам в 1916 г. показали, что пластичные тела характеризуются в первом приближении двумя константами пределом текучести и пластической вязкостью — постоянной выше предела текучести, тогда как обычная эффективная вязкость уменьшается в этой области с возрастанием напряжения сдвига. Эта зависимость [c.11]

    Бингам [109, 110] упростил уравнение пластично-вязкого течения, введя величину Р,с —условного динамического предела текучести (Рк >Рк) и наименьшую пластическую вязкость Цт- [c.63]

    Шведов и Бингам показали, что пластические тела характеризуются в первом приближении двумя константами — пределом текучести Я, и так называемой пластической вязкостью rii, остающейся в некоторой области выше предела текучести практически постоянной, тогда как эффективная вязкость в этой области с увеличением напряжения сдвига падает. Из уравнения Шведова— Бингама Р = Рц+ т)ь где —градиент скорости, следует, что в отличие от вычисления эффективной вязкости для вычисления пластической вязкости вместо действующего напряжения Р берется его избыток над пределом текучести Р — Рк- [c.25]

    Жидкости, подчиняющиеся закону Ньютона, наз.ывают ньютс-новскими жидкостями, или ньютоновскими телами. Пластичные системы, являющиеся промежуточными между ньютоновскими телами и твердыми системами, называются неньютоновскими телами. Большинство агрегированных или структурированных осадков при приложении к ним напряжений сдвига (механического воздействия) 5, больших определенного критического значения 5, р, начинают медленно деформироваться (течь). Осадок начинает течь при соблюдении условия 5 — 5кр > 0. Такое течение Бингам назвал пластическим, а критическое (предельное) напряжение сдвига — пределом текучести. [c.63]

    Бингамовские жидкости (рис. 6-27, кривая J) начинают течь только после приложения напряжения Tq (Tq-начальное напряжение сдвига, или предел текучести), превышающего предел текучести. При этом структура пластичной жидкости разрушается, и она ведет себя как ньютоновская, т. е. зависимость от dy/dx для них также прямо пропорциональна. При снижении напряжения (х < Xq) структура бингамовских жидкостей восстанавливается. К бинга-мовским жидкостям относятся густые суспензии (различные пасты и шламы, масляные краски и т. п.). [c.145]

    Уравнению Шведова—Бингама, как это показал Бингам, соответствует характер течения некоторых красок и водных суспензий глины. В 30-х годах в результате вискозиметрических исследований М. П. Воларовича к этой группе были причислены типографские краски, суспензии торфа, пшеничное тесто и консистентные смазки [97]. Однако вскоре выяснилось, чтс многие структурированные дисперсии, в том числе консистентные смазки, суспензии глин и др. подчиняются этому уравнению только при малых напряжениях сдвига. Уже в вискозиметрических исследованиях мыльных консистентных смазок Арвесона [98] было показано, что при значительных напряжениях сдвига скорость их течения начинает возрастать гораздо быстрее, чем напряжение сдвига. Таким образохм, по характеру течения они становятся в ряд квазнпластичных тел. В таких случаях предлагалось использовать уравнение (14) и находить предел текучести экстраполяцией линейного участка кривой течения (см. рис. 13, кривая г) до пересечения с осью напряжения сдвига Т2. [c.90]

    Основы реологии коллоидных растворов впервые изучены Ф.Н.Шведовым, Бингамом и Грином. В 1889 году Ф.Н. Шведов, позже в 1916 году Бингам установили, что течение системы с пространственной структурой начинается лишь тогда, когда напряжение сдвига х превышает определенное критическое значение т (рис. 2.3), необходимое для разрушения в жидкости структурной сетки. Такое течение было названо пластическим, а критическое напряжение сдвига -пределом те>д>чести или предельным напряжением сдвига. [c.11]

    К бинг иювск[1м пластичным жидкостям относят жидкости, име-юн ие начальный предел текучести т , ниже которого они не текут и проявляют себя как твердые тела. Изменение нх вязкости подчиняется закону Ньютона ири т > т  [c.142]

    Измерению реологических свойств пены на нефтяных месторождениях стали уделять внимание в саязи с ее использованием для повышения нефтеотдачи пласта. В начале 60-х годов вязкость пены была измерена в усовершенствованном вискозиметре Фэнна. Позднее измерения этого параметра стали проводить в трубках малого диаметра. Установлено, что главным фактором, влияющим на поведение движущейся пены, является качество пены, определяемое соотношением объемов газа и пены (или объемная доля газа) при заданных температуре и давлении. При повышении этого соотношения с 0,85 до 0,96 (предел устойчивости пены) эффективная вязкость пены быстро возрастает. В предположении, что пена ведет себя как бинга-92 [c.92]

    Определение вязкости и предела текучести было первым шагом к научно обоснованному измерению реологических свойств смазок. Изучение этих параметров основывалось на предположении, что смазки могут описываться как простые пластичные тела. В частности, бьши сделаны попытки показать, что они подчиняются уравнению деформации тела Бингам-Воларовича. Однако уже первые измерения установили, что смазки обладают аномальной, неньютоновской вязкостью, а предел текучести не вполне отчетлив и может несколько смещаться в зависимости от времени действия нагрузки. [c.241]

    При увеличении скорости гидросмеси нарушенные структурные связи не успевают восстанавливаться такой режим течения называют структурным, или бинга-мовским. При переходе от шведовского режима к бин-гамовскому структурная вязкость уменьшается по мере увеличения скорости (касательного напряжения), но, когда достигается динамический предел текучести, структурная вязкость становится постоянной. Динамиче- [c.206]

    Бингем для суспензий глина — вода ввел дополнительное значение предела пластичности . Течение в капиллярной трубке ньютоновских жидкостей йодчнняется [c.348]

---