Для
изучения процессов с дискретными
состояниями пользуются так называемым
графом состояний, в котором состояния
системы обозначаются прямоугольниками
или кружочками, а возможные переходы
из состояния в состояние − ориентированными
дугами графа.
-
Рассмотрим
марковский процесс с дискретным
состоянием и дискретным временем.
Пусть
имеется физическая система
,
которая может находиться в состояниях
,
,
…,
,
причем переход системы из состояния в
состояние осуществляется скачками
только в моменты времени
,
,
…,
,
…, для которых разности
равны постоянному числу — шагу, для
простоты принимаемому за единицу
времени. Такие марковские процессы
называются марковскими цепями.
Определение.
Вероятностью состояния
называется вероятность системы
находиться в состоянии
после
-го
шага.
Очевидно,
что для каждого шага
.
Будем
считать, что вероятности
перехода системы из состояния
в состояние
(они называются переходными вероятностями)
одинаковые для всех шагов (такая цепь
называется однородной).
Введем
так называемую матрицу вероятностей
перехода
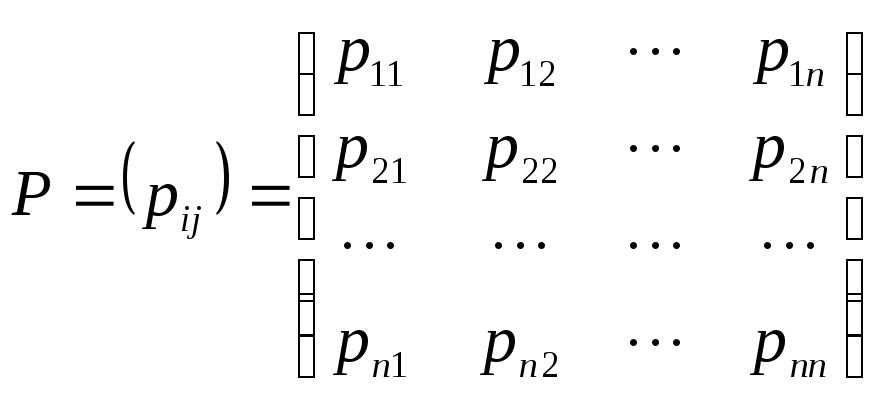
(1)
Элементы
матрицы
неотрицательны, но могут равняться 0:
,
если переход системы
из состояния
в состояние
невозможен. Сумма элементов любой строки
матрицы
равна 1. Такие матрицы называются
стохастическими.
1.
Вероятности перехода из состояния
в состояние
за
шагов
определяются матрицей
,
где
,
откуда следует, что
,
.
(2)
2.
Теорема Маркова. Если при
некотором
все элементы матрицы
положительны, то существуют такие
положительные числа
,
,
…,
,
что независимо от начального состояния
системы
имеют место равенства
,
причем
.
(3)
Вектор
называется предельным распределением,
а числа
— предельными вероятностями состояний.
Предельное
распределение
можно найти как собственный вектор
матрицы
(
транспонированная), соответствующий
собственному значению
.
Пример
2. Задана матрица
вероятностей перехода цепи Маркова из
состояния
в состояние
за один шаг. Найти матрицу
перехода из состояния
в состояние
за
два шага и вероятность появления цепочки
состояний
—
—
за два шага. Выяснить, можно ли к матрице
применить теорему Маркова. Если да,
найти предельное распределение.
Решение.
Матрицу
получаем по формуле (2)
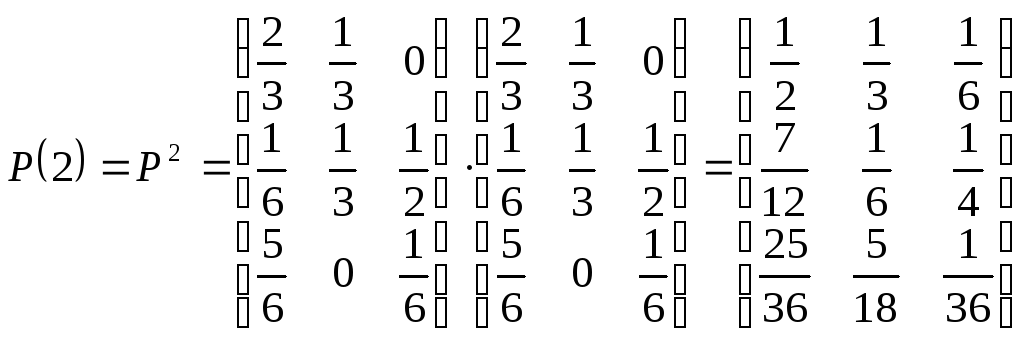
Вероятность
появления цепочки состояний
—
—
за два шага равна
,
т.е. такой последовательности состояний
наблюдаться не может.
Матрица
получилась положительной, а это означает,
что предельные вероятности существуют.
Найдем вектор
как собственный вектор матрицы
из
матричного уравнения
(4)
при
,
т.е.
или
из системы
Эта
система равносильна системе
Решая
ее, например методом Жордана-Гаусса,
получим


,
откуда
А
с учетом (3)
,
т.е.
в стационарном режиме система в среднем
всего времени находится в состоянии
,
— в состоянии
и
— в состоянии
.
-
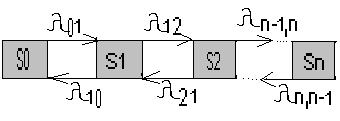
Рассмотрим
марковский процесс с дискретным
состоянием и непрерывным временем
временем.
Для
таких процессов рисуется граф состояний,
вершины которого соответствуют состояниям
S0, S1,…,Sn,
а дуги − переходам из одного состояния
в другое. Как правило, переход из одного
состояния в другое происходит под
действием простейшего потока событий
с интенсивностью
.
Граф, дугам которого приписаны
интенсивности
,
называется размеченным.
− вероятность
того, что в момент времени
система
находиться в состоянии
.
Для
вероятностей
имеет место условие нормировки:
(1)
и
система уравнений Колмогорова:
(2)
Гдеберётся
по всем состояниям
,
дуги из которых идут в состояния
.
Во второй сумме берутся все состояния,
в которые идут дуги из состояния
.
Особый
интерес представляет случай, когда
система может перейти в стационарный
режим.
,
− это предельные вероятности, получающиеся
при
.
Их находят из системы:
(3)
Среди
системы уравнений (3) одно лишнее (любое),
его следует отбросить и добавить условие
(1). Доказано, что если число состояний
конечно и из каждого состояния можно
перейти в любое другое, то предельные
вероятности существуют.
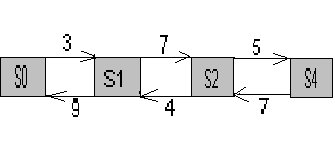
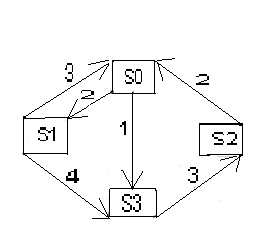
Пример:
Найти
предельные вероятности для системы,
размеченный граф которой имеет вид.
,
,
,
.
С
учетом условия нормировки получаем
систему
Отбрасываем
третье из уравнений, получаем:
§
4 Процессы гибели и размножения
описывают
изменение численности биологических
популяций.
Граф
состояний процесса гибели и размножения
имеет вид
т.к.
переход из любого состояния может
осуществляться только в состояния с
соседними номерами.
,
,
т.к.
,
то остается
,
и
далее аналогично
,
…………………..
,
.
Получаем
систему
из
которой с учетом условия нормировки
получаем окончательно
и
далее из системы находим
,
,…,
.
Пример.
Дан граф процесса гибели и размножения.
предельные вероятности состояний.
Решение.
,
,
,
.
Отбрасываем
последнее уравнение, добавляем условие
нормировки и получаем систему
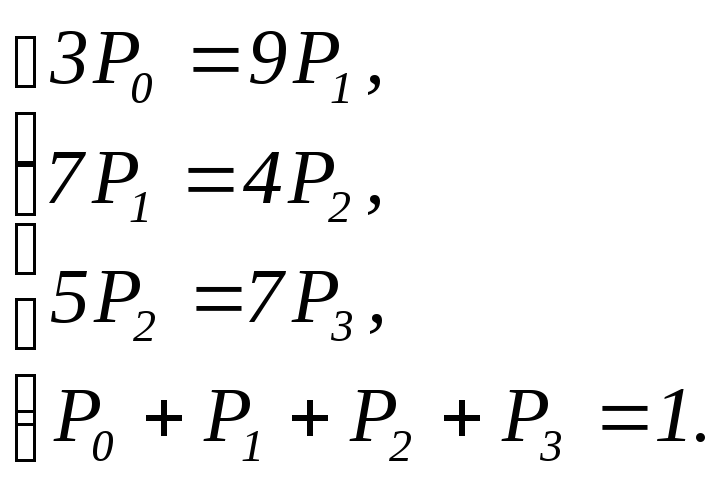
Окончательно
§
5. Некоторые задачи теории массового
обслуживания
Системы
массового обслуживания СМО − системы,
предназначенные для многократного
использования при решении однотипных
задач. Каждая система состоит из
определенного количества обслуживающих
единиц − каналов.
Будем
рассматривать многоканальные СМО с
отказами (т.е. такие, в которых в случае
занятости всех каналов заявка покидает
систему необслуженной). Для них введем
следующие показатели.
1.
интенсивность потока заявок, т.е. среднее
количество заявок, поступающих за
единицу времени;
2.
— абсолютная пропускная способность
СМО, т.е. среднее число заявок,
рассматриваемых в единицу времени.
3.
— относительная пропускная способность,
т.е. средняя доля пришедших заявок,
обслуживаемых системой.
4.
— вероятность отказа, т.е. того, что
заявка покинет систему необслуженной.
5.
— среднее число занятых каналов для
многоканальной системы.
6.
— интенсивность обслуживания, т.е.
количество заявок, обслуживаемых одним
каналом за единицу времени.
7.
— среднее время обслуживания, т.е.
.
Итак,
имеется
каналов, на которые поступает поток
заявок с интенсивностью
.
Поток обслуживания каждого канала имеет
интенсивность
.
Найдем предельные вероятности состояний
системы и показатели ее эффективности.
Система
имеет следующие состояния
,
,
,
…,
,
…,
,
пронумерованные по числу заявок,
находящихся в системе, т.е.
— состояние системы, когда в ней находятся
заявок (занято
каналов).
Г
состояний соответствует процессу гибели
и размножения.
Переход
в соседнее состояние с большим номером
всегда происходит под действием
простейшего потока с интенсивностью
,
а вот переход из состояния
в состояние
происходит под действием потока
интенсивности
,
так как освободиться может любой из
занятых каналов.
Формула
для предельной вероятности состояния
примет вид
,
(1)
где
— так называемая интенсивность
нагрузки канала, а
,
,
…,
,
…,
.
(2)
Найдем
показатели эффективности СМО.
Вероятность
отказа системы есть предельная вероятность
того, что все
каналов будут заняты, т.е.
.
Относительная
пропускная способность — вероятность
того, что заявка будет обслужена
.
Абсолютная
пропускная способность
.
Среднее
число занятых каналов
,
т.е. математическое ожидание числа
занятых каналов
или
иначе
.
Далее
разбирайте задачи к практическому
занятию и используйте методички (см.
список литературы).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В 1998 году Лоуренс Пейдж, Сергей Брин, Раджив Мотвани и Терри Виноград опубликовали статью «The PageRank Citation Ranking: Bringing Order to the Web», в которой описали знаменитый теперь алгоритм PageRank, ставший фундаментом Google. Спустя чуть менее двух десятков лет Google стал гигантом, и даже несмотря на то, что его алгоритм сильно эволюционировал, PageRank по-прежнему является «символом» алгоритмов ранжирования Google (хотя только немногие люди могут действительно сказать, какой вес он сегодня занимает в алгоритме).
С теоретической точки зрения интересно заметить, что одна из стандартных интерпретаций алгоритма PageRank основывается на простом, но фундаментальном понятии цепей Маркова. Из статьи мы увидим, что цепи Маркова — это мощные инструменты стохастического моделирования, которые могут быть полезны любому эксперту по аналитическим данным (data scientist). В частности, мы ответим на такие базовые вопросы: что такое цепи Маркова, какими хорошими свойствами они обладают, и что с их помощью можно делать?
Краткий обзор
В первом разделе мы приведём базовые определения, необходимые для понимания цепей Маркова. Во втором разделе мы рассмотрим особый случай цепей Маркова в конечном пространстве состояний. В третьем разделе мы рассмотрим некоторые из элементарных свойств цепей Маркова и проиллюстрируем эти свойства на множестве мелких примеров. Наконец, в четвёртом разделе мы свяжем цепи Маркова с алгоритмом PageRank и увидим на искусственном примере, как цепи Маркова можно применять для ранжирования узлов графа.
Примечание. Для понимания этого поста необходимы знания основ вероятностей и линейной алгебры. В частности, будут использованы следующие понятия: условная вероятность, собственный вектор и формула полной вероятности.
Что такое цепи Маркова?
Случайные переменные и случайные процессы
Прежде чем вводить понятие цепей Маркова, давайте вкратце вспомним базовые, но важные понятия теории вероятностей.
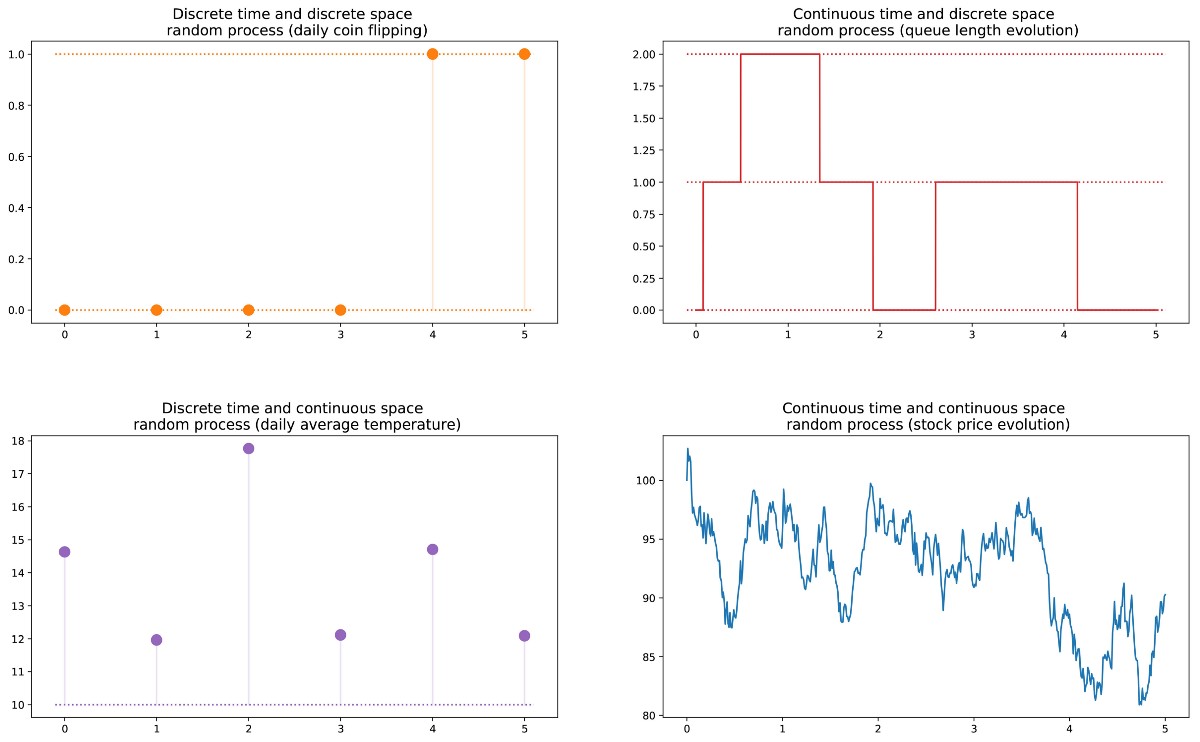
Во-первых, вне языка математики случайной величиной X считается величина, которая определяется результатом случайного явления. Его результатом может быть число (или «подобие числа», например, векторы) или что-то иное. Например, мы можем определить случайную величину как результат броска кубика (число) или же как результат бросания монетки (не число, если только мы не обозначим, например, «орёл» как 0, а «решку» как 1). Также упомянем, что пространство возможных результатов случайной величины может быть дискретным или непрерывным: например, нормальная случайная величина непрерывна, а пуассоновская случайная величина дискретна.
Далее мы можем определить случайный процесс (также называемый стохастическим) как набор случайных величин, проиндексированных множеством T, которое часто обозначает разные моменты времени (в дальнейшем мы будем считать так). Два самых распространённых случая: T может быть или множеством натуральных чисел (случайный процесс с дискретным временем), или множеством вещественных чисел (случайный процесс с непрерывным временем). Например, если мы будем бросать монетку каждый день, то зададим случайный процесс с дискретным временем, а постоянно меняющаяся стоимость опциона на бирже задаёт случайный процесс с непрерывным временем. Случайные величины в разные моменты времени могут быть независимыми друг от друга (пример с подбрасыванием монетки), или иметь некую зависимость (пример со стоимостью опциона); кроме того, они могут иметь непрерывное или дискретное пространство состояний (пространство возможных результатов в каждый момент времени).
Разные виды случайных процессов (дискретные/непрерывные в пространстве/времени).
Марковское свойство и цепь Маркова
Существуют хорошо известные семейства случайных процессов: гауссовы процессы, пуассоновские процессы, авторегрессивные модели, модели скользящего среднего, цепи Маркова и другие. Каждое из этих отдельных случаев имеет определённые свойства, позволяющие нам лучше исследовать и понимать их.
Одно из свойств, сильно упрощающее исследование случайного процесса — это «марковское свойство». Если объяснять очень неформальным языком, то марковское свойство сообщает нам, что если мы знаем значение, полученное каким-то случайным процессом в заданный момент времени, то не получим никакой дополнительной информации о будущем поведении процесса, собирая другие сведения о его прошлом. Более математическим языком: в любой момент времени условное распределение будущих состояний процесса с заданными текущим и прошлыми состояниями зависит только от текущего состояния, но не от прошлых состояний (свойство отсутствия памяти). Случайный процесс с марковским свойством называется марковским процессом.
Марковское свойство обозначает, что если мы знаем текущее состояние в заданный момент времени, то нам не нужна никакая дополнительная информация о будущем, собираемая из прошлого.
На основании этого определения мы можем сформулировать определение «однородных цепей Маркова с дискретным временем» (в дальнейшем для простоты мы их будем называть «цепями Маркова»). Цепь Маркова — это марковский процесс с дискретным временем и дискретным пространством состояний. Итак, цепь Маркова — это дискретная последовательность состояний, каждое из которых берётся из дискретного пространства состояний (конечного или бесконечного), удовлетворяющее марковскому свойству.
Математически мы можем обозначить цепь Маркова так:
где в каждый момент времени процесс берёт свои значения из дискретного множества E, такого, что
Тогда марковское свойство подразумевает, что у нас есть
Снова обратите внимание, что эта последняя формула отражает тот факт, что для хронологии (где я нахожусь сейчас и где я был раньше) распределение вероятностей следующего состояния (где я буду дальше) зависит от текущего состояния, но не от прошлых состояний.
Примечание. В этом ознакомительном посте мы решили рассказать только о простых однородных цепях Маркова с дискретным временем. Однако существуют также неоднородные (зависящие от времени) цепи Маркова и/или цепи с непрерывным временем. В этой статье мы не будем рассматривать такие вариации модели. Стоит также заметить, что данное выше определение марковского свойства чрезвычайно упрощено: в истинном математическом определении используется понятие фильтрации, которое выходит далеко за пределы нашего вводного знакомства с моделью.
Характеризуем динамику случайности цепи Маркова
В предыдущем подразделе мы познакомились с общей структурой, соответствующей любой цепи Маркова. Давайте посмотрим, что нам нужно, чтобы задать конкретный «экземпляр» такого случайного процесса.
Сначала заметим, что полное определение характеристик случайного процесса с дискретным временем, не удовлетворяющего марковскому свойству, может быть сложным занятием: распределение вероятностей в заданный момент времени может зависеть от одного или нескольких моментов в прошлом и/или будущем. Все эти возможные временные зависимости потенциально могут усложнить создание определения процесса.
Однако благодаря марковскому свойству динамику цепи Маркова определить довольно просто. И в самом деле. нам нужно определить только два аспекта: исходное распределение вероятностей (то есть распределение вероятностей в момент времени n=0), обозначаемое
и матрицу переходных вероятностей (которая даёт нам вероятности того, что состояние в момент времени n+1 является последующим для другого состояния в момент n для любой пары состояний), обозначаемую
Если два этих аспекта известны, то полная (вероятностная) динамика процесса чётко определена. И в самом деле, вероятность любого результата процесса тогда можно вычислить циклически.
Пример: допустим, мы хотим знать вероятность того, что первые 3 состояния процесса будут иметь значения (s0, s1, s2). То есть мы хотим вычислить вероятность
Здесь мы применяем формулу полной вероятности, гласящую, что вероятность получения (s0, s1, s2) равна вероятности получения первого s0, умноженного на вероятность получения s1 с учётом того, что ранее мы получили s0, умноженного на вероятность получения s2 с учётом того, что мы получили ранее по порядку s0 и s1. Математически это можно записать как
И затем проявляется упрощение, определяемое марковским допущением. И в самом деле, в случае длинных цепей мы получим для последних состояний сильно условные вероятности. Однако в случае цепей Маркова мы можем упростить это выражение, воспользовавшись тем, что
получив таким образом
Так как они полностью характеризуют вероятностную динамику процесса, многие сложные события можно вычислить только на основании исходного распределения вероятностей q0 и матрицы переходной вероятности p. Стоит также привести ещё одну базовую связь: выражение распределения вероятностей во время n+1, выраженное относительно распределения вероятностей во время n
Цепи Маркова в конечных пространствах состояний
Представление в виде матриц и графов
Здесь мы допустим, что во множестве E есть конечное количество возможных состояний N:
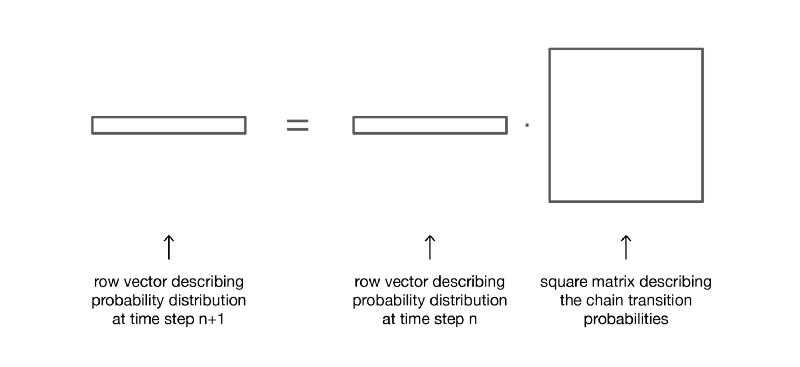
Тогда исходное распределение вероятностей можно описать как вектор-строку q0 размером N, а переходные вероятности можно описать как матрицу p размером N на N, такую что
Преимущество такой записи заключается в том, что если мы обозначим распределение вероятностей на шаге n вектором-строкой qn, таким что его компоненты задаются
тогда простые матричные связи при этом сохраняются
(здесь мы не будем рассматривать доказательство, но воспроизвести его очень просто).
Если умножить справа вектор-строку, описывающий распределение вероятностей на заданном этапе времени, на матрицу переходных вероятностей, то мы получим распределение вероятностей на следующем этапе времени.
Итак, как мы видим, переход распределения вероятностей из заданного этапа в последующий определяется просто как умножение справа вектора-строки вероятностей исходного шага на матрицу p. Кроме того, это подразумевает, что у нас есть
Динамику случайности цепи Маркова в конечном пространстве состояний можно с лёгкостью представить как нормированный ориентированный граф, такой что каждый узел графа является состоянием, а для каждой пары состояний (ei, ej) существует ребро, идущее от ei к ej, если p(ei,ej)>0. Тогда значение ребра будет той же вероятностью p(ei,ej).
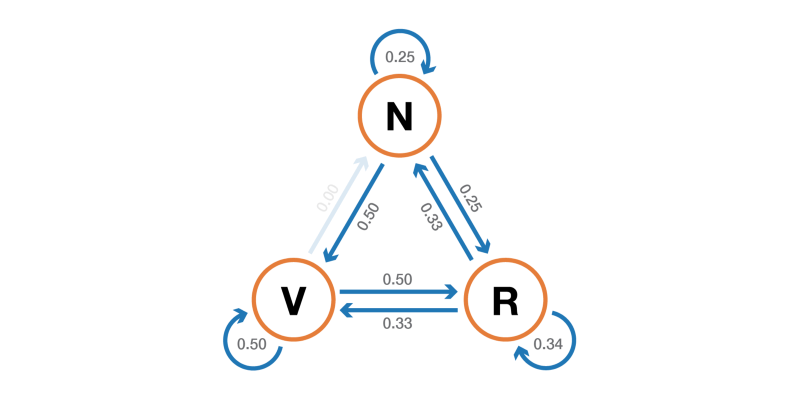
Пример: читатель нашего сайта
Давайте проиллюстрируем всё это простым примером. Рассмотрим повседневное поведение вымышленного посетителя сайта. В каждый день у него есть 3 возможных состояния: читатель не посещает сайт в этот день (N), читатель посещает сайт, но не читает пост целиком (V) и читатель посещает сайт и читает один пост целиком (R ). Итак, у нас есть следующее пространство состояний:
Допустим, в первый день этот читатель имеет вероятность 50% только зайти на сайт и вероятность 50% посетить сайт и прочитать хотя бы одну статью. Вектор, описывающий исходное распределение вероятностей (n=0) тогда выглядит так:
Также представим, что наблюдаются следующие вероятности:
- когда читатель не посещает один день, то имеет вероятность 25% не посетить его и на следующий день, вероятность 50% только посетить его и 25% — посетить и прочитать статью
- когда читатель посещает сайт один день, но не читает, то имеет вероятность 50% снова посетить его на следующий день и не прочитать статью, и вероятность 50% посетить и прочитать
- когда читатель посещает и читает статью в один день, то имеет вероятность 33% не зайти на следующий день (надеюсь, этот пост не даст такого эффекта!), вероятность 33% только зайти на сайт и 34% — посетить и снова прочитать статью
Тогда у нас есть следующая переходная матрица:
Из предыдущего подраздела мы знаем как вычислить для этого читателя вероятность каждого состояния на следующий день (n=1)
Вероятностную динамику этой цепи Маркова можно графически представить так:
Представление в виде графа цепи Маркова, моделирующей поведение нашего придуманного посетителя сайта.
Свойства цепей Маркова
В этом разделе мы расскажем только о некоторых самых базовых свойствах или характеристиках цепей Маркова. Мы не будем вдаваться в математические подробности, а представим краткий обзор интересных моментов, которые необходимо изучить для использования цепей Маркова. Как мы видели, в случае конечного пространства состояний цепь Маркова можно представить в виде графа. В дальнейшем мы будем использовать графическое представление для объяснения некоторых свойств. Однако не стоит забывать, что эти свойства необязательно ограничены случаем конечного пространства состояний.
Разложимость, периодичность, невозвратность и возвратность
В этом подразделе давайте начнём с нескольких классических способов характеризации состояния или целой цепи Маркова.
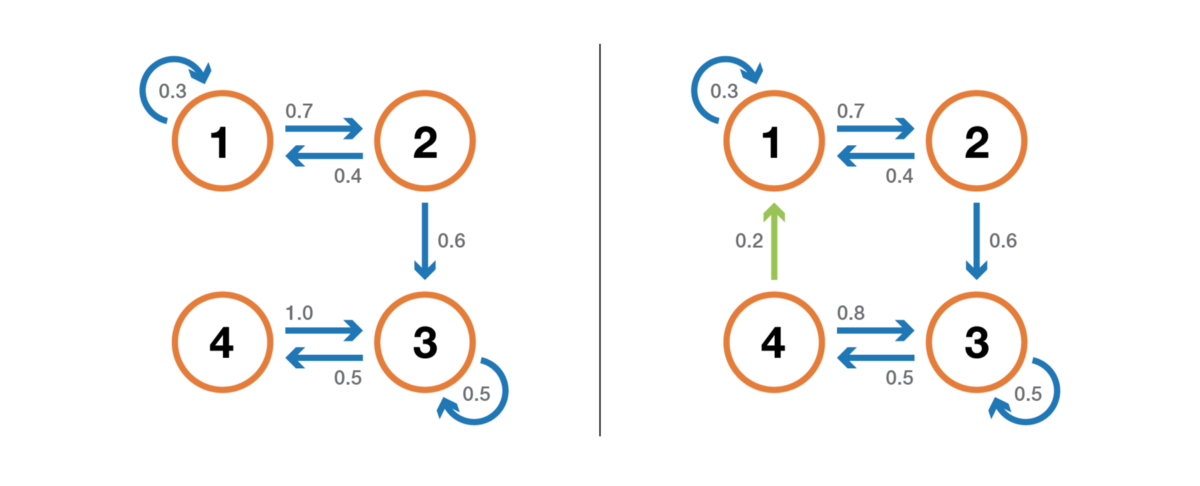
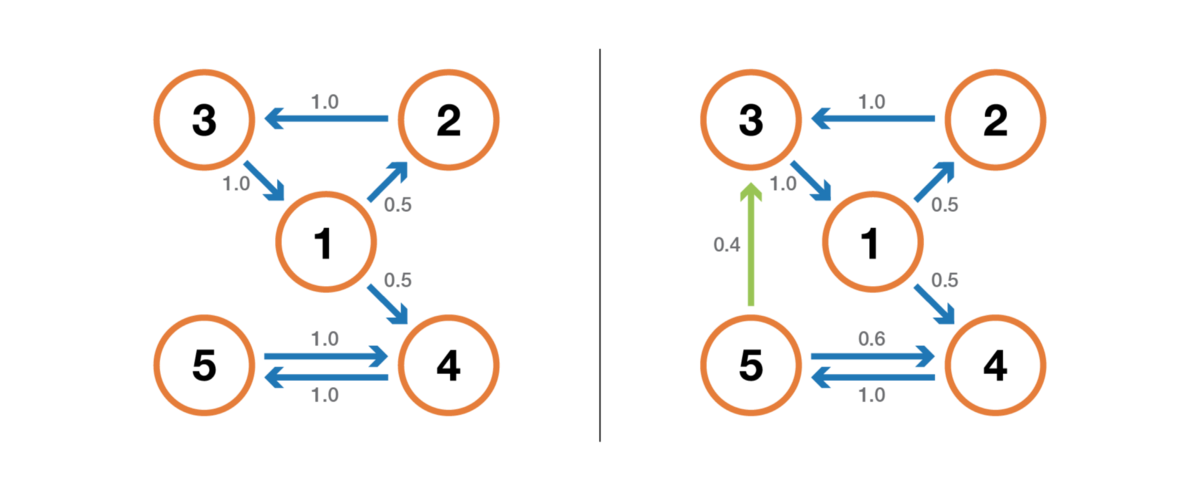
Во-первых, мы упомянем, что цепь Маркова неразложима, если можно достичь любого состояния из любого другого состояния (необязательно, что за один шаг времени). Если пространство состояний конечно и цепь можно представить в виде графа, то мы можем сказать, что граф неразложимой цепи Маркова сильно связный (теория графов).
Иллюстрация свойства неразложимости (несокращаемости). Цепь слева нельзя сократить: из 3 или 4 мы не можем попасть в 1 или 2. Цепь справа (добавлено одно ребро) можно сократить: каждого состояния можно достичь из любого другого.
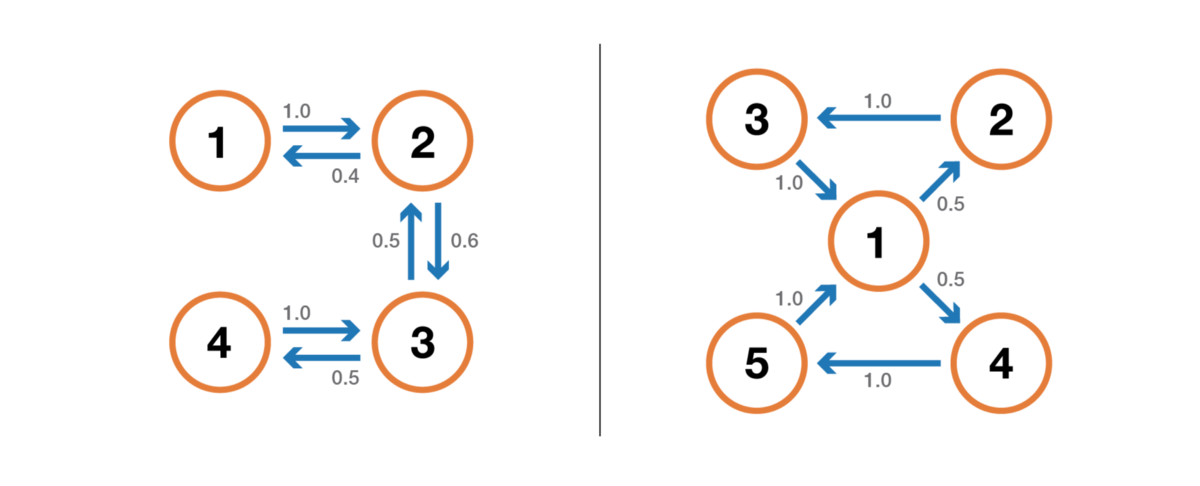
Состояние имеет период k, если при уходе из него для любого возврата в это состояние нужно количество этапов времени, кратное k (k — наибольший общий делитель всех возможных длин путей возврата). Если k = 1, то говорят, что состояние является апериодическим, а вся цепь Маркова является апериодической, если апериодичны все её состояния. В случае неприводимой цепи Маркова можно также упомянуть, что если одно состояние апериодическое, то и все другие тоже являются апериодическими.
Иллюстрация свойства периодичности. Цепь слева периодична с k=2: при уходе из любого состояния для возврата в него всегда требуется количество шагов, кратное 2. Цепь справа имеет период 3.
Состояние является невозвратным, если при уходе из состояния существует ненулевая вероятность того, что мы никогда в него не вернёмся. И наоборот, состояние считается возвратным, если мы знаем, что после ухода из состояния можем в будущем вернуться в него с вероятностью 1 (если оно не является невозвратным).
Иллюстрация свойства возвратности/невозвратности. Цепь слева имеет такие свойства: 1, 2 и 3 невозвратны (при уходе из этих точек мы не можем быть абсолютно уверены, что вернёмся в них) и имеют период 3, а 4 и 5 возвратны (при уходе из этих точек мы абсолютно уверены, что когда-нибудь к ним вернёмся) и имеют период 2. Цепь справа имеет ещё одно ребро, делающее всю цепь возвратной и апериодической.
Для возвратного состояния мы можем вычислить среднее время возвратности, которое является ожидаемым временем возврата при покидании состояния. Заметьте, что даже вероятность возврата равна 1, то это не значит, что ожидаемое время возврата конечно. Поэтому среди всех возвратных состояний мы можем различать положительные возвратные состояния (с конечным ожидаемым временем возврата) и нулевые возвратные состояния (с бесконечным ожидаемым временем возврата).
Стационарное распределение, предельное поведение и эргодичность
В этом подразделе мы рассмотрим свойства, характеризующие некоторые аспекты (случайной) динамики, описываемой цепью Маркова.
Распределение вероятностей π по пространству состояний E называют стационарным распределением, если оно удовлетворяет выражению
Так как у нас есть
Тогда стационарное распределение удовлетворяет выражению
По определению, стационарное распределение вероятностей со временем не изменяется. То есть если исходное распределение q является стационарным, тогда оно будет одинаковых на всех последующих этапах времени. Если пространство состояний конечно, то p можно представить в виде матрицы, а π — в виде вектора-строки, и тогда мы получим
Это снова выражает тот факт, что стационарное распределение вероятностей со временем не меняется (как мы видим, умножение справа распределения вероятностей на p позволяет вычислить распределение вероятностей на следующем этапе времени). Учтите, что неразложимая цепь Маркова имеет стационарное распределение вероятностей тогда и только тогда, когда одно из её состояний является положительным возвратным.
Ещё одно интересное свойство, связанное с стационарным распределением вероятностей, заключается в следующем. Если цепь является положительной возвратной (то есть в ней существует стационарное распределение) и апериодической, тогда, какими бы ни были исходные вероятности, распределение вероятностей цепи сходится при стремлении интервалов времени к бесконечности: говорят, что цепь имеет предельное распределение, что является ничем иным, как стационарным распределением. В общем случае его можно записать так:
Ещё раз подчеркнём тот факт, что мы не делаем никаких допущений об исходном распределении вероятностей: распределение вероятностей цепи сводится к стационарному распределению (равновесному распределению цепи) вне зависимости от исходных параметров.
Наконец, эргодичность — это ещё одно интересное свойство, связанное с поведением цепи Маркова. Если цепь Маркова неразложима, то также говорится, что она «эргодическая», потому что удовлетворяет следующей эргодической теореме. Допустим, у нас есть функция f(.), идущая от пространства состояний E к оси (это может быть, например, цена нахождения в каждом состоянии). Мы можем определить среднее значение, перемещающее эту функцию вдоль заданной траектории (временное среднее). Для n-ных первых членов это обозначается как
Также мы можем вычислить среднее значение функции f на множестве E, взвешенное по стационарному распределению (пространственное среднее), которое обозначается
Тогда эргодическая теорема говорит нам, что когда траектория становится бесконечно длинной, временное среднее равно пространственному среднему (взвешенному по стационарному распределению). Свойство эргодичности можно записать так:
Иными словами, оно обозначает, что в пределе ранее поведение траектории становится несущественным и при вычислении временного среднего важно только долговременное стационарное поведение.
Вернёмся к примеру с читателем сайта
Снова рассмотрим пример с читателем сайта. В этом простом примере очевидно, что цепь неразложима, апериодична и все её состояния положительно возвратны.
Чтобы показать, какие интересные результаты можно вычислить с помощью цепей Маркова, мы рассмотрим среднее время возвратности в состояние R (состояние «посещает сайт и читает статью»). Другими словами, мы хотим ответить на следующий вопрос: если наш читатель в один день заходит на сайт и читает статью, то сколько дней нам придётся ждать в среднем того, что он снова зайдёт и прочитает статью? Давайте попробуем получить интуитивное понятие о том, как вычисляется это значение.
Сначала мы обозначим
Итак, мы хотим вычислить m(R,R). Рассуждая о первом интервале, достигнутом после выхода из R, мы получим
Однако это выражение требует, чтобы для вычисления m(R,R) мы знали m(N,R) и m(V,R). Эти две величины можно выразить аналогичным образом:
Итак, у нас получилось 3 уравнения с 3 неизвестными и после их решения мы получим m(N,R) = 2.67, m(V,R) = 2.00 и m(R,R) = 2.54. Значение среднего времени возвращения в состояние R тогда равно 2.54. То есть с помощью линейной алгебры нам удалось вычислить среднее время возвращения в состояние R (а также среднее время перехода из N в R и среднее время перехода из V в R).
Чтобы закончить с этим примером, давайте посмотрим, каким будет стационарное распределение цепи Маркова. Чтобы определить стационарное распределение, нам нужно решить следующее уравнение линейной алгебры:
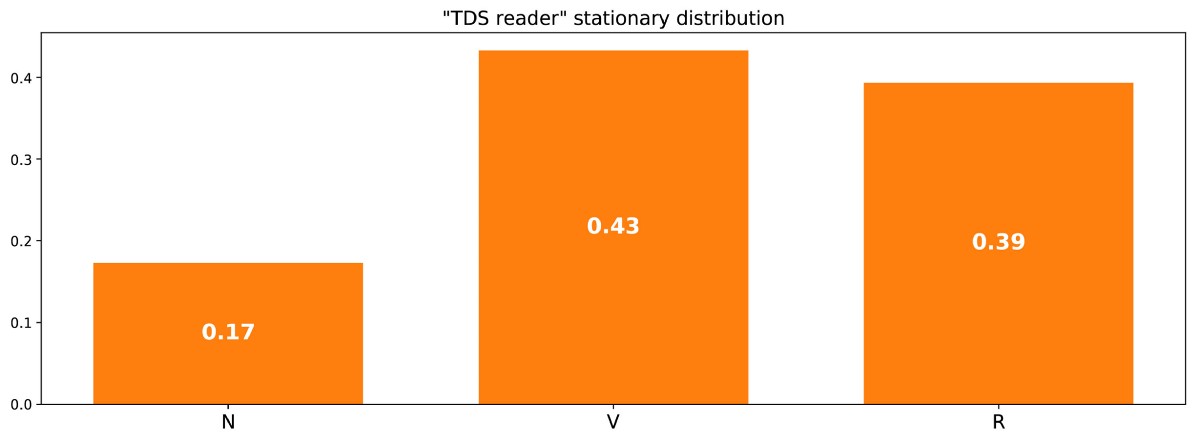
То есть нам нужно найти левый собственный вектор p, связанный с собственным вектором 1. Решая эту задачу, мы получаем следующее стационарное распределение:
Стационарное распределение в примере с читателем сайта.
Можно также заметить, что π( R ) = 1/m(R,R), и если немного поразмыслить, то это тождество довольно логично (но подробно об этом мы говорить не будем).
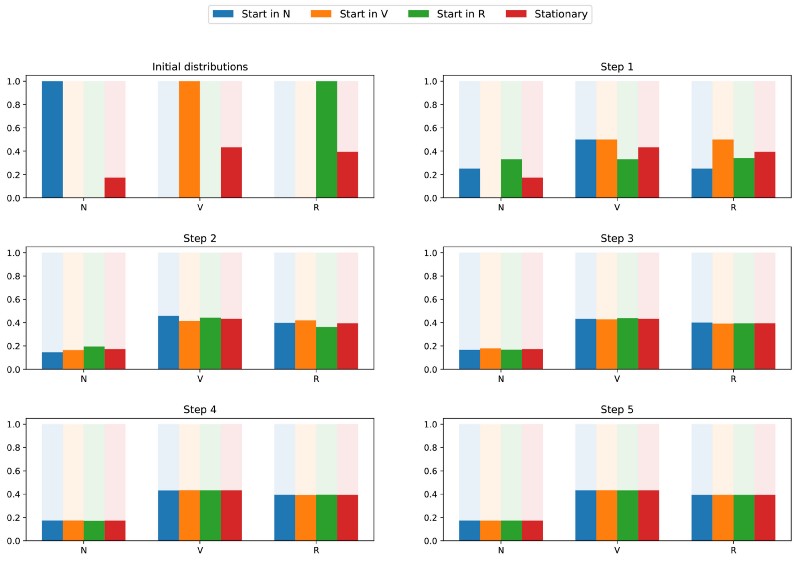
Поскольку цепь неразложима и апериодична, это означает, что в длительной перспективе распределение вероятностей сойдётся к стационарному распределению (для любых исходных параметров). Иными словами, каким бы ни было исходное состояние читателя сайта, если мы подождём достаточно долго и случайным образом выберем день, то получим вероятность π(N) того, что читатель не зайдёт на сайт в этот день, вероятность π(V) того, что читатель зайдёт, но не прочитает статью, и вероятность π® того, что читатель зайдёт и прочитает статью. Чтобы лучше уяснить свойство сходимости, давайте взглянем на следующий график, показывающий эволюцию распределений вероятностей, начинающихся с разных исходных точек и (быстро) сходящихся к стационарному распределению:
Визуализация сходимости 3 распределений вероятностей с разными исходными параметрами (синяя, оранжевая и зелёная) к стационарному распределению (красная).
Классический пример: алгоритм PageRank
Настало время вернуться к PageRank! Но прежде чем двигаться дальше, стоит упомянуть, что интерпретация PageRank, данная в этой статье, не единственно возможная, и авторы оригинальной статьи при разработке методики не обязательно рассчитывали на применение цепей Маркова. Однако наша интерпретация хороша тем, что очень понятна.
Произвольный веб-пользователь
PageRank пытается решить следующую задачу: как нам ранжировать имеющееся множество (мы можем допустить, что это множество уже отфильтровано, например, по какому-то запросу) с помощью уже существующих между страницами ссылок?
Чтобы решить эту задачу и иметь возможность отранжировать страницы, PageRank приблизительно выполняет следующий процесс. Мы считаем, что произвольный пользователь Интернета в исходный момент времени находится на одной из страниц. Затем этот пользователь начинает случайным образом начинает перемещаться, щёлкая на каждой странице по одной из ссылок, которые ведут на другую страницу рассматриваемого множества (предполагается, что все ссылки, ведущие вне этих страниц, запрещены). На любой странице все допустимые ссылки имеют одинаковую вероятность нажатия.
Так мы задаём цепь Маркова: страницы — это возможные состояния, переходные вероятности задаются ссылками со страницы на страницу (взвешенными таким образом, что на каждой странице все связанные страницы имеют одинаковую вероятность выбора), а свойства отсутствия памяти чётко определяются поведением пользователя. Если также предположить, что заданная цепь положительно возвратная и апериодичная (для удовлетворения этим требованиям применяются небольшие хитрости), тогда в длительной перспективе распределение вероятностей «текущей страницы» сходится к стационарному распределению. То есть какой бы ни была начальная страница, спустя длительное время каждая страница имеет вероятность (почти фиксированную) стать текущей, если мы выбираем случайный момент времени.
В основе PageRank лежит такая гипотеза: наиболее вероятные страницы в стационарном распределении должны быть также и самыми важными (мы посещаем эти страницы часто, потому что они получают ссылки со страниц, которые в процессе переходов тоже часто посещаются). Тогда стационарное распределение вероятностей определяет для каждого состояния значение PageRank.
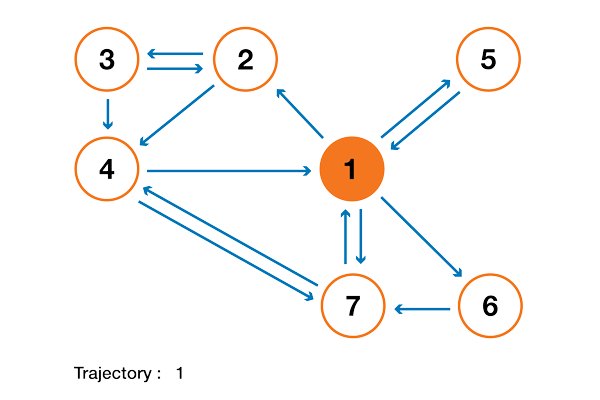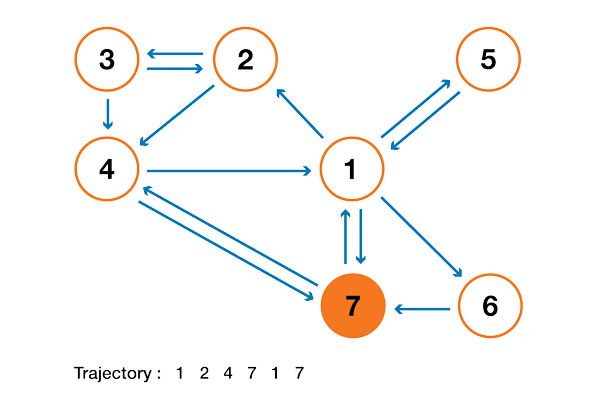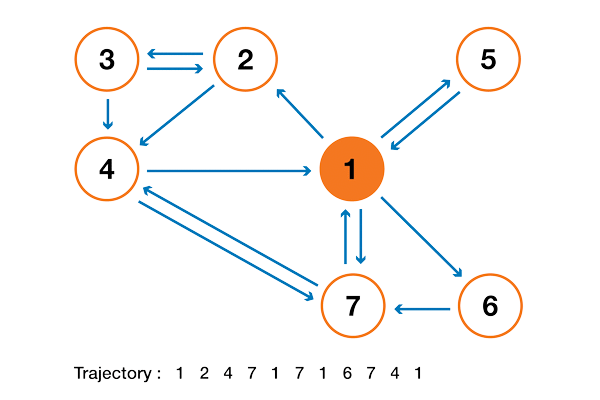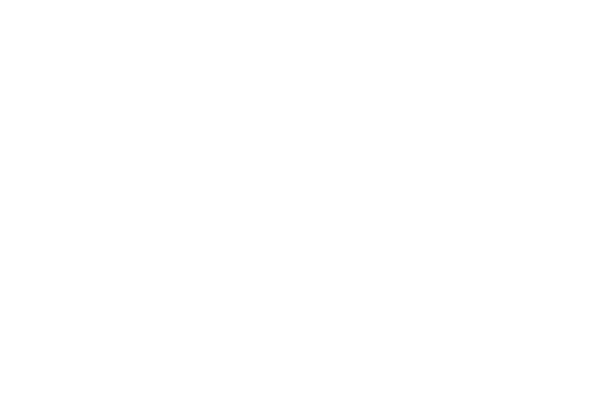
Искусственный пример
Чтобы это стало намного понятнее, давайте рассмотрим искусственный пример. Предположим, что у нас есть крошечный веб-сайт с 7 страницами, помеченными от 1 до 7, а ссылки между этими страницами соответствуют следующему графу.
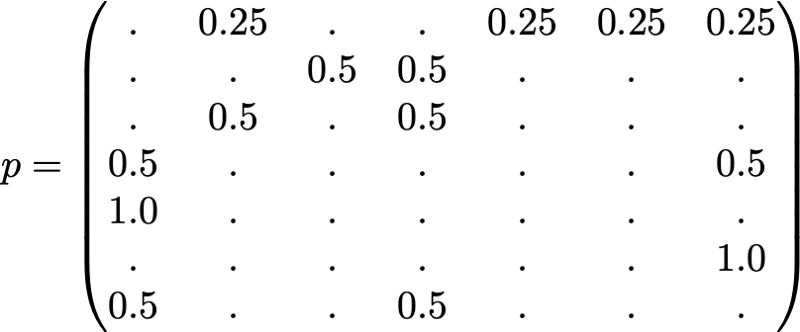
Ради понятности вероятности каждого перехода в показанной выше анимации не показаны. Однако поскольку подразумевается, что «навигация» должна быть исключительно случайной (это называют «случайным блужданием»), то значения можно легко воспроизвести из следующего простого правила: для узла с K исходящими ссылками (странице с K ссылками на другие страницы) вероятность каждой исходящей ссылки равна 1/K. То есть переходная матрица вероятностей имеет вид:
где значения 0.0 заменены для удобства на «.». Прежде чем выполнять дальнейшие вычисления, мы можем заметить, что эта цепь Маркова является неразложимой и апериодической, то есть в длительной перспективе система сходится к стационарному распределению. Как мы видели, можно вычислить это стационарное распределение, решив следующую левую задачу собственного вектора
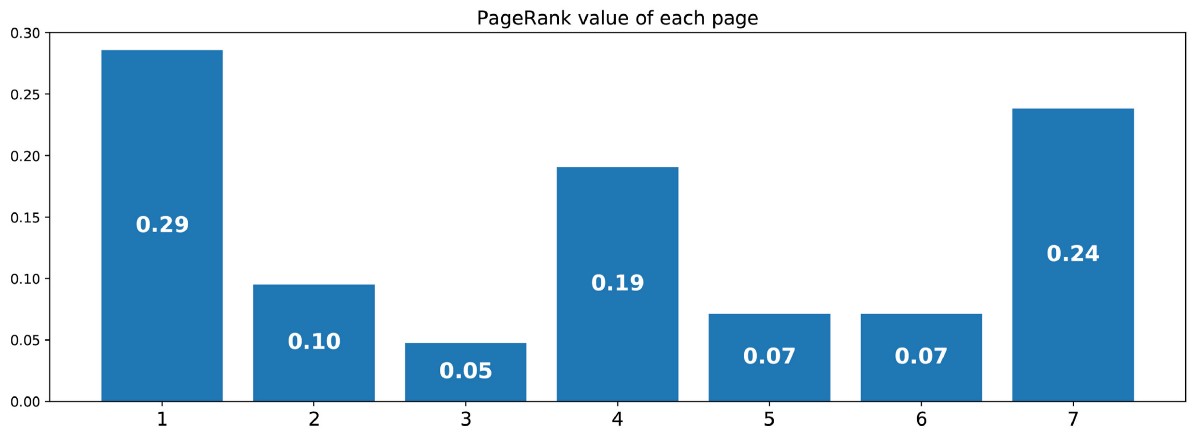
Сделав так, мы получим следующие значения PageRank (значения стационарного распределения) для каждой страницы
Значения PageRank, вычисленные для нашего искусственного примера из 7 страниц.
Тогда ранжирование PageRank этого крошечного веб-сайта имеет вид 1 > 7 > 4 > 2 > 5 = 6 > 3.
Выводы
Основные выводы из этой статьи:
- случайные процессы — это наборы случайных величин, часто индексируемые по времени (индексы часто обозначают дискретное или непрерывное время)
- для случайного процесса марковское свойство означает, что при заданном текущем вероятность будущего не зависит от прошлого (это свойство также называется «отсутствием памяти»)
- цепь Маркова с дискретным временем — это случайные процессы с индексами дискретного времени, удовлетворяющие марковскому свойству
- марковское свойство цепей Маркова сильно облегчает изучение этих процессов и позволяет вывести различные интересные явные результаты (среднее время возвратности, стационарное распределение…)
- одна из возможных интерпретаций PageRank (не единственная) заключается в имитации веб-пользователя, случайным образом перемещающегося от страницы к странице; при этом показателем ранжирования становится индуцированное стационарное распределение страниц (грубо говоря, на самые посещаемые страницы в устоявшемся состоянии должны ссылаться другие часто посещаемые страницы, а значит, самые посещаемые должны быть наиболее релевантными)
В заключение ещё раз подчеркнём, насколько мощным инструментом являются цепи Маркова при моделировании задач, связанных со случайной динамикой. Благодаря их хорошим свойствам они используются в различных областях, например, в теории очередей (оптимизации производительности телекоммуникационных сетей, в которых сообщения часто должны конкурировать за ограниченные ресурсы и ставятся в очередь, когда все ресурсы уже заняты), в статистике (хорошо известные методы Монте-Карло по схеме цепи Маркова для генерации случайных переменных основаны на цепях Маркова), в биологии (моделирование эволюции биологических популяций), в информатике (скрытые марковские модели являются важными инструментами в теории информации и распознавании речи), а также в других сферах.
Разумеется, огромные возможности, предоставляемые цепями Маркова с точки зрения моделирования и вычислений, намного шире, чем рассмотренные в этом скромном обзоре. Поэтому мы надеемся, что нам удалось пробудить у читателя интерес к дальнейшему изучению этих инструментов, которые занимают важное место в арсенале учёного и эксперта по данным.
From Wikipedia, the free encyclopedia
In probability theory and statistics, the marginal distribution of a subset of a collection of random variables is the probability distribution of the variables contained in the subset. It gives the probabilities of various values of the variables in the subset without reference to the values of the other variables. This contrasts with a conditional distribution, which gives the probabilities contingent upon the values of the other variables.
Marginal variables are those variables in the subset of variables being retained. These concepts are «marginal» because they can be found by summing values in a table along rows or columns, and writing the sum in the margins of the table.[1] The distribution of the marginal variables (the marginal distribution) is obtained by marginalizing (that is, focusing on the sums in the margin) over the distribution of the variables being discarded, and the discarded variables are said to have been marginalized out.
The context here is that the theoretical studies being undertaken, or the data analysis being done, involves a wider set of random variables but that attention is being limited to a reduced number of those variables. In many applications, an analysis may start with a given collection of random variables, then first extend the set by defining new ones (such as the sum of the original random variables) and finally reduce the number by placing interest in the marginal distribution of a subset (such as the sum). Several different analyses may be done, each treating a different subset of variables as the marginal distribution.
Definition[edit]
Marginal probability mass function[edit]
Given a known joint distribution of two discrete random variables, say, X and Y, the marginal distribution of either variable – X for example – is the probability distribution of X when the values of Y are not taken into consideration. This can be calculated by summing the joint probability distribution over all values of Y. Naturally, the converse is also true: the marginal distribution can be obtained for Y by summing over the separate values of X.
, and
|
X Y |
x1 | x2 | x3 | x4 | pY(y) ↓ |
|---|---|---|---|---|---|
| y1 | 4/32 | 2/32 | 1/32 | 1/32 | 8/32 |
| y2 | 3/32 | 6/32 | 3/32 | 3/32 | 15/32 |
| y3 | 9/32 | 0 | 0 | 0 | 9/32 |
| pX(x) → | 16/32 | 8/32 | 4/32 | 4/32 | 32/32 |
A marginal probability can always be written as an expected value:
Intuitively, the marginal probability of X is computed by examining the conditional probability of X given a particular value of Y, and then averaging this conditional probability over the distribution of all values of Y.
This follows from the definition of expected value (after applying the law of the unconscious statistician)
Therefore, marginalization provides the rule for the transformation of the probability distribution of a random variable Y and another random variable X=g(Y):
Marginal probability density function[edit]
Given two continuous random variables X and Y whose joint distribution is known, then the marginal probability density function can be obtained by integrating the joint probability distribution, f, over Y, and vice versa. That is
where ![xin [a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce)
![{displaystyle yin [c,d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44a51655f18baf55ecb29903da6b8edb9d628646)
Marginal cumulative distribution function[edit]
Finding the marginal cumulative distribution function from the joint cumulative distribution function is easy. Recall that:
- For discrete random variables,
- For continuous random variables,
If X and Y jointly take values on [a, b] × [c, d] then
and
If d is ∞, then this becomes a limit 

Marginal distribution vs. conditional distribution[edit]
Definition[edit]
The marginal probability is the probability of a single event occurring, independent of other events. A conditional probability, on the other hand, is the probability that an event occurs given that another specific event has already occurred. This means that the calculation for one variable is dependent on another variable.[2]
The conditional distribution of a variable given another variable is the joint distribution of both variables divided by the marginal distribution of the other variable.[3] That is,
- For discrete random variables,
- For continuous random variables,
Example[edit]
Suppose there is data from a classroom of 200 students on the amount of time studied (X) and the percentage of correct answers (Y).[4] Assuming that X and Y are discrete random variables, the joint distribution of X and Y can be described by listing all the possible values of p(xi,yj), as shown in Table.3.
|
X Y |
Time studied (minutes) | |||||
|---|---|---|---|---|---|---|
|
% correct |
x1 (0-20) | x2 (21-40) | x3 (41-60) | x4(>60) | pY(y) ↓ | |
| y1 (0-20) | 2/200 | 0 | 0 | 8/200 | 10/200 | |
| y2 (21-40) | 10/200 | 2/200 | 8/200 | 0 | 20/200 | |
| y3 (41-59) | 2/200 | 4/200 | 32/200 | 32/200 | 70/200 | |
| y4 (60-79) | 0 | 20/200 | 30/200 | 10/200 | 60/200 | |
| y5 (80-100) | 0 | 4/200 | 16/200 | 20/200 | 40/200 | |
| pX(x) → | 14/200 | 30/200 | 86/200 | 70/200 | 1 |
The marginal distribution can be used to determine how many students scored 20 or below: 
The conditional distribution can be used to determine the probability that a student that studied 60 minutes or more obtains a scored of 20 or below: 
Real-world example[edit]
Suppose that the probability that a pedestrian will be hit by a car, while crossing the road at a pedestrian crossing, without paying attention to the traffic light, is to be computed. Let H be a discrete random variable taking one value from {Hit, Not Hit}. Let L (for traffic light) be a discrete random variable taking one value from {Red, Yellow, Green}.
Realistically, H will be dependent on L. That is, P(H = Hit) will take different values depending on whether L is red, yellow or green (and likewise for P(H = Not Hit)). A person is, for example, far more likely to be hit by a car when trying to cross while the lights for perpendicular traffic are green than if they are red. In other words, for any given possible pair of values for H and L, one must consider the joint probability distribution of H and L to find the probability of that pair of events occurring together if the pedestrian ignores the state of the light.
However, in trying to calculate the marginal probability P(H = Hit), what is being sought is the probability that H = Hit in the situation in which the particular value of L is unknown and in which the pedestrian ignores the state of the light. In general, a pedestrian can be hit if the lights are red OR if the lights are yellow OR if the lights are green. So, the answer for the marginal probability can be found by summing P(H | L) for all possible values of L, with each value of L weighted by its probability of occurring.
Here is a table showing the conditional probabilities of being hit, depending on the state of the lights. (Note that the columns in this table must add up to 1 because the probability of being hit or not hit is 1 regardless of the state of the light.)
|
L H |
Red | Yellow | Green |
|---|---|---|---|
| Not Hit | 0.99 | 0.9 | 0.2 |
| Hit | 0.01 | 0.1 | 0.8 |
To find the joint probability distribution, more data is required. For example, suppose P(L = red) = 0.2, P(L = yellow) = 0.1, and P(L = green) = 0.7. Multiplying each column in the conditional distribution by the probability of that column occurring results in the joint probability distribution of H and L, given in the central 2×3 block of entries. (Note that the cells in this 2×3 block add up to 1).
|
L H |
Red | Yellow | Green | Marginal probability P(H) |
|---|---|---|---|---|
| Not Hit | 0.198 | 0.09 | 0.14 | 0.428 |
| Hit | 0.002 | 0.01 | 0.56 | 0.572 |
| Total | 0.2 | 0.1 | 0.7 | 1 |
The marginal probability P(H = Hit) is the sum 0.572 along the H = Hit row of this joint distribution table, as this is the probability of being hit when the lights are red OR yellow OR green. Similarly, the marginal probability that P(H = Not Hit) is the sum along the H = Not Hit row.
Multivariate distributions[edit]
Many samples from a bivariate normal distribution. The marginal distributions are shown in red and blue. The marginal distribution of X is also approximated by creating a histogram of the X coordinates without consideration of the Y coordinates.
For multivariate distributions, formulae similar to those above apply with the symbols X and/or Y being interpreted as vectors. In particular, each summation or integration would be over all variables except those contained in X.[5]
That means, If X1,X2,…,Xn are discrete random variables, then the marginal probability mass function should be
if X1,X2,…,Xn are continuous random variables, then the marginal probability density function should be
See also[edit]
- Compound probability distribution
- Joint probability distribution
- Marginal likelihood
- Wasserstein metric
- Conditional distribution
References[edit]
- ^ Trumpler, Robert J. & Harold F. Weaver (1962). Statistical Astronomy. Dover Publications. pp. 32–33.
- ^ «Marginal & Conditional Probability Distributions: Definition & Examples». Study.com. Retrieved 2019-11-16.
- ^ «Exam P [FSU Math]». www.math.fsu.edu. Retrieved 2019-11-16.
- ^ Marginal and conditional distributions, retrieved 2019-11-16
- ^ A modern introduction to probability and statistics : understanding why and how. Dekking, Michel, 1946-. London: Springer. 2005. ISBN 9781852338961. OCLC 262680588.
{{cite book}}: CS1 maint: others (link)
Bibliography[edit]
- Everitt, B. S.; Skrondal, A. (2010). Cambridge Dictionary of Statistics. Cambridge University Press.
- Dekking, F. M.; Kraaikamp, C.; Lopuhaä, H. P.; Meester, L. E. (2005). A modern introduction to probability and statistics. London : Springer. ISBN 9781852338961.
Уравнения Колмогорова.
Предельные вероятности состояний
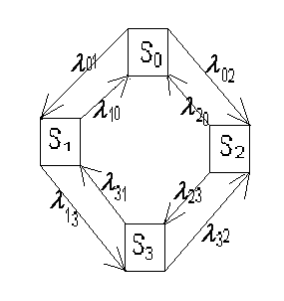
Рассмотрим математическое описание марковского процесса с дискретными состояниями и непрерывным временем* на примере случайного процесса из примера 1, граф которого изображен на рис. 1. Будем полагать, что все переходы системы из состояния в
происходят под воздействием простейших потоков событий с интенсивностями
; так, переход системы из состояния
в
будет происходить под воздействием потока отказов первого узла, а обратный переход из состояния
в
— под воздействием потока «окончаний ремонтов» первого узла и т.п.
Граф состояний системы с проставленными у стрелок интенсивностями будем называть размеченным (см. рис. 1). Рассматриваемая система имеет четыре возможных состояния:
.
Вероятностью i-го состояния называется вероятность того, что в момент
система будет находиться в состоянии
. Очевидно, что для любого момента
сумма вероятностей всех состояний равна единице:
(8)
Рассмотрим систему в момент и, задав малый промежуток
, найдем вероятность
того, что система в момент
будет находиться в состоянии
. Это достигается разными способами.
1. Система в момент с вероятностью
находилась в состоянии
, а за время
не вышла из него.
Вывести систему из этого состояния (см. граф на рис. 1) можно суммарным простейшим потоком с интенсивностью , т.е. в соответствии с формулой (7), с вероятностью, приближенно равной
. А вероятность того, что система не выйдет из состояния
, равна
. Вероятность того, что система будет находиться в состоянии
по первому способу (т.е. того, что находилась в состоянии
и не выйдет из него за время
), равна по теореме умножения вероятностей:
2. Система в момент с вероятностями
(или
) находилась в состоянии
или
и за время
перешла в состояние
.
Потоком интенсивностью (или
— с- рис. 1) система перейдет в состояние
с вероятностью, приближенно равной
(или
). Вероятность того, что система будет находиться в состоянии
по этому способу, равна
(или
).
Применяя теорему сложения вероятностей, получим
откуда
Переходя к пределу при (приближенные равенства, связанные с применением формулы (7), перейдут в точные), получим в левой части уравнения производную
(обозначим ее для простоты
):
Получили дифференциальное уравнение первого порядка, т.е. уравнение, содержащее как саму неизвестную функцию, так и ее производную первого порядка.
Рассуждая аналогично для других состояний системы , можно получить систему дифференциальных уравнений Колмогорова для вероятностей состояний:
(9)
Сформулируем правило составления уравнений Колмогорова. В левой части каждого из них стоит производная вероятности i-го состояния. В правой части — сумма произведений вероятностей всех состояний (из которых идут стрелки в данное состояние) на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного (i-го состояния).
В системе (9) независимых уравнений на единицу меньше общего числа уравнений. Поэтому для решения системы необходимо добавить уравнение (8).
Особенность решения дифференциальных уравнений вообще состоит в том, что требуется задать так называемые начальные условия, т.е. в данном случае вероятности состояний системы в начальный момент . Так, например, систему уравнений (9) естественно решать при условии, что в начальный момент оба узла исправны и система находилась в состоянии
, т.е. при начальных условиях
.
Уравнения Колмогорова дают возможность найти все вероятности состояний как функции времени. Особый интерес представляют вероятности системы в предельном стационарном режиме, т.е. при
, которые называются предельными (или финальными) вероятностями состояний.
В теории случайных процессов доказывается, что если число состояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое состояние, то предельные вероятности существуют.
Предельная вероятность состояния имеет четкий смысл: она показывает среднее относительное время пребывания системы в этом состоянии. Например, если предельная вероятность состояния
, т.е.
, то это означает, что в среднем половину времени система находится в состоянии
.
Так как предельные вероятности постоянны, то, заменяя в уравнениях Колмогорова их производные нулевыми значениями, получим систему линейных алгебраических уравнений, описывающих стационарный режим. Для системы с графом состояний, изображенном на рис. 1), такая система уравнений имеет вид:
(10)
Систему (10) можно составить непосредственно по размеченному графу состояний, если руководствоваться правилом, согласно которому слева в уравнениях стоит предельная вероятность данного состояния , умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а справа — сумма произведений интенсивностей всех потоков, входящих в i-е состояние, на вероятности тех состояний, из которых эти потоки исходят.
Пример 2. Найти предельные вероятности для системы из примера 1, граф состояний которой приведен на рис. 1, при
Решение. Система алгебраических уравнений, описывающих стационарный режим для данной системы, имеет вид (10) или
(11)
(Здесь мы вместо одного «лишнего» уравнения системы (10) записали нормировочное условие (8)).
Решив систему (11), получим , т.е. в предельном, стационарном режиме система
в среднем 40% времени будет находиться в состоянии
(оба узла исправны), 20% — в состоянии
(первый узел ремонтируется, второй работает), 27% — в состоянии
(второй узел ремонтируется, первый работает) и 13% времени — в состоянии
(оба узла ремонтируются)
Пример 3. Найти средний чистый доход от эксплуатации в стационарном режиме системы в условиях примеров 1 и 2, если известно, что в единицу времени исправная работа первого и второго узлов приносит доход соответственно в 10 и 6 ден.ед., а их ремонт требует затрат соответственно в 4 и 2 ден.ед. Оценить экономическую эффективность имеющейся возможности уменьшения вдвое среднего времени ремонта каждого из двух узлов, если при этом придется вдвое увеличить затраты на ремонт каждого узла (в единицу времени).
Решение. Из примера 2 следует, что в среднем первый узел исправно работает долю времени, равную , а второй узел —
. В то же время первый узел находится в ремонте в среднем долю времени, равную
, а второй узел —
. Поэтому средний чистый доход
в единицу времени от эксплуатации системы, т.е. разность между доходами и затратами, равен
ден. ед.
Уменьшение вдвое среднего времени ремонта каждого из узлов в соответствии с (6) будет означать увеличение вдвое интенсивностей потока «окончаний ремонтов» каждого узла, т.е. теперь
и система линейных алгебраических уравнений (10), описывающая стационарный режим системы
, вместе с нормировочным условием (8) примет вид:
Решив систему, получим .
Учитывая, что , а затраты на ремонт первого и второго узла составляют теперь соответственно 8 и 4 ден.ед., вычислим средний чистый доход
в единицу времени:
ден.ед.
Так как больше
(примерно на 20%), то экономическая целесообразность ускорения ремонтов узлов очевидна.
Процесс гибели и размножения
В теории массового обслуживания широкое распространение имеет специальный класс случайных процессов — так называемый процесс гибели и размножения. Название этого процесса связано с рядом биологических задач, где он является математической моделью изменения численности биологических популяций.
Граф состояний процесса гибели и размножения имеет вид, показанный на рис. 4.
Рассмотрим упорядоченное множество состояний системы . Переходы могут осуществляться из любого состояния только в состояния с соседними номерами, т.е. из состояния
возможны переходы только либо в состояние
, либо в состояние
.
Предположим, что все потоки событий, переводящие систему по стрелкам графа, простейшие с соответствующими интенсивностями или
.
По графу, представленному на рис. 4, составим и решим алгебраические уравнения для предельных вероятностей состояний (их существование вытекает из возможности перехода из каждого состояния в каждое другое и конечности числа состояний).
В соответствии с правилом составления таких уравнений (см. 13) получим: для состояния
(12)
для состояния имеем
, которое с учетом (12) приводится к виду
(13)
Аналогично, записывая уравнения для предельных вероятностей других состояний, можно получить следующую систему уравнений:
(14)
к которой добавляется нормировочное условие
(15)
При анализе численности популяций считают, что состояние соответствует численности популяции, равной
, и переход системы из состояния
в состояние
происходит при рождении одного члена популяции, а переход в состояние
— при гибели одного члена популяции.
Решая систему (14), (15), можно получить
(16)
(17)
Легко заметить, что в формулах (17) для коэффициенты при
есть слагаемые, стоящие после единицы в формуле (16). Числители этих коэффициентов представляют произведение всех интенсивностей, стоящих у стрелок, ведущих слева направо до данного состояния
, а знаменатели — произведение всех интенсивностей, стоящих у стрелок, ведущих справа налево до состояния
.
Пример 4. Процесс гибели и размножения представлен графом (рис. 5). Найти предельные вероятности состояний.
Решение. По формуле (16) найдем
по (17)
т.е. в установившемся, стационарном режиме в среднем 70,6% времени система будет находиться в состоянии , 17,6% — в состоянии
и 11,8% — в состоянии
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.


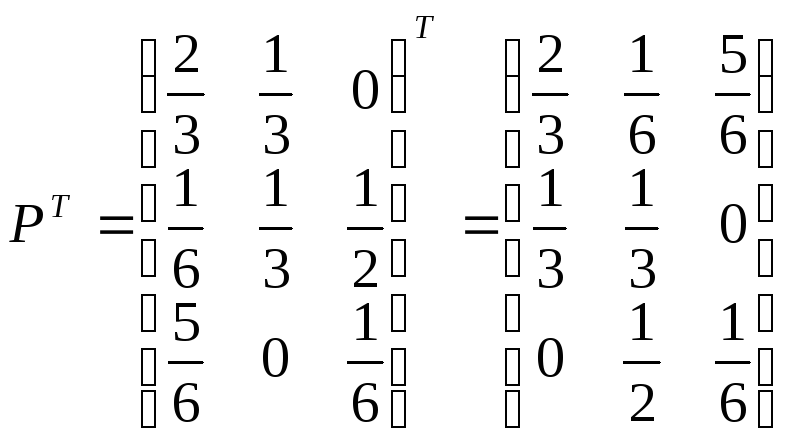
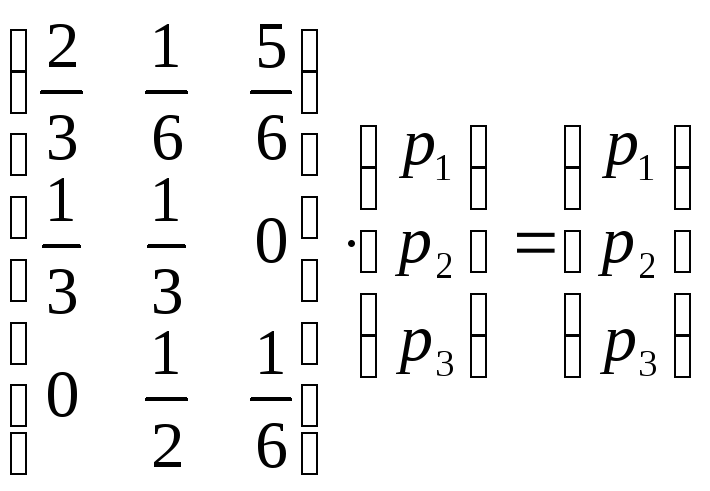
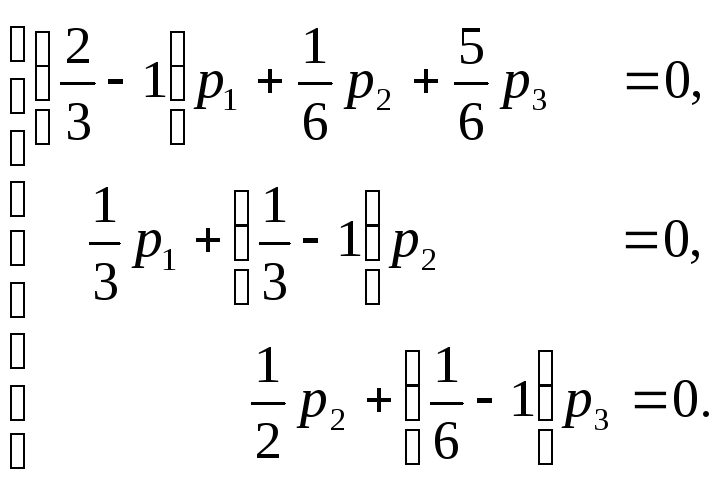
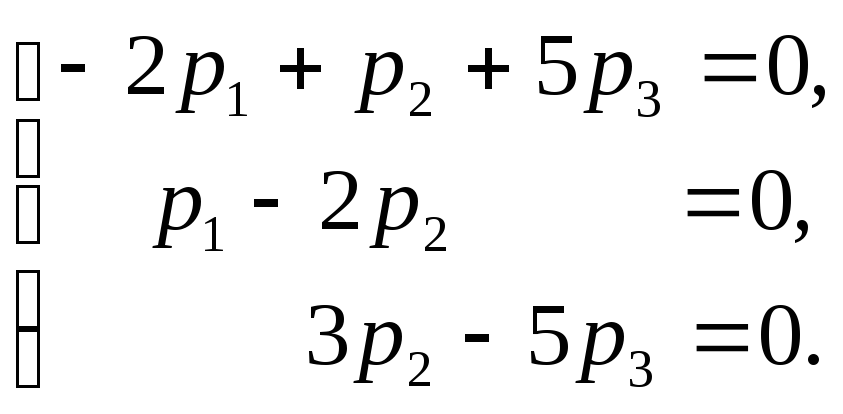
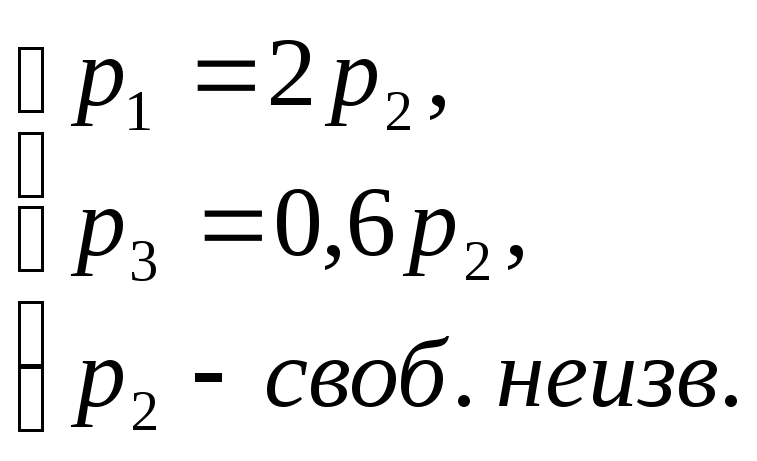
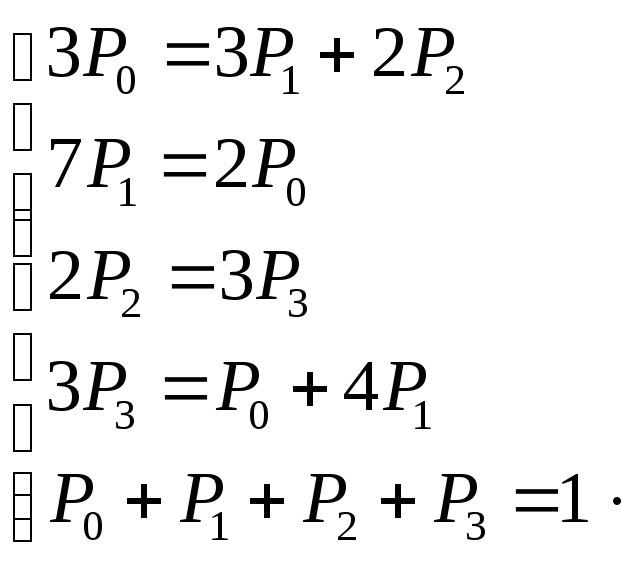


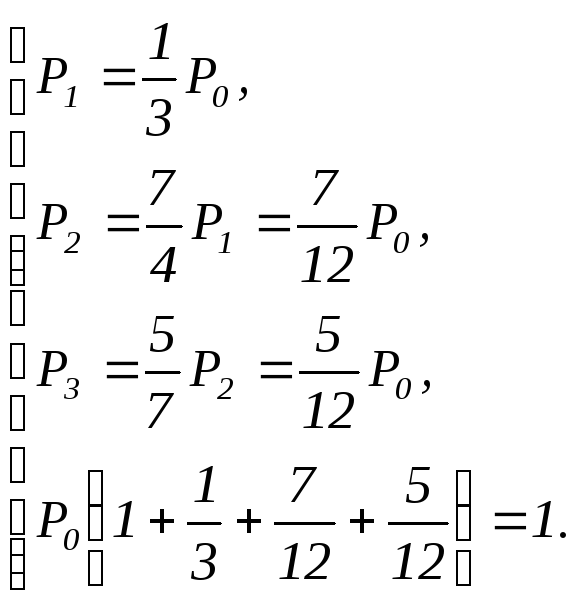
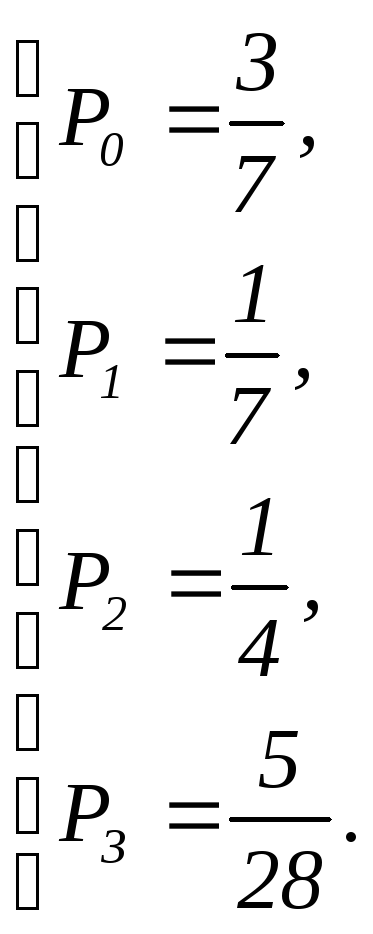
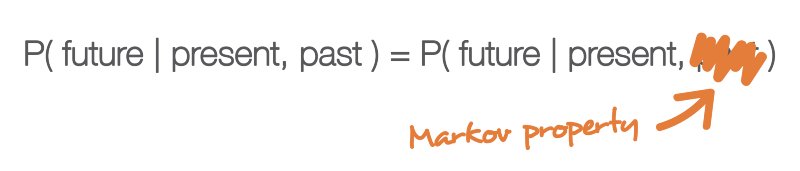
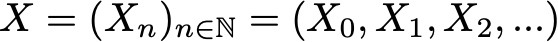

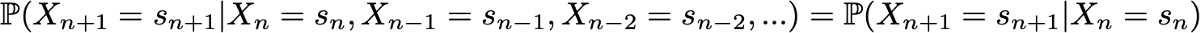
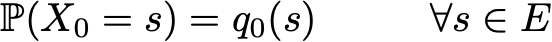
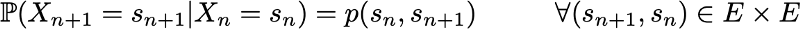
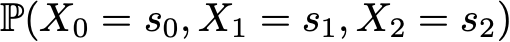
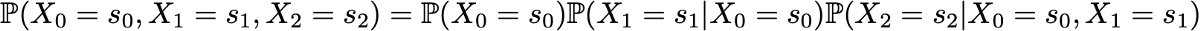
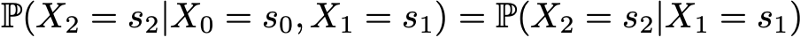
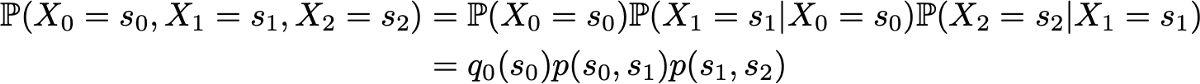
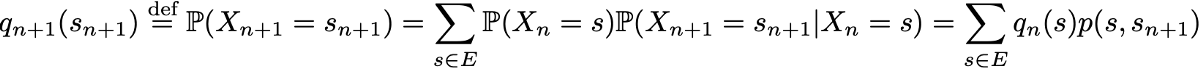
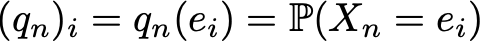
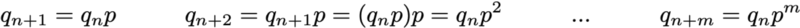

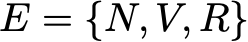
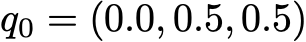


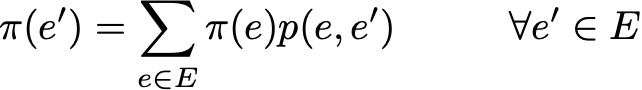
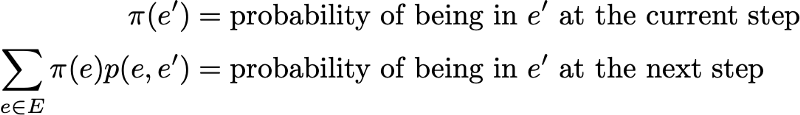
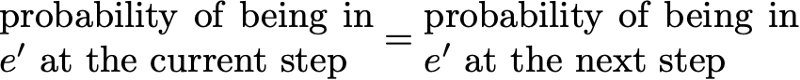
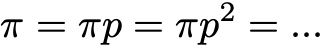
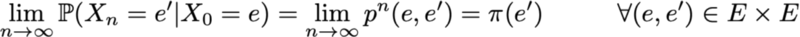
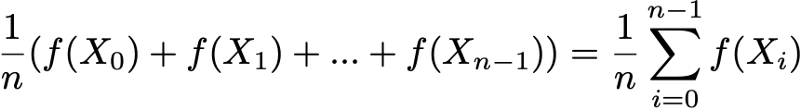
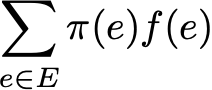
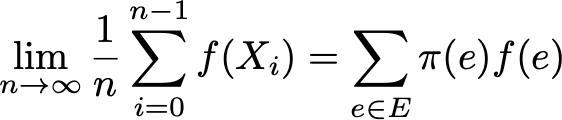
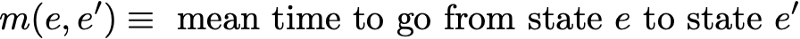
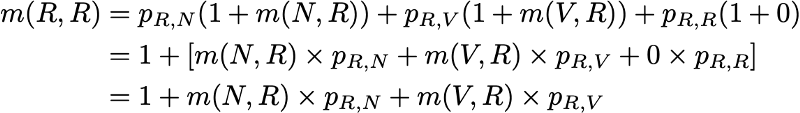
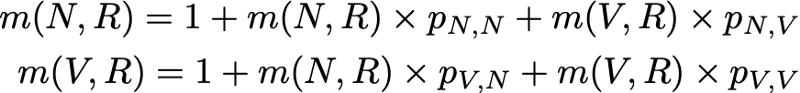
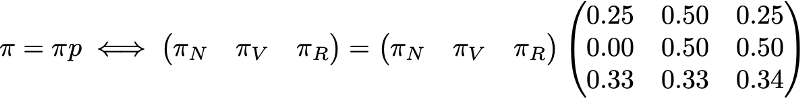
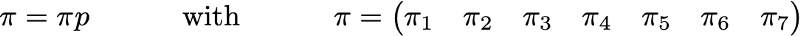


![{displaystyle p_{X}(x)=int _{y}p_{Xmid Y}(xmid y),p_{Y}(y),mathrm {d} y=operatorname {E} _{Y}[p_{Xmid Y}(xmid y)];.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3be350f4abd775f622107a8b4a809ef491e8e458)
![{displaystyle operatorname {E} _{Y}[f(Y)]=int _{y}f(y)p_{Y}(y),mathrm {d} y.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/275f3fc53bf6fac27de9a9a11bc3ee47455094e1)













