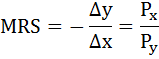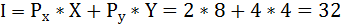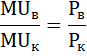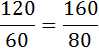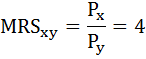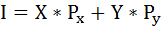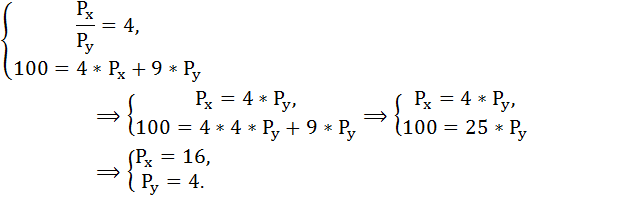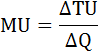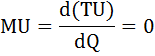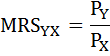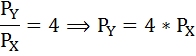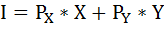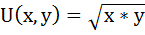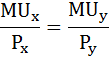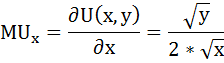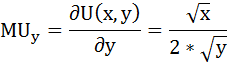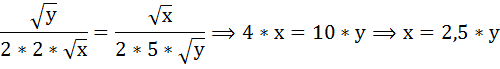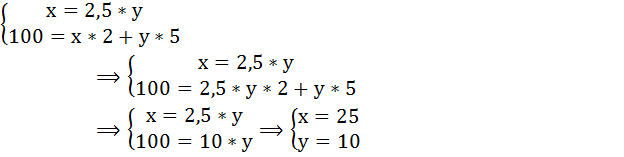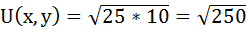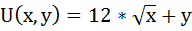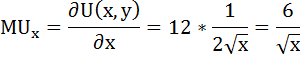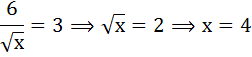Общая TU и предельная MU полезности товаров А, В, С представлены в таблице. Заполнить пропуски в таблице.
| Количество товара | А | В | С | |||
|---|---|---|---|---|---|---|
| TU | MU | TU | MU | TU | MU | |
| 1 | … | 20 | 19 | … | 22 | … |
| 2 | … | 15 | 30 | … | … | 10 |
| 3 | … | 12 | 38 | … | 39 | … |
| 4 | … | 8 | 43 | … | 44 | … |
| 5 | … | 6 | 45 | … | … | 3 |
Решение:
Найдём общую полезность товара А.
Общая полезность N-й единицы товара = Предельная полезность N-й единицы товара + Общая полезность N-1-й единицы товара
TU(1)=MU(1)=20
TU(2)=MU(2) + TU(1)=15 + 20=35
TU(3)=MU(3) + TU(2)=12 + 35=47
TU(4)=MU(4) + TU(3)=8 + 47=55
TU(5)=MU(5) + TU(4)=6 + 55=61
Найдём предельную полезность товара В.
Предельная полезность N-й единицы товара=Общая полезность N-й единицы товара — Общая полезность N-1-й единицы товара
MU(1)=TU(1)=19
MU(2)= TU(2) — TU(1)=30 – 19 = 11
MU(3)= TU(3) — TU(2)=38 – 30 = 8
MU(4)= TU(4) — TU(3)=43 – 38=5
MU(5)= TU(5) — TU(4)=45 – 43=2
Найдём общую и предельную полезности товара С.
MU(1)=TU(1)=22
TU(2)=MU(2) + TU(1)=10 + 22=32
MU(3)= TU(3) — TU(2)=39 – 32=7
MU(4)= TU(4) — TU(3)=44 – 39=5
TU(5)=MU(5) + TU(4)=3 + 44=47
Заполним пропуски в таблице:
| Количество товара | А | В | С | |||
|---|---|---|---|---|---|---|
| TU | MU | TU | MU | TU | MU | |
| 1 | 20 | 20 | 19 | 19 | 22 | 22 |
| 2 | 35 | 15 | 30 | 11 | 32 | 10 |
| 3 | 47 | 12 | 38 | 8 | 39 | 7 |
| 4 | 55 | 8 | 43 | 5 | 44 | 5 |
| 5 | 61 | 6 | 45 | 2 | 47 | 3 |
Задача № 1 Расчёт дохода потребителя
Индивид покупает 8 единиц товара Х и 4 единицы товара Y. Найти его доход, если известно, что цена товара Х равна 2 ден. ед., а предельная норма замены равна 0,5.
Решение:
В точке оптимума выполняется равенство:
По условию MRS = 0,5 и Рх = 2. Следовательно, Ру = Рх / MRS = 2/0,5=4.
Найдём доход индивида, используя бюджетное ограничение:
где I – доход,
Рх и Ру – цены двух рассматриваемых благ,
Х и Y – их количества.
Задача № 2. Расчёт общей и предельной полезности
Общая TU и предельная MU полезности товаров А, В, С представлены в таблице. Заполнить пропуски в таблице.
Решение:
Найдём общую полезность товара А.
Общая полезность N-й единицы товара = Предельная полезность N-й единицы товара + Общая полезность N-1-й единицы товара
TU(1)=MU(1)=20
TU(2)=MU(2) + TU(1)=15 + 20=35
TU(3)=MU(3) + TU(2)=12 + 35=47
TU(4)=MU(4) + TU(3)=8 + 47=55
TU(5)=MU(5) + TU(4)=6 + 55=61
Найдём предельную полезность товара В.
Предельная полезность N-й единицы товара=Общая полезность N-й единицы товара — Общая полезность N-1-й единицы товара
MU(1)=TU(1)=19
MU(2)= TU(2) — TU(1)=30 – 19 = 11
MU(3)= TU(3) — TU(2)=38 – 30 = 8
MU(4)= TU(4) — TU(3)=43 – 38=5
MU(5)= TU(5) — TU(4)=45 – 43=2
Найдём общую и предельную полезности товара С.
MU(1)=TU(1)=22
TU(2)=MU(2) + TU(1)=10 + 22=32
MU(3)= TU(3) — TU(2)=39 – 32=7
MU(4)= TU(4) — TU(3)=44 – 39=5
TU(5)=MU(5) + TU(4)=3 + 44=47
Заполним пропуски в таблице:
Задача № 3. Расчёт общей полезности
Предельная полезность первой единицы блага равна 420. При потреблении первых трёх единиц блага предельная полезность каждой последующей единицы уменьшается в 2 раза; предельная полезность каждой последующей единицы блага при дальнейшем потреблении падает в 4 раза. Найти общую полезность блага при условии, что его потребление составляет 8 единиц.
Решение:
Распишем условие задачи следующим образом:
MU(1) = 420,
MU(2) = 420/2=210,
MU(3) = 210/2=105,
MU(4) = 105/4=26,25,
MU(5) = 26,25/4=6,5625,
MU(6) = 6,5625/4=1,640625,
MU(7) = 1,640625/4=0,410156,
MU(8) = 0,410156/4=0,102539.
Найдём общую полезность блага при условии, что его потребление составляет 8 единиц.
TU(8) = MU(8) + TU(7) = MU(8) + MU(7) + TU(6) =…=
= MU(8) + MU(7) + MU(6) + MU(5) + MU(4) + MU(3) + MU(2) + MU(1) =
= 420 + 210 + 105 + 26,25 + 6,5625 + 1,640625 + 0,410156 + 0,102539 = 769,96582
Задача № 4. Расчёт оптимального объёма потребления двух благ
В таблице представлены следующие данные о предельной полезности двух благ.
| Количество, кг | Конфеты | Виноград |
|---|---|---|
| 1 | 60 | 150 |
| 2 | 40 | 120 |
| 3 | 20 | 90 |
Цена 1 кг конфет 80 ден. ед., а цена 1 кг винограда 160 ден. ед.
Бюджет потребителя составляет 400 ден. ед.
Определить оптимальный объём потребления конфет и винограда.
Решение:
Оптимальный объём потребления конфет и винограда достигается тогда, когда отношение предельных полезностей равно отношению цен этих благ.
Среди перечисленных вариантов таким свойством обладает комбинация 2 кг винограда (MUв=120) и 1 кг конфет (MUк=60).
Предельная полезность винограда, разделённая на предельную полезность конфет равна отношению их цен:
Проверим соответствие этой комбинации бюджетному ограничению:
80*1 + 160*2 = 400
Бюджет полностью израсходован.
Задача № 5. Расчёт цен товаров Х и Y
Потребитель покупает 4 единицы блага Х и 9 единиц блага Y, имея доход 100 ден. ед. Найти цены товаров X и Y, если известно, что предельная норма замены товара Y товаром X (MRSxy) равна 4.
Решение:
Предельную норму замены товара Y товаром X(MRSxy) можно определить как отношение цены товара Х к цене товара Y:
Запишем бюджетное ограничение:
100 = 4*Px + 9*Py,
где
Px, Py – цены благ Х и Y соответственно.
Составим и решим систему уравнений:
Задача № 6. Расчёт оптимального объёма потребления
У студента Иванова в холодильнике сыр и колбаса нарезаны для удобства кусочками по 100 г. Общая полезность их потребления представлена в таблице. Определите количество съеденного им в день, если известно, что он в целом употребляет 700 г названных продуктов и при этом добивается максимума полезности.
| Количество, г | Колбаса (общая польза) | Сыр (общая польза) |
| 100 | 2000 | 1900 |
| 200 | 3900 | 3750 |
| 300 | 5700 | 5550 |
| 400 | 7400 | 7300 |
| 500 | 8000 | 9000 |
| 600 | 9500 | 10650 |
Решение:
Рассчитаем предельную полезность от потребления этих двух продуктов.
Предельная полезность в дискретном случае определяется по формуле:
где
ΔTU – приращение общей полезности (TU1 – TU0),
ΔQ – приращение количества потребляемого блага (Q1 – Q0).
Вычисления занесём в таблицу.
| Количество, г | Колбаса (общая польза) | Сыр (общая польза) | Предельная полезность колбасы | Предельная полезность сыра |
| 100 | 2000 | 1900 | 2000 | 1900 |
| 200 | 3900 | 3750 | 1900 | 1850 |
| 300 | 5700 | 5550 | 1800 | 1800 |
| 400 | 7400 | 7300 | 1700 | 1750 |
| 500 | 9000 | 9000 | 1600 | 1700 |
| 600 | 10500 | 10650 | 1500 | 1650 |
Известно, что в целом студент употребляет 700 г колбасы и сыра, то есть всего 7 кусочков, и при этом добивается максимума полезности.
Решение об оптимальном объёме потребления можно представить в виде таблицы, где на каждом шаге будем сравнивать предельную полезность каждого кусочка колбасы и сыра и выбирать наибольшую величину предельной полезности, что в сумме даст их максимум.
Итак, на первом шаге наибольшая предельная полезность, равная 2000 будет получена от потребления 1 кусочка/100 грамм колбасы. Дальше студенту без разницы, что употребить, так как первый кусочек сыра и второй кусочек колбасы приносят одинаковую полезность – 1900. Пусть, например, это будет сначала сыр, а затем колбаса. Но вот на четвёртом шаге наибольшую полезность принесёт второй кусочек сыра. Предельная полезность, полученная от его потребления 1850 больше, чем 1800 – предельная полезность третьего куска колбасы или третьего кусочка сыра. На пятом шаге студенту опять всё равно, что съесть первым, третий кусочек сыра или третий кусочек колбасы, так как полезность от дополнительного потребления этих продуктов одинакова. И наконец, седьмым кусочком должен стать сыр, поскольку предельная полезность четвёртого кусочка сыра (1750), больше чем предельная полезность четвёртого кусочка колбасы (1700).
Общая полезность от потребления 3 кусочков колбасы и 4 кусочков сыра будет максимальной и составит:
TU = 2000 + 1900 + 1900 + 1850 + 1800 + 1800 + 1750 = 13 000
Таким образом, студент Иванов получит максимум полезности при употреблении 3 кусочков (300 грамм) колбасы и 4 кусочков (400 грамм) сыра.
Задача № 7. Расчёт отимального объёма потребления
Определите оптимальный для потребителя объем блага Q, если известно, что функция полезности индивида от обладания этим благом имеет вид:
1) U(Q)= 1 – 5 × Q2
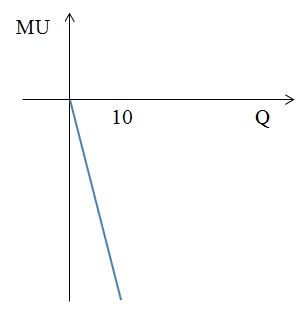
2) U(Q)= 5 + Q – Q2
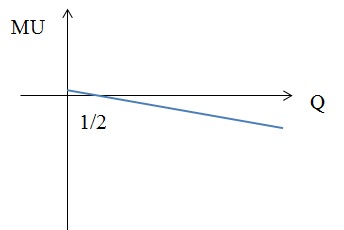
3) U(Q) = Q2 – 5 × Q3
Как будут выглядеть функции предельной полезности? Проиллюстрируйте ответ.
Решение:
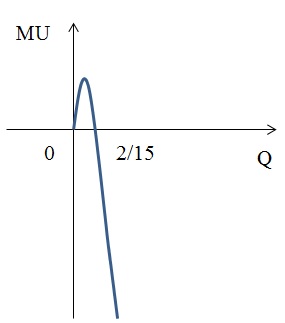
Оптимальный для потребителя объем блага Q будет определяться в точке, где потребитель получит максимум удовлетворения полезности. Задача сводится к нахождению экстремума функции полезности. Найдём производную функции полезности (предельную полезность MU) и приравняем её к нулю.
1) MU = –10 × Q = 0, следовательно, Q = 0;
2) MU = 1 – 2 × Q = 0, следовательно, Q = 1/2;
3) MU = 2 × Q – 15 × Q2 = 0, следовательно, Q = 0; Q = 2/15.
Задача № 8. Расчёт цен товаров X и Y
Индивид покупает 4 единицы блага X и 9 единиц блага Y, имея доход равный 100 денежным единицам. Найти цены товаров X и Y, если известно, что предельная норма замены X на Y равна 4.
Решение:
По условию задачи предельная норма замены благом Y блага X () равно 4. Это значит, что количество блага Х должно быть сокращено на 4 единицы в обмен на увеличение количества блага Y на единицу, при неизменном уровне удовлетворения потребителя.
Равновесие потребителя может быть представлено математически как:
— это предельная норма замещения, равная отношению цен благ Y и X. Данное условие оптимума потребителя следует понимать так. Соотношение, в котором потребитель при данных ценах способен замещать один товар другим, равно соотношению, в котором потребитель согласен замещать один товар другим, не изменяя уровень своего удовлетворения.
Отсюда
Далее воспользуемся формулой бюджетного ограничения:
где I – доход или бюджет потребителя.
100 = 4 × PX + 9 × PY
100 = 4 × PX + 9 × 4 × PX
100 = 40 × PX
PX = 2,5
PY = 4 × 2,5 = 10.
Ответ: PX = 2,5; PY = 10.
Задача № 9. Определение рационального выбора потребителя
Потребитель имеет функцию полезности:
и может на свой доход равный 100 единицам приобретать только эти два товара по ценам:
Px = 2
Py = 5
Определить рациональный выбор потребителя. Какой максимальный уровень полезности достижим?
Решение:
Рациональный выбор потребителя осуществляется в соответствии со вторым законом Госсена:
Предельная полезность товара х будет равна производной функции общей полезности по аргументу х:
Аналогично находим предельную полезность товара y:
Далее воспользуемся бюджетным ограничением:
Из условия задачи известно, что:
I = 100
Px = 2
Py = 5
Составим и решим систему уравнений:
При х = 25 и у = 10 общая полезность достигнет максимума:
Задача № 10. Расчёт оптимального объёма потребления
У Оксаны есть 30 рублей. Она хочет купить шоколадки «Шок» ценой 3 р. Полезность от этой покупки она оценивает функцией:
х – приобретённое количество шоколадок,
y – оставшаяся часть дохода.
Сколько купит шоколадок «Шок» рациональная Оксана?
Решение:
Рациональное поведение потребителя можно определить, как стремление максимизировать излишек потребителя. Потребитель будет покупать дополнительные единицы до тех пор, пока они приносят дополнительный избыток, т.е. пока цена, которую потребитель готов уплатить за единицу блага, превосходит реальную цену:
MU > P
Однако каждая последующая единица потребления обычно приносит уменьшающийся прирост полезности, т.е. при покупке благ «одно за другим» рано или поздно предельная полезность какого-то блага сравняется с его ценой:
MU = P
После того как предельная полезность сравняется с ценой, потребитель прекратит дальнейшие покупки: оптимальный объём потребления достигнут.
Найдём предельную полезность MU, как производную функции общей полезности по аргументу х:
Оптимальный объём потребления будет достигнут при МU = P:
Таким образом, рациональная Оксана купит 4 шоколадки, потратив на эту покупку 12 рублей.
Как найти предельную полезность
Любой товар представляет для покупателей определенную ценность, которая лежит в основе желания его приобрести. Свойство той или иной вещи удовлетворять потребительские нужды называется полезностью.

Инструкция
Полезность материального или нематериального блага, которое человек приобретает за деньги, является его способностью удовлетворять нужды покупателей. По мере того, как рынок насыщается, происходит и падение ценности вещей, т.е. свойство полезности имеет обыкновение снижаться в связи с уменьшением спроса.
Различают общую и предельную полезность. Если общая полезность – это совокупная величина всех реализованных единиц товара, то предельная является добавочной и равна отношению прироста общей полезности к дополнительному объему продукции:MV = ∆TV/∆Q.
Таким образом, чтобы найти предельную полезность, необходимо вычислить общую полезность дополнительных единиц товара и разделить на его количество. Эта величина постепенно снижается, в то время как общая растет. В определенный момент ее значение становится нулевым, что говорит о том, что достигнуто полное насыщение.
Если производитель не остановится и продолжит выпуск продукции, то предельная полезность станет отрицательной. Предприятие будет нести убытки, производя блага, которые никто не захочет покупать. Трудно предугадать потребительские вкусы, но можно спрогнозировать порог насыщения блага.
Есть еще один фактор, который влияет на величину предельной полезности помимо покупательского спроса. Это ограниченный запас определенных благ, в особенности тех, которые подразумевают использование редких природных ресурсов, невозможных к воспроизведению человеком. Например, алмазы. Предельная полезность дополнительной единицы этого товара гораздо выше, чем, скажем, у бутылки газированной воды, поскольку потребность в нем труднее удовлетворить. Отсюда вытекает принцип формирования рыночной цены, который основан не на общей полезности, а именно на предельной.
Видео по теме
Источники:
- найти общую полезность
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Предельная полезность помогает как экономистам, так и отдельным людям придать товарам количественную ценность. Предприятия используют предельную полезность для определения успешности продукта или услуги и корректировки производства по мере необходимости. Крупные корпорации используют сложные расчеты, но предельную полезность можно найти с помощью простой формулы. В этой статье мы обсудим, что такое предельная полезность и как ее рассчитать на примере.
Что такое предельная полезность?
Предельная полезность оценивает удовлетворенность клиентов, заказчиков и потребителей после получения большего количества единиц товара или услуги. Экономисты используют предельную полезность для оценки того, сколько товара или услуги хотят купить покупатели. Когда потребляется больше одной и той же единицы товара и общая полезность возрастает, возникает положительная предельная полезность. Когда происходит обратное, продукт получает отрицательную предельную полезность.
Третий распространенный тип предельной полезности известен как нулевая предельная полезность. Это происходит, когда наличие более чем одного предмета не приносит дальнейшего удовлетворения потребителю. Например, нулевая предельная полезность возникает, если потребитель покупает два одинаковых выпуска комикса, и второй экземпляр не дает никакой дополнительной ценности.
Откуда взялась идея предельной полезности?
В 19 веке экономисты собрались вместе, чтобы проанализировать концепцию цены. Преобладающей идеей было то, что цена влияет на полезность. Однако они столкнулись с парадоксом, когда заметили, что цены на некоторые товары не первой необходимости намного выше, чем на товары первой необходимости. Например, бриллианты имеют большую ценность, чем хлеб, несмотря на то, что хлеб имеет большую полезность. Это явление стало известно как парадокс стоимости, который позже был решен с помощью предельной полезности. Поскольку алмазы редки, потребители готовы платить больше, чтобы получить их, что делает их предельную полезность выше, чем у хлеба, который менее дефицитен.
Почему важна предельная полезность?
Общая удовлетворенность продуктом или услугой позволяет оценить будущие решения потребителей.
Например, производитель закусок создает новое сэндвич-печенье со вкусом, который никогда ранее не использовался. Сэндвич-печенье распространяется только на тестовых рынках. По прошествии некоторого времени в Интернете появляются отзывы о продукте, показывающие, что людям он нравится. Остатки продукта быстро уходят с полок, так как потребители покупают сразу несколько единиц товара. Это доказывает производителю, что положительная предельная полезность имеет место, и он может расширить свой рыночный ассортимент.
Закон убывающей предельной полезности
Благодаря своему успеху производитель заключает сделки с большим количеством поставщиков, что позволяет продавать товар по всей стране. Однако этот успех сглаживается законом убывающей предельной полезности. Этот закон, разработанный экономистами, гласит, что со временем предельная полезность уменьшается с каждой единицей, полученной потребителем. Если предположить, что все остальные переменные, связанные с продуктом, остаются неизменными, потребители в конечном итоге переходят от одного продукта к другому, подобно причуде.
Как рассчитать предельную полезность
Полезность можно рассматривать как ценность, которую клиент придает определенному товару или услуге. Проще говоря, его можно определить как то, сколько человек готов заплатить за товар.
Например, коллекционер произведений искусства замечает в социальных сетях, что работа одного из его любимых художников выставлена на аукцион. Инкассатор мчится на аукцион, готовый выписать чек. Хотя стартовая цена составляет $800, он сразу же делает ставку в $5 000, чтобы обеспечить себе приобретение этого предмета. Поскольку вещь доставляет ему большое удовлетворение, он придает ей большую ценность или стоимость.
В экономике стандартное правило гласит, что предельная полезность равна изменению общей полезности, деленному на изменение количества товара. Формула выглядит следующим образом:
Предельная полезность = разность общей полезности и количества товаров
-
Найдите общую полезность первого события.
-
Найдите общую полезность второго события.
-
Найдите разницу между обоими (или всеми) событиями.
-
Найти разницу между количеством товаров между обоими (или всеми) событиями.
-
Примените формулу.
1. Найдите общую полезность первого события
Нахождение предельной полезности предполагает сравнение двух или более событий для нахождения среднего значения. Если эти события связаны с оценкой цены покупки, сложите каждую цену вместе, чтобы найти общую полезность первого события.
2. Найдите общую полезность второго события
Рассмотрим информацию, полученную во время второго события. Определите количество измененных товаров, а также предложенную цену покупки. Сложите все покупки вместе, чтобы найти общую полезность второго события.
3. Найдите разницу между обоими (или всеми) событиями
Соберите итоговые суммы по обоим или всем событиям и найдите их разность. Полученный ответ становится общей разницей полезности для формулы.
4. Найдите разницу между количеством товаров между обоими (или всеми) событиями
Сложите все купленные товары с первого мероприятия и найдите общую сумму. Затем соберите вместе все купленные товары из второго (и всех последующих) событий. Вычтите итоговые значения друг из друга и найдите решение.
5. Примените формулу
Найдя обе конечные разницы, примените полученную информацию к формуле. Разделите обе разницы и установите их равными предельной полезности.
Пример расчета предельной полезности
Во время своего обеденного перерыва доктор. Авасарала направляется к ближайшей тележке, продающей тако. Каждое тако стоит всего $2, но Dr. Авасарала так голодна, что готова заплатить по $5 за каждую порцию. Несмотря на то, что тако стоят всего два доллара каждый, она оценивает полезность в $5.
Во время пребывания в грузовике она хочет съесть два тако. Зная, что после первого тако она будет почти сыта, она готова заплатить только $3 за второе тако, что снижает ее полезность. Чтобы найти общую полезность, она складывает оба итога вместе:
Общая полезность = 5 + 3
Общая полезность = 8
Dr. Авасарала кладет $8 общей полезности на два тако.
Во время отдельного посещения продуктового фургона, Др. Авасарала решает, что она готова съесть 5 тако. Заплатив $5 за первое тако, она решает, что второе тако стоит всего $4, потому что она наелась до отвала. После второго тако она заплатит по $1 за оставшиеся 3 тако. Чтобы найти общую полезность второго посещения, она складывает все покупки вместе:
Общая полезность = 5 + 4 + 1 + 1 + 1
Общая полезность = 12
Доктор. Авасарала оценивает общую полезность пяти тако в $12.
Чтобы найти предельную полезность, она находит разницу между обоими посещениями.
Разница в общей полезности = 12 — 8
Общая разница в полезности = 4
Далее, Dr. Авасарала вычитает количество тако из каждого посещения друг из друга:
Разница в количестве товаров = 5 — 2
Разница в количестве товаров = 3
Доктор. У Авасаралы есть разница в 3 тако.
Имея на руках эту информацию, Др. Авасарала применяет формулу:
Предельная полезность = 4 3
Предельная полезность = ~1.3 = 1.4
Доктор. Авасарала обнаруживает, что ее предельная полезность составляет около $1.40 на каждое тако.
Представители
количественной теории полезности (К.
Менгер, Е. Бем-Баверк, Г. Госсен и др.)
основывали свои рассуждения на
следующих предположениях (гипотезах):
—
при расходовании своего бюджета
потребитель стремится получить
максимум полезности (удовлетворения)
от приобретаемых благ;
—
потребитель способен произвести
количественную оценку полезности
благ;
—
последовательно потребляемые количества
какого-либо блага обладают убывающей
полезностью для потребителя.
Ученые
различали общую и предельную полезность
и измеряли ее в условных единицах —
утилях.
Общая
полезность TU
—
это удовлетворение, которое получает
потребитель от потребления определенного
количества благ. Эта зависимость
выражается функцией полезности
TU
= f(Qi).
Предельная
полезность MU—
это дополнительное удовлетворение,
получаемое от потребления еще одной
добавочной единицы потребленного
товара. Ее можно определить по двум
формулам:
1) MU(Qi)
=
2) как частную производную общей
полезности
MU(Qi)
= .
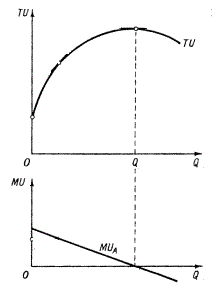
Графическое
изображение кривых общей и предельной
полезности дано на рис. 3.1. Геометрически
значение предельной полезности равно
тангенсу угла наклона касательной к
кривой TU.
Из рисунка видно, что когда функция
общей полезности достигает максимума,
то одновременно предельная полезность
товара становится нулевой.
Принцип
убывающей полезности (закон насыщения
потребности)
называют
первым законом Госсена — по имени
экономиста, впервые сформулировавшего
его. Он
содержит
два положения: первое констатирует
убывание последующих единиц блага в
одном непрерывном акте потребления,
так что в пределе достигается полное
насыщение этим благом; второе указывает
на убывание полезности первых единиц
блага при повторных актах потребления.
Рис.
3.1 — Зависимость между общей и предельной
полезностью
В
обычной жизни каждый потребитель
стремится повысить общую полезность
потребляемого блага. Принцип
максимизации
общей
полезности состоит
в следующем: каждый потребитель.
приобретая какой-то набор товаров,
должен распределить свой доход так,
чтобы полезность денежной единицы
(доллара, рубля и т. д.), израсходованной
на тот или иной товар, была одинаковой.
Второй закон Госсена — это закон
выравнивания предельных полезностей.
Условие
равновесия потребителя
выражается
формулой
,
где
λ — предельная полезность денег;
х,у,п
— виды приобретаемых товаров.
Последнюю
часть равенства можно записать как MUn
= Рпλ,
т.е.
предельная полезность блага равна
предельным затратам потребителя [10].
Пример
3.1
Потребитель
собирается приобрести на свой доход,
равный 10 денежным единицам, набор из
двух товаров: А
по цене 1 денежная единица за штуку
и В
по цене 2 денежных единицы за штуку.
Полезность товаров для потребителя в
утилях представлена в таблице.
Необходимо найти такую комбинацию
товаров, при которой предельная полезность
покупки окажется максимальной.
Расчет максимальной суммарной предельной полезности от покупки набора товаров
|
Единицы товара |
Предельная |
|||
|
Товар |
Товар |
|||
|
в |
в |
в |
в |
|
|
1-я |
20 |
20 |
48 |
24 |
|
2-я |
16 |
16 |
40 |
20 |
|
3-я |
14 |
14 |
36 |
18 |
|
4-я |
12 |
12 |
32 |
16 |
|
5-я |
10 |
10 |
24 |
12 |
|
6-я |
8 |
8 |
12 |
6 |
|
7-я |
6 |
6 |
8 |
4 |
Решение.
Прежде
всего следует купить 1 штуку товара В
за 2 денежных единицы, так как она
обеспечит наиболее возможную предельную
полезность первой покупки в расчете на
1 денежную единицу.
В
качестве второй покупки можно купить
товар А
либо товар В,
так как и тот и другой обеспечивают
одинаковую предельную полезность,
равную 20 утилям. Если мы купим товар А,
то третьей покупкой будет товар В.
Итак, на три единицы товара мы израсходовали
5 денежных единиц. Оставшиеся 5 денежных
единиц будут израсходованы в следующей
последовательности: 4-я штука — товар
В
дает 18 утилей; 5-я и 6-я штуки — товары А
и В,
так как у них одинаковая предельная
полезность. Итого
будет
приобретено
2 штуки товара А
и 4 штуки товара В.
Суммарная предельная полезность при
этом будет равна 192 утилям. Это
максимальная
величина полезности.
-
Порядковая
теория полезности
Авторы
порядкового направления (Ф. Эджуорт, Е.
Слуцкий, Дж.
Хикс)
предложили измерять субъективную
полезность с помощью
предпочтений.
При этом потребителю необходимо нишь
сделать
выбор между двумя наборами потребительских
благ.
Этот подход
базируется на следующих постулатах
[11]:
1)
предпочтения у потребителя уже сложились
и упорядочены;
2)
потребитель согласен отказаться от
небольшого количества блага у, если
ему предложат взамен большее количество
блага х;
3)
потребитель стремится иметь большее
количество любых товаров и услуг, если
он не пресыщен ни одним из них;
4)
удовлетворение потребителя зависит
только от количества потребляемых
им благ и не зависит от количества благ,
потребляемых другими.
Для
исследования равновесия потребителя
используются следующие понятия: кривая
безразличия, предельная норма замещения,
бюджетная линия.
Кривая
безразличия
U
—
это модель, представленная в виде кривой.
Каждая точка кривой представляет такой
набор из двух товаров, что потребителю
безразлично, какой из них выбрать.
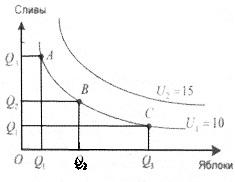
Чтобы построить кривую безразличия
(рис. 3.2), необходимо по оси абсцисс
отложить один вид товара, а по оси
ординат — другой. Точки А,
В,
С, лежащие на кривой, показывают наборы,
дающие одинаковую полезность (например,
10 утилей) для потребителя, и его выбор.
Все
множество кривых безразличия в
пространстве двух благ образует карту
безразличия. Кривые безразличия,
расположенные правее кривой U1,
показывают более высокий уровень
удовлетворенности потребителя.
Рис.
3.2 — Кривые безразличия
Кривые
безразличия для отдельного потребителя
обладают следующими свойствами:
1)кривые
безразличия, лежащие выше и правее
первой кривой, имеют большую полезность;
2)кривые
безразличия имеют отрицательный наклон;
3)они
выпуклы к началу координат;
4)они
никогда не пересекаются.
Основным
рабочим понятием порядковой теории
полезности является предельная
норма замещения
MRSху.
Она показывает то количество блага х,
которое потребитель желает получить в
обмен на единицу блага у,
с тем чтобы уровень удовлетворения
остался неизменным, и определяется по
формуле
MRSху
=
.
Предельная
норма замещения может принимать различные
значения: может быть равна нулю, быть
неизменной, меняться при движении вдоль
кривой безразличия. В случае выпуклости
к началу координат MRS
убывает,
т. е. потребитель соглашается отдавать
все меньшее количество замещаемого
блага за одно и то же количество
замещенного. Для двух взаимозаменяемых
товаров она является неизменной. В
случае двух взаимодополняемых товаров
кривая безразличия принимает вид двух
взаимно перпендикулярных отрезков.
Предельная
норма замещения, показывая возможности
замены
одного
блага другим, не позволяет в то же время
определить, какой именно набор товаров
потребитель считает наиболее выгодным.
Эту информацию дает бюджетная
линия
I.
Она представляет
собой
прямую линию с отрицательным наклоном,
графически
отображающую
множество наборов из двух товаров,
требующих одинаковых затрат на их
приобретение. Уравнение
бюджетной
линии имеет следующий вид:
I
= Рхх
+ Руу,
где
I
— доход потребителя;
Рх
— цена блага х;
Pу
—
цена блага у;
х,
у
—
соответственно количества приобретенных
благ.
Эту
формулу можно преобразовать в более
привычный вид
у
= а
— bх
или у
=,
где
угловой
коэффициент наклона прямой.
Точка
М
на оси ординат определяется делением
дохода на цену товара у
(рис. 3.3), если потребитель приобретает
только один товар — сливы. Точка N
определяется
делением дохода на цену товара х
при условии приобретения потребителем
тиара х
(яблок).
Следовательно,
бюджетная линия MN
характеризует
реальную покупательскую способность
и соотношение цен приобретаемых
товаров.
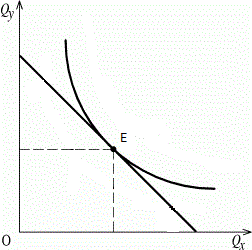
Точка
касания бюджетной линии с кривой
безразличия означает равновесие
потребителя
(см.
рис. 3.3). В точке равновесия Е
предельная норма замещения равна
соотношению цен товаров х
и у:
Рис.
3.3 — Равновесие потребителя
Изменение
соотношения цен на товары приводит к
изменению угла наклона бюджетной
линии.
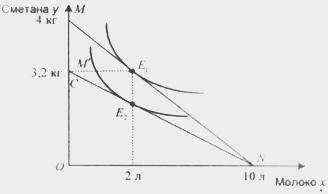
Пример
3.2
Доход
потребителя, расходуемый на два товара
(молоко и
сметану),
равен 80 руб. Цена 1 л молока равна 8 руб.,
цена 1 кг
сметаны
— 20 руб. Предположим, что в состоянии
равновесия потребитель приобретает 2
л молока и 3,2 кг сметаны.
Необходимо:
а)построить
бюджетную линию и определить угол ее
наклона;
б)построить
новую бюджетную линию и определить yгoл
ее
наклона после повышения цены сметаны
до 25 руб. за 1 кг
при
сохранении неизменной цены молока.
Решение.
1.Для
построения бюджетной линии MN
на
нижеприведенном рисунке определим
значения крайних точек бюджетной линии,
находящиеся на осях абсцисс и ординат.
Значение точки М
на
оси ординат наймем, используя уравнение
бюджетной линии:
Значение
точки N
на
оси абсцисс определим по аналогичным
формулам:
I
= Pxx;
y
=
=
=
10.
2.Выбираем
произвольно на бюджетной линии MN
точку
потребительского
равновесия и строим кривую безразличия.
Точка касания кривой безразличия и
бюджетной линии показывает
равновесный
набор, состоящий из двух товаров. Согласно
графику потребитель предпочитает набор
Е1,
в котором больше сметаны и меньше молока.
3.Определим
наклон бюджетной линии MN
двумя
способами. Первый способ позволяет
определить наклон бюджетной линии по
формуле
наклон
бюджетной линии =
=
=
= 0.4.
Второй
способ предполагает использование
соотношения цен товаров x
и у.
Наклон бюджетной линии определим по
формуле
наклон
бюджетной линии
=
=
=
0,4.
Крутизна
бюджетной линии в точке потребительского
равновесия показывает, от какого
количества единиц товара у
следует отказаться потребителю, чтобы
получить дополнительное количество
единиц товара х.
В нашем примере потребителю следует
отказаться от двух единиц товара у,
чтобы приобрести дополнительно пять
единиц товара х.
4.Повышение
цены сметаны с 20 руб. до 25 руб. приведет
к смещению точки М
вниз. Построим новую бюджетную линию
М’N
.
Значение точки М’
определим по формулам
Потребитель
после роста цены сможет купить только
3,2 кг сметаны. Новая бюджетная линия М‘N
станет
более пологой по сравнению с бюджетной
линией MN,
и
ее наклон будет равен
Новое
равновесие потребителя может находиться
на любой точке новой бюджетной линии
M‘N
в
зависимости от его предпочтений.
Предположим, что наш потребитель не
желает изменять количество потребляемого
молока. Тогда новая точка равновесия
установится в точке Е2.
Таким
образом, рост цены сметаны при неизменной
цене молока и неизменных предпочтениях
потребителя приводит его к выбору
набора, содержащего меньше сметаны и
столько же молока.
Используя
изменение соотношения цен, ученые
построили кривую «цена потребления».
Допустим, что цена яблок снижается
с Р]
до Р2,
а
доход является неизменным. Снижение
цены товара л- при неизменной цене товара
у
и неизменном доходе приводит к изменению
наклона бюджетной линии MN>
(рис.
3.4, а,
б).
Она становится длиннее и с меньшим углом
наклона MN’.
Для
каждой новой бюджетной линии можно
найти соответствующие кривые безразличия
U1,U2,
которые
будут соприкасаться с бюджетными линиями
в точках
Е1
и
Е2.
Соединив эти точки, получим кривую
цена-потребление
Gp.
Рис.
3.4 — Взаимосвязь кривой «цена-потребление»
(а)
и
кривой индивидуального спроса (б)
На
основе кривой «цена-потребление»
строится линия индивидуального
спроса на товар х.
Взаимодействие этих кривых показывает,
что наклон кривой спроса зависит от
предпочтений потребителя.
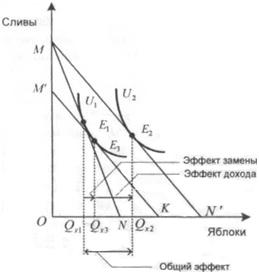
Изменение
цены какого-либо товара влияет на объем
спроса через эффект замены и эффект
дохода. Первым ученым, предложившим
разложить общий эффект от изменения
цен на эффект дохода и эффект замены,
является Е. Слуцкий, но более простым
для понимания является подход Дж. Хикса.
На
рис. 3.5 в точке Е2
показан набор товаров х,
у,
который выбрал потребитель в результате
снижения цены товара х.
Общий эффект выразился в увеличении
количества яблок с Qx1
до
Qx2,
(при абстрагировании от эффекта товара
у).
Этот эффект
раскладывается
на два эффекта: эффект замещения (Qx1
—
Qx3)
и
эффект
дохода (Qx3
—
Qx2).
Рис.
3.5 — Разложение общего эффекта
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
11.05.2015110.59 Кб2pr.doc
- #
- #
- #