Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
практикум математика часть 2.pdf
Скачиваний:
94
Добавлен:
15.02.2015
Размер:
3.83 Mб
Скачать
|
y |
D2 |
|||||
|
x) |
||||||
|
( |
||||||
|
2 |
||||||
|
y |
||||||
|
D1 |
y3(x) |
|||||
|
x) |
D3 |
|||||
|
y |
1( |
|||||
|
a |
b |
c |
d |
x |
|
b |
y2 ( x) |
||
|
∫∫= ∫∫+ ∫∫+ ∫∫= ∫dx |
∫ f (x, y)dy + |
||
|
D |
D1 D2 D3 |
a |
y1 ( x) |
|
c |
y2 ( x) |
d |
y3 ( x) |
|
∫dx |
∫ f (x, y)dy + ∫dx ∫ f (x, y)dy |
||
|
b |
y3 ( x) |
b |
y1 ( x) |
Рис. 3.2
Пусть область D построена в полярной системе координат. Напомним связь прямоугольных и полярных координат: x = rcosϕ , y = rsinϕ ,
|
r = x2 + y 2 , ϕ = arctg |
y |
, где r – полярный радиус, ϕ — полярный угол, |
|
|
x |
|||
|
0 ≤ ϕ ≤ 2π , 0 ≤ r ≤ ∞ . |
В двойном интеграле произойдёт замена переменных интегрирования x, y на новые переменные ϕ , r по известным формулам: x = rcosϕ , y = rsinϕ ,
при этом dxdy = rdrdϕ (доказательство не приводим).
В некоторых случаях такая замена переменных упрощает подынтегральную функцию, аналитическое выражение области интегрирования, что приводит к облегчению расстановки пределов и, самое главное, упрощает вычисление самого интеграла.
Правила вычисления двойного интеграла в полярной системе координат
1.Вычисление внутреннего интеграла.
• Внутренний интеграл однозначно берётся по переменной r, при этом область D, должна быть правильной (выпуклой), т.е. полярный радиус проведённый через любую внутреннюю точку области D пересекает её не более в двух точках. Если область D окажется неправильной, то с помощью дополнительных полярных радиусов разбить область D на правильные части
60
D1, D2, …, Dn , вычислить интеграл по этим частям и сложить согласно свойству 3.
• Пределами интегрирования внутреннего интеграла являются функции r(ϕ ). Нижний предел – функция r1(ϕ ) , график которой есть граница области D при вхождении в эту область возрастающего полярного радиуса (в частном случае это ноль, если точка (0; 0) входит в область D). Верхний предел – функция r2(ϕ ), график которой есть граница области D при выходе указанного полярного радиуса из области D.
•Нижний и верхний пределы интегрирования – функции – должны быть заданы одним аналитическим выражением (границы области D должны быть гладкими). Если это правило не соблюдается, разбить область D полярными радиусами на части D1, D2, …, Dn , удовлетворяющие этому правилу и произвести расчёт интеграла по свойству 3.
•Вычисление внутреннего интеграла произвести аналогично такому же пункту вычисления в прямоугольной системе координат.
2.Вычисление внешнего интеграла.
Это обычный определённый интеграл по переменной ϕ , пределы которого ϕ1 — нижний, ϕ2 — верхний есть полярные углы между которыми заключена область D.
На рис. 3.3. представлены варианты расчёта двойного интеграла в полярной системе координат согласно приведённым правилам.
|
y |
y |
||
|
r |
2( |
ϕ) |
|
D
|
ϕ2 |
r |
1( |
ϕ) |

x
|
D2 |
||
|
) |
||
|
ϕ |
r |
|
|
( |
||
|
1 |
D1 |
|
|
r |
||
ϕ4 ϕ3ϕ2

|
r |
3 |
( |
ϕ) |
||||
|
D3 |
|||||||
|
) |
|||||||
|
ϕ |
|||||||
|
r |
( |
||||||
|
) |
4 |
||||||
|
ϕ |
|||||||
|
(2 |
|||||||
x
61

∫∫ f (x, y)dxdy = ∫∫ f (r cosϕ, r sin ϕ)rdrdϕ =
D D
ϕ1 r1 (ϕ)
y
r2(ϕ
D1

ϕ2
|
ϕ3 |
r2 |
(ϕ) |
||||
|
∫∫= ∫∫+ ∫∫+ ∫∫= ∫dϕ |
∫F(r,ϕ)rdr + |
|||||
|
D |
D1 |
D2 |
D3 ϕ1 |
r1 (ϕ) |
||
|
ϕ4 |
r3 |
(ϕ) |
ϕ3 |
r3 |
(ϕ) |
|
|
+ ∫dϕ |
∫F(r,ϕ)rdr + ∫dϕ |
∫F (r,ϕ)rdr |
||||
|
ϕ3 |
r1 (ϕ) |
ϕ2 |
r4 (ϕ) |
∫∫= ∫∫+ ∫∫=
|
D D1 |
D2 |
||||
|
ϕ2 |
r1 |
( ϕ ) |
ϕ3 |
r2 |
( ϕ ) |
|
= ∫dϕ |
∫F( r,ϕ )rdr + ∫dϕ |
∫F( r,ϕ )rdr |
|||
|
ϕ1 |
0 |
ϕ2 |
0 |
Рис. 3.3
3.2..3. Некоторые приложения двойных интегралов
Эти приложения основаны на геометрическом и физическом смыслах двойного интеграла.
Двойной интеграл применяется для вычисления следующих величин.
1.Вычисление объёма V тела (см. геометрический смысл).
V = ∫∫ f (x, y)dxdy
D
2.Вычисление площади S плоской фигуры D.
S = ∫∫dxdy ; S = ∫∫rdrdϕ (полярная система).
DD
3.Вычисление массы m плоского тела (пластинки) с поверхностной
плотностью распределения массы f(x, y).
m = ∫∫ f (x, y)dxdy .
D
4.Вычисление координат (хс, ус) центра массы m плоского тела D.
|
xc = |
My |
= |
∫∫xf (x, y)dxdy |
; yc = |
Mx |
= |
∫∫yf (x, y)dxdy |
, |
|
|
D |
D |
||||||||
|
m |
m |
m |
m |
||||||
62
где Мх , Му – статические моменты пластинки относительно осей Ох и Оу.
5.Вычисление моментов инерции Ix, Iy, Io относительно осей Ох, Оу
иначала координат плоского тела D.
|
Ix = ∫∫y2 f (x, y)dxdy ; |
Iy = ∫∫x2 f (x, y)dxdy ; Io = Ix + Iy = ∫∫(x2 + y 2 ) f (x, y)dxdy . |
|
D |
D |
3.2.4. Типовые примеры решения двойных интегралов
Напомним, что для расчёта любых примеров и задач на двойные интегралы нужно обязательно построить область интегрирования D, а затем руководствоваться правилами расчёта.
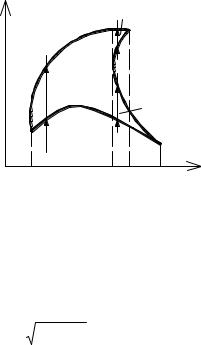
Пример1.Составить двукратный интеграл от функции f(x,y) по областиD, если f(x, y) задана в области D, ограниченной кривыми y2 = 2x ; x – y – 4 = 0.
|
y |
|||||||||
|
4 |
y2= 2x |
B(8,4) |
|||||||
|
3 |
D |
||||||||
|
2 |
|||||||||
|
1 |
x-y-4 = 0 |
||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
−2 |
A(2,-2) |
||||||||
|
Рис. 3.4 |
Решение. Область D (рис. 3.4) правильная в направлении переменной х, значит внутренний интеграл берётся по х, внешний по у. Стрелка возрастания
xпеременной х при вхождении в область D встречается на границе области D с кривой
|
х = |
у2 |
(нижний предел интегрирования |
|
|
2 |
|||
внутреннего интеграла) и при выходе из области D встречается с прямой х = =у + 4 (верхний предел).
Проектируем область D на ось Оу. Границы проекции есть числа -2 (нижний предел интегрирования внешнего интеграла), 4 (верхний предел).
Напомним, точки А и В пересечения кривых находятся в результате решения системы уравнений этих кривых.
63
|
4 |
y+4 |
|||||||||||||||||||||||||
|
Составляем интеграл: ∫∫ f (x, y)dxdy = ∫dy ∫ f (x, y)dx . |
||||||||||||||||||||||||||
|
D |
−2 |
y2 |
||||||||||||||||||||||||
|
2 |
||||||||||||||||||||||||||
|
Пример 2. |
В условиях примера 1 изменить порядок интегрирования. |
|||||||||||||||||||||||||
|
Решение. Область D (рис. 3.5) в направлении переменной у правильная, |
||||||||||||||||||||||||||
|
но нарушено правило задания нижнего предела интегрирования внутреннего |
||||||||||||||||||||||||||
|
интеграла одним аналитическим выражением (в точке A излом). Разбиваем |
||||||||||||||||||||||||||
|
y |
область D на две части D1 и D2 составляем |
|||||||||||||||||||||||||
|
4 |
B(8,4) |
сумму |
двух |
интегралов |
по |
известному |
||||||||||||||||||||
|
x |
||||||||||||||||||||||||||
|
3 |
2 |
правилу: |
||||||||||||||||||||||||
|
y= |
D2 |
-4 |
||||||||||||||||||||||||
|
2 |
f (x, y)dxdy + |
f (x, y)dxdy = |
||||||||||||||||||||||||
|
x |
∫∫ |
f ( x, y )dxdy = |
∫∫ |
∫∫ |
||||||||||||||||||||||
|
1 |
D1 |
= |
||||||||||||||||||||||||
|
y |
||||||||||||||||||||||||||
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
x |
D |
D1 |
D2 |
|||||||||||||||
|
1 |
2 |
2 x |
8 |
2 x |
||||||||||||||||||||||
|
y = — 2x |
A(2,-2) |
∫dx |
∫ |
f (x, y)dy + ∫dx ∫ f (x, y)dxdy. |
||||||||||||||||||||||
|
0 |
− |
2 x |
2 |
x−4 |
||||||||||||||||||||||
|
Рис. 3.5 |
||||||||||||||||||||||||||
|
y |
Пример |
3. |
Изменить |
порядок |
||||||||||||||||||||||
|
интегрирования |
||||||||||||||||||||||||||
|
1 |
D3 |
1 |
e y +2 |
|||||||||||||||||||||||
|
0.5 |
3 |
y |
D2 |
y 2 |
∫ |
dy |
∫ |
f (x, y)dx. |
||||||||||||||||||
|
+ |
||||||||||||||||||||||||||
|
x |
= |
e |
0 |
3 y |
||||||||||||||||||||||
|
= |
||||||||||||||||||||||||||
|
D1 |
||||||||||||||||||||||||||
|
x |
e+2 |
x |
||||||||||||||||||||||||
|
1 |
2 |
3 |
4 |
|||||||||||||||||||||||
|
Рис. 3.6 |
Решение. По условиям примера |
|||||||||||||||||||||||||
|
строим область D (рис. 3.6), разбиваем её на 3 части D1, D2, D3 и составляем |
интеграл:
|
1 |
e y +2 |
1 |
x3 |
3 |
1 |
e+2 |
1 |
||
|
∫dy |
∫ |
f (x, y)dx = ∫dx ∫ f (x, y)dy + ∫dx∫ f (x, y)dy + ∫ |
dx |
∫ f (x, y)dy . |
|||||
|
0 |
3 y |
0 |
0 |
1 |
0 |
3 |
ln( x−2) |
Пример 4. Вычислить∫∫x2 ydxdy ,D: x2 + y2 = 4x , x = 0 , x = 4 , y = 3 , y≥0
D
64
|
Решение. Область D (рис. 3.7) правильная в |
||||||||||||||||||||||||||||||||||||
|
y |
y = 3 |
направлении у. |
||||||||||||||||||||||||||||||||||
|
3 |
3 |
|||||||||||||||||||||||||||||||||||
|
D |
4 |
3 |
4 |
y |
2 |
|||||||||||||||||||||||||||||||
|
2 |
4 |
∫∫x2 ydxdy = ∫dx |
∫ |
x2 ydy = ∫dxx2 |
= |
|||||||||||||||||||||||||||||||
|
y |
= 4x-x |
2 |
x = |
D |
0 |
4 x−x2 |
0 |
2 |
4 x−x2 |
|||||||||||||||||||||||||||
|
1 |
4 |
9 − 4x − x |
2 |
4 |
9x |
2 |
− 4x |
3 |
+ x |
4 |
||||||||||||||||||||||||||
|
= |
dx = |
|||||||||||||||||||||||||||||||||||
|
∫ |
x2 |
dx = |
∫ |
|||||||||||||||||||||||||||||||||
|
2 |
2 |
2 |
||||||||||||||||||||||||||||||||||
|
1 |
2 |
3 |
4 |
x |
0 |
0 |
||||||||||||||||||||||||||||||
|
1 |
x3 |
x4 |
x5 |
4 |
1 |
1024 |
||||||||||||||||||||||||||||||
|
− 4 |
+ |
64 |
− 256 + |
|||||||||||||||||||||||||||||||||
|
9 |
= |
3 |
= 70,4. |
|||||||||||||||||||||||||||||||||
|
Рис. 3.7 |
2 |
3 |
4 |
5 |
2 |
5 |
||||||||||||||||||||||||||||||
|
0 |
||||||||||||||||||||||||||||||||||||
|
y |
||||||||||||||||||||||||||||||||||||
|
3 |
Пример 5. Вычислить площадь фигуры, |
|||||||||||||||||||||||||||||||||||
|
y = 2 |
||||||||||||||||||||||||||||||||||||
|
2 |
ограниченной линиями y = −2, |
|||||||||||||||||||||||||||||||||||
|
y = x + 2, |
||||||||||||||||||||||||||||||||||||
|
x+2 |
2 |
x |
||||||||||||||||||||||||||||||||||
|
1 |
= |
|||||||||||||||||||||||||||||||||||
|
= |
D |
y |
y = 2, y 2 |
= x. |
||||||||||||||||||||||||||||||||
|
y |
||||||||||||||||||||||||||||||||||||
|
−4 |
−3 |
−2 |
−1 |
1 |
2 |
3 |
4 |
x |
Решение. |
Область |
D |
(рис.3.8) |
||||||||||||||||||||||||
|
−1 |
||||||||||||||||||||||||||||||||||||
|
−2 |
y = -2 |
правильная в направлении x. |
||||||||||||||||||||||||||||||||||
|
Рис. 3.8 |
2 |
y2 |
2 |
y2 |
||||||||||||||||||||||||||||||||
|
S = ∫∫dxdy = ∫dy ∫dx = ∫dy x |
= |
|||||||||||||||||||||||||||||||||||
|
D |
−2 |
y−2 |
−2 |
y−2 |
||||||||||||||||||||||||||||||||
|
= |
2 |
3 |
y |
2 |
2 |
= 8 − 4 + 2 2 + 8 + 2 + 4 = 40 кв.ед. |
||||||||||||||||||||||||||||||
|
∫ |
(y2 − y + 2)dy = y |
− |
+ 2 y |
|||||||||||||||||||||||||||||||||
|
3 |
2 |
3 2 |
3 |
3 |
||||||||||||||||||||||||||||||||
|
−2 |
−2 |
|||||||||||||||||||||||||||||||||||
|
Пример |
6. |
Вычислить |
площадь |
фигуры, |
ограниченной |
кривой |
||||||||||||||||||||||||||||||
|
(x2 + y2 )3 = a2 x2 y2 , a > 0. |
||||||||||||||||||||||||||||||||||||
|
S1 |
Решение. |
Переходим |
к |
полярным |
||||||||||||||||||||||||||||||||
|
координатам: |
x = r cosϕ, y = r sin ϕ. |
|||||||||||||||||||||||||||||||||||
|
Тогда: (r 2 cos2 ϕ + r 2 sin 2 ϕ)3 = a2 r 2 cos2 ϕ r 2 sin 2 ϕ, |
||||||||||||||||||||||||||||||||||||
|
r 6 |
= a2 r 4 cos2 ϕ sin 2 ϕ, |
|||||||||||||||||||||||||||||||||||
|
Рис. 3.9 |
r 2 |
= 1 a2 sin 2 |
2ϕ, r = a |
sin 2ϕ . |
||||||||||||||||||||||||||||||||
|
4 |
2 |
|||||||||||||||||||||||||||||||||||
|
Строим область D (рис. 3.9) в координатах r, φ и вычисляем двойной |
интеграл согласно правил его расчета в полярных координатах.
65
|
π 2 |
a |
sin 2ϕ |
π 2 |
r 2 |
a |
sin 2ϕ |
||||||||||||||||||||||||
|
S = 4S1 = 4∫∫rdrdϕ = 4 ∫dϕ |
2 ∫rdr =4 ∫dϕ |
2 |
= |
|||||||||||||||||||||||||||
|
D |
0 |
0 |
0 |
2 |
0 |
|||||||||||||||||||||||||
|
π 2 |
a2 |
2 |
a2 |
π 2 |
1 − cos 4ϕ |
a2 |
1 |
π 2 |
1 |
2 |
||||||||||||||||||||
|
= 2 ∫ |
sin |
2ϕdϕ = |
∫ |
dϕ = |
ϕ − |
sin 4ϕ |
= |
πa |
. |
|||||||||||||||||||||
|
4 |
2 |
2 |
4 |
4 |
8 |
|||||||||||||||||||||||||
|
0 |
0 |
0 |
3.2.5.Задания на контрольную работу
Задание 1. Изменить порядок интегрирования.
|
3 |
25−x2 |
|||
|
1а. ∫dx |
∫ f (x, y)dy . |
|||
|
0 |
0 |
|||
|
2а. ∫1 dx ∫x f (x, y)dy . |
||||
|
0 |
x 3 |
|||
|
3а. ∫4 dx ∫x f (x, y)dy . |
||||
|
1 |
0 |
|||
|
4 |
25−x2 |
|||
|
4а. ∫dx ∫ f (x, y)dy . |
||||
|
0 |
3 |
x |
||
|
4 |
||||
|
1 |
1−y2 |
|||
|
5а. ∫dy ∫ f (x, y)dx . |
||||
|
−2 |
y−1 |
|||
|
2 |
4−x2 |
|||
|
6а. ∫ dx ∫ f (x, y)dy . |
||||
|
− 2 |
x2 |
|||
|
1 |
y−1 |
|||
|
7а. ∫dy |
∫ f (x, y)dx . |
|||
|
0 |
− 1−y2 |
|||
|
0 |
−x2 |
|||
|
8а. ∫dx |
∫ f (x, y)dy . |
|||
|
−1 |
x2 −2 |
|||
|
1 |
2−x2 |
|||
|
9а. ∫dx |
∫ f (x, y)dy . |
|||
|
0 |
x2 |
|
π 4 |
sin x |
π 2 |
cos x |
||||||||||
|
1б.. ∫ dx |
∫ |
f (x, y)dy + |
∫ |
dx ∫ |
f (x, y)dy |
||||||||
|
0 |
0 |
π 4 |
0 |
||||||||||
|
− |
3 |
4 |
−x2 |
0 |
2− |
4−x2 |
|||||||
|
2б. ∫ |
dx |
∫ f (x, y)dy + ∫ dx |
∫ f (x, y)dy . |
||||||||||
|
−2 |
0 |
− |
3 |
0 |
|||||||||
|
3б. ∫1 dx ∫1 |
f (x, y)dy + ∫e dx ∫1 |
f (x, y)dy . |
|||||||||||
|
0 |
1−x2 |
1 |
ln x |
||||||||||
|
4б. −∫1dx ∫0 |
f (x, y)dy + ∫0 dx ∫0 |
f (x, y)dy . |
|||||||||||
|
−2 |
−2−x |
−1 |
3 |
x |
|||||||||
|
y |
|||||||||||||
|
5б. ∫1 dy ∫ f (x, y)dx + ∫e dy ∫1 |
f (x, y)dx . |
||||||||||||
|
0 |
0 |
1 |
ln y |
||||||||||
|
6б. ∫3 dx ∫0 |
f (x, y)dy + ∫2 dx ∫0 |
f (x, y)dy . |
|||||||||||
|
0 |
4−x2 −2 |
3 |
− 4−x2 |
||||||||||
|
2+y |
− y |
||||||||||||
|
7б. −∫1dy ∫ f (x, y)dx + ∫0 dy ∫ f (x, y)dx . |
|||||||||||||
|
−2 |
0 |
−1 |
0 |
||||||||||
|
1 |
2 arcsin y |
1 |
arccos y |
||||||||||
|
8б. ∫ dy ∫ f (x, y)dx + ∫ dy ∫ f (x, y)dx. |
|||||||||||||
|
0 |
0 |
1 |
2 |
0 |
|||||||||
|
3 |
2− 4−x2 |
2 |
4−x2 |
||||||||||
|
9б. ∫dx |
∫ |
f (x, y)dy + ∫dx |
∫ f (x, y)dy . |
||||||||||
|
0 |
0 |
3 |
0 |
66
|
10а. ∫4 dx ∫2 f (x, y)dy . |
10б. ∫1 |
3 |
|
|
dxx∫ f (x, y)dy + ∫2 dx2∫−x f (x, y)dy . |
|||
|
0 4 x−x2 |
0 |
0 |
1 0 |
|
Задание 2. Вычислить. |
|||
|
1. ∫∫(8xy +9x2 y2 )dxdy; D : x =1, y = 3 |
x, y = −x3 . |
||
|
D |
|||
|
∫∫12 y sin 2xydxdy; D : y = π 4, y = π 2, x = 2, x = 3. |
|||
|
D |
|||
|
2. ∫∫(12xy + 27x2 y2 )dxdy; D : x =1, y = x2 , y = −3 x |
(x ≥ 0). |
||
|
D |
∫∫ye−xy
D
|
4 |
9 |
2 |
2 |
3 |
||||||||
|
3. ∫∫ |
xy + |
x |
y |
dxdy; D : x =1, y = x |
, y = − x. |
|||||||
|
5 |
11 |
|||||||||||
|
D |
∫∫y cos xydxdy; D : x = 0, x = 2, y =π, y = 5π.
D
|
4. |
∫∫(24xy − 48x3 y3 )dxdy; D : x =1, y = x2 , y = − x. |
|
D |
|
|
∫∫4 y sin 2xydxdy; D : x = 0, x =1, y = 2π, y = 3π. |
|
|
D |
|
|
5. |
∫∫(4xy +16x3 y3 )dxdy; D : x =1, y = 3 x, y = −x3 . |
|
D |
|
|
∫∫3y cos xydxdy; D : x = 0, x = 0,5, y =π, y = 2π. |
|
|
D |
|
|
6. |
∫∫(44xy +16x3 y3 )dxdy; D : x =1, y = x2 , y = −3 x. |
|
D |
∫∫ye−xy
D
|
7. |
∫∫(xy − 4x3 y3 )dxdy; D : x =1, y = x3 , y = − |
x. |
||||||||||||
|
D |
||||||||||||||
|
∫∫y cos 2xydxdy; D : x = 0, x =1, y = |
π |
, y = 2π. |
||||||||||||
|
D |
2 |
|||||||||||||
|
8. |
2 |
2 |
25 |
4 |
4 |
2 |
||||||||
|
∫∫ 6x |
y |
+ |
x |
y |
dxdy; D : x =1, y = x |
, y = − x. |
||||||||
|
3 |
||||||||||||||
|
D |
67
|
∫∫3ysin |
xy |
dxdy; D : x = 0, x =1y = |
4π |
, y = |
2π |
. |
|||||
|
3 |
3 |
||||||||||
|
D |
2 |
||||||||||
|
50 |
|||||||||||
|
9. ∫∫ |
3x2 y2 + |
x4 y4 |
dxdy; D : x =1, y = 3 x, y |
= −x3 . |
|||||||
|
3 |
|||||||||||
|
D |
∫∫ye−xy
D
10. ∫∫(54x2 y2 +150x4 y4 )dxdy; D : x =1, y = x2 , y = −3 x (x ≥ 0).
D
∫∫y cos xydxdy; D : x = 0, x =1, y =π, y = 2π.
D
Задание 3. Найти площадь фигуры,
1. y = 24 − x2 , 2 3y = x2 , x ≥ 0.
3 y = 


5. y = 2
7. y = 3

ограниченной линиями.
|
2. |
y = 20 − x2 , y = −8x. |
|
4. |
y = 32 − x2 , y = −4x. |
|
6. |
x2 + y 2 = 36, 3 2 y = x2 (y ≥ 0). |
|
8. |
y = 6 − 36 − x2 , y = 36 − x2 , x ≥ 0. |
10. y = x, y = 1x , x =16.
Задание 4. Вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах (a > 0).
|
1. |
x6 |
= a2 (x4 − y4 ). |
2. |
(x2 + y2 )2 = ax3 . |
|
3. |
x4 |
= a2 (x2 −3y2 ). |
4. |
x4 = a2 (x2 − y2 ). |
|
5. |
y6 = a2 (y4 − x4 ). |
6. |
(x2 |
+ y 2 )2 = a2 (x2 + 4 y 2 ). |
|
7. |
(x2 + y 2 )2 = a2 (2x2 + 3y2 ). |
8. |
(x2 |
+ y 2 )3 = a2 x4 . |
|
9. |
y6 |
= a2 (3y2 − x2 ) (y2 + x2 ). |
10. (x2 + y 2 )2 = a2 (3x2 + y 2 ). |
68
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Алгоритм вычисления двойных интегралов при переходе к полярным координатам детально приведен как в настоящей статье, так и предыдущих публикациях с теорией. Для перехода к полярным координатам нужно найти якобиан, который несколько раз здесь повторим. Дальше сами уравнения кривых, которые ограничивают область интегрирования следует также перевести в полярные координаты. В теории все хорошо описано и выглядит понятным, однако на практике во многих студентов возникают трудности и немало вопросов, поэтому внимательно пересмотрите приведенные дальше решения.
Пример 2.1 Вычислить двойной интеграл, используя полярные координаты:
Решение: Построим область интегрирования ограниченную кривыми
-3≤x≤3
Эти кривые записываем из пределов интегрирования, внимательно пересмотрите в каких пределах изменяются «икс» и «игрек».
Нижний предел по оси «игреков» приведем к каноническому виду
x2+y2=9.
Получили уравнение круга с центром в точке O(0;0) и радиусом 3 (нижняя половина).
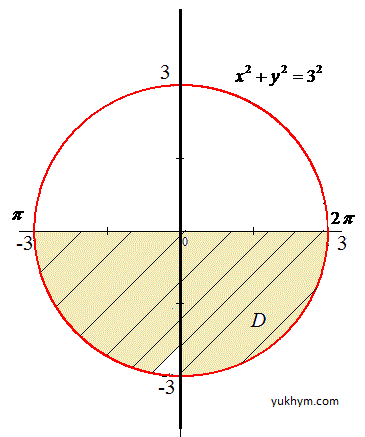
Перейдем к полярной системе координат с помощью превращения координат:
найдем якобиан перехода:
Найдем подынтегральную функцию в полярных координатах:
Внимательно пересмотрите формулы двойного синуса, косинуса и им подобных.
Они достаточно часто встречаются при упрощении подынтегральных функций, все сделано умышленно для того, чтобы Вы без проблем могли интегрировать.
Запишем пределы интегрирования в полярной системе координат:
0≤r≤3, π≤φ≤2 π.
Вычислим двойной интеграл:
Поскольку переменные разделены, то интегрирование не тяжелое, достаточно воспользоваться табличными интегралами и подставить пределы.
Пример 2.2 Найти двойной интеграл, используя полярные координаты:
Решение: Из интеграла выписываем область интегрирования
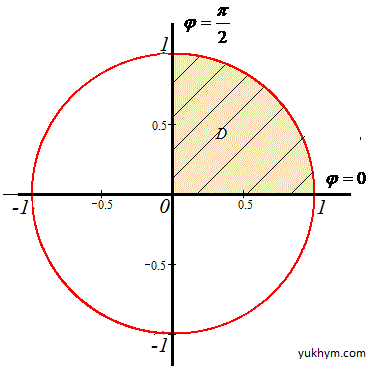
0≤x≤1
Она ограничена прямыми, которые совпадают с-осями координат
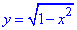
Получили круг с центром в точке O(0;0) и радиусом r=1 (верхняя половина).
Якобиан перехода к ПСК I=r.
Запишем подынтегральную функцию в полярной системе координат:
Для круговых областей не трудно записать пределы интегрирования при переходе к полярной системе координат:
0≤r≤1, 0≤φ≤π/2.
Находим двойной интеграл:
В результате интегрирования в ответе получили выражение которое содержит логарифм двойки, и число Пи.
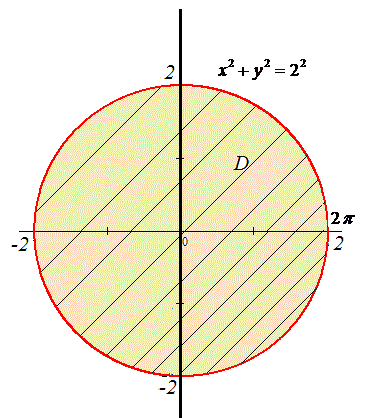
Пример 2.3 Вычислить значение двойного интеграла, перейдя к полярным координатам:
Решение: Выпишем область интегрирования, которая ограничена кривыми
— 2≤x≤2,
По «игреку» имеем ограничения ветками круга 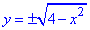
Перейдем к полярной системе координат:
якобиан переходу: I=r.
С учетом формул перехода подынтегральная функция в полярной системе координат примет вид корневой зависимости:
Пределы интегрирования в ПСК следующие:
0≤r≤2, 0≤φ≤2π.
Переходим от двойного интеграла в декартовых координатах к двойному в полярных координатах и находим его значение:
Интеграл равен 16π/3.
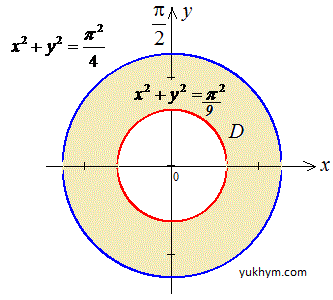
Пример 2.4 Найти двойной интеграл, используя полярные координаты:
D: {x2+y2=π2/9; x2+y2=π2/4}.
Решение: Выпишем область интегрирования ограниченную кривыми
Первая кривая x2+y2=π2/9 — круг с центром в начале координат O(0;0) и радиусом π/3;
второе уравнение описывает x2+y2=π2/4 — больший круг с центром в той же точке O(0;0) и радиусом π/2.
Область между кругами образует кольцо, по которому выполняем интегрирование.
Найдем подынтегральную функцию в полярной СК:
Круги в полярной системе координат можно задать радиусами и центрами:
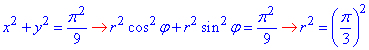
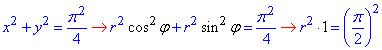
Пределы интегрирования в полярной системе координат следующие:
π/3≤r≤π/2, 0≤φ≤2π.
Выполняем вычисление двойного интеграла:
Переход к полярной СК значительно упрощает вычисление интегралов для круговых и кольцевых областей.
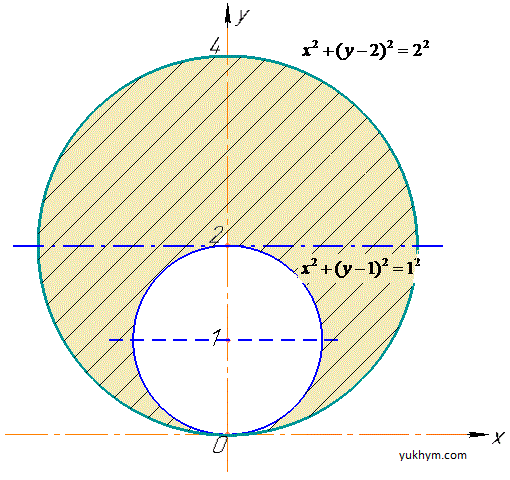
Пример 2.5 Найти двойной интеграл, используя полярные координаты:
D: {x2+y2— 2y=0; x2+y2— 4y=0}.
Решение: На основе предыдущих примеров делаем вывод, что область интегрирования, ограниченная x2+(y-1)2=1 — кругом с центром в точке O(0;1) и радиусом 1;
Вторая кривая x2+(y-2)2=2— круг с центром в точке O(0;2) и радиусом 2.
Графически они формируют следующую область интегрирования.
Переходим к полярной системе координат с помощью якобиана перехода I=r.
Дальше записываем кривые в полярной системе координат:
расставляем корректные пределы интегрирования:
2sin(φ)≤r≤4sin(φ), 0≤φ≤2π.
Вычисляем двойной интеграл в полярной СК:
Нахождение двойных интегралов не тяжелое занятие, если часто самостоятельно практиковать и иметь перед собой таблицу основных интегралов.
Все остальные манипуляции не тяжелые и их Вы повсюду в математике выполняете.
Дальше рассмотрим еще несколько примеров на вычисление двойных интегралов в полярных координатах.
-
Теоретический минимум
Двойной интеграл представляет собой обобщение определённого интеграла на случай функций двух переменных. Строится он совершенно
аналогично определённому интегралу. Сравним процедуры построения интегралов обоих типов. Подчеркнём, что излагается лишь общая идея
построения интегралов, не претендующая на строгость формулировок.Определённый интеграл
Интеграл функции, вычисляемый по отрезку
. Отрезок разбивается на малые необязательно равные частичные отрезки
длиной, внутри каждого такого отрезка выбирается точка
, и составляется интегральная сумма
.
Затем осуществляется переход к пределу разбиения отрезка на бесконечно малые частичные отрезки, а именно требуют, чтобы длина самого
большого частичного отрезка стремилась к нулю. Величина предела и является интегралом.
Двойной интеграл
Интеграл функции, вычисляемый по двумерной области
. Область разбивается на малые части. Эти малые части
характеризуются их площадямии длинами
наибольшего отрезка, который можно провести внутри частичной области. Этот
отрезок называется диаметром частичной области. В каждой частичной области выбирается точка, и составляется интегральная сумма
. Затем осуществляется переход к пределу разбиения области
на бесконечно малые частичные области,
а именно требуют, чтобы длина самого большого диаметра частичной области стремилась к нулю. Величина предела и является интегралом
.
Вычисление двойного интеграла сводится к вычислению двух определённых интегралов. Не станем формулировать общие теоремы, а сразу покажем
конкретные примеры расчётов, так как они по сути дублируют содержание общих теорем в их конструктивной части.Примеры вычисления двойных интегралов сведением к повторному интегрированию
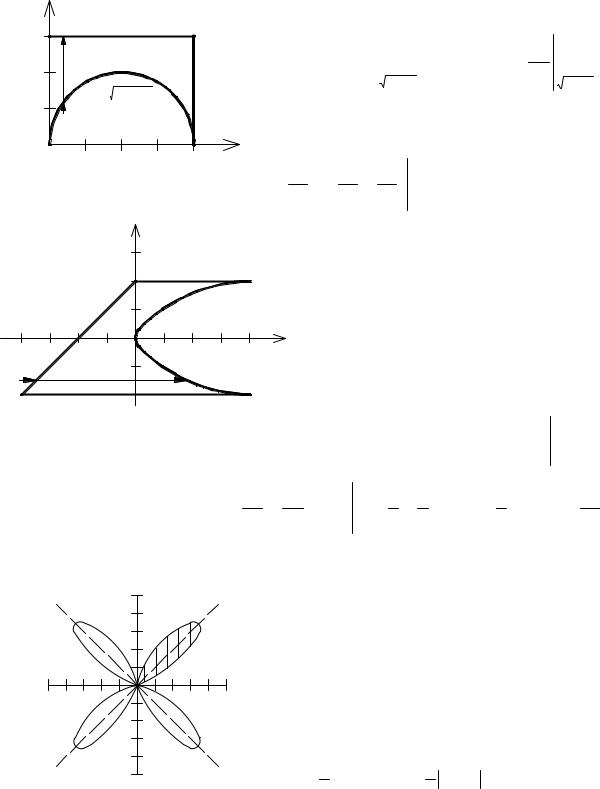
Пример 1. Прямоугольная область интегрирования.
Вычислить интегралпо области
.
Это самый простой пример, однако он же и основополагающий с точки зрения теории, как станет ясно потом. Фактически здесь нужно сначала
вычислить интеграл по одной из переменных, например, по переменной, считая вторую переменную константой (есть некоторая
аналогия с вычислением частных производных). Затем выполняется и второе интегрирование.
.
После вычисления зададимся вопросом: имел ли значение порядок интегрирования? Ответ: если оба повторных интеграла существуют, то порядок
интегрирования не важен, и его следует выбирать таким, чтобы вычисление проводилось по возможности удобнее.Пример 2. Область интегрирования не является прямоугольной.
Вычислить интегралпо области, ограниченной параболой
и прямой
.
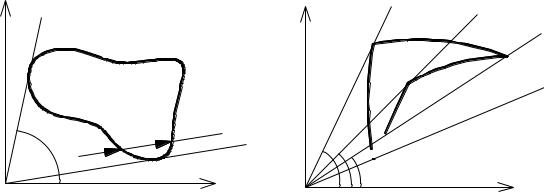
Сделав чертёж (см. рис. 1), оценим, в каком порядке легче интегрировать. Прежде всего, поясним, что мы планируем придерживаться прежнего плана
действий: сначала проинтегрировать по одной переменной, считая вторую постоянной, а затем проинтегрировать по второй переменной. И тут возникает
вопрос о расстановке пределов интегрирования. При интегрировании по прямоугольнику такого вопроса не было. Обратимся к построению двойного интеграла.
Основным элементом этого построения является разбиение на малые (в пределе бесконечно малые) части области интегрирования. Мы умеем выполнять
интегрирование по прямоугольнику. Разобьём область интегрирования на малые прямоугольники. Если они будут бесконечно малыми, то они покроют область
с криволинейной границей полностью. Двойной интеграл обладает свойством аддитивности. Если область интегрирования разбить на две части, то интеграл
будет равен сумме интегралов по полученным областям. Это верно для любого числа областей. Теперь посмотрим на такое разбиение с геометрической точки
зрения. Если мы фиксируем, например, переменную, считая её постоянной, то мы выделяем набор прямоугольников, выстроенных по прямой, параллельной
оси абсцисс (см. рис. 2). Тогда понятно в каких пределах следует интегрировать по переменнойпри данном значении
. Но при другом
значениипределы интегрирования по переменной
будут уже другими. Это значит, что эти пределы интегрирования являются функциями
.
Т.е. интегрирование можно выполнять по формуле Ньютона-Лейбница, но пределы интегрирования будут переменными. Второе интегрирование выполняется
уже стандартно, пределы определяются всеми возможными значениями, исходя из области интегрирования.
Применим эти рассуждения к нашему конкретному примеру. Допустим, мы хотим, чтобы внутреннее интегрирование было по переменной
. Это значит,
что во внутреннем интегрировании переменнаяиграет роль константы. Постоянным значениям
соответствуют горизонтальные прямые (теперь уже,
конечно, нет рядов прямогольников). Проведём несколько таких прямых (см. рис. 3). Видно, что где бы ни была проведена прямая, она всегда «входит» в кривую
, а «выходит» из прямой
. Вот так мы и расставим пределы интегрирования во внутреннем интеграле.
Осталось лишь определить, в каких пределах изменяется. Для этого нужно решить уравнение
.
Расставляем пределы интегрирования и вычисляем интеграл:
.
Ничто не мешало вычислять интеграл в другом порядке. Расставьте пределы интегрирования для этого случая самостоятельно и покажите прямым
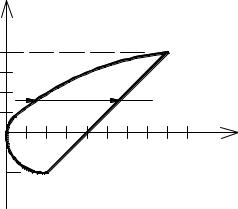
вычислением, что ответ получается такой же.Пример 3. Разбиение области интегрирования на части.
Вычислить интегралпо области, ограниченной параболой
и прямыми
,
.
С целью определения пределов интегрирования снова будем проводить прямые, пересекающие область интегрирования. Только прямые
на этот раз будут вертикальными, а следовательно, внутреннее интегрирование будет по переменной. Выбран именно этот порядок
интегрирования, так как из уравнения параболы неудобно выражать. На чертеже (см. рис. 4) показаны четыре из возможных вертикальных
прямых. Как видно, все они «выходят» из параболы, но две «входят» через прямую, а две – через прямую
.
Это наводит на мысль, что нужно разбивать область интегрирования на две части. Граница этого разбиения – часть оси ординат. К слову,
другой порядок интегрирования в этом смысле был бы ничуть не лучше: область интегрирования всё равно пришлось бы разбивать.
-
Теоретический минимум (продолжение)
Обсудим тему расстановки пределов интегрирования в полярных координатах. И для начала напомним, как вводятся полярные координаты.
Вводится точка, играющая роль начала координат — полюс — и выходящий из неё луч — полярная ось. Положение точки на плоскости характеризуется
расстоянием до полюсаи углом
, который составляет с полярной осью отрезок, соединяющий точку и полюс (см. рис. 5).
Связь декартовых прямоугольных и полярных координат задаётся соотношениями
Отсюда следует, что
,
т.е. уравнениезадаёт на плоскости окружность радиуса
, а уравнение
задаёт на плоскости
прямую, проходящую через начало координат. Полезно изобразить сеть координатных линий (т.е. линий, на которых та или иная координата постоянна)
для случая прямоугольных и полярных координат (см. рис. 6).Вернёмся к двойным интегралам. При интегрировании с использованием прямоугольных координат для определения пределов интегрирования
мы проводили прямые, отвечающие постоянным значениям одной или другой переменной интегрирования. При интегрировании в полярных
координатах мы должны проводить линии, соответствующие постоянным значениям расстояния до начала координат (окружности) и полярного угла
(прямые, проходящие через начало координат). Снова проследим это на конкретных примерах. В этих примерах мы не проводим интегрирования,
ограничиваясь расстановкой пределов интегрирования. Связано это с некоторой спецификой интегрирования в полярных координатах, которая будет
пояснена позже. Кроме того, ничего нового по сравнению с уже приведёнными выше примерами проведение повторного интегрирования не даст.Примеры расстановки пределов интегрирования при использовании полярных координат
Пример 4. Кольцевая область интегрирования.
Расставить пределы интегрирования в полярных координатах в интеграле, где область интегрирования –
кольцо.
Этот пример аналогичен примеру 1 в том смысле, что это простейший случай интегрирования в полярных координатах. Границу области
интегрирования образуют координатные линии полярной системы координат (см. рис. 7). Поэтому пределы интегрирования расставляются элементарно:
Так как подынтегральная функция не конкретизирована, то за порядком интегрирования не следим: если повторные интегралы существуют,
то они равны. При конкретных вычислениях, разумеется, выбирается тот порядок интегрирования, при котором вычисления проще.Пример 5. Квадратная область интегрирования.
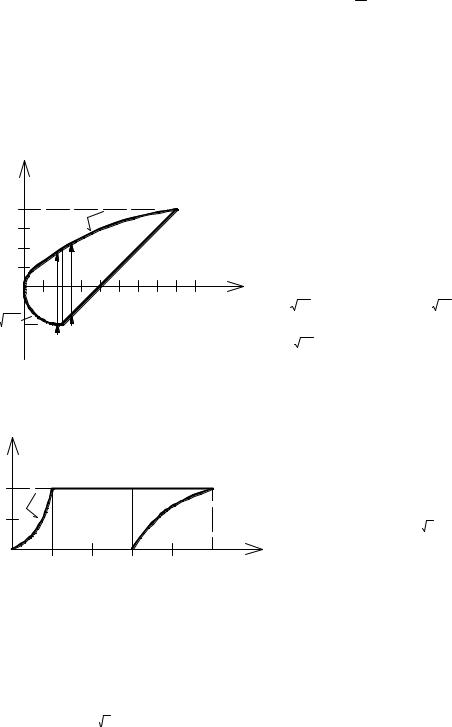
Расставить пределы интегрирования в полярных координатах в интеграле, где область интегрирования –
квадрат.
При интегрировании в прямоугольных координатах этот пример был простейшим. Теперь он несколько усложнился. Мы расставим пределы для обоих
порядков интегрирования. Но сначала запишем уравнения сторон квадратав полярных координатах:
.
Первым рассмотрим случай, когда внутреннее интегрирование выполняется по переменной
, тогда полярный угол фиксирован,
т.е. для определения пределов интегрирования следует проводить лучи, исходящие из начала координат (см. рис. 8). Полярный угол в целом будет
изменяться от нуля до. Но заметьте, что прямые могут «выходить» из вертикальной прямой, а могут – из горизонтальной. В связи с этим
интеграл распадётся на два:
Теперь проведём интегрирование в другом порядке: внутреннее интегрирование проведём по полярному углу, тогда переменнаясчитается
константой. Для определения пределов интегрирования проводим дуги окружностей (см. рис. 9). Как видно, до некоторого значения радиуса окружности
она пересекает стороны квадрата, соответствующие значениям полярного угла 0 (горизонтальная сторона) и(вертикальная сторона).
Когда радиус окружности становится равным единице, то она начинает пересекать две другие стороны. Наконец, после достижения радиусом окружности
значенияокружность вообще перестаёт пересекать стороны квадрата. Таким образом, расстановка пределов интегрирования следующая:
-
Теоретический минимум (окончание)
Наконец, рассмотрим замену переменных при вычислении двойного интеграла. Цель замены переменных та же, что и в случае определённого интеграла —
сделать вычисление технически проще. Кроме того, при замене может заметно упроститься расстановка пределов интегрирования. Это уже можно было
видеть на примерах 1 и 5, когда при интегрировании по одной и той же области в одних координатах расстановка пределов была элементарной, а в
других потребовалось разбивать интеграл на две части.Проследим аналогию в выполнении замены в определённом и двойном интеграле. Напомним процедуру замены переменной в определённом интеграле.
Пусть требуется в интегралеперейти к переменной интегрирования
, причём
:
.
Выделим три момента: 1) выполнение замены в подынтегральной функции; 2) преобразование дифференциала; 3) преобразование пределов интегрирования.
Первый и третий пункты особых комментариев не требуют, остановимся подробнее на втором. В определённом интеграле он достаточно очевиден,
а потому именно здесь удобно отследить его геометрический смысл. Переход от дифференциала старой переменной к дифференциалу новой переменной
происходит с помощью производной. Геометрически это связано с тем, что некоторому малому приращению старой переменной соответствует вполне определённое
приращение новой переменной в силу наличия между ними функциональной зависимости. Это показано на рис. 10. Производная, появляющаяся при замене,
представляет собой тангенс угла наклона касательной к графику функции, а потому она позволяет выразить один катет в изображённом
прямоугольном треугольнике (приращение) через другой катет (приращение
).
Обратимся к случаю двойного интеграла и начнём с частного случая перехода к полярным координатам. Замена в подынтегральной функции выполняется
элементарно, расстановка пределов интегрирования обсуждалась ранее. Остановимся на преобразовании дифференциалов. В случае определённого
интеграла преобразование дифференциала представляло собой переход к дифференциалу новой переменной с поправкой на изменение длины отрезка, который
сначала представлял собой приращение, а потом представляет собой приращение
. В случае двойного интеграла
нужно рассмотреть преобразование элемента площадипри замене переменных. Рассмотрим подробно, как образуется
элемент площади в координатах. Строятся координатные линии
. Они и
ограничивают элемент площади. Как это выглядит в случае полярных координат, показано на рис. 11.
Легко вычислить площадь изображённого элемента в полярных координатах. Так как речь идёт о бесконечно малых приращениях переменных
и
, то изображённую фигуру можно считать прямоугольником. Его стороны равны
(такова разница
в радиусах дуг окружностей) и(дуга окружности радиуса
, на которую опирается центральный угол
).
Итак, элемент площади в полярных координатах.
Понятно, что такое вычисление может быть не столь простым для других систем координат, и вообще хотелось бы иметь общую методику замены
переменных в двойном интеграле. Можно доказать, что общая методика такова: вместо дифференциаловследует записать
дифференциалыи умножить их на модуль якобиана перехода
.
Этот якобиан как раз и выражает изменение элемента площади, связанное с его деформацией при замене переменных.
Например, в случае полярных координат
,
что согласуется с результатом нашего расчёта, сделанного с помощью чертежа.Итак, замена переменных в двойном интеграле проводится следующим образом:
.
Изменение обозначения области интегрирования сна
связано с необходимостью изменить пределы интегрирования.
Запомнить формулу достаточно просто: во-первых, по сути она повторяет формулу замены в определённом интеграле, а во-вторых, порядок
перечисления переменных в якобиане такой, что новые переменныедолжны «сокращаться», чтобы оставались старые переменные
.
Подчеркнём, что это исключительно мнемоническое правило, позволяющее лучше запомнить формулу. Никакой доказательной силы оно, конечно,
не имеет. Ещё одно замечание касается появления в формуле модуля. При замене в определённом интеграле мы не ставили производную под
знак модуля. Однако знак автоматически учитывала расстановка пределов интегрирования, ведь в определённом интеграле существует общая
методика изменения пределов интегрирования, а в двойном интеграле их приходится расставлять заново.Примеры
Пример 1. Площадь эллипса.
Вычислить интегралпо области, ограниченной эллипсом
.
В соответствии с геометрическим смыслом двойного интеграла мы сейчас фактически вычислим площадь эллипса. Проводить вычисление
в прямоугольных координатах неудобно, и принципиально этот метод не отличается от нахождения площади фигуры с помощью определённого
интеграла. Здесь удобно перейти к так называемым обобщённым полярным координатам:
.
В этих координатах уравнение эллипса принимает предельно простой вид, полярный угол принимает все значения от нуля до
.
Якобиан такого преобразования отличается от случая полярных координат только дополнительным множителем. Это достаточно очевидно,
но можно и проверить это расчётом. Итак,
.
Пример 2. Вид замены диктуется областью интегрирования.
Вычислить интегралпо области, ограниченной кривыми
.
Область интегрирования показана на рис. 12. Понятно, что вычисление в прямоугольных координатах очень неудобно. Можно ввести такую
замену координат, чтобы область интегрирования существенно упростилась. В этом примере вид замены подсказывается уравнениями,
определяющими границы области интегрирования:
.
После применения такой замены нужно будет интегрировать по области, т.е. по квадрату.
Остаётся вычислить якобиан перехода:
.
Обратите внимание: был вычислен якобиан обратного перехода (здесь такое вычисление удобнее), т.е. при подстановке в интеграл нужно взять
обратную величину по отношению к этому якобиану, так как.
Поделиться этой страницей





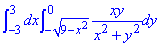
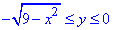
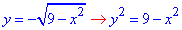
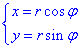
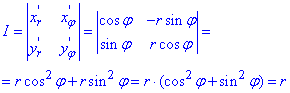
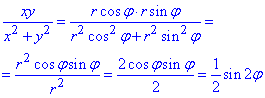
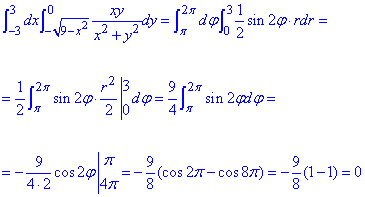
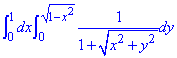
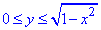
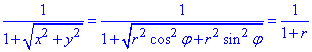
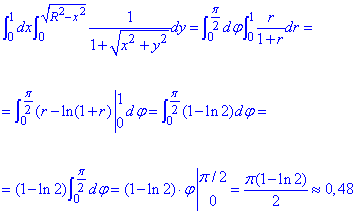
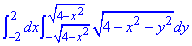
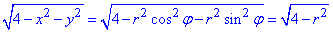
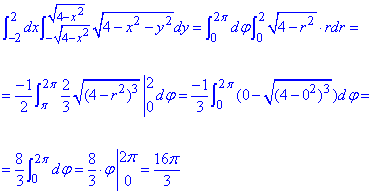
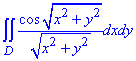
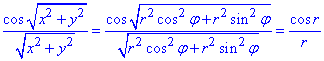
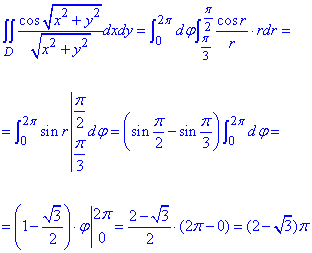
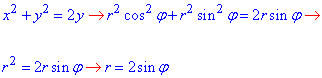
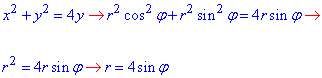
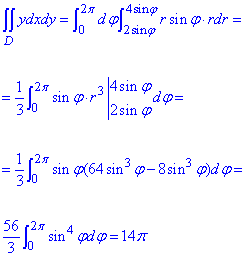
![[IMG]](http://corum.mephist.ru/tex/images/4ab76939d161dfd785c9aecb76012178.gif) , вычисляемый по отрезку
, вычисляемый по отрезку ![[IMG]](http://corum.mephist.ru/tex/images/051f64bba458bf213f344c609f8ad9d8.gif) . Отрезок разбивается на малые необязательно равные частичные отрезки
. Отрезок разбивается на малые необязательно равные частичные отрезки ![[IMG]](http://corum.mephist.ru/tex/images/80a15ae9b42d82e8676bae47fcab70b3.gif) , внутри каждого такого отрезка выбирается точка
, внутри каждого такого отрезка выбирается точка ![[IMG]](http://corum.mephist.ru/tex/images/6c2dd1abf1d12257789c1ff16ffaf6c3.gif) , и составляется интегральная сумма
, и составляется интегральная сумма ![[IMG]](http://corum.mephist.ru/tex/images/ea1fabe348727dd9f58a8ecc7158d284.gif) .
. ![[IMG]](http://corum.mephist.ru/tex/images/b80b4aacc97d175a63b9b58496ddd368.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/9d90daf3b83524bb04c47f2248b7d6b5.gif) , вычисляемый по двумерной области
, вычисляемый по двумерной области ![[IMG]](http://corum.mephist.ru/tex/images/3e41496c50f64ea502eb85888ab10489.gif) . Область разбивается на малые части. Эти малые части
. Область разбивается на малые части. Эти малые части ![[IMG]](http://corum.mephist.ru/tex/images/fad6beda9f607f0e4319bd522986f952.gif) и длинами
и длинами ![[IMG]](http://corum.mephist.ru/tex/images/913d03aa0a280da1a666282e2541c33a.gif) наибольшего отрезка, который можно провести внутри частичной области. Этот
наибольшего отрезка, который можно провести внутри частичной области. Этот ![[IMG]](http://corum.mephist.ru/tex/images/17eebd8689a1ffafe1e31352ad01fce0.gif) , и составляется интегральная сумма
, и составляется интегральная сумма ![[IMG]](http://corum.mephist.ru/tex/images/014361a9b8864de546519af5dd0fb6bc.gif) . Затем осуществляется переход к пределу разбиения области
. Затем осуществляется переход к пределу разбиения области ![[IMG]](http://corum.mephist.ru/tex/images/62de2bc13156020514a37aa3881acf94.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/ebaa8d8c69f88a2e51b7b35f81e77cca.gif) по области
по области ![[IMG]](http://corum.mephist.ru/tex/images/e17f4d7246c330517c5e8e288efe61c4.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/8725029ea89712eed8670bae64d30e47.gif) , считая вторую переменную константой (есть некоторая
, считая вторую переменную константой (есть некоторая![[IMG]](http://corum.mephist.ru/tex/images/c1a034d27979142b0ae545ecd42cbd49.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/add841dcc0aecc0303318bf76e3b8f49.gif) по области, ограниченной параболой
по области, ограниченной параболой ![[IMG]](http://corum.mephist.ru/tex/images/210312eec856b81b6a70066aa051e7d7.gif) и прямой
и прямой ![[IMG]](http://corum.mephist.ru/tex/images/11ff7b6f3a7bddd0d7340441e0fb6696.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/36a4dc9ccf2bdc09d800556724231fc6.gif) , считая её постоянной, то мы выделяем набор прямоугольников, выстроенных по прямой, параллельной
, считая её постоянной, то мы выделяем набор прямоугольников, выстроенных по прямой, параллельной![[IMG]](http://corum.mephist.ru/uploads/1369078311/med_gallery_20527_327_3432.png)
![[IMG]](http://corum.mephist.ru/tex/images/65a39b7d463138310b96e632ae95aff1.gif) , а «выходит» из прямой
, а «выходит» из прямой ![[IMG]](http://corum.mephist.ru/tex/images/e634174260a16b48c3747c584eff5c25.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/5d4dfe7a9cd89b9d0ab429b3042c8357.gif)
![[IMG]](http://corum.mephist.ru/tex/images/e533a82173f3bb5038aa2d2a3246dd4f.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/5e2da6e12b2afbcd0e9b3b4afcc88982.gif) по области, ограниченной параболой
по области, ограниченной параболой ![[IMG]](http://corum.mephist.ru/tex/images/cb6a98225fb63d2ee1e20c34633ad5da.gif) и прямыми
и прямыми ![[IMG]](http://corum.mephist.ru/tex/images/a88f5c713480ec47b80c753d54879b60.gif) ,
, ![[IMG]](http://corum.mephist.ru/tex/images/21079da8ca28b01cd167f8b4374e394f.gif) .
.![[IMG]](http://corum.mephist.ru/uploads/1369078311/gallery_20527_327_1221.png)
![[IMG]](http://corum.mephist.ru/tex/images/5d75f5d72536275a8074ad1d64933421.gif) , а две – через прямую
, а две – через прямую ![[IMG]](http://corum.mephist.ru/tex/images/f9c30e2a9d312812ebd6f5f732110b56.gif) .
. ![[IMG]](http://corum.mephist.ru/tex/images/45e8e5d9ff8a2a3bd7f7684ca83b1203.gif)
![[IMG]](http://corum.mephist.ru/tex/images/06b15f13cee2d9f9f2d6b8fb74c99363.gif)
![[IMG]](http://corum.mephist.ru/tex/images/253178e1cb99b0a83e42a84d883300c4.gif)
![[IMG]](http://corum.mephist.ru/tex/images/aa7bb4b05fbd27db7ca594893f166b47.gif) и углом
и углом ![[IMG]](http://corum.mephist.ru/tex/images/3e47ab3d63aa5c76c7d345ccb7bebda7.gif) , который составляет с полярной осью отрезок, соединяющий точку и полюс (см. рис. 5).
, который составляет с полярной осью отрезок, соединяющий точку и полюс (см. рис. 5).![[IMG]](http://corum.mephist.ru/uploads/1369078311/gallery_20527_327_9584.png)
![[IMG]](http://corum.mephist.ru/tex/images/c78baefc40eed1b1dbad56a4a3450105.gif)
![[IMG]](http://corum.mephist.ru/tex/images/7b1e1993138869b4790256a63feac83e.gif) ,
,![[IMG]](http://corum.mephist.ru/tex/images/7103153f7f6f3b156370be9ea15d65a6.gif) задаёт на плоскости окружность радиуса
задаёт на плоскости окружность радиуса ![[IMG]](http://corum.mephist.ru/tex/images/3eb6ae1764eedc74c52098315f61dcd1.gif) задаёт на плоскости
задаёт на плоскости![[IMG]](http://corum.mephist.ru/tex/images/54423b789f1c8afadb25780e21b2b73b.gif) , где область интегрирования –
, где область интегрирования – ![[IMG]](http://corum.mephist.ru/tex/images/b1ace5b81b0a9be1c8b009d42f0d3a32.gif) .
.![[IMG]](http://corum.mephist.ru/uploads/1369078311/gallery_20527_327_705.png)
![[IMG]](http://corum.mephist.ru/tex/images/619c01b25eca0ccd6793219e29de8e4f.gif)
![[IMG]](http://corum.mephist.ru/tex/images/0703eb54e241d1872045447c790f6460.gif) в полярных координатах:
в полярных координатах:![[IMG]](http://corum.mephist.ru/tex/images/2abdbc2bd5f0471595c50f3070540ee2.gif) .
.![[IMG]](http://corum.mephist.ru/uploads/1369078311/gallery_20527_327_5962.png)
![[IMG]](http://corum.mephist.ru/tex/images/f1c3c82ecacef5ad48bbf83066497a64.gif) . Но заметьте, что прямые могут «выходить» из вертикальной прямой, а могут – из горизонтальной. В связи с этим
. Но заметьте, что прямые могут «выходить» из вертикальной прямой, а могут – из горизонтальной. В связи с этим ![[IMG]](http://corum.mephist.ru/tex/images/6a2e69f3ea16343f2a8c3fe753bcca90.gif)
![[IMG]](http://corum.mephist.ru/tex/images/60fc0ee50857029f56d99b512a03b28a.gif) окружность вообще перестаёт пересекать стороны квадрата. Таким образом, расстановка пределов интегрирования следующая:
окружность вообще перестаёт пересекать стороны квадрата. Таким образом, расстановка пределов интегрирования следующая:![[IMG]](http://corum.mephist.ru/tex/images/700316fc58f5389c00a542958a6f1d7f.gif)
![[IMG]](http://corum.mephist.ru/tex/images/30b2ab8dc1496d06b230a71d8962af5d.gif) , причём
, причём ![[IMG]](http://corum.mephist.ru/tex/images/c1b022f3eaa49d0fcac18c001fe4d3c8.gif) :
:![[IMG]](http://corum.mephist.ru/tex/images/6c5e4efa2b0b8cbb1c0ea25422bef419.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/9055916c231182e459aa3e773d163215.gif) ) через другой катет (приращение
) через другой катет (приращение ![[IMG]](http://corum.mephist.ru/tex/images/768667a5b42d77660d4f5133cb9a7d47.gif) ).
).![[IMG]](http://corum.mephist.ru/uploads/1369078311/gallery_20527_327_242.png)
![[IMG]](http://corum.mephist.ru/tex/images/9884bf92207a6a1641c7b564f7e5198e.gif) при замене переменных. Рассмотрим подробно, как образуется
при замене переменных. Рассмотрим подробно, как образуется![[IMG]](http://corum.mephist.ru/tex/images/5019c4d599c3882c028227da07aff111.gif) . Строятся координатные линии
. Строятся координатные линии ![[IMG]](http://corum.mephist.ru/tex/images/82bc9682317a9acefb6b9d3e42caefbd.gif) . Они и
. Они и![[IMG]](http://corum.mephist.ru/uploads/1369078311/gallery_20527_327_1220.png)
![[IMG]](http://corum.mephist.ru/tex/images/f1b0dd5189d3cbd59c47c074189f0eee.gif) и
и ![[IMG]](http://corum.mephist.ru/tex/images/efd4fe2d29680169ad9c93bb782a08e1.gif) , то изображённую фигуру можно считать прямоугольником. Его стороны равны
, то изображённую фигуру можно считать прямоугольником. Его стороны равны ![[IMG]](http://corum.mephist.ru/tex/images/ec09a42445c3c62e910ad48baf566053.gif) (дуга окружности радиуса
(дуга окружности радиуса ![[IMG]](http://corum.mephist.ru/tex/images/114d1d5822840a96e11baf531fb02c4b.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/4e95552b283741eb2a72d0fdae3871cf.gif) и умножить их на модуль якобиана перехода
и умножить их на модуль якобиана перехода![[IMG]](http://corum.mephist.ru/tex/images/890fcf8cb6ee4da070032605e79da94d.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/1796650365aaa991bf5095ffcf38ea1e.gif) ,
,![[IMG]](http://corum.mephist.ru/tex/images/9baf220ed6d8b3880043fb4a75c43c0d.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/70007ddb70e7b9cd05fdb7cf0b5d85c7.gif) связано с необходимостью изменить пределы интегрирования.
связано с необходимостью изменить пределы интегрирования.![[IMG]](http://corum.mephist.ru/tex/images/95c08be48ddd5c8423e8610375e6fce1.gif) должны «сокращаться», чтобы оставались старые переменные
должны «сокращаться», чтобы оставались старые переменные ![[IMG]](http://corum.mephist.ru/tex/images/7781dfecc39de21fd1d92eec917a9c4a.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/196a85aacba475cc033dd60421efb85c.gif) по области, ограниченной эллипсом
по области, ограниченной эллипсом ![[IMG]](http://corum.mephist.ru/tex/images/126cf096ed5d16bf53b47bab75a4446e.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/62dfa410d095f885064bd4c917b86f23.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/b6c3d077e9902b461291bc4d37c09526.gif) , полярный угол принимает все значения от нуля до
, полярный угол принимает все значения от нуля до ![[IMG]](http://corum.mephist.ru/tex/images/aa6ec90581e52f6f39e16d63f37276e9.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/c78c1d9d58c60eea485f034a5efb368c.gif) . Это достаточно очевидно,
. Это достаточно очевидно,![[IMG]](http://corum.mephist.ru/tex/images/607898399d95a343d54c071810577968.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/2b09cad7a38e662a4b19e22c849a83b7.gif) .
.![[IMG]](http://corum.mephist.ru/uploads/1369078311/gallery_20527_327_1855.png)
![[IMG]](http://corum.mephist.ru/tex/images/a64c5abdba8e5039295d38433dca41c6.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/e457239934831fdfd70cb131d37aeaa5.gif) , т.е. по квадрату.
, т.е. по квадрату.![[IMG]](http://corum.mephist.ru/tex/images/dd567f3103feea77814400f8dddfe70f.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/283aa04a6c0eba3f47232706f4fa51f2.gif) .
.![[IMG]](http://corum.mephist.ru/tex/images/e99d5ee7ff72e6f96da63dcb6701a217.gif)