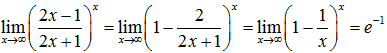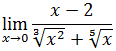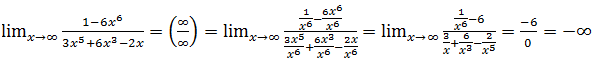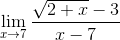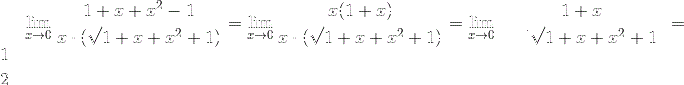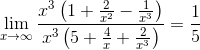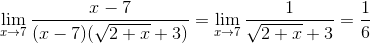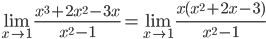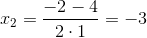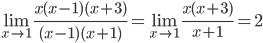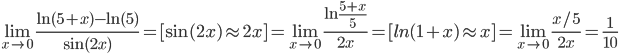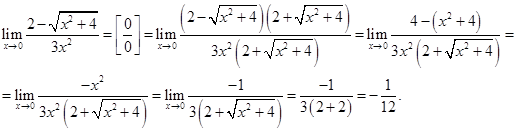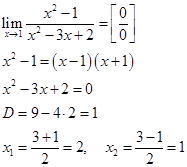Пример 1:
Найти предел, не пользуясь правилом Лопиталя:
Решение от преподавателя:
Так как числитель и знаменатель обратились в нуль при x=-5, то -5 – корень обоих многочленов, а значит, каждый из них разлагается на множители, одним из которых будет (x — (-5)) .
Найдем корни первого многочлена:
x2 +0 x — 25 = 0
D=02 — 4*1(-25)=100
Найдем корни второго многочлена:
2 x2 +9 x — 5 = 0
D=92 — 4*2(-5)=121
Получаем:
Пример 2:
Вычислить предел функции не пользуясь правилом Лопиталя.
Решение от преподавателя:
Пример 3:
Найти пределы функций (не используя правило Лопиталя):
Решение от преподавателя:
Пример 4:
Найти пределы функций (не используя правило Лопиталя):
Решение от преподавателя:
Пример 5:
Найти предел, не пользуясь правилом Лопиталя:
Решение от преподавателя:
=е
Пример 6:
Вычислить предел функции не пользуясь правилом Лопиталя.
Решение от преподавателя:
Пример 7:
Найти пределы функций (не используя правило Лопиталя):
Решение от преподавателя:
Пример 8:
Найти пределы функций (не используя правило Лопиталя):
Решение от преподавателя:
Пример 9:
Найти предел, не пользуясь правилом Лопиталя:
Решение от преподавателя:
Используем свойство первого замечательного предела:
-2sin(x) ≈ -2x
Пример 10:
Вычислить предел функций не пользуясь правилом Лопиталя.
Решение от преподавателя:
Пример 11:
Найти пределы функций (не используя правило Лопиталя):
Решение от преподавателя:
Пример 12:
Найти пределы функций (не используя правило Лопиталя):
Решение от преподавателя:
Пример 13:
Найти предел, не пользуясь правилом Лопиталя:
Решение от преподавателя:
Используем свойство первого замечательного предела:
arcsin(2x) ≈ 2x
Пример 14:
Вычислить предел функции, не пользуясь правилом Лопиталя.
Решение от преподавателя:
Пример 15:
Найти пределы функций (не используя правило Лопиталя):
Решение от преподавателя:
Пример 16:
Найти пределы функций (не используя правило Лопиталя):
Решение от преподавателя:
Пример 17:
Вычислить предел, не пользуясь правилом Лопиталя.
Решение от преподавателя:
Пример 18:
Вычислить предел функции, не пользуясь правилом Лопиталя.
Решение от преподавателя:
Пример 19:
Найти пределы функций (не используя правило Лопиталя):
Решение от преподавателя:
Так как числитель и знаменатель обратились в нуль при x=2, то 2 – корень обоих многочленов, а значит, каждый из них разлагается на множители, одним из которых будет (x — 2) .
Найдем корни первого многочлена:
x2 -8 x + 12 = 0
D=(-8)2 — 4*1*12=16
Найдем корни второго многочлена:
x2 -6 x + 8 = 0
D=(-6)2 — 4*1*8=4
Получаем:
Пример 20:
Найти пределы функций (не используя правило Лопиталя):
Решение от преподавателя:
Пример 21:
Вычислить предел, не пользуясь правилом Лопиталя.
Решение от преподавателя:
Пример 22:
Вычислить предел функции, не пользуясь правилом Лопиталя.
Решение от преподавателя:
Пример 23:
Найти пределы функций (не используя правило Лопиталя):
Решение от преподавателя:
Пример 24:
Вычислить предел функции, не пользуясь правилом Лопиталя.
Решение от преподавателя:
Пример 25:
Найти пределы функций (не используя правило Лопиталя):
Решение от преподавателя:
Пример 26:
Вычислить предел функции, не пользуясь правилом Лопиталя.
Решение от преподавателя:
Пример 27:
Найти пределы функций (не используя правило Лопиталя):
Решение от преподавателя:
Пример 28:
Вычислить предел функции, не пользуясь правилом Лопиталя.
Решение от преподавателя:
Пример 29:
Вычислить предел функции, не пользуясь правилом Лопиталя.
Решение от преподавателя:
Пример 30:
Вычислить пределы функций, не пользуясь правилом Лопиталя.
Решение от преподавателя:
Используем свойство первого замечательного предела:
Ответ:
Пример 31:
Вычислить пределы функций, не пользуясь правилом Лопиталя.
Решение от преподавателя:
Пример 32:
Вычислить пределы функций, не пользуясь правилом Лопиталя.
Решение от преподавателя:
Пример 33:
Вычислить пределы функций, не пользуясь правилом Лопиталя.
Решение от преподавателя:
Пример 34:
Вычислить пределы функций, не пользуясь правилом Лопиталя.
Решение от преподавателя:
Пример 35:
Найти пределы функций (не используя правило Лопиталя):
Решение от преподавателя:
=
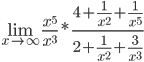
=
Пример 36:
Найти пределы функций (не используя правило Лопиталя):
Решение от преподавателя:
Для выражения
сопряженным является
Умножим его на числитель и знаменатель. =
Учитывая, что (a-b)(a+b) = a2-b2, получаем:
Решение пределов
Число A называется пределом функции y=f(x) в точке x0, если для любой последовательности точек из области определения функции, отличных от x0, сходящейся к точке x0(lim xn = x0), последовательность соответствующих значений функции сходится к числу A.
- Решение онлайн
- Видеоинструкция
- Оформление Word
- Также решают
Если выбрать вид предела, то подробное решение по шагам будет доступно в MS Word:
1. Не знаю
2. Пределы вида 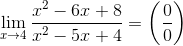
3. Вычислить предел, используя правило Лопиталя.
4. Пределы простейших иррациональности вида
5. Нахождение пределов, используя свойства первого замечательного предела ,
6. Нахождение пределов, используя свойства второго замечательного предела ,
,
Для нахождения предела слева
используйте знак -, справа
: +. Например, 0-, 1+
Примечание: число «пи» (π) записывается как pi, знак ∞ как infinity
Некоторые виды записи пределов
Например, найти предел 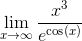
см. также нахождение пределов, используя свойства первого замечательного предела и второго замечательного предела.
Примеры.
Вычислить указанные пределы:
1. 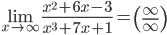
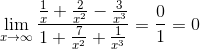
2. 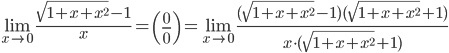
3. 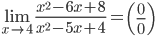
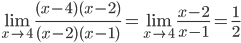
4. 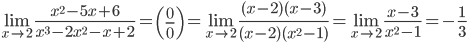
5. 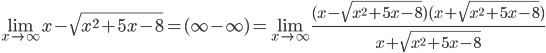
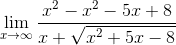
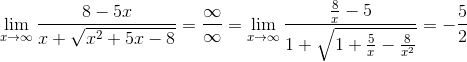
6. 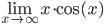
7. 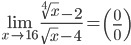
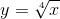
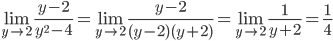
8. 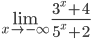
9. 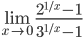
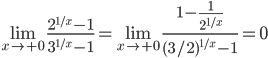
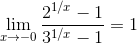
Следовательно, 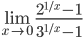
Найти пределы функции, не применяя правило Лопиталя.
а)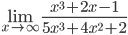
Ответ: 1/5
б) 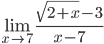
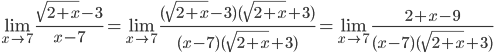
Ответ: 1/6
в) 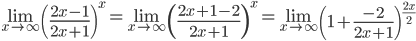
e-2/2 = e-1
Ответ: 1/e
г)
Так как числитель и знаменатель обратились в нуль при x=1, то 1 – корень обоих многочленов, а значит, каждый из них разлагается на множители, одним из которых будет (x-1).
Найдем корни первого многочлена: x2+2x-3=0
D=22-4•1•(-3)=16
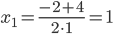
Найдем корни второго многочлена: x2-1=(x-1)(x+1)
Получаем:
Ответ: 2
д) 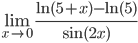
Ответ: 1/10
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Вычисление пределов, без использования правила Лопиталя.
Найти указанные пределы, не пользуясь правилом Лопиталя.
1. 
Решение.
Ответ: 0.
2.
Решение.
Таким образом, 
Отсюда находим

Ответ: 0.
3. 
Решение.
Ответ:
4. 
Решение.

Ответ:
5.
Решение.
Ответ:
6.
Решение.

Ответ: -5.
7.
Решение.

Таким образом, 
Отсюда находим
Ответ: 1.
8. 
Решение.

Ответ: 36.
9. 
Решение.
Ответ: 0.
10.
Решение.

Ответ:
11. $limlimits_{xrightarrowinfty}frac{3x^2+2x-1}{4x^3+3x^2+4}.$
Решение.
$$limlimits_{xrightarrowinfty}frac{3x^2+2x-1}{4x^3+3x^2+4}=left[frac{infty}{infty}right]=limlimits_{xrightarrowinfty}frac{frac{3x^2}{x^3}+frac{2x}{x^3}-frac{1}{x^3}}{frac{4x^3}{x^3}+frac{3x^2}{x^3}+frac{4}{x^3}}=limlimits_{xrightarrowinfty}frac{frac{3}{x}+frac{2}{x^2}-frac{1}{x^3}}{4+frac{3}{x}+frac{4}{x^3}}=frac{0}{4}=0.$$
Ответ: 0.
12. $limlimits_{xrightarrowinfty}left(frac{3x+1}{3x-2}right)^{2x}.$
Решение.
$$limlimits_{xrightarrowinfty}left(frac{3x+1}{3x-2}right)^{2x}=limlimits_{xrightarrowinfty}left(frac{3x-2+3}{3x-2}right)^{2x}=limlimits_{xrightarrowinfty}left(1+frac{3}{3x-2}right)^{frac{3x-2}{3}cdotfrac{3}{3x-2}cdot 2x}=$$
$$=e^{limlimits_{xrightarrowinfty}frac{3}{3x-2}cdot 2x}=e^{limlimits_{xrightarrowinfty}frac{6x}{3x-2}}=e^{limlimits_{xrightarrowinfty}frac{6}{3-frac{2}{x}}}=e^{frac{6}{3-0}}=e^2.$$
Ответ: $e^2$.
13. $limlimits_{xrightarrowinfty}frac{sqrt x-6x}{3x+1}.$
Решение.
$$limlimits_{xrightarrowinfty}frac{sqrt x-6x}{3x+1}=left[frac{infty}{infty}right]=limlimits_{xrightarrowinfty}frac{frac{sqrt x}{x}-frac{6x}{x}}{frac{3x}{x}+frac{1}{x}}=limlimits_{xrightarrowinfty}frac{frac{1}{sqrt x}-6}{3+frac{1}{x}}=frac{-6}{3}=-2.$$
Ответ: $-2.$
14. 
Решение.

Ответ: 3
15.
Решение.
Таким образом,

Отсюда находим
Ответ: -2.
16. 
Решение.
Ответ: 3/20.
17. $limlimits_{xrightarrow 1}frac{-x+1}{-x+sqrt{x}}.$
Решение.
Ответ: 2.
Пример решения задачи. Нахождение предела функции.
Найти пределы
функций, не пользуясь правилом Лопиталя в пунктах а)-г); с использованием
правила Лопиталя в пункте д)
a)
Имеем неопределенность
, т.к. пределы числителя и знаменателя равны нулю.
Следовательно,
теорему о пределе частного здесь применять нельзя. Для раскрытия этой
неопределенности разложим числитель и знаменатель на множители:
Таким
образом:
б)
Имеем
неопределенность вида
, так как пределы числителя и знаменателя равны нулю.
Для
раскрытия этой неопределенности умножим числитель и знаменатель дроби на
выражение, сопряженное числителю, т.е. на
. Таким
образом,
в)
Имеем
неопределенность вида
, так как:
Преобразуем
функцию так, чтобы использовать второй замечательный предел:
Таким образом:
г)
Имеем
неопределенность вида
. Для раскрытия
этой неопределенности воспользуемся формулой
и
первым замечательным пределом:
Таким
образом:
д)
Имеем
неопределенность вида
. Преобразуем исходную функцию:
Таким образом:
Имеем
неопределенность вида
. Для раскрытия этой неопределенности воспользуемся
правилом Лопиталя:
Окончательно
имеем:
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная оплата переводом на карту СберБанка.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
2. Следствием второго замечательного предела является предел 
________________________________________________________
Читабельней 

Вы нарушаете рекомендации начинающим: «Прежде всего, осуществите поиск по ключевым словам — возможно, Ваш или близкий к Вашему вопрос рассматривался ранее. Если Вы не нашли ответ на свой вопрос или подходящей темы, где бы рассматривались близкие вопросы
, Вы можете создать свою тему.» [Выделение курсивом GAA]
Добавлено спустя 46 минут 26 секунд:
1. Вычисление 
и bot
.