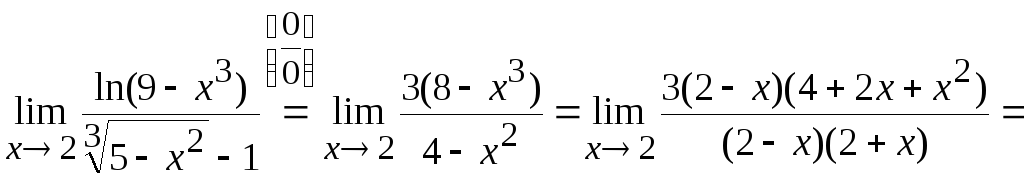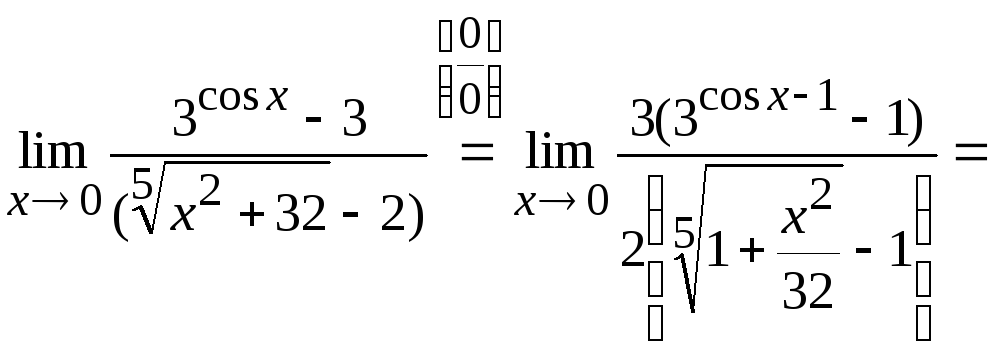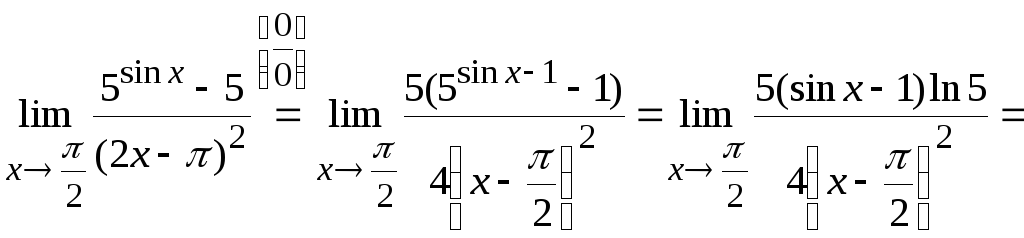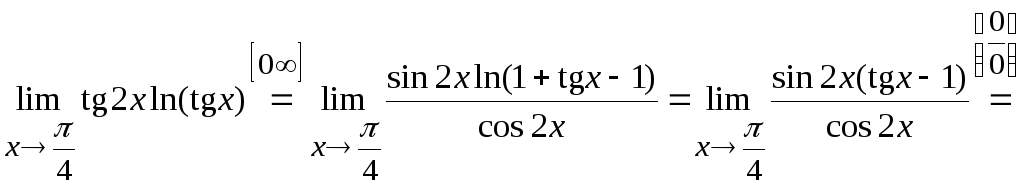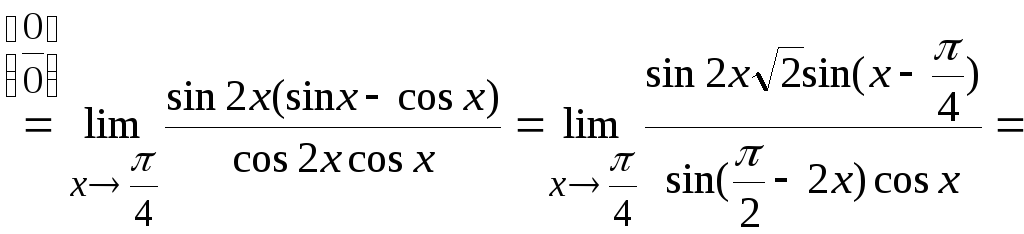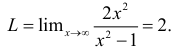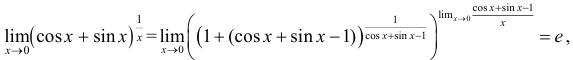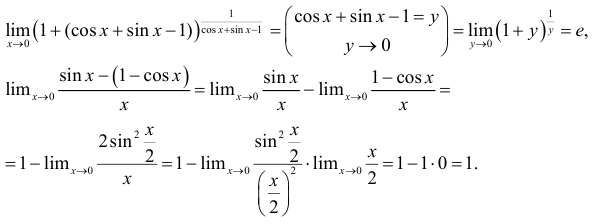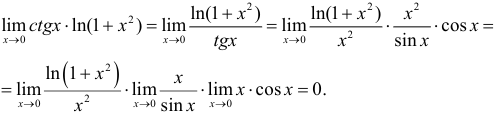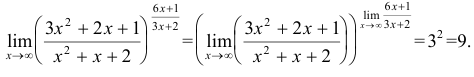Как найти пределы со степенями - Исправление недочетов и поиск решений вместе с Examum.ru

Пределы со степенями: показательная, степенная и показательно-степенная функции

Пределы со степенями бывают различных видов в зависимости от положения неизвестной $x$ в пределе. Рассмотрим примеры решений для следующих ситуаций:

Показательная функция
$$limlimits_{xto a} a^{f(x)} = a^{limlimits_{xto a} f(x)} $$
Степенная функция
$$ limlimits_{xto a} (f(x))^a = bigg(limlimits_{xto a} f(x) bigg)^a $$
Показательно-степенная функция
$$limlimits_{xto a} bigg(f(x)bigg)^{g(x)} = limlimits_{xto a} frac{ln(f(x))}{frac{1}{g(x)}} $$

Пример 1

Найти предел показательной функции $limlimits_{xto 2} 2^{frac{x^2-4}{x-2}}$

Решение

Подставив точку $x=2$ в предел получим неопределенность $2^{big(frac{0}{0}big)}$. Итак, перенесем знак предела в показатель и попробуем его вычислить путем разложения числителя по формуле разности квадратов $a^2-b^2 = (a-b)(a+b)$.

$$limlimits_{xto 2} 2^{frac{x^2-4}{x-2}} = 2^{limlimits_{xto 2} frac{(x-2)(x+2)}{x-2}} = $$

Сокращаем числитель со знаменателем на $x-2$ и вычисляем предел степени.

$$ =2^{limlimits_{xto 2} (x+2)} = 2^{2+2} = 2^4 = 16 $$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$limlimits_{xto 2} 2^{frac{x^2-4}{x-2}} = 16$$

Пример 2

Решить предел степенной функции $limlimits_{xto 0} bigg(frac{sin x^2}{1-cos x}bigg)^3$

Решение

Внесем знак предела внутрь скобок, а степень останется при этом снаружи.

$$limlimits_{xto 0} bigg(frac{sin x^2}{1-cos x}bigg)^3 = bigg(limlimits_{xto 0} frac{sin x^2}{1-cos x}bigg)^3 = $$

При подстановке точки $x=0$ в предел получаем неопределенность $frac{0}{0}$. Для её устранения воспользуемся таблицей эквивалентностей пределов.

$$sin x^2 sim x^2$$ $$ 1-cos x sim frac{x^2}{2}$$

Подставляем эквивалентные функции в предел и сокращаем $x$.

$$ = bigg(limlimits_{xto 0} frac{x^2}{frac{x^2}{2}}bigg)^3 = bigg(limlimits_{xto 0} frac{2x^2}{x^2} bigg)^3 = 2^3 = 8$$

Ответ

$$limlimits_{xto 0} bigg(frac{sin x^2}{1-cos x}bigg)^3 = 8$$

Пример 3

Вычислить предел показательно-степенной функции $limlimits_{xto 0} (tg x)^{sin x} $

Решение

Если подставим $x=0$, то получим предел ноль в степени ноль $(0^0)$. Превратим это в другую неопределенность $(frac{infty}{infty})$ с помощью третьей формулы.

$$limlimits_{xto 0} (tg x)^{sin x} = limlimits_{xto 0} frac{ln (tg ;x)}{frac{1}{sin x}} = frac{infty}{infty} = $$

Используем правило Лопиталя для продолжения решения. По нему, как известно, предел отношения функций равен пределу отношения производных от этих функций.

$$ = limlimits_{xto 0} frac{(ln (tg ;x))’}{(frac{1}{sin x})’} = limlimits_{xto 0} frac{frac{frac{1}{cos^2 x}}{tg ;x}}{-frac{cos x}{sin^2 x}} = $$

Преобразуем числитель в нормальный вид с помощью формулы $tg ; x = frac{sin x}{cos x}$ и выполняем все необходимые сокращения.

$$ = limlimits_{xto 0} frac{frac{1}{sin x cos x}}{-frac{cos x}{sin^2 x}} = -limlimits_{xto 0} frac{sin x}{cos^2 x} = $$

Теперь подставляя точку $x=0$ возможно получить окончательный ответ.

$$ = — frac{sin 0}{cos^2 x} = -frac{0}{1} = 0 $$

Ответ

$$limlimits_{xto 0} (tg x)^{sin x} = 0$$

Источник

Вычисление пределов степенно-показательных функций

Пусть функции

и

заданы на множестве

и функция

на нем положительна. Функция

называется степенно
— показательной.

Предположим, что

– точка сгущения множества

и существуют конечные пределы

,
,

где
.
Нужно найти

Воспользовавшись
тождествами
,
запишем исходное выражение в виде

В силу теоремы 6.1
получим

При заданных
значениях пределов будем иметь

Из проведенного
рассуждения видно, что предположение
о существовании конечных пределов

и

можно отбросить. Действительно, для
нахождения предела выражения

достаточно знать предел произведения

(конечный или бесконечный).

1) Пусть
.
Тогда
.

2) Если
,
то
.

3) Если
,
то
.

Заметим, что
произведение

может оказаться неопределенностью типа
.
Тогда и исходное выражение

представляет собой неопределенность.
Перечислим возникающие здесь
неопределенности.

1) Если
,
то вычисление предела

приводит к неопределенности типа
.

2) Если
,
то вычисление предела

приводит к неопределенности типа
.

3) Если
,
то вычисление предела

приводит к неопределенности типа
.

Во всех указанных
случаях (,

)
можно раскрыть неопределенность

в показателе степени, преобразуя ее к
типу

и используя соответствующие эквивалентные
бесконечно малые.

Замечание 8.3.
Приведенные выше рассуждения справедливы
и для вычисления предела степенно-показательной
функции в бесконечно удаленной точке:
.

Пример 8.2.
Вычислить
.

Решение.
Здесь
,
,
поэтому имеем неопределенность типа
.
Преобразуем выражение под знаком
предела:

В показателе
степени имеем неопределенность типа
.
Заменой

при

на эквивалентную бесконечно малую

раскрываем ее:

Таким образом,

Замечание 8.4.
Аналогично доказывается равенство
.

Пределы

образуют две формы
одного и того же равенства, которое
также является замечательным
пределом
и часто служат определением числа
.

Задачи к §8

Задача
1. Вычислить
.

Решение.
Здесь имеем
неопределенность типа
.
Преобразуем числитель дроби к форме
произведения:

Затем
заменим бесконечно малую в точке

функцию

эквивалентной бесконечно малой
.

Тогда
получим

Ответ:
.

Задача
2. Вычислить
.

Решение.
Здесь возникает неопределенность типа
.
Преобразуем знаменатель, воспользовавшись
свойствами логарифмической функции, и
выделим в аргументе логарифма слагаемое,
равное 1:

Заменим
бесконечно малую в точке

функцию

эквивалентной бесконечно малой
.
Числитель разложим на множители:

Тогда
получим:

Ответ:
.

Задача
3. Вычислить
.

Решение.
Здесь возникает неопределенность типа
.
Представим числитель в виде:

Затем
заменим его эквивалентной бесконечно
малой в точке

функцией
.

Функцию

в точке

тоже заменим на эквивалентную бесконечно
малую
.

Тогда

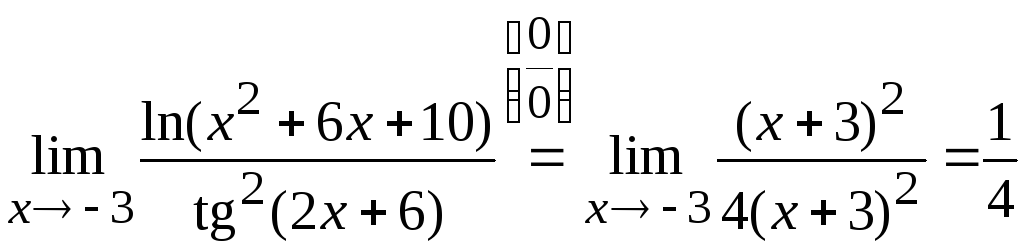
Ответ:
.

Задача
4. Вычислить

Решение.
Здесь возникает неопределенность типа
.
Представим числитель в виде:

Затем
заменим его эквивалентной бесконечно
малой в точке

функцией
.

Преобразуем
знаменатель:

и
заменим его на эквивалентную бесконечно
малую
.
Тогда получим

Ответ:
.

Задача
5. Вычислить
.

Решение.
Здесь возникает неопределенность типа
.
Числитель

можно заменить эквивалентной бесконечно
малой
.

Чтобы
воспользоваться соотношением (8.4),
преобразуем знаменатель:

и
заменим его эквивалентной бесконечно
малой
.

Тогда

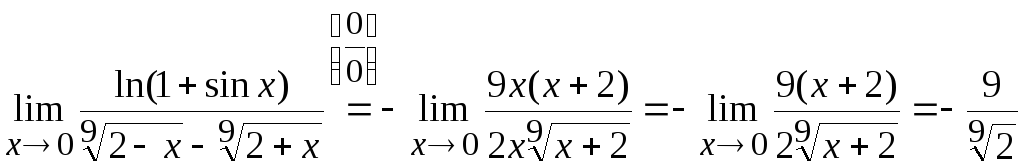
Ответ:

.

Задача
6. Вычислить
.

Решение.
Здесь имеем неопределенность типа
.
Чтобы применить к выражению

соотношение (8.3), представим его в виде:

и
заменим бесконечно малую функцию

эквивалентной бесконечно малой
.
Знаменатель же представим в виде:

и,
используя соотношения (8.2) и (8.8), заменим
его эквивалентной бесконечно малой
.
Учитывая проведенные выкладки и
соотношение (8.4), получим:

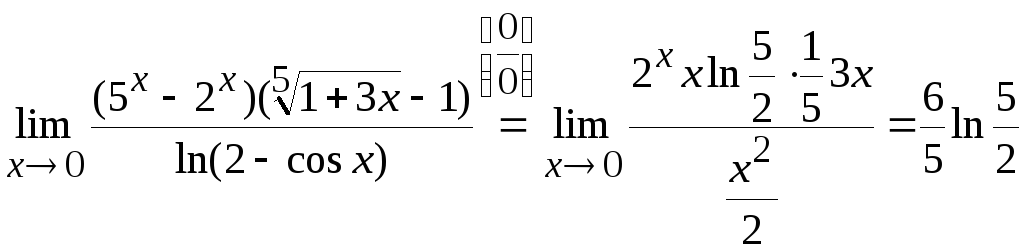
Ответ:

.

Задача
7. Вычислить
.

Решение.
Здесь имеем неопределенность типа
.
Используя ряд приемов, примененных в
задачах 1–7, получим

Ответ:

.

Задача
8. Вычислить
.

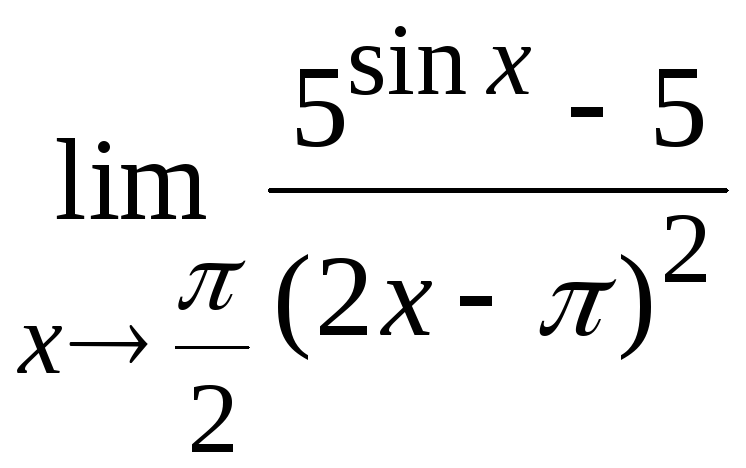
Решение.
Здесь имеем неопределенность типа
.
Используя ряд приемов, примененных в
задачах 1–7 и формулы приведения для
тригонометрических функций, получим

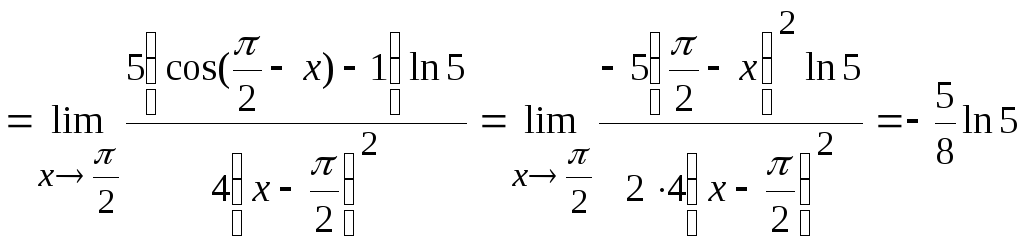
Ответ:

.

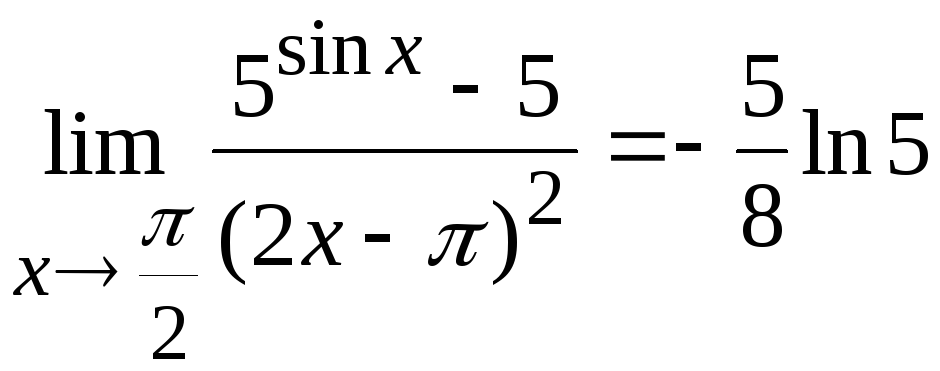
Задача
9. Вычислить
.

Решение.
Здесь имеем неопределенность типа
.
Чтобы применить к числителю соотношение
(8.2), преобразуем его следующим образом:

Теперь
числитель согласно соотношению (8.2)
можно заменить эквивалентной бесконечно
малой
.

Преобразуем
знаменатель

Заменяем,
используя соотношение (8.1),

эквивалентной бесконечно малой
.

Тогда

Ответ:

.

Задача
10. Вычислить
.

Решение.
Здесь имеем неопределенность типа
.
Используя приемы, описанные выше, получим

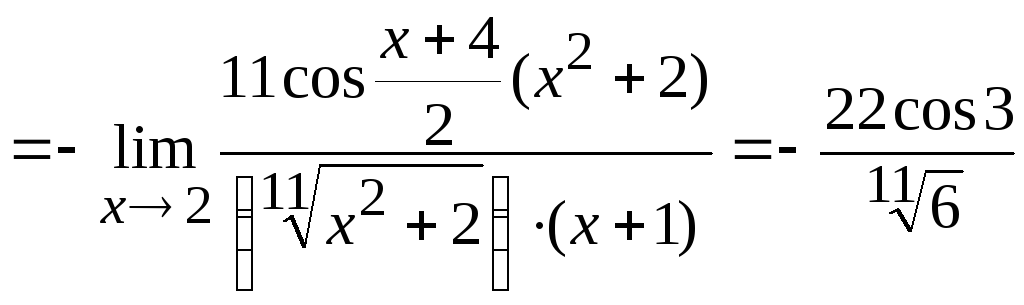
Ответ:
.

Задача
11. Вычислить
.

Решение.
Здесь имеем неопределенность типа
.
Используя теоремы 6.2 и 6.1, получим

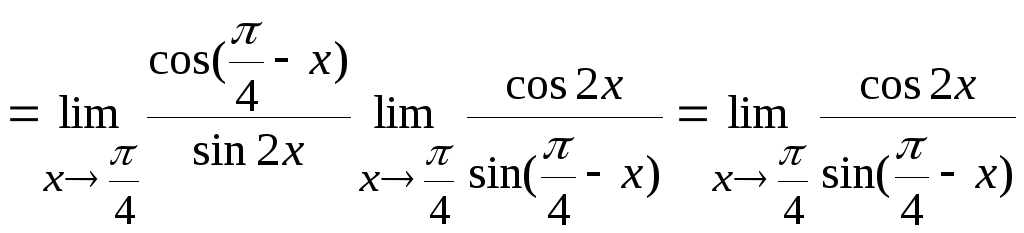
Получили
неопределенность типа
.
Преобразуем выражение с помощью формул
приведения, затем переходим к эквивалентным
бесконечно малым. В итоге получим

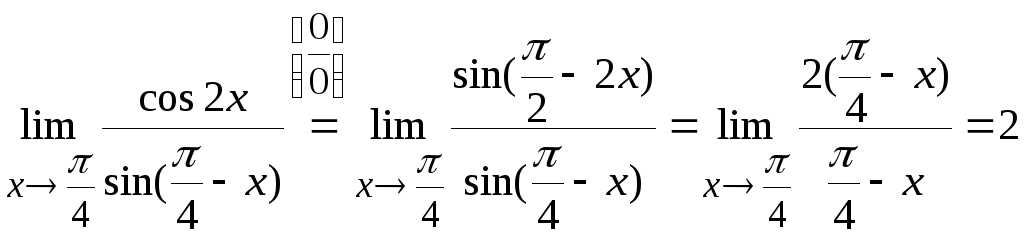
Ответ:
.

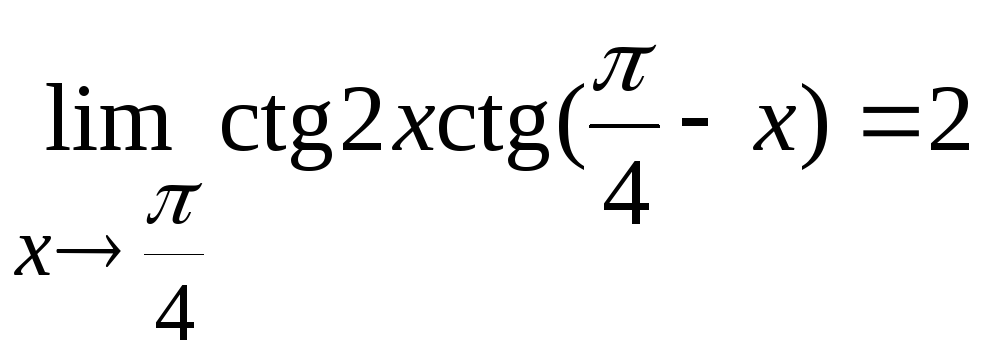
Задача
12. Вычислить
.

Решение.
Здесь имеем неопределенность типа
.
Выделим

в основании степени:

Заметим,
что

при
.

Справедлива
цепочка равенств

Заменяя
логарифм эквивалентной бесконечно
малой согласно соотношению (8.2) и используя
замечание 6.4 для раскрытия неопределенности,
получим

Ответ:
.

Задача
13^⁴.
Вычислить
.

Решение.
Здесь имеем неопределенность типа
.
Введем переменную
.
Если
,
то
.

Выделим

в основании степени:

тогда

Заметим,
что

при
.
Заменим функцию

эквивалентной бесконечно малой
,
будем иметь

Используя
теорему 7.3, окончательно получим

Ответ:
.

Задача
14. Вычислить
.

Решение.
Здесь возникает неопределенность типа
.
Поскольку

вычислим
сначала
.
Мы имеем дело с неопределенностью типа
.

Воспользовавшись
последовательно соотношениями (8.2) и
(8.1), будем иметь

Ответ:
.

Задача
15. Вычислить
.

Решение.
Здесь возникает неопределенность типа
.
Воспользуемся формулой

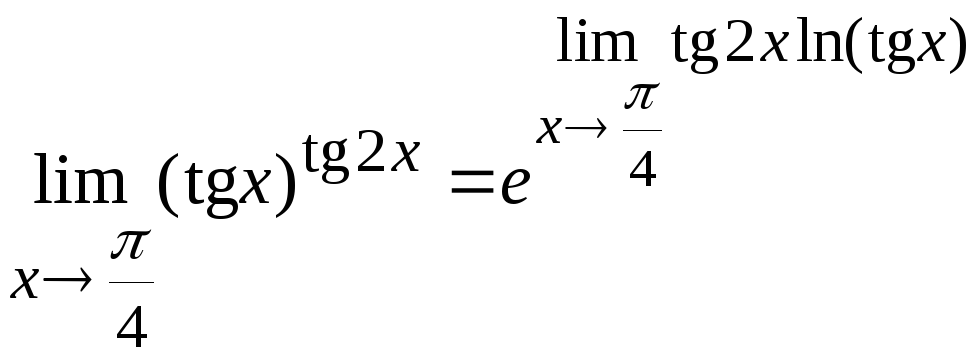
Вычислим
предел, стоящий в показателе степени.
Для этого требуется раскрыть
неопределенность типа
.
Преобразуем ее в неопределенность типа

и воспользуемся эквивалентностью
бесконечно малых:

Ответ:
.

Задача
16. Вычислить
.

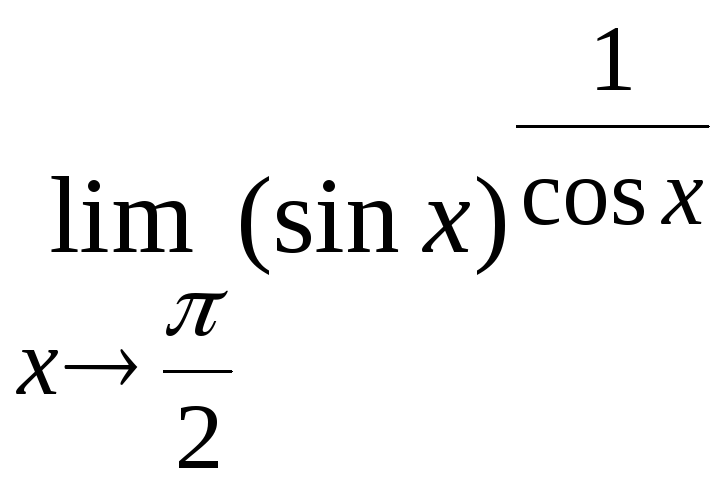
Решение.
Здесь возникает неопределенность типа

.
Преобразуем исходное предельное
выражение

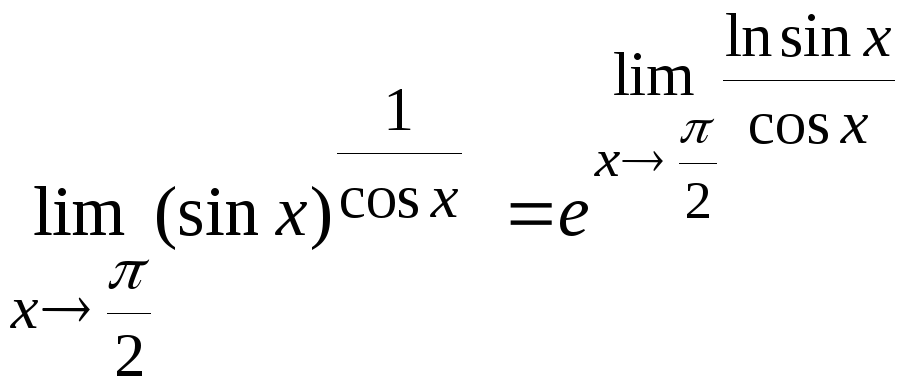
Вычислим
предел, стоящий в показателе степени.

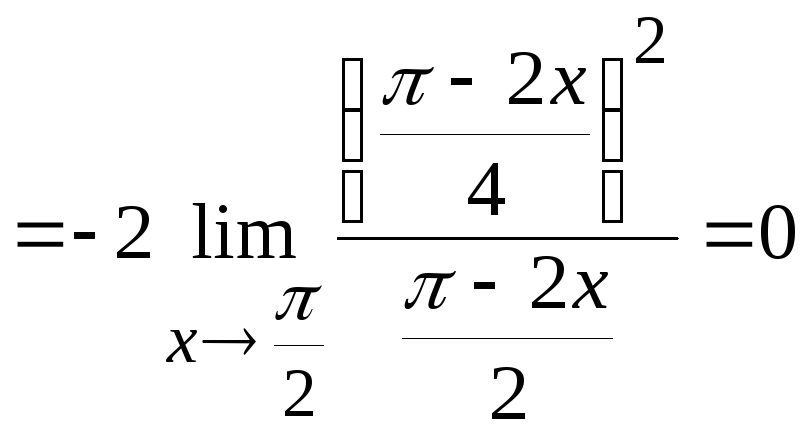
Ответ:
.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Второй замечательный предел

Обычно второй замечательный предел записывают в такой форме:

$$
begin{equation}
lim_{xtoinfty}left(1+frac{1}{x}right)^x=e
end{equation}
$$

Число $e$, указанное в правой части равенства (1), является иррациональным. Приближённое значение этого числа таково: $eapprox{2{,}718281828459045}$. Если сделать замену $t=frac{1}{x}$, то формулу (1) можно переписать в следующем виде:

$$
begin{equation}
lim_{tto{0}}biggl(1+tbiggr)^{frac{1}{t}}=e
end{equation}
$$

Как и для первого замечательного предела, неважно, какое выражение стоит вместо переменной $x$ в формуле (1) или вместо переменной $t$ в формуле (2). Главное – выполнение двух условий:

Основание степени (т.е. выражение в скобках формул (1) и (2)) должно стремиться к единице;
Показатель степени (т.е. $x$ в формуле (1) или $frac{1}{t}$ в формуле (2)) должен стремиться к бесконечности.

Говорят, что второй замечательный предел раскрывает неопределенность $1^infty$. Заметьте, что в формуле (1) мы не уточняем, о какой именно бесконечности ($+infty$ или $-infty$) идёт речь. В любом из этих случаев формула (1) верна. В формуле (2) переменная $t$ может стремиться к нулю как слева, так и справа.

Отмечу, что есть также несколько полезных следствий из второго замечательного предела. Примеры на использование второго замечательного предела, равно как и следствий из него, очень популярны у составителей стандартных типовых расчётов и контрольных работ.

Пример №1

Вычислить предел $lim_{xtoinfty}left(frac{3x+1}{3x-5}right )^{4x+7}$.

Решение

Сразу отметим, что основание степени (т.е. $frac{3x+1}{3x-5}$) стремится к единице:

$$
lim_{xtoinfty}frac{3x+1}{3x-5}=left|frac{infty}{infty}right|
=lim_{xtoinfty}frac{3+frac{1}{x}}{3-frac{5}{x}}
=frac{3+0}{3-0}
=1.
$$

При этом показатель степени (выражение $4x+7$) стремится к бесконечности, т.е. $lim_{xtoinfty}(4x+7)=infty$.

Основание степени стремится к единице, показатель степени – к бесконечности, т.е. мы имеем дело с неопределенностью $1^infty$. Применим формулу (1) для раскрытия этой неопределённости. В основании степени формулы (1) расположено выражение $1+frac{1}{x}$, а в рассматриваемом нами примере основание степени таково: $frac{3x+1}{3x-5}$. Посему первым действием станет формальная подгонка выражения $frac{3x+1}{3x-5}$ под вид $1+frac{1}{x}$. Для начала прибавим и вычтем единицу:

$$
lim_{xtoinfty}left(frac{3x+1}{3x-5}right )^{4x+7}
=|1^infty|
=lim_{xtoinfty}left(1+frac{3x+1}{3x-5}-1right)^{4x+7}
$$

Следует учесть, что просто так добавить единицу нельзя. Если мы вынуждены добавить единицу, то её же нужно и вычесть, дабы не изменять значения всего выражения. Для продолжения решения учтём, что

$$
frac{3x+1}{3x-5}-1
=frac{3x+1}{3x-5}-frac{3x-5}{3x-5}
=frac{3x+1-3x+5}{3x-5}
=frac{6}{3x-5}.
$$

Так как $frac{3x+1}{3x-5}-1=frac{6}{3x-5}$, то:

$$
lim_{xtoinfty}left(1+ frac{3x+1}{3x-5}-1right)^{4x+7}
=lim_{xtoinfty}left(1+frac{6}{3x-5}right )^{4x+7}
$$

Продолжим «подгонку». В выражении $1+frac{1}{x}$ формулы (1) в числителе дроби находится 1, а в нашем выражении $1+frac{6}{3x-5}$ в числителе находится $6$. Чтобы получить $1$ в числителе, опустим $6$ в знаменатель с помощью следующего преобразования:

$$
1+frac{6}{3x-5}
=1+frac{1}{frac{3x-5}{6}}
$$

Таким образом,

$$
lim_{xtoinfty}left(1+frac{6}{3x-5}right )^{4x+7}
=lim_{xtoinfty}left(1+frac{1}{frac{3x-5}{6}}right )^{4x+7}
$$

Итак, основание степени, т.е. $1+frac{1}{frac{3x-5}{6}}$, подогнано под вид $1+frac{1}{x}$, который требуется в формуле (1). Теперь начнём работать с показателем степени. Заметьте, что в формуле (1) выражения, стоящие в показатели степени и в знаменателе, одинаковы:

Значит, и в нашем примере показатель степени и знаменатель нужно привести к одинаковой форме. Чтобы получить в показателе степени выражение $frac{3x-5}{6}$, просто домножим показатель степени на эту дробь. Естественно, что для компенсации такого домножения, придется тут же домножить на обратную дробь, т.е. на $frac{6}{3x-5}$. Итак, имеем:

$$
lim_{xtoinfty}left(1+frac{1}{frac{3x-5}{6}}right )^{4x+7}
=lim_{xtoinfty}left(1+frac{1}{frac{3x-5}{6}}right )^{frac{3x-5}{6}cdotfrac{6}{3x-5}cdot(4x+7)}
=lim_{xtoinfty}left(left(1+frac{1}{frac{3x-5}{6}}right)^{frac{3x-5}{6}}right)^{frac{6cdot(4x+7)}{3x-5}}
$$

Отдельно рассмотрим предел дроби $frac{6cdot(4x+7)}{3x-5}$, расположенной в степени:

$$
lim_{xtoinfty}frac{6cdot(4x+7)}{3x-5}
=left|frac{infty}{infty}right|
=lim_{xtoinfty}frac{6cdotleft(4+frac{7}{x}right)}{3-frac{5}{x}}
=6cdotfrac{4}{3}
=8.
$$

Согласно формуле (1) имеем $lim_{xtoinfty}left(1+frac{1}{frac{3x-5}{6}}right )^{frac{3x-5}{6}}=e$. Кроме того, $lim_{xtoinfty}frac{6cdot(4x+7)}{3x-5}=8$, поэтому возвращаясь к исходному пределу, получим:

$$
lim_{xtoinfty}left(left(1+frac{1}{frac{3x-5}{6}}right )^{frac{3x-5}{6}}right)^{frac{6cdot(4x+7)}{3x-5}}
=e^8.
$$

Полное решение без промежуточных пояснений будет иметь такой вид:

$$
lim_{xtoinfty}left(frac{3x+1}{3x-5}right )^{4x+7}=left|1^inftyright|
=lim_{xtoinfty}left(1+frac{3x+1}{3x-5}-1right)^{4x+7}
=lim_{xtoinfty}left(1+frac{6}{3x-5}right)^{4x+7}=\

=lim_{xtoinfty}left(1+frac{1}{frac{3x-5}{6}}right)^{4x+7}
=lim_{xtoinfty}left(1+frac{1}{frac{3x-5}{6}}right )^{frac{3x-5}{6}cdotfrac{6}{3x-5}cdot(4x+7)}
=lim_{xtoinfty}left(left(1+frac{1}{frac{3x-5}{6}}right)^{frac{3x-5}{6}}right)^{frac{6cdot(4x+7)}{3x-5}}
=e^8.
$$

Кстати сказать, вовсе не обязательно использовать первую формулу. Если учесть, что $frac{6}{3x-5}to{0}$ при $xtoinfty$, то применяя формулу (2), получим:

$$
lim_{xtoinfty}left(frac{3x+1}{3x-5}right )^{4x+7}=left|1^inftyright|
=lim_{xtoinfty}left(1+frac{3x+1}{3x-5}-1right)^{4x+7}
=lim_{xtoinfty}left(1+frac{6}{3x-5}right)^{4x+7}=\

=lim_{xtoinfty}left(1+frac{6}{3x-5}right)^{frac{3x-5}{6}cdotfrac{6}{3x-5}cdot(4x+7)}
=lim_{xtoinfty}left(left(1+frac{6}{3x-5}right)^{frac{3x-5}{6}}right)^{frac{6cdot(4x+7)}{3x-5}}
=e^8.
$$

Ответ: $lim_{xtoinfty}left(frac{3x+1}{3x-5}right)^{4x+7}=e^8$.

Пример №2

Найти предел $lim_{xto{1}}biggl(7-6xbiggr)^{frac{x}{3x-3}}$.

Решение

Выражение, стоящее в основании степени, т.е. $7-6x$, стремится к единице при условии $xto{1}$, т.е. $lim_{xto{1}}(7-6x)=7-6cdot1=1$. Для показателя степени, т.е. $frac{x}{3x-3}$, получаем: $lim_{xto{1}}frac{x}{3x-3}=infty$. Итак, здесь мы имеем дело с неопределенностью вида $1^infty$, которую раскроем с помощью второго замечательного предела.

Для начала отметим, что в формуле (1) переменная $x$ стремится к бесконечности, в формуле (2) переменная $t$ стремится к нулю. В нашем случае $xto{1}$, поэтому имеет смысл ввести новую переменную, чтобы она стремилась или к нулю (тогда применим формулу (2)), или к бесконечности (тогда применим формулу (1)). Введение новой переменной, вообще говоря, не является обязательным, это будет сделано просто для удобства решения. Проще всего новую переменную $y$ ввести так: $y=x-1$. Так как $xto{1}$, то ${x-1}to{0}$, т.е. $yto{0}$. Подставляя $x=y+1$ в рассматриваемый пример, и учитывая $yto{0}$, получим:

$$
lim_{xto{1}}biggl(7-6xbiggr )^{frac{x}{3x-3}}
=left|begin{aligned}&y=x-1;;x=y+1\&yto{0}end{aligned}right|=\
=lim_{yto{0}}biggl(7-6cdot(y+1)biggr)^{frac{y+1}{3cdot(y+1)-3}}
=lim_{yto{0}}biggl(1-6ybiggr)^frac{y+1}{3y}
=lim_{yto 0}biggl(1+(-6y)biggr)^frac{y+1}{3y}
$$

Применим формулу (2). Выражение в основании степени в формуле (2), т.е. $1+t$, соответствует форме выражения в основании степени нашего примера, т.е. $1+(-6y)$ (выражение $-6y$ играет роль $t$). Формула (2) предполагает, что показатель степени будет иметь вид $frac{1}{t}$, т.е. в нашем случае в показателе степени следует получить $frac{1}{-6y}$. Домножим показатель степени на выражение $frac{1}{-6y}$. Для компенсации такого домножения нужно домножить показатель степени на обратную дробь, т.е. на выражение $frac{-6y}{1}=-6y$:

$$
lim_{yto{0}}biggl(1-6ybiggr)^frac{y+1}{3y}=lim_{yto{0}}biggl(1+(-6y)biggr)^{frac{1}{-6y}cdot(-6y)cdotfrac{y+1}{3y}}
=lim_{yto{0}}left(biggl(1+(-6y)biggr)^{frac{1}{-6y}}right)^{-2(y+1)}
$$

Так как $lim_{yto{0}}biggl(1+(-6y)biggr)^{frac{1}{-6y}}=e$ и $lim_{yto{0}}(-2(y+1))=-2$, то получим:

$$
lim_{yto{0}}left(biggl(1+(-6y)biggr)^{frac{1}{-6y}}right)^{-2(y+1)}
=e^{-2}
=frac{1}{e^2}.
$$

Полное решение без пояснений таково:

$$
lim_{xto{1}}biggl(7-6xbiggr)^{frac{x}{3x-3}}
=left|begin{aligned}&y=x-1;;x=y+1\&yto{0}end{aligned}right|
=lim_{yto{0}}biggl(7-6cdot(y+1)biggr)^{frac{y+1}{3cdot(y+1)-3}}=\

=lim_{yto{0}}biggl(1-6ybiggr)^frac{y+1}{3y}
=lim_{yto{0}}biggl(1+(-6y)biggr)^{frac{1}{-6y}cdot(-6y)cdotfrac{y+1}{3y}}
=lim_{yto{0}}left(biggl(1+(-6y)biggr)^{frac{1}{-6y}}right)^{-2(y+1)}
=e^{-2}
=frac{1}{e^2}.
$$

Ответ: $lim_{xto{1}}biggl(7-6xbiggr)^{frac{x}{3x-3}}=frac{1}{e^2}$.

Пример №3

Найти предел $lim_{xto{0}}biggl(cos{2x}biggr)^{frac{1}{sin^2{3x}}}$.

Решение

Так как $lim_{xto{0}}(cos{2x})=1$ и $lim_{xto{0}}frac{1}{sin^2{3x}}=infty$ (напомню, что $sin{u}to{0}$ при $uto{0}$), то мы имеем дело с неопределённостью вида $1^infty$. Преобразования, аналогичные рассмотренным в примерах №1 и №2, укажем без подробных пояснений, ибо они были даны ранее:

$$
lim_{xto{0}}biggl(cos{2x}biggr)^{frac{1}{sin^2{3x}}}
=|1^infty|
=lim_{xto{0}}biggl(1+cos{2x}-1biggr)^{frac{1}{sin^2{3x}}}
$$

Так как $sin^2x=frac{1-cos{2x}}{2}$, то $cos{2x}-1=-2sin^2x$, поэтому:

$$
lim_{xto{0}}biggl(1+cos{2x}-1biggr)^{frac{1}{sin^2{3x}}}
=lim_{xto{0}}biggl(1+left(-2sin^2xright)biggr)^{frac{1}{-2sin^2x}cdot(-2sin^2x)cdotfrac{1}{sin^2 3x}}=\

=lim_{xto{0}}left(biggl(1+left(-2sin^2xright)biggr)^{frac{1}{-2sin^2x}}right)^{frac{-2sin^2{x}}{sin^2{3x}}}
=e^{-frac{2}{9}}.
$$

Здесь мы учли, что $lim_{xto{0}}frac{sin^2{x}}{sin^2{3x}}=frac{1}{9}$. Подробное описание того, как находить этот предел, дано в соответствующей теме.

Ответ: $lim_{xto{0}}biggl(cos{2x}biggr)^{frac{1}{sin^2{3x}}}=e^{-frac{2}{9}}$.

Пример №4

Найти предел $lim_{xto+infty}xleft(ln(x+1)-ln{x}right)$.

Решение

Так как при $x>0$ имеем $ln(x+1)-ln{x}=lnleft(frac{x+1}{x}right)$, то:

$$
lim_{xto+infty}xleft(ln(x+1)-ln{x}right)
=lim_{xto+infty}left(xcdotlnleft(frac{x+1}{x}right)right)
$$

Раскладывая дробь $frac{x+1}{x}$ на сумму дробей $frac{x+1}{x}=1+frac{1}{x}$ получим:

$$
lim_{xto+infty}left(xcdotlnleft(frac{x+1}{x}right)right)
=lim_{xto+infty}left(xcdotlnleft(1+frac{1}{x}right)right)
=lim_{xto+infty}left(lnleft(frac{x+1}{x}right)^xright)
=ln{e}
=1.
$$

Ответ: $lim_{xto+infty}xleft(ln(x+1)-ln{x}right)=1$.

Пример №5

Найти предел $lim_{xto{2}}biggl(3x-5biggr)^{frac{2x}{x^2-4}}$.

Решение

Так как $lim_{xto{2}}(3x-5)=6-5=1$ и $lim_{xto{2}}frac{2x}{x^2-4}=infty$, то мы имеем дело с неопределенностью вида $1^infty$. Подробные пояснения даны в примере №2, здесь же ограничимся кратким решением. Сделав замену $t=x-2$, получим:

$$
lim_{xto{2}}biggl(3x-5biggr)^{frac{2x}{x^2-4}}
=left|begin{aligned}&t=x-2;;x=t+2\&tto{0}end{aligned}right|
=lim_{tto{0}}biggl(1+3tbiggr)^{frac{2t+4}{t^2+4t}}=\

=lim_{tto{0}}biggl(1+3tbiggr)^{frac{1}{3t}cdot 3tcdotfrac{2t+4}{t^2+4t}}
=lim_{tto{0}}left(biggl(1+3tbiggr)^{frac{1}{3t}}right)^{frac{6cdot(t+2)}{t+4}}
=e^3.
$$

Можно решить данный пример и по-иному, используя замену: $t=frac{1}{x-2}$. Разумеется, ответ будет тем же:

$$
lim_{xto{2}}biggl(3x-5biggr)^{frac{2x}{x^2-4}}
=left|begin{aligned}&t=frac{1}{x-2};;x=frac{2t+1}{t}\&ttoinftyend{aligned}right|
=lim_{ttoinfty}left(1+frac{3}{t}right)^{tcdotfrac{4t+2}{4t+1}}=\

=lim_{ttoinfty}left(1+frac{1}{frac{t}{3}}right)^{frac{t}{3}cdotfrac{3}{t}cdotfrac{tcdot(4t+2)}{4t+1}}
=lim_{ttoinfty}left(left(1+frac{1}{frac{t}{3}}right)^{frac{t}{3}}right)^{frac{6cdot(2t+1)}{4t+1}}
=e^3.
$$

Ответ: $lim_{xto{2}}biggl(3x-5biggr)^{frac{2x}{x^2-4}}=e^3$.

Пример №6

Найти предел $lim_{xtoinfty}left(frac{2x^2+3}{2x^2-4}right)^{3x} $.

Решение

Выясним, к чему стремится выражение $frac{2x^2+3}{2x^2-4}$ при условии $xtoinfty$:

$$
lim_{xtoinfty}frac{2x^2+3}{2x^2-4}
=left|frac{infty}{infty}right|
=lim_{xtoinfty}frac{2+frac{3}{x^2}}{2-frac{4}{x^2}}
=frac{2+0}{2-0}=1.
$$

Таким образом, в заданном пределе мы имеем дело с неопределенностью вида $1^infty$, которую раскроем с помощью второго замечательного предела:

$$
lim_{xtoinfty}left(frac{2x^2+3}{2x^2-4}right)^{3x}
=|1^infty|
=lim_{xtoinfty}left(1+frac{2x^2+3}{2x^2-4}-1right)^{3x}=\

=lim_{xtoinfty}left(1+frac{7}{2x^2-4}right)^{3x}
=lim_{xtoinfty}left(1+frac{1}{frac{2x^2-4}{7}}right)^{3x}=\

=lim_{xtoinfty}left(1+frac{1}{frac{2x^2-4}{7}}right)^{frac{2x^2-4}{7}cdotfrac{7}{2x^2-4}cdot 3x}
=lim_{xtoinfty}left(left(1+frac{1}{frac{2x^2-4}{7}}right)^{frac{2x^2-4}{7}}right)^{frac{21x}{2x^2-4}}
=e^0
=1.
$$

Ответ: $lim_{xtoinfty}left(frac{2x^2+3}{2x^2-4}right)^{3x}=1$.

Источник

При вычислении пределов от показательно-степенной функции пользуются либо формулой 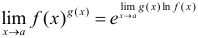, либо вторым замечательным пределом.

Пример №1.

Вычислить .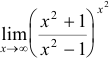

Решение:

, так как

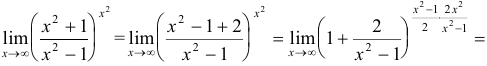
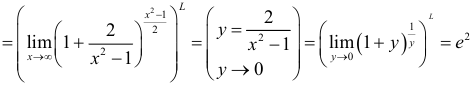
Пример №1.

Вычислить .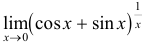

Решение:

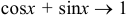
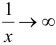
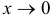
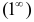
Заметим, что , а при . Следовательно, имеется неопределенность вида . Для ее раскрытия воспользуемся вторым замечательным пределом. Получим, что

так как

Пример №2.

Вычислить .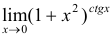

Решение:

в силу непрерывности . Вычислим

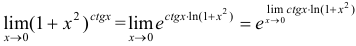
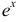
Следовательно, .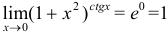

Пример №3.

Вычислить .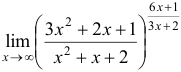

Решение:

Так как 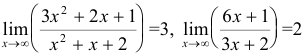, то в данном случае отсутствует неопределенность и

На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:

Высшая математика краткий курс лекций для заочников

Возможно вам будут полезны эти страницы:

Источник

Предел показательно степенной функции, примеры нахождения

В процессе нахождения предела показательно-степенной функции типа lim x → x 0 ( f ( x ) ) g ( x ) часто работаем с такими степенными неопределенностями, как 1 ∞ , 0 0 , ∞ 0 .

Для их раскрытия необходимо задействовать логарифмирование a = e ln ( a ) , свойство логарифма a · ln ( b ) = ln ( b a ) и применение его предела заданной непрерывной функции, причем ее знак разрешено менять местами.

Для этого производятся преобразования вида:

lim x → x 0 ( f ( x ) ) g ( x ) = e ln lim x → x 0 f ( x ) ) g ( x ) = e lim x → x 0 ( ln ( f ( x ) ) g ( x ) = e lim x → x 0 ( g ( x ) ln ( f ( x ) ) ) = = e lim x → x 0 ln ( f ( x ) ) 1 g ( x )

Отсюда видно, что задание приводится к нахождению предела заданной функции вида e lim x → x 0 ln ( f ( x ) ) 1 g ( x ) = ∞ ∞ или 0 0 .

Данный случай рассматривает методы:

непосредственного вычисления;
использования правила Лопиталя;
с заменой эквивалентных бесконечно малых функций;
применение первого замечательного предела.

Для того, чтобы неопределенность была раскрыта, необходимо применять второй замечательный предел, при наличии 1 ∞ .

Рассмотрим теорию на элементарных примерах заданий.

Найти предел заданной функции lim x → 0 ( x 3 + 2 x + 1 ) 3 2 x 3 + x .

Для решения необходимо произвести подстановку. Получаем :

lim x → 0 ( x 3 + 2 x + 1 ) 3 2 ( x 3 + x ) = ( 0 3 + 2 · 0 + 1 ) 3 2 ( 0 3 + 0 ) = 1 ∞

Получение единицы в степени бесконечность называют неопределенностью, значит, необходимо решить другим методом.

Следует произвести преобразования данного предела. Получаем:

lim x → 0 ( x 3 + 2 x + 1 ) 3 2 ( x 3 + x ) = e ln lim x → 0 ( x 3 + 2 x + 1 ) 3 2 ( x 3 + x ) = = e lim x → 0 ln ( x 3 + 2 x + 1 ) 3 2 ( x 3 + x ) = e lim x → 0 3 ln ( x 3 + 2 x + 1 ) 2 ( x 3 + x )

Видим, что преобразование сводится к пределу вида lim x → 0 3 ln ( x 3 + 2 x + 1 ) 2 ( x 3 + x ) .

lim x → 0 3 ln ( x 3 + 2 x + 1 2 ( x 3 + x ) = 0 0 = 3 2 lim x → 0 ln ( x 3 + 2 x + 1 ) x 3 + x = = 3 2 lim x → 0 x 3 + 2 x x 3 + x = 3 2 lim x → 0 x 2 + 2 x 2 + 1 = 3 2 · 0 2 + 2 0 2 + 1 = 3

Данные преобразования были выполнены при помощи применения замены логарифма на эквивалентную бесконечно малую функцию.

Тогда исходный предел принимает вид lim x → 0 ( x 2 + 2 x + 1 ) 3 2 ( x 3 + x ) = e 3 .

Вычисление данного предела возможно с применением второго замечательного предела. Тогда получаем:

lim x → 0 ( x 2 + 2 x + 1 ) 3 2 ( x 3 + x ) = lim x → 0 ( 1 + ( x 3 + 2 x ) 1 x 3 + 2 x ( x 3 + 2 x ) 3 2 ( x 3 + x ) = = lim x → 0 ( 1 + ( x 3 + 2 x ) ) 1 x 3 + 2 x 3 ( x 3 + 2 x ) 2 ( x 3 + x ) = lim x → 0 1 + ( x 3 + 2 x ) ) 1 x 3 + 2 x 3 ( x 2 + 2 ) 2 ( x 2 + 1 ) = = lim x → 0 ( 1 + ( x 3 + 2 x ) 1 x 3 + 2 x 3 = e 3

Найти и вычислить предел lim x → π 2 ( t g x ) 2 c o s x

Если произведем подстановку, в результате получим ответ в виде бесконечности в степени ноль, а это является знаком, что необходимо применить другой метод для преобразования. Получаем:

lim x → π 2 ( t g x ) 2 c o s x = ∞ 0 = e ln lim x → π 2 ( t g x ) 2 cos x = = e 2 lim x → π 2 ( t g x ) 2 cos x = e lim x → π 2 ( 2 cos x · ln · ( t g x ) ) = = e 2 lim x → π 2 ln ( t g x ) 1 cos x

Отсюда видно, что решение сводится к переделу lim x → π 2 ln ( t g x ) 1 cos x = ∞ ∞ .

Для дальнейшего преобразования применим правило Лопиталя, так как получили неопределенность в виде частного бесконечностей. Видим, что

lim x → π 2 ln ( t g x ) 1 cos x = ∞ ∞ = lim x → π 2 = ln ( t g x ) ‘ 1 cos ( x ) ‘ = = lim x → π 2 1 t g ( x ) · 1 cos 2 ( x ) sin ( x ) cos 2 ( x ) = lim x → π 2 cos ( x ) sin 2 ( x ) = cos π 2 sin 2 π 2 = 0 1 2 = 0

Отсюда следует, что пределом показательно-степенной функции является результат, полученный при вычислении. Имеем вы предел вида lim x → π 2 ( t g x ) 2 cos x = e 2 · 0 = e 0 = 1 .

Второй замечательный предел

Обычно второй замечательный предел записывают в такой форме:

Число $e$, указанное в правой части равенства (1), является иррациональным. Приближённое значение этого числа таково: $eapprox718281828459045>$. Если сделать замену $t=frac$, то формулу (1) можно переписать в следующем виде:

Основание степени (т.е. выражение в скобках формул (1) и (2)) должно стремиться к единице;
Показатель степени (т.е. $x$ в формуле (1) или $frac$ в формуле (2)) должен стремиться к бесконечности.

Сразу отметим, что основание степени (т.е. $frac$) стремится к единице:

При этом показатель степени (выражение $4x+7$) стремится к бесконечности, т.е. $lim_(4x+7)=infty$.

Основание степени стремится к единице, показатель степени – к бесконечности, т.е. мы имеем дело с неопределенностью $1^infty$. Применим формулу (1) для раскрытия этой неопределённости. В основании степени формулы (1) расположено выражение $1+frac$, а в рассматриваемом нами примере основание степени таково: $frac$. Посему первым действием станет формальная подгонка выражения $frac$ под вид $1+frac$. Для начала прибавим и вычтем единицу:

Продолжим «подгонку». В выражении $1+frac$ формулы (1) в числителе дроби находится 1, а в нашем выражении $1+frac$ в числителе находится $6$. Чтобы получить $1$ в числителе, опустим $6$ в знаменатель с помощью следующего преобразования:

Итак, основание степени, т.е. $1+frac>$, подогнано под вид $1+frac$, который требуется в формуле (1). Теперь начнём работать с показателем степени. Заметьте, что в формуле (1) выражения, стоящие в показатели степени и в знаменателе, одинаковы:

Значит, и в нашем примере показатель степени и знаменатель нужно привести к одинаковой форме. Чтобы получить в показателе степени выражение $frac$, просто домножим показатель степени на эту дробь. Естественно, что для компенсации такого домножения, придется тут же домножить на обратную дробь, т.е. на $frac$. Итак, имеем:

Отдельно рассмотрим предел дроби $frac$, расположенной в степени:

Согласно формуле (1) имеем $lim_left(1+frac>right )^>=e$. Кроме того, $lim_frac=8$, поэтому возвращаясь к исходному пределу, получим:

Полное решение без промежуточных пояснений будет иметь такой вид:

Кстати сказать, вовсе не обязательно использовать первую формулу. Если учесть, что $fracto$ при $xtoinfty$, то применяя формулу (2), получим:

Выражение, стоящее в основании степени, т.е. $7-6x$, стремится к единице при условии $xto$, т.е. $lim_>(7-6x)=7-6cdot1=1$. Для показателя степени, т.е. $frac$, получаем: $lim_>frac=infty$. Итак, здесь мы имеем дело с неопределенностью вида $1^infty$, которую раскроем с помощью второго замечательного предела.

Для начала отметим, что в формуле (1) переменная $x$ стремится к бесконечности, в формуле (2) переменная $t$ стремится к нулю. В нашем случае $xto$, поэтому имеет смысл ввести новую переменную, чтобы она стремилась или к нулю (тогда применим формулу (2)), или к бесконечности (тогда применим формулу (1)). Введение новой переменной, вообще говоря, не является обязательным, это будет сделано просто для удобства решения. Проще всего новую переменную $y$ ввести так: $y=x-1$. Так как $xto$, то $to$, т.е. $yto$. Подставляя $x=y+1$ в рассматриваемый пример, и учитывая $yto$, получим:

Применим формулу (2). Выражение в основании степени в формуле (2), т.е. $1+t$, соответствует форме выражения в основании степени нашего примера, т.е. $1+(-6y)$ (выражение $-6y$ играет роль $t$). Формула (2) предполагает, что показатель степени будет иметь вид $frac$, т.е. в нашем случае в показателе степени следует получить $frac$. Домножим показатель степени на выражение $frac$. Для компенсации такого домножения нужно домножить показатель степени на обратную дробь, т.е. на выражение $frac=-6y$:

Полное решение без пояснений таково:

Так как $lim_>(cos)=1$ и $lim_>frac>=infty$ (напомню, что $sinto$ при $uto$), то мы имеем дело с неопределённостью вида $1^infty$. Преобразования, аналогичные рассмотренным в примерах №1 и №2, укажем без подробных пояснений, ибо они были даны ранее:

Так как $sin^2x=frac>$, то $cos-1=-2sin^2x$, поэтому:

Здесь мы учли, что $lim_>frac>>=frac$. Подробное описание того, как находить этот предел, дано в соответствующей теме.

Так как при $x>0$ имеем $ln(x+1)-ln=lnleft(fracright)$, то:

Раскладывая дробь $frac$ на сумму дробей $frac=1+frac$ получим:

Так как $lim_>(3x-5)=6-5=1$ и $lim_>frac=infty$, то мы имеем дело с неопределенностью вида $1^infty$. Подробные пояснения даны в примере №2, здесь же ограничимся кратким решением. Сделав замену $t=x-2$, получим:

Можно решить данный пример и по-иному, используя замену: $t=frac$. Разумеется, ответ будет тем же:

Выясним, к чему стремится выражение $frac$ при условии $xtoinfty$:

Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).

Замечательные пределы: Первый и второй замечательный предел.

Понятие замечательных пределов используется на просторах бывшего Советского Союза для обозначения хорошо известных математических тождеств со взятием предела. Замечательны они потому, что они уже доказаны великими математиками и нам нам остается лишь пользоваться ими для удобства нахождения пределов. Из них наиболее известны первый и второй замечательные пределы. Дальнейшее чтение статье будет намного интереснее, если вы уже знакомы с понятием пределов. Если для вас lim , это то что новое, то рекомендуем к прочтению статью «Пределы. Понятие пределов. Вычисление пределов.»

Теперь со спокойной душой переходим к рассмотрению замечательных пределов.
Первый замечательный предел имеет вид .

Вместо переменной х могут присутствовать различные функции, главное, чтобы они стремились к 0.

Необходимо вычислить предел

Как видно, данный предел очень похож на первый замечательный, но это не совсем так. Вообще, если Вы замечаете в пределе sin, то надо сразу задуматься о том, возможно ли применение первого замечательного предела.

Согласно нашему правилу №1 подставим вместо х ноль:

Получаем неопределенность .

Теперь попробуем самостоятельно организовать первый замечательный предел. Для этого проведем нехитрую комбинацию:

Таким образом мы организовываем числитель и знаменатель так, чтобы выделить 7х. Вот уже и проявился знакомый замечательный предел. Желательно при решении выделять его:

Подставим решение первого замечательного примера и получаем:

Как видите – все очень просто.

Второй замечательный предел имеет вид , где e = 2,718281828… – это иррациональное число.

Вместо переменной х могут присутствовать различные функции, главное, чтобы они стремились к .

Необходимо вычислить предел

Здесь мы видим наличие степени под знаком предела, значит возможно применение второго замечательного предела.

Как всегда воспользуемся правилом №1 – подставим вместо х:

Видно, что при х основание степени , а показатель – 4x > , т.е. получаем неопределенность вида :

Воспользуемся вторым замечательным пределом для раскрытия нашей неопределенности, но сначала надо его организовать. Как видно – надо добиться присутствия в показателе, для чего возведем основание в степень 3х, и одновременно в степень 1/3x, чтобы выражение не менялось:

Не забываем выделять наш замечательный предел:

Дальше знак предела перемещаем в показатель:

Вот такие действительно замечательные пределы!
Если у вас остались какие то вопросы по первому и второму замечательным пределам, то смело задавайте их в комментариях.
Всем по возможности ответим.

Также вы можете позаниматься с педагогом по этой теме.

Мы рады предложить вам услуги подбора квалифицированного репетитора в вашем городе. Наши партнеры оперативно подберут для вас хорошего преподавателя на выгодных для вас условиях.

Источник