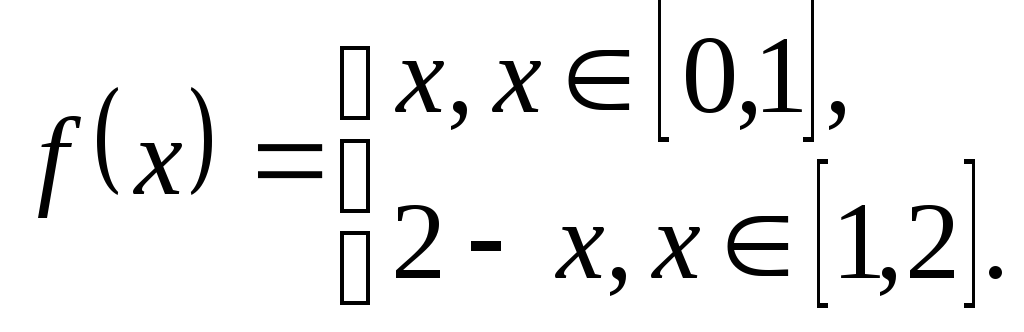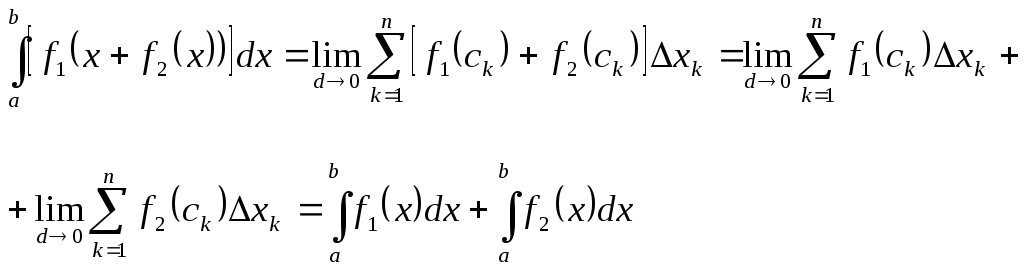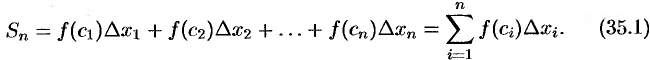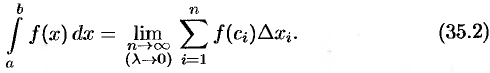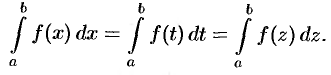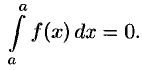Здесь напрашивается способ сведения к интегральным суммам. Слагаемое номер $%k$% имеет вид $%frac{k}{n^2+k^2}=frac1ncdotfrac{k/n}{1+(k/n)^2}$%. Вводим функцию $%f(x)=frac{x}{1+x^2}$% на отрезке $%xin[0;1]$%, и тогда выражение под знаком предела имеет вид интегральной суммы $%frac{f(1/n)+f(2/n)+cdots+f(n/n)}n$% при разбиении отрезка на $%n$% равных частей.
При $%ntoinfty$% такие суммы стремятся к значению определённого интеграла $%intlimits_0^1f(x),dx=intlimits_0^1frac{x,dx}{1+x^2}=frac12ln2$% (первообразная равна $%frac12ln(1+x^2)$%).
Пусть
на отрезке
,
где b>a, задана функция.
Выполним следующие четыре операции:
-
разобьем
отрезок
на части точками
Положим
.
Набор точек деленияназовем разбиением отрезка
,
а величину d –диаметром разбиения; -
на
каждом отрезке
выберем какую-нибудь точку
,
вычислим значениев этой точке. Точки
назовем отмеченными точками;
-
умножим
значение
на длину соответствующего отрезка
и сложим все найденные произведения.
Суммы вида
,
где
(4)
назовем
(одномерными) интегральными
суммами Римана
для функции f по заданному разбиению
отрезка
;
-
измельчим
разбиение
,
т.е. добавим новые точки деления и найдем
предел интегральных сумм (4) при(если
он существует).
Введем
понятие предела интегральных сумм
при
.
Определение
1. Число I
называется пределом интегральных сумм
Римана
при
,
если для любогосуществует
такое, что
при любом разбиении
отрезка
с диаметром разбиения
независимо от выбора отмеченных точек
.
Принята
следующая запись этого определения:
.
Замечание.
Очевидно, что число I не зависит от
разбиения
отрезка
и от выбора
отмеченных точек
.
Определение
2. Если
интегральные суммы Римана (4) имеют
предел при
,
то этот предел называется определенным
(однократным) интегралом от функции f
по отрезкуи обозначается
.
Итак, по определению имеем
(5)
В
этом случае функцию f называют интегрируемой
по Риману на отрезке
.
Числа a, b называют соответственно нижним
и верхним пределами интегрирования,
функцию f – подынтегральной функцией,
а выражение— подынтегральным выражением.
Замечания:
-
Определение
2 можно кратко сформулировать так:
определенным интегралом от заданной
функции по заданному отрезку называется
предел интегральных сумм Римана для
заданной функции при стремлении к нулю
диаметров разбиений отрезков, порождающих
интегральные суммы. -
Так
как другие интегралы мы не рассматриваем,
то вместо термина “интеграл Римана”
будем просто употреблять интеграл.
В
приведенных выше определениях существенно
предполагалось, что
.
Обобщим
понятие определенного интеграла на
случай
и
.
3. Основные свойства определенного интеграла.
При
по определения полагаем
(6)
Равенство
(6) означает, что при перемене пределов
интегрирования знак определенного
интеграла меняется на противоположный.
При
по определению полагаем
(7)
Равенство (7)
означает, что определенный интеграл с
совпадающими пределами интегрирования
равен нулю.
Так
как интегральная сумма (4) не зависит от
того, какой буквой обозначен аргумент
данной функции, то и ее предел, т.е.
определенный интеграл не зависит от
обозначения переменной интегрирования:
.
Приведем условия,
при которых функция является интегрируемой.
Теорема
1. (необходимое
условие интегрируемости).
Если
функция f интегрируема на отрезке
,
то она ограничена на
этом отрезке.
Доказательство.
Допустим, что интегрируемая на
функция не ограничена на нем. Тогда при
любом разбиенииона окажется неограниченной по крайней
мере на одном из отрезковразбиения. В этом случае, выбирая
различными способами точку,
можно сделать произведениесколь угодно большим. Значит интегральные
суммы становятся сколь угодно большими
за счет только выбора точеки не могут стремиться ни к какому пределу
при.
Следовательно, f не ин6тегрируема на.
Из полученного противоречия и вытекает
доказательство теоремы.
Теорема
2. (достаточное
условие интегрируемости). Непрерывная
на отрезке
функция f интегрируема на этом отрезке.
Замечание.
Свойство непрерывности функции является
лишь достаточным условием ее
интегрируемости. Иными словами могут
существовать разрывные на
,
но интегрируемые на этом отрезке функции.
Пример.
Вычислить интеграл
.
Решение.
Так как функция
непрерывна на
,
то в силу теоремы 2 искомый интеграл
существует. Вычислим его по формуле
(5). Разобьем отрезок интегрированияна n равных частей и построим n полос
одинаковой ширины.
Абсциссы точек разбиения таковы:В качестве отмеченной точки
выберем левый конец
основания k- ой полосы. Составим
интегральную сумму Римана:
так
как выражение в скобках есть сумма n
членов геометрической прогрессии со
знаменателем
которая равна
.
Используя формулу (5), находим
.
Поскольку
имеем
.
На основании
правила Лопиталя получим
Следовательно,
.
Этот
пример показывает, что вычисление
интеграла по формуле (5) громоздко и
вызывает значительные трудности. Поэтому
нам необходимо получить эффективный
метод вычисления определенного интеграла.
Такой метод будет изложен позже; он
является следствием связи между
определенными и неопределенными
интегралами, открытой Ньютоном и
Лейбницем.
Вернемся
к задаче о площади криволинейной
трапеции. Так как правая часть равенства
(2) есть интегральная сумма Римана, то
учитывая формулу (5), получаем: если f(x)
интегрируема и неотрицательна на
,
то определенный интеграл f(x) по отрезкуравен площади криволинейной трапеции,
ограниченной линиями(геометрический смысл определенного
интеграла в случае неотрицательности
подынтегральной функции). Если
подынтегральная функция отрицательная
или меняет знак на,
то в интегральной сумме (2) некоторые
члены будут иметь знак минус. Тогда
предел интегральной суммы, то есть
определенный интеграл, будет равен
алгебраической сумме площадей частей
криволинейной трапеции, причем площади
частей, лежащих выше оси Ox, берутся со
знаком плюс, а площади частей, лежащих
ниже оси Ox, — со знаком минус.
Перейдем
теперь к задаче о пройденном пути. Так
как правая часть формулы (3) есть
интегральная сумма, то в силу формулы
(5), получаем: если скорость v(t) непрерывна
и положительна на
,
то определенный интеграл от скорости
v(t) по отрезку времениравен пути, пройденному точкой от момента
t=a до момента t=b (механический смысл
определенного интеграла).
Пример.
Вычислить
,
где
Решение.
Построим график подынтегральной функции.
В силу геометрического определенного
интеграла имеем
,
где S – площадь прямоугольного треугольника
ABC. Так както
Перечислим
свойства, выраженные равенствами и
неравенствами.
1) Если подынтегральная
функция равна единице, то
(8)
Доказательство.
Составим интегральную сумму; имеем
.
Переходя к пределу при,
получаем равенство (8).
2)
Если A
– некоторое число и функция f(x)
интегрируема на
,
то
(9)
Доказательство.
Составим интегральную сумму для функции
Af(x);
имеем
.
Переходя к пределу при,
получаем равенство (9).
3)
Если
и
— две интегрируемые функции, определенные
на отрезке,
то
(10)
т.е.
интеграл от суммы двух функций равен
сумме интегралов от этих функций.
(Свойство 3)
очевидным образом распространяется на
сумму любого числа интегрируемых
функций)
Доказательство.
Составим интегральную сумму
(11)
4)
Аддитивность интеграла как функции
отрезка интегрирования. Если
интегрируема на отрезке
,
то
(12)
т.е. если отрезок
разделен на части, то интеграл по всему
отрезку равен сумме интегралов по его
частям.
Доказательство.
При разбиении отрезка
на части включим точкуc
в число точек деления. Если
,
то
Каждая
из написанных выше сумм является
интегральной соответственно для отрезков
,
и
.
Переходя к пределу при,
получаем равенство (12).
5)
Если
интегрируема на отрезке
и еслиa,
b,
c
– точки этого отрезка, то
(13)
Доказательство.
Если из точек a,
b
и c
то крайней мере две совпадают, то
равенство (13) очевидно. Пусть все эти
точки различны. Если a<b<c,
то равенство справедливо на основании
свойства 4). Если же c<b<a,
то
,
откуда.
Домножая на (-1) и меняя пределы
интегрирования в третьем интеграле,
получаем формулу (13). Другие случаи
взаимного расположения точек можно
свести к свойству 4).
6)
Монотонность. Если функции
и
интегрируемы и удовлетворяют условию
и нижний предел интеграла не больше
верхнего,
то
(14)
Доказательство. При
a=bравенство
(14) очевидно. Если жеa<b,
то справедливо неравенство.
Переходя к пределу при,
получим требуемое неравенство.
7) Оценка
определенного интеграла. Если
интегрируема на отрезке
и нижний предел интеграла не больше
верхнего иf(x)
удовлетворяет условию,
то
(15)
В частности, если
,
то
Свойство 7) имеет
простой геометрический смысл: в случае,
если подынтегральная функция неотрицательна
на
,
то площадь криволинейной трапеции
больше площади прямоугольника с высотойm, но меньше площади
прямоугольника с высотойM.

Теорема о среднем значении. Если
интегрируема на отрезке
иf(x)
удовлетворяет условию,
тогда существует такое число,
что
(16)
Доказательство. Если
a=bтогда
равенство (16) очевидно. Если,
то положим
(17)
Тогда из неравенств
(15) вытекает, что
,
еслиa<b.
Так как обе части равенства (16) изменяют
знаки при перестановке пределовaиb, то оно справедливо и
приb<a.
Число, определяемое равенством (17),
называетсясредним значениемфункцииfна отрезке.
Из свойства 
следующее свойство.
9) Если
функция f(x)
непрерывна на отрезке,
то найдется значениетакое, что
(18)
Для доказательства
достаточно взять
.
Контрольные
вопросы по теме занятия:
-
Напомните
определение первообразной. -
Дайте
определение определенного интеграла. -
Вспомните
формулу Ньютона-Лейбница.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
02.04.2015132.61 Кб1013.doc
- #
- #
02.04.2015310.78 Кб6014.doc
- #
- #
- #
02.04.2015390.66 Кб2316.doc
- #
- #
Определенный интеграл как предел интегральных сумм
Остановимся на еще одном подходе к задаче о площади криволинейной трапеции, который приводит к несколько иной, более общей трактовке определенного интеграла. Простоты ради по-прежнему будем считать заданную на отрезке [а; Ь] непрерывную функцию у = f(x) неотрицательной, но не обязательно возрастающей — ее график изображен на рис. 8.7.
На чертеже кроме криволинейной трапеции ААВВ изображена ступенчатая фигура, образованная прямоугольни-
ками с основаниями Дг, = Дг2 =. = Ах„ =-, так что правая
верхняя вершина каждого из них лежит на графике данной функции. Площадь S„ этой фигуры выражается в виде суммы площадей всех составляющих ее прямоугольников следующим образом:
Написанное выражение называется интегральной суммой; S„ дает приближенное значение площади S криволинейной трапеции, причем погрешность будет уменьшаться с ростом п, т.е. с увеличением числа прямоугольников. Точное равенство получится, если в интегральной сумме устремить п к бесконечности.
Определение 8.3. Предел последовательности интегральных сумм Sn называется определенным интегралом функции у = f(x) на отрезке [а; Ь]:
Символ J есть стилизованная буква S — от латинского слова «Summa», тот же смысл имеет и греческая буква I (читается: «сигма») используемая для обозначения суммирования.
Таким образом, определенный интеграл есть число, геометрически выражающее площадь криволинейной трапеции.
Проиллюстрируем сказанное на простом примере, в котором несложность выкладок облегчит понимание дела.
Будем рассматривать линейную функцию: у = he, заданную на отрезке [0; й], — в этом случае криволинейная трапеция превращается в треугольник ОВВ (рис. 8.8).
Рис. 8.8
Запишем интегральную сумму S,v выражающую в этом примере площадь составленной из прямоугольников ступенчатой фигуры, «описывающей» треугольник ОВВ:
Несложными тождественными преобразованиями оно приводится к виду:
Перейдем к предел)’ при п—
Замечание. Разумеется, проще найти площадь треугольника ОВВ по формуле Ньютона — Лейбница:
или вообще пе применяя интегралов, а иростр по элементарной формуле, перемножая длины катетов ОВ и ВВ:
Но нашей целью было проследовать в этом примере тем маршрутом, который приводит к определенному интегралу в новом, более общем понимании, которое как раз и отражено в приведенном выше рассуждении Льва Толстого об интегрировании как о суммировании бесконечного числа бесконечно малых элементов: при п —»°° каждое слагаемое в интегральной сумме является бесконечно малым, а число слагаемых стремится к бесконечности.
Определенный интеграл как предел суммы
К понятию определенного интеграла приводят многие физические задачи. В конечном счете, все они сводятся к определению площади криволинейной трапеции.
Рассмотрим плоскую фигуру ограниченную отрезком оси
, двумя вертикальными прямыми
и
, а также кривой
(для определенности мы нарисовали кривую над осью
).
Площадь такой трапеции можно найти приближенно. Для этого разбиваем отрезок на
не обязательно равных частей точками:
,
и на каждом отрезке выберем точку
. Произведение
есть площадь прямоугольника со сторонами
и
. При малых
сумма площадей этих прямоугольников будет мало отличаться от площади всей трапеции. Строгое определение определенного интеграла следующее (интеграл Римана).
Обозначим длину наибольшего отрезка через
. Составим интегральную сумму
. Конечно, эта сумма зависит еще и от самого разбиения и от выбора точек
. Так вот, если предел таких интегральных сумм при
существует, то он называется определенным интегралом от функции
по промежутку
:
Мы не останавливаемся на построении строгой теории интеграла Римана. Отметим только, что кусочно — непрерывные функции интегрируемы по Риману. Хотя теория интеграла Римана вполне законченная, но имеет свои недостатки. В частности, интегралы от неограниченных функций, а также интегралы по неограниченным промежуткам (несобственные интегралы) не существуют, как интегралы Римана.
Приведем несколько примеров, показывающих, как вычисляются определенные интегралы через пределы частичных сумм.
Пример 1 Вычислить определенный интеграл, как предел интегральных сумм, производя надлежащим образом разбиение промежутка интеграции:
.
Разбиение промежутка интегрирования проведем так: .
Значения функции для определенности возьмем в правых концах промежутков.
Воспользуемся формулой: .
Тогда, продолжая дальше цепочку равенств, получим окончательно: 
Пример 2 Вычислить определенный интеграл, как предел интегральных сумм:
.
Разбиение промежутка интегрирования проведем, как и в предыдущем примере:
Оставим интегральные суммы. Значения функции берем в левых концах промежутков:
Воспользуемся формулой для суммы членов геометрической прогрессии:
У нас . В результате получим:
Теперь используем следствие второго замечательного предела:
Согласно этой формуле, закончим вычисления: 
.
Длины волн инфракрасного света достаточно велики, чтобы перемещаться сквозь облака, которые в противном случае блокировали бы наш обзор. Используя большие инфракра сные телескопы, астрономы смогли заглянуть в ядро нашей галактики. Большое количество звезд излучают часть своей электромагнитной энергии в виде видимого света, крошечной части спектра, к которой чувствительны наши глаза.
Так как длина волны коррелирует с энергией, цвет звезды говорит нам, насколько она горячая. Используя телескопы, чувствительные к различным диапазонам длин волн спектра, астрономы получают представление о широком круге объектов и явлений во вселенной.
Пример №1 Постройте центральную симметрию тетраэдра, относительно точки O, изображенных на рисунке 3.
Решение.
Для построения такой центральной симметрии сначала проведем через все точки тетраэдра прямые, каждая из которых будет проходить через точку O. На них построим отрезки, удовлетворяющие условиям |AO|=|A?O|, |BO|=|B?O|, |CO|=|C?O|, |DO|=|D?O| Таким образом, и получим искомую симметрию (рис. 4).
В ряду разных механических движений особенным значением обладают колебания. Это движения и процессы, имеющие периодичность во времени.
В среде электромагнитных явлений также значительное место заняли электромагнитные колебания. В этих колебаниях заряды, токи, электрические и магнитные поля изменяются согласно периодическим законам.
Совет №1 Велосипедист, имеющий скорость 300 м/с, или идеальный газ, оказывающий давление 100 паскалей в большой тепловой машине — это странно.
Определенный интеграл как предел интегральных сумм. Геометрический и экономический смысл
Пусть функция у=f(х) определена на отрезке [а; b], а < b. Выполним следующие действия.
2. В каждом чacтичном отрезке [xi-1; xi], i= 1,2,…, n выберем произвольную точку ci [xi-1; xi] и вычислим значение функции в ней, т. е. величину f(ci).
3. Умножим найденное значение функции f(ci) на длину соответствующего частичного отрезка: f(ci)
4. Составим сумму Sn всех таких произведений:
Сумма вида (1) называется uнтегралънoй суммой функции у=f(х) на отрезке [а; b]. Обозначим через λ длину наибольшего частичного отрезка: (i = 1,2, . ,n).
5. Найдем предел интегральной суммы (1), когда n что .
Если при этом интегральная сумма Sn имеет предел I, который не зависит ни от способа разбиения отрезка [а; b] на частичные отрезки, ни от выбора точек в них, то число I называется определенным интегралом от функции у = f(x) на отрезке [а; b] и обозначается . Таким образом,
Числа а и b называются соответственно нижним и верхним пределом интегрирования, f(x) – подынтегральной функцией, f(x)dx – подынтегральным выражением, х – переменной интегрирования, отрезок [а; b] –областью (отрезком) интегрирования
Функция у = f(x), для которой на отрезке [а; b] существует определенный интеграл , называется интегрируемой на этом отрезке.
Сформулируем теорему существования определенного интеграла.
Теорема (Коши). Если функция у = f(x) непрерывна на отрезке [а; b], то определенный интеграл существует.
Отметим, что непрерывность функции является достаточным условием ее интегрируемости. Однако определенный интеграл может существовать и некоторых разрывных функций, в частности для всякой ограниченной на отрезке функции, имеющей на нем конечное число точек разрыва.
Укажем некоторые свойства определенного интеграла, непосредственно вытекающие из его определения (2).
1. Определенный интеграл не зависит от обозначения переменной интегрирования.
Это следует из того, что интегральная сумма (1), а, следовательно, и ее предел (2) не зависят от того, какой буквой обозначается аргумент данной функции.
2. Определенный интеграл с одинаковыми пределами интегрирования равен нулю:
3. Для любого действительного числа с: .
Площадь криволинейной трапеции. Пусть на отрезке [a;b] задана непрерывная функция у = f(x) 0. Фигура, ограниченная сверху графиком функции у = f(x) , снизу — осью Ох, сбоку — прямыми х = а и х = b, называется криволинейной трапецией. Найдем площадь этой трапеции.
Для этого отрезок [a;b]точками a = x0, x1, …, b=xn (x0 < x1 < … < xn) разобьем на n частичных отрезков [x0,x1], [x1;x2], …, [xn-1;xn]. В каждом частичном отрезке [xi-1;xi] (i=1,2,…n) возьмем произвольную точку сi и вычислим значение функции в ней, т. е. f(ci). Умножим значение функции f(ci) на длину соответствующего частичного отрезка. Произведение f(ci) равно площади прямоугольника с основанием и высотой f(ci). Сумма всех таких произведений
равна площади ступенчатой фигуры и приближенно равна площади S криволинейной трапеции:
С уменьшением всех величин точность приближения криволинейной трапеции ступенчатой фигурой и точность полученной формулы увеличиваются. Поэтому за точное значение площади S криволинейной трапеции принимается предел S, к которому стремится площадь ступенчатой фигуры Sn, когда n неограниченно возрастает так, что :
Итак, определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции.
В этом и состоит геометрический смысл определенного интеграла.
Экономический смысл интеграла. Пусть функция z=f(t) описывает изменение производительности с течением времени. Найдем объем продукции и, произведенной за промежуток времени [0,Т].
Отметим, что если производительность не изменяется с течением времени (f(t) — постоянная функция), то объем продукции , произведенной за некоторый промежуток времени [t, t+ t], задается формулой . В общем случае справедливо приближенное равенство , где , которое оказывается тем более точным, чем меньше . Разобьем отрезок [0,Т] на промежутки времени точками: . Для величины объема продукции , произведенной за промежуток времени , имеем , где . Тогда
При стремлении к нулю каждое из использованных приближенных равенств становится все более точным, поэтому
Учитывая определение определенного интеграла, окончательно получаем
т.е. если f(t) – производительность труда в момент t, то есть объем выпускаемой продукции за промежуток [0,Т].
Сравнение данной задачи с задачей о площади криволинейной трапеции показывает, что величина и объем продукции, произведенной за промежуток времени [0,Т], численно равна площади под графиком функции z=f(t), описывающей изменение производительности труда с течением времени, на промежутке [0,T] или .
I. Вычисление с помощью интегральных сумм. Предварительно изучите по учебнику Г М. Фихтенгольца главу XI, п° 176, 177, 180, 184. Обратите особое внимание на примеры, решенные в п° 184.
Способ вычисления определенных интегралов методом суммирования основан на понятии «интегральных сумм», подробно изложенном в п°п° 176, 184.
321. Вычислить интеграл:
Решение. В теоретическом курсе (п° 176) доказывается, что
где f(x) — непрерывная на сегменте
точка, произвольно выбранная внутри частичного сегмента 
не зависит ни от способа разбиения сегмента
частичные сегменты
внутри каждого из частичных сегментов. Руководствуясь этим, разобьем сегмент [О, I] на п равных частей. Точками деления сегмента будут:

Получим п частичных сегментов:
Длина каждого из частичных сегментов равна

Выберем внутри каждого частичного сегмента наиболее удобное для вычисления положение точек Ii. Пусть это будут самые правые точки каждого частичного сегмента:
Вычислим значение функции /(Ii) в этих точках:
Составим интегральную сумму:
Вычислим предел интегральной суммы при
Таким образом,
Покажем, что и при другом выборе точек

Вычислим значения функции в этих точках:
Составим интегральную сумму:
Вычислим предел полученной интегральной суммы при стремлении к нулю наибольшего из частичных сегментов:
Полученный предел является значением определенного интеграла.
322. Вычислить интеграл:
Решение. Разобьем отрезок [О, I] на п равных частей точками
Получим п частичных сегментов:
Длина каждого частичного сегмента равна

Вычислим значения функции
Составим интегральную сумму:
Вычислим предел интегральной суммы при
323. Вычислить интеграл:
Решение. Разсбьем сегмент ач bI течками деления
и потребуем, чтобы эти точки составляли геометрическую прогрессию
Знаменатель прогрессии
Длины частичных сегментов будут:

В качестве точек Ii выберем самые правые точки
частичных сегментов:
Составим интегральную сумму:
Вычислим предел интегральной суммы при
Таким образом,
Вычислим значения функции. _
324. Вычислить интеграл:
Решение. Для удобства вычислений разобьем сегмент [I, 2] точками


Длины частичных сегментов будут:
В качестве точек
Вычислим значения функции
Составим интегральную сумму:
Вычислим предел интегральной суммы при
Заменим переменную под знаком предела, положив


будет

поскольку
Таким образом,
325. Вычислить интеграл разбивая сегмент 
326. Вычислить интеграл

327. Вычислить интеграл

328. Вычислить интеграл

329. Вычислить
так, чтобы точки деления сегмента составляли геометрическую прогрессию.
330. Вычислить интеграл
так, чтобы точки деления сегмента составляли геометрическую прогрессию.
2. Вычисление определенных интегралов из геометрических соображений. Предварительно изучите по учебнику Г. М. Фихтенгольца главу X, п° 156 и главу XI, п° 175.
Как известно из теоретического курса (п° 175), определенный интеграл dx численно равен площади кри
волинейнойтрапеции аАВЬ (рис. I), ограниченной сверху кривой
ком оси абсцисс.
331. Используя геометрические соображения, вычислить:
Решение. Обозначив подынтегральную функцию через у, получим:

332. Используя геометрические соображения, вычислить:
Решение. Обозначим подынтегральную функцию через у. Кривая у = sin х изображена на рисунке 3. Разобьем
промежуток интегрирования



жена на сегменте [0, я] над осью Ох, а на сегменте



Используя геометрические соображения, вычислить следующие интегралы:
3. Основные свойства определенных интегралов. Предварительно изучите по учебнику Г. М. Фихтенгольца главу XI, п° 180— 183.
341. Оценить интеграл:
Решение. Так как в данной задаче 0 <х < I, следовательно, 0 < X2 < I, то для подынтегральной функции справедливы неравенства:
Воспользовавшись теперь свойством 8 определенного интеграла (см. учебник, п° 182), находим оценку заданного интеграла:
или окончательно
Решение. На заданном отрезке подынтегральная функция монотонно убывает. В самом деле, если
всюду на отрезке
По определению монотонно убывающей функции из неравенств следуют неравенства
следовательно, по указанному выше свойству определенного интеграла
или
откуда
В задачах 343—346 оценить интегралы.
347. Найти среднее значение функции
Решение. Средним значением функции

В данном случае
Используя свойства 3 и 4 определенного интеграла (см. учебник, п°181), получим:
Из геометрических соображений ясно, что

348. He вычисляя значений интегралов
Решение. Как известно (п° 182),если функции и g(x) интегрируемы на сегменте


Обозначим через f(x) подынтегральную функцию первого интеграла, т. е. f(x) — x, а через g (х) подынтегральную функцию второго интеграла, т. е.
Функции f(x) и g (х) непрерывны на сегментеГО. 11, следовательно, и интегрируемы на нем, и
349. Доказать неравенство:
Решение. Рассмотрим интегралы, Обо
значим через соответствующие подынтеграль-
ные функции, т. е.

непрерывны на сегменте [О, I], причем
геометрических соображений ясно, чтс
тельно,
Левая часть неравенств доказана. Рассмотрим интегралы 
интегралов соответственно через г
Эти функции непрерывны на сегменте [О, I], причем


часть неравенств доказана. Таким образом, неравенства доказаны полностью.
350. Найти среднее значение функции / (х) на указанных сегментах:
351. He вычисляя интегралов, установить, величина какого из указанных ниже интегралов больше:
352. Доказать неравенства:
353. Найти производную функции:
Решение. Из теоретического курса известно, что производная интеграла с постоянным нижним пределом и переменным верхним пределом равна подынтегральной функции при значении ее аргумента, равном верхнему пределу. Пользуясь свойствами определенного интеграла, преобразуем данный интеграл:
Найдем теперь Производную заданной функции, пользуясь правилом дифференцирования сложной функции
354. Функция задана параметрически:
Найти производную
Решение. Если функция задана параметрически уравнениями
то
Найдем предварительно

Таким образом,
В задачах 355 — 356 найти производные следующих функций:
357. Кривая задана уравнениями в параметрической форме:
Определить величину угла, образованного касательной к этой кривой с положительным направлением оси Ох.
358. Кривая задана уравнением:
Определить величину угла, образованного касательной к этой кривой в точкес положительным направ
лением оси Ох.
359. Найти точки экстремума функции
в области х > 0.
360. Найти точки экстремума и точки перегиба для функции
| < Предыдущая | Следующая > |
|---|
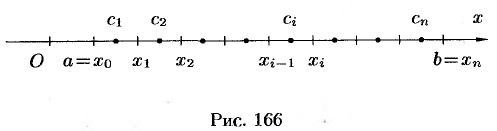
Определенный интеграл как предел интегральной суммы
Пусть функция 
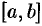
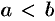
1. С помощью точек 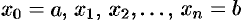
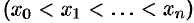
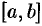
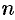
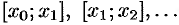
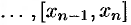
2. В каждом частичном отрезке 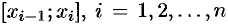
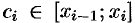
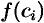
3. Умножим найденное значение функции 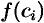
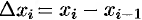
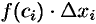
4. Составим сумму 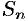
Сумма вида (35.1) называется интегральной суммой функции 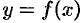
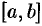
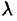
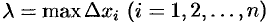
5. Найдем предел интегральной суммы (35.1), когда 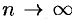
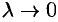
Если при этом интегральная сумма 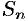
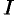
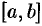
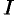
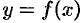
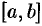
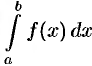
Числа 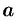
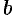
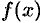
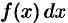
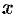
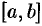
Функция 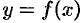
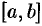
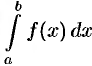
Сформулируем теперь теорему существования определенного интеграла.
Теорема 35.1 (Коши). Если функция 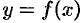
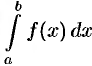
Отметим, что непрерывность функции является достаточным условием ее интегрируемости. Однако определенный интеграл может существовать и для некоторых разрывных функций, в частности для всякой ограниченной на отрезке функции, имеющей на нем конечное число точек разрыва.
Укажем некоторые свойства определенного интеграла, непосредственно вытекающие из его определения (35.2).
1. Определенный интеграл не зависит от обозначения переменной интегрирования:
Это следует из того, что интегральная сумма (35.1), а следовательно, и ее предел (35.2) не зависят от того, какой буквой обозначается аргумент данной функции.
2. Определенный интеграл с одинаковыми пределами интегрирования равен нулю:
3. Для любого действительного числа 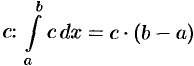
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
- Решение задач по высшей математике
Другие темы по высшей математике возможно вам они будут полезны: