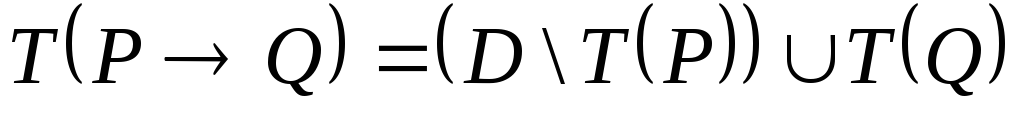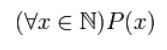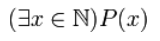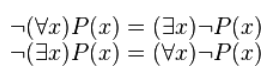Как найти предикат в логике

Логика предикатов

Предикаты
– это отображения произвольных множеств
во множество высказываний. Логика
предикатов представляет собой развитие
логики высказываний. Исторически понятие
о предикатах явилось следствием
логического анализа высказываний, т.е.
выяснения их логической структуры.

Определение
предиката

Пусть
Х₁,
Х₂,
…, Х_п
произвольные переменные. Эти переменные
будем называть предметными.
Пусть наборы переменных выбираются из
множества X,
которые будем называть предметной
областью.
Предикатом
местности n
(n —
местным предикатом), определенным на
предметной области X,
называют отображение множества X
во множество высказываний. Обозначение:
P( )- n — местный предикат, определенный
на X:=( ).

Пример:
«х
простое
число».

Это
выражение не является высказыванием,
но если в нем переменную х
заменить на определенное число, то
получим высказывание. Причем при замене
х
на число 3
получим истинное высказывание, тогда
как при замене х
на 8 получим ложное высказывание.

Таким
образом, выражение: «х
простое число» можно рассматривать как
функцию Р(х),
зависящую от переменной х.
Область определения Р(х)
— множество
чисел, а область значения — высказывание.

Предикаты
— отображения произвольных множеств во
множество высказываний. Пусть х₁,
х₂,
. . . , х_n
—
произвольные переменные. Эти переменные
будем называть предметными.
Пусть наборы переменных х₁,
х₂,
. . . , х_n
выбираются из множества X,
которые будем называть предметной
областью.

Предикатом
местности n
(n-местным
предикатом),
определенным на предметной области X,
называют отображение множества X
во множество высказываний.

Обозначение:
P(х₁,
х₂,
. . . , х_n)
— n-местный
предикат, определенный на X:={х₁,
х₂,
. . . , х_n}.

Дадим
другое определение предиката.

N—местный
предикат — это
связное повествовательное предложение,
содержащее n
переменных и обладающее следующим
свойством: при фиксации всех переменных
о нем (предложении) можно сказать, истинно
оно или ложно.

Примеры.

1)
Р(х₁,
х₂)
«Натуральное число х₁
делится
(без остатка) на натуральное число х₂»
— двуместный предикат, определенный на
множестве пар натуральных чисел (х₁,
х₂
N
).
Очевидно
Р(4, 2) =1; Р(5,
3) = 0

2)
Р(х) = “x²
< -1, xR”
— одноместный предикат, определенный
на R.

Ясно,
что Р(-1) = 0 и
вообще предикат P(x)
— тождественно ложен, т.е. Р(x)
= 0

3)
Р(х, y,
z)
= “x²
+ y²
≤ z,
x,y,xR”
— трехместный предикат, определенный
на R³.
Р(1, 1, -2) = 0,
Р(1, 1, 2) = 1

Предикат
— это функция, значениями которой
являются высказывания о п
объектах, представляющих значения
аргументов.

С
помощью формальных теорий можно описать
обширный класс высказываний, называемых
предикатами. Дадим опреде­ление
исчисления предикатов как формальной
теории, а затем подробно остановимся
на интерпретации.

Определение
1
(предиката).
Функция
Р(х₁,
… ,х_п),
опре­деленная
на некотором множестве М
и
принимающая одно из двух значений: И
(истина)
или Л
(ложь):

Р:
М →
{И,
Л},

называется
п-местным
предикатом.

Произвольная
функция Р:
Мⁿ→В,
заданная
на произвольном множестве М,
называется
n-местным
предикатом
Р(х₁,
х₂,
. . .,x_n),
т.е. Р
задает
семантическую характеристику.

Формальная
теория S
= <A,
F,
Р, R>
называется
исчислением
предикатов
первого
порядка, если заданы алфавит, формулы,
ак­сиомы и правила вывода.

1. Алфавит
А:

х,
у, z…
—
предметные переменные, принимающие
конкрет­ные значения из некоего
множества D.
Тогда
х₀,
y₀,
z₀
…
—
значе­ния предметных переменных, т.е.
предметные постоянные (кон­станты);

р,
q,
r
…
—
переменные высказывания, принимающие
два зна­чения: 1 (истина) и 0 (ложь). Тогда
p₀,
q₀,
r₀
…
— фиксированные
значения;

Р,
Q,
F
—
переменные, символизирующие само
высказыва­ние; Р₀,
Q₀(
)
— постоянные предикаты;

—символы
логических операций; дополнительно
исполь­зуются символы
;

—кванторы
общности и существования;

служебные
символы ),
(
— нужны для установления порядка
выполнения связок и области действия
кванторов;

можно
использовать также знаки !
— единственность, :
— «та­кой, что…» и другие символы
метаязыка. Например,
.

1. Формулы:
   F:

переменные
есть формулы;

если
А,
В
—
формулы, х
—
переменная, то А(х),

,

,

и

— формулы.

3. Аксиомы:

исчисления
высказываний:

Р₁:

;

Р₂:

;

Р₃:

;

кванторные:

Р₄:

;

Р₅:
.

4. Правила
вывода:

R₁
:
modus
ponens;

R₂:



введение квантора общности;

R₃:



введение квантора существования.

Построенная
формальная теория S
описывает весьма общие объекты, поэтому
нужно ее интерпретировать в то, с чем
можно работать.

Заметим,
что предикаты дают возможность
математически ана­лизировать суждения.
В классической логике предикатом
называ­ется
сказуемое
суждения,
т.е. то, что утверждается или отрицается
относительно субъекта этого суждения,
имени предмета мысли, фиксирующее его
определенные свойства. А в математической
логике понятие предиката рассматривается
как тождественное суждению, содержащему
местоимения, т.е. пропозиционная фун­кция,
аргументами которой служат имена.

Пример.
О высказывательной форме «Он получил
специальность программиста» нельзя
сказать, истинна она или ложна, пока не
произведена замена местоимения «он»
на существительное: «М. А. Иванов стал
про­граммистом» (истинно), «Дом стал
программистом» (ложно).

Далее
подробно опишем все составляющие
формальной тео­рии исчисления
предикатов в такой интерпретации.

Чтобы
задать п-местный
предикат Р(х₁,
х₂,
…, х_п),
следует указать множества Х₁,
Х₂,
…, Х_п
— области
изменения переменных х₁,
х₂,
…, х_п,
причем чаще всего рассматривается
случай, когда Х₁
= Х₂
= …= Х_п.

С
теоретико-множественной точки зрения
предикат определяется заданием
подмножества М
в декартовом произведении X₁
x
Х₂
x
… x
Х_п.

Переменные
х₁,
х₂,
…, х_п
называются предметными
переменными. Элементы
множеств Х₁,
Х₂,
…, Х_п
называются предметами.
Множество М
— множество
кортежей длины п
<х₁,
х₂,
…, х_п>
называется полем
предиката Р(х₁,
х₂,
…, х_п).

Будем
обозначать предметные переменные малыми
буквами конца латинского алфавита
(иногда будем снабжать эти буквы
индексами) x,
y,
z,
…, х₁,
х₂,
…, х_п
.

Предметы
из множеств Х₁,
Х₂,
…, Х_п
— малыми буквами начала латинского
алфавита а,
b,
с, …, a₁,
a₂,
…

Предикаты
— большими буквами латинского алфавита
с приписанными предметными переменными
или без них
А(х, х). В, F(x,
y),
Р(х₁,
х₂,
…, х_п).

Число
переменных будем указывать как верхний
индекс у предиката: Р^k(х₁,
х₂,
…, х_k)
— k—местный
предикат,
Q²(x,
у) —
двуместный предикат, Р(х)
— одноместный
предикат.

Итак,
k—местный
предикат — Р^k(х₁,
х₂,
…, х_k)
есть функция, предметные переменные
которой принимают значения из некоторого
множества М_k,
а сама она принимает только два значения:
истина (1)
или ложь (0),
т.е.

Р^k(х₁,
х₂,
…, х_k):
М_k
→ {1,0}.

Например,
если Х
— множество
действительных чисел, то х²
> 1 —
одноместный
предикат.

Если
X, У
— множества действительных чисел, то
ху = 5
— двуместный предикат.

Предикат
называется разрешимым,
если существуют такие кортежи, компоненты
которых обращают предикат в истинное
высказывание.

Если
предикат при подстановке любых конкретных
элементов из соответствующих множеств
обращается в истинное высказывание, он
называется
тождественно истинным.

Если
предикат при подстановке любых конкретных
элементов из соответствующих множеств
обращается в ложное высказывание, он
называется тождественно
ложным.

К предикатам,
определенным на одном и том же множестве,
можно применять операции алгебры
высказываний: конъюнкцию, дизъюнкцию,
импликацию, эквивалентность, отрицание
и получать новые предикаты.

Например,
если к предикатам «х
= y»
и «х < у»
— обозначим
их соответственно Р(х,
у) и Q(x,
у) —
применить операцию конъюнкции, то
получим новый предикат Р(х,
у)Q(x,
у).

Язык
логики предикатов.

Символами
X,
Y,
Z,
X_i,
Y_i,
…
в
логике предикатов принято обозначать
предметные
переменные, т.е.
от­дельные предметы
— имена. Они
могут быть простыми и сложны­ми. Если
такие предметы (имена) не содержат
дополнительной информации о себе, то
они называются собственными
(простыми),
например «земля», «студент» и др. Если
такое имя содержит наряду с самим
предметом его отдельные свойства, то
оно является слож­ным,
например
«автор романа «Анна Каренина»,
«перпендикуляр­ные прямые»,
«взаимно-однозначное соответствие» и
др.

Символами
а,
b,
с,
a_i
b_i
… принято
обозначать константы
или
предметные
постоянные, т.
е. конкретные значения имен предметов
из указанной предметной области.
Высказывательные формы, вхо­дящие в
предикаты, называют также препозиционными
функция­ми,
или
предикаторами.

Любое
непустое множество содержит два
подмножества: само себя и пустое. Это
свойство автоматически выделяет из
области определения два случая.

Тождественно-истинным
называется
предикат, истинный всю­ду на области
определения: Т(Р)
= D(P).

Тождественно-ложным
называется
предикат, множество истинности которого
пусто: Т(Р)
= 0.

Два
предиката в одной и той же области
определения различны
в
том и только в том случае, если их
множества истинности не совпадают. Это
определение совпадает с отрицанием
обычного оп­ределения равенства
функций.

Логические
операции (связки) над предикатами

Связки,
анало­гичные связкам булевой алгебры
и исчисления высказываний, соответствуют
логическим операциям над предикатами.
Операции над n-местными
предикатами вводятся аналогично
одноместным.

Пусть,
например, Р(х,
…)
и Q(x,
…)
— предикаты, которые
определены на
множестве D,
причем
Т(Р)
и
T(Q)
—
их множества истинности.

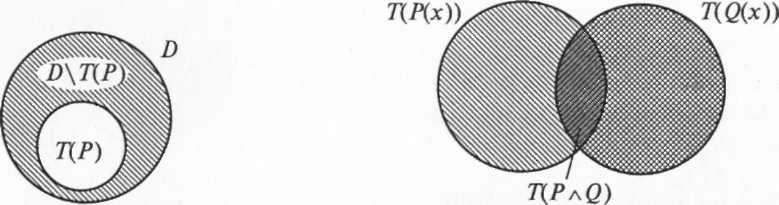
Отрицанием
предиката
Р(х,...)
называется предикат Р(х),
также
определенный на множестве D
и
истинный при тех значениях переменной
х,
при
которых Р(х,
...)
ложен, т.е. Т(Р)
= DT(P)
(рис.
5.1).

Рассмотрим
примеры.

1.
Для предикатов Р(х):
«х
— четное число» и Q(x):
«х
кратно 7» конъюнкцией Р(х)
л Q(x)
служит
предикат «х — четное и
кратное
7 число» или «х — число, кратное 14».

Рис.
5.1. Множество истинности Рис. 5.2.
Множество истинности

предиката
Р(х) конъюнкции
предикатов

Пример.

Предикат
Р(х):
«х —
простое
число»
определен на множестве D
=
Z
целых чисел, а его областью истинности
являют­ся только простые числа, т. е.
числа, имеющие два делителя: х
и 1.
Тогда предикат «х
— составное (целое) число»,
также определен­ный на Z,
будет отрицанием предиката Р(х),
т.е.
,
а
его обла­стью истинности будет
множество всех
целых
составных чисел (имеющих три и более
делителей):
T(P).

Аналогично
вводятся и остальные операции.

Конъюнкция
предикатов
Р(х,
…)
и Q(x,
…)
есть новый преди­кат
,
определенный
на множестве D
и
истинный при тех значениях переменной
х,
при которых истинны одновременно оба
предиката
Р(х,
…)
и Q(x,
...),
поэтому

(рис.
5.2).

Пример.

Для
предикатов P(x):
«x – четное число»
и Q(x):
«x – кратное 7»
конъюнкцией
служит предикат«x
– четное и кратное 7 число»
или «x
–число, кратное 14»

Пример.

Решить
систему неравенств
означает:
решить первое неравенство, т.е. определитьТ(Р₁),
решить
второе неравенство — определить Т(Р₂):

,<=>.
Определить, при какихх
верны и
первое,
и
второе
неравенства. В данном случае система
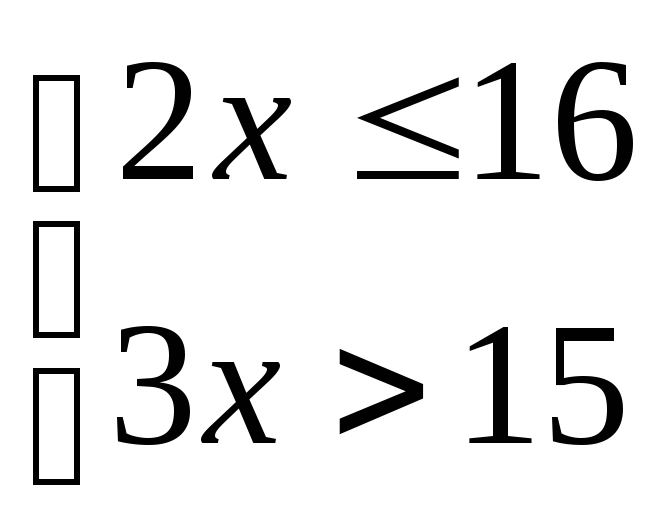
означает конъюнкцию высказываний<=>5
< х =< 8,
а ответ является пересечением Т(Р₁)
и
T(Р₂)
(рис. 5.3), т. е. интервалом 5 < х < 8.

Рис.
5.3. Графическое решение системы неравенств

Обратите
внимание, что в итоговый ответ вошла
конъюнкция высказываний, эквивалентных
данным в условии, а не самих ис­ходных.

Дизъюнкцией
предикатов
Р(х,
…)
и Q(x,
…)
называется пре­дикат Р(х)vQ(x),
определенный
на множестве D
и
истинный при тех значениях переменной
х,
при которых истинен хотя бы один из
предикатов Р(х)
или
Q(x).

Поэтому

(рис.
5.4).

Рис.
5.4. Множество истинности дизъюнкции
предикатов

Пример.

Для
предикатов Р(х):
«х—
число, кратное 3»
и Q(x):
«х — число, оканчивающееся на 3»,
определенных на N,
дизъюнк­цией Р(х)vQ(x)
служит
предикат: «х
— число или
кратное
3, или
оканчивающееся
цифрой 3».

Так,
при решении уравнений (неравенств),
левая часть кото­рых есть произведение
нескольких множителей, а правая — нуль,
они разбиваются на совокупность уравнений
(неравенств).

Пример.

х²
— 8х — 20 = 0 <=> (х — 10)(х + 2) = 0 <=> х — 10 = 0
(Р₁)
или
х
+ 2 = 0
(Р₂).
Таким
образом, нужно найти T(P₁)
= {10}, T(Р₁)
= {-2}
и их объединение: Т(Р)
=
{-2, 10}.

Импликациейпредиката
Р(х,
…)
в Q(x,
…)
называется преди­кат Р(х)
→ Q(x),
определенный на множестве D
и
ложный только при тех значениях переменной
х,
при которой предикат Р(х,
…)
истинен, а предикат Q(x,
…)
ложен. В полном соответствии с формулой
алгебры логики
имеем:и
(рис.
5.5).

Рис.
5.5. Множество истинности импликации
предикатов

Пример.

Импликацией
предикатов Р(х):
«х — нечетное число»
и Q(x):
«х
кратно 5»,
определенных на
,
служит предикатР(х)
→
Q(x):
«Если
х — нечетное число, то х кратно 5».

Здесь
Т(Р)
= {y|(ymod2)
= 1}
= {1, 3, 5, …};

T(Q)
= {y|(ymod5)
=
0}
=
{0, 5, 10, …}.

Тогда
D/T(Р)
= {у|(ymod2)
= 0} ={0, 2, 4,…};

Импликация
верна, если число кратно двум или пяти.

Замечание.
Поскольку в данном нами алфавите связка
→ является основной, a
и— дополнительными, то дадим введение
конъюнкции и дизъюнкции черези

:

,

.

Эквиваленцией
предикатов Р(х,
…)
и Q(x,
…)
называется пре­дикат Р(х)
в Q(x),
определенный на множестве D
и
истинный при тех значениях переменной
х,
при которых либо оба предиката истинны,
либо оба предиката ложны.

Поэтому

.

В
силу законов Де Мор­гана
.
Если
Т(Р)
= T(Q),
то
Т(Р
= Q)
= D.

Пример.

Эквивалентны
преди­каты Р(х):
«х — натуральное число, кратное 3»
и Q{x):
«х — нату­ральное
число, сумма цифр которого делится на
3».

Кванторы

Помимо
операций алгебры высказываний, в логике
предикатов есть две операции, которые
связаны с природой предикатов. Пусть
дан предикат Р(х),
зависящий от одной переменной и
определенный на поле М.

а)
Выражение (х)Р(х)
означает высказывание, истинное только
в том случае, когда предикат Р(х)
истинен для всех предметов из поля М.
Выражение (х)Р(х)
читается «для всякого х,
Р(х)», здесь
символ

— квантор общности.

б)
Выражение (х)Р(х)
означает высказывание, истинное только
в том случае, когда предикат Р(х)
истинен хотя бы для одного предмета из
поля М.
Выражение (х)Р(х)
читается «существует х,
что Р(х)»,
символ

— квантор существования.

Рассмотрим примеры
применения операций квантирования к
предикатам. Пусть даны предикаты над
полем натуральных чисел:

1)
х²
= х х,
тогда (х)
(х²
= х х) —
истинное высказывание;

2)
х + 2 = 7,
тогда (х)
(х+2 = 7) —
ложное высказывание; а (х)
(х + 2 = 7) —
истинное высказывание;

3)
х + 2 = х,
тогда (х)
(х + 2 = х)
— ложное
высказывание.

Название	Прочтение	Обозначение
Квантор общности	«все», «всякий», «каждый», «любой»
Квантор существования	«Хотя бы один», «найдется», «существует»

Квантор
общности —
это оператор, приводящий в соответствии
любому заданному предикату у
= Р(х) такую
двузначную логическую переменную z,
которая принимает значение 1
тогда и только тогда, когда у
= 1 при всех
значениях х.

Квантор
существования —
это оператор, приводящий в соответствии
любому одноместному предикату у
= Р(х) такую
двузначную логическую переменную z,
которая принимает значение 0
тогда и только тогда, когда у
= 0 при всех
значениях х.

Рассмотрим
некоторые общие свойства введенных
операторов. В соответствии с определениями
кванторов логическая переменная z
в выражениях

z
= (х)Р(х)

z
= (х)Р(х)

уже
не является функцией предметной
переменной х.

Для
того чтобы отметить отсутствие
функциональной зависимости z
от х,
предметную переменную х
в таких случаях называют связанной.
Несвязанные
переменные называют свободными.

Например, в предикате

(х)A(х,y)(z)
B(z,v)

переменные
х
и z
— связанные,
а у
и v
— свободные.

Если
квантор общности или квантор существования
применяется не к одноместному предикату,
а к какому-нибудь k-местному
предикату, то в результате этого
получается снова предикат, но за счет
связывания одной предметной переменной
получаемый предикат будет (k-1)-местным.

Кванторы.

Для
количественных характеристик обычно
исполь­зуют понятия «все», «некоторые»,
«существуют» и др., кото­рые называют
кванторами
(от
лат. quantum
— сколько).
Мы часто пользовались символами
и,
заменяющими слова «любой» и «существует».
Покажем действие этих кванторов в
высказыва­тельных формах. Часть
формулы, на которую распространяется
действие квантора, называетсяобластью
действия
этого
кван­тора. Вхождение переменной в
формулу может быть связанным,
если
переменная расположена либо непосредственно
после знака квантора, либо в области
действий квантора, после которого стоит
переменная. Все прочие вхождения —
свободные. Напри­мер, в выражении
переменнаях
связывает свойство пре­диката и
квантор общности. Грубо говоря, от этой
переменной, ее конкретного вида и имени,
ничего не зависит, т.е.

и

суть
одно и то же. Так, можно произвольно
называть индекс суммирования в рядах
и переменную интегрирования в определенных
интегралах. В частности, в определении
множества как совокупности всех
объектов,
удовлетворяющих характери­стическому
свойству, использовалась запись G
= {хР(х)}.
Оче­видно,
что в предикате со связанной переменной
ее так же легко можно заменить на любую
другую. При этом множество все равно
будет совокупностью тех же элементов,
удовлетворяющих свой­ству Р.
Переменная,
не являющаяся связанной, называется
сво­бодной,
если
после подстановки вместо нее имени
некоторых конкретных объектов предикат
превращается в осмысленное пред­ложение.

Между
кванторами
ии логическими операциями существу­ет
тесная связь. Пусть предикатР(х)
определен
на конечном мно­жестве D=
{a₁,
а₂,
. . . ,а_n}.
Тогда
высказывание
будет истинным только в том случае, если
истинны одновременно все высказыванияР(а₁),
Р(а₂),.
. ., Р(а_п),
т.е.
если истинна их конъ­юнкция:
.
Аналогично
высказывание
означает,
что оно истинно, когда истинно хотя бы
одно из высказываний Р(а₁),
Р(а₂),…,
Р(а_п).
Тогда
должна быть ис­тинной дизъюнкция
высказываний
.
По­этому
для конечной области определения
выполняются равно­сильности:
и.

Таким
образом, кванторы общности и существования
являют­ся дополнениями и аналогами
соответственно логических опера­ций
конъюнкции и дизъюнкции.

Поскольку
конъюнкцию можно выразить через отрицание
и дизъюнкцию, то, вообще говоря, символ
можно было не вклю­чать в число основных
символов, так как квантор существова­ния
по сути является сокращенной записью
формулы
,
выражающей так называемуюдвойственность.

Пример.

Записать
с помощью формул логики предикатов
следующее утверждение: «Для лечения
любого известного компьютерного вируса
имеются программы. Существуют новые
(неизвестные) компьютерные вирусы, для
лечения которых программы еще не
разработаны»

Решение.

Введем
обозначения элементарных формул:

A(x)
– известен компьютерный вирус x;

B(x)
– для лечения вируса x
существует
программа;

Тогда
с помощью логических связок и кванторов
получим формулы:

—
против вируса x
нет программы;

— любой вирус
известен;

— существуют новые
(неизвестные) вирусы;

— если вирус давно
известен, то имеется программа для его
лечения;

— существуют
(появились) новые вирусы, для лечения
которых программы еще не разработаны.

Тогда
формализованное исходное утверждение
примет вид:

Отношение
следования и равносильности между
высказывательными формами связаны с
тождественно-истинными импликацией и
эквиваленцией, следовательно, их можно
записать с помощью кванторов общности:

тождественно

тождественно

Пример.

Запись
х²
— 5х = 0 <=> х(х — 5) = 0 является не форму­лой,
а истинным высказыванием о равносильности
двух формул, представленных в виде
уравнений. В то же время справедлива
за­пись (х²
— 5х = 0) ≡ (х(х — 5) = 0), выражающая истинное
высказывание, которое включает операцию
эквиваленции в каче­стве составляющей.

Поэтому
логическое следование можно определить
через имп­ликацию, а равносильность
через эквиваленцию. Так, для эквива­ленции
справедливо: «Две высказывательные
формы Q₁
и
Q₂
ис­тинны
или ложны (Q₁
<=>
Q₂)
одновременно
с высказыванием »,
что
и было ранее введено.

Существует
различие в употреблении знаков и «»,«»,
«»
и «».

Знаки
«»,
«»
обозначают логические операции
импли­кации и равносильности и входят
составной частью в формулы.

Знаки
«»
и «»
обозначают определенные отношения
между высказывательными формами, не
входя в них в качестве состав­ной
части.

Квантификация
многоместных высказывательных форм

Пусть
Q(x₁,
х₂,
. . ., х_n)
— n-местная
высказывательная форма. Ее замену на
высказывательную форму
x_i
Q(x₁,
х₂,
. . ., х_n)
либо на
x_i
Q(x₁,
х₂,
. . ., х_n)
называют квантификацией
высказывательной
формы Q(x₁,
х₂,
. . ., х_n)
по переменной x_i.

В
процессе такой квантификации эта i-я
переменная связыва­ется одним из
кванторов, а n-местная
высказывательная форма превращается
в (п—1)-местную.

Это
аналогично тому, что если функцию f(x₁,
х₂,
…,
х_n)
проинтегрировать от а
до
b
по
пере­менной x_i,
то
полученный результат будет функцией
от п-1
пе­ременной и не будет зависеть от
х_i:
I(х₁,…,
х_i-1,
x_i+1,
…,
х_n)
=
Так,
интеграл от функции одной (п
=
1)
переменной является константой и вообще
ни от чего не зависит.

Пусть
дана двухместная высказывательная
форма х
—
у
< 0,
определенная на
.
Произведем
квантификацию по переменной у
(«навесим»
квантор общности). Получим одномест­ную
высказывательную форму
со свободной пере­меннойх.
Если для фиксированного х
= х₀
будет выполнено
,
то эта высказывательная форма превращается
в истин­ное высказывание, например,
прих
= -2,
а при х
= 3
— в ложное.

Если
в одноместной высказывательной форме
связать кванто­ром и вторую переменную
х,
то можно получить высказывание: либо
— истинное высказывание;— ложное высказывание.

При
«навешивании» кванторов на двухместную
высказывательную форму Q(x,у)
можно
получить одну из восьми комбинаций:

1. 
   — «для
   любого х
   и любого у
   Q(x,у)»;

2. 
   — «для
   любого у
   и
   любого х
   Q(x,у)»;

1. )
   — «существует
   х
   и существует у,
   такие,
   что Q(x,у)»;

2. 
   — «существует
   у
   и
   существует х,
   такие, что Q(x,у))»;

3. 
   —«существует
   х,
   такой, что для любого у
   Q(x,у)»;

4. 
   — «для
   всякого х
   существует у,
   такой,
   что Q(x,у)»;

7)

— «существуету,
такой,
что для любого х
Q(x,
у)»;

— «для
всякого у
существует
х,
такой, что Q(x,
у)».

Очевидно,
что первое и второе высказывания, а
также третье и четвертое тождественны
между собой, их значения истинности
совпадают. Между остальными полученными
высказываниями нельзя установить
тождественности: если истинно высказывание
5, то истинным будет и высказывание 8,
причем обратное неверно. Аналогично,
если истинно высказывание 7, то истинно
и выска­зывание 6, но не наоборот. То
есть, если кванторы одноименны (1 — 4),
то их порядок не играет роли и полученные
высказывания эквивалентны. Если кванторы
разноименные (5 — 8), то их поря­док в
полученном высказывании принципиально
важен.

Например,
для двухместного предиката «Город х
находится в стране у»
высказывание

имеет
вид 0-местного
пре­диката и читается «В каждой стране
у
есть
некоторый город х».
Оно будет истинным, в то время как
высказывание

чита­ется
«Существует город х,
находящийся во всех странах у»
будет
ложным.

Пусть
даны х,
у
— две
различные переменные, F(x),
Ф(х)
и Q(x,у)
—
любые формулы логики предикатов и М
—
формула, не содержащая свободных
вхождений х.
Тогда справедливы равно­сильности,
представленные с учетом двойственности
кванторов
ив табл. 5.5.

Таблица
5.5

Логика предикатов

Предикаты вслед за высказываниями являются следующим важным предметом, исследуемым математической логикой. Понятие предиката обобщает понятие высказывания, а теория предикатов представляет собой более тонкий инструмент, по сравнению с теорией высказываний, для изучения закономерностей процессов умозаключения и логического следования, составляющих предмет математической логики. В настоящей главе рассматриваются основы теории предикатов.

Понятие предиката

В высказывании все четко: это — конкретное утверждение о конкретных объектах — истинное или ложное. Предикат — предложение, похожее на высказывание, но все же им не являющееся: о нем нельзя судить, истинно оно или ложно. Дадим точное определение.

Определение 18.1. Определенным на множествах n-местным предикатом называется предложение, содержащее переменных , превращающееся в высказывание при подстановке вместо этих переменных любых конкретных элементов из множеств соответственно.

Для n-местного предиката будем использовать обозначение . Переменные называют предметными, а элементы множеств , которые эти переменные пробегают, — конкретными предметами. Всякий n-местный предикат , определенный на множествах , представляет собой функцию п аргументов, заданную на указанных множествах и принимающую значения в множестве всех высказываний. Поэтому предикат называют также функцией-высказыванием.

Рассмотрим пример. Предложение «Река впадает в озеро Байкал» является одноместным предикатом, определенным над множеством всех названий рек. Подставив вместо предметной переменной название «Баргузин», получим высказывание «Река Баргузин впадает в озеро Байкал». Это высказывание истинно. Подставив вместо предметной переменной название «Днепр», получим ложное высказывание «Река Днепр впадает в озеро Байкал».

Другой пример. Предложение (выражение) «» является двухместным предикатом, заданным над множествами . Множества, на которых задан двухместный предикат, совпадают (говорят, что «двухместный предикат задан на множестве «). Пара действительных чисел 2, 2 превращает данный предикат в истинное высказывание: ««, а пара чисел 2, 3 — в ложное: ««.

Отметим еще один подход к понятию предиката. Как отмечалось, предикат , определенный на множествах , превращается в конкретное высказывание , если вместо предметных переменных подставить в него конкретные предметы (элементы ) из множеств соответственно. Это высказывание может быть либо истинным, либо ложным, т. е. его логическое значение равно 1 или 0. Следовательно, данный предикат определяет функцию аргументов, заданную на множествах принимающую значение в двухэлементном множестве . Иногда эту функцию и называют предикатом.

---

Классификация предикатов

Определение 18.2. Предикат , заданный на множествах , называется:

а) тождественно истинным, если при любой подстановке вместо переменных любых конкретных предметов из множеств соответственно он превращается в истинное высказывание ;

б) тождественно ложным, если при любой подстановке вместо переменных любых конкретных предметов из множеств соответственно он превращается в ложное высказывание;

в) выполнимым (опровержимым), если существует по меньшей мере один набор конкретных предметов из множеств соответственно, при подстановке которых вместо соответствующих предметных переменных в предикат последний превратится в истинное (ложное) высказывание .

Приведем примеры предикатов.

Одноместный предикат «Город расположен на берегу реки Волги», определенный на множестве названий городов, является выполнимым, потому что существуют города, названия которых превращают данный предикат в истинное высказывание, или, иначе, удовлетворяют этому предикату (например, Ульяновск, Саратов и т. д.). Но данный предикат не будет тождественно истинным, потому что существуют города, названия которых превращают его в ложное высказывание, или, иначе, не удовлетворяют этому предикату (например, Прага, Якутск и т.д.). Этот же предикат являет собой пример опровержимого, но не тождественно ложного предиката (продумайте!).

В другом примере одноместный предикат ««, определенный на множестве действительных чисел, тождественно истинный. Наконец, двухместный предикат ««, заданный также на множестве действительных чисел, является тождественно ложным предикатом, потому что любая пара действительных чисел превращает его в ложное высказывание (не удовлетворяет ему).

Отметим некоторые достаточно очевидные закономерности взаимосвязей между предикатами различных типов (рекомендуется осмыслить их):

1) каждый тождественно истинный предикат является выполнимым, но обратное неверно;
2) каждый тождественно ложный предикат является опровержимым, но обратное неверно;
3) каждый не тождественно истинный предикат будет опровержимым, но, вообще говоря, не будет тождественно ложным;
4) каждый не тождественно ложный предикат будет выполнимым, но, вообще говоря, не будет тождественно истинным.

---

Множество истинности предиката

Определение 18.3. Множеством истинности предиката , заданного на множествах , называется совокупность всех упорядоченных n-систем , в которых , таких, что данный предикат обращается в истинное высказывание при подстановке . Это множество будем обозначать . Таким образом,

Множество истинности «-местного предиката представляет собой n-арное отношение между элементами множеств . Если предикат — одноместный, заданный над множеством , то его множество истинности является подмножеством множества .

Например, множеством истинности двухместного предиката «Точка принадлежит прямой «, заданного на множестве всех точек плоскости и на множестве всех прямых этой плоскости, является бинарное отношение принадлежности (инцидентности) между точками и прямыми плоскости. Другой пример. Множество истинности двухместного предиката , заданного на множестве , есть множество всех таких пар действительных чисел, которые являются координатами точек плоскости, образующими окружность с центром в начале координат и радиуса 3. Наконец, если «» — одноместный предикат над , то , или .

В терминах множества истинности легко выразить понятия, связанные с классификацией предикатов (определение 18.2). В самом деле, n-местный предикат , заданный на множествах , будет:

а) тождественно истинным тогда и только тогда, когда ;
б) тождественно ложным тогда и только тогда, когда ;
в) выполнимым тогда и только тогда, когда ;
г) опровержимым тогда и только тогда, когда .

На языке множеств истинности еще более отчетливо проясняются закономерности взаимосвязей между предикатами различных типов, отмеченные в конце предыдущего пункта. Проанализируйте их еще раз.

---

Равносильность и следование предикатов

Определение 18.4. Два n-местных предиката и , заданных над одними и теми же множествами , называются равносильными, если набор предметов (элементов) превращает первый предикат в истинное высказывание в том и только в том случае, когда этот набор предметов превращает второй предикат в истинное высказывание .

Другими словами (на языке множеств истинности), предикаты и равносильны тогда и только тогда, когда их множества истинности совпадают. .

Утверждение о равносильности двух предикатов и символически будем записывать так: . Отношение равносильности предикатов является отношением эквивалентности, так что совокупность всех n-местных предикатов, определенных на множествах , распадается на непересекающиеся классы равносильных предикатов (все они определяют одну и ту же функцию, заданную на множествах и принимающую значения в двухэлементном множестве ). Переход от предиката к равносильному ему предикату называется равносильным преобразованием первого. Это понятие очень важно для школьной математики, потому что изучаемые в ней уравнения и неравенства представляют собой частные виды предикатов. Решение уравнения и неравенства есть поиск их множеств истинности. При таком поиске мы проделываем над уравнением и неравенством различные преобразования, и здесь важно, чтобы эти преобразования были равносильными, т. е. чтобы найденное множество оказалось бы множеством истинности именно исходного уравнения или неравенства. Аналогична ситуация при решении систем уравнений или неравенств.

Рассмотрим простой пример. Пусть требуется решить уравнение (найти множество истинности предиката): . Преобразуем его равносильным образом:

Ответ: — множество всех решений данного уравнения (множество истинности данного предиката).

Отметим следующее немаловажное обстоятельство: может быть так, что два предиката равносильны, если их рассматривать над одним множеством, и неравносильны, если их рассматривать над другим (в частности, объемлющим первое) множеством. Такова, например, ситуация с предикатами: и .

---

Определение 18.5. Предикат , заданный над множествами , называется следствием предиката , заданного над теми же множествами, если он превращается в истинное высказывание на всех тех наборах значений предметных переменных из соответствующих множеств, на которых в истинное высказывание превращается предикат .

Другими словами (в терминах множеств истинности), можно сказать, что предикат является следствием предиката тогда и только тогда, когда .

Утверждение о том, что предикат является следствием предиката , будем символически записывать так: .

Например, одноместный предикат, определенный на множестве натуральных чисел, « делится на 3″ является следствием одноместного предиката, определенного на том же множестве, « делится на 6″. Из двух предикатов, упомянутых перед последним определением, первый будет следствием второго, если считать, что оба предиката заданы на множестве целых чисел.

Язык множеств истинности позволяет установить взаимосвязь между понятиями равносильности и следования предикатов: два предиката, определенные на одних и тех же множествах, равносильны тогда и только тогда, когда каждый из них является следствием другого. Кроме того, этот же язык дает возможность без труда установить следующие простые теоремы.

Теорема 18.6. Каждые два тождественно истинных (тождественно ложных) предиката, заданных на одних и тех же множествах, равносильны. Обратно, всякий предикат, равносильный тождественно истинному (тождественно ложному) предикату, сам является тождественно истинным (тождественно ложным) предикатом.

Теорема 18.7. Каждый тождественно истинный n-местный предикат является следствием любого другого n-местного предиката, определенного на тех же множествах. Каждый n-местный предикат является следствием любого тождественно ложного n-местного предиката, определенного на тех же множествах.

Теорема 18.8. Пусть и — два n-местных предиката, определенные на одних и тех же множествах, такие, что есть следствие . Тогда:

а) если тождественно истинный (выполнимый), то и тождественно истинный (выполнимый);

б) если тождественно ложный (опровержимый), то и тождественно ложный (опровержимый).

Доказательство теоремы 18.8:

а) Поскольку , поэтому . Если теперь тождественно истинный предикат, то

(где — множества, на которых определены n-местные предикаты и ).

Но . Поэтому , а, значит, предикат — тождественно истинный предикат. Если же — выполнимый предикат, то . Но . Тогда и — выполнимый предикат.

б) Пусть — тождественно ложный предикат. Тогда . Но , поэтому . Следовательно, предикат — тождественно ложный. Наконец, пусть — опровержимый предикат. Тогда . Поскольку, кроме того,

и , то .

Следовательно, предикат — опровержимый.

Отыщите самостоятельно в настоящем и предыдущем пунктах данной лекции утверждения, обосновывающие остальные сформулированные теоремы.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Понятие предиката

Предикат называется тождественно-истинным, если на любом наборе аргументов он принимает истинное значение:

$P (x_1, dots, x_n)=1$

Предикат называется тождественно-ложным, если на любом наборе аргументов он принимает ложное значение:

$P (x_1, dots, x_0)=0$

Предикат называется выполнимым, если хотя бы на одном наборе аргументов он принимает истинное значение.

Т.к. предикаты могут принимать только два значения (истинно/ложно или $0/1$), то к ним можно применять все операции алгебры логики: отрицание, конъюнкция, дизъюнкция и т.д.

Примеры предикатов

Пусть предикат $R(x, y)$: $«x = y»$ обозначает отношение равенства, где $x$ и $y$ принадлежат множеству целых чисел. В этом случае предикат R будет принимать истинное значение для всех равных $x$ и $y$.

Другой пример предиката — РАБОТАЕТ($x, y, z$) для отношения «$x$ работает в городе y в компании $z$».

Еще один пример предиката — НРАВИТСЯ($x, y$) для «x нравится y» для $x$ и $y$, которые принадлежат $M$ — множеству всех людей.

Таким образом, предикатом является все то, что утверждается или отрицается о субъекте суждения.

«Предикаты и кванторы» 👇

Операции над предикатами

Рассмотрим применение операций алгебры логики к предикатам.

Логические операции:

Кванторы

Чаще всего используют кванторы:

• квантор всеобщности (обозначается символом $forall x$) — выражение «для всех $x$» («для любого $x$»);

• квантор существования (обозначается символом $exists x$) — выражение «существует $x$ такое, что… »;

• квантор единственности и существования (обозначается $exists !x$) — выражение «существует точно одно такое $x$, что… ».

В математической логике существует понятие связывание или квантификация, которые обозначают приписывание квантора к формуле.

Примеры применения кванторов

Пусть — предикат «$x$ кратно $7$».

С помощью квантора всеобщности можно записать следующие ложные высказывания:

1. любое натуральное число делится на $7$;

2. каждое натуральное число делится на $7$;

3. все натуральные числа делятся на $7$;

который будет иметь вид:

Для записи истинных высказываний используем квантор существования:

1. существуют натуральные числа, которые делятся на $7$;

2. найдётся натуральное число, которое делится на $7$;

3. хотя бы одно натуральное число делится на $7$.

Запись будет иметь вид:

Пусть на множестве $x$ простых чисел задан предикат : «Простое число является нечетным». Поставив перед предикатом слово «любое», получим ложное высказывание: «Любое простое число является нечетным» (например, $2$ является простым четным числом).

Поставим перед предикатом слово «существует» и получим истинное высказывание: «Существует простое число , которое является нечетным» (например, $x=3$ ).

Таким образом, предикат можно превратить в высказывание, если поставить перед предикатом квантор.

Операции над кванторами

Для построения отрицания высказываний, которые содержат кванторы, применяется правило отрицания кванторов:

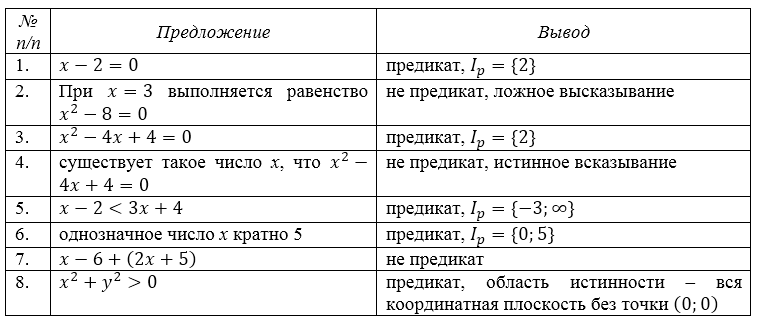
Рассмотрим предложения и выделим среди них предикаты, указав область истинности каждого из них: