| Определение: |
| Префикс-функция (англ. prefix-function) от строки — массив длин наибольших бордеров для каждой позиции этой строки |
Здесь и далее считаем, что символы в строках нумеруются с .
Определим префикс-функцию от строки в позиции следующим образом: . Если мы не нашли такого , то .
Содержание
- 1 Наивный алгоритм
- 1.1 Псевдокод
- 1.2 Пример
- 1.3 Время работы
- 2 Эффективный алгоритм
- 2.1 Псевдокод
- 2.2 Время работы
- 3 Построение префикс-функции по Z-функции
- 3.1 Постановка задачи
- 3.2 Описание алгоритма
- 3.3 Псевдокод
- 4 Построение строки по префикс-функции
- 4.1 Постановка задачи
- 4.2 Описание алгоритма
- 4.3 Реализация
- 4.4 Доказательство корректности алгоритма
- 5 Критерий корректности значений префикс-функции
- 5.1 Решение
- 5.2 Доказательство корректности
- 5.3 Псевдокод
- 6 См. также
- 7 Источники информации
Наивный алгоритм
Наивный алгоритм вычисляет префикс-функцию непосредственно по определению, сравнивая префиксы и суффиксы строк. Обозначим длину строки за . Будем считать, что префикс-функция хранится в массиве .
Псевдокод
int[] prefixFunction(string s):
int[] p = int[s.length]
fill(p, 0)
for i = 0 to s.length - 1
for k = 0 to i - 1
if s[0..k] == s[i - k..i]
p[i] = k
return p
Пример
Рассмотрим строку , для которой значение префикс-функции равно .
| Шаг | Строка | Значение функции |
|---|---|---|
| a | 0 | |
| ab | 0 | |
| abc | 0 | |
| abca | 1 | |
| abcab | 2 | |
| abcabc | 3 | |
| abcabcd | 0 |
Время работы
Всего итераций цикла, на каждой из который происходит сравнение строк за , что дает в итоге .
Эффективный алгоритм
Вносятся несколько важных замечаний:
- Заметим, что . Чтобы показать это, рассмотрим суффикс,оканчивающийся на позиции и имеющий длину , удалив из него последний символ, мы получим суффикс, оканчивающийся на позиции и имеющий длину , следовательно неравенство неверно.
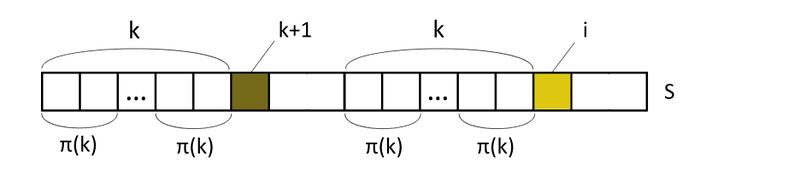
- Избавимся от явных сравнений строк. Пусть мы вычислили , тогда, если , то . Если окажется, что , то нужно попытаться попробовать подстроку меньшей длины. Хотелось бы сразу перейти к такому бордеру наибольшей длины, для этого подберем такое , что . Делаем это следующим образом. За исходное необходимо взять , что следует из первого пункта. В случае, когда символы и не совпадают, — следующее потенциальное наибольшее значение , что видно из рисунка. Последнее утверждение верно, пока , что позволит всегда найти его следующее значение. Если , то при , иначе .
Псевдокод
int[] prefixFunction(string s):
p[0] = 0
for i = 1 to s.length - 1
k = p[i - 1]
while k > 0 and s[i] != s[k]
k = p[k - 1]
if s[i] == s[k]
k++
p[i] = k
return p
Время работы
Время работы алгоритма составит . Для доказательства этого нужно заметить, что итоговое количество итераций цикла определяет асимптотику алгоритма. Теперь стоит отметить, что увеличивается на каждом шаге не более чем на единицу, значит максимально возможное значение . Поскольку внутри цикла значение лишь уменьшается, получается, что не может суммарно уменьшиться больше, чем раз. Значит цикл в итоге выполнится не более раз, что дает итоговую оценку времени алгоритма .
Построение префикс-функции по Z-функции
Постановка задачи
Дан массив с корректной Z-функцией для строки , получить за массив с префикс-функцией для строки .
Описание алгоритма
Пусть Z-функция хранится в массиве . Префикс-функцию будем записывать в массив .
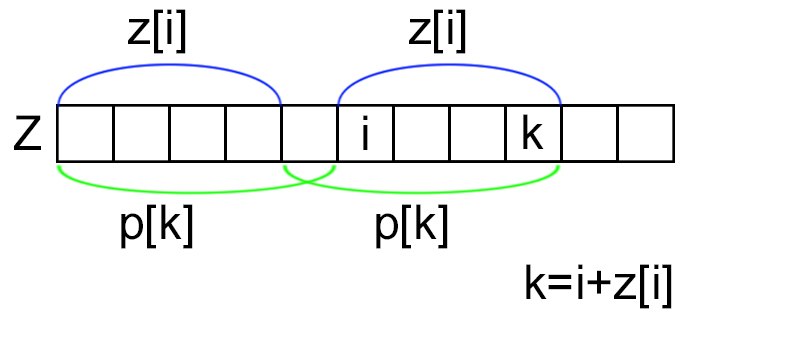
Заметим, что если то для всех элементов с индексом , где , значение будет не меньше, чем длина подстроки с по , что равно (как изображено на рисунке).
Также заметим, что если мы уже установили в какую-то позицию значение с позиции , а потом пытаемся установить значение c позиции , причём и , то изменение с позиции только уменьшит значение . Действительно, значение после первого присвоения . В итоге получаем алгоритм: идем слева направо по массиву и, находясь на позиции , пытаемся записать в от позиции до значение где пробегает все значения , пока не наткнемся на уже инициализированный элемент. Слева от него все значения тоже нет смысла обновлять, поэтому прерываем эту итерацию.
Убедимся, что алгоритм работает за линейное время (см. псевдокод). Каждый элемент устанавливается ровно один раз. Дальше на нем может случиться только . Поэтому в итоге внутренний цикл суммарно отработает за количество установленных значений и количество . Количество установленных значений — . А число тоже будет не больше , так как каждый переводит внешний цикл на следующую итерацию, откуда получаем итоговую асимптотику .
Псевдокод
int[] buildPrefixFunctionFromZFunction(int[] z):
int[] p = int[z.length]
fill(p, 0)
for i = 1 to z.length - 1
for j = z[i] - 1 downto 0
if p[i + j] > 0
break
else
p[i + j] = j + 1
return p
Построение строки по префикс-функции
Постановка задачи
Восстановить строку по префикс-функции за , считая алфавит неограниченным.
Описание алгоритма
Пусть в массиве хранятся значения префикс-функции, в будет записан ответ. Пойдем по массиву слева направо.
Пусть мы хотим узнать значение . Для этого посмотрим на значение : если , тогда в запишем новый символ, иначе . Обратим внимание, что нам уже известно, так как .
Реализация
string buildFromPrefix(int[] p):
s = ""
for i = 0 to p.length - 1
if p[i] == 0
s += new character
else
s += s[p[i] - 1]
return s
Доказательство корректности алгоритма
Докажем, что если нам дали корректную префикс-функцию, то наш алгоритм построит строку с такой же префикс-функцией. Также заметим, что строк с такой префикс-функцией может быть много, и алгоритм строит только одну из них.
Пусть — данная префикс-функция, строку построил наш алгоритм, — массив значений префикс-функции для .
Докажем корректность индукцией по длине массива префикс-функции полученной строки. Для начала заметим, что на предыдущие значения массива прибавление нового символа не влияет, так как при подсчёте префикс-функции на -ой позиции рассматриваются символы на позициях не больше . Поэтому достаточно показать, что очередное значение префикс-функции будет вычислено правильно.
- База очевидна для строки длины .
- Переход: пусть до -ой позиции мы построили строку, что . Возможны два случая:
- . Тогда мы добавляем новый символ, поэтому тоже будет равно .
- . Бордер строки имеет длину . Поэтому если дописать к строке символ , то бордер нашей новой строки станет равен , как можно увидеть на рисунке.
Критерий корректности значений префикс-функции
| Задача: |
| Дан массив значений префикс-функции некоторой строки , необходимо проверить, корректен ли он за . Так же узнать размер минимального алфавита, при котором он корректен. |
Решение
Если выполняется неравенство , то мы можем построить строку из алгоритма выше, значит префикс-функция корректна.
Найдем минимальный алфавит, при котором префикс-функция корректна. Если значение префикс-функции в текущей ячейке больше нуля, буква известна и алфавит не нуждается в добавлении новой буквы. Иначе, необходимо исключить все ранее известные буквы, возвращаясь и проверяя для меньших префиксов. Если все уже известные буквы использованы, понятно что, необходимо добавить новую букву.
Доказательство корректности
Докажем, что найденнный выше алфавит минимален от противного. Допустим, существует строка, использующая алфавит меньшей мощности. Рассмотрим первое вхождение буквы, которая есть в нашем алфавите, а в их отсутствует. Понятно, что для этого символа префикс-функция равна 0, т.к. мы добавили новую букву. Пройдемся циклом по подпрефиксам. Т.к. в меньшем решении буква не новая, то она увеличит подпрефикс и префикс-функция в новой строке будет отличаться от нуля в этом символе, а должна равняться нулю. Противоречие, следовательно не существует алфаивта меньшей мощности, чем найденный алгоритмом выше.
Псевдокод
bool is_correct(int[] p):
for i = 0 to p.length - 1
if i > 0 && p[i] > p[i - 1] + 1 || p[i] < 0
return false
return true
int minimal_alphabet(int[] p):
c = 1
s[0] = 0
for i = 1 to p.length - 1
if p[i] == 0
fill(used, false)
k = p[i - 1]
while k > 0
used[s[k]] = true
k = p[k - 1]
s[i] = -1
for j = 1 to c
if !used[j]
s[i] = j;
break
if s[i] == -1
s[i] = c++
else
s[i] = s[p[i] - 1]
return c
См. также
- Z-функция
- Алгоритм Кнута-Морриса-Пратта
Источники информации
- Википедия — Префикс-функция
- MAXimal :: algo :: Префикс-функция
- Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. — 2-е изд. — М.: Издательский дом «Вильямс», 2007. — С. 1296 ISBN 978-5-8459-0857-5
Определение. Префикс-функцией от строки $s$ называется массив $p$, где $p_i$ равно длине самого большого префикса строки $s_0 s_1 s_2 ldots s_i$, который также является и суффиксом $i$-того префика (не считая весь $i$-й префикс).
Например, самый большой префикс, который равен суффиксу для строки «aataataa» — это «aataa»; префикс-функция для этой строки равна $[0, 1, 0, 1, 2, 3, 4, 5]$.
vector<int> slow_prefix_function(string s) {
int n = (int) s.size();
vector<int> p(n, 0);
for (int i = 1; i < n; i++)
for (int len = 1; len <= i; len++)
// если префикс длины len равен суффиксу длины len
if (s.substr(0, len) == s.substr(i - len + 1, len))
p[i] = len;
return p;
}
Этот алгоритм пока что работает за $O(n^3)$, но позже мы его ускорим.
#Как это поможет решить исходную задачу?
Давайте пока поверим, что мы умеем считать префикс-функцию за линейное от размера строки, и научимся с помощью нее искать подстроку в строке.
Соединим подстроки $s$ и $t$ каким-нибудь символом, который не встречается ни там, ни там — обозначим пусть этот символ #. Посмотрим на префикс-функцию получившейся строки s#t.
string s = "choose";
string t =
"choose life. choose a job. choose a career. choose a family. choose a fu...";
cout << s + "#" + t << endl;
cout << slow_prefix_function(s + "#" + t) << endl;
choose#choose life. choose a job. choose a career. choose a family. choose a fu...
0000000123456000000012345600000000123456000100000001234560000000000012345600000000
Видно, что все места, где значения равны 6 (длине $s$) — это концы вхождений $s$ в текст $t$.
Такой алгоритм (посчитать префикс-функцию от s#t и посмотреть, в каких позициях она равна $|s|$) называется алгоритмом Кнута-Морриса-Пратта.
#Как её быстро считать
Рассмотрим ещё несколько примеров префикс-функций и попытаемся найти закономерности:
aaaaa
01234
abcdef
000000
abacabadava
00101230101
Можно заметить следующую особенность: $p_{i+1}$ максимум на единицу превосходит $p_i$.
Доказательство. Если есть префикс, равный суффиксу строки $s_{:i+1}$, длины $p_{i+1}$, то, отбросив последний символ, можно получить правильный суффикс для строки $s_{:i}$, длина которого будет ровно на единицу меньше.
Попытаемся решить задачу с помощью динамики: найдём формулу для $p_i$ через предыдущие значения.
Заметим, что $p_{i+1} = p_i + 1$ в том и только том случае, когда $s_{p_i} =s_{i+1}$. В этом случае мы можем просто обновить $p_{i+1}$ и пойти дальше.
Например, в строке $underbrace{aabaa}toverbrace{aabaa}$ выделен максимальный префикс, равный суффиксу: $p_{10} = 5$. Если следующий символ равен будет равен $t$, то $p_{11} = p_{10} + 1 = 6$.
Но что происходит, когда $s_{p_i}neq s_{i+1}$? Пусть следующий символ в этом же примере равен не $t$, а $b$.
- $implies$ Длина префикса, равного суффиксу новой строки, будет точно меньше 5.
- $implies$ Помимо того, что искомый новый супрефикс является суффиксом «aabaab», он ещё является префиксом подстроки «aabaa».
- $implies$ Значит, следующий кандидат на проверку — это значение префикс-функции от «aabaa», то есть $p_4 = 2$, которое мы уже посчитали.
- $implies$ Если $s_2 = s_{11}$ (т. е. новый символ совпадает с идущим после префикса-кандидата), то $p_{11} = p_2 + 1 = 2 + 1 = 3$.
В данном случае это действительно так (нужный префикс — «aab»). Но что делать, если, в общем случае, $p_{i+1} neq p_{p_i+1}$? Тогда мы проводим такое же рассуждение и получаем нового кандидата, меньшей длины — $p_{p_{p_i}}$. Если и этот не подошел — аналогично проверяем меньшего, пока этот индекс не станет нулевым.
vector<int> prefix_function(string s) {
int n = (int) s.size();
vector<int> p(n, 0);
for (int i = 1; i < n; i++) {
// префикс функция точно не больше этого значения + 1
int cur = p[i - 1];
// уменьшаем cur значение, пока новый символ не сматчится
while (s[i] != s[cur] && cur > 0)
cur = p[cur - 1];
// здесь либо s[i] == s[cur], либо cur == 0
if (s[i] == s[cur])
p[i] = cur + 1;
}
return p;
}
Асимптотика. В худшем случае этот while может работать $O(n)$ раз за одну итерацию, но в среднем каждый while работает за $O(1)$.
Префикс-функция каждый шаг возрастает максимум на единицу и после каждой итерации while уменьшается хотя бы на единицу. Значит, суммарно операций будет не более $O(n)$.
Задача про обезьян и бесконечность
Время на прочтение
9 мин
Количество просмотров 32K
Всем известно, что если посадить обезьяну за печатную машинку и заставить ее вечно случайно стучать по клавишам, то, рано или поздно, она напечатает «Войну и мир», собрание трудов Пифагора и даже статью, которую вы сейчас читаете.
Потрясающий факт, но еще интереснее попытаться понять, сколько же времени ей понадобится для набора конкретного текста. Чтобы не водить лишний параметр — скорость набора обезьяной — будем искать ответ на вопрос: сколько нажатий на клавиши ей потребуется в среднем. А вам очевидно, что строку «abc» набирать гораздо легче чем «aaa»? Решению этой задачи и посвящен этот пост. Попутно объясняется префикс функция и ее свойства.
Понятно, что время, потраченное обезьяной на набор конкретного текста — это некоторая случайная величина. Поэтому логично спросить про ее математическое ожидание.
Формальная постановка задачи
Дана строка s, состоящая из прописных латинских букв („a“-„z“). Нужно найти мат. ожидание количества случайных нажатий на клавиши до того, как будет набрана вся строка s, если все символы набираются равновероятно (с вероятностью 1/26).
Код решения
Чтобы понять, почему это работает и что это за функция Pi() нужно прочитать всю статью :(.
string s; //строка, которую набирает обезьяна
int n = s.length();
vector<int> p = Pi(s);
vector<long double> pow(n+1);
pow[0] = 1;
int i;
for (i = 1; i <= n; i++) {
pow[i] = pow[i-1]*26;
}
long double ans = 0;
for (i = n; i>0; i = p[i-1]) {
ans += pow[i];
}
cout << ans;Префикс функция
Именно эта функция поможет нам решить поставленную задачу. Префикс функция была введена Д. Кнутом и М. Праттом (и параллельно Д. Моррисом) для их знаменитого алгоритма поиска подстроки в строке (алгоритм КМП). Префикс функция для строки s возвращает длину самого длинного собственного префикса строки, который также является ее суффиксом.
Префиксы и суффиксы
Префикс — это просто начало строки, если отбросить сколько-то символов с конца. Так у строки «aba» есть 4 префикса: «» (пустая строка), «a», «ab» и «aba». Суффикс — тоже самое, но символы удаляются с начала. При этом некоторые суффиксы и префиксы могут совпасть. Для строки «aba» есть 3 таких префикса-суффикса: «»,»a» и «aba» (четвертый суффикс «ba» не совпадает с префиксом «ab»). Суффикс или префикс называется собственным, если он короче всей строки.
Формально говоря:
Где prefk (s) — это префикс длины k строки s, а sufk(s) — это суффикс длины k строки s.
Как в алгоритме КМП, так и в других применениях, гораздо полезнее рассматривать префикс функцию сразу для всех префиксов данной строки. Да, звучит страшно — для каждого префикса нужно найти наибольший собственный префикс, который совпадает с суффиксом префикса. Но на самом деле все просто:
Такая расширенная префикс функция полезна прежде всего тем, что ее проще вычислять, чем просто . Ниже показаны значения
для s=«ababac».
k: 1 2 3 4 5 6 s: a b a b a c P(i): 0 0 1 2 3 0
Вычисление префикс функции
Код вычисления
vector<int> Pi(string s) {
int n = s.length();
vector<int> p(n);
p[0] = 0;
for (int i = 1; i < n; i++) {
int j = p[i-1];
while (j > 0 && s[i] != s[j]) {
j = p[j];
}
if (s[i] == s[j]) j++;
p[i] = j;
}
return p;
}Быстрое, за O(N), вычисление префикс функции основано на двух простых наблюдениях.
(1) Чтобы получить префикс-суффикс для позиции k надо взять какой-то префикс-суффикс для позиции k-1 и дописать к нему в конец символ на позиции k.
(2) Все префиксы-суффиксы строки s длины n можно получить как и так далее, пока очередное значение не станет равным 0. Это свойство можно проверить на строке «abacaba». Тут
, что соответствует всем префиксам-суффиксам («aba», «a» и «»). Так получается потому, что максимальный префикс-суффикс имеет длину
. Следующий по длине префикс-суффикс будет короче. Но поскольку первый префикс-суффикс встречается как в начале, так и на конце строки s, то следующий префифкс-суффикс будет длиннейшим префиксом-суффиксом в первом префиксе-суффиксе.
Поэтому для построения префикс функции для позиции i достаточно проитерироваться начиная со значения префикс функции в предыдущей позиции пока продолжение суффикса новым символом не будет также и префиксом (для этого надо проверить только один новый символ). Такой алгоритм выполняется за линейное время, потому что значение префикс функции каждый раз увеличивается максимум на 1, поэтому оно не может уменьшится более чем n раз, а значит, вложенный цикл суммарно выполнится не более чем n раз.
Конечный автомат KMP
Следующий математический объект, необходимый в решении поставленной задачи — это конечный автомат, принимающий строки, заканчивающиеся на заданную строку s. Этот автомат используется в другой, менее известной модификации алгоритма Кнута-Морисса-Пратта. В этой версии алгоритма строится конечный автомат, который принимает все строки, которые заканчиваются на заданную строку (шаблон). Затем автомату передается строка-текст. Каждый раз, когда автомат принимает переданный ему текст, найдено очередное вхождение шаблона. Именно этот автомат и поможет нам решить задачу об обезьяне за печатоной машинкой.
Что такое конечный автомат
Конечный автомат — это математический объект который проще всего представить себе как некоторую коробку у которой есть какое-то внутреннее состояние. Изначально коробка находится в начальном состоянии. В коробку можно вводить строки, по одному символу за раз. После каждого символа коробка меняет свое состояние, при чем в зависимости от текущего состояния и введенного символа. Так же некоторые состояния являются хорошими (математический термин — конечные состояния). Говорят, что автомат принимает строку, если после скармливания ему этой строки символ-за-символом, автомат находится в хорошем состоянии.
Для определения КА нужно определить начальное состояние, хорошие состояния и функцию перехода — для каждого состояния и символа нужно указать новое состояние, в которое автомат перейдет. Удобно рисовать автомат как полный ориентированный граф, где вершины — это стостояния, а на каждом ребре написан ровно один символ. Из каждой вершины должно быть ровно одно ребро с каждым символом. Тогда для обработки какой-то строки надо просто перейти по ребрам с символами из этой строки. Если путь закончился в конечном состоянии, то автомат такую строку принимает.
Для построения этого автомата мы будем использовать уже известную нам префикс функцию.
В автомате будет n+1 состояние, пронумерованные от 0 до n. Состояние k соответствует совпадению последних k набранных символов с префиксом шаблона длины k (Если мы ищем строку «abac» то нам от текущего текста интересно только что там на конце: «abac», «aba», «ab», «a» или что-то друге. Этой информации достаточно чтоб получить такуюже после дописывания одного символа). Состояние 0 будет начальным, а состояние n — конечным. Иногда может быть неразбериха: например, для сроки «ababccc» при скормленой автамату строке «zzzabab» можно выбрать как состояние 2, так и 4. Но, чтобы не терять нужную информацию о набранном тексте, мы всегда будем выбирать наибольшее состояние.
пример конечного автомата KMP
Вот автомат для строки «ababac». Для примера алфавит состоит только из символов ‘a’-‘c’. Параллельные ребра объединены для наглядности. На самом деле каждому ребру соответствует только один символ. Начальное состояние — 0, конечное — 6.
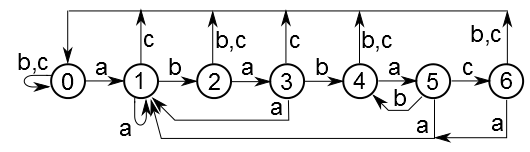
Несложно убедиться, что любой путь из состояния 0 в состояние 6, каким бы сложным он не был, обязательно кончается на строку «ababac». И наоборот, любой такой путь обязательно закончится в состоянии 6.
Код построения конечного автомата
string s; //исходная строка.
int n = s.length();
vector< vector<int> > nxt(n+1, vector<int>(256));
// функция перехода nxt[состояние][символ] == новое состояние
vector<int> p = Pi(s); // Префикс функция. См. код выше
nxt[0][s[0]] = 1; //единственный переход из состояния 0 не в 0.
for (int i = 1; i <= n; i++) {
for (int c = 0; c < 256; c++)
nxt[i][c] = nxt[p[i-1]][c]; //p[] индексируется с нуля, поэтому нужно -1
if (i < n) nxt[i][s[i]] = i+1;
}Обратите внимание, как строятся переходы. Для расчета переходов из состояния i мы рассматриваем 2 варианта. Если новый символ — это s[i] — то переход будет в состояние i+1. Тут все очевидно: если было совпадение в i символов — то добавив следующий символ из строки s мы увеличим длину совпадения на 1. Если же символ не совпал, то мы просто копируем переходы из состояния . Почему? Переход в этом случае будет точно в состояние с номером ≤i. Значит после перехода мы забудем часть информации о набранном тексте. Можно сделать это перед переходом. Самый минимум, что мы можем стереть, это притвориться что на самом деле сейчас состояние не i, а
. Это как в том примере выше, можно было считать что текст кончается на «abab» или «ab». Если из «abab» никаких переходов нет — можно использовать переходы из «ab».
Решение
Теперь мы готовы решить поставленную задачу.
Построим для строки s автомат KMP. Поскольку все символы набираются обезьяной случайно, нам не важны сами символы, а только ребра в графе переходов. Задачу можно переформулировать так: найти мат. ожидание количества переходов в случайном блуждании из состояния 0 пока не достигнуто состояние n.
Логично в такой постановке ввести переменные: Ek, 0≤k≤n — матожидание количества переходов до достижения состояния n. E0 будет ответом к исходной задаче. Пусть Z — это множество допустимых символов (алфавит). Можно составить систему уравнений:
Уравнение (1) означает, что достигнув состояния n случайное блуждание останавливается.
Для любого другого состояния будет сделан какой-то переход, поэтому в уравнении (2) присутствует слагаемое 1. Второе слагаемое — это сумма по всем возможным вариантам, умноженным на вероятность этих вариантов. Все вероятности одинаковы — поэтому она вынесена за знак суммы.
Вот уже есть решение задачи за O(n^3): построенную систему линейных уравнений можно решить методом Гаусса. Но если немного посмотреть на эту систему и вспомнить, что есть префикс функция, то есть решение гораздо проще и быстрее.
Вспомним построение конечного автомата. (Для простоты далее вместо я буду использовать просто
). Переходы из состояния k почти полностью совпадают с переходами из состояния
. Отличие в переходе только по символу s[k-1]. Поэтому правые части уравнений (2) для состояний k и
отличаются только одним слагаемым. В уравнении для
стоит
вместо
в уравнении для k. При чем nxt[k][s[k-1]]=k+1. Используя этот факт можно переписать уравнения (2):
Теперь нужно сделать еще одно наблюдение. Оказывается
Т.е. чтобы найти префикс функцию для какого-то состояния, надо взять префикс функцию от предыдущего состояния и перейти оттуда по символу, ведущему в следующее состояние.
Действительно, если рассмотреть состояние , то оно соответствует строке, заканчивающейся на символ s[k-1]. Значит туда есть переходы по этому символу. Рассмотрим самое большое состояние, из которого такой переход есть, но которое имеет номер < k. Если после перехода по символу s[k-1] мы получили какой-то суффикс
, то до перехода это был суффикс
. Поскольку это было самое правое такое состояние, то оно соответствует максимальному префиксу-суффиксу
, а значит оно имеет номер
. Вот мы и получили этот удивительный и полезный факт.
Тогда (3) преобразуется в:
Или по-другому:
С обеих сторон от знака равенства тут отрицательные числа (логично, что чем больше k, тем меньше Ek). Умножим обе части на -1.
Но (4) справедливо только для k>0. Для k=0 можно явно выписать уравнение (2), ведь только один из |Z| переходов ведет в состояние 1, а все остальные возвращаются в состояние 0:
Теперь соберем все переменные слева, домножим уравнение на |Z| и заменим (префикс функция для одного символа всегда равна 0, т.к. непустых собственных префиксов у одного символа нет):
Я позволю себе повторить уравнения (1), (4) и (5), так как они составляют систему, которую мы теперь решим аналитически:
Подставляя первое уравнение в левую часть второго при k=1, затем при k=2 и т.д. получаем:
Вот уже решение почти готово: теперь рассмотрим (6) при k=n и вспомним, что , получаем:
Подставляем это значение в (6) при — получаем:
Аналогично, получаем:
И так можно продолжать то тех пор, пока не получим выражение для , что, кстати, и является ответом к задаче. Обозначим
примененную k раз подряд функцию
, тогда:
Таким образом, мы получили решение задачи за O(n): построить префикс функцию к строке s и итерироваться по ней начиная с n пока не достигнем 0, попутно складывая степени |Z| равные текущей длине префикса. Это и есть то самое решение, приведенное в начале статьи.
Глядя на (*) становится понятно, почему строку «aaa» набрать сложнее чем «abc», ведь в у «aaa» только третья итерация равна нулю, а у второй строки вообще нет непустых префиксов равным суффиксам и
сразу дает ноль.
Замечания
Префикс функция и автомат КМП очень полезные инструменты для работы со строками. Если у уважаемых читателей есть интерес, то я могу разобрать решения других задач. О любых опечатках прошу сообщать в личку, спасибо.
Update:
Во-первых, спасибо огромное parpalak за его замечательный сервис для подготовке статьей с формулами на Хабре (https://habrahabr.ru/post/264709/). Без него этой статьи бы не было. Очень стыдно, что забыл сразу об этом написать.
Во-вторых, очень многих комментаторов путает их интуиция. В теорвере это часто случается. Да, вероятности набрать тексты одинаковой длины с первого раза одинаковы. Да, частота вхождения одинаковых по длине текстов одинакова в бесконечном случайном тексте. Все это верно, но из этих фактов не следует, что мат.ожидания количества символов до первого вхождения строк будут одинаковыми. И наоборот, из того, что строка «чч» в бесконечном тексте встретится позже, чем строка «чк» никак не следует, что в казино надо после черного ставить на красное.
Давайте на пальцах посчитаем матожидания до выпадания двух строк «чч» и «чк». Матожидание — это сумма по всем i: вероятности набрать строку за i символов в первый раз умноженной на i. Фраза выделенная жирным означает что, во-первых, последние набранные символы совпадают с искомыми (эта вероятность одинакова для обеих строк), и, во-вторых, среди первых i-2 символов искомая строка не встречается. Этот второй множитель и отличается для разных строк. Вероятность не найти строку — это просто количество всех текстов, в которых этой строки нет, деленное на количество всех текстов такой длины.
Теперь важное: строк длины k не содержащих строку «чк» всего k+1: «к…к», «к…кч», «к…кчч», «к…ккччч», …, «кч…ч» и «ч…ч». Это потому, что после символа «ч» может быть только «ч».
Сток же длины k не содержащих строку «чч» будет гораздо больше, а именно Fk+1 — число Фиббоначи под номером k+1 (это числа 1, 1, 2, 3, 5, 8, 13,… — каждое следующее есть сумма двух предыдущих). Например, для k=2 3 строки будут «кк», «кч», «чк». Эти числа очень быстро растут и поэтому все слагаемые для мат ожидания для строки «кк» будут больше, так как там вероятность больше.
Обратите внимание, все из-за того, что вероятности напечатать текст в первый раз за сколько-то нажатий зависят от вероятности не напечатать текст ни разу в начале и середине текста. Эта вероятность прямо пропорциональна количеству строк не содержащих заданную строку, а оно для разных шаблонов разное.
Еще раз, это не я придумал, это известный факт, хоть и крайне неинтуитивный. Посмотрите, например, на эту статью (ищите там задачу про Алису и Боба — 4 абзац): https://habrahabr.ru/post/279337/
Материал из Algocode wiki
Перейти к: навигация, поиск
Постановка и наивное решение
Определение:
Префикс-функция —это массив $p$, где $p_i$ равно длине самого большого префикса строки $s_0 s_1 s_2 ldots s_i$, который также является и суффиксом $i$-того префика (не считая весь $i$-й префикс).
Например, самый большой префикс, который равен суффиксу для строки «aataataa» — это «aataa»; префикс-функция для этой строки равна $[0, 1, 0, 1, 2, 3, 4, 5]$.
vector<int> slow_prefix_function(string s) { int n = (int) s.size(); vector<int> p(n, 0); for (int i = 1; i < n; i++) for (int len = 1; len <= i; len++) // если префикс длины len равен суффиксу длины len if (s.substr(0, len) == s.substr(i - len + 1, len)) p[i] = len; return p; }
Этот алгоритм пока что работает за $O(n^3)$, но позже мы его ускорим.
Решение за $O(n)$
Рассмотрим ещё несколько примеров префикс-функций и попытаемся найти закономерности:
aaaaa 01234 abcdef 000000 abacabadava 00101230101
Можно заметить следующую особенность: $p_{i+1}$ максимум на единицу превосходит $p_i$.
Доказательство. Если есть префикс, равный суффиксу строки $s_{:i+1}$, длины $p_{i+1}$, то, отбросив последний символ, можно получить правильный суффикс для строки $s_{:i}$, длина которого будет ровно на единицу меньше.
Попытаемся решить задачу с помощью динамики: найдём формулу для $p_i$ через предыдущие значения.
Заметим, что $p_{i+1} = p_i + 1$ в том и только том случае, когда $s_{p_i} =s_{i+1}$. В этом случае мы можем просто обновить $p_{i+1}$ и пойти дальше.
Например, в строке $underbrace{aabaa}toverbrace{aabaa}$ выделен максимальный префикс, равный суффиксу: $p_{10} = 5$. Если следующий символ равен будет равен $t$, то $p_{11} = p_{10} + 1 = 6$.
Но что происходит, когда $s_{p_i}neq s_{i+1}$? Пусть следующий символ в этом же примере равен не $t$, а $b$.
- $implies$ Длина префикса, равного суффиксу новой строки, будет точно меньше 5.
- $implies$ Помимо того, что искомый новый супрефикс является суффиксом «aabaab», он ещё является префиксом подстроки «aabaa».
- $implies$ Значит, следующий кандидат на проверку — это значение префикс-функции от «aabaa», то есть $p_4 = 2$, которое мы уже посчитали.
- $implies$ Если $s_2 = s_{11}$ (т. е. новый символ совпадает с идущим после префикса-кандидата), то $p_{11} = p_2 + 1 = 2 + 1 = 3$.
В данном случае это действительно так (нужный префикс — «aab»). Но что делать, если, в общем случае, $p_{i+1} neq p_{p_i+1}$? Тогда мы проводим такое же рассуждение и получаем нового кандидата, меньшей длины — $p_{p_{p_i}}$. Если и этот не подошел — аналогично проверяем меньшего, пока этот индекс не станет нулевым.
vector<int> prefix_function(string s) { int n = (int) s.size(); vector<int> p(n, 0); for (int i = 1; i < n; i++) { // префикс функция точно не больше этого значения + 1 int cur = p[i - 1]; // уменьшаем cur значение, пока новый символ не сматчится while (s[i] != s[cur] && cur > 0) cur = p[cur - 1]; // здесь либо s[i] == s[cur], либо cur == 0 if (s[i] == s[cur]) p[i] = cur + 1; } return p; }
Асимптотика. В худшем случае этот while может работать $O(n)$ раз за одну итерацию, но в среднем каждый while работает за $O(1)$.
Префикс-функция каждый шаг возрастает максимум на единицу и после каждой итерации while уменьшается хотя бы на единицу. Значит, суммарно операций будет не более $O(n)$.
Z-функция
Материал позаимствован с сайта e-maxx.ru.
Определение
Здесь и далее строки индексируются с нуля, т.е. первый символ строки имеет номер (0). Также, здесь и далее (s[i ldots j]) обозначает подстроку строки (s) от (i)-го символа до (j)-го включительно.
Пусть дана строка (s) длины (n). Тогда (Z(s)) — это массив длины (n), (i)-ый элемент которого равен наибольшему числу символов, начиная с позиции (i), совпадающих с первыми символами строки (s).
Иными словами, (z[i]) — это длина наибольшего общего префикса строки (s) и её (i)-го суффикса.
Первый элемент (Z)-функции, (z[0]), обычно считают неопределённым. В данной статье мы будем считать, что он равен нулю (хотя ни в алгоритме, ни в приведённой реализации это ничего не меняет).
Далее будет привиден алгоритм вычисления (Z)-функции за время (O(n)), а также различные применения этого алгоритма.
Примеры
Приведём для примера подсчитанную (Z)-функцию для нескольких строк:
-
«aaaaa»:
z[0] = 0, z[1] = 4, z[2] = 3, z[3] = 2, z[4] = 1.
-
«aaabaab»:
z[0] = 0, z[1] = 2, z[2] = 1, z[3] = 0, z[4] = 2, z[5] = 1, z[6] = 0.
-
«abacaba»:
z[0] = 0, z[1] = 0, z[2] = 1, z[3] = 0, z[4] = 3, z[5] = 0, z[6] = 1.
Тривиальный алгоритм
Формальное определение можно представить в виде следующей элементарной реализации за (O(n^2)):
def z_func(s, n): z = [0] * n for i in range(1, n - 1): while i + z[i] < n and s[z[i]] == s[i + z[i]]: z[i] += 1 return z
Мы просто для каждой позиции (i) перебираем ответ для неё (z[i]), начиная с нуля, и до тех пор, пока мы не обнаружим несовпадение или не дойдём до конца строки.
Разумеется, эта реализация слишком неэффективна, перейдём теперь к построению эффективного алгоритма.
Эффективный алгоритм вычисления Z-функции
Чтобы получить эффективный алгоритм, будем вычислять значения (z[i]) по очереди — от (i=1) до (n-1), и при этом постараемся при вычислении очередного значения (z[i]) максимально использовать уже вычисленные значения.
Назовём для краткости подстроку, совпадающую с префиксом строки (s), отрезком совпадения. Например, значение искомой Z-функции (z[i]) — это длина длиннейшего отрезок совпадения, начинающийся в позиции (i) (и заканчиваться он будет в позиции (i + z[i] — 1)).
Для этого будем поддерживать координаты (boldsymbol{[l;r]}) самого правого отрезка совпадения, т.е. из всех обнаруженных отрезков будем хранить тот, который оканчивается правее всего. В некотором смысле, индекс (r) — это такая граница, до которой наша строка уже была просканирована алгоритмом, а всё остальное — пока ещё не известно.
Тогда если текущий индекс, для которого мы хотим посчитать очередное значение (Z)-функции, — это (i), мы имеем один из двух вариантов:
-
(i > r) — т.е. текущая позиция лежит за пределами того, что мы уже успели обработать.
Тогда будем искать (z[i]) тривиальным алгоритмом, т.е. просто пробуя значения (z[i]=0), (z[i]=1), и т.д. Заметим, что в итоге, если (z[i]) окажется (> 0), то мы будем обязаны обновить координаты самого правого отрезка ([l; r]) — т.к. (i + z[i] — 1) гарантированно окажется больше (r).
-
(i le r) — т.е. текущая позиция лежит внутри отрезка совпадения ([l; r]).
Тогда мы можем использовать уже подсчитанные предыдущие значения (Z)-функции, чтобы проинициализировать значение (z[i]) не нулём, а каким-то возможно бОльшим числом.
Для этого заметим, что подстроки (s[l ldots r]) и (s[0 ldots r-l]) совпадают. Это означает, что в качестве начального приближения для (z[i]) можно взять соответствующее ему значение из отрезка (s[0 ldots r-l]), а именно, значение (z[i-l]).
Однако значение (z[i-l]) могло оказаться слишком большим: таким, что при применении его к позиции (i) оно «вылезет» за пределы границы (r). Этого допустить нельзя, т.к. про символы правее (r) мы ничего не знаем, и они могут отличаться от требуемых.
Приведём пример такой ситуации, на примере строки «aaaabaa».
Когда мы дойдём до последней позиции ((i=6)), текущим самым правым отрезком будет ([5;6]). Позиции (6) с учётом этого отрезка будет соответствовать позиция (6-5=1), ответ в которой равен (z[1] = 3). Очевидно, что таким значением инициализировать (z[6]) нельзя, оно совершенно некорректно. Максимум, каким значением мы могли проинициализировать — это (1), поскольку это наибольшее значение, которое не вылезает за пределы отрезка ([l;r]).
Таким образом, в качестве начального приближения для (z[i]) безопасно брать только такое выражение:
begin{equation*}
z_0[i] = min (r-i+1, z[i-l]).
end{equation*}Проинициализировав (z[i]) таким значением (z_0[i]), мы снова дальше действуем тривиальным алгоритмом — потому что после границы (r), вообще говоря, могло обнаружиться продолжение отрезка совпадение, предугадать которое одними лишь предыдущими значениями (Z)-функции мы не можем.
Таким образом, весь алгоритм представляет из себя два случая, которые фактически различаются только начальным значением (z[i]): в первом случае оно полагается равным нулю, а во втором — определяется по предыдущим значениям по указанной формуле. После этого обе ветки алгоритма сводятся к выполнению тривиального алгоритма, стартующего сразу с указанного начального значения.
Алгоритм получился весьма простым. Несмотря на то, что при каждом (i) в нём так или иначе выполняется тривиальный алгоритм — мы достигли существенного прогресса, получив алгоритм, работающий за линейное время (действительно, на каждый символ мы «посмотрим», т.е. сравним его с каким-либо предыдущим всего один раз).
Упражнение №1: (Z)-функция
Напишите (Z)-функцию. Пусть заголовком ее будет def z_func(s, n):
Упражнение №2: Поиск подстроки
Пусть даны две строки. Найти все вхождения второй строки в первую.
Упражнение №3: Количество разных подстрок
Найти число всех различных подстрок входящих в данную.
Упражнение №4: Период строки
Для данной строки (s) найти строку (p) минимальной длины, такую что (s) можно предстваить как конкатенацию одной или нескольких копий (p).
Префикс-функция. Алгоритм Кнута-Морриса-Пратта
Материал частично позаимствован с сайта тоже e-maxx.ru.
Префикс-функция. Определение
Пусть дана строка (s) длины (n). Тогда (pi(s)) — это массив длины (n), (i)-ый элемент которого ((pi[i])) определяется следующим образом: это длина наибольшего собственного суффикса подстроки (s[0 ldots i]), совпадающего с её префиксом (собственный суффикс — значит не совпадающий со всей строкой). В частности, значение (pi[0]) полагается равным нулю.
Примечение: вообще говоря, в теории множеств собственным считается не пустое подмножество, не совпдающее с самим множеством. В данной статье, для простоты суффикс и префикс нулевой длины также считаются собственными.
Математически определение префикс-функции можно записать следующим образом:
begin{equation*}
pi[i] = max_{k=0 ldots i} { k : s[0 ldots k — 1] = s[i — k + 1 ldots i]}.
end{equation*}
Например, для строки «abcabcd» префикс-функция равна: ([0, 0, 0, 1, 2, 3, 0]), что означает:
у строки "a" нет нетривиального префикса, совпадающего с суффиксом; у строки "ab" нет нетривиального префикса, совпадающего с суффиксом; у строки "abc" нет нетривиального префикса, совпадающего с суффиксом; у строки "abca" префикс длины 1 совпадает с суффиксом; у строки "abcab" префикс длины 2 совпадает с суффиксом; у строки "abcabc" префикс длины 3 совпадает с суффиксом; у строки "abcabcd" нет нетривиального префикса, совпадающего с суффиксом.
Другой пример — для строки «aabaaab» она равна: ([0, 1, 0, 1, 2, 2, 3]).
Тривиальный алгоритм
Непосредственно следуя определению, можно написать такой алгоритм вычисления префикс-функции:
def prefix_func(s, n): pi = [0] * n for i in range(n - 1): for k in range(1, i + 1): equal = True for j in range(k): if s[j] != s[i - k + 1 + j]: equal = False break if equal: pi[i] = k return pi
Как нетрудно заметить, работать он будет за (O(n^3)), что слишком медленно.
Эффективный алгоритм
Для удобства будем обозначать подстроки строки (s) следующим образом: пусть (p^k) — префикс (s) длины (k), (s^k_i) — подстрока длины (k) заканчивающаяся символом с номером (i). Напомним, что первый символ строки имеет номер (0).
Будем вычислять (pi[i]) последовательно, начиная с (pi[1]). (pi[0]) очевидно (= 0). Постараемся на (i) шаге получить решение, используя уже известную информацию, т.е. предыдущие значения (pi).
Во-первых заметим, что (pi[i]) превосходит (pi[i — 1]) не более чем на 1. Действительно, раз уж (p^{pi[i]}) = (s^{pi[i]}_i), значит и (p^{pi[i]-1}=s^{pi[i]-1}_{i-1}), а значит (pi[i — 1]) как минимум будет (pi[i] — 1). Это иллюстрирует схема (для (pi[i] = 4)):
begin{equation*}
underbrace{ overbrace{s_0 s_1 s_2}^{pi[i-1]} overbrace{s_3}^{s_3 = s_i }}_{pi[i] = 4} ldots underbrace{ overbrace{s_{i-3} s_{i-2} s_{i-1}}^{pi[i-1] >= 3} overbrace{s_i}^{s_3 = s_i} }_{pi[i] = 4}
end{equation*}
Будем рассматривать убывающую последовательность ({k_j}: p^{k_j} = s^{k_j}_{i — 1}, i > k_j, k_j > k_{j + 1}, j = 0, 1, …), т.е. собственные суффиксы строки (p^i), являющиеся одновременно ее префиксами, упорядоченные по убыванию длины. Очевидно, что первый из них, для которого выполнено (s[k_j] = s[i]) даст нам (pi[i] = k_j + 1). Осталось только понять, как можно быстро перебрать такие (k_j). Иллюстрация, в предположении что (k_{j+1} = 2):
begin{equation*}
overbrace{overbrace{s_0 s_1}^{k_{j+1}} s_2 ldots s_{k_j-1}}^{k_j} s_{k_j} ldots overbrace{s_{i-k_{j-1}} ldots overbrace{s_{i-2} s_{i-1}}^{k_{j+1}}}^{k_j} s_i
end{equation*}
begin{equation*}
ldots
end{equation*}
begin{equation*}
s_{k_j} = s_i Rightarrow pi[i] = k_j + 1, text{переходим к следующему i}
end{equation*}
begin{equation*}
s_{k_{j+1}} = s_i Rightarrow pi[i] = k_{j+1} + 1, text{переходим к следующему i}
end{equation*}
begin{equation*}
ldots
end{equation*}
По определению префикс-функции, очевидно, что (k_0 = pi[i — 1]). Пусть мы теперь знаем (k_j), найдем (k_{j+1}). (p^{k_j} = s^{k_j}_{i — 1}), значит, (p^{k_{j+1}} = s^{k_{j+1}}_{k_j — 1}), причем (p^{k_{j+1}}) максимален из всех таких собственных префиксов строки (p^{k_j}). Значит, (k_{j+1} = pi[k_j — 1]). Иллюстрация, в предположении что (k_{j+1} = 2):
begin{equation*}
overbrace{underbrace{s_0 s_1}_{k_{j+1}} s_2 ldots underbrace{s_{k_j-1} s_{k_j-1}}_{k_{j+1} = pi[k_j — 1]}}^{k_j} s_{k_j} ldots overbrace{s_{i-k_j} ldots underbrace{s_{i-2} s_{i-1}}_{k_{j+1}}}^{k_j} s_i
end{equation*}
Ясно, что последовательность (k_j) заканчивается первым получившимся нулем. Если при этом условие (s[k_j] = s[i]) так и не было удовлетворено, то очередное (pi[i] = 0).
Итак, (pi[0] = 0), далее, на каждом шагу алгоритма будем вычислять последовательность (k_j). Если для очередного (k_j) выполнено (s[k_j] = s[i]), то (pi[i] = k_j + 1), переходим к следующему (i). Если перебрали все (k_j) вплоть до нуля и совпадения нет, то (pi[i] = 0). Заметим, что дойдя до нуля совпадение тоже нужно проверить, в этом случае можно получить (pi[i] = 0 + 1 = 1).
Этот алгоритм был разработан Кнутом (Knuth) и Праттом (Pratt) и независимо от них Моррисом (Morris) в 1977 г. (как основной элемент для алгоритма поиска подстроки в строке). Легко видеть, что алгоритм имеет сложность (O(n)): действительно, сложность шага, на котором префикс-функция возрастает, т.е. (pi[i] = pi[i — 1] + 1) есть (O(1)), сложность шага на котором функция убывает есть (O(pi[i] — pi[i — 1])). Т.е. общая сложность есть (O(sum_i| pi[i] — pi[i — 1]|)). Сумма положительных приростов префикс-функции не превышает (n). А сумма отрицательных изменений не может превысить сумму положительных (иначе мы уйдем в минус). Значит сумма модулей изменений функции не превысит (2n), значит общая сложность (O(n)).
Как нетрудно заметить, этот алгоритм является онлайновым, т.е. он обрабатывает данные по ходу поступления — можно, например, считывать строку по одному символу и сразу обрабатывать этот символ, находя ответ для очередной позиции. Алгоритм требует хранения самой строки и предыдущих вычисленных значений префикс-функции, однако, как нетрудно заметить, если нам заранее известно максимальное значение, которое может принимать префикс-функция на всей строке, то достаточно будет хранить лишь на единицу большее количество первых символов строки и значений префикс-функции.
Поиск подстроки в строке. Алгоритм Кнута-Морриса-Пратта
Эта задача является классическим применением префикс-функции (и, собственно, она и была открыта в связи с этим).
Дан текст (t) и строка (s), требуется найти и вывести позиции всех вхождений строки (s) в текст (t).
Обозначим для удобства через (n) длину строки (s), а через (m) — длину текста (t).
Образуем строку (s + # + t), где символ (#) — это разделитель, который не должен нигде более встречаться. Посчитаем для этой строки префикс-функцию. Теперь рассмотрим её значения, кроме первых (n+1) (которые, как видно, относятся к строке (s) и разделителю). По определению, значение (pi[i]) показывает наидлиннейшую длину подстроки, оканчивающейся в позиции (i) и совпадающего с префиксом. Но в нашем случае это (pi[i]) — фактически длина наибольшего блока совпадения со строкой (s) и оканчивающегося в позиции (i). Больше, чем (n), эта длина быть не может, за счёт разделителя. А вот равенство (pi[i] = n) (там, где оно достигается), означает, что в позиции (i) оканчивается искомое вхождение строки (s) (только не надо забывать, что все позиции отсчитываются в склеенной строке (s+#+t)).
Таким образом, если в какой-то позиции (i) оказалось (pi[i] = n), то в позиции (i — (n + 1) — n + 1 = i — 2n) строки (t) начинается очередное вхождение строки (s) в строку (t).
Как уже упоминалось при описании алгоритма вычисления префикс-функции, если известно, что значения префикс-функции не будут превышать некоторой величины, то достаточно хранить не всю строку и префикс-функцию, а только её начало. В нашем случае это означает, что нужно хранить в памяти лишь строку (s + #) и значение префикс-функции на ней, а потом уже считывать по одному символу строку (t) и пересчитывать текущее значение префикс-функции.
Итак, алгоритм Кнута-Морриса-Пратта решает эту задачу за (O(n+m)) времени и (O(n)) памяти.
Упражнение №5: Префикс-функция
Напишите префикс-функцию. Пусть заголовком ее будет def p_func(s, n):
Упражнение №6: Поиск подстроки
Пусть даны две строки. Найти все вхождения второй строки в первую с помощью алгоритма Кнута-Морриса-Пратта.
Упражнение №7: Поиск подстроки онлайн
В первой строке ввода — число (n), количество букв в паттерне.
Во второй строке — паттерн, строка которую нужно искать в тексте.
В каждой из последующих строк — символы текста, по одному в каждой строке. Необходимо вывести позиции вхождений паттерна в текст. Длина текста заранее не известна, он может быть очень большим.
Упражнение №8: Количество разных подстрок
Найти число всех различных подстрок входящих в данную с помощью префикс-функции.
Упражнение №9: Период строки
Для данной строки (s) найти строку (p) минимальной длины, такую что (s) можно предстваить как конкатенацию одной или нескольких копий (p). Используйте префикс-функцию.

