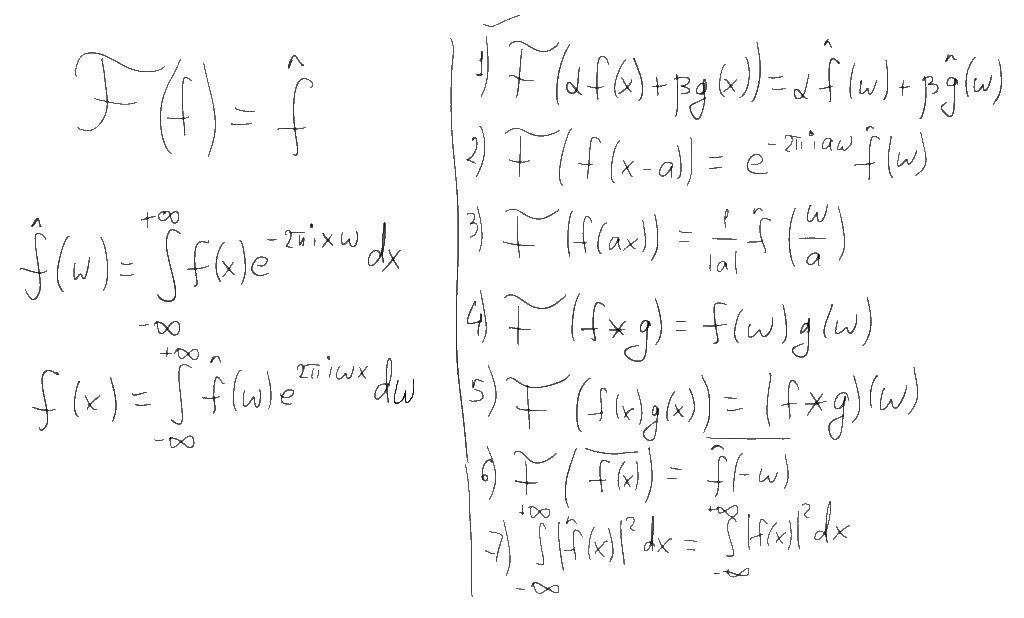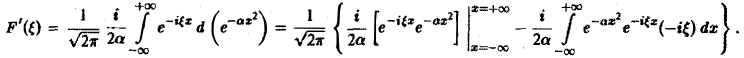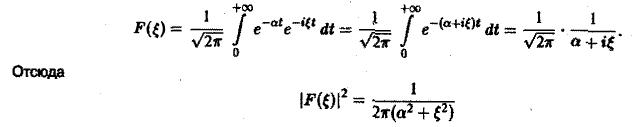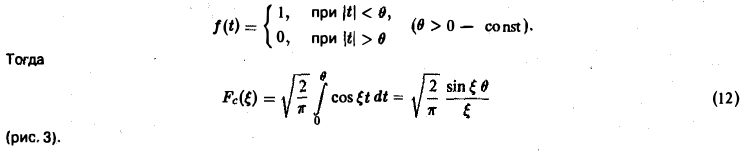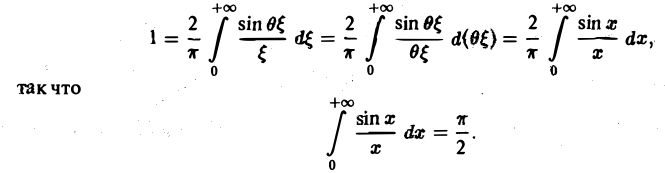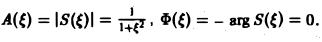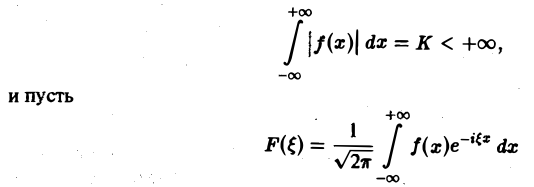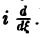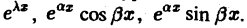Загрузить PDF
Загрузить PDF
Преобразование Фурье — это интегральное преобразование, которое нашло широкое применение в физике и инженерных расчетах. Его часто используют для анализа сигналов и решения некоторых дифференциальных уравнений в частных производных.
Критерии сходимости преобразования Фурье (а именно, что функция должна быть абсолютно интегрируемой в вещественной области) довольно строги из-за отсутствия члена с экспоненциальным затуханием, который имеется в преобразовании Лапласа, и это означает, что такие функции, как полиномы, экспоненты и тригонометрические функции, не имеют преобразования Фурье в обычном смысле. Тем не менее с помощью дельта-функции Дирака можно осуществить преобразование Фурье этих функций корректным образом.
Такая процедура может потребоваться даже для самых простых функций, поэтому для лучшего понимания изложенного ниже материала желательно ознакомиться со свойствами преобразования Лапласа. Кроме того, лучше начать со свойств преобразования Фурье, и лишь затем переходить к рассмотрению конкретных примеров.
Предварительные сведения
-
1
Найдем преобразование Фурье производной. Простое интегрирование по частям и учет того, что
должна стремиться к нулю на бесконечности, дают следующий результат:
-
2
Найдем преобразование Фурье функции, умноженной на
. Симметрия преобразования Фурье дает аналогичное свойство в пространстве частот. Сначала рассмотрим случай
, а затем обобщим полученный результат.
-
3
-
4
-
5
Найдем преобразование Фурье функции
. В этом случае имеем свойство растяжения, которое наблюдается и для преобразования Лапласа:
-
6
Найдем преобразование Фурье свертки двух функций. Как и в случае преобразования Лапласа, свертка в реальном пространстве соответствует умножению в пространстве Фурье:
-
7
Рассмотрим преобразование Фурье четных и нечетных функций. Четные и нечетные функции обладают особой симметрией. Для получения результата используем формулу Эйлера и свойства умножения четных и нечетных функций.
Реклама
-
1
Подставьте функцию в формулу для преобразования Фурье. Как и в случае преобразования Лапласа, преобразование Фурье функции можно выполнить непосредственно с помощью его определения. В качестве примера рассмотрим функцию
, которая однозначно удовлетворяет критериям сходимости.
-
2
Оценим интеграл с помощью доступных методов. Хотя данный интеграл не вычисляется элементарными методами, его можно найти с помощью теории вычетов.
- Чтобы использовать метод вычетов, проведем контур
, состоящий из линии вдоль действительной оси и соединенной с ней полукруглой дуги в нижней полуплоскости, которая обходится по часовой стрелке. Действительный интеграл равен интегралу по контуру, а интеграл вдоль дуги обращается в нуль:
- Можно разложить знаменатель на множители и показать, что функция имеет простые полюсы в
. Поскольку контур охватывает лишь
, можно использовать теорему вычетов, чтобы вычислить интеграл по контуру:
- Обратите внимание на дополнительный знак «–», который появился из-за того, что мы двигаемся по контуру по часовой стрелке.
- Не менее важно показать, что интеграл вдоль дуги равен нулю. Это можно сделать с помощью леммы Жордана. Хотя в лемме не говорится непосредственно, что интеграл равен нулю, она позволяет оценить разность между интегралом по контуру и вещественным интегралом. Применим лемму к нижней полуплоскости для функции
, где
. С параметризацией
, где
, лемма Жордана дает следующее ограничение для интеграла:
- Теперь осталось показать, что
стремится к нулю при больших
, что в данном случае тривиально, поскольку функция уменьшается как
:
- Какова в данном случае область определения
? Как отмечалось выше, лемма Жордана применима лишь для
. Тем не менее, если повторить данный расчет для контура в верхней полуплоскости, найти вычет для второго полюса, еще раз применить лемму Жордана и убедиться, что интеграл вдоль дуги равен нулю, мы получим
, и в этом случае областью определения
будут отрицательные действительные числа. Таким образом, получаем окончательный результат:
- Чтобы использовать метод вычетов, проведем контур
-
3
-
4
Рассмотрим преобразование Фурье функции Гаусса. Функция Гаусса относится к тем немногим функциям, которые при преобразовании Фурье сохраняют свой вид. Дополним показатель степени до полного квадрата и проинтегрируем:
Реклама
-
1
Рассмотрим преобразование Фурье функции
. Если вы знакомы с преобразованием Лапласа, то знаете, что экспоненциальная функция имеет очень «простое» преобразование Лапласа. В случае преобразования Фурье дело обстоит сложнее, поскольку модуль данной функции не стремится к 0 при
. Тем не менее ее образ Фурье представляет собой дельта-функцию:
-
2
Рассмотрим преобразование Фурье функции
. С помощью свойства сдвига можно найти преобразование Фурье степенной функции, а следовательно, и любых полиномов. Обратите внимание, что при этом вычисляются производные дельта-функции:
-
3
Реклама
Советы
- Существуют также две другие распространенные формы записи преобразования Фурье.
Реклама
Об этой статье
Эту страницу просматривали 18 536 раз.
Была ли эта статья полезной?
Простыми словами о преобразовании Фурье
Уровень сложности
Средний
Время на прочтение
14 мин
Количество просмотров 989K
Я полагаю что все в общих чертах знают о существовании такого замечательного математического инструмента как преобразование Фурье. Однако в ВУЗах его почему-то преподают настолько плохо, что понимают как это преобразование работает и как им правильно следует пользоваться сравнительно немного людей. Между тем математика данного преобразования на удивление красива, проста и изящна. Я предлагаю всем желающим узнать немного больше о преобразовании Фурье и близкой ему теме того как аналоговые сигналы удается эффективно превращать для вычислительной обработки в цифровые.

Без использования сложных формул и матлаба я постараюсь ответить на следующие вопросы:
- FT, DTF, DTFT — в чем отличия и как совершенно разные казалось бы формулы дают столь концептуально похожие результаты?
- Как правильно интерпретировать результаты быстрого преобразования Фурье (FFT)
- Что делать если дан сигнал из 179 сэмплов а БПФ требует на вход последовательность по длине равную степени двойки
- Почему при попытке получить с помощью Фурье спектр синусоиды вместо ожидаемой одиночной “палки” на графике вылезает странная загогулина и что с этим можно сделать
- Зачем перед АЦП и после ЦАП ставят аналоговые фильтры
- Можно ли оцифровать АЦП сигнал с частотой выше половины частоты дискретизации (школьный ответ неверен, правильный ответ — можно)
- Как по цифровой последовательности восстанавливают исходный сигнал
Я буду исходить из предположения что читатель понимает что такое интеграл, комплексное число (а так же его модуль и аргумент), свертка функций, плюс хотя бы “на пальцах” представляет себе что такое дельта-функция Дирака. Не знаете — не беда, прочитайте вышеприведенные ссылки. Под “произведением функций” в данном тексте я везде буду понимать “поточечное умножение”
Начать надо, наверное, с того что обычное преобразование Фурье — это некая такая штука которая, как можно догадаться из названия, преобразует одни функции в другие, то есть ставит в соответствие каждой функции действительного переменного x(t) её спектр или фурье-образ y(w):
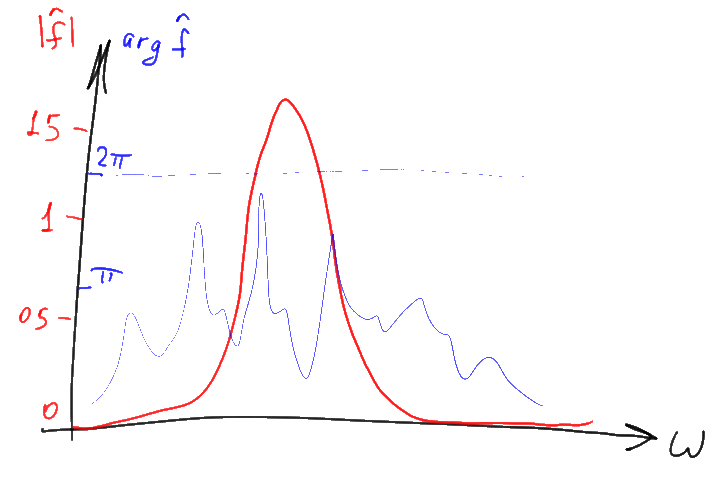
Если приводить аналогии, то примером аналогичного по смыслу преобразования может послужить например дифференцирование, превращающее функцию в её производную. То есть преобразование Фурье — такая же, по сути, операция как и взятие производной, и её часто обозначают схожим образом, рисуя треугольную “шапочку” над функцией. Только в отличие от дифференцирования которое можно определить и для действительных чисел, преобразование Фурье всегда “работает” с более общими комплексными числами. Из-за этого постоянно возникают проблемы с отображением результатов этого преобразования, поскольку комплексные числа определяются не одной, а двумя координатами на оперирующем действительными числами графике. Удобнее всего, как правило, оказывается представить комплексные числа в виде модуля и аргумента и нарисовать их по раздельности как два отдельных графика:
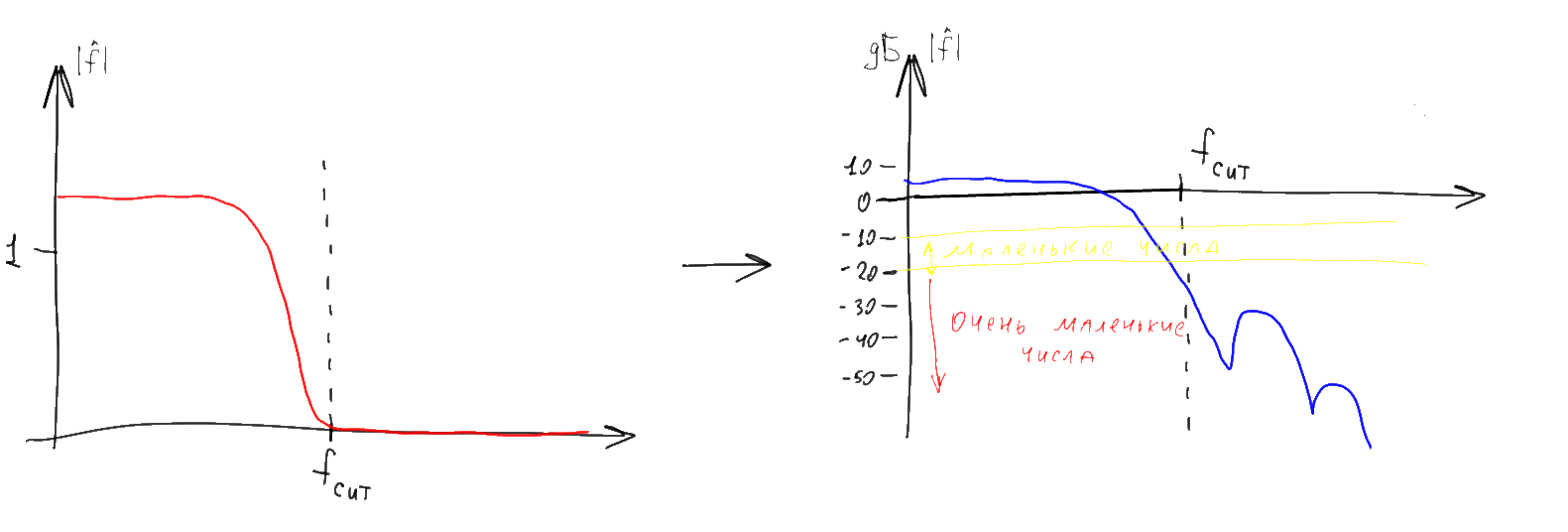
График аргумента комплексного значения часто называют в данном случае “фазовым спектром”, а график модуля — “амплитудным спектром”. Амплитудный спектр как правило представляет намного больший интерес, а потому “фазовую” часть спектра нередко пропускают. В этой статье мы тоже сосредоточимся на “амплитудных” вещах, но забывать про существование пропущенной фазовой части графика не следует. Кроме того, вместо обычного модуля комплексного значения часто рисуют его десятичный логарифм умноженный на 10. В результате получается логарифмический график, значения на котором отображаются в децибелах (дБ).
Обратите внимание что не очень сильно отрицательным числам логарифмического графика (-20 дБ и менее) при этом соответствуют практически нулевые числа на графике “обычном”. Поэтому длинные и широкие “хвосты” разнообразных спектров на таких графиках при отображении в “обычные” координаты как правило практически исчезают. Удобство подобного странного на первый взгляд представления возникает из того что фурье-образы различных функций часто необходимо перемножать между собой. При подобном поточечном умножении комплекснозначных фурье-образов их фазовые спектры складываются, а амплитудные — перемножаются. Первое выполняется легко, а второе — сравнительно сложно. Однако логарифмы амплитуды при перемножении амплитуд складываются, поэтому логарифмические графики амплитуды можно, как и графики фаз, просто поточечно складывать. Кроме того, в практических задачах часто удобнее оперировать не «амплитудой» сигнала, а его «мощностью» (квадратом амплитуды). На логарифмической шкале оба графика (и амплитуды и мощности) выглядят идентично и отличаются только коэффициентом — все значения на графике мощности ровно вдвое больше чем на шкале амплитуд. Соответственно для построения графика распределения мощности по частоте (в децибелах) можно не возводить ничего в квадрат, а посчитать десятичный логарифм и умножить его на 20.
Заскучали? Погодите, еще немного, с занудной частью статьи, объясняющей как интерпретировать графики, мы скоро покончим :). Но перед этим следует понять одну крайне важную вещь: хотя все вышеприведенные графики спектров были нарисованы для некоторых ограниченных диапазонов значений (в частности, положительных чисел), все эти графики на самом деле продолжаются в плюс и минус бесконечность. На графиках просто изображается некоторая “наиболее содержательная” часть графика, которая обычно зеркально отражается для отрицательных значений параметра и зачастую периодически повторяется с некоторым шагом, если рассматривать её в более крупном масштабе.
Определившись с тем, что же рисуется на графиках, давайте вернемся собственно к преобразованию Фурье и его свойствам. Существует несколько разных способов как определить это преобразование, отличающихся небольшими деталями (разными нормировками). Например в наших ВУЗах почему-то часто используют нормировку преобразования Фурье определяющую спектр в терминах угловой частоты (радианов в секунду). Я буду использовать более удобную западную формулировку, определяющую спектр в терминах обычной частоты (герцах). Прямое и обратное преобразование Фурье в этом случае определяются формулами слева, а некоторые свойства этого преобразования которые нам понадобятся — списком из семи пунктов справа:
Первое из этих свойств — линейность. Если мы берем какую-то линейную комбинацию функций, то преобразование Фурье этой комбинации будет такой же линейной комбинацией образов Фурье этих функций. Это свойство позволяет сводить сложные функции и их фурье-образы к более простым. Например, фурье-образ синусоидальной функции с частотой f и амплитудой a является комбинацией из двух дельта-функций расположенных в точках f и -f и с коэффициентом a/2:
Если взять функцию, состоящую из суммы множества синусоид с разными частотами, то согласно свойству линейности, фурье-образ этой функции будет состоять из соответствующего набора дельта-функций. Это позволяет дать наивную, но наглядную интерпретацию спектра по принципу “если в спектре функции частоте f соответствует амплитуда a, то исходную функцию можно представить как сумму синусоид, одной из которых будет синусоида с частотой f и амплитудой 2a”. Строго говоря, эта интерпретация неверна, поскольку дельта-функция и точка на графике — это совершенно разные вещи, но как мы увидим дальше, для дискретных преобразований Фурье она будет не так уж и далека от истины.
Второе свойство преобразования Фурье — это независимость амплитудного спектра от сдвига сигнала по времени. Если мы подвинем функцию влево или вправо по оси x, то поменяется лишь её фазовый спектр.
Третье свойство — растяжение (сжатие) исходной функции по оси времени (x) пропорционально сжимает (растягивает) её фурье-образ по шкале частот (w). В частности, спектр сигнала конечной длительности всегда бесконечно широк и наоборот, спектр конечной ширины всегда соответствует сигналу неограниченной длительности.
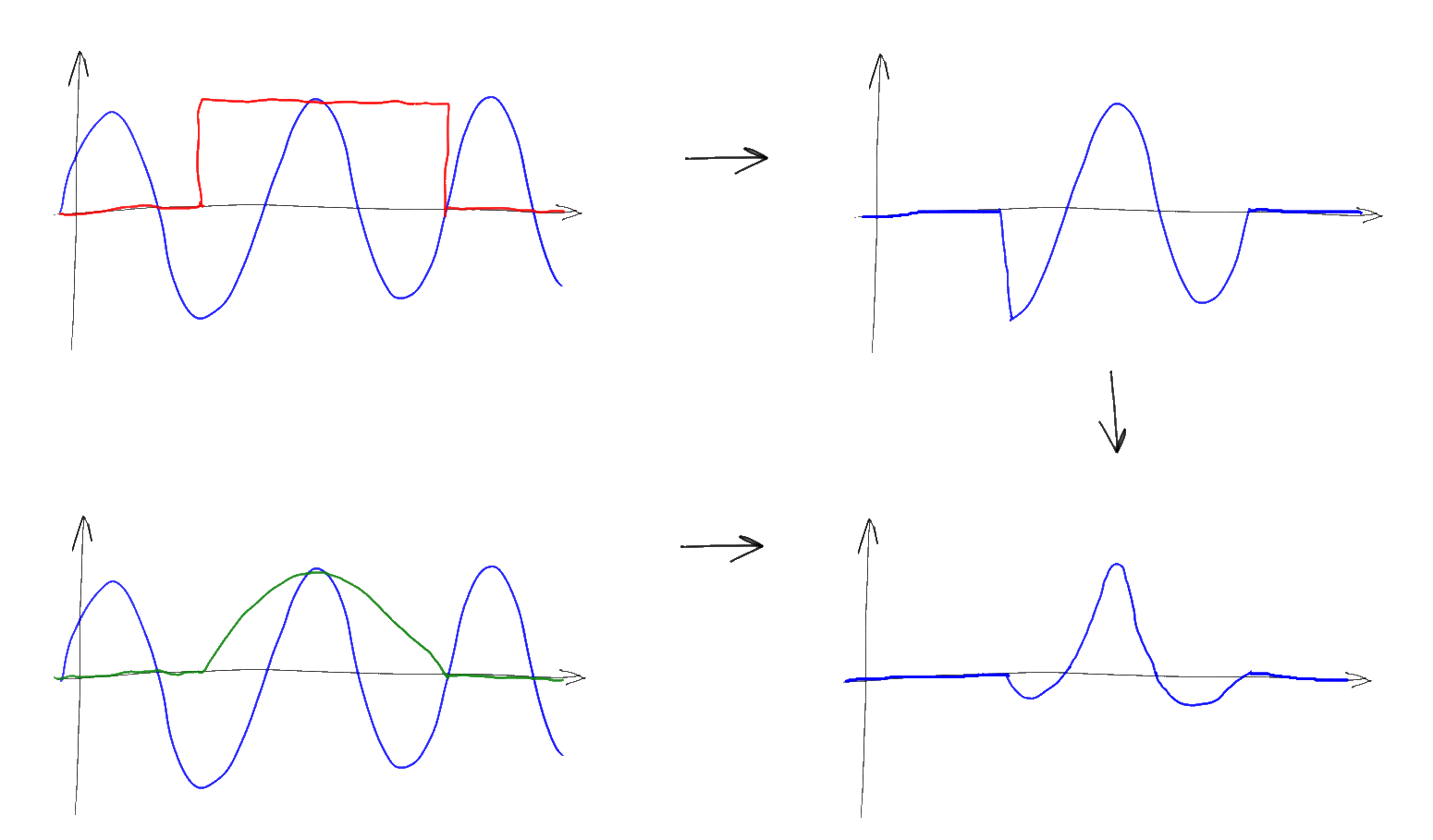
Четвертое и пятое свойства самые, пожалуй, полезные из всех. Они позволяют свести свертку функций к поточечному перемножению их фурье-образов и наоборот — поточечное перемножение функций к свертке их фурье-образов. Чуть дальше я покажу насколько это удобно.
Шестое свойство говорит о симметрии фурье-образов. В частности, из этого свойства следует что в фурье-образе действительнозначной функции (т.е. любого “реального” сигнала) амплитудный спектр всегда является четной функцией, а фазовый спектр (если его привести к диапазону -pi…pi) — нечетной. Именно по этой причине на графиках спектров практически никогда не рисуют отрицательную часть спектра — для действительнозначных сигналов она не дает никакой новой информации (но, повторюсь, и нулевой при этом не является).
Наконец последнее, седьмое свойство, говорит о том, что преобразование Фурье сохраняет “энергию” сигнала. Оно осмысленно только для сигналов конечной продолжительности, энергия которых конечна, и говорит о том, что спектр подобных сигналов на бесконечности быстро приближается к нулю. Именно в силу этого свойства на графиках спектров как правило изображают только “основную” часть сигнала, несущую в себе львиную долю энергии — остальная часть графика просто стремится к нулю (но, опять же, нулем не является).
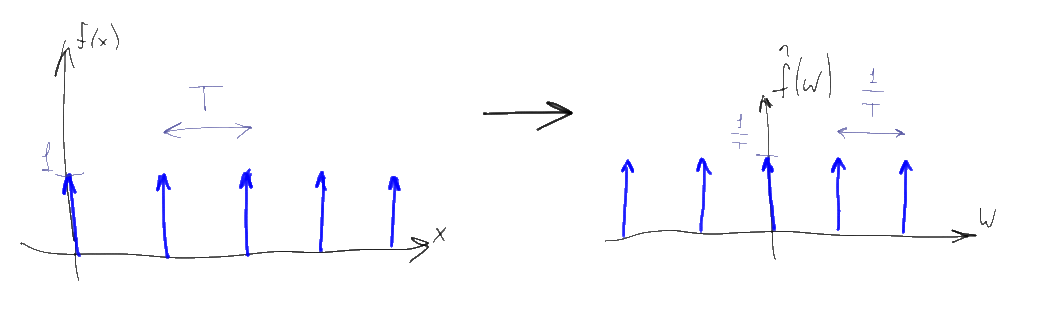
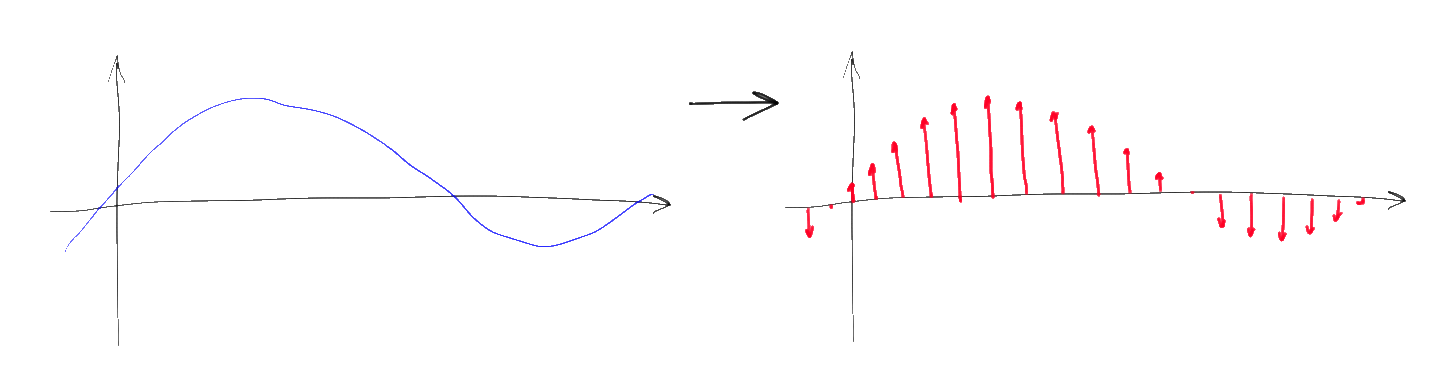
Вооружившись этими 7 свойствами, давайте посмотрим на математику “оцифровки” сигнала, позволяющую перевести непрерывный сигнал в последовательность цифр. Для этого нам понадобится взять функцию, известную как “гребенка Дирака”:
Гребенка Дирака — это просто периодическая последовательность дельта-функций с единичным коэффициентом, начинающаяся в нуле и идущая с шагом T. Для оцифровки сигналов, T выбирают по возможности малым числом, T<<1. Фурье-образ этой функции — тоже гребенка Дирака, только с гораздо большим шагом 1/T и несколько меньшим коэффициентом (1/T). С математической точки зрения, дискретизация сигнала по времени — это просто поточечное умножение исходного сигнала на гребенку Дирака. Значение 1/T при этом называют частотой дискретизации:
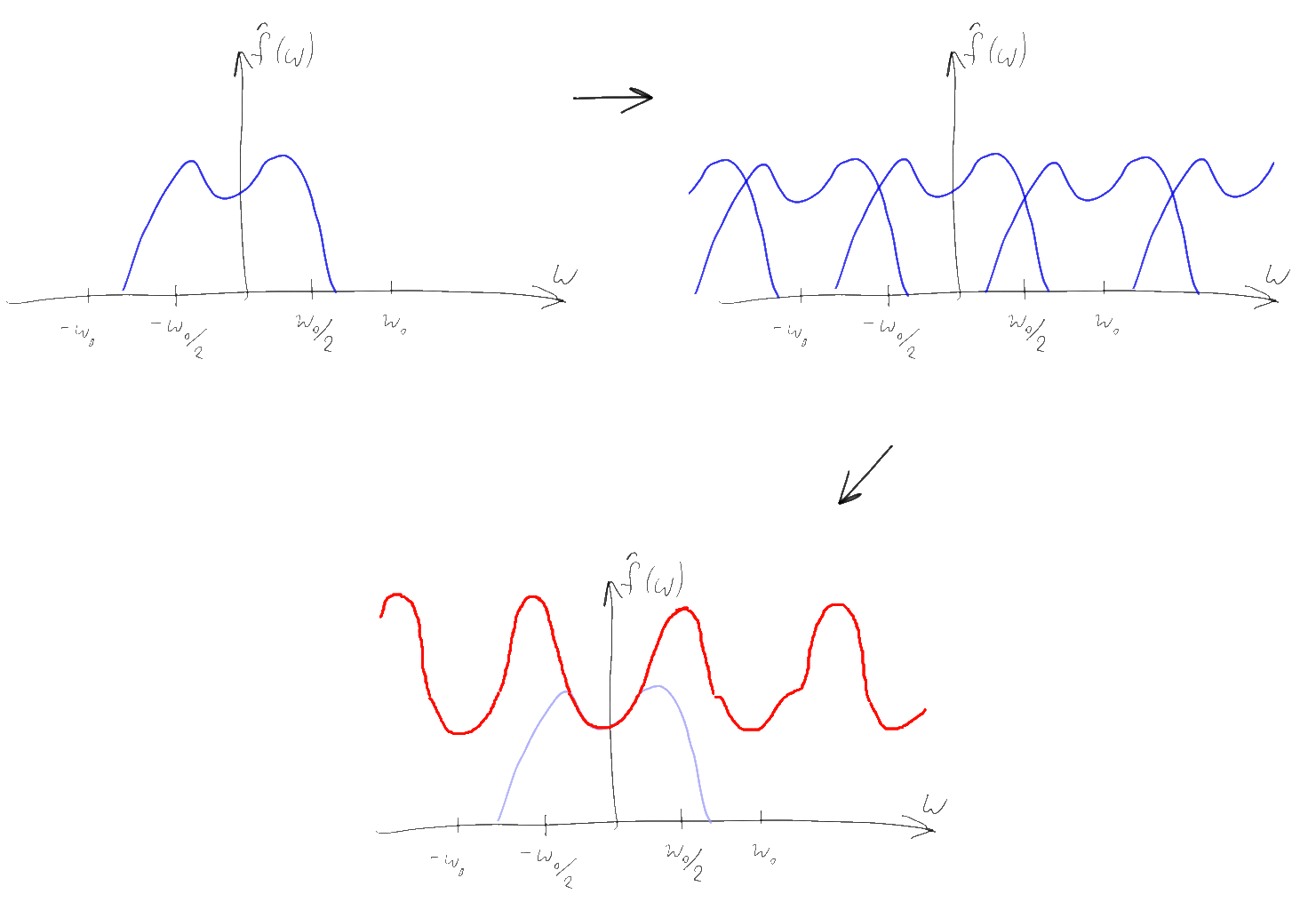
Вместо непрерывной функции после подобного перемножения получается последовательность дельта-импульсов определенной высоты. При этом согласно свойству 5 преобразования Фурье, спектр получившегося дискретного сигнала есть свертка исходного спектра с соответствующей гребенкой Дирака. Несложно понять, что исходя из свойств свертки, спектр исходного сигнала при этом как бы “копируется” бесконечное число раз вдоль оси частот с шагом 1/T, а затем суммируется.
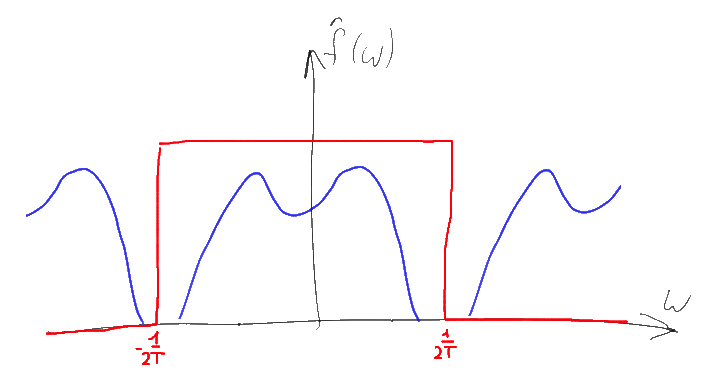
Заметим, что если исходный спектр имел конечную ширину и мы использовали достаточно большую частоту дискретизации, то копии исходного спектра не будут перекрываться, а следовательно и суммироваться друг с другом. Несложно понять что по подобному “свернутому” спектру будет легко восстановить исходный — достаточно будет просто взять компоненту спектра в районе нуля, “обрезав” лишние копии уходящие на бесконечность. Простейший способ это сделать — это домножить спектр на прямоугольную функцию, равную T в диапазоне -1/2T…1/2T и нулю — вне этого диапазона. Подобный Фурье-образ соответствует функции sinc(Tx) и согласно свойству 4, подобное умножение равнозначно свертке исходной последовательности дельта-функций с функцией sinc(Tx)
То есть с помощью преобразования Фурье мы получили способ легко восстановить исходный сигнал из дискретизированного по времени, работающий при условии что мы используем частоту дискретизации, по крайней мере вдвое (из-за наличия в спектре отрицательных частот) превышающую максимальную частоту присутствующую в исходном сигнале. Этот результат широко известен и называется “теорема Котельникова / Шеннона-Найквиста”. Однако, как несложно теперь (понимая доказательство) заметить, этот результат вопреки широко распространенному заблуждению определяет достаточное, но не необходимое условие для восстановления исходного сигнала. Все что нам требуется — это добиться того, чтобы интересующая нас часть спектра после дискретизации сигнала не накладывалась друг на друга и если сигнал достаточно узкополосный (имеет малую “ширину” ненулевой части спектра), то этого результата часто можно добиться и при частоте дискретизации намного ниже чем удвоенная максимальная частота сигнале. Подобная техника называется “undersampling” (субдискретизация, полосовая дискретизация) и довольно широко используется при обработке всевозможных радиосигналов. Например, если мы берем FM-радио действующее в полосе частот от 88 до 108 МГц, то для его оцифровки можно использовать АЦП с частотой всего 43.5 МГц вместо предполагающихся по теореме Котельникова 216 МГц. При этом, правда, понадобится качественный АЦП и хороший фильтр.
Замечу, что “дублирование” высоких частот частотами меньших порядков (алиасинг) — непосредственное свойство дискретизации сигнала, необратимо “портящее” результат. Поэтому если в сигнале в принципе могут присутствовать частоты высокого порядка (то есть практически всегда) перед АЦП ставят аналоговый фильтр, “отсекающий” все лишнее непосредственно в исходном сигнале (так как после дискретизации делать это уже будет поздно). Характеристики этих фильтров, как аналоговых устройств, неидеальны, поэтому некоторая “порча” сигнала при этом все равно происходит, и на практике из этого следует что наибольшие частоты в спектре, как правило, недостоверны. Чтобы уменьшить эту проблему, сигнал нередко сэмплируют с завышенной частотой дискретизации, ставя при этом входной аналоговый фильтр на меньшую полосу пропускания и используя только нижнюю часть теоретически доступного частотного диапазона АЦП.
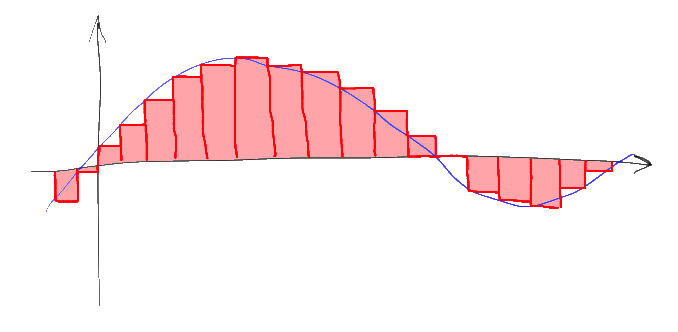
Еще одно распространенное заблуждение, кстати, — это когда сигнал на выходе ЦАП рисуют “ступеньками”. “Ступеньки” соответствуют свертке дискретизированной последовательности сигналов с прямоугольной функцией ширины T и высоты 1:
Спектр сигнала при таком преобразовании умножается на фурье-образ этой прямоугольной функции, а у подобной прямоугольной функции это снова sinc(w), “растянутый” тем сильнее, чем меньше ширина соответствующего прямоугольника. Спектр дискретизированного сигнала при подобном “ЦАП” поточечно умножается на этот спектр. При этом ненужные высокие частоты с “лишними копиями” спектра обрезаются не полностью, а верхняя часть “полезной” части спектра, напротив, ослабляется.
На практике так, естественно, никто не делает. Существует много разных подходов к построению ЦАП, но даже в наиболее близких по смыслу ЦАП взвешивающего типа прямоугольные импульсы в ЦАП напротив выбираются по возможности короткими (приближающимися к настоящей последовательности дельта-функций) чтобы избежать излишнего подавления полезной части спектра. “Лишние” частоты в получившемся широкополосном сигнале практически всегда гасят, пропуская сигнал через аналоговый фильтр низких частот, так что «цифровых ступенек» нет ни «внутри» преобразователя, ни, тем более, на его выходе.
Однако вернемся обратно к преобразованию Фурье. Описанное выше преобразование Фурье, примененное к заранее дискретизированной последовательности сигналов называется преобразованием Фурье дискретного времени (DTFT). Спектр получаемый подобным преобразованием всегда 1/T-периодичен, поэтому спектр DTFT полностью определяется её значениями на отрезке [0…1/T), поэтому часто этим отрезком спектр DTFT и ограничивают. При этом результат DTFT несмотря на то что это спектр дискретизированного сигнала — по-прежнему “аналоговая” функция. Кроме того, для “обычных” действительнозначных сигналов вторая половина этого спектра в силу свойства 6 зеркально повторяет левую половину, отраженную относительно частоты Найквиста 1/2T.
До сих пор мы предполагали что на вход наших преобразований поступает сигнал определенный от минус до плюс бесконечности. Однако реальные доступные нам сигналы всегда имеют конечную длину — что делать? Для решения этой проблемы в FT и DTFT конечный сигнал просто дополняют слева и справа на бесконечность нулями. Если исходный сигнал изначально был конечным (скажем, это отдельный импульс) и в преобразование Фурье он попал полностью, то этот подход напрямую дает желаемый результат. Однако часто «конечный» сигнал используемый для преобразования Фурье на самом деле является частью более длинного, возможно бесконечного сигнала, такого как, например, синусоида. В этом случае дополнение конечного отрезка нулями интерпретируют следующим образом: считают что исходный сигнал имеет бесконечно большую длину, но затем умножается на некоторую взвешивающую функцию — “окно”, обращающуюся в ноль вне доступного нам для измерения отрезка. В простейшем случае роль “окна” играет просто прямоугольная функция, соответствующая тому что мы просто дополняем конечный сигнал слева и справа бесконечным числом нулей. В более сложных — исходную последовательность умножают на весовые коэффициенты определяемые функцией “окна” и затем, опять же, дополняют нулями.
Пользуясь уже хорошо нам знакомым свойством 5, несложно сообразить, что при подобном умножении исходный сигнал прсто сворачивается со спектром функции окна. Например если мы пытаемся измерить спектр синусоиды (дельта-функцию), но ограничиваем интервал измерений прямоугольным окном, то в получившимся спектре на месте дельта-функции мы увидим спектр окна — т.е. Tsinc(T(x-f)):
В данном случае T — это длина интервала которым мы ограничили наш сигнал, так что чем длиннее будет входной сигнал — тем “уже” и ближе к истинной дельта-функции будет наблюдаемый нами спектр. Конечная “ширина” главного лепестка приводит к невозможности уверенно различать наличие в исходном сигнале синусоид близких друг к другу по частоте, а наличие “боковых лепестков” вносит небольшие искажения и в далеко расположенные частоты, мешая точному измерению амплитуды отдельных частот, особенно если нужно измерять спектр в областях небольшой амплитуды при наличии в спектре на порядок более мощных компонент. Этот эффект называют “спектральной утечкой” и полностью победить его для конечных сигналов невозможно, но чем длиннее интервал на котором измеряется сигнал — тем меньше влияние этой утечки. Выбором функции окна можно контролировать “ширину” этой утечки, либо концентрируя её вокруг главной частоты (сильно “размывая” спектр, но зато не мешая соседним частотам), либо размазывая её повсюду (размытие пиков уменьшается но сильно растет “шум” и как следствие — погрешность измерения амплитуды отдельных частот). Заметьте, что выбранная частота дискретизации в спектральной утечке почти не играет роли — короткий отрезок сигнала можно сэмплировать хоть на 10 ГГц, но это увеличит только количество поддающихся измерению частот, тогда как точность определения каждой отдельной частоты все равно останется низкой.
Интересным частным случаем является ситуация, в которой сигнал с набором дискретных частот nF дискретизируется на частоте mF, где m,n — целые числа. В этом случае нули “окна” и расположение дельта-функций в спектре в точности совпадают и хотя частоты все равно “размазываются”, но их амплитуда в точках mF совпадает с истинной — “шум” равен нулю. Это свойство позволяет доказать аналог теоремы Котельникова для дискретного преобразования Фурье, но на практике такие сигналы, к сожалению, фактически не встречаются.
Итак, со “входом” мы разобрались — из непрерывной функции бесконечной длины мы получили конечное число дискретных отсчетов, с которыми можем работать а взамен получили ограничения по ширине спектра и утечку частот. Однако “выход” DTFT по-прежнему является непрерывной функцией, работать с которой компьютеру проблематично. На практике эту проблему решают очень просто — полный отрезок [0,1/T) делят на k равных частей и считают DTFT в точках fi=i/kT, где i = 0,1,… k-1. Получившуюся конструкцию называют “дискретным преобразованием Фурье” (DFT).
Последнее преобразование удобно нормализовать, убрав из него T и вопросы связанные с выбором “окна”. Эту нормализованную запись часто используют в качестве определения DFT как преобразования последовательности из N комплексных чисел:
Прелесть преобразования Фурье записанного в такой форме — в том что сохраняя все достоинства DTFT, подобное DTF для “гладких” k (например, степеней двойки) можно вычислять чрезвычайно быстро, за время порядка k log(k). Соответствующие алгоритмы называют “быстрым преобразованием Фурье” (БПФ, FFT) и их, вообще говоря, существует несколько. С практической точки зрения, впрочем, их все можно рассматривать как “черные ящики”, получающие последовательность комплексных чисел на входе и выдающих последовательность комплексных чисел на выходе. Таким образом, работа с дискретизированным сигналом конечной длины сводится к тому, что этот сигнал вначале умножается на подходящую взвешивающую функцию, затем дополняется нужным числом нулей справа и передается в алгоритм БПФ.
Как интерпретировать получившийся результат? С учетом всего вышеизложенного,
- Получившиеся значения есть равномерная сетка отсчетов по спектру DTFT. Чем больше отсчетов — тем мельче сетка, тем подробнее виден спектр. Дописывая к известной последовательности нужное число нулей можно посчитать сколь угодно близкое приближение к непрерывному спектру
- Спектр DTFT задан на отрезке частот от 0 до 1/T (где 1/T — частота дискретизации) и периодически повторяется на бесконечность вне этого отрезка
- Этот спектр задан комплексными числами (парами действительных). Амплитуда определяется как модуль комплексного числа, фаза — как аргумент.
- Для действительнозначного входного сигнала, спектр в диапазоне 1/2T…1/T просто зеркально повторяет спектр 0…1/2T и не несет соответственно полезной нагрузки (для визуализации спектра его можно просто обрезать)
- Если исходный сигнал содержал частоты выше половины частоты дискретизации, то они будут отображены в более низкие частоты (возможно накладываясь поверх уже существующего сигнала этой частоты) — алиасинг
- В спектре всегда присутствует “спектральная утечка” определяющаяся выбранной взвешивающей “оконной функцией”. Чем длиннее исходный сигнал (до дополнения нулями!) — тем эта утечка меньше.
- Спектральная утечка ограничивает осмысленность расчета БПФ с большим дополнением нулями. Однако дополнение все же часто бывает полезным, поскольку, например, позволяет точнее определить максимум узкополосного синусоидального сигнала, если он не попадает точно в одну из частот вида k/T.
- Синусоиде амплитуды A в амплитудном спектре (при выбранной мной нормировке преобразования Фурье) соответствует значение A*N/2, за исключением нулевой частоты, которая не раскладывается на “плюс” и “минус” частоту и потому имеет амплитуду A*N, а также частоты Найквиста 1/2T в которой касаются в предельном случае друг друга отдельные копии спектра (там тоже будет A*N, но, в отличие от нуля в выход БПФ это значение не попадает да и достоверным в реальных схемах все равно никогда не является). Здесь N = T1/T0, где T1 — это длина исходного сигнала (она определяет коэффициент перед спектром «окна»), а T0 — длина одного периода дискретизации (она определяет коэффициент у гребенки Дирака) и по смыслу это, как несложно видеть, попросту число отсчетов в исходном сигнале (до его дополнения нулями)
Ну вот, в общем, и всё. Надеюсь преобразование Фурье и алгоритмы БПФ будут теперь для Вас простыми, понятными и приятными в обращении инструментами.
Одним из мощных средств исследования задач математической физики является метод интегральных преобразований.
Пусть функция f(x) задана на интервале (а, 6), конечном или бесконечном. Интегральным преобразованием функции f(х) называется функция (*)
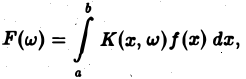
где К(х, w) — фиксированная для данного преобразования функция, называемая ядром преобразования (предполагается, что интеграл (*) существует в собственном или несобственном смысле).
Интеграл Фурье
Всякая функция f(x), которая на отрезке [— l, l] удовлетворяет условиям разложимости в ряд Фурье, может быть на этом отрезке представлена тригонометрическим рядом (1)
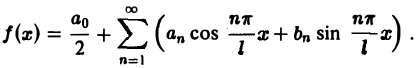
Коэффициенты аn и bn ряда (1) определяются по формулам Эйлера—Фурье:
(2)
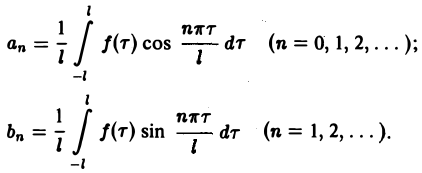
Ряд в правой части равенства (1) можно записать в иной форме. С этой целью внесем в него из формул (2) значения коэффициентов аn и bn, подведем под знаки интегралов cos 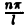
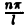
(3)
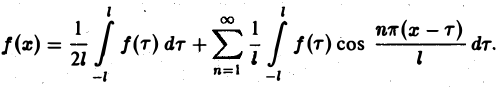
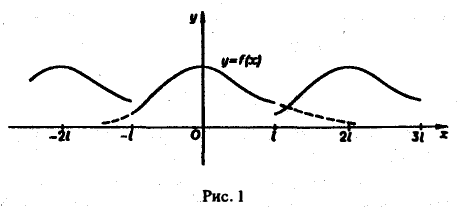
Если функция f(x) первоначально была определена на интервале числовой оси, большем, чем отрезок [-l, l] (например, на всей оси), то разложение (3) воспроизведет значения этой функции только на отрезке [-l, l] и продолжит ее на всю числовую ось как периодическую функцию с периодом 2l (рис. 1).
Поэтому, если функция f(x) (вообще говоря, непериодическая) определена на всей числовой оси, в формуле (3) можно попытаться перейти к пределу при l → +∞. При этом естественно потребовать выполнения следующих условий:
1, f(x) удовлетворяет условиям разложимости в ряд Фурье на любом конечном отрезке оси Ох;
2. функция f(x) абсолютно интегрируема на всей числовой оси,
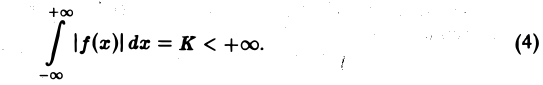
При выполнении условия 2 первое слагаемое правой части равенства (3) при l → +∞ стремится к нулю. В самом деле,
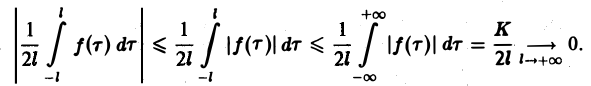
Попытаемся установить, во что перейдет в пределе при l → +∞ сумма в правой части (3). Положим
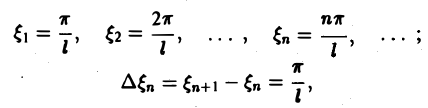
так, что 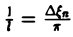
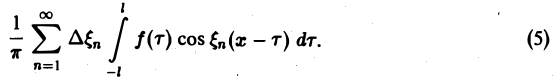
В силу абсолютной сходимости интеграла эта сумма при больших l мало отличается от выражения
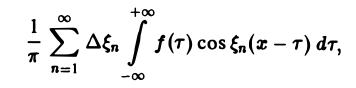
которое напоминает интегральную сумму для функции переменного ξ
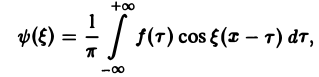
составленную для интервала (0, + ∞) изменения Поэтому естественно ожидать, что при l → +∞ (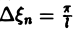
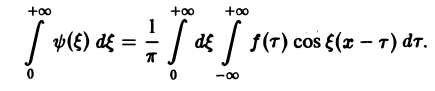
С другой стороны, при l → +∞ (х фиксировано) из формулы (3) вытекает, что
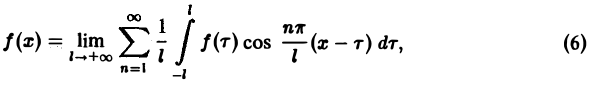
и мы получаем равенство
(7)
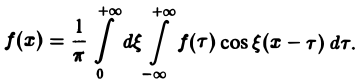
Достаточное условие справедливости формулы (7) выражается следующей теоремой.
Теорема:
Если функция f(x) абсолютно интегрируема на всей числовой оси — ∞ < х < + ∞ и имеет вместе со своей производной конечное число точек разрыва первого рода на любом отрезке [а, b], то справедливо равенство
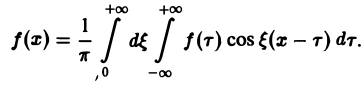
При этом во всякой точке xq, являющейся точкой разрыва 1-го рода функции f(x), значение интеграла в правой части (7) равно
j [/(^о — 0) + f(xo + 0)].
Формулу (7) называют интегральной формулой Фурье, а стоящий в ее правой части интеграл — интегралам Фурье.
Если воспользоваться формулой для косинуса разности, то формулу (7) можно записать в виде (8)
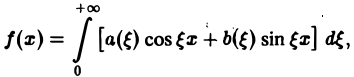
где
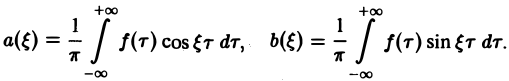
Функции а( ξ ), b( ξ ) являются аналогами соответствующих коэффициентов Фурье an и bn 2π-периодической функции, но последние определены для дискретных значений п, в то время как а( ξ ), b( ξ ) определены для непрерывных значений ξ ∈ (— ∞, + ∞).
Комплексная форма интеграла Фурье
Предполагая f(x) абсолютно интегрируемой на всей оси Ох, рассмотрим интеграл
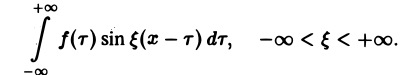
Этот интеграл равномерно сходится для — ∞ < ξ < + ∞, так как
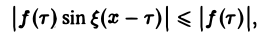
и потому представляет собой непрерывную и, очевидно, нечетную функцию от ξ. Но тогда
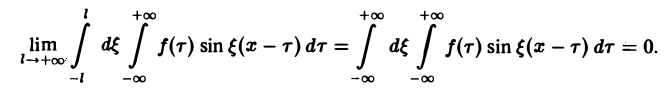
С другой стороны, интеграл
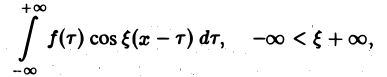
есть четная функция переменной так что
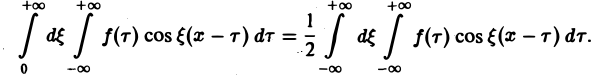
Поэтому интегральную формулу Фурье можно записать так:
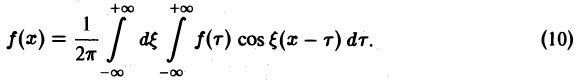
Умножим равенство
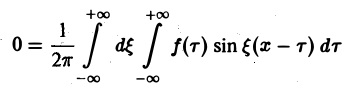
на мнимую единицу i и прибавим к равенству (10). Получим
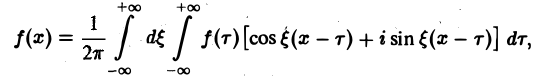
откуда, в силу формулы Эйлера (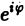
(11)
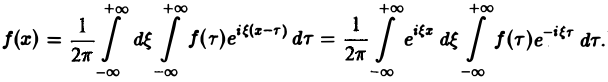
Это — комплексная форма интеграла Фурье. Здесь внешнее интегрирование по ξ понимается в смысле главного значения по Коши:
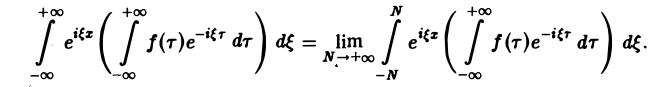
Преобразование Фурье. Косинус- и синус-преобразования Фурье
Пусть функция f(x) является кусочно-гладкой на любом конечном отрезке оси Ох и абсолютно интегрируема на всей оси.
Определение:
Функция
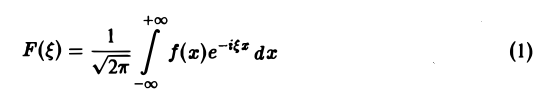
называется преобразованием Фурье функции f(x) (спектральной функцией).
Это — интегральное преобразование функции f(x) на интервале (- ∞ ,+ ∞) с ядром
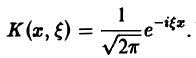
Используя интегральную формулу Фурье
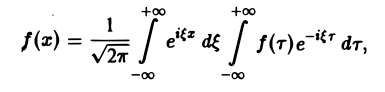
получаем
(2)
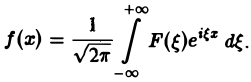
Это так называемое обратное преобразование Фурье, дающее переход от F( ξ ) к f(x). Иногда прямое преобразование Фурье задают так:
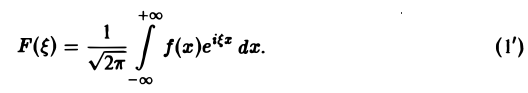
Тогда обратное преобразование Фурье определится формулой
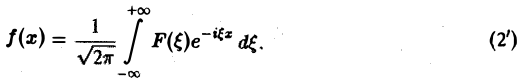
Преобразование Фурье F( ξ ) функции f(х) определяют также следующим образом:
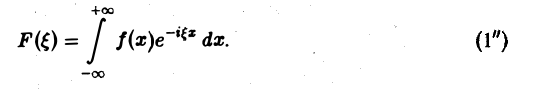
Тогда, в свою очередь,
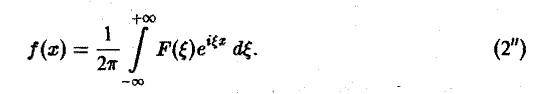
При этом положение множителя 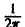
Пример:
Найти преобразование Фурье функции
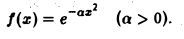
Имеем
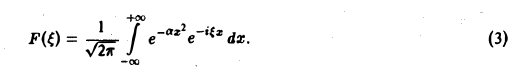
Это равенство допускает дифференцирование по ξ под знаком интеграла (получающийся после дифференцирования интеграл равномерно сходится, когда ξ принадлежит любому конечному отрезку):
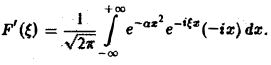
Интегрируя по частям, будем иметь
Внеинтегральное слагаемое обращается в нуль, и мы получаем
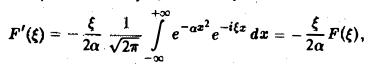
откуда

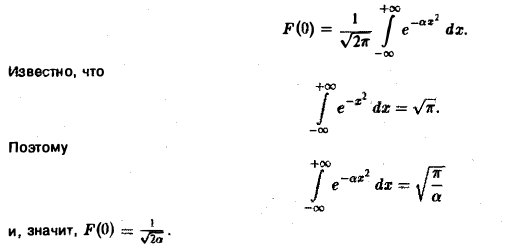
(С — постоянная интегрирования). Полагая в (4) ξ = 0, найдем С —F(0). В силу (3) имеем
Таким образом,
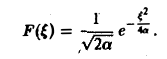
В частности, для
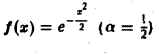
получаем, что
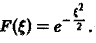
Пример:
Разряд конденсатора через сопротивление. Рассмотрим функцию
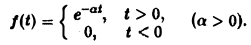
Для спектральной функции F( ξ ) получаем
(рис. 2).
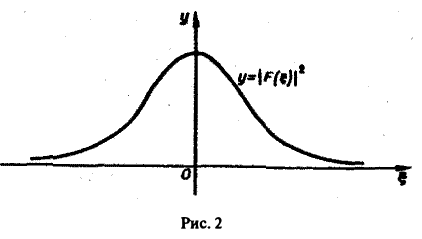
Условие абсолютной интегрируемости функции f(x) на всей числовой оси является весьма жестким. Оно исключает, например, такие элементарные функции, как f(x) = 1. f(x) = x3, f(х) = cosx, f(х) = ех, для которых преобразования Фурье (в рассматриваемой здесь классической форме) не существует.
Фурье-образ имеют только те функции, которые достаточно быстро стремятся к нулю при |х| → + ∞ (как в примерах 1 и 2).
Косинус- и синус-преобразования Фурье
Используя формулу косинуса, разности, перепишем интегральную формулу Фурье
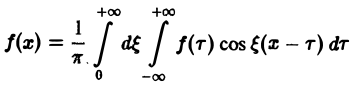
в следующем виде:
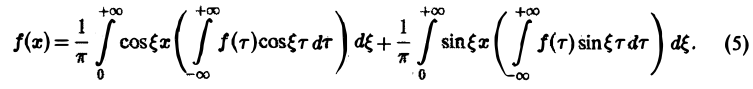
Пусть f(x) — четная функция. Тогда
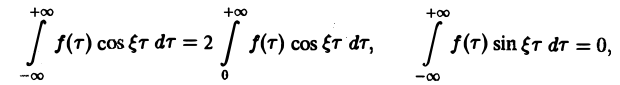
так что из равенства (5) имеем
(6)
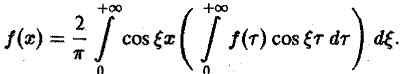
В случае нечетной f(x) аналогично получаем
(7)
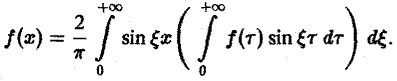
Если f(х) задана лишь на (0, + ∞), то формула (6) продолжает f(x) на всю ось Ох четным образом, а формула (7) — нечетным.
Определение:
Функция
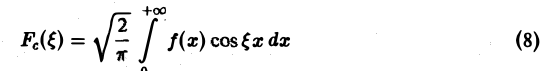
называется косинус-преобразованием Фурье функции f(x). Из (6) следует, что для четной функции f(x)
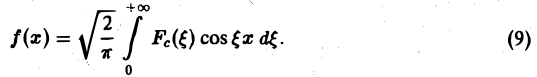
Это означает, что f(x), в свою очередь, является косинус-преобразованием для Fc( ξ ). Иными словами, функции f и Fc являются взаимными косинус-преобразованиями.
Определение:
Функция
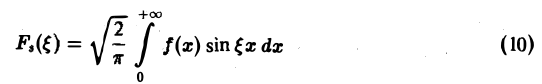
называется синус-преобразованием Фурье функции f(x).
Из (7) получаем, что для нечетной функции f(х)
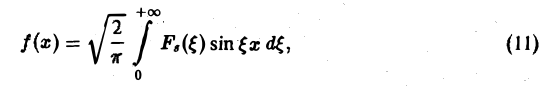
т.е. f и Fs являются взаимными синус-преобразованиями.
Пример:
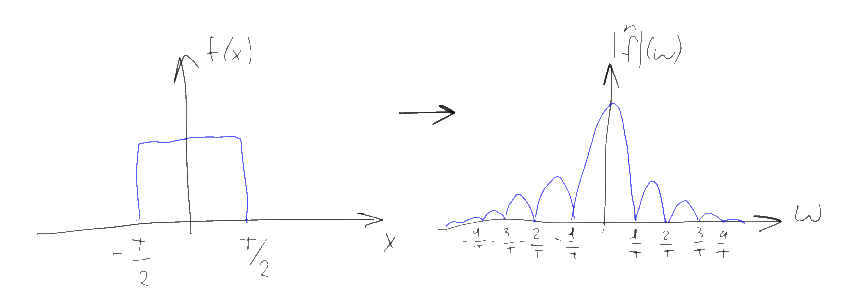
Прямоугольный импульс. Пусть f(t) — четнaя функция, определенная следующим образом:
Воспользуемся полученным результатом для вычисления интеграла
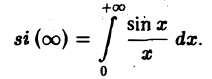
В силу формулы (9) имеем
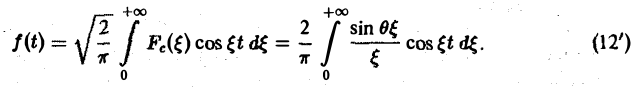
В точке t = 0 функция f(t) непрерывна и равна единице.
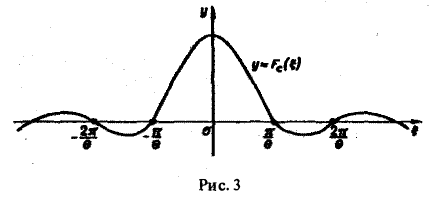
Поэтому из (12′) получим
Амплитудный и фазовый спектры интеграла Фурье
Пусть периодическая с периодом 2π функция f(х) разлагается в ряд Фурье
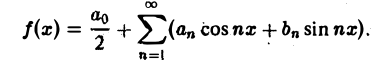
Это равенство можно записать в виде
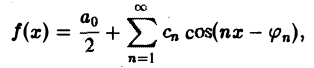
где Cn = 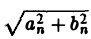
Для непериодической функции f(x), заданной на (- ∞, + ∞), при определенных условиях оказывается возможным представить ее интегралом Фурье
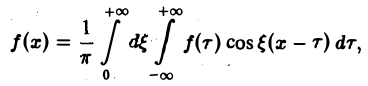
осуществляющим разложение этой функции по всем частотам 0 < ξ < + ∞ (разложение по непрерывному спектру частот).
Определение:
Спектральной функцией, или спектральной плотностью интеграла Фурье, называется выражение
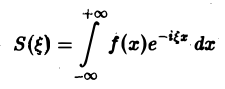
(прямое преобразование Фурье функции f(х)).
Функция
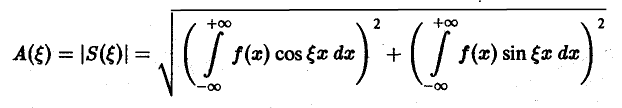
называется амплитудным спектром, а функция
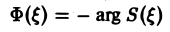
(0 — фазовым спектром функции f(x).
Амплитудный спектр A (ξ) служит мерой вклада частоты ξ в функцию f(х).
Пример:
Найти амплитудный и фазовый спектры функции
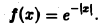
Находим спектральную функцию
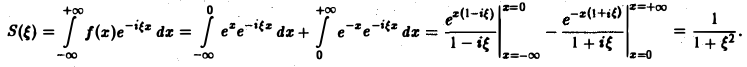
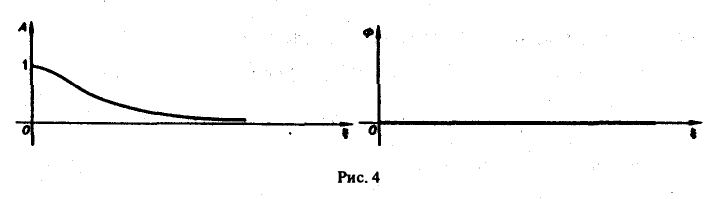
Отсюда
Графики этих функций изображены на рис. 4.
Свойства преобразования Фурье
1, Линейность. Если F( ξ ) и G( ξ ) — преобразования Фурье функций f(х) и g(х) соответственно, то при любых постоянных а и β преобразованием Фурье функции а f(х) + β g(х) будет функция a F( ξ ) + βG( ξ ).
Пользуясь свойством линейности интеграла, имеем
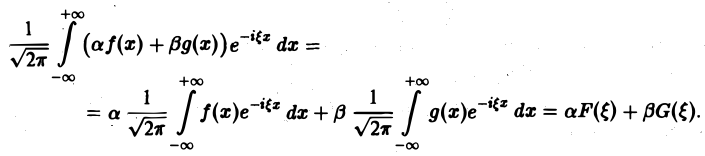
Таким образом, преобразование Фурье есть линейный оператор. Обозначая его через 
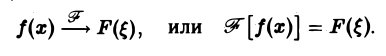
Если F( ξ ) есть преобразование Фурье абсолютно интегрируемой на всей числовой оси функции f(х), то F( ξ ) ограничена при всех ξ ∈ (— ∞, + ∞).
Пусть функция f(х) абсолютно интегрируема на всей оси — ∞ < х < + ∞,
— преобразование Фурье функции f(х). Тогда
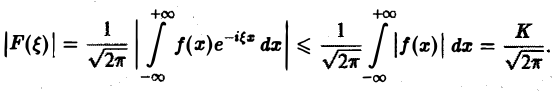
Задача:
Пусть f(x) — функция, допускающая преобразование Фурье, h — действительное число. Функция fh(x) = f(x-h) называется сдвигом функции f(x). Пользуясь определением преобразования Фурье, показать, что
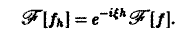
Задача:
Пусть функция f(x) имеет преобразование Фурье F( ξ ), h — действительное число. Показать, что
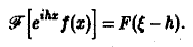
3. Преобразование Фурье и операция дифференцирования. Пусть абсолютно интегрируемая функция f(х) имеет производную f'(х), также абсолютно интегрируемую на всей оси Ох, так что f(х) стремится к нулю при |х| —► + ∞. Считая f'(х) гладкой функцией, запишем
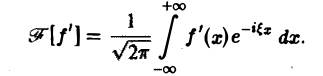
Интегрируя по частям, будем иметь
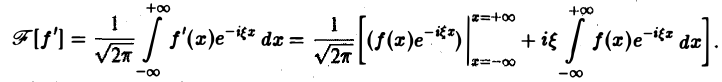
Внеинтегральное слагаемое обращается в нуль (так как f(х) → 0 при |х| → + ∞), и мы получаем (1)
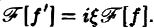
Таким образом, дифференцированию функции f(х) отвечает умножение ее образа Фурье 
Если функция f(х) имеет гладкие абсолютно интегрируемые производные до порядка m включительно и все они, как и сама функция f(х), стремятся к нулю при |x| → + ∞, то, интегрируя по частям нужное число раз, получим
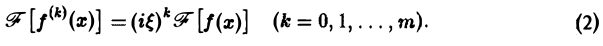
Преобразование Фурье очень полезно именно потому, что оно заменяет операцию дифференцирования операцией умножения на величину iξ и тем самым упрощает задачу интегрирования некоторых видов дифференциальных уравнений.
Так как преобразование Фурье 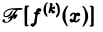
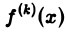

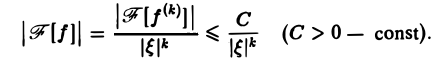
Из этой оценки следует: чем больше функция f(х) имеет абсолютно интегрируемых производных, тем быстрее ее преобразование Фурье стремится к нулю при | ξ | → + ∞.
Замечание:
Условие 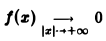
4. Связь между скоростью убывания функции f(x) при |х| → + ∞ и гладкостью ее преобразования Фурье. Предположим, что не только f(x), но и ее произведение хf(х) является абсолютно интегрируемой функцией на всей оси Ох. Тогда преобразование Фурье
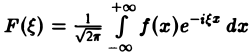
функции f(x) будет дифференцируемой функцией.
Действительно, формальное дифференцирование по параметру ξ подынтегральной функции приводит к интегралу
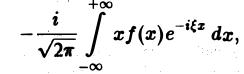
который является абсолютно и равномерно сходящимся относительно параметра Следовательно, дифференцирование возможно, и
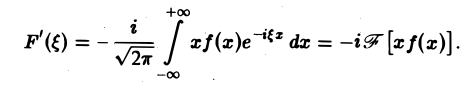
Таким образом,
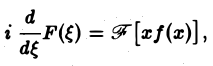
т. е. операция умножения f(х) на аргумент х переходит после преобразования Фурье в операцию
Если вместе с функцией f(х) абсолютно интегрируемыми на всей оси Ох являются функции хf(х)…..хmf(х), то процесс дифференцирования можно продолжить.
Получим, что функция F( ξ ) = 
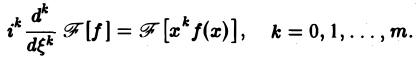
Таким образом, чем быстрее функция f(х) убывает при |х| → + ∞, тем более гладкой получается функция F( ξ ) = 
Теорема:
О свертке. Пусть F1( ξ ) и F2( ξ ) — преобразования Фурье функций f1(x) и f2(x) соответственно. Тогда
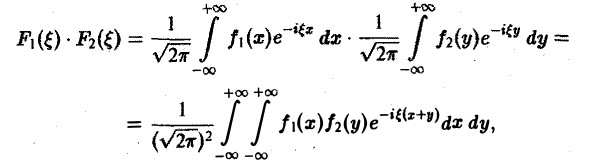
причем двойной интеграл в правой части сходится абсолютно.
Положим х + у = т, так что у = т — х. Тогда будем иметь
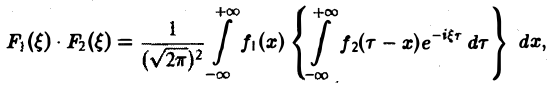
или, меняя порядок интегрирования,
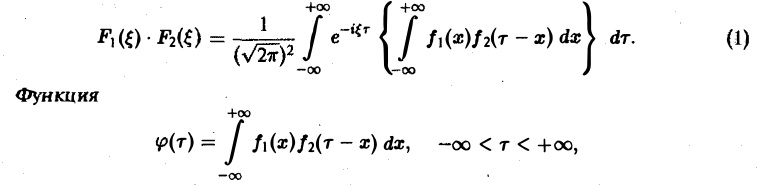
называется сверткой функций f(x) и f2(x) и обозначается символом 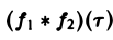
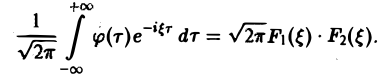
Отсюда видно, что преобразование Фурье свертки функций f1(x) и f2(x) равно умноженному на 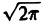
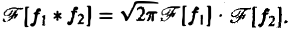
Замечание:
Нетрудно установить следующие свойства свертки:
1) линейность:
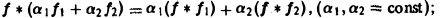
2) коммутативность:
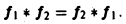
Приложения преобразования Фурье
1, Пусть 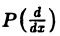
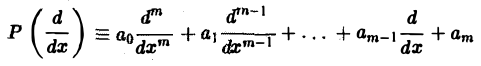
(аo, a1,… ,ат = const). Используя формулу для преобразования Фурье производных функции у(х), находим
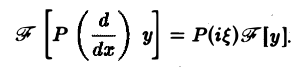
Рассмотрим дифференциальное уравнение

где 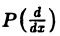
Предположим, что искомое решение у(х) имеет преобразование Фурье y(ξ), а функция f(x) имеет преобразование f( ξ ). Применяя преобразование Фурье к уравнению (1), получим вместо дифференциального алгебраическое уравнение на оси Oξ относительно y(ξ)
так что формально
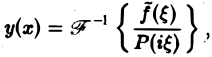
где символ 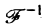
Основное ограничение применимости этого метода связано со следующим фактом. Решение обыкновенного дифференциального уравнения с постоянными коэффициентами содержит функции вида
Они не являются абсолютно интегрируемыми на оси — ∞ < х < + ∞, и преобразование Фурье для них не определено, так что, строго говоря, применять данный метод нельзя. Это ограничение можно обойти, если ввести в рассмотрение так называемые обобщенные функции. Однако в ряде случаев преобразование Фурье все же применимо в своей классической форме.
Пример:
Найти решение u = u(x,t) уравнения
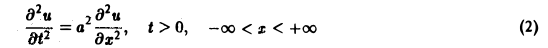
(а = const), при начальных условиях
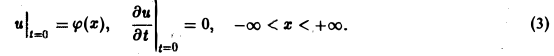
Это — задача о свободных колебаниях бесконечной однородной струны, когда задано начальное отклонение φ(х) точек струны, а начальные скорости отсутствуют.
Поскольку пространственная переменная х изменяется в пределах от — ∞ до + ∞, подвергнем уравнение и начальные условия преобразованию Фурье по переменной х. Будем предполагать, что
1) функции u(z, t) и φ(x) — достаточно гладкие и стремятся к нулю при х → + ∞ и ∀t ≥ О настолько быстро, что существуют преобразования Фурье
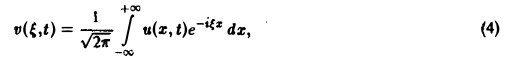
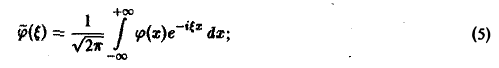
2) допустимы операции дифференцирования, так что
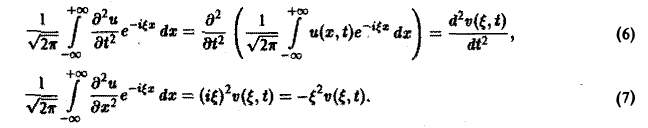
Умножая обе части (2) на 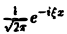

а из начальных условий (3) найдем

Таким образом, применяя к задаче (2)-(3) преобразование Фурье, приходим к задаче Коши (8)—(10) для обыкновенного дифференциального уравнения, где ξ — параметр. Решением уравнения (8) является функция
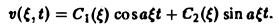
Из условий (9) и (10) находим, что С1( ξ ) = φ( ξ ). C2( ξ ) = 0, так что v( ξ, t) = φ( ξ )cos aξt. Применяя обратное преобразование Фурье, получим
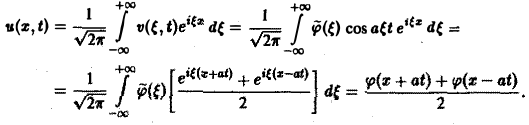
Это частный случай формулы Даламбера решения задачи (2)-(3).
2. Преобразование Фурье может быть использовано при решении некоторых интегральных уравнений, т. е. уравнений, в которых неизвестная функция входит под знак интеграла.
Рассмотрим, например, уравнение
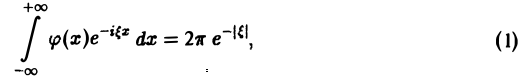
где φ(х) — искомая функция. Записав (1) в виде
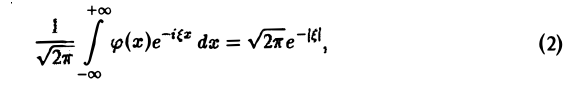
замечаем, что левую часть (2) можно рассматривать как преобразование Фурье функции φ(х), так что (2) равносильно следующему равенству:
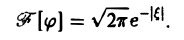
Тогда по формуле обращения
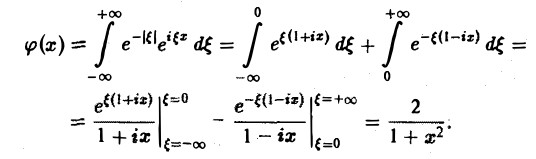
Функция 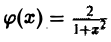
Понятие о многомерном преобразовании Фурье
Преобразование Фурье:

Пусть
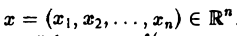
Многомерным преобразованием Фурье абсолютно интегрируемой функции f(х1, х2,…, хb) называется функция
или, короче,
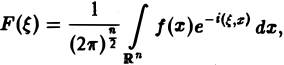
где
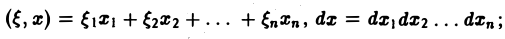
символ 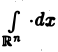
Свойства многомерного преобразования аналогичны соответствующим свойствам преобразования Фурье функции одной переменной. В специальном случае, когда
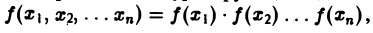
имеем
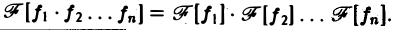
Дополнение к преобразованию Фурье
Смотрите также:
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат


















![phi in [0,pi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/885d893a88ce10762161016fa3db3a37828df879)
![{Bigg |}int _{{C}}f(t){mathrm {d}}t{Bigg |}leq {frac {pi }{omega }}max _{{phi in [0,pi ]}}g(Re^{{-iphi }})](https://wikimedia.org/api/rest_v1/media/math/render/svg/452ffbc41fa70c8f4fc159cbaae784942172224b)