Задача 36488 № 11.3.23 Вычислить приближенно:…
Условие
№ 11.3.23 Вычислить приближенно: arctg(1.02/9.95)

математика ВУЗ
2841
Решение
★
Вводим в рассмотрение функцию
z=arctg(y/x)
Применяем формулу ( см. рис.)
f`_(x)=(y/x)`_(x)/(1+(y/x)^2)=(-y/x^2)/((x^2+y^2)/x^2)= -y/(x^2+y^2)
f`_(y)=(y/x)`_(y)/(1+(y/x)^2)=(1/x)/((x^2+y^2)/x^2)= x/(x^2+y^2)
x_(o)=1
y_(o)=1
Δ x=0,95-1=-0,05
Δy=1,02-1=0,02
f`_(x)(x_(o);y_(o))= -1/(1^2+1^2)=-1/2
f`_(y)(x_(o);y_(o))=1/(1^2+1^2)=1/2
Осталось подставить в формулу и сосчитать
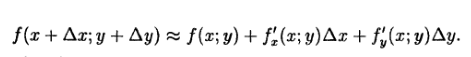
Написать комментарий
Нахождение значений арксинуса, арккосинуса, арктангенса и арккотангенса
В данной статье рассматриваются вопросы нахождения значений арксинуса, арккосинуса, арктангенса и арккотангенса заданного числа. Для начала вводятся понятия арксинуса, арккосинуса, арктангенса и арккотангенса. Рассматриваем основные их значения, по таблицам, в том числе и Брадиса, нахождение этих функций.
Значения арксинуса, арккосинуса, арктангенса и арккотангенса
Необходимо разобраться в понятиях «значения арксинуса, арккосинуса, арктангенса, арккотангенса».
Определения арксинуса, арккосинуса, арктангенса и арккотангенса числа помогут разобраться в вычислении заданных функций. Значение тригонометрических функций угла равняется числу a , тогда автоматически считается величиной этого угла. Если a – число, тогда это и есть значение функции.
Для четкого понимания рассмотрим пример.
Если имеем арккосинус угла равного π 3 , то значение косинуса отсюда равно 1 2 по таблице косинусов. Данный угол расположен в промежутке от нуля до пи, значит, значение арккосинуса 1 2 получим π на 3 . Такое тригонометрическое выражение записывается как a r cos ( 1 2 ) = π 3 .
Величиной угла может быть как градус, так и радиан. Значение угла π 3 равняется углу в 60 градусов (подробней разбирается в теме перевода градусов в радианы и обратно). Данный пример с арккосинусом 1 2 имеет значение 60 градусов. Такая тригонометрическая запись имеет вид a r c cos 1 2 = 60 °
Основные значения arcsin, arccos, arctg и arctg
Благодаря таблице синусов, косинусов, тангенсов и котангенсов, мы имеет точные значения угла при 0 , ± 30 , ± 45 , ± 60 , ± 90 , ± 120 , ± 135 , ± 150 , ± 180 градусов. Таблица достаточно удобна и из нее можно получать некоторые значения для аркфункций, которые имеют название как основные значения арксинуса, арккосинуса, арктангенса и арккотангенса.
Таблица синусов основных углов предлагает такие результаты значений углов:
sin ( — π 2 ) = — 1 , sin ( — π 3 ) = — 3 2 , sin ( — π 4 ) = — 2 2 , sin ( — π 6 ) = — 1 2 , sin 0 = 0 , sin π 6 = 1 2 , sin π 4 = 2 2 , sin π 3 = 3 2 , sin π 2 = 1
Учитывая их, можно легко высчитать арксинус числа всех стандартных значений, начиная от — 1 и заканчивая 1 , также значения от – π 2 до + π 2 радианов, следуя его основному значению определения. Это и является основными значениями арксинуса.
Для удобного применения значений арксинуса занесем в таблицу. Со временем придется выучить эти значения, так как на практике приходится часто к ним обращаться. Ниже приведена таблица арксинуса с радианным и градусным значением углов.
в р а д и а н а х
| α | — 1 | — 3 2 | — 2 2 | — 1 2 | 0 | 1 2 | 2 2 | 3 2 |
| a r c sin α к а к у г о л | — π 2 | — π 3 | — π 4 | — π 6 | 0 | π 6 | π 4 | π 3 |
| в г р а д у с а х | — 90 ° | — 60 ° | — 45 ° | — 30 ° | 0 ° | 30 ° | 45 ° | 60 ° |
| a r c sin α к а к ч и с л о | — π 2 | — π 3 | — π 4 | — π 6 | 0 | π 6 | π 4 | π 3 |
Для получения основных значений арккосинуса необходимо обратиться к таблице косинусов основных углов. Тогда имеем:
cos 0 = 1 , cos π 6 = 3 2 , cos π 4 = 2 2 , cos π 3 = 1 2 , cos π 2 = 0 , cos 2 π 3 = — 1 2 , cos 3 π 4 = — 2 2 , cos 5 π 6 = — 3 2 , cos π = — 1
Следуя из таблицы, находим значения арккосинуса:
a r c cos ( — 1 ) = π , arccos ( — 3 2 ) = 5 π 6 , arcocos ( — 2 2 ) = 3 π 4 , arccos — 1 2 = 2 π 3 , arccos 0 = π 2 , arccos 1 2 = π 3 , arccos 2 2 = π 4 , arccos 3 2 = π 6 , arccos 1 = 0
в р а д и а н а х
| α | — 1 | — 3 2 | — 2 2 | — 1 2 | 0 | 1 2 | 2 2 | 3 2 | 1 |
| a r c cos α к а к у г о л | π | 5 π 6 | 3 π 4 | 2 π 3 | π 2 | π 3 | π 4 | π 6 | 0 |
| в г р а д у с а х | 180 ° | 150 ° | 135 ° | 120 ° | 90 ° | 60 ° | 45 ° | 30 ° | 0 ° |
| a r c cos α к а к ч и с л о | π | 5 π 6 | 3 π 4 | 2 π 3 | π 2 | π 3 | π 4 | π 6 | 0 |
Таким же образом, исходя из определения и стандартных таблиц, находятся значения арктангенса и арккотангенса, которые изображены в таблице арктангенсов и арккотангенсов ниже.
| α | — 3 | — 1 | — 3 3 | 0 | 3 3 | 1 | 3 | |
| a r c t g a к а к у г о л | в р а д и а н а х | — π 3 | — π 4 | — π 6 | 0 | π 6 | π 4 | π 3 |
| в г р а д у с а х | — 60 ° | — 45 ° | — 30 ° | 0 ° | 30 ° | 45 ° | 60 ° | |
| a r c t g a к а к ч и с л о | — π 3 | — π 4 | — π 6 | 0 | π 6 | π 4 | π 3 |
Нахождение значений по таблицам синусов, косинусов, тангенсов и котангенсов Брадиса
a r c sin , a r c cos , a r c t g и a r c c t g
Для точного значения a r c sin , a r c cos , a r c t g и a r c c t g числа а необходимо знать величину угла. Об этом сказано в предыдущем пункте. Однако, точное значении функции нам неизвестно. Если необходимо найти числовое приближенное значение аркфункций, применяют таблицу синусов, косинусов, тангенсов и котангенсов Брадиса.
Такая таблица позволяет выполнять довольно точные вычисления, так как значения даются с четырьмя знаками после запятой. Благодаря этому числа выходят точными до минуты. Значения a r c sin , a r c cos , a r c t g и a r c c t g отрицательных и положительных чисел сводится к нахождению формул a r c sin , a r c cos , a r c t g и a r c c t g противоположных чисел вида a r c sin ( — α ) = — a r c sin α , a r c cos ( — α ) = π — a r c cos α , a r c t g ( — α ) = — a r c t g α , a r c c t g ( — α ) = π — a r c c t g α .
Рассмотрим решение нахождения значений a r c sin , a r c cos , a r c t g и a r c c t g с помощью таблицы Брадиса.
Если нам необходимо найти значение арксинуса 0 , 2857 , ищем значение, найдя таблицу синусов. Видим, что данному числу соответствует значение угла sin 16 градусов и 36 минут. Значит, арксинус числа 0 , 2857 – это искомый угол в 16 градусов и 36 минут. Рассмотрим на рисунке ниже.
Правее градусов имеются столбцы называемые поправки. При искомом арксинусе 0 , 2863 используется та самая поправка в 0 , 0006 , так как ближайшим числом будет 0 , 2857 . Значит, получим синус 16 градусов 38 минут и 2 минуты, благодаря поправке. Рассмотрим рисунок с изображением таблицы Брадиса.
Бывают ситуации, когда искомого числа нет в таблице и даже с поправками его не найти, тогда отыскивается два самых близких значения синусов. Если искомое число 0,2861573, то числа 0,2860 и 0,2863 являются ближайшими его значениями. Этим числам соответствуют значения синуса 16 градусов 37 минут и 16 градусов и 38 минут. Тогда приближенное значение данного числа можно определить с точностью до минуты.
Таким образом находятся значения a r c sin , a r c cos , a r c t g и a r c c t g .
Нахождение значения arcsin, arccos, arctg и arcctg
Чтобы найти арксинус через известный арккосинус данного числа, нужно применить тригонометрические формулы a r c sin α + a r c cos α = π 2 , a r c t g α + a r c c t g α = π 2 (не обходимо просмотреть тему формул суммы арккосинуса и арксинуса, суммы арктангенса и арккотангенса).
При известном a r c sin α = — π 12 необходимо найти значение a r c cos α , тогда необходимо вычислить арккосинус по формуле:
a r c cos α = π 2 − a r c sin α = π 2 − ( − π 12 ) = 7 π 12 .
Если необходимо найти значение арктангенса или арккотангенса числа a с помощью известного арксинуса или арккосинуса, необходимо производить долгие вычисления, так как стандартных формул нет. Рассмотрим на примере.
Если дан арккосинус числа а равный π 10 , а вычислить арктангенс данного числа поможет таблица тангенсов. Угол π 10 радиан представляет собой 18 градусов, тогда по таблице косинусов видим, что косинус 18 градусов имеет значение 0 , 9511 , после чего заглядываем в таблицу Брадиса.
При поиске значения арктангенса 0 , 9511 определяем, что значение угла имеет 43 градуса и 34 минуты. Рассмотрим по таблице ниже.
Фактически, таблица Брадиса помогает в нахождении необходимого значения угла и при значении угла позволяет определить количество градусов.
Обратные тригонометрические функции и их графики
Обратные тригонометрические функции — это арксинус, арккосинус, арктангенс и арккотангенс.
Сначала дадим определения.
Арксинусом числа а называется число , такое, что Или, можно сказать, что это такой угол , принадлежащий отрезку , синус которого равен числу а.
Арккосинусом числа а называется число , такое, что
Арктангенсом числа а называется число , такое, что
Арккотангенсом числа а называется число , такое, что
Расскажем подробно об этих четырех новых для нас функциях — обратных тригонометрических.
Например, арифметический квадратный корень из числа а — такое неотрицательное число, квадрат которого равен а.
Логарифм числа b по основанию a — такое число с, что
Мы понимаем, для чего математикам пришлось «придумывать» новые функции. Например, решения уравнения — это и Мы не смогли бы записать их без специального символа арифметического квадратного корня.
Понятие логарифма оказалось необходимо, чтобы записать решения, например, такого уравнения: Решение этого уравнения — иррациональное число Это показатель степени, в которую надо возвести 2, чтобы получить 7.
Так же и с тригонометрическими уравнениями. Например, мы хотим решить уравнение
Ясно, что его решения соответствуют точкам на тригонометрическом круге, ордината которых равна И ясно, что это не табличное значение синуса. Как же записать решения?
Здесь не обойтись без новой функции, обозначающей угол, синус которого равен данному числу a. Да, все уже догадались. Это арксинус.
Угол, принадлежащий отрезку , синус которого равен — это арксинус одной четвертой. И значит, серия решений нашего уравнения, соответствующая правой точке на тригонометрическом круге, — это
А вторая серия решений нашего уравнения — это
Подробнее о решении тригонометрических уравнений — здесь.
Осталось выяснить — зачем в определении арксинуса указывается, что это угол, принадлежащий отрезку ?
Дело в том, что углов, синус которых равен, например, , бесконечно много. Нам нужно выбрать какой-то один из них. Мы выбираем тот, который лежит на отрезке .
Взгляните на тригонометрический круг. Вы увидите, что на отрезке каждому углу соответствует определенное значение синуса, причем только одно. И наоборот, любому значению синуса из отрезка отвечает одно-единственное значение угла на отрезке . Это значит, что на отрезке можно задать функцию принимающую значения от до
Повторим определение еще раз:
Арксинусом числа a называется число , такое, что
Обозначение: Область определения арксинуса — отрезок Область значений — отрезок .
Можно запомнить фразу «арксинусы живут справа». Не забываем только, что не просто справа, но ещё и на отрезке .
Мы готовы построить график функции
Как обычно, отмечаем значения х по горизонтальной оси, а значения у — по вертикальной.
Поскольку , следовательно, х лежит в пределах от -1 до 1.
Значит, областью определения функции y = arcsin x является отрезок
Мы сказали, что у принадлежит отрезку . Это значит, что областью значений функции y = arcsin x является отрезок .
Заметим, что график функции y=arcsinx весь помещается в области, ограниченной линиями и
Как всегда при построении графика незнакомой функции, начнем с таблицы.
По определению, арксинус нуля — это такое число из отрезка , синус которого равен нулю. Что это за число? — Понятно, что это ноль.
Аналогично, арксинус единицы — это такое число из отрезка , синус которого равен единице. Очевидно, это
Продолжаем: — это такое число из отрезка , синус которого равен . Да, это
Строим график функции
1. Область определения
2. Область значений
3. , то есть эта функция является нечетной. Ее график симметричен относительно начала координат.
4. Функция монотонно возрастает. Ее наименьшее значение, равное — , достигается при , а наибольшее значение, равное , при
5. Что общего у графиков функций и ? Не кажется ли вам, что они «сделаны по одному шаблону» — так же, как правая ветвь функции и график функции , или как графики показательной и логарифмической функций?
Представьте себе, что мы из обычной синусоиды вырезали небольшой фрагмент от до , а затем развернули его вертикально — и мы получим график арксинуса.
То, что для функции на этом промежутке — значения аргумента, то для арксинуса будут значения функции. Так и должно быть! Ведь синус и арксинус — взаимно-обратные функции. Другие примеры пар взаимно обратных функций — это при и , а также показательная и логарифмическая функции.
Напомним, что графики взаимно обратных функций симметричны относительно прямой
Аналогично, определим функцию Только отрезок нам нужен такой, на котором каждому значению угла соответствует свое значение косинуса, а зная косинус, можно однозначно найти угол. Нам подойдет отрезок
Арккосинусом числа a называется число , такое, что
Легко запомнить: «арккосинусы живут сверху», и не просто сверху, а на отрезке
Обозначение: Область определения арккосинуса — отрезок Область значений — отрезок
Очевидно, отрезок выбран потому, что на нём каждое значение косинуса принимается только один раз. Иными словами, каждому значению косинуса, от -1 до 1, соответствует одно-единственное значение угла из промежутка
Арккосинус не является ни чётной, ни нечётной функцией. Зато мы можем использовать следующее очевидное соотношение:
Построим график функции
Нам нужен такой участок функции , на котором она монотонна, то есть принимает каждое свое значение ровно один раз.
Выберем отрезок . На этом отрезке функция монотонно убывает, то есть соответствие между множествами и взаимно однозначно. Каждому значению х соответствует свое значение у. На этом отрезке существует функция, обратная к косинусу, то есть функция у = arccosx.
Заполним таблицу, пользуясь определением арккосинуса.
Арккосинусом числа х, принадлежащего промежутку , будет такое число y, принадлежащее промежутку , что
Вот график арккосинуса:
1. Область определения
2. Область значений
Эта функция общего вида — она не является ни четной, ни нечетной.
4. Функция является строго убывающей. Наибольшее значение, равное , функция у = arccosx принимает при , а наименьшее значение, равное нулю, принимает при
5. Функции и являются взаимно обратными.
Следующие — арктангенс и арккотангенс.
Арктангенсом числа a называется число , такое, что
Обозначение: . Область определения арктангенса — промежуток Область значений — интервал .
Почему в определении арктангенса исключены концы промежутка — точки ? Конечно, потому, что тангенс в этих точках не определён. Не существует числа a, равного тангенсу какого-либо из этих углов.
Построим график арктангенса. Согласно определению, арктангенсом числа х называется число у, принадлежащее интервалу , такое, что
Как строить график — уже понятно. Поскольку арктангенс — функция обратная тангенсу, мы поступаем следующим образом:
— Выбираем такой участок графика функции , где соответствие между х и у взаимно однозначное. Это интервал Ц На этом участке функция принимает значения от до
Тогда у обратной функции, то есть у функции , область, определения будет вся числовая прямая, от до а областью значений — интервал
Дальше рассуждаем так же, как при построении графиков арксинуса и арккосинуса.
А что же будет при бесконечно больших значениях х? Другими словами, как ведет себя эта функция, если х стремится к плюс бесконечности?
Мы можем задать себе вопрос: для какого числа из интервала значение тангенса стремится к бесконечности? — Очевидно, это
А значит, при бесконечно больших значениях х график арктангенса приближается к горизонтальной асимптоте
Аналогично, если х стремится к минус бесконечности, график арктангенса приближается к горизонтальной асимптоте
На рисунке — график функции
1. Область определения
2. Область значений
3. Функция нечетная.
4. Функция является строго возрастающей.
5. Прямые и — горизонтальные асимптоты данной функции.
6. Функции и являются взаимно обратными — конечно, когда функция рассматривается на промежутке
Аналогично, определим функцию арккотангенс и построим ее график.
Арккотангенсом числа a называется число , такое, что
1. Область определения
2. Область значений
3. Функция — общего вида, то есть ни четная, ни нечетная.
4. Функция является строго убывающей.
5. Прямые и — горизонтальные асимптоты данной функции.
6. Функции и являются взаимно обратными, если рассматривать на промежутке
Урок 9. Обратные тригонометрические функции. Теория
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На этом уроке мы рассмотрим особенности обратных функций и повторим обратные тригонометрические функции. Отдельно будут рассмотрены свойства всех основных обратных тригонометрических функций: арксинуса, арккосинуса, арктангенса и арккотангенса.
Данный урок поможет Вам подготовиться к одному из типов задания В7 и С1.
http://interneturok.ru/lesson/algebra/11-klass/bzadachi-iz-egeb/urok-9-obratnye-trigonometricheskie-funktsii-teoriya
Сообщения без ответов | Активные темы
Вычислить приближенно арктангенс, заменяя полное приращение
Модераторы: Prokop, mad_math
| Автор | Сообщение | ||
|---|---|---|---|
|
Shwed |
Заголовок сообщения: Вычислить приближенно арктангенс, заменяя полное приращение
|
||
|
Как вычислить приближенно арктангенс, заменяя полное приращение функции полным дифференциалом [math]operatorname{arctg}!left(frac{1,98}{1,03}-1 right)[/math]
|
||
| Вернуться к началу |
|
||
|
Ellipsoid |
Заголовок сообщения: Re: вычислить приближенно
|
|
Требуется найти приближенное значение функции [math]operatorname{arctg} left(frac{1,98}{1,03}-1 right)[/math]. Пусть[math]z=operatorname{arctg} left(frac{x}{y}-1 right)[/math]. Далее, [math]Delta z= f(x+Delta x,y+Delta y)-f(x,y)[/math], [math]dz=frac{partial z}{partial x}dx + frac{partial z}{partial y}dy=frac{partial z}{partial x}Delta x + frac{partial z}{partial y}Delta y[/math]. Известно, что [math]Delta z approx dz[/math], тогда [math]f(x+Delta x,y+Delta y)-f(x,y) approx frac{partial z}{partial x}Delta x + frac{partial z}{partial y}Delta y Leftrightarrow f(x+Delta x,y+Delta y) approx f(x,y) +frac{partial z}{partial x}Delta x + frac{partial z}{partial y} Delta y[/math]. Положим [math]x=2, Delta x=-0,02, y=1, Delta y=0,03[/math]. Находим частные производные и вычисляем значение функции…
|
|
| Вернуться к началу |
|
| За это сообщение пользователю Ellipsoid «Спасибо» сказали: mad_math, pewpimkin, Shwed |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Как вычислить арктангенс?
в форуме Тригонометрия |
Mirtu |
5 |
1262 |
22 июн 2016, 19:45 |
|
Как вычислить интеграл 1/арктангенс х
в форуме Интегральное исчисление |
gail-ul |
4 |
821 |
02 дек 2016, 10:37 |
|
Вычислить приближенное значение, заменив в точке приращение
в форуме Теория вероятностей |
darthanyan |
1 |
331 |
22 дек 2018, 19:46 |
|
Вычислить приближенно
в форуме Дифференциальное исчисление |
photographer |
5 |
408 |
08 янв 2018, 21:40 |
|
Вычислить приближенно
в форуме Ряды |
SkiprDAG |
4 |
213 |
21 апр 2021, 07:53 |
|
Приближённо вычислить
в форуме Ряды |
devnulled |
1 |
290 |
27 май 2017, 20:37 |
|
Вычислить приближенно
в форуме Ряды |
zdorove |
2 |
204 |
15 янв 2019, 13:14 |
|
Вычислить приближенно
в форуме Дифференциальное исчисление |
cincinat |
1 |
402 |
16 окт 2015, 22:11 |
|
Вычислить приближенно
в форуме Дифференциальное исчисление |
wr00m |
2 |
348 |
19 июн 2017, 18:46 |
|
Вычислить приближённо с помощью диф-ла
в форуме Дифференциальное исчисление |
sfanter |
1 |
367 |
04 ноя 2015, 10:42 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 1 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Powered by phpBB © 2000, 2002, 2005, 2007 phpBB Group
Вы можете создать форум бесплатно PHPBB3 на Getbb.Ru, Также возможно сделать готовый форум PHPBB2 на Mybb2.ru
Русская поддержка phpBB
Приближенные вычисления с использованием дифференциалов.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Выражение для дифференциала имеет вид $$dy(x_0, dx)=f'(x_0)dx,$$ где $dx=Delta x.$
Если $f'(x_0)neq 0,$ то при $Delta xrightarrow 0$ приращение функции и ее дифференциал $dy$ в фиксированной точке являются эквивалентными бесконечно малыми, что позволяет записать приближенное равенство:
$Delta yapprox dy$ при $|Delta x|ll1.$
Примеры.
5.298. Вычислить приближенно:
а) $arcsin 0,05;$
Решение.
Будем пользоваться формулой $Delta yapprox dy=y'(x_0)dx.$
$y(x)=arcsin x$
$x_0=0,$ $Delta x=dx=0,05,$
$Delta y=y(x)-y(x_0)Rightarrow arcsin 0,05approx y'(0)cdot 0,05;$
$y(x)=arcsin xRightarrow y'(x)=frac{1}{sqrt{1-x^2}}.$ Таким образом, $y'(x_0)=1.$
Подставляя все полученные значения в формулу $Delta yapprox dy=y'(x_0)dx,$ получаем $arcsin 0,05approx 1cdot 0,05=0,05;$
Ответ: 0,05.
в) $ln 1,2.$
Решение.
Будем пользоваться формулой $Delta yapprox dy=y'(x_0)dx.$
$y(x)=ln x$
$x_0=1,$ $Delta x=dx=0,2,$
$Delta y=y(x)-y(x_0)Rightarrow ln 1,2approx y'(1)cdot 0,2;$
$y(x)=ln xRightarrow y'(x)=frac{1}{x}.$ Таким образом, $y'(x_0)=1.$
Подставляя все полученные значения в формулу $Delta yapprox dy=y'(x_0)dx,$ получаем $ln 1,2approx 1cdot 0,2=0,2;$
Ответ: 0,2.
Домашнее задание.
5.298. Вычислить приближенно:
б) $arctg 1,04;$
Ответ: 0,805.
5.299. Обосновать приближенную формулу $$sqrt[3]{x+Delta x}approxsqrt[3]{x}+frac{Delta x}{3sqrt[3]{x^2}}$$ и вычислить по этой формуле $sqrt[3]{25}.$
Ответ: 2,93.
Приращение $delta y$ функции
$y=f(x)$ представимо в виде:
$$Delta y=f^{prime}(x) cdot Delta x+alpha(Delta x) cdot Delta x$$
где функция $alpha(Delta x)$ является
б.м. функцией при
стремлении аргумента $Delta x$ к нулю. Так как
$Delta x=dx$, то
$$Delta y=f^{prime}(x) d x+alpha(Delta x) cdot Delta x=d y+alpha(Delta x) cdot Delta x$$
В силу того, что второе слагаемое
$alpha(Delta x) cdot Delta x$ является бесконечно малым, то им можно пренебречь, а поэтому
$$Delta y approx d y$$
А так как в нахождении дифференциал значительно проще, чем приращение функции, то данная формула активно используется на практике.
Для приближенного вычисления значения функции применяется следующая формула:
$$fleft(x_{0}+Delta xright) approx fleft(x_{0}right)+f^{prime}left(x_{0}right) cdot Delta x$$
Пример
Задание. Вычислить приближенно $text { arctg } 1,02$ ,
заменяя приращение функции ее дифференциалом.
Решение. Рассмотрим функцию $y=operatorname{arctg} x$.
Необходимо вычислить ее значение в точке $x=1,02$ .
Представим данное значение в виде следующей суммы:
$x=x_0+Delta x$
Величины $x_0$ и $delta x$
выбираются так, чтобы в точке $x_0$ можно было бы
достаточно легко вычислить значение функции и ее производной, а $delta x$
было бы достаточно малой величиной. С учетом этого, делаем вывод, что
$x=1,02=1+0,02$ , то есть $x_0=1$, $Delta x=0,02$.
Вычислим значение функции $y=operatorname{arctg} x$ в точке
$x_0=1$:
$$yleft(x_{0}right)=y(1)=operatorname{arctg} 1=frac{pi}{4}$$
Далее продифференцируем рассматриваемую функцию и найдем значение
$y^{prime}left(x_{0}right)$:
$$y^{prime}=(operatorname{arctg} x)^{prime}=frac{1}{1+x^{2}}$$
Тогда
$$y^{prime}(1)=frac{1}{2}$$
Итак,
$$begin{aligned}
y(1,02) &=operatorname{arctg} 1,02=y(1+0,02) approx y(1)+y^{prime}(1) cdot Delta x=\
&=frac{pi}{4}+frac{1}{2} cdot 0,02 approx 0,7852+0,01=0,7952
end{aligned}$$
Ответ. $operatorname{arctg} 1,02 approx 0,7952$
Читать дальше: геометрический и механический смысл производной.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!


















