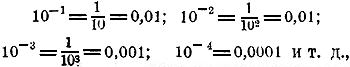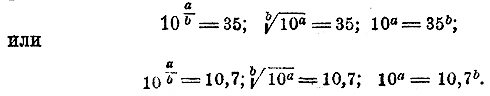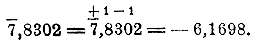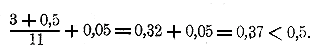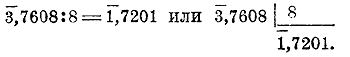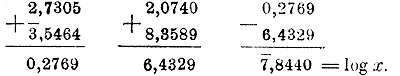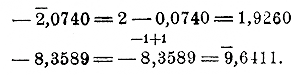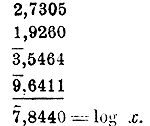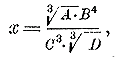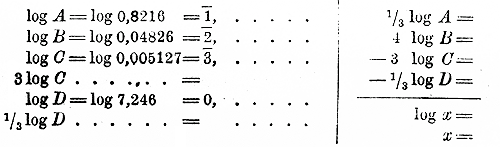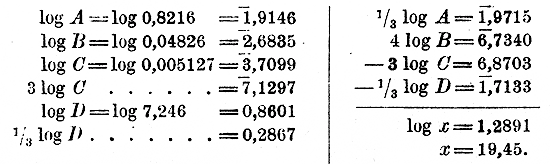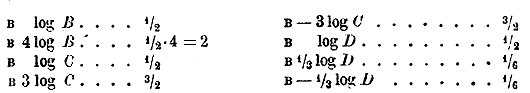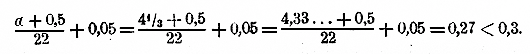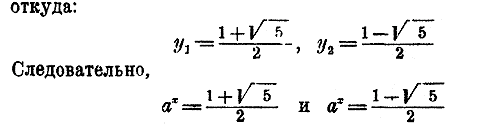Как найти приближенное значение функции логарифм

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания,
берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта
готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием
сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом
администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта
и представлены на сайте исключительно для ознакомления. Авторские права на материалы
принадлежат их законным авторам. Частичное или полное копирование материалов сайта без
письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой
зрения авторов.

Вычисление логарифмов: способы, примеры, решения

Вычисление логарифмов по определению

В простейших случаях возможно достаточно быстро и легко выполнить нахождение логарифма по определению. Давайте подробно рассмотрим, как происходит этот процесс.

Его суть состоит в представлении числа b в виде a c , откуда по определению логарифма число c является значением логарифма. То есть, нахождению логарифма по определению отвечает следующая цепочка равенств: log_ab=log_aa c =c .

Итак, вычисление логарифма по определению сводится к нахождению такого числа c , что a c =b , а само число c есть искомое значение логарифма.

Учитывая информацию предыдущих абзацев, когда число под знаком логарифма задано некоторой степенью основания логарифма, то можно сразу указать, чему равен логарифм – он равен показателю степени. Покажем решения примеров.

Найдите log₂2 −3 , а также вычислите натуральный логарифм числа e 5,3 .

Определение логарифма позволяет нам сразу сказать, что log₂2 −3 =−3 . Действительно, число под знаком логарифма равно основанию 2 в −3 степени.

Аналогично находим второй логарифм: lne 5,3 =5,3 .

log₂2 −3 =−3 и lne 5,3 =5,3 .

Если же число b под знаком логарифма не задано как степень основания логарифма, то нужно внимательно посмотреть, нельзя ли прийти к представлению числа b в виде a c . Часто такое представление бывает достаточно очевидно, особенно когда число под знаком логарифма равно основанию в степени 1 , или 2 , или 3 , …

Вычислите логарифмы log₅25 , и .

Несложно заметить, что 25=5 2 , это позволяет вычислять первый логарифм: log₅25=log₅5 2 =2 .

Переходим к вычислению второго логарифма . Число можно представить в виде степени числа 7 : (при необходимости смотрите степень с дробным показателем ). Следовательно, .

Перепишем третий логарифм в следующем виде . Теперь можно увидеть, что , откуда заключаем, что . Следовательно, по определению логарифма .

Коротко решение можно было записать так: .

log₅25=2 , и .

Когда под знаком логарифма находится достаточно большое натуральное число, то его не помешает разложить на простые множители. Это часто помогает представить такое число в виде некоторой степени основания логарифма, а значит, вычислить этот логарифм по определению.

Найдите значение логарифма .

Разложение на простые множители числа под знаком логарифма имеет вид 7776=2 5 ·3 5 , откуда следует, что 7776=6 5 . Полученное выражение несложно представить в виде степени числа . Так как , то (в последнем переходе мы использовали свойство степени в степени ). Таким образом, . На этом вычисление логарифма завершено.

.

В заключение этого пункта отметим, что мы не ставили целью рассмотреть все способы представления числа под знаком логарифма в виде некоторой степени основания. Наша цель заключалась в том, чтобы дать самые часто используемые варианты действий, приводящие к результату при вычислении логарифмов по определению.

Как решать «вложенные» логарифмические уравнения

Сегодня мы продолжаем изучать логарифмические уравнения и разберем конструкции, когда один логарифм стоит под знаком другого логарифма. Оба уравнения мы будем решать с помощью канонической формы.Сегодня мы продолжаем изучать логарифмические уравнения и разберем конструкции, когда один логарифм стоит под знаком другого. Оба уравнения мы будем решать с помощью канонической формы. Напомню, если у нас есть простейшее логарифмическое уравнение вида log _a f ( x ) = b , то для решения такого уравнения мы выполняем следующие шаги. В первую очередь, нам нужно заменить число b :

Заметьте: a b — это аргумент. Точно так же в исходном уравнении аргументом является функция f ( x ). Затем мы переписываем уравнение и получаем вот такую конструкцию:

log _a f ( x ) = log _a a b

Уже затем мы можем выполнить третий шаг — избавится от знака логарифма и просто записать:

В результате мы получим новое уравнение. При этом никаких ограничений на функцию f ( x ) не накладывается. Например, на ее месте также может стоять логарифмическая функция. И тогда мы вновь получим логарифмическое уравнение, которое снова сведем к простейшему и решим через каноническую форму.

Впрочем, хватит лирики. Давайте решим настоящую задачу. Итак, задача № 1:

Как видим, перед нами простейшее логарифмическое уравнение. В роли f ( x ) выступает конструкция 1 + 3 log₂ x , а в роли числа b выступает число 2 (в роли a также выступает двойка). Давайте перепишем эту двойку следующим образом:

Важно понимать, что первые две двойки пришли к нам из основания логарифма, т. е. если бы в исходном уравнении стояла 5, то мы бы получили, что 2 = log₅ 5 2 . В общем, основание зависит исключительно от логарифма, который изначально дан в задаче. И в нашем случае это число 2.

Итак, переписываем наше логарифмическое уравнение с учетом того, что двойка, которая стоит справа, на самом деле тоже является логарифмом. Получим:

Переходим к последнему шагу нашей схемы — избавляемся от канонической формы. Можно сказать, просто зачеркиваем знаки log. Однако с точки зрения математики «зачеркнуть log» невозможно — правильнее сказать, что мы просто просто приравниваем аргументы:

Отсюда легко находится 3 log₂ x :

Мы вновь получили простейшее логарифмическое уравнение, давайте снова приведем его к канонической форме. Для этого нам необходимо провести следующие изменения:

Почему в основании именно двойка? Потому что в нашем каноническом уравнении слева стоит логарифм именно по основанию 2. Переписываем задачу с учетом этого факта:

Снова избавляемся от знака логарифма, т. е. просто приравниваем аргументы. Мы вправе это сделать, потому что основания одинаковые, и больше никаких дополнительных действий ни справа, ни слева не выполнялось:

Вот и все! Задача решена. Мы нашли решение логарифмического уравнения.

Обратите внимание! Хотя переменная х и стоит в аргументе (т. е. возникают требования к области определения), мы никаких дополнительных требований предъявлять не будем.

Как я уже говорил выше, данная проверка является избыточной, если переменная встречается лишь в одном аргументе лишь одного логарифма. В нашем случае х действительно стоит лишь в аргументе и лишь под одним знаком log. Следовательно, никаких дополнительных проверок выполнять не требуется.

Тем не менее, если вы не доверяете данному методу, то легко можете убедиться, что х = 2 действительно является корнем. Достаточно подставить это число в исходное уравнение.

Давайте перейдем ко второму уравнению, оно чуть интересней:

Если обозначить выражение внутри большого логарифма функцией f ( x ), получим простейшее логарифмическое уравнение, с которого мы начинали сегодняшний видеоурок. Следовательно, можно применить каноническую форму, для чего придется представить единицу в виде log₂ 2 1 = log₂ 2.

Переписываем наше большое уравнение:

Изваляемся от знака логарифма, приравнивая аргументы. Мы вправе это сделать, потому что и слева, и справа основания одинаковые. Кроме того, заметим, что log₂ 4 = 2:

log_1/2 (2 x − 1) + 2 = 2

Перед нами снова простейшее логарифмическое уравнение вида log _a f ( x ) = b . Переходим к канонической форме, т. е. представляем ноль в виде log_1/2 (1/2)0 = log_1/2 1.

Переписываем наше уравнение и избавляемся от знака log, приравнивая аргументы:

Опять же мы сразу получили ответ. Никаких дополнительных проверок не требуется, потому что в исходном уравнении лишь один логарифм содержит функцию в аргументе.

Следовательно, никаких дополнительных проверок выполнять не требуется. Мы можем смело утверждать, что х = 1 является единственным корнем данного уравнения.

А вот если бы во втором логарифме вместо четверки стояла бы какая-то функция от х (либо 2х стояло бы не в аргументе, а в основании) — вот тогда потребовалось бы проверять область определения. Иначе велик шанс нарваться на лишние корни.

Откуда возникают такие лишние корни? Этот момент нужно очень четко понимать. Взгляните на исходные уравнения: везде функция х стоит под знаком логарифма. Следовательно, поскольку мы записали log₂ x , то автоматически выставляем требование х > 0. Иначе данная запись просто не имеет смысла.

Однако по мере решения логарифмического уравнения мы избавляемся от всех знаков log и получаем простенькие конструкции. Здесь уже никаких ограничений не выставляется, потому что линейная функция определена при любом значении х.

Именно эта проблема, когда итоговая функция определена везде и всегда, а исходная — отнюдь не везде и не всегда, и является причиной, по которой в решении логарифмических уравнениях очень часто возникают лишние корни.

Но повторю еще раз: такое происходить лишь в ситуации, когда функция стоит либо в нескольких логарифмах, либо в основании одного из них. В тех задачах, которые мы рассматриваем сегодня, проблем с расширением области определения в принципе не существует.

Тонкости и хитрости решения

Сегодня мы переходим к более сложным задачам и будем решать логарифмическое уравнение, в основании которого стоит не число, а функция.

И пусть даже эта функция линейна — в схему решения придется внести небольшие изменения, смысл которых сводится к дополнительным требованиям, накладываемым на область определения логарифма.

Логарифмические уравнения. Методы решения

На самом деле существует целая масса подходов: это и разложение на множители, и потенцирование, и замена, и работа с основаниями…

Но все методы решения логарифмических уравнения роднит одно: их цель свести логарифмические уравнения к простейшему виду::

Если уравнение сведено к такому, что слева и справа от знака «равно» стоят логарифмы с одним основанием, то логарифмы мы «зачеркиваем» и решаем оставшееся уравнение.

Однако, тут есть один подводный камень: поскольку логарифм определен только тогда, когда

то после нахождения корней логарифмического уравнения, мы обязаны сделать проверку. Я не поленюсь и повторю еще раз:

В ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЯХ МЫ ВСЕГДА ДЕЛАЕМ ПРОВЕРКУ ПОЛУЧЕННЫХ КОРНЕЙ!!

Те учащиеся, которые игнорируют это требование, как правило допускают глупейшие и непростительные ошибки!

Согласись, обидно решить правильно уравнение, а потом не сделать самую малость: проверку, и записать лишние корни, и записать из-за этого неправильный ответ!

Формулы логарифмов. Логарифмы примеры решения

Теперь на основе этих формул(свойств), покажем примеры решения логарифмов.

Примеры решения логарифмов на основании формул

Логарифм положительного числа b по основанию a (обозначается logab) — это показатель степени, в которую надо возвести a, чтобы получить b, при этом b > 0, a > 0, а 1.

Согласно определения logab = x, что равносильно ax = b, поэтому logaax = x.

log749 = 2, т.к. 72 = 49

Десятичный логарифм — это обычный логарифм, в основании которого находится 10. Обозначается как lg.

log10100 = 2, т.к. 102 = 100

Натуральный логарифм — также обычный логарифм логарифм, но уже с основанием е (е = 2,71828… — иррациональное число). Обозначается как ln.

Формулы или свойства логарифмов желательно запомнить, потому что они понадобятся нам в дальнейшем при решении логарифмов, логарифмических уравнений и неравенств. Давайте еще раз отработаем каждую формулу на примерах.

Основное логарифмическое тождество
a logab = b
Пример.
82log83 = (82log83)2 = 32 = 9

Логарифм произведения равен сумме логарифмов loga (bc) = logab + logac
Пример.
log38,1 + log310 = log3 (8,1*10) = log381 = 4

Логарифм частного равен разности логарифмов
loga (b/c) = logab — logac
Пример.
9 log550/9 log52 = 9 log550- log52 = 9 log525 = 9 2 = 81

Свойства степени логарифмируемого числа и основания логарифма

Показатель степени логарифмируемого числа logab m = mlogab

Показатель степени основания логарифма loganb =1/n*logab

loganb m = m/n*logab,

если m = n, получим loganb n = logab

log49 = log223 2 = log23

Переход к новому основанию
logab = logcb/logca,

если c = b, получим logbb = 1

тогда logab = 1/logba

log0,83*log31,25 = log0,83*log0,81,25/log0,83 = log0,81,25 = log4/55/4 = -1

Как видите, формулы логарифмов не так сложны как кажутся. Теперь рассмотрев примеры решения логарифмов мы можем переходить к логарифмическим уравнениям.

Область допустимых значений (ОДЗ) логарифма

Теперь поговорим об ограничениях (ОДЗ – область допустимых значений переменных).

Мы помним, что, например, квадратный корень нельзя извлекать из отрицательных чисел; или если у нас дробь, то знаменатель не может быть равен нулю. Подобные ограничения есть и у логарифмов:

То есть и аргумент, и основание должны быть больше нуля, а основание еще и не может равняться .

Начнем с простого: допустим, что . Тогда, например, число не существует, так как в какую бы степень мы не возводили , всегда получается . Более того, не существует ни для какого . Но при этом может равняться чему угодно (по той же причине – в любой степени равно ). Поэтому объект не представляет никакого интереса, и его просто выбросили из математики.

Похожая проблема у нас и в случае : в любой положительной степени – это , а в отрицательную его вообще нельзя возводить, так как получится деление на ноль (напомню, что ).

При мы столкнемся с проблемой возведения в дробную степень (которая представляется в виде корня: . Например, (то есть ), а вот не существует.

Поэтому и отрицательные основания проще выбросить, чем возиться с ними.

Ну а поскольку основание a у нас бывает только положительное, то в какую бы степень мы его ни возводили, всегда получим число строго положительное. Значит, аргумент должен быть положительным. Например, не существует, так как ни в какой степени не будет отрицательным числом (и даже нулем, поэтому тоже не существует).

В задачах с логарифмами первым делом нужно записать ОДЗ. Приведу пример:

Вспомним определение: логарифм – это степень, в которую надо возвести основание , чтобы получить аргумент . И по условию, эта степень равна : .

Получаем обычное квадратное уравнение: . Решим его с помощью теоремы Виета: сумма корней равна , а произведение . Легко подобрать, это числа и .

Но если сразу взять и записать оба этих числа в ответе, можно получить 0 баллов за задачу. Почему? Давайте подумаем, что будет, если подставить эти корни в начальное уравнение?

– это явно неверно, так как основание не может быть отрицательным, то есть корень – «сторонний».

Чтобы избежать таких неприятных подвохов, нужно записать ОДЗ еще до начала решения уравнения:

Тогда, получив корни и , сразу отбросим корень , и напишем правильный ответ.

Использование свойств логарифмов при вычислении

Мощным инструментом вычисления логарифмов является использование свойств логарифмов .

Некоторые свойства логарифмов позволяют сразу указать значение логарифмов. К таким свойствам относятся свойство логарифма единицы и свойство логарифма числа, равного основанию: log₁1=log_aa 0 =0 и log_aa=log_aa 1 =1 . То есть, когда под знаком логарифма находится число 1 или число a , равное основанию логарифма, то в этих случаях логарифмы равны 0 и 1 соответственно.

Чему равны логарифмы и lg10 ?

Так как , то из определения логарифма следует .

Во втором примере число 10 под знаком логарифма совпадает с его основанием, поэтому десятичный логарифм десяти равен единице, то есть, lg10=lg10 1 =1 .

и lg10=1 .

Отметим, что вычисление логарифмов по определению (которое мы разобрали в предыдущем пункте) подразумевает использование равенства log_aa p =p , которое является одним из свойств логарифмов.

На практике, когда число под знаком логарифма и основание логарифма легко представляются в виде степени некоторого числа, очень удобно использовать формулу , которая соответствует одному из свойств логарифмов. Рассмотрим пример нахождения логарифма, иллюстрирующий использование этой формулы.

Вычислите логарифм .

Число под знаком логарифма и основание логарифма можно записать в виде степени двойки: и . Таким образом, . Для вычисления полученного логарифма воспользуемся свойством логарифма , получаем (при затруднениях с вычислениями смотрите статью действия с обыкновенными дробями ).

.

Не упомянутые выше свойства логарифмов также используются при вычислении, но об этом поговорим в следующих пунктах.

Зачем в жизни нужны логарифмы?

Я уже говорил, что математики СУПЕРленивые люди? Это правда.

Вот представь себе, им лень умножать и они придумали логарифмы, которые позволяют заменить умножение сложением!

Им еще больше лень возводить в степень и они используют логарифмы, чтобы заменить возведение в степень умножением или делением!

То есть они используют логарифмы, чтобы быстро проделывать громоздкие вычисления.

Пример Найдите корень уравнения.

Здесь для решения данного логарифмического уравнения будем использовать свойство логарифма:

То есть внесем число 3 справа под знак логарифма.

Если показатели степени равны, основания степени равны, то равны числа, получаемые в результате, то есть получим

Делаем проверку:

Получаем:

Ответ:

Степень можно выносить за знак логарифма

log a b p =p log a b (a>0,a≠1,b>0) (7)

И вновь хотелось бы призвать к аккуратности. Рассмотрим следующий пример:

log a (f (x) 2 =2 log a f(x)

Левая часть равенства определена, очевидно, при всех значениях f(х), кроме нуля. Правая часть — только при f(x)>0! Вынося степень из логарифма, мы вновь сужаем ОДЗ. Обратная процедура приводит к расширению области допустимых значений. Все эти замечания относятся не только к степени 2, но и к любой четной степени.

Формула перехода к новому основанию

log a b= log c b log c a (a>0,a≠1,b>0,c>0,c≠1) (8)

Тот редкий случай, когда ОДЗ не изменяется при преобразовании. Если вы разумно выбрали основание с (положительное и не равное 1), формула перехода к новому основанию является абсолютно безопасной.

Если в качестве нового основания с выбрать число b, получим важный частный случай формулы (8):

log a b= 1 log b a (a>0,a≠1,b>0,b≠1) (9)

Десятичным логарифмом числа x называется логарифм по основанию 10. Десятичные логарифмы используются довольно часто, поэтому для них введено специальное обозначение: log10x = lg x. Все перечисленные выше формулы сохраняют актуальность для десятичных логарифмов. Например, lg(xy)=lgx+lgy (x>0,y>0) .

Натуральным логарифмом числа x (обозначение lnx) называется логарифм х по основанию e. Число e — иррациональное, приближенно равно 2,71. Например, ln e = 1. Пользуясь формулой (8), можно любой логарифм свести к десятичным или натуральным логарифмам: log a b= lgb lga = lnb lna (a>0,a≠1,b>0)

Несколько простых примеров с логарифмами

Пример 1. Вычислите: lg2 + lg50. Решение. lg2 + lg50 = lg100 = 2. Мы воспользовались формулой суммы логарифмов (5) и определением десятичного логарифма.

Пример 2. Вычислите: lg125/lg5. Решение. lg125/lg5 = log5125 = 3. Мы использовали формулу перехода к новому основанию (8).

a log a b =b (a>0,a≠1)

log a a=1 (a>0,a≠1)

log a 1=0 (a>0,a≠1)

log a (bc)= log a b+ log a c (a>0,a≠1,b>0,c>0)

log a b c = log a b− log a c (a>0,a≠1,b>0,c>0)

log a b p =p log a b (a>0,a≠1,b>0)

log a b= log c b log c a (a>0,a≠1,b>0,c>0,c≠1)

log a b= 1 log b a (a>0,a≠1,b>0,b≠1)

Сложные задачи

Этот урок будет довольно длинным. В нем мы разберем два довольно серьезных логарифмических уравнения, при решении которых многие ученики допускают ошибки. За свою практику работы репетитором по математике я постоянно сталкивался с двумя видами ошибок:

1. Возникновение лишних корней из-за расширения области определения логарифмов. Чтобы не допускать такие обидные ошибки, просто внимательно следите за каждым преобразованием;
2. Потери корней из-за того, что ученик забыл рассмотреть некоторые «тонкие» случаи — именно на таких ситуациях мы сегодня и сосредоточимся.

Это последний урок, посвященный логарифмическим уравнениям. Он будет длинным, мы разберем сложные логарифмические уравнения. Устраивайтесь поудобней, заварите себе чай, и мы начинаем.

Первое уравнение выглядит вполне стандартно:

Сразу заметим, что оба логарифма являются перевернутыми копиями друг друга. Вспоминаем замечательную формулу:

Однако у этой формулы есть ряд ограничений, которые возникают в том случае, если вместо чисел а и b стоят функции от переменной х:

Эти требования накладываются на основание логарифма. С другой стороны, в дроби от нас требуется 1 ≠ a > 0, поскольку не только переменная a стоит в аргументе логарифма ( следовательно, a > 0), но и сам логарифм находится в знаменателе дроби. Но log _b 1 = 0, а знаменатель должен быть отличным от нуля, поэтому a ≠ 1.

Итак, ограничения на переменную a сохраняется. Но что происходит с переменной b ? С одной стороны, из основания следует b > 0, с другой — переменная b ≠ 1, потому что основание логарифма должно быть отлично от 1. Итого из правой части формулы следует, что 1 ≠ b > 0.

Но вот беда: второе требование ( b ≠ 1) отсутствует в первом неравенстве, посвященном левому логарифму. Другими словами, при выполнении данного преобразования мы должны отдельно проверить, что аргумент b отличен от единицы!

Вот давайте и проверим. Применим нашу формулу:

[Подпись к рисунку]

А теперь, прежде чем идти дальше, выпишем все требования области определения, накладываемые на исходную задачу:

1 ≠ х − 0,5 > 0; 1 ≠ х + 1 > 0

Вот мы и получили, что уже из исходного логарифмического уравнения следует, что и а, и b должны быть больше 0 и не равны 1. Значит, мы спокойно можем переворачивать логарифмическое уравнение:

Предлагаю ввести новую переменную:

В этом случае наша конструкция перепишется следующим образом:

Заметим, что в числителе у нас стоит разность квадратов. Раскрываем разность квадратов по формуле сокращенного умножения:

Дробь равна нулю, когда ее числитель равен нулю, а знаменатель отличен от нуля. Но в числителе стоит произведение, поэтому приравниваем к нулю каждый множитель:

Как видим, оба значения переменной t нас устраивают. Однако на этом решение не заканчивается, ведь нам требуется найти не t , а значение x . Возвращаемся к логарифму и получаем:

Давайте приведем каждое из этих уравнений к канонической форме:

Избавляемся от знака логарифма в первом случае и приравниваем аргументы:

Такое уравнение не имеет корней, следовательно, первое логарифмическое уравнение также не имеет корней. А вот со вторым уравнением все намного интересней:

Решаем пропорцию — получим:

Напоминаю, что при решении логарифмических уравнений гораздо удобней приводить все десятичные дроби обычные, поэтому давайте перепишем наше уравнение следующим образом:

x 2 + x − 1/2 x − 1/2 − 1 = 0;

x 2 + 1/2 x − 3/2 = 0.

Перед нами приведенное квадратное уравнение, оно легко решается по формулам Виета:

Получили два корня — они являются кандидатами на решение исходного логарифмического уравнения. Для того чтобы понять, какие корни действительно пойдут в ответ, давайте вернемся к исходной задаче. Сейчас мы проверим каждый из наших корней на предмет соответствия области определения:

1,5 ≠ х > 0,5; 0 ≠ х > −1.

Эти требования равносильны двойному неравенству:

Отсюда сразу видим, что корень х = −1,5 нас не устраивает, а вот х = 1 вполне устраивает. Поэтому х = 1 — окончательное решение логарифмического уравнения.

Переходим ко второй задаче:

На первый взгляд может показаться, что у всех логарифмов разные основания и разные аргументы. Что делать с такими конструкциями? В первую очередь заметим, что числа 25, 5 и 625 — это степени 5:

А теперь воспользуемся замечательным свойством логарифма. Дело в том, что можно выносить степени из аргумента в виде множителей:

На данное преобразование также накладываются ограничения в том случае, когда на месте b стоит функция. Но у нас b — это просто число, и никаких дополнительных ограничений не возникает. Перепишем наше уравнение:

Получили уравнение с тремя слагаемыми, содержащими знак log. Причем аргументы всех трех логарифмов равны.

Самое время перевернуть логарифмы, чтобы привести их к одному основанию — 5. Поскольку в роли переменной b выступает константа, никаких изменений области определения не возникает. Просто переписываем:

Как и предполагалось, в знаменателе «вылезли» одни и те же логарифмы. Предлагаю выполнить замену переменной:

В этом случае наше уравнение будет переписано следующим образом:

Выпишем числитель и раскроем скобки:

2 ( t + 3) ( t + 2) + t ( t + 2) − 4 t ( t + 3) = 2 ( t 2 + 5 t + 6) + t 2 + 2 t − 4 t 2 − 12 t = 2 t 2 + 10 t + 12 + t 2 + 2 t − 4 t 2 − 12 t = − t 2 + 12

Возвращаемся к нашей дроби. Числитель должен быть равен нулю:

А знаменатель — отличен от нуля:

Последние требования выполняются автоматически, поскольку все они «завязаны» на целые числа, а все ответы — иррациональные.

Итак, дробно-рациональное уравнение решено, значения переменной t найдены. Возвращаемся к решению логарифмического уравнения и вспоминаем, что такое t :

Приводим это уравнение к канонической форме, получим число с иррациональной степенью. Пусть это вас не смущает — даже такие аргументы можно приравнять:

У нас получилось два корня. Точнее, два кандидата в ответы — проверим их на соответствие области определения. Поскольку в основании логарифма стоит переменная х, потребуем следующее:

С тем же успехом утверждаем, что х ≠ 1/125, иначе основание второго логарифма обратится в единицу. Наконец, х ≠ 1/25 для третьего логарифма.

Итого мы получили четыре ограничения:

1 ≠ х > 0; х ≠ 1/125; х ≠ 1/25

А теперь вопрос: удовлетворяют ли наши корни указанным требованиям? Конечно удовлетворяют! Потому что 5 в любой степени будет больше нуля, и требование х > 0 выполняется автоматически.

С другой стороны, 1 = 5 0 , 1/25 = 5 −2 , 1/125 = 5 −3 , а это значит, что данные ограничения для наших корней (у которых, напомню, в показателе стоит иррациональное число) также выполнены, и оба ответа являются решениями задачи.

Итак, мы получили окончательный ответ. Ключевых моментов в данной задаче два:

1. Будьте внимательны при перевороте логарифма, когда аргумент и основание меняются местами. Подобные преобразования накладывают лишние ограничения на область определения.
2. Не бойтесь преобразовывать логарифмы: их можно не только переворачивать, но и раскрывать по формуле суммы и вообще менять по любым формулам, которые вы изучали при решении логарифмических выражений. Однако при этом всегда помните: некоторые преобразования расширяют область определения, а некоторые — сужают.

Логарифм: что это? Все формулы. Простейшие уравнения и неравенства

Сейчас речь пойдет о трех страшных буквах: l o g.Существовать в нашем бытии они просто так не могут. Обязательно должен быть какой-нибудь индекс — число снизу (основание логарифма) и число после букв (аргумент логарифма).

Прежде, чем мы перейдем к тому, что такое логарифм, решим парочку подводящих примеров.

Чтобы справиться с этим примером, мы проговариваем в голове: какое число нужно дважды (т.к. корень квадратный) умножить само на себя, чтобы получить 81.

А этот пример можно решить по алгоритму (решения показательных уравнений), а можно так же провести разговор с самим собой (главное не вслух, я считаю это нормально, но кого-то вы можете напугать разговором с самим собой): сколько раз нужно число 3 умножить само на себя, чтобы получить 27. Постепенным перемножением мы дойдем до ответа.

Тогда, если дело касается логарифма:

можно сказать так: в какую степень нужно возвести 3 (число снизу — основание логарифма), чтобы получить 27 (число слева — аргумент логарифма). Не напоминает выше стоящий пример?

На самом деле в этом и заключается основная формула (определение логарифма):

Логарифм говорит нам (кому-то кричит): логарифм числа «b» по основанию «a» равняется числу «c». Тогда без логарифма это можно сформулировать так: чтобы получить число «b», требуется число «a» возвести в степень «c». Логарифм — это действие, обратное возведению в степень.

У отца log есть два родных сына: ln и lg. Так же, как сыновья отличаются возрастом (мы говорим о максимальной точности), так и эти логарифмы отличаются основанием (числовым индексом снизу).

Данные логарифмы придумали для упрощения записи. На самом деле в прикладной математики именно логарифмы по такому основанию встречаются чаще всех остальных. А мы все в глубине души народ ленивый, так что почему бы себе жизнь не упростить?

Что нужно запомнить: ln — это обычный логарифм только по основанию e ( e — это число Эйлера, e = 2,7182…, мой номер телефона, кстати, — это последние 11 цифр числа Эйлера, так что буду ждать звонка).

А lg — это обычный логарифм по основанию 10 (10ая система — это система счисления, в которой мы живем, столько пальцев на руках у среднего человека. В общем 10 — это как 9, только на 1 больше).

Как мы не можем существовать без еды, воды, интернета… Так и логарифм не представляет свое существование без ОДЗ.

Всегда, когда существует логарифм, должно быть:

«Почему это так?» — это первый вопрос, который я предоставляю тебе. Советую начать с того, что логарифм — это обратное действие от возведения в степень.

А теперь разберем теорию на практике:

В какую степень нужно возвести два (число в основании), чтобы получить шестнадцать (аргумент логарифма).

Два нужно четыре раза умножить само на себя, чтобы получить 16.

Нахождение логарифмов через другие известные логарифмы

Информация этого пункта продолжает тему использования свойств логарифмов при их вычислении. Но здесь основное отличие состоит в том, что свойства логарифмов используются для того, чтобы выразить исходный логарифм через другой логарифм, значение которого известно. Приведем пример для пояснения. Допустим, мы знаем, что log₂3≈1,584963 , тогда мы можем найти, например, log₂6 , выполнив небольшое преобразование с помощью свойств логарифма: log₂6=log₂(2·3)=log₂2+log₂3≈ 1+1,584963=2,584963 .

В приведенном примере нам было достаточно использовать свойство логарифма произведения. Однако намного чаще приходится применять более широкий арсенал свойств логарифмов, чтобы вычислить исходный логарифм через заданные.

Вычислите логарифм 27 по основанию 60 , если известно, что log₆₀2=a и log₆₀5=b .

Итак, нам нужно найти log₆₀27 . Несложно заметить, что 27=3 3 , и исходный логарифм в силу свойства логарифма степени можно переписать как 3·log₆₀3 .

Теперь посмотрим, как log₆₀3 выразить через известные логарифмы. Свойство логарифма числа, равного основанию, позволяет записать равенство log₆₀60=1 . С другой стороны log₆₀60=log60(2 2 ·3·5)= log₆₀2 2 +log₆₀3+log₆₀5= 2·log₆₀2+log₆₀3+log₆₀5 . Таким образом, 2·log₆₀2+log₆₀3+log₆₀5=1 . Следовательно, log₆₀3=1−2·log₆₀2−log₆₀5=1−2·a−b .

Наконец, вычисляем исходный логарифм: log₆₀27=3·log₆₀3= 3·(1−2·a−b)=3−6·a−3·b .

Отдельно стоит сказать о значении формулы перехода к новому основанию логарифма вида . Она позволяет от логарифмов с любыми основаниями переходить к логарифмам с конкретным основанием, значения которых известны или есть возможность их отыскать. Обычно от исходного логарифма по формуле перехода переходят к логарифмам по одному из оснований 2 , e или 10 , так как по этим основаниям существуют таблицы логарифмов, позволяющие с определенной степенью точности вычислять их значения. В следующем пункте мы покажем, как это делается.

Методика решения логарифмических уравнений

Разделы: Математика

Введение

Увеличение умственной нагрузки на уроках математики заставляет задуматься над тем как поддержать у студентов интерес к изучаемому материалу, их активность на протяжении всего урока. В связи с этим ведутся поиски новых эффективных методов обучения и таких методических приемов, которые активизировали бы мысль студентов, стимулировали бы их к самостоятельному приобретению знаний.

Возникновение интереса к математике у значительного числа студентов зависит в большей степени от методики ее преподавания, от того, на сколько умело будет построена учебная работа. Вовремя обращая внимание студентов на то, что математика изучает общие свойства объектов и явлений окружающего мира, имеет дело не с предметами, а с отвлеченными абстрактными понятиями, можно добиться понимания того, что математика не нарушает связи с действительностью, а, напротив, дает возможность изучить ее глубже, сделать обобщенные теоретические выводы, которые широко применяются в практике.

Участвуя в фестивале педагогических идей «Открытый урок» 2004-2005 учебного года, я представила урок-лекцию по теме «Логарифмическая функция» (диплом № 204044). Считаю этот метод наиболее удачным в данном конкретном случае. В результате изучения у студентов имеется подробный конспект и краткая схема по теме, что облегчит им подготовку к следующим урокам. В частности, по теме «Решение логарифмических уравнений», которая полностью опирается на изучение логарифмической функции и ее свойств.

При формировании основополагающих математических понятий важно создать у студентов представление о целесообразности введения каждого из них и возможности их применения. Для этого необходимо, чтобы при формулировке определения некоторого понятия, работе над его логической структурой, рассматривались вопросы об истории возникновения данного понятия. Такой подход поможет студентам осознать, что новое понятие служит обобщением фактов реальной действительности.

История возникновения логарифмов подробно представлена в работе прошлого года.

Учитывая важность преемственности при обучении математике в среднем специальном учебном заведении и в вузе и необходимость соблюдения единых требований к студентам считаю целесообразным следующую методику ознакомления студентов с решением логарифмических уравнений.

Уравнения, содержащие переменную под знаком логарифма (в частности, в основании логарифма), называются логарифмическими. Рассмотрим логарифмические уравнения вида:

(1)

Решение этих уравнений основано на следующей теореме.

Теорема 1. Уравнение равносильно системе

(2)

Для решения уравнения (1) достаточно решить уравнение

(3)

и его решения подставить в систему неравенств

(4),

задающую область определения уравнения (1).

Корнями уравнения (1) будут только те решения уравнения (3), которые удовлетворяют системе (4), т.е. принадлежат области определения уравнения (1).

При решения логарифмических уравнений может произойти расширение области определения (приобретение посторонних корней) или сужение (потеря корней). Поэтому подстановка корней уравнения (3) в систему (4), т.е. проверка решения, обязательна.

Пример 1: Решить уравнение

Оба значения х удовлетворяют условиям системы.

Ответ:

Рассмотрим уравнения вида:

(5)

Их решение основано на следующей теореме

Теорема 2: Уравнение (5) равносильно системе

(6)

Корнями уравнения (5) будут только те корни уравнения , которые

принадлежат области определения, задаваемой условиями .

Логарифмическое уравнение вида (5) можно решить различными способами. Рассмотрим основные из них.

1. ПОТЕНЦИНИРОВАНИЕ (применение свойств логарифма).

Пример 2: Решить уравнение

Решение: В силу теоремы 2 данное уравнение равносильно системе:

Всем условиям системы удовлетворяет лишь один корень. Ответ:

2. ИСПОЛЬЗОВАНИЕ ОПРЕДЕЛЕНИЯ ЛОГАРИФМА .

Пример 3: Найти х, если

Значение х = 3 принадлежит области определения уравнения. Ответ х = 3

3. ПРИВЕДЕНИЕ К КВАДРАТНОМУ УРАВНЕНИЮ.

Пример 4: Решить уравнение

Оба значения х являются корнями уравнения.

Ответ:

Пример 5: Решить уравнение

Решение: Прологарифмируем обе части уравнения по основанию 10 и применим свойство «логарифм степени».

Оба корня принадлежат области допустимых значений логарифмической функции.

Ответ: х = 0,1; х = 100

5. ПРИВЕДЕНИЕ К ОДНОМУ ОСНОВАНИЮ.

Пример 6: Решить уравнение

Воспользуемся формулой и перейдем во всех слагаемых к логарифму по основанию 2:

Тогда данное уравнение примет вид:

Так как , то это корень уравнения.

Ответ: х = 16

6. ВВЕДЕНИЕ ВСПОМОГАТЕЛЬНОЙ ПЕРЕМЕННОЙ.

Решим способом введения вспомогательной переменной уравнение, заданное в примере 6.

Пусть ; тогда

Учитывая, что

После проверки, проведенной устно, легко убеждаемся в правильности найденного ответа.

Многие уравнения, содержащие переменную не только под знаком логарифма или в показателе степени, удобно решать графически.

Графически решением уравнения являются абсциссы точек пересечения графиков функций, заданных в уравнении.

Пример 7: Решить уравнение

Решение: Построим графики функций и y = x

Графики функций не пересекаются, и, значит, уравнение не имеет корней (см. рисунок).

Ответ: корней нет

Пример 8: Найти х, если

Решение: С помощью рассмотренных выше способов корни уравнения найти не удается. Найдем какой-нибудь корень методом подбора.

Пусть, например, х = 10. Проверкой убедимся в том, что 10 — корень уравнения. Действительно,

истинно

Докажем, что других корней данное уравнение не имеет.

Эти корни следует искать во множестве значений х.

Допустимые значения х находятся в промежутке

На этом промежутке функция убывает, а функция возрастает. И, значит, если уравнение имеет решение, то оно единственное.

Логарифмические уравнения и системы

п.1. Методы решения логарифмических уравнений

При решении логарифмических уравнений используются следующие основные методы:
1) переход от логарифмического уравнения к равносильному уравнению (f(x)=g(x)) с системой неравенств, описывающих ОДЗ;
2) графический метод;
3) замена переменной.

п.2. Решение уравнений вида (log_a f(x)=log_a g(x))

Неравенства ( begin f(x)gt 0\ g(x)gt 0 end ) в системе соответствуют ограничению ОДЗ для аргумента логарифмической функции.

Решать логарифмическое уравнение принято в таком порядке:
1) решить систему неравенств и получить промежутки допустимых значений для (x) в явном виде;
2) решить уравнение (f(x)=g(x));
3) из полученных корней выбрать те, что входят в промежутки допустимых значений. Записать ответ.

Однако, если выражения (f(x)) и (g(x)) слишком сложны для явного решения, возможен другой порядок действий:
1) решить уравнение (f(x)=g(x));
2) провести подстановку: полученные корни подставить в выражения для (f(x)) и (g(x)), и проверить, получатся ли положительные значения для этих функций;
3) из корней выбрать те, для которых подстановка оказалась успешной. Записать ответ.

Например:
Решим уравнение (lg(2x+3)+lg(x+4)=lg(1-2x))
Найдем ОДЗ в явном виде:
( begin 2x+3gt 0\ x+4gt 0\ 1-2xgt 0 end Rightarrow begin xgt-frac32\ xgt-4\ xltfrac12 end Rightarrow -frac32lt xltfrac12Rightarrow xinleft(-frac32;frac12right) )
Решаем уравнение:
(lgleft((2x+3)(x+4)right)=lg(1-2x))
((2x+3)(x+4)=1-2x)
(2x^2+11x+12-1+2x=0)
(2x^2+13x+11=0)
((2x+11)(x+1)=0)
( left[ begin x_1=-5,5\ x_2=-1 end right. )
Корень (x_1=-5,5notin left(-frac32;frac12right),) т.е. не подходит.
Корень (x_2=-1in left(-frac32;frac12right)) — искомое решение.
Ответ: -1

п.3. Решение уравнений вида (log_ f(x)=log_ g(x))

Как и в предыдущем случае, можно сначала найти ОДЗ, а потом решать уравнение.
Или же, можно решить уравнение, а потом проверить требования ОДЗ прямой подстановкой полученных корней.

Например:
Решим уравнение (log_(x^2-4)=log_(2-x))
Найдем ОДЗ в явном виде:
( begin x^2-4gt 0\ 2-xgt 0\ x+5gt 0\ x+5ne 1 end Rightarrow begin xlt -2cup xgt 2\ xlt 2\ xgt -5\ xne -4 end Rightarrow begin -5lt xlt -2\ xne -4 end Rightarrow xin (-5;-4)cup(-4;-2) )
Решаем уравнение:
(x^2-4=2-x)
(x^2+x-6=0)
((x+3)(x-2)=0)
( left[ begin x_1=-3\ x_2=2 — text <не подходит>end right. )
Ответ: -3

В логарифмическом уравнении перед отбрасыванием логарифмов основания обязательно должны быть равны. Не забывайте это проверять!

Например:
Решим уравнение (log_<2>(x+1)=log_<4>(x+3))
Основания (2ne 4), и нельзя сразу написать (x+1=x+3).
Нужно привести к одному основанию, преобразовав левую часть:
(log_2(x+1)=log_<2^2>(x+1)^2=log_4(x+1)^2)
Тогда исходное уравнение примет вид: (log_4(x+1)^2=log_4(x+3))
И теперь: ((x+1)^2=x+3)
(x^2+x-2=0)
((x+2)(x-1)=0)
( left[ begin x_1=-2\ x_2=1 end right. )
Что касается ОДЗ, то её нужно искать для исходного уравнения:
( begin x+1gt 0\ x+3gt 0 end Rightarrow begin xgt -1\ xgt -3 end Rightarrow xgt -1 )
Корень (x_1=-2lt -1) — не подходит.
Ответ: 1

Преобразования могут расширить первоначальную область допустимых значений (например, при возведении в квадрат), и вы включите в решение лишние корни.
Преобразования также могут сузить ОДЗ (например, при взятии корня), и некоторые решения окажутся потеряны.
Поэтому ОДЗ определяется для исходного уравнения (выражения, неравенства), а не того, которое получено после преобразований.

п.4. Примеры

Пример 1. Решите уравнения:
a) ( log_2(x+1)-log_2(x-1)=1 )
ОДЗ: ( begin x+1gt 0\ x-1gt 0 end Rightarrow begin xgt -1\ xgt 1 end Rightarrow xgt 1 )
(log_2left((x+1)(x-1)right)=log_22)
(x^2-1=2Rightarrow x^2 =3)
( left[ begin x_1=-sqrt<3>lt 2 — text<не подходит>\ x_2=sqrt <3>end right. )
Ответ: (sqrt<3>)

б) ( 2log_5(x-1)=log_5(1,5x+1) )
ОДЗ: ( begin x-1gt 0\ 1,5x+1gt 0 end Rightarrow begin xgt 1\ xgt-frac23 end Rightarrow xgt 1 )
Преобразуем: (2log_5(x-1)=log_5(x-1)^2)
Получаем: (log_5(x-1)^2=log_5(1,5x+1))
((x-1)^2=1,5x+1)
(x^2-2x+1-1,5x-1=0Rightarrow x^2-3,5x=0Rightarrow x(x-3,5)=0)
( left[ begin x_1=0lt 1 — text<не подходит>\ x_2=3,5 end right. )
Ответ: 3,5

в) ( log_3(3-x)+log_3(4-x)=1+2log_3 2 )
ОДЗ: ( begin 3-xgt 0\ 4-xgt 0 end Rightarrow begin xlt 3\ xlt 4 end Rightarrow xlt 3 )
Преобразуем: (1+2log_3 2=log_3 3+log_3 2^2=log_3(3cdot 4)=log_3 12)
Получаем: (log_3left((3-x)(4-x)right)=log_3 12)
((3-x)(4-x)=12Rightarrow 12-7x+x^2=12Rightarrow x(x-7)=0)
( left[ begin x_1=0\ x_2=7gt 3 — text <не подходит>end right. )
Ответ: 0

г) ( log_2^2x+log_2 x^2+1=0 )
ОДЗ: (xgt 0)
(log_2x^2=2log_2x)
Получаем: (log_2^2x+2log_2x+1=0)
Замена: (t=log_2 x)
(t^2+2t+1=0Rightarrow(t+1)^2=0Rightarrow t=-1)
Возвращаемся к исходной переменной: (log_2x=-1)
(x=2^<-1>=frac12)
Ответ: (frac12)

д) ( x^<lg x>=10 )
ОДЗ: (xgt 0)
Замена: (t=lg ⁡x). Тогда (x=10^t)
Подставляем:
((10^t)^t=10Rightarrow 10^=10^1Rightarrow t^2=1Rightarrow t=pm 1)
Возвращаемся к исходной переменной:
( left[ begin lg x=-1\ lg x=1 end right. Rightarrow left[ begin x=10^<-1>\ x=10 end right. Rightarrow left[ begin x_1=0,1\ x_2=10 end right. )
Оба корня подходят.
Ответ:

e) ( sqrtcdot log_5(x+3)=0 )
ОДЗ: ( begin xgeq 0\ x+3gt 0 end Rightarrow begin xgeq 0\ xgt -3 end Rightarrow xgeq 0 )
( left[ begin sqrt=0\ log_5(x+3)=0 end right. Rightarrow left[ begin x=0\ x+3=5^0=1 end right. Rightarrow left[ begin x_1=0\ x_2=-2lt 0 — text <не подходит>end right. )
Ответ: 0

ж) ( log_<5x-2>2+2log_<5x-2>x=log_<5x-2>(x+1) )
ОДЗ: ( begin xgt 0\ x+1gt 0\ 5x-2gt 0\ 5x-2ne 1 end Rightarrow begin xgt 0\ xgt -1\ xgtfrac25\ xnefrac35 end Rightarrow begin xgtfrac25\ xnefrac35 end )
Преобразуем: (log_<5x-2>2+2log_<5x-2>x=log_<5x-2>(2x^2))
Подставляем: (log_<5x-2>(2x^2)=log_<5x-2>(x+1))
( 2x^2=x+1Rightarrow 2x^2-x-1=0Rightarrow (2x+1)(x-1)=0 Rightarrow left[ begin x_1=-frac12 — text<не подходит>\ x_2=1 end right. )
Ответ: 1

Пример 2*. Решите уравнения:
a) ( log_4log_2log_3(2x-1)=frac12 )
ОДЗ: ( begin 2x-1gt 0\ log_3(2x-1)gt 0\ log_2log_3(2x-1)gt 0 end Rightarrow begin xgtfrac12\ 2x-1gt 3^0\ log_3(2x-1)gt 2^0 end Rightarrow begin xgtfrac12\ xgt 1\ 2x-1gt 3^1 end Rightarrow )
( Rightarrow begin xgtfrac12\ xgt 1\ xgt 2 end Rightarrow xgt 2 )
Решаем:
(log_2log_3(2x-1)=4^<1/2>=2)
(log_3(2x-1)=2^2=4)
(2x-1=3^4=81)
(2x=82)
(x=41)
Ответ: 41

б) ( log_2(9-2^x)=25^<log_5sqrt<3-x>> )
ОДЗ: ( begin 9-2xgt 0\ 3-xgt 0 end Rightarrow begin 2^xlt 9\ xlt 3 end Rightarrow begin xltlog_2 9\ xlt 3 end Rightarrow xlt 3 )
Преобразуем: (25^<log_5sqrt<3-x>>=25^<log_<5^2>(sqrt<3-x>)^2>=25^<log_<25>(3-x)>=3-x)
Подставляем: (log_2(9-2^x)=3-x)
(9-2^x=2^<3-x>)
(9-2^x-frac<8><2^x>=0)
Замена: (t=2^xgt 0)
( 9-t-frac8t=0Rightarrow frac<-t^2+9t-8>=0Rightarrow begin t^2-9t+8gt 0\ tne 0 end Rightarrow begin (t-1)(t-8)=0\ tne 0 end Rightarrow left[ begin t_1=1\ t_2=8 end right. )
Возвращаемся к исходной переменной:
( left[ begin 2^x=1\ 2^x=8 end right. Rightarrow left[ begin 2^x=2^0\ 2^x=2^3 end right. Rightarrow left[ begin x_1=0\ x_2=3 end right. )
По ОДЗ (xlt 3), второй корень не подходит.
Ответ: 0

в) ( lgsqrt+lgsqrt<2x-3>+1=lg 30 )
ОДЗ: ( begin x-5gt 0\ 2x-3gt 0 end Rightarrow begin xgt 5\ xgtfrac32 end Rightarrow xgt 5 )
Преобразуем: (lg 30-1=lg 30-lg 10=lgfrac<30><10>=lg 3)
Подставляем: (lgsqrt+lgsqrt<2x-3>=lg 3)
(frac12lg(x-5)+frac12lg(2x-3)=lg 3 |cdot 2)
(lg(x-4)+lg(2x-3)=2lg 3)
(lgleft((x-5)(2x-3)right)=lg 3^2)
((x-5)(2x-3)=9Rightarrow 2x^2-13x+15-9=0 Rightarrow 2x^2-13x+6=0)
( (2x-1)(x-6)=0Rightarrow left[ begin x_1=frac12lt 5 — text<не подходит>\ x_2=6 end right. )
Ответ: 6

г) ( frac<1><lg x>+frac<1><lg 10x>+frac<3><lg 100x>=0 )
ОДЗ: ( begin xgt 0\ lg xne 0\ lg 10xne 0\ lg 100xne 0 end Rightarrow begin xgt 0\ xne 1\ 10xne 1\ 100xne 1 end Rightarrow begin xgt 0\ xneleft<frac<1><100>;frac<1><10>;1right> end )
Преобразуем: (lg 10x=lg 10+lg x=1+lg 10)
(lg 100x=lg 100+lg x=2+lg x)
Подставляем: (frac<1><lg x>+frac<1><1+lg x>+frac<3><2+lg x>=0)
Замена: (t=lg x)
begin frac1t+frac<1><1+t>+frac<3><2+t>=0Rightarrow frac1t+frac<1><1+t>=-frac<3><2+t>Rightarrow frac<1+t+t>=-frac<3><2+t>Rightarrow (1+2t)(2+t)=(1+t)\ 2_5t+2t^2=-3t-3t^2Rightarrow 5t^2+8t+2=0\ D=8^2-4cdot 5cdot 2=24, t=frac<-8pm 2sqrt<6>><10>=frac<-4pm sqrt<6>> <5>end Возвращаемся к исходной переменной:
$$ left[ begin lg x=frac<-4- sqrt<6>><5>\ lg x=frac<-4+ sqrt<6>> <5>end right. Rightarrow left[ begin x=10frac<-4- sqrt<6>><5>\ x=10frac<-4+ sqrt<6>> <5>end right. $$ Оба корня подходят.
Ответ: (left<10frac<-4pmsqrt<6>><5>right>)

e) ( x^<frac<lg x+7><4>>=10^ <lg x+1>)
ОДЗ: (xgt 0)
Замена: (t=lg x.) Тогда (x=10^t)
Подставляем: begin (10^t)^<frac<4>>=10^\ frac<4>=t+1Rightarrow t(t+7)=4(t+1)Rightarrow t^2+7t-4t-4=0\ t^2+3t-4=0Rightarrow (t+4)(t-1)=0Rightarrow left[ begin t_1=-4\ t_2=1 end right. end Возвращаемся к исходной переменной:
$$ left[ begin lg x=-4\ lg x=1 end right. Rightarrow left[ begin x=10^<-4>\ x=10 end right. Rightarrow left[ begin x_1=0,0001\ x_2=10 end right. $$ Оба корня подходят.
Ответ: (left<0,0001; 10right>)

ж) ( 4^<log_3(1-x)>=(2x^2+2x+5)^ <log_3 2>)
ОДЗ: ( begin 1-xgt 0\ 2x^2+2x+5gt 0 end Rightarrow begin xlt 1\ Dlt 0, xinmathbb end Rightarrow xlt 1 )
По условию: begin log_3(1-x)=log_4left((2x^2+2x+5)^<log_32>right)\ log_3(1-x)=log_32cdotlog_4(2x^2+2x+5) end Перейдем к другому основанию: $$ frac<lg(1-x)><lg 3>=frac<lg 2><lg 3>cdotfrac<lg(2x^2+2x+5)><lg 4> |cdot lg 3 $$ (frac<lg 2><lg 4>=frac<lg 2><lg 2^2>=frac<lg 2><2lg 2>=frac12) begin lg(1-x)=frac12cdotlg(2x^2+2x+5) |cdot 2\ 2lg(1-x)=lg(2x^2+2x+5)\ lg(1-x)^2=lg(2x^2+2x+5)\ (1-x)^2=2x^2+2x+5\ 1-2x+x^2=2x^2+2x+5\ x^2+4x+4=0\ (x+2)^2=0\ x=-2 end Ответ: -2

Пример 3. Решите систему уравнений:
a) ( begin lg x+lg y=lg 2\ x^2+y^2=5 end )
ОДЗ: ( begin xgt 0\ ygt 0 end )
Из первого уравнения: (lg(xy)=lg 2Rightarrow xy=2)
Получаем: ( begin xy=2\ x^2+y^2=5 end Rightarrow begin y=frac2x\ x^2+left(frac2xright)^2-5=0 end )
Решаем биквадратное уравнение: begin x^2+frac<4>-5=0Rightarrowfrac=0Rightarrow begin x^4-5x^2+4=0\ xne 0 end \ (x^2-4)(x^2-1)=0Rightarrow left[ begin x^2=4\ x^2=1 end right. Rightarrow left[ begin x=pm 2\ x=pm 1 end right. end Согласно ОДЗ, оставляем только положительные корни.
Получаем две пары решений: ( left[ begin begin x=1\ y=frac2x=2 end \ begin x=2\ y=frac22=1 end end right. )
Ответ: (left<(1;2),(2,1)right>)

б) ( begin x^=27\ x^<2y-5>=frac13 end )
ОДЗ: (xgt 0, xne 1)
Логарифмируем: ( begin y+1=log_x27=log_x3^3=3log_x3\ 2y-5=log_xfrac13=log_x3^<-1>=-log_x3 end )
Замена: (z=log_x3) begin begin y+1=3z\ 2y-5=-z |cdot 3 end Rightarrow begin y+1=3z\ 6y-15=-3z end Rightarrow begin 7y-14=0\ z=5-2y end Rightarrow begin y=2\ z=1 end end Возвращаемся к исходной переменной: $$ begin y=2\ log_x3=1 end Rightarrow begin x^1=3\ y=2 end Rightarrow begin x=3\ y=2 end $$
Ответ: (3;2)

в*) ( begin 3(log_y x-log_x y)=8\ xy=16 end )
ОДЗ: ( begin xgt 0, xne 1\ ygt 0, yne 1 end )
Сделаем замену (t=log_x y). Тогда (log_y x=frac<1><log_x y>=frac1t)
Подставим в первое уравнение и решим его: begin 3left(frac1t-tright)=8Rightarrowfrac<1-t^2>=frac83Rightarrow begin 3(1-t^2)=8t\ tne 0 end\ 3t^2+8t-3=0Rightarrow (3t-1)(t+3)=0Rightarrow left[ begin t_1=frac13\ t_2=-3 end right. end Прологарифмируем второе уравнение по (x): $$ log_x(xy)=log_x16Rightarrow 1+log_x y=log_x16Rightarrow 1+t=log_x 16 $$ Получаем: begin left[ begin begin t=frac13\ log_x16=1+t=frac43 end \ begin t=-3\ log_x16=1+t=-2 end end right. Rightarrow left[ begin begin t=frac13\ x^<frac43>=16 end \ begin t=-3\ x^<-2>=16 end end right. Rightarrow left[ begin begin t=frac13\ x=(2^4)^<frac34>=2^3=8 end \ begin t=-3\ x=(16)^<-frac12>=frac14 end end right. end Возвращаемся к исходной переменной: begin left[ begin begin x=8\ log_x y=frac13 end \ begin x=frac14\ log_x y=-3 end end right. Rightarrow left[ begin begin x=8\ y=8^<frac13>=2 end \ begin x=frac14\ y=left(frac14right)^<-3>=64 end end right. end
Ответ: (left<(8;2),left(frac14; 64right)right>)

г*) ( begin (x+y)cdot 3^=frac<5><27>\ 3log_5(x+y)=x-y end )
ОДЗ: (x+ygt 0)
Прологарифмируем первое уравнение по 3: begin log_3left((x+y)cdot 3^right)=log_3frac<5><27>\ log_3(x+y)+(y-x)=log_3frac<5><27>\ log_3(x+y)-log_3frac<5><27>=x-y end Получаем:(x-y=3log_5(x+y)=log_3(x+y)-log_3frac<5><27>)
Решим последнее уравнение относительно (t=x+y) begin 3log_5 t=log_3 t-log_3frac<5><27>\ 3cdotfrac<log_3t><log_35>-log_3t=-log_3frac<5><27>\ log_3tcdotleft(frac<3><log_35>-1right)=-log_3frac<5><27>\ log_3t=-frac<log_3frac<5><27>><frac<3><log_35>-1>=-frac<(log_35-3)log_35><3-log_35>=log_35\ t=5 end Тогда: (x-y=3log_5t=3log_55=3)
Получаем систему линейных уравнений: begin begin x+y=5\ x-y=3 end Rightarrow begin 2x=5+3\ 2y=5-3 end Rightarrow begin x=4\ y=1 end end Требование ОДЗ (x+y=4+1gt 0) выполняется.
Ответ: (4;1)

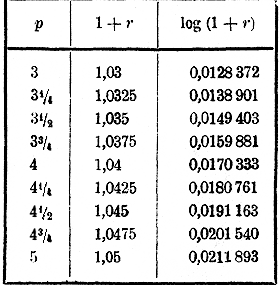
274. Замечания.

а) Если в выражении, которое требуется вычислить, встречается сумма или разность чисел, то их надо находить без помощи таблиц обыкновенным сложением или вычитанием. Напр.:

log (35 +7,24)⁵ = 5 log (35 + 7,24) = 5 log 42,24.

б) Умея логарифмировать выражения, мы можем, обратно, по данному результату логарифмирования найти то выражение, от которого получился этот результат; так, если

log х = log a + log b — 3 log с,

то легко сообразить, что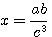

в) Прежде чем перейти к рассмотрению устройства логарифмических таблиц, мы укажем некоторые свойства десятичных логарифмов, т.е. таких, в которых за основание принято число 10 ( только такие логарифмы употребляются для вычислений).

Глава вторая.

Свойства десятичных логарифмов.

275. а) Так как 10¹ = 10,  10² = 100,  10³ =1000,   10⁴ = 10000 и т. д., то  log 10 = 1, log 100 = 2, log 1000 = 3, log 10000 = 4, и т. д.

Значит, логарифм целого числа, изображаемого единицею с нулями, есть целое положительное число, содержащее столько единиц, сколько нулей в изображении числа.

Таким образом: log 100 000 = 5, log 1000 000 = 6, и т. д.

б) Так как

то:

log 0,1 = —l;     log 0,01 = — 2;     log 0,001 == —3;    log 0,0001 = — 4, и т. д.

Значит, логарифм десятичной дроби, изображаемой единицею с предшествующими нулями, есть целое отрицательное число содержащее столько отрицательных единиц, сколько нулей в изображении дроби, считая в том числе и 0 целых.

Таким образом: log 0,00001= — 5, log 0,000001 = —6, и т. д.

в) Возьмем целое число, не изображаемое единицею с нулями, напр. 35, или целое число с дробью, напр. 10,7. Логарифм такого числа не может быть целым числом, так как, возвысив 10 в степень с целым показателем (положительным или отрицательным), мы получим 1 с нулями (следующими за 1, или ей предшествующими). Предположим теперь, что логарифм такого числа  есть какая-нибудь дробь ^a/_b. Тогда мы имели
бы равенства

Но эти равенства невозможны, как как 10^а есть 1 с нулями, тогда как степени 35^b и 10,7^b ни при каком показателе b не могут дать 1 c нулями. Значит, нельзя допустить, чтобы log 35 и log 10,7 были равны дробям. Но из свойств логарифмической функции мы знаем (§ 270, 2), что всякое положительное число имеет логарифм; следовательно, каждое из чисел 35
и 10,7 имеет свой логарифм, и так как он не может быть ни числом целым, ни числом дробным, то он есть число иррациональное и, следовательно,
не может быть выражен точно посредством цифр. Обыкновенно иррациональные логарифмы выражают приближенно в виде десятичной дроби с несколькими десятичными знаками. Целое число этой дроби (хотя бы это было „0 целых») называется характеристикой, а дробная часть — мантиссой логарифма. Если, напр., логарифм есть 1,5441, то характеристика его равна 1, а мантисса есть 0,5441.

г) Возьмем какое-нибудь целое или смешанное число, напр. 623 или 623,57. Логарифм такого числа состоит из характеристики и мантиссы. Оказывается, что десятичные логарифмы обладают тем удобством, что характеристику их мы всегда можем найти по одному виду числа. Для этого сосчитаем, сколько цифр в данном целом числе, или в целой части смешанного числа, В наших примерах этих цифр 3. Поэтому каждое из чисел 623 и 623,57  больше
 100, но меньше  1000; значит, и логарифм каждого из них больше log 100, т. е. больше 2, но меньше log 1000, т. е. меньше 3 (вспомним, что большее число имеет  и больший логарифм). Следовательно, log 623 = 2,…, и log 623,57 = 2,… (точки заменяют собою неизвестные мантиссы).

Подобно этому найдем:

10 < 56,7 < 100 1 < log56,7 < 2 log 56,7 = 1,…

1000 < 8634 < 10 000 3 < log8634 < 4 log 8634 = 3,…

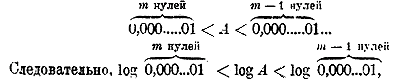
Пусть вообще в данной целом числе, или в целой части данного смешанного числа, содержится m цифр. Так как самое малое целое число, содержащее m цифр, есть 1 с m — 1 нулями на конце, то (обозначая данное число N) можем написать неравенства:

и следовательно,

m — 1 < log N < m,

и потому

log N = (m — 1) +  положительная дробь.

Значит, характеристика logN = m — 1.

Мы видим таким образом, что характеристика логарифма целого или смешанного числа содержит столько положительных единиц, сколько цифр в целой части числа без одной.

Заметив это,  мы   можем   прямо   писать:  

 log 7,205 = 0,…;  log 83 = 1,…;    log 720,4 = 2,…   и т. п.

д) Возьмем несколько десятичных дробей, меньших 1 (т. е. имеющих 0 целых): 0,35; 0,07; 0,0056; 0,0008, и т. п.

Таким образом, каждый из этих логарифмов заключен между  двумя целыми отрицательными числами, различающимися на одну единицу; поэтому каждый из них равен меньшему из этих отрицательных чисел, увеличенному на некоторую положительную дробь. Напр., log0,0056= —3 + положительная дробь. Предположим, что эта дробь будет 0,7482. Тогда, значит:

log 0,0056 = — 3 + 0,7482 (= — 2,2518).

Такие суммы, как — 3 + 0,7482, состоящие из целого oтрицательного числа.и положительной десятичной дроби, условились при логарифмических вычислениях писать сокращенно так: 3,7482  ( Такое число читается: 3 с минусом, 7482 десятитысячных.), т. е. ставят знак минус над характеристикой с целью показать, что он относится только к этой характеристике, а не к мантиссе, которая
остается положительной. Таким образом, из приведенной выше таблички видно, что

log 0,35 == 1,….; log 0,07 = 2,….; log 0,0008 = 4,….

Пусть вообще . есть десятичная дробь, у которой перед первой значащей цифрой α стоит m нулей, считая в том числе и 0 целых. Тогда, очевидно, что

т. е.

— m < log A < — (m — 1).

Так как из двух целых чисел:— m  и — (m — 1) меньшее есть — m , то

log А =   — m + положительная дробь,

и потому характеристика log А =   — m   (при положительной мантиссе).

Таким образом, характеристика логарифма десятичной дроби, меньшей 1, содержит в себе столько отрицательных единиц, сколько нулей в изображении десятичной дроби перед первой значащей цифрой, считая в том числе и нуль целых; мантисса же такого логарифма положительна.

е) Умножим какое-нибудь число N (целое или дробное — всe равно) на 10, на 100 на 1000…, вообще на 1 c нулями. Посмотрим, как от этого изменится log N. Так как логарифм произведения равен сумме логарифмов сомножителей, то

log (N•10) = log N +  log 10 =  log N +  1;

log (N•100) = log N +  log 100 =  log N +  2;

log (N•1000) = log N +  log 1000 =  log N +  3;  и т. д.

Когда к log N  мы прибавляем какое-нибудь целое число, то это число мы может всегда прибавлять к характеристике, а не к мантиссе.

Так, если log N = 2,7804, то 2,7804 + 1 =3,7804;  2,7804 + 2 = 4,7801 и т. п.;

или если log N = 3,5649, то 3,5649 + 1 = 2,5649; 3,5649  + 2 = 1,5649, и т. п.

Поэтому:

От умножения числа на 10, 100, 1000,.., вообще на 1 с нулями, мантисса логарифма не изменяется, а характеристика увеличивается на столько единиц, сколько нулей  во множителе.

Подобно этому, приняв во внимание, что логарифм частного равен логарифму делимого без логарифма делителя, мы получим:

 log ^N/₁₀ = log N— log 10 = log N —1;

 log ^N/₁₀₀ = log N— log 100 = log N —2;

 log ^N/₁₀₀₀ = log N— log 1000 = log N —3; и т. п.

Если условимся при вычитании целого числа из логарифма вычитать это целое число всегда из характеристики, а мантиссу оставлять без изменения, то можно сказать:

От деления числа на 1 с нулями мантисса логарифма не изменяется, а характеристика уменьшается   на  столько  единиц, сколько нулей в делителе.

276. Следствия. Из свойства (е) можно вывести следующие два следствия:

а) Мантисса логарифма десятичного числа не изменяется от перенесения в числе запятой, потому что перенесение запятой равносильно умножению или делению на 10, 100, 1000 и т. д. Таким образом, логарифмы чисел:

0,00423,    0,0423,  4,23,    423

отличаются только характеристиками, но не мантиссами (при условии, что все мантиссы положительны).

б) Мантиссы чисел, имеющих одну и ту же значащую часть, но отличающихся только нулями на конце, одинаковы: так, логарифмы чисел: 23, 230, 2300, 23 000 отличаются только характеристиками.

Замечание. Из указанных свойств десятичных логарифмов видно, что характеристику логарифма целого числа и десятичной дроби мы можем находить без помощи таблиц (в этом заключается большое удобство десятичных логарифмов); вследствие этого в логарифмических таблицах помещаются только одни мантиссы; кроме того, так как нахождение логарифмов дробей сводится к нахождению логарифмов целых чисел (логарифм дроби = логарифму числителя без логарифма знаменателя),
то в таблицах помещаются мантиссы
логарифмов только целых чисел.

Глава третья.

Устройство и употребление четырехзначных таблиц.

277.  Системы логарифмов. Системою логарифмов называется совокупность  логарифмов, вычисленных  для  ряда  последовательных целых чисел по одному и тому же основанию. Употребительны две системы: система обыкновенных или десятичных логарифмов, в которых за основание взято число 10, и система так называемых натуральных логарифмов, в которых за основание (по некоторым причинам, которые уясняются в  других  отделах  математики)  взято
  иррациональное
  число 2,7182818…  Для вычислений употребляются десятичные логарифмы, вследствие тех удобств, которые были нами указаны, когда мы перечисляли свойства таких логарифмов.

Натуральные логарифмы называются также Неперовыми по имени изобретателя логарифмов, шотландского математика Непера (1550—1617 гг.), а десятичные логарифмы — Бригговыми по имени профессора Бригга (современника и друга Непера), впервые составившего таблицы этих логарифмов ¹⁾.

278.  Преобразование  отрицательного  логарифма  в  такой, у которого мантисса положительна, и обратное преобразование. Мы видели, что  логарифмы чисел, меньших  1, отрицательны. Значит, они состоят из отрицательной характеристики и отрицательной мантиссы. Такие логарифмы всегда можно преобразовать так, что у них мантисса будет положительная, а характеристика   останется   отрицательной.  Для   этого   достаточно
прибавить  к мантиссе  положительную  единицу, а к характеристике — отрицательную (от чего, конечно, величина логарифма не  изменится).  

Если, напр.,  мы  имеем   логарифм — 2,0873,  то можно написать:

— 2,0873 = — 2 — 1 + 1 — 0,0873 = — (2 + 1) + (1 — 0,0873) = — 3 + 0,9127,

или сокращенно:

Обратно, всякий логарифм с отрицательной характеристикой и положительной мантиссой можно превратить в отрицательный. Для этого достаточно к положительной мантиссе приложить отрицательную единицу, а к отрицательной характеристике — положительную ²⁾: так, можно написать:

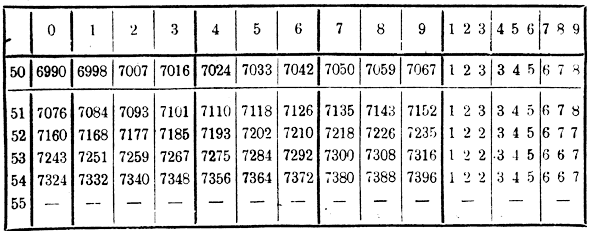
279. Описание четырехзначных таблиц. Для решения большинства практических задач вполне достаточны четырехзначные таблицы, обращение с которыми весьма просто ³⁾. Таблицы эти (с надписью на верху их „логарифмы») помещены в конце этой книги, а небольшая часть их (для объяснения расположения) напечатана на этой странице. В них содержатся мантиссы

Логарифмы.

логарифмов всех целых чисел от 1 до 9999 включительно, вычисленные с четырьмя десятичными знаками, причем последний из этих знаков увеличен на 1 во всех тех случаях, когда 5-й десятичный знак должен был бы оказаться 5 или более 5; следовательно, 4-значные таблицы дают приближенные мантиссы с точностью до ¹/₂ десятитысячной доли (с недостатком или с избытком).

Так как характеристику логарифма целого числа или десятичной дроби мы можем, на основании свойств десятичных логарифмов, проставить непосредственно, то из таблиц мы должны взять только мантиссы; при этом надо вспомнить, что положение запятой в десятичном числе, а также число нулей, стоящих в конце числа, не имеют влияния на величину мантиссы. Поэтому при нахождении мантиссы по данному числу мы отбрасываем в этом числе запятую, а также и нули на конце его, если таковые есть,
и находим мантиссу образовавшегося после этого целого числа. При этом могут представиться следующие случаи.

1)  Целое число состоит из 3-х цифр. Напр., пусть надо найти мантиссу логарифма числа 536. Первые две цифры этого числа, т. е.  53, находим  в  таблицах  в   первом  слева  вертикальном столбце (см. таблицу). Найдя  число   53,   продвигаемся   от   него   по   горизонтальной строке  вправо до пересечения  этой строчки с вертикальным столбцом,
проходящим через ту из цифр 0, 1, 2, 3,… 9, поставленных наверху (и внизу) таблицы, которая представляет собою 3-ю   цифру  данного числа, т. е. в  нашем  примере  цифру 6. В пересечении получим мантиссу 7292 (т. е. 0,7292), принадлежащую логарифму  числа   536. Подобно этому для числа 508 найдем мантиссу 0,7059, для числа 500 найдем 0,6990 и т. п.

2)  Целое число состоит из 2-х или из 1-й цифры. Тогда мысленно приписываем к этому  числу  один или два нуля и находим мантиссу для образовавшегося таким образом трехзначного числа. Напр., к числу 51 приписываем один нуль, от чего получаем 510 и находим мантиссу 7070; к числу 5 приписываем 2 нуля и находим мантиссу 6990 и т. д.

3) Целое число выражается 4  цифрами. Напр., надо найти мантиссу log 5436. Тогда сначала находим в таблицах, как было сейчас указано, мантиссу для числа, изображенного первыми 3-мя цифрами данного числа, т. е. для 543 (эта мантисса будет 7348); затем продвигаемся от найденной мантиссы по горизонтальной строке направо (в правую часть таблицы, расположенную за жирной вертикальной чертой) до пересечения с вертикальным столбцом, проходящим через ту из цифр:
1, 2 3,… 9, стоящих на верху (и в низу) этой части таблицы, которая представляет собою 4-ю цифру данного числа, т. е. в нашем примере цифру 6. В пересечении находим поправку (число 5), которую надо приложить в уме к мантиссе 7348, чтобы получить мантиссу числа 5436; мы получим таким образом мантиссу 0,7353.

4) Целое число выражается 5-ю или более цифрами. Тогда отбрасываем все цифры, кроме первых 4-х, и берем приближенное четырехзначное число, причем последнюю цифру этого числа увеличиваем на 1 в том. случае, когда отбрасываемая 5-я цифра числа есть 5 или больше 5. Так, вместо 57842 мы берем 5784, вместо 30257 берем 3026, вместо 583263 берем 5833 и т. и. Для этого округленного четырехзначного числа находим мантиссу так, как было сейчас объяснено.

Руководствуясь этими указаниями, найдем для примера логарифмы следующих чисел:

36,5; 804,7; 0,26; 0,00345;  7,2634; 3456,06.

Прежде  всего, не обращаясь пока к таблицам, проставим одни характеристики, оставляя место для мантисс, которые выпишем после:

log   36,5   = 1,….                     log 0,00345 = 3,….

log 804,7   = 2,….                     log 7,2634   = 0,….

log     0,26 = 1,….                     log 3456,86 = 3,….

Далее по таблицам выставляем прямо мантиссы:

log  36,5   = 1,5623;               log 0,00345 =  3,5378;

log 804,7   =  2,9057;              log 7,2634  = 0,8611;

log     0,26 = 1,4150;               log 3456,86 = 3,5387.

280. Замечание. В некоторых четырехзначных таблицах  (напр, в таблицах В. Лорченко и Н. Оглоблина, С. Глазенапа, Н. Каменьщикова) поправки на 4-ю цифру данного числа не помещены. Имея дело с такими таблицами, приходится поправки эти находить при помощи простого вычисления, которое можно выполнять на основании следующей истины: если числа превосходят 100, а разности между ними меньше 1, то без чувствительной погрешности можно принять, что разности
между логарифмами пропорциональны разностям между соответствующими числами ⁴⁾. Пусть, напр., надо найти мантиссу, соответствующую числу 5367. Мантисса эта, конечно, та же самая, что и для числа 536,7. Находим в таблицах для числа 536 мантиссу 7292. Сравнивая эту мантиссу с соседней вправо мантиссой 7300, соответствующей числу 537, мы замечаем, что если число 536 увеличится на 1, то мантисса его увеличится на 8 десятитысячных (8 есть так называемая табличная
разность между двумя соседними мантиссами); если же число 536 увеличится на 0,7, то мантисса его увеличится не на 8 десятитысячных, а на некоторое меньшее число х десятитысячных, которое, согласно допущенной пропорциональности, должно удовлетворять пропорции:

х : 8 = 0,7 : 1; откуда х = 8•07 = 5,6,

что по округлении составляет 6 десятитысячных. Значит, мантисса для числа 536,7 (и следовательно, для числа 5367) будет: 7292 + 6 = 7298.

Заметим, что нахождение по двум рядом стоящим в таблицах числам промежуточного числа называется интерполированием. Интерполирование, описанное здесь, называется пропорциональным, так как оно основано на допущении, что изменение логарифма пропорционально изменению числа. Оно называется также линейным, так как предполагает, что графически изменение логарифмической
функции выражается прямою линией.

281. Предел погрешности приближенного логарифма. Если число, которого логарифм отыскивается, есть число т о ч н о е, то за предел погрешности его логарифма, найденного но 4-значным таблицам, можно, как мы говорили в § 279, принять ¹/₂ десятитысячной доли. Если же данное число не точное, то к этому пределу погрешности надо еще добавить предел другой погрешности, происходящей
от неточности самого числа. Доказано (мы опускаем это доказательство), что за такой предел можно принять произведение

a (d +1) десятитысячных.,

в котором а есть предел погрешности самого неточного числа в предположении, что в его целой части взяты 3 цифры, a d табличная разность мантисс, соответствующих двум последовательным трехзначным  числам, между которыми заключается данное неточное число. Таким образом предел окончательной погрешности логарифма выразится тогда формулой:

¹/₂ + a (d +1) десятитысячных

Пример. Найти log π, принимая за π приближенное число 3,14, точное до ¹/₂сотой.

Перенеся в числе 3,14 запятую после 3-й цифры, считая слева, мы получим трехзначное число 314, точное до ¹/₂ единицы; значит, предел погрешности неточного числа, т. е. то, что мы обозначили буквой а, есгь ¹/₂ Из таблиц находим:

log 3,14 = 0,4969.

Табличная разность d между мантиссами чисел 314 и 315 равна 14, поэтому погрешность найденного логарифма будет менее

¹/₂ + ¹/₂ (14 +1) = 8 десятитысячных.

Так как о логарифме 0,4969 мы не знаем, с недостатком ли он или с избытком, то можем только ручаться, что точный логарифм π заключается между 0,4969 — 0,0008 и 0,4969 + 0,0008, т. е. 0,4961 < log π < 0,4977.

282. Найти число по данному логарифму. Для нахождения числа по данному логарифму могут служить те же таблицы, по которым отыскиваются мантиссы данных чисел; но удобнее пользоваться другими таблицами, в которых помещены так называемые антилогарифмы, т. е. числа, соответствующие данным мантиссам. Таблицы эти, обозначенные надписью сверху „антилогарифмы», помещены в конце этой книги вслед за таблицами логарифмов; небольшая часть их помещена на этой странице (для
объяснения).

Пусть дана 4-значная мантисса 2863 (на характеристику не обращаем внимания) и требуется найти соответствующее целое число. Тогда, имея таблицы антилогарифмов, надо пользоваться ими совершенно так же, как было раньше объяснено для нахождения мантисс по данному числу, а именно: первые 2 цифры мантиссы мы находим в первом слева столбце. Затем продвигаемся от этих цифр по горизонтальной строке вправо до пересечения с вертикальным столбцом, идущим от 3-й цифры мантиссы, которую
надо искать в верхней строке (или в нижней). В пересечении находим четырехзначное число 1932, соответствующее мантиссе 286. Затем от этого числа продвигаемся дальше по горизонтальной строке направо до пересечения с вертикальным столбцом, идущим от 4-й цифры мантиссы, которую надо найти наверху (или внизу) среди поставленных там цифр 1, 2, 3,… 9. В пересечении мы находим поправку 1, которую надо приложить (в уме) к найденному раньше числу 1032, чтобы получить число, соответствующее мантиссе 2863.

Таким образом, число это будет 1933. После этого, обращая внимание  на характеристику, надо в числе 1933  поставить занятую на надлежащем месте. Например:

если  log x = 3,2863,           то х = 1933,

„     log x = 1,2863,            „   х = 19,33,

,,     log x = 0,2&63,           „   х = 1,933,

„     log x = 2,2863,             „   х = 0,01933

и т.п.

Вот еще примеры:

log x =  0,2287,           х = 1,693,

log x = 1,7635,                х = 0,5801,

log x = 3,5029,               х = 3184,

log x =  2,0436,                х = 0,01106.

Если в мантиссе указано 5 или более цифр, то берем только первые 4 цифры, отбрасывая остальные (и увеличивая 4-ю цифру на 1, если 5-я цифра есть пять или более). Напр., вместо мантиссы 35478 берем 3548, вместо 47562 берем 4756.

283. Замечание. Поправку на 4-ю и следующие цифры мантиссы можно находить и посредством интерполирования. Так, если мантисса будет 84357, то, найдя число 6966, соответствущее мантиссе 843  мы можем рассуждать далее так :: если мантисса увеличивается на 1 (тысячную), т. е. сделаетоя 844, то число, как видно из таблиц, увеличится на 16 единиц; если же мантисса увеличится не на 1 (тысячную), а на 0,57 (тысячной), то число увеличится на х
единиц, причем х должно удовлетворять пропорции:

х  :  16 = 0,57  :  1, откуда х = 16•0,57 = 9,12.

Значит, искомое число будет 6966+ 9,12 = 6975,12 или (ограничиваясь только четырьмя цифрами) 6975.

284. Предел погрешности найденного числа. Доказано, что в том случае, когда в найденном числе запятая стоит после 3-й слева цифры, т. е. когда характеристика логарифма есть 2, за предел погрешности можно принять сумму

где а есть предел погрешности логарифма (выраженный в десятитысячных долях), по которому отыскивалось число, и d — разность между мантиссами двух трехзначных последовательных чисел, между которыми заключается найденное число (с запятой после 3-й цифры слева). Когда характеристика будет не 2, а какая-нибудь иная, то в найденном числе запятую придется перенести влево или вправо, т. е. разделить или умножить число на некоторую степень 10. При этом
погрешность результата также разделится или умножится на ту же степень 10.

Пусть, например, мы отыскиваем число по логарифму 1,5950, о котором известно, чго он точен до 3 десятитысячных; значит, тогда а = 3. Число, соответствующее этому логарифму, найденное по таблице антилогарифмов, есть 39,36. Перенеся запятую после 3-й цифры слева, будем иметь число 393,6, заключающееся между 393 и 394. Из таблиц логарифмов видим, что разность между мантиссами, соответствующими этим двум числам, составляет
11 десятитысячных; значит d = 11. Погрешность числа 393,6 будет меньше

Значит, погрешность числа 39,36 будет меньше 0,05.

285. Действия над логарифмами с отрицательными характеристиками. Сложение и вычитание логарифмов не представляют никаких затруднений, как это видно из следующих примеров:

Не представляет никаких затруднений также и умножение логарифма на положительное число, напр.:

В последнем примере отдельно умножена положительная мантисса на 34, затем отрицательная характеристика на 34.

Если логарифм о отрицательной характеристикой и положительной мантиссой умножается на отрицательное число, то поступают двояко: или предварительно данный логарифм обращают в отрицательный, или же умножают отдельно мантиссу и характеристику и результаты соединяют вместе, например:

3,5632 • ( — 4) = — 2,4368 • (— 4) = 9,7472;

3,5632 •( — 4) = + 12 — 2,2528 = 9,7472.

При делении могут представиться два случая: 1) отрицательная характеристика делится и 2) не делится на делитель. В первом случае отдельно делят характеристику и мантиссу:

10,3784 : 5 = 2,0757.

Во втором случае прибавляют к характеристике столько отрицательных единиц, чтобы образовавшееся число делилось на делитель; к мантиссе прибавляют столько же положительных единиц:

3,7608 : 8 = ( — 8 + 5,7608) : 8 = 1,7201.

Это преобразование надо совершать в уме, так что действие располагается так:

286. Замена вычитаемых логарифмов слагаемыми.  При вычислении какого-нибудь сложного выражения помощью логарифмов приходится некоторые логарифмы складывать, другие вычитать; в таком случае, при обыкновенном способе совершения действий, находят отдельно сумму слагаемых логарифмов, потом   сумму вычитаемых и из первой суммы вычитают вторую. Напр., если имеем:

log х = 2,7305 — 2,0740 + 3,5464 — 8,3589,

то обыкновенное выполнение действий расположится так:

Есть однако возможность заменить вычитание сложением. Так:

Теперь можно расположить вычисление так:

287. Примеры вычислений.

Пример 1. Вычислить выражение:

если А = 0,8216, В = 0,04826,  С= 0,005127 и D = 7,246.

Логарифмируем данное выражение:

log х = ¹/₃ log A   +   4 log В   —   3 log С   —   ¹/₃ log D

Теперь, для избежания излишней потери времени и для уменьшения возможности ошибок, прежде всего расположим все вычисления, не исполняя пока их и не обращаясь, следовательно, к таблицам:

После этого берем таблицы и проставляем логарифмы на оставленных свободных местах:

Прeдел погрешности. Сначала найдем предел погрешности числа x₁ = 194,5, равный:

Значит, прежде всего надо найти а, т. е. предел погрешности приближенного логарифма, выраженный в десятитысячных долях. Допустим, что данные числа А, В, С и D все точные. Тогда погрешности в отдельных логарифмах будут следующие (в десятитысячных долях):

в logА………. ¹/₂

в ¹/₃ log A………¹/₆  +  ¹/₂  =  ²/₃

(¹/₂ прибавлена потому, что при делении на 3 логарифма 1,9146 мы округлили частное, отбросив 5-ю цифру его, и, следовательно, сделали еще ошибку,меньшую ¹/₂ десятитысячной).

Теперь находим предел погрешности логарифма:

а = ²/₃ + 2 + ³/₂ + ¹/₆ = 4 ¹/₃ (десятитысячных).

Определим далее d . Так как  x₁ = 194,5, то 2 целых последовательных числа, между которыми заключается x₁ будут 194 и 195. Табличная разность d между мантиссами, соответствующими этим числам, равна 22. Значит, предел погрешности числа x₁ есть:

Так как x = x₁ : 10, то предел погрешности в числе x равен 0,3:10 = 0,03. Таким образом, найденное нами число 19,45 разнится от точного числа менее, чем на 0,03. Так как мы не знаем, с недостатком или с избытком найдено наше приближение, то можем только ручаться, что

19,45 + 0,03 > х > 19,45 — 0,03, т. е.

19,48 > х > 19,42,

и потому,  если примем х =19,4, то будем иметь  приближение  с недостатком с точностью до 0,1.

Пример 2. Вычислить:

х = (— 2,31)^{3  5}√72 = — (2,31)^{3  5}√72.

Так как отрицательные числа не имеют логарифмов, то предварительно находим:

х’ = (2,31)^{3  5}√72

по разложению:

log х’ = 3 log 2,31  + ¹/₅  log72.

После вычисления окажется:

х’ = 28,99;

следовательно,

x = — 28,99.

Пример 3. Вычислить:

Сплошного логарифмирования здесь применить нельзя, так как под знаком корня стоит с у м м а. В подобных случаях вычисляют формулу по частям.

Сначала находим N = ⁵√8, потом N₁ = ⁴√3; далее простым сложением определяем N + N₁, и, наконец, вычисляем ³√N + N₁;       окажется:

N = 1,514,       N₁ = 1,316;     N + N₁ = 2,830.

log x  = log   ³√2,830 = ¹/₃ log 2,830   =  0,1506;

x = 1,415.

Глава  четвертая.

Показательные и логарифмические уравнения.

288. Показательными уравнениями называются такие, в которых неизвестное входит в показатель степени,   а   логарифмическими — такие, в которых неизвестное входит под знаком log. Такие уравнения могут быть разрешаемы только в частных случаях, причем приходится основываться на свойствах логарифмов и на том начале, что если числа равны, то равны и их логарифмы, и,
обратно, если логарифмы равны, то равны и соответствующие им числа.

Пример 1. Решить уравнение: 2^x = 1024.

Логарифмируем обе части уравнения:

Пример 2. Решить уравнение: a^2x — a^x = 1. Положив a^x = у, получим квадратное уравнение:

y² — у — 1 = 0,

Так как 1—√5 < 0,  то   последнее   уравнение   невозможно (функция a^x всегда есть число положительное), а первое дает:

Пример 3. Решить уравнение:

log (а + x) + log (b + х) = log (с + x).

Уравнение можно написать так:

log [(а + x) (b + х)] = log (с + x).

Из равенства логарифмов заключаем о равенстве чисел:

(а + x) (b + х) = с + x.

Это есть квадратное уравнение, решение которого не представляет затруднений.

Глава пятая.

Сложные  проценты, срочные  уплаты  и срочные взносы.

289. Основная задача на сложные проценты. В какую сумму обратится капитал а рублей, отданный в рост по р сложных процентов, по прошествии t лет (t — целое число)?

Говорят, что капитал отдан по сложным процентам, если принимаются во внимание так называемые  „проценты на проценты», т. е. если причитающиеся на капитал процентные деньги присоединяются в конце каждого года к капиталу для наращения их процентами в следующие годы.

Каждый рубль капитала, отданного по р %, в течение одного года принесет прибыли ^p/₁₀₀ рубля, и,  следовательно, каждый рубль капитала через 1 год обратится в 1+ ^p/₁₀₀  рубля (напр., если капитал отдан по 5% , то каждый рубль его через год обратится в 1+ ⁵/₁₀₀, т. е. в 1,05 рубля).

Обозначив для
краткости дробь ^p/₁₀₀  одною буквою, напр, r, можем сказать, что каждый рубль капитала через год обратится в 1 + r рублей; следовательно, а рублей обратятся через 1 год в а(1 + r) руб. Еще через год, т. е. через 2 года от начала роста, каждый рубль из этих а (1 + r) руб. обратится снова в 1 + r  руб.; значит, весь
капитал обратится в а (1 + r) ² руб. Таким же образом найдем, что через три года капитал будет а (1 + r) ³, через четыре года будет а (1 + r) ⁴,… вообще через t лет, если t есть целое число, он обратится в а (1 + r) ^t руб. Таким образом,
обозначив через А окончательный капитал, будем иметь следующую формулу сложных процентов:

А = а (1 + r) ^t  где r =  ^p/₁₀₀.

Пример. Пусть a =2 300 руб., p = 4, t =20 лет; тогда формула дает:

r =  ⁴/₁₀₀= 0,04;     А = 2 300 • (1,04)²⁰.

Чтобы вычислить А, применяем логарифмы:

log a = log 2 300 + 20 log 1,04 = 3,3617 + 20 • 0,0170 = 3,3617+0,3400 = 3,7017.

A = 5031 рубль.

Замечание. В этом примере нам пришлось log 1,04 умножить на 20. Так как число 0,0170 есть приближенное значение log 1,04 с точностью до  ¹/₂ десятитысячной доли, то произведение этого числа на 20 будет точно только до ¹/₂ • 20, т. е. до 10 десятитысячных =1 тысячной. Поэтому в сумме 3,7017 мы не можем ручаться не только за цифру десятитысячных,
но и за цифру тысячных. Чтобы в подобных случаях можно было получить большую точность, лучше для числа 1 + r брать логарифмы не 4-значные, а с большим числом цифр, напр. 7-значные. Для этой цели мы приводим здесь небольшую табличку, в которой выписаны 7-значные логарифмы для наиболее употребительных значений р.

290. Основная задача на срочные уплаты. Некто занял а рублей по р % с условием погасить долг, вместе с причитающимися на него процентами, в t лет, внося в конце каждого года одну и ту же сумму. Какова должна быть эта сумма?

Сумма x, вносимая ежегодно при таких условиях, называется срочною  уплатою.  Обозначим  опять буквою  r ежегодные процентные деньги с  1  руб., т. е. число ^p/₁₀₀.  Тогда к концу первого года долг а возрастает до а (1 + r), аза уплатою х рублей он сделается а (1 + r)—х.

К концу второго года каждый рубль этой суммы снова обратится в 1 + r рублей, и потому долг будет [а (1 + r)—х](1 + r) = а (1 + r)² — x(1 + r), а за уплатою x рублей окажется: а (1 + r)² — x(1
+ r) — х. Таким же образом убедимся, что к концу 3-го года долг будет

а (1 + r)³ — x(1 + r)² — x(1 + r) — x,

и вообще и концу t-го года он окажется:

а (1 + r)^t — x(1 + r)^{t —1} — x(1 + r)^{t —2}… — x(1 + r) — x, или

а (1 + r)^t — x [ 1 + (1 + r) + (1 + r)² + …+ (1 + r)^{t —2}+ (1 + r)^{t —1}]

Многочлен, стоящий внутри скобок [], представляет сумму членов геометрической прогрессии; у которой первый член есть 1, последний (1 + r)^{t —1}, а знаменатель (1 + r). По формуле для суммы членов геометрической прогрессии (отдел 10 глава 3 § 249) находим:

и величина долга после t-ой уплаты будет:

По условию задачи, долг в конце t-го года должен равняться 0; поэтому:

 откуда

При вычислении этой формулы срочных уплат помощью логарифмов мы должны сначала найти вспомогательное число N = (1 + r)^t по логарифму: log N= t log (1 + r); найдя N, вычтем из него 1, тогда получим знаменатель формулы для х, после чего вторичным логарифмированием найдем:

log х = log a + log N +  log r — log (N — 1).

291. Основная задача на срочные взносы. Некто вносит в банк в начале каждого года одну и ту же сумму а руб. Определить, какой капитал образуется из этих взносов по прошествии t лет, если банк платит по р сложных процентов.

Обозначив через r ежегодные процентные деньги с 1 рубля, т. е. ^p/₁₀₀, рассуждаем так: к концу первого года капитал будет а (1 + r);

в начале 2-го года к этой сумме прибавится а рублей; значит, в это время капитал окажется а (1 + r) + a . К концу 2-го года он будет   а (1 + r)²  + а (1 + r);

в начале 3-го года снова вносится а рублей; значит, в это время капитал будет а (1 + r)²  + а (1 + r) + а; к концу 3-го он окажется а (1 + r)³  + а (1 + r)²  + а (1 + r) Продолжая эти рассуждения
далее, найдем,
чтo к концу t-го года искомый капитал A будет:

Такова формула срочных взносов, делаемых в начале каждого года.

Ту же формулу можно получить и таким рассуждением:. первый взнос в а рублей, находясь в банке t лет, обратится, согласно формуле сложных процентов, в а (1 + r)^t  руб. Второй взнос, находясь в банке одним годом меньше, т. е. t — 1 лет, обратится в а (1 + r)^{t— 1}  руб. Подобно этому третий взнос даст а
(1 + r)^{t— 2} и
т. д., и, наконец, последний взнос, находясь в банке только 1 год, обратится в а
(1 + r) руб. Значит, окончательный капитал A руб. будет:

A = а (1 + r)^t + а (1 + r)^{t— 1} + а
(1 + r)^{t— 2}+ . . . + а
(1 + r),

что, после упрощения, дает найденную выше формулу.

При вычислении помощью логарифмов этой формулы надо поступить так же, как и при вычислении формулы срочных уплат, т. е. сначала найти число N = (1 + r)^t  по его логарифму: log N= t log (1 + r), затем число N— 1 и уже тогда логарифмировить формулу:

log A = log a + log (1 + r) + log (N — 1) — 1оg r

Замечание. Если бы срочный взнос в а руб. производился не в начале, а в конце каждого года (как, напр., вносится срочная уплата х для погашения долга), то, рассуждая подобно предыдущему, найдем, что к концу t-го года искомый капитал А’ руб. будет (считая в том числе и последний взнос а руб., не приносящий процентов):

A’ =  а (1 + r)^{t— 1} + а
(1 + r)^{t— 2}+ . . . + а
(1 + r) + а 

что равно:

т. е. А’ оказывается в (1 + r) pаз менее А, что и надо было ожидать, так как каждый рубль капитала А’ лежит в банке годом меньше, чем соответствующий рубль капитала А.

Приближенные вычисления в инженерных задачах (от простого к сложному)

• Авторы
• Руководители
• Файлы работы
• Наградные документы

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

Однажды мне довелось наблюдать за работой опытного инженера. Делая чертеж какого-то замысловатого устройства, он постоянно что-то считал. Причем считал много, и без привычных нам «столбиков» и «уголков», и без калькулятора. Иногда на черновичке появлялась строчка промежуточных цифр и, после небольшой паузы, сразу появлялся результат. Я поняла – человек просто считает «в уме». Заинтересовавшись темой устных вычислений, я попыталась найти на просторах интернета методику таких вычислений.

Разных пособий по математике с изложением вычислительных приемов оказалось много, особенно с изложением приемов устного счета [1 — 6]. Эти пособия в основном ориентированы на широкий круг читателей, разных по возрасту и профессиональной деятельности. Даже просто запомнить этот объемный перечень правил устного счета обычному человеку довольно сложно. Обычно всеми этими правилами владеют либо преподаватели математики, либо отдельные любители устных вычислений.

Актуальность данной работы связана с востребованностью техники приближенных вычислений при решении инженерных (технических) задач.

Цель работы – создать набор правил, позволяющих устно либо вручную, без калькулятора быстро производить приближенные вычисления от простых арифметических до тригонометрических и логарифмирования.

Для достижения цели сформулированы следующие задачи:

Провести анализ приемов устного счета и выбрать ограничения на количество значащих цифр аргументов для вычислений с точностью около 1%;

Сформулировать правила применения техники устного счета при выполнении основных математических операций с вещественными числами;

Изложить особенности приближенных вычислений с тригонометрическими функциями и логарифмами.

Приемы приближенного выполнения основных математических операций могут быть полезны учащимся старших классов и студентам технических вузов.

1. Точные операции с натуральными числами до четырех знаков

Для решения инженерно-технических задач не требуется высокой точности вычислений. Обычно бывает достаточно двух-трех верных знаков.

Однако, чтобы их получить, нужно освоить приемы точного выполнения арифметических операций в диапазоне 4-значных чисел. Главные принципы для упрощения вычислений заключаются в следующем:

Разделение операций на прямые (сложение, умножение) и обратные (вычитание, деление);

Выделение чисел, удобных для выполнения устных вычислений;

Выполнение операций от старшего разряда к младшему.

1.1. Удобные числа и формулы сокращенного умножения

Устное сложение и вычитание чисел в 4-значном диапазоне обычно затруднений не вызывает. Операции выполняются на основе формул сокращенного умножения, которые можно записать в следующей форме:

а) для произведения одинаковых чисел (возведение в квадрат):

a² = (a+c) ∙ (a—c) + c²

б) для произведения разных чисел (или возведение в куб):

a∙b = (a+c)∙b — c∙b

a∙b = (a-c)∙b + c∙b

В этих формулах число свыбирается так, чтобы полученная сумма (a+c) или разность (a—c) было числом, удобным для выполнения устных операций.

1.2. Приемы умножения и возведение в степень натуральных чисел

Рассмотрим подробнее прямые операции быстрого умножения и возведения в степень натуральных с результатом до 10000. На первых порах можно вычислять, записывая промежуточные результаты на листе бумаги.

1) Умножение 2-значного числа на 1-значный множитель. Сначала перемножаем десятки, затем прибавляем (или отнимаем) произведение единиц:

22 ∙ 4 = 20 ∙ 4 + 2 ∙ 4 = 80 + 8 = 88

76 ∙ 7 = 80 ∙ 7 — 4 ∙ 7 = 560 — 28 = 532

2) Возведение в квадрат 2-значных чисел. Выбираем ближайшее «удобное» число, затем вычисляем результат по формуле сокращенного умножения:

29² = 30 ∙ (29 — 1) + 1² = 30 ∙ 28 + 1 = 0840 + 1 = 0841

89² = 100 ∙ (89 — 11) + 11² = 100 ∙ 89 + 121 = 8900 + 121 = 9021

3) Умножение 3-значного числа на 1-значный множитель. Выполняем через приведение к двузначному:

118 ∙ 6 = 110 ∙ 6 + 8 ∙ 6 = 660 + 48 = 0708

788 ∙ 6 = 800 ∙ 6 — 12 ∙ 6 = 4800 + 72 = 4872

4) Произведение 2-значных чисел. Один из сомножителей приводим к «удобным десяткам» вычитанием (или добавлением) единиц. После перемножения десятков, к полученному результату добавляем (или вычитаем) произведение этих единиц на другой сомножитель:

32 ∙ 97 = 100 ∙ 32 — 3 ∙ 32 = 3200 — 96 = 3104

42 ∙ 37 = 40 ∙ 42 — 3 ∙ 42 = 1680 + 126 = 1554

Реже возникает необходимость возведения в куб и в 4-ю степень.

Возведение в куб – через возведение в квадрат и перемножение:

21³ = 21 ∙ 441 = 20 ∙ 441 + 441 = 8820 + 441 = 9261

7³ = 7 ∙ 49 = 7 ∙ 50 — 7 = 350 — 7 = 343

Возведение в 4-ю степень – через двойное возведение в квадрат:

6⁴ = 36² = 40 ∙ 32 + 4² = 1280 + 16 = 1296

7⁴ = 49² = 50 ∙ 48 + 1² = 2400 + 1 = 2401

Таким образом для быстрого умножения и возведения в степень натуральных чисел нужно владеть всего четырьмя основными навыками.

2. Прямые операции с вещественными числами. Нормировка

2.1. Нормировка при операциях с вещественными числами

Рассмотренные в первом разделе навыки выполнение прямых операций умножения и возведения в степень натуральных чисел можно также применять при умножении и возведении в степень вещественных чисел, если предварительно провести их нормировку. В данном случае нормировкой мы называем процесс приведения сомножителей к форме натуральных чисел, дающих результат до четырех значащих цифр, а именно при нормировке десятичная запятая переносится таким образом, чтобы можно было применить одно из 4-х правил в первом разделе. Иначе говоря, вначале записывается (запоминается) на сколько позиций вправо (+) или влево (-) надо перенести десятичную запятую результата:

76 ∙ 0,041 = 10^-3 ∙ (76 ∙ 41 = 40 ∙ 76 + 1 ∙ 76 = 3040 + 76 = 3116) = 10^-3 ∙ 3116 = 3,116

380² = 10⁺² ∙ (38² = 40 ∙ 36 + 4 = 1440 + 4 = 1444) = 10⁺² ∙ 1444 = 144400.

2.2. Минимизация погрешности округлений

Поскольку мы определились, что точность вычислений порядка 1% вполне допустима, то в результате операций с вещественными числами нам достаточно иметь итоговое число с 2 — 3 значащими цифрами. Однако было бы неверным, например, округлять до 3-х знаков результаты, приведенные в п. 2.1, так как этим действием мы заведомо вносим погрешность в уже выполненные вычисления.

В то же время, если исходные числа имеют больше значащих цифр, чем нужно для применения освоенных навыков, то округлять исходные числа просто необходимо.

В этих случаях при нормировке «лишние» значащие цифры следует отбросить, минимизируя, по возможности, погрешность вычислений. Принципы минимизации погрешности округлений поясним на следующих примерах. Здесь и далее в конце строки в фигурных скобках будем показывать относительную погрешность приближенного результата в процентах.

Округление одного сомножителя:

0,00742 ∙ 1,8 ≈ 10^-5 ∙ (74∙18 = 20∙74 — 2∙74 = 1480–148 = 1332) ≈ 0,01332 { -0,27 %}

3,141593 ∙ 5,46 ≈ 10^-2 ∙ (3∙546 = 1638) ≈ 16,38 { -4,51 %}

Округление двух сомножителей в разные стороны:

0,096417² ≈ 10^-6 ∙ (96∙97 = 100∙96 – 3∙96 = 9600–288 = 9412) ≈ 0,009412 {+1,25 %}

3,141593 ∙ 5,46 ≈ 10^-2 ∙ (31∙55 = 60∙31– 5∙31 = 1860–155 = 1705) ≈ 17,05 {-0,60 %}

Округление с добавлением остатка:

Минимизировать погрешность при округлении одного сомножителя можно дополнительно уже при записи итогового значения путем добавления произведения отброшенной части на второй сомножитель, например:

0,00742 ∙ 1,8 ≈ 10^-5 ∙ (74∙18 = 20∙74-2∙74 = 1480–148 = 1332) ≈ 0,01336 { +0,03 %}

3,141593 ∙ 5,46 ≈ 10^-2 ∙ (3∙546 = 1638) ≈ 17,18 { +0,16 %}

В этих примерах приближенные результаты 0,01332 и 16,38 скорректированы соответственно на величины 0,0004 (0,00002∙1,8) и 0,8 (0,141593∙5,46).

В последнем примере вычисления длины окружности диаметром 5,46 (3,141593∙5,46) показано, как правильно выбранный способ округления позволил снизить погрешность вычисления с 4,51 % до 0,16 %. Хотя, если внимательно присмотреться к последнему примеру, можно заметить, что добавление остатка без вычислений (просто «угадыванием» — при соответствующих навыках) даст вполне удовлетворительный результат. Так, например, и без вычислений понятно, что отбрасывание величины 0,141593∙5,46 повышает погрешность. Просто «угадывая» в качестве приближенного ответа, можно было бы сразу записать значение 17,2.

3. Обратные операции с вещественными числами. Интерполяция

3.1. Применение интерполяции при выполнении обратных операций

В предыдущем разделе мы научились выполнять прямые операции умножения и вычисления с вещественными числами. Приближенность таких вычислений заключалась лишь в отбрасывании «лишних» знаков с целью применения навыки целочисленных вычислений. Иное дело – обратные операции: деление и извлечение корня. При делении и извлечении корней даже из натуральных чисел мы получаем вещественные с неограниченным числом значащих цифр.

Для поиска результата от деления чисел или извлечения корней сокращение числителя и знаменателя на общий множитель, равно как и вынос общего числа за знак радикала, лишь удлиняет цепочку вычислений, никак не упрощая их.

Намного эффективнее оказывается поиск ближайших граничных значений с последующей интерполяцией между ними. Поскольку мы уже овладели приемами устного умножения и возведения в степень, нам проще определить интервал, внутри которого находится искомый результат. Интерполяция в пределах этого интервала позволяет с некоторой степенью точности «предсказать» приближенное значение результата деления или извлечения корня. Графически схема интерполяции показана на рис.1.

Рис. 1. Схемы интерполяции: а) линейная, б) нелинейная.

При вычислениях следует стремиться к тому, чтобы целочисленные значения границ интервала отличались друг от друга лишь на единицу. Это упрощает интерполяцию и позволяет пренебречь влиянием нелинейности основных математических функций вследствие незначительности вносимой погрешности.

3.2. Приемы деления и извлечения корней из вещественных чисел

Рассмотрим практические приемы выполнения обратных операций.

Деление четырехзначного числа на двухзначное. Например, 3749 / 76:

Пусть 1-е граничное частное равно 50, тогда делимое 50∙76 = 3800

Пусть 2-е граничное частное равно 49, тогда делимое 3800 — 76 = 3724

Искомое частное 50-25∙1/76 ≈ 49,3. Сокращенно будет выглядеть так:

3849/76=50 или 49 => 50∙76=3800 или 3800-76=3724 => 50-25/76 ≈ 49,3{-0,06 %}

Вычисление квадратного корня. Например, корень из 4432:

Пусть 1-й граничный корень равен 65, тогда 65² = 4225

Пусть 2-й граничный корень равен 67, тогда 67² = 4489

Искомый корень ≈ 67 — 2∙57/264 ≈ 66,5. Или сокращенно:

√4432 = 65 или 67 -> 65² =4225 или 67² =4489 -> 274-2∙57/264 ≈ 66,5 {-0,11 %}

Вычисление кубического корня. Например, из 1715:

Пусть 1-й граничный корень равен 12, т.е. 12³ = 144∙10+2∙144=1728

Пусть 2-й граничный корень равен 11, т.е. 11³ = 121∙10+2∙121=1331

Искомый корень ≈ 12 — 13/397 ≈ 11,97. Или сокращенно:

= 12 или 11 => 12³ =1728 или 11³ =1331 => 12 — 13/397 ≈ 11,97 { 0,00 %}

Примеры операций с вещественными числами:

1) При делении делимое нормируем до 4-значного, а делитель до 2-значного числа, причем округление делителя и делимого производим в одну сторону:

149,29/0,247=10⁺¹ ∙ (1492,9/24,7 ≈ (1492,9+30) / 25 ≈ 1523/25∙ (60 или 61 =>

=> 60∙25=1500 или 61∙25=1500+25=1525) => 61-2/25 ≈ 60,9) ≈ 609 {+0,76 %}

2) При извлечении корней нормируем до 4-знаков, перенося десятичную запятую кратно 2-м позициям для квадратного (или 3-м – для кубического) корней:

≈10⁺² ∙ ≈10⁺² ∙ (24 или 23 => 24² = 576 или 23² = 529 =>

=> 24 — 20/47 ≈ 23,8) ≈ 2380 {+0,90 %}

3 ≈ 10- ≈ 10 — 1 ∙ (5 или 6 => 53=125 или 63=216 =>

=> 5+(149 — 125)/(216 — 125) = 5 + 24/91 ≈ 5,26) ≈ 0,526 {-0,72 %}

4. Приближенные операции с тригонометрическими функциями

4.1. Тригонометрический круг и замечательное число «пи»

Приближенные вычисления в инженерных задачах немыслимы без навыков работы с тригонометрическими функциями. Несмотря на кажущуюся сложность, приближенное определение основных тригонометрических функций (синус, косинус, тангенс и котангенс) на основе тригонометрического круга (см. рис. 2) дают точность, достаточную для большинства практических задач.

Рис. 2. Фрагмент тригонометрического круга для приближенных вычислений

При работе с тригонометрическими функциями не обойтись без замечательного числа π, численно равному отношению длины окружности к ее диаметру. Значение числа π, приблизительно равное 3,141593 запомнить не сложно, используя сочетание 3,14 и 1593 г. – год опубликования французским математиком Франсуа Виетом широко известной формулы Виета [4] для вычисления числа π:

4.2. Приемы вычислений на основе тригонометрического круга

Для приближенных вычислений тригонометрических функций необходимо помнить правила перехода от градусной меры к радианам:

1 радиан = 180⁰/π ≈ 57,3⁰

1⁰ = π/180⁰/π ≈ 0,01745 рад.

Масштабная сетка на рис.2 позволяет получить 2 верных знака при вычислении тригонометрических функций любых углов. Однако, с учетом того, что часть значений тангенса и котангенса (больше 1) выходит за пределы изображения, могут оказаться полезными следующие формулы:

ctg a = 1 / tg a;

arctg a = arcctg (1 / a).

Существенно облегчает вычисления свойство малых углов (менее 0,1 радиана ≈ π/30 ≈ 6⁰), которое гласит, что «синус малого угла примерно равен его тангенсу и самому углу п радианах» (погрешность менее 0,5%).

В то же время для углов, близких к 0 или к π/2, зачастую требуется более высокая точность, которую можно достичь, применяя формулы:

cos a = ;

sina = cos (π/2 –a).

Полезно помнить значения тригонометрические функции основных углов, позволяющих производить вычисления с помощью приемов интерполяции:

sin(π/6) = sin(30⁰) = ½ = 0,5

sin(π/4) = sin 45⁰ = ≈ 0,707

sin(π/3) = sin(60⁰) = ≈ 0,866

tg(π/6) = tg(30⁰) = ≈ 0,577

tg(π/4) = tg(45⁰) = 1

tg(π/3) = tg(60⁰) = ≈ 1,732 .

Рассмотрим несколько примеров:

sin(7π/3) = sin(2π + π /3) = sin(π /3) = /2 ≈ 0,866; {0,00 %}

tg(35⁰) (чуть более tg(30⁰) = 0,577, но менее tg(45⁰) = 1,0) ≈ 0,70; {-0,03 %}

ctg( /12) = 1/tg( /12) ≈ 1/0,27 ≈ 10^-1∙(1000/27) ≈ 3,7;{-0,86 %}

sin(1) ≈ sin(57,3⁰) ≈ 0,85, т.е. чуть менее sin(π/3);{+1,0 %}

arctg( /3) ≈ arctg(1,05) ≈ 0,8, т.е. чуть более /4;{-1,2 %}

cos(200⁰) ≈ -0,925 , т.е. примерно между -0,9 и -0,95; {-1,6 %}

arctg(2) = arcctg(1/2) ≈ 63⁰, т.е. немного более 60⁰, но менее 70⁰; {+1,9 %}

sin(1/6) ≈ 0,166 (почти малый угол, округлим 0,16666 в < сторону); {+0,1 %}

cos(1/10) = = = = 10^-2 ∙ ≈ 10^-2 ∙ (99 или 100 => 99² =9801 или 100² = 10000) => 10^-2 ∙ (99+100)/2 ≈ 0,995. { 0,00 %}

Как видно из примеров, имея под рукой тригонометрический круг с масштабной сеткой и линейку, значения тригонометрических функций можно находить с достаточной точностью. Несколько грубее (примерно с точностью до 1 — 2%) можно вычислять и по памяти, просто мысленно представляя перед собой графическое изображение тригонометрического круга.

5. Приближенные операции с логарифмами

В естественных науках (особенно в информатике и инженерных расчетах) логарифмы востребованы почти на уровне тригонометрических функций. Одним из основных принципов природных процессов является принцип пропорциональности прироста самой измеряемой величине, это делает логарифмическую функцию удобной, например, в физике — для измерения уровня восприятия человеком звуковых и световых явлений, в информатике – для описания информационной энтропии (формула Шеннона), в теории ракетных двигателей (формула Циолковского), в статистической термодинамике (формула Планкадля энтропии вещества). Освоение методов приближенного вычисления логарифмов несомненно облегчит решение подобных задач.

5.1. Применение формул логарифма произведения и логарифма частного

Логарифмирование есть операция отыскания показателя степени (x), в которую надо возвести основание (a), чтобы получить значение аргумента (b). Иными словами, это решение уравнения вида a^x = b. Традиционно записывается в форме x = log_a b, предложенной Джоном Непером в 1614 году. Из сказанного следует, что, по сути, логарифмирование есть операция, обратная возведению в степень. Таблица 1 иллюстрирует взаимосвязь прямых и обратных операций.

Таблица 1

Прямые и обратные операции

Прямая операция	Обратная операция
А	+	Х	= В	В	—	A	= Х
А	х	Х	= В	В	/	A	= Х
А	↑	Х	= В	В	↓	A	= Х
АХ = В	logАВ = Х

В этой таблице знаком ↑ обозначена операция «возведения» исходного числа А в степень Х, а знаком ↓ обозначена обратная операция, которую условно можно назвать «извлечением степени Х из числа В по основанию А», т.е. отыскания степени Х, в которую возвели исходное число Адля получения результата В(в чем собственно и заключается операция логарифмирования). Из сказанного следует, что при определении численных значений логарифмов мы также можем использовать приемы интерполяции, изложенные в п.3.1.

В отличие от операций сложения и умножения при возведении в степень перестановка операндов (аргументов операции) недопустима. Кроме того, при вычислении логарифмов с применением техники линейной интерполяции необходимо более внимательно следить за вносимой погрешностью, особенно когда результат от двухзначного числа приближается к единице.

Для практических вычислений нам потребуются вспомнить следующие свойства показательных функций:

Любое чисто в степени ноль равно единице: a⁰ = 1;

Произведение a^b ∙ a^c = a^b+c;

Частное a^b / a^c = a^b—c ;

и вытекающих из них формул для логарифмов:

Логарифм по любому основанию от единицы равен нулю: log_a 1 = 0;

Логарифм произведения log_a (b∙с) = log_a b + log_a с;

Логарифм частного log_a (b/с) = log_a b — log_a с.

Если бы Д. Неппер вместо обозначения log_a b придумал бы какой-нибудь знак попроще (ну хотя бы как в таблице 1), логарифмирование с точки зрения вычислительных операций, воспринималось бы гораздо проще.

Поскольку нас главным образом интересует вопрос приближенного нахождения численных значений логарифмов, как операций, обратных возведению в степень, исключительно в целях сокращения записей заменим традиционную форму записи x = log_a b на упрощенную _аb = x, ассоциирующуюся с привычной операцией возведения в степень b =a^x. Тогда упомянутые ранее формулы логарифма произведения и логарифма частного запишутся в виде:

_a (b∙с) = _a b + _aс; _a (b/с) = _a b — _aс.

Нам представляется, что допущенная вольность облегчит устные операции за счет сокращения записи.

Итак, при вычислении численного значения логарифма перед нами стоит задача определить, на сколько порядков (степеней) число, стоящее за признаком логарифма, больше (или меньше) основания.

Поясним сказанное на примере вычисления десятичного и двоичного логарифма, используя договоренность об упрощении записи

x = log_a b тождественно _аb = x.

Двоичный (бинарный) логарифм. Например, из числа 1565 и 0,1565.

Пусть 1-я граничная степень равна 10-ти, т.е. 2¹⁰ = 1024.

Пусть 2- я граничная степень равна 11-ти, т.е. 2¹¹ = 2048.

Искомая степень ≈ 10 + 541/1024 ≈ 10,5. Или сокращенно:

₂1565 = 10 или 11 => 2¹⁰ = 1024 или 2¹¹ = 2048 => 10 + 541/1024 ≈ 10,5 {-1,1 %}

₂0,1565 ≈ ₂(1/6,4) =—₂6,4= —2 или -3 => 2²=4 или 2³=8 => -(2+2,4/4) ≈ 2,6 {-2,8 %}

Десятичный логарифм. Из числа 1565 и 0,1565.

Пусть 1-я граничная степень равна 3-м, т.е. 10³ = 1000.

Пусть 2- я граничная степень равна 4-м, т.е. 10⁴ = 10000.

Искомая степень ≈ 3 + 565/9000 ≈ 3,1. Или сокращенно:

₁₀1565 = 3 или 4 => 10³ = 1000 или 10⁴ = 10000 => 3 + 565/9000 ≈ 3,1 {-3,0 %}

₁₀0,1565 = ₁₀(1565/10000) = — (₁₀10000) — ₁₀1565) ≈ — (4 – 3,1) ≈ -0,9 {+11,7 %}

Как видно из примеров, погрешность вычисления из-за нелинейности функции зависит от степени приближения результата к единице. Для двухзначного результата (более 10-ти) нелинейность можно не учитывать.

5.2. Особенности натуральных логарифмов и замечательное число «е»

Если в тригонометрических функциях базовой является константа π, характеризующая связь между линейными и сферическими измерениями, то для функций логарифмирования базовой константой является число e=2,718281828…, служащее основанием натурального логарифма (ln). Запомнить константу e не трудно 2,7 + 1828 + 1828 (год рождения Л.Н. Толстого). Вычислить численное значение константы е можно с помощью ряда:

е= 1 + 1/1! + 1/2! + 1/3! + … ≈ 2,718281828 или ≈ 2,72.

Важное свойство: производная от натурального логарифма является обратная функция (ln x)’ =1/x.Благодаря этому свойству натуральный логарифм нашел широкое применение в самых разных областях математики, в технических науках, в экономике и финансах.

Для приближенных вычислений натуральных логарифмов кроме упомянутых ранее формул суммы (разности) логарифмов полезно запомнить некоторые «удобные» числа в 4-значном интервале, являющиеся приближенным результатом возведения числа е в целую однозначную степень:

е²≈ 7,4; е³≈20; е⁴≈55; е⁵≈148; е⁶≈403; е⁷≈1096; е⁸≈2981; е⁹≈8103.

Примеры приближенного вычисления натуральных логарифмов:

Натуральный логарифм из целого четырехзначного числа 1565:

_е1565 = 7 или 8 => е⁷ ≈ 1096 или е⁸ ≈ 2981 => — (7+469/1885) ≈ 7,25 {+0,6%}

Натуральный логарифм из десятичной дроби 0,1565:

_е0,1565 = _е(1/6,4) = — _е6,4 => -1 или -2 => —е¹ ≈ 2,27 или –е² ≈ 7,4 =>

=> — (2 — 1/5,13) ≈ 1,8 {-2,9%}

Как видно из примеров, приведенных в п.5.1 и 5.2, основным приемов приближенного вычисления логарифмов является представление исходного числа в виде произведения (или частного) двух чисел, одно из которых наиболее близко подходит к основанию в целочисленной степени, а логарифм от второго числа (по возможности) мал по сравнению с логарифмом от первого числа.

Заключение

В результате анализа существующих публикаций по способам устного умножения и возведения в степень натуральных чисел в настоящей работе выбран ограниченный набор правил, позволяющих быстро выполнять операции точного умножения и возведения в степень произвольных натуральных чисел. Показано, что достижение 4-значного результата умножения и возведения в степень достаточно для выполнения произвольных приближенных вычислений с точностью порядка 1 — 2%.

С учетом того, что в инженерной практике в основном востребованы вычисления с точностью до 2 — 3 верных знаков, в результате проведенного исследования разработана методика быстрого выполнения вычислительных операций с произвольными вещественными числами без применения калькулятора и другой счетной техники.

Новизна предложенной методики заключается в следующем своде приемов приближенных вычислений:

Исходные числа приводятся к форме, позволяющей применять способы устного умножения и возведения в степень с результатом до 4-х знаков.

Обратные операции (деление и извлечение корней) выполняются с применением правил линейной интерполяции.

Специфика операций с тригонометрическими функциями учитывается с помощью тригонометрического круга.

Специфика вычисления логарифмов основана на применении свойств показательной функции.

Предложенная методика помогает закрепить математическую подготовку уровня школьной программы и сохранить полученные навыки в дальнейшей учебе и производственной деятельности.

Список источников и литературы

1. Арутюнян Е., Левитас Г. Занимательная математика. – М.: АСТ-ПРЕСС, 1999. – 368 с.

2. Владимиров А.И. Интересные способы быстрого счета / А.И. Владимиров, В.В. Михайлова, С.П. Шмелева // Юный ученый. 2016. — № 6.1 (9.1). — стр. 15–17.

3. Гарднер М. Математические чудеса и тайны. – М.: Наука, 1978. – 128 с.

4. История математики. С древнейших времен до начала Нового времени // История математики / Под редакцией А. П. Юшкевича, в трёх томах. Том.1 — М.: Наука, 1970. — стр. 314 – 315.

5. Камаев П.М. Устный счет, 2007. — стр. 4 – 29.

6. Trachtenberg, Yakow, The Trachtenberg’s Speed System of Basic Mathematics, 2004. – 207 p.

Просмотров работы: 104