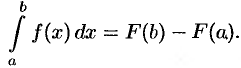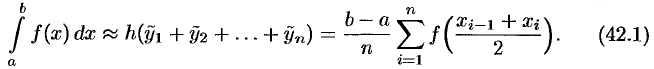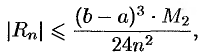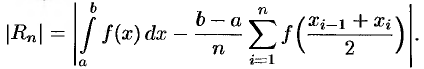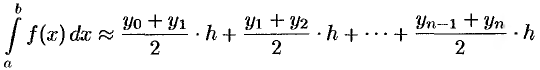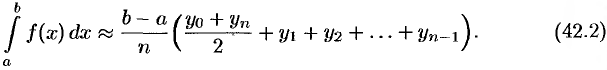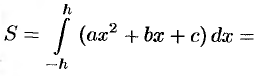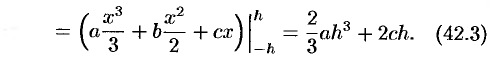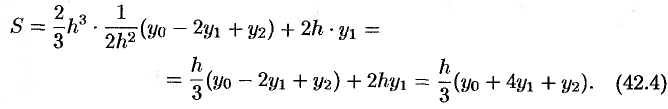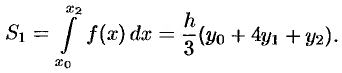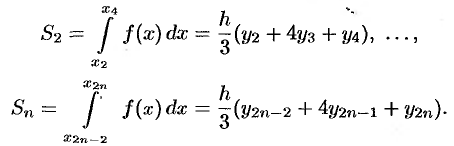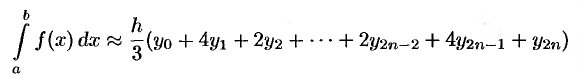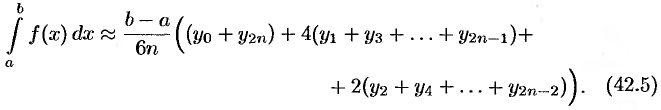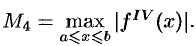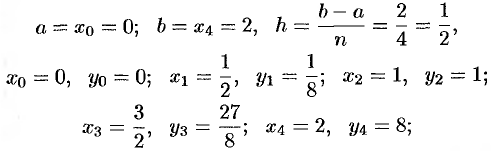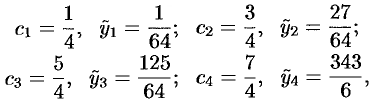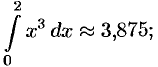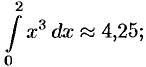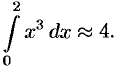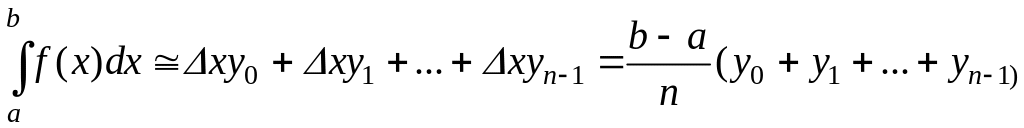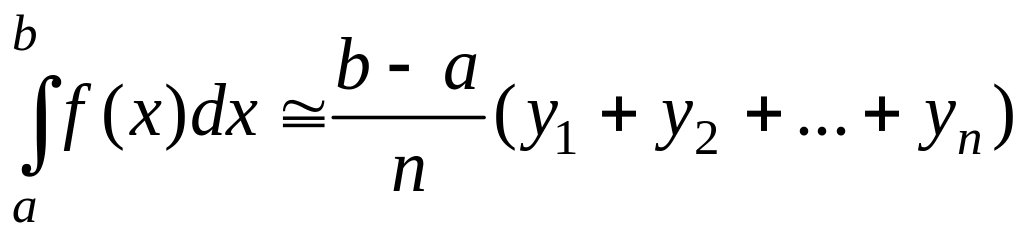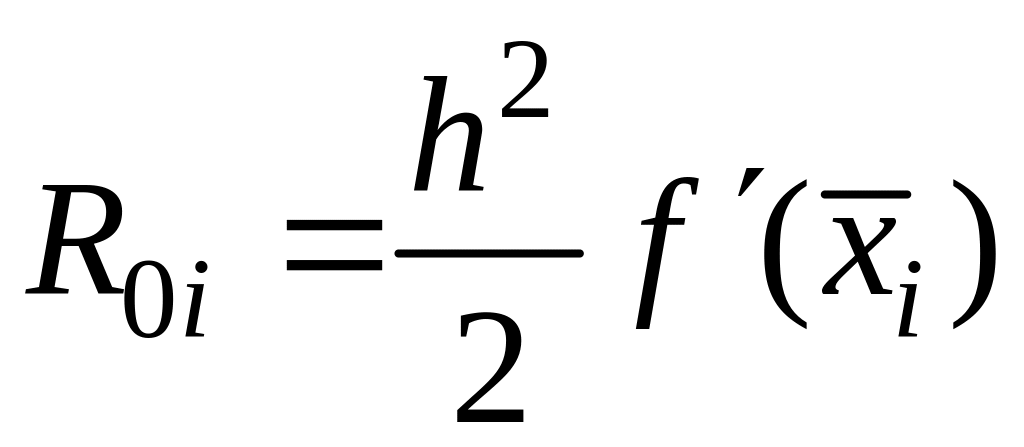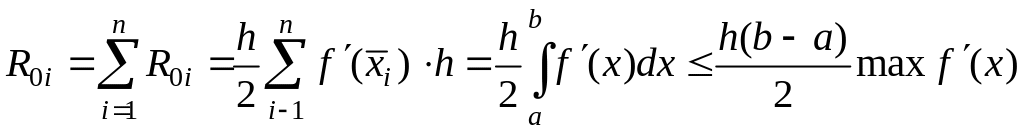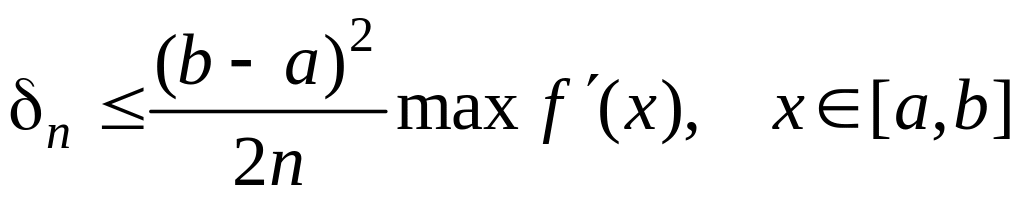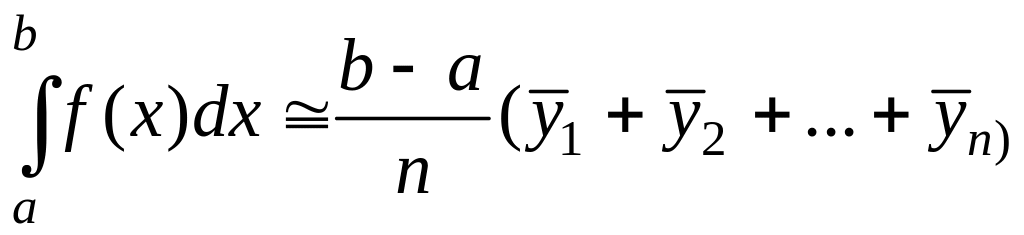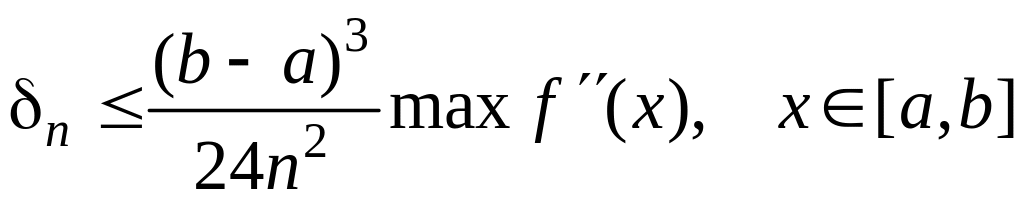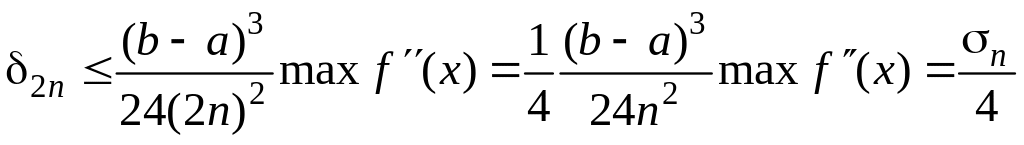Как найти приближенное значение определенного интеграла

Приближенное вычисление определенного интеграла

Пусть требуется найти определенный интеграл 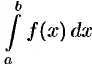от непрерывной функции . Если можно найти первообразную функции , то интеграл вычисляется по формуле Ньютона-Лейбница:

Но отыскание первообразной функции иногда весьма сложно; кроме того, как известно, не для всякой непрерывной функции ее первообразная выражается через элементарные функции. В этих и других случаях (например, функция 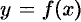задана графически или таблично) прибегают к приближенным формулам, с помощью которых определенный интеграл находится с любой степенью точности.

Рассмотрим три наиболее употребительные формулы приближенного вычисления определенного интеграла — формулу прямоугольников, формулу трапеций, формулу парабол (Симпсона), основанные на геометрическом смысле определенного интеграла.

Формула прямоугольников

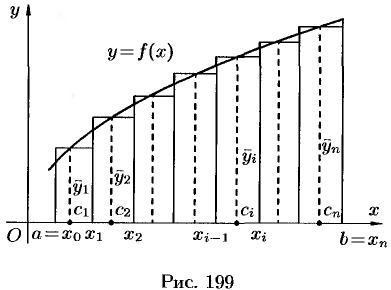
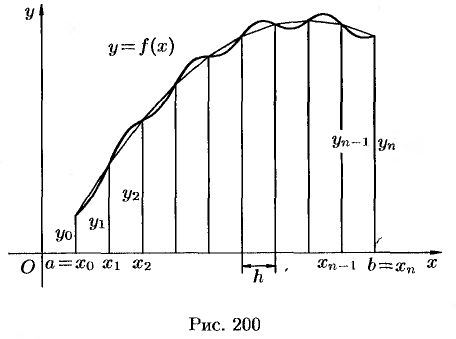
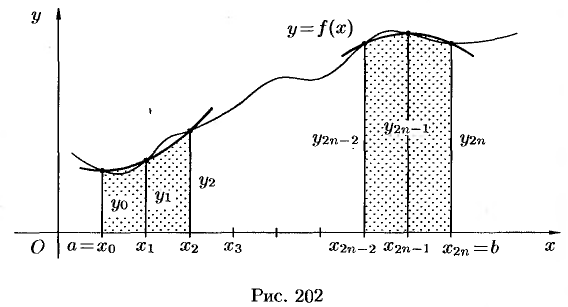
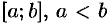
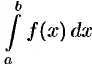
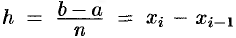
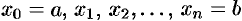
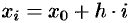
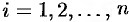
Пусть на отрезке , задана непрерывная функция . Требуется вычислить интеграл , численно равный площади соответствующей криволинейной трапеции. Разобьем основание этой трапеции, т. е. отрезок , на равных частей (отрезков) длины (шаг разбиения) с помощью точек . Можно записать, что , где (см. рис. 199).

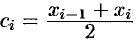
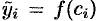
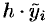
В середине каждого такого отрезка построим ординату графика функции . Приняв эту ординату за высоту, построим прямоугольник с площадью .

Тогда сумма площадей всех прямоугольников дает площадь ступенчатой фигуры, представляющую собой приближенное значение искомого определенного интеграла

Формула (42.1) называется формулой средних прямоугольников.

Абсолютная погрешность приближенного равенства (42.1) оценивается с помощью следующей формулы:

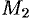
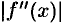
где — наибольшее значение на отрезке ,

Отметим, что для линейной функции 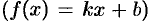формула (42.1) дает точный ответ, поскольку в этом случае .

Формула трапеций

Формулу трапеций получают аналогично формуле прямоугольников: на каждом частичном отрезке криволинейная трапеция заменяется обычной.

Разобьем отрезок на равных частей длины . Абсциссы точек деления (рис. 200). Пусть — соответствующие им ординаты графика функции. Тогда

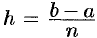
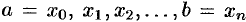
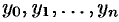
расчетные формулы для этих значений примут вид , , ; .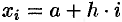

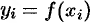
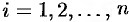
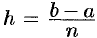
Заменим кривую ломаной линией, звенья которой соединяют концы ординат и (). Тогда площадь криволинейной трапеции приближенно равна сумме площадей обычных трапеций с основаниями , и высотой :

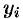
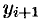
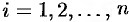
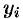
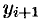
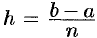
или

Формула (42.2) называется формулой, трапеций.

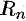
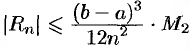
Абсолютная погрешность приближения, полученного по формуле трапеций, оценивается с помощью формулы ,
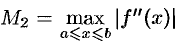
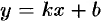
где . Снова для линейной функции формула (42.2) — точная.

Формула парабол (Симпсона)

Если заменить график функции на каждом отрезке разбиения не отрезками прямых, как в методах трапеций и прямоугольников, а дугами парабол, то получим более точную формулу приближенного вычисления интеграла .

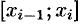
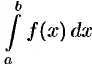
Предварительно найдем площадь криволинейной трапеции, ограниченной сверху графиком параболы , сбоку — прямыми и снизу — отрезком .

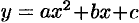
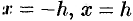
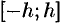
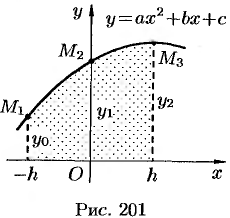
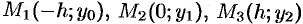
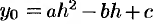
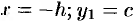
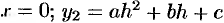
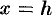
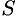
Пусть парабола проходит через три точки , где — ордината параболы в точке — ордината параболы в точке — ордината параболы в точке (см. рис. 201). Площадь равна

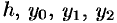
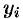
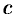
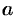
Выразим эту площадь через . Из равенств для ординат находим, что . Подставляя эти значения и в равенство (42.3), получаем

Получим теперь формулу парабол для вычисления интеграла .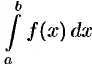

Для этого отрезок разобьем на равных частей (отрезков) длиной точками . В точках деления вычисляем значения подынтегральной функции : , где (см. рис. 202).

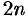
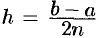
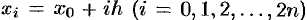
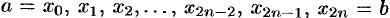
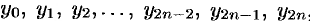
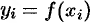
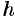
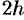
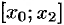
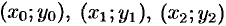
Заменяем каждую пару соседних элементарных криволинейных трапеций с основаниями, равными , одной элементарной параболической трапецией с основанием, равным . На отрезке парабола проходит через три точки . Используя формулу (42.4), находим

Аналогично находим

Сложив полученные равенства, имеем

или

Формула (42.5) называется формулой парабол (или Симпсона).

Абсолютная погрешность вычисления по формуле (42.5) оценивается соотношением

, где

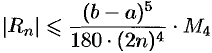
Отметим, что формула (42.5) лает точное значение интеграла 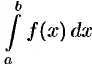во всех случаях, когда — многочлен, степень которого меньше или равна трем (тогда ).

Пример №42.1.

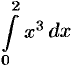
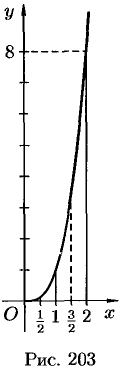
Вычислить , разбив отрезок интегрирования [0; 2] на 4 части.

Решение:

Имеем: ,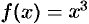

(см. рис. 203)

а) по формуле прямоугольников:

, т.е.

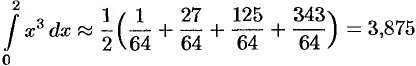
б) по формуле трапеции:

т.е.

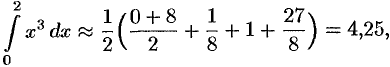
в) по формуле парабол:

т.е.

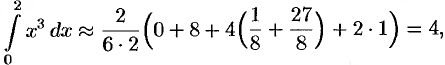
Точное значение интеграла .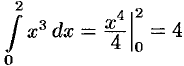

Абсолютные погрешности соответствующих формул таковы:

.

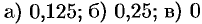
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:

• Решение задач по высшей математике

Другие темы по высшей математике возможно вам они будут полезны:

Методические указания к расчетной работе

«Приближенное вычисление определенных интегралов»

I. Теоретическая часть

1. Постановка задачи

Пусть требуется вычислить,  где  непрерывная на промежутке  функция. Если можно найти первообразную  функции , то
интеграл вычисляется по формуле Ньютона – Лейбница  Но
формула Ньютона – Лейбница не всегда позволяет вычислить данный определенный
интеграл. Во многих случаях первообразные функции либо вообще не выражаются
через элементарные функции, либо оказываются слишком сложными для расчетов.
Если же подынтегральная функция  задана в виде таблицы,
то понятие первообразной вообще теряет смысл. Здесь на помощь приходит
приближенное вычисление определенных интегралов с необходимой точностью. (Кстати
на практике часто не требуется знать точное значение данного интеграла).

   Задача численного интегрирования состоит в нахождении приближенного
значения интеграла  по заданным или вычисленным
значениям подынтегральной функции  в некоторых точках
(узлах) отрезка  Численное определение
однократного интеграла называется механической квадратурой, а
соответствующие формулы численного интегрирования – квадратурными.
Рассмотри простейшие из них.

2. Метод  прямоугольников

Если   на сегменте , то  представляет собой площадь криволинейной
трапеции , ограниченной сверху графиком функции  снизу отрезком  оси
Ox, с боков отрезками прямых  

                                                                                     

                       Рис.
3.1                                                                  Рис. 3.2

Составим интегральную   сумму, соответствующую делению отрезка  на  равных
частей (отрезков) длины  точками  . Обозначим далее через  значения функции   в
точках  деления        

Составим суммы   Каждая из этих сумм
является интегральной суммой для  на отрезке  и поэтому приближенно выражает интеграл.  Обозначив,
      получим                                                 (3.1)

                                                              (3.2)       
              Формулы (3.1) и (3.2) называют формулами
прямоугольников.

   Формула (3.1) выражает площадь ступенчатой фигуры, составленной из
«входящих» прямоугольников (см. рис. 3.1)), а формула (3.2) – площадь
ступенчатой фигуры, составленной из «выходящих» прямоугольников (см. рис. 3.2)).

    Ошибка, совершаемая при вычислении интеграла по формулам прямоугольников,
будет тем меньше, чем больше число  (т.е. чем меньше шаг
деления ).

  Абсолютная погрешность приближенных равенств (3.1) и (3.2)
оценивается с помощью следующей формулы  

                                             (3.3)

3. Метод трапеций

  Естественно ожидать, что мы получим более точное значение
определенного интеграла, если данную кривую  заменим
не ступенчатой линией, как это было в формуле прямоугольников, а вписанной
ломаной (см. рис. 3.3).

Разобьем отрезок  на  равных частей длины  Абсциссы   точек деления   Пусть  —
соответствующие им ординаты графика функции. Тогда расчетные формулы для этих
значений примут вид

                                                                             

                                                                        
         

                                                                              
Заменим кривую  ломаной

                                                                              
линией,      звенья              которой

                                                                              
соединяют      концы         ординат

                              Рис. 3.3                                                                                  

 Тогда площадь криволинейной трапеции приближенно
равна сумме площадей обычных трапеций с основаниями  и
высотой   :

                                              или

                                                      (3.4)

   Формулу (3.4) называют  формулой трапеций, так
как её геометрический смысл связан с заменой площади каждой прямоугольной
полоски, на которые  разбивается криволинейная трапеция, на площадь
прямоугольной трапеции (рис. 3.3).

    Заметим, что формулы (3.1), (3.2), (3.4) приближают интеграл  тем лучше, чем больше , т.е. число делений промежутка . Известно, что абсолютная ошибка R_n
, которая получается при
замене определённого интеграла на  его приближенным
значением по формуле трапеций –

                           , где .                                  (3.5)

    Отсюда видно, что при возрастании  ошибка
убывает примерно как  

4. Метод парабол  (метод Симпсона [1])

    Если заменить график функции  на
каждом отрезке  разбиения не отрезками прямых,
как в методах трапеций и прямоугольников, а дугами парабол, то получим более
точную формулу приближенного интеграла      Предварительно
     найдём   площадь    S  криволинейной трапеции,

ограниченной сверху графиком параболы  сбоку – прямыми    и  снизу  –  отрезком .  Пусть  парабола  проходит  через  три точки
          

где  — ордината параболы в точке

 —
ордината параболы   в точке

;  —
ордината параболы в

точке  (см. рис 3.4). Площадь S
равна                                                      

                                                                                                                    
Рис. 3.4.

                                (3.6)

Выразим эту площадь через  Из равенств для
ординат  находим, что   Подставляя эти значения  и  в
равенство (3.6), получаем

 

                                                                                              (3.6?)

Получим теперь формулу парабол для вычисления интеграла
 

Для этого отрезок  разобьём на  равных частей (отрезков) длинной  точками  В
точках деления  вычисляем значения
подынтегральной функции  где   (см. рис.3.5)

Заменяем каждую пару соседних элементарных криволинейных трапеций с
основаниями, равными , одной элементарной  параболической
трапецией с основанием, равным .

На отрезке  парабола проходит
через три точки  Используя формулу (3.6) находим
        

Аналогично находим ,…,

Сложив полученные равенства, имеем

            или

. (3.7)

Формула (3.7) называется формулой парабол (или Симпсона).

Абсолютная погрешность вычисления по формуле (3.7) оценивается соотношением         
          где         (3.8)

 убывает примерно как .

Если, например то формулы прямоугольников и
трапеций дают ошибку порядка , а параболическая  формула
–.

Отметим, что формула (3.7) даёт точное значение интеграла  во всех случаях, когда  — многочлен, степень которого меньше или
равна трём (тогда ).

   Если отыскание четвертой производной подынтегральной функции
затруднительно, то для оценки погрешности вычисления интеграла  по формуле Симпсона можно применить
следующий прием.

   Полагая , вычисляют приближенное
значение данного интеграла по формуле Симпсона для шага ;
пусть найденное значение интеграла есть ; затем
шаг  удваивают, и вычисление по формуле
Симпсона проводят для шага ; пусть найденное
значение интеграла есть ; погрешность второго
вычисления приблизительно в 16 раз больше погрешности первого и обе они имеют
одинаковый знак. Поэтому погрешность первого вычисления

( при шаге ) определяется следующей
формулой (учитывающей и знак погрешности):     (этот
способ можно назвать оценкой погрешности формулы Симпсона по методу удвоения
шага вычислений).

5. Графическое интегрирование

  Это еще один способ вычисления определенного интеграла, который
применяется тогда, когда подынтегральная функция задана графически. Этот метод
основан на теореме о среднем.

Теорема о среднем. Если непрерывная на функция, то внутри этого промежутка
найдется, по крайней мере одно значение такое,
что,                                                                             (3.9)

т.е. в точке , где  функция принимает свое среднее значение.

    Равенство (3.9) представим в виде   и
предположим, что  на , тогда
геометрический смысл теоремы состоит в том, что площадь криволинейной трапеции
равна площади прямоугольника с тем же основанием  и
высотой, равной среднему значению функции или ординате в точке  (рис. 3.6). На рис. 3.6 функция достигает
среднего значения в двух точках

                          Рис.
3.6                                                               Рис. 3.7

Рассмотрим криволинейную трапецию (рис. 3.7), площадь ее по теореме о
среднем  равна —
площади прямоугольника с высотой , и длиной .  Проведем «на глаз» горизонтальную
прямую, примерно так чтобы получить нужный прямоугольник. Абсциссы точек
пересечения прямой и кривой будут те точки , о
которых упоминается в теореме о среднем. Отложим на оси Ox,
слева от начала координат
масштабную единицу, (на рис. 3.7 ) и продолжим
проведенную горизонтальную прямую до пересечения с осью ординат. (Если a<0,
то лучше вначале слева от a провести вертикальную прямую, и при дальнейших действиях заменить ось Oy этой прямой). Пусть прямая пересекает ось Oy в точке Q, тогда OQ=f().
Соединим точки P и
Q и
из точки a проведем
прямую aM параллельно PQ до
пересечения в точке M с
ординатой из точки b.

    Покажем, что , т.е. величина
отрезка bM численно равна значению определенного
интеграла.

    Действительно . Отсюда

                               .

        

Замечание. На рис.3.7 функция f(x)>0
 и bM>0. Высказанное предложение имеет место для любой
непрерывной на функции f(x). Например,  на рис. 3.8 функция f(x) меняет знак.

Заштрихованные площади равны по модулю и  противоположны по знаку,        будет

               Рис. 3.8                           отрицателен. Проведя
предыдущие построения, получаем отрезок bM, величина которого отрицательна и здесь .

II. Порядок выполнения работы

Задание 3.1

Вычислить  по формуле Ньютона – Лейбница и
по приближенным формулам прямоугольников, трапеций и Симпсона, разбивая
интервал интегрирования на  равных частей. Оценить
в процентах погрешность результатов, полученных по приближенным формулам.

Решение:

1.    
Вычислим по формуле
Ньютона – Лейбница .

2.    
Делим интервал интегрирования
 на  равных
частей длиной  точками ,
при этом . (Для формулы  Симпсона на  частей с шагом ).

3.    
Вычислим значения
подынтегральной функции

4.    
Полученные значения
занесем в таблицу 3.1:

                   Таблица 3.1          5.  Вычислим данный
интеграл по   приближенным

                                           формулам:

k	xk=x0+kh	yk=f(xk)
0	x0=a	y0
1	x1=a+h	y1
…	…	…
n	xn=a+nh	yn

                1) по первой формуле
прямоугольников

                   .

      Найдем абсолютную ошибку этого приближения

        (по недостатку)  и   относительную

(процентную) ошибку     .

2) по второй формуле прямоугольников     .

Найдем для этого приближения абсолютную и относительную (по избытку)
(см.1)).

3) по формуле трапеций          .

Найдем абсолютную и относительные ошибки.

4) по формуле
Симпсона    .

Найдем абсолютную и
относительные ошибки этого приближения.

5.    
Результаты занесем в
таблицу 3.2.                                                   Таблица 3.2

Методы вычисления	Фор-ла Ньютона- Лейбница	Фор-ла  прямоугол.	Фор-ла трапеций	Фор-ла Симпсона
по недост.	по избыт.
	—
	—

Задание 3.2

Определить на какое число частей следует разделить интервал
интегрирования , для приближенного вычисления
интеграла  методом:

а) прямоугольников;  б) трапеций;  в) Симпсона, чтобы получить заданную
точность вычисления .

Решение:

а). Найдем  для формул
прямоугольников:

1. Найдем производную подынтегральной функции .

2. Найдем наибольшее значение  на   .

3. Подставив значения , запишем выражение  предельной
абсолютной погрешности   .

4. Решая неравенство , где — заданное значение, найдем искомое  число
 .

б) Найдем  для формулы трапеций:

1. Найдем , дифференцируя найденное
значение  второй раз.

2. Найдем наибольшее значение  на  .

3. Подставив значения , запишем выражение
предельной абсолютной погрешности: .

4. Решая неравенство , где — заданное значение точности, найдем
искомое число .

в) Найдем    для формулы
Симпсона:

1. Найдем , дважды дифференцируя найденную
вторую производную .

2. Найдем наибольшее значение  на   .

3. Подставив значения , запишем выражение
предельной абсолютной погрешности: .

4. Решая неравенство , где — заданная степень точности, найдем
искомое число .

Задание 3.3.

   Пусть функция   представлена на кривой, изображенной на рис. Графически
проинтегрировать эту кривую.

Решение:

1.    
Разобьем  на n не
обязательно равных частей, но так, чтобы на каждом частичном интервале
функция вела себя монотонно точками . Отмечаем середину
каждого из частичных интервалов: , проводим ординаты
точек  до пересечения с кривой и проектируем
точки пересечения на ось Oy. Получаем OQ₁=f(), OQ₂=f(),…, OQ_n=f(). Будем
считать, что точки , это точки, фигурирующие в
теореме о среднем на промежутке , т.е. . Так как промежуток  мал, то мы считаем, что — середина промежутка.

2.    
Слева от начала координат
на оси  Ox откладываем
отрезок OP, причем
(масштабная единица) и соединяем P с
точками Q_1, Q_2,…,Q_n.

3.    
Из точки a проводим прямую  aM₁//PQ₁ до пересечения в точке M₁ с ординатой из x₁. Согласно
высказанного вначале предложения

                                                     .

4.    
 Далее из точки M₁ проводим прямую M₁M₂//PQ₂ до
пересечения в точке M₂ с ординатой из  x₂.

                                                      .

5.    
Из точки M₂ проводим прямую M₂M₃//PQ₃ до
пересечения в точке M₃ с
ординатой из x₃.

                                                         
.                  И т.д.

6.    
Из точки M_n-1 проводим прямую M_n-1M_n//PQ_n до
пересечения в точке M_n с
ординатой из  x_n=b.  

                                                           .

Замечание. Ломанная   aM₁M₂…M_n  изображает (приближенно) график функции   (см.
рис. 3.9). Так что если взять какое-то значение x, то ордината ломанной, соответствующая этому
значению x, будет
величина . Конечно, чем больше n,
тем точнее получается
результат.

III. Примеры

Задание 3.1

Вычислить  по формуле Ньютона – Лейбница и
по приближенным формулам прямоугольников, трапеций и Симпсона, разбивая
интервал интегрирования на 8 равных частей. Оценить в процентах погрешность
результатов, полученных по приближенным формулам.

Решение:

1.    
Вычислим по формуле
Ньютона – Лейбница   .

1.    
Делим интервал
интегрирования  на  равных
частей длиной точками .

3.    
Вычислим значения
подынтегральной функции

4. Полученные значения
занесем в таблицу 3:

                                                                  
                                         Таблица 3.3       

k	0	1	2	3	4	5	6	7	8
xk	1	2	3	4	5	6	7	8	9
yk	1,0000	2,6458	3,6056	4,3589	5,0000	5,5678	6,0828	6,5574	7,0000

   5.  Вычислим
данный интеграл по     приближенным формулам:

1) по первой формуле прямоугольников:       .

Найдем абсолютную ошибку этого приближения (по недостатку) =

=  и относительную (процентную) ошибку  

                               =

2) по второй формуле прямоугольников      .

Найдем для этого приближения абсолютную ошибку (по избытку)   и относительную ошибку

                             

3) по формуле трапеций           .

Найдем абсолютную ошибку этого
приближения        и        относительную        ошибку

                             

4) по формуле
Симпсона .

Найдем абсолютную
ошибку  и относительную ошибку этого приближения

                                

4.    
Результаты занесем в
таблицу 3.4.

Таблица 3.4

Методы вычисления	Фор-ла Ньютона- Лейбница	Фор-ла  прямоугол.	Фор-ла трапеций	Фор-ла Симпсона
по недост.	по избыт.
	38	34,8183	40,8183	37,8183	37,9655
	—	3,1817	2,8183	0,1817	0,0345
	—	8,37%	7,42%	0,48%	0,09%

Задание 3.2

  Определить на какое число частей следует разделить интервал
интегрирования , для приближенного вычисления
интеграла  методом:

а) прямоугольников;  б) трапеций;  в) Симпсона  с точностью  

Решение:

а). Найдем  для формул
прямоугольников:

1. Найдем производную подынтегральной функции .

2. Найдем наибольшее значение  на  .

3. Подставив значения , запишем выражение 
предельной абсолютной погрешности   .

4. Решая неравенство ,  найдем искомое
число . Т.к. 0,00001=10^-5, то,
 Следовательно, чтобы

вычислить данный интеграл с точностью до 0,00001 надо разделить
интервал интегрирования на n=123246 равных частей.

б) Найдем  для
формулы трапеций:

1. Найдем , дифференцируя найденное
значение  второй раз.

                                       

2. Найдем наибольшее значение  на

                                      

3. Подставив значения
, запишем выражение предельной абсолютной погрешности:

4. Решая неравенство

Нашли число n=180 (как ближайшее целое число к 179,58), на которое надо разбить
интервал интегрирования, чтобы вычислить приближенно по формуле трапеций данный
интеграл с точностью 0,00001

в) Найдем    для формулы
Симпсона:

1. Найдем , дважды дифференцируя найденную
вторую производную :

2. Найдем наибольшее значение  на   .

3. Подставив значения
, запишем выражение предельной абсолютной
погрешности: .

4. Решая неравенство

     Ближайшее четное число  большее 8,5
 — n=10 ,
следовательно, интервал интегрирования надо разделить на 10 равных частей,
чтобы при вычислении данного интеграла получить  его приближенное значение  по
формуле Симпсона с точностью  до 0,00001.

Задание 3.3.

Графически проинтегрировать кривую, изображенную на рис. 3.9.

                 

                                                 Рис. 3.9

Решение:

   Пусть функция   представлена на кривой, изображенной на рис.8.

1.    
Разобьем на n не
обязательно равных частей, но так, чтобы на каждом частичном интервале
функция вела себя монотонно. На рис. 3.9  n=4 и точки деления a=x_0, x_{1 ,}x_{2 ,}x_3,x₄=b.

2.    
Отмечаем середину каждого
из частичных интервалов: , проводим ординаты
точек  до пересечения с кривой и проектируем
точки пересечения на ось Oy. Получаем OQ₁=f(), OQ₂=f(), OQ₃=f(), OQ₄=f(). Будем
считать, что точки , это точки, фигурирующие в
теореме о среднем на промежутке , т.е. . Так как промежуток  мал, то мы считаем, что — середина промежутка.

3.    
Слева от начала координат
на оси  Ox откладываем
отрезок OP, причем
(масштабная единица) и соединяем P с
точками Q_1, Q_2,Q_3,Q₄.

4.    
Из точки a проводим прямую  aM₁//PQ₁ до пересечения в точке M₁ с ординатой из x₁. Согласно
высказанного вначале предложения

                                                     .

5.    
Далее из точки M₁ проводим прямую M₁M₂//PQ₂ до
пересечения в точке M₂ с ординатой из  x₂.

                                                      .

6.    
Из точки M₂ проводим прямую M₂M₃//PQ₃ до
пересечения в точке M₃ с
ординатой из  x₃.

                                                       .

7.    
Из точки M₃ проводим прямую M₃M₄//PQ₄ до
пересечения в точке M₄ с
ординатой из  x₄=b.  

                                                           .

         IV. Контрольные вопросы

1. В каких случаях применяется приближенное вычисление определенных
интегралов?

2. Формулы прямоугольников.

3. Формула трапеций.

4. Формула Симпсона.

5. Формула абсолютной погрешности.

6. Формула относительной погрешности.

7.
Когда применяется графическое интегрирование?

8. Сформулировать теорему о среднем.

9. Графический смысл теоремы о среднем.

10. Алгоритм метода графического интегрирования?

           V. Индивидуальные задания

       Задание 3.1      Вычислить  по формуле Ньютона – Лейбница и по
приближенным формулам прямоугольников, трапеций и Симпсона, разбивая интервал
интегрирования на  равных частей. Оценить в
процентах погрешность результатов, полученных по приближенным формулам.
Вычисления вести с четырьмя знаками после запятой.

Таблица 3.5

№ вар	,	№ вар	,	№ вар	,
1	n=10.	11		21
2	, n=10.	12		22
3	n=10.	13		23
4	n=10.	14		24
5	, n=10.	15		25
6	n=10.	16		26
7	, n=10.	17		27
8	n=10.	18		28
9	, n=10.	19		29
10	, n=10.	20		30

Задание 3.2

     Определить на какое число частей следует разделить интервал
интегрирования , для приближенного вычисления
интеграла  методом: а) прямоугольников;  б)
трапеций;  в) Симпсона, чтобы получить заданную точность вычисления .

Таблица 3.6

№ вар     ,	№ вар     ,	№ вар     ,
1. ,	11.	21.
2. ,	12.	22.
3. ,	13.	23.
4. ,	14.	24.
5.	15.	25.
6.	16.	26.
7. ,	17.	27.
8. ,	18.	28.
9.	19.	29.
10.	20.	30.

Вычисление
линейного интеграла с помощью
неопределенного по формуле Ньютона-Лейбница
на практике, как уже отмечалось, не
всегда возможно. Во-первых, первообразная
не всегда выражается через элементарные
функции или через известные неэлементарные,
т.е. не всегда её можно найти. Во-вторых,
найденная первообразная может оказаться
очень громоздкой. И наконец функция
f(х),
которую надо проинтегрировать, может
быть задана не формулой, а , например,
таблицей значений или графиком.

Во
всех этих случаях линейный интеграл
вычисляют приближенно с помощью
численного интегрирования. Существует
много различных способов и формул для
приближенного вычисления линейного
интеграла. Сущность большинства из них
состоит в замене подынтегральной функции
f(х)
аппроксимирующей функцией φ(х),
для которой можно легко найти первообразную,
т.е.

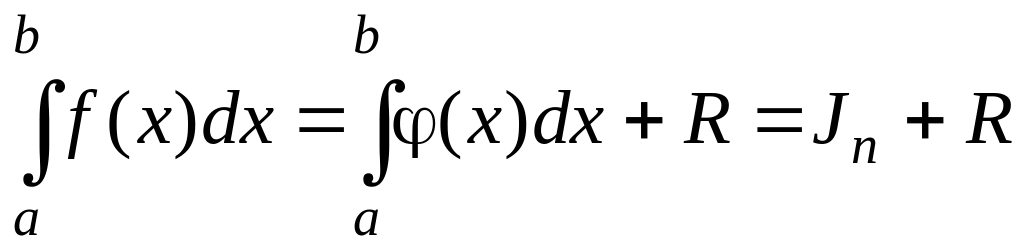
где
J_n
– приближенное
значение интеграла,

R
– погрешность вычисления.

Мы
рассмотрим некоторые простейшие методы
класса Ньютона-Котеса исходя из
геометрического смысла
линейного интеграла. В этих методах
подынтегральную функцию заменяют
многочленом, от степени которого зависит
количество узлов, где необходимо
вычислить значение функции f(х).
Алгоритмы этих методов просты и легко
поддаются программной реализации.

3.8.1. Формула прямоугольников

Отметим, что при
выводе этой формулы подынтегральную
функцию заменяют многочленом нулевой
степени, т.е. числом.

Требуется
вычислить:

,
где f(х)
– непрерывна в замкнутом интервале [а,
b].
Будем исходить из того, что величина
интеграла

равна площади криволинейной трапеции
(рис.1). Вычислим эту площадь следующим
образом. Разобьем интервал [а,
b]
на n
равных
частей, так что:

(Рис.3.8.1).

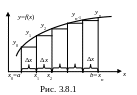
На
всех частных интервалах построим
прямоугольники, с высотами, равными
значениям функции в
начале
каждого частного интервала:

у₀,
у₁,
…, у_n-1.

Тогда
за площадь криволинейной трапеции
приближенно можно принять сумму площадей
построенных прямоугольников, т.е.

(3.8.1)

Если
на каждом частном интервале длиною Δх
построить прямоугольники с высотами
у₁,
у₂,
…, у_n
– равными значениям функции в конце
каждого частичного интервала, то величина
интеграла приближенно будет равна:

(3.8.2)

Формулы
(3.8.1) и (3.8.2) называют формулами левых и
правых прямоугольников. В случае
возрастающей функции, как показано на
рисунке 3.8.1, формула (3.8.1) дает значение
интеграла с недостатком (нижняя сумма
Дарбу), а формула (3.8.2) с избытком.

Обе
формулы имеют сравнительно большую
погрешность (первого порядка малости).
Так для левых прямоугольников главный
член погрешности на частичном интервале
равен

.

Суммирование
по всему интервалу [а,
b]
дает общую ошибку

.

Если
учесть, что

,
то верхнюю
границу абсолютной ошибки можно записать
так

.

При
уменьшении
в два раза числа разбиений интервала
[а,
b]
абсолютная ошибка возрастает также в
два раза.

По
сравнению с формулами (3.8.1) и (3.8.2) более
точным является метод средних
прямоугольников,
т.е. когда значения функции f(х)
вычисляют в срединах каждого частного
интервала:

(3.8.3)

При этом верхняя
граница абсолютной ошибки равна

.

Если число точек
(узлов) увеличить в два раза, точность
формулы (3.8.3) улучшится в четыре раза. В
самом деле

.

Однако,
если подынтегральная функция f(х)
определяется из эксперимента в дискретном
наборе узлов, то метод средних
прямоугольников применить нельзя из-за
отсутствия значений f(х)
в средних точках

.
В этом случае для интегрирования
используют другие методы Ньютона-Котеса.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #