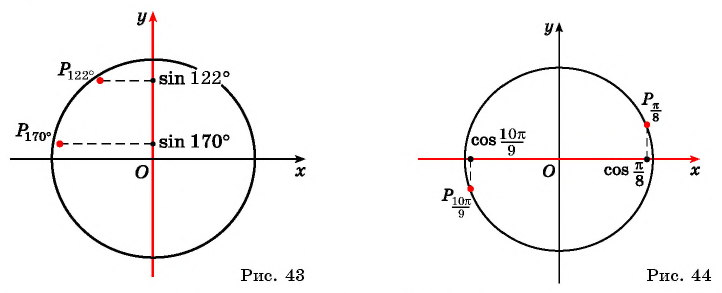
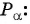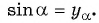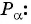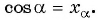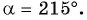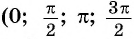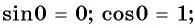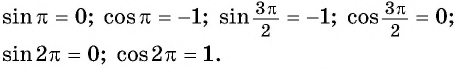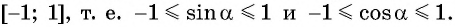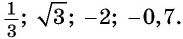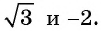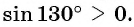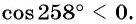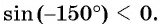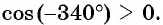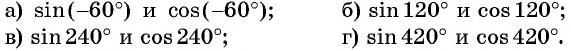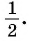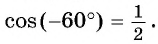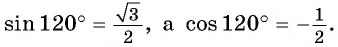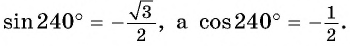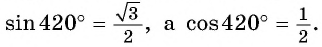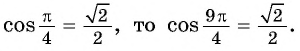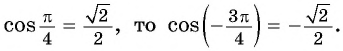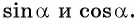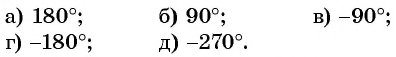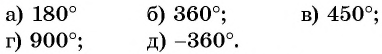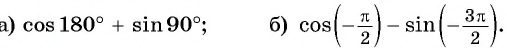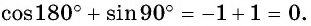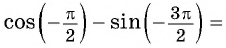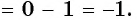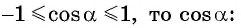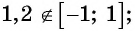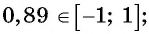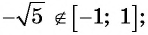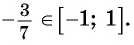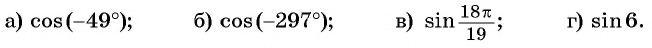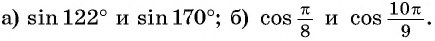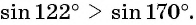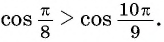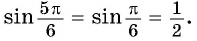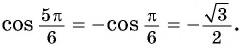Содержание:
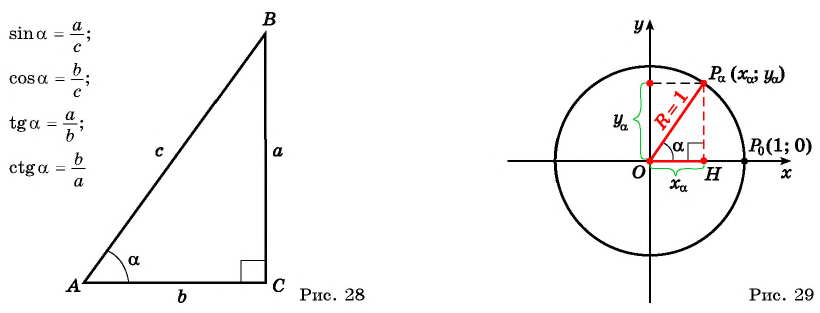
При изучении геометрии вы рассматривали отношения сторон в прямоугольном треугольнике и познакомились с понятиями синуса, косинуса, тангенса и котангенса острого угла (рис. 28).
Построение синуса и косинуса произвольного угла
Построим точку
Рассмотрим прямоугольный треугольник 
Таким образом, синус угла 
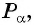
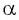
Поскольку в тригонометрии рассматриваются углы 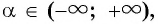
Определение синуса произвольного угла
Определение:
Синусом угла 
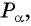
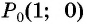
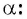
Определение косинуса произвольного угла
Определение:
Косинусом угла 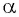
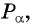
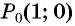
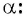
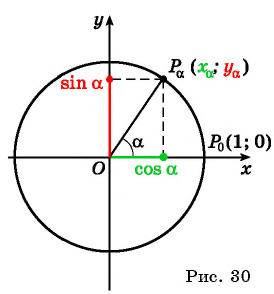
Для того чтобы найти синус и косинус произвольного угла 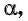
- Построить точку
единичной окружности.
- Найти ординату точки
- Найти абсциссу точки
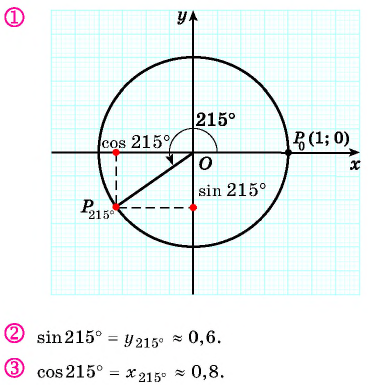
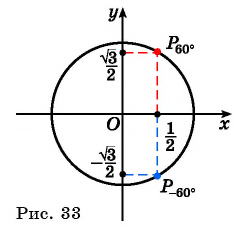
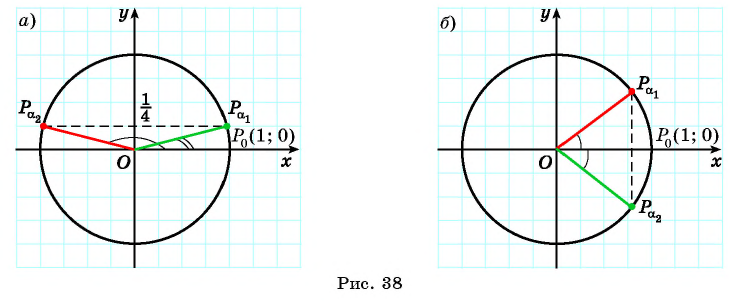
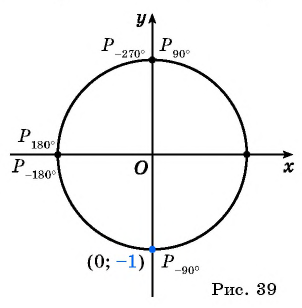
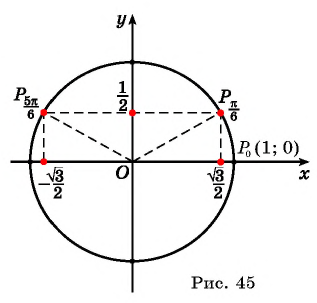
Найдите синус и косинус угла
Значения синуса и косинуса произвольного угла с помощью единичной окружности в основном можно указать только приближенно.
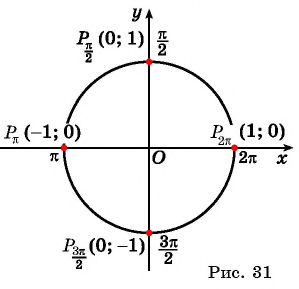
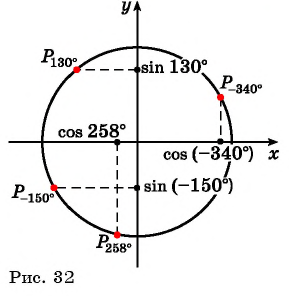
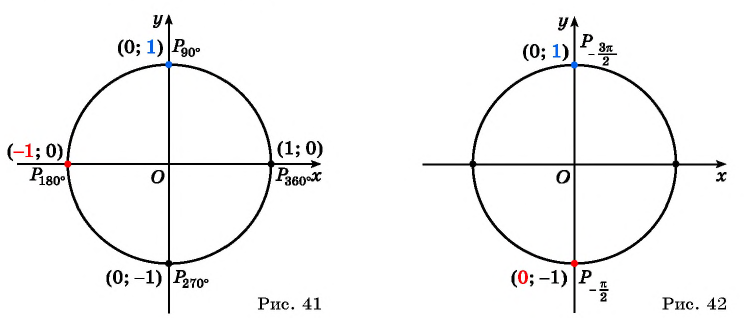
Однако для некоторых углов значения синуса и косинуса можно указать точно. Определим значения синуса и косинуса для углов, которые соответствуют точкам пересечения окружности с осями координат 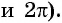
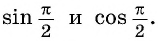
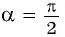
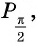
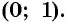
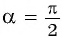
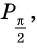
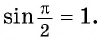
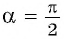
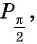
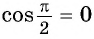
Пользуясь определением синуса и косинуса угла 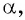
Так как ординаты и абсциссы точек единичной окружности изменяются от -1 до 1, то значения синуса и косинуса произвольного угла принадлежат промежутку
Например, выясним, может ли 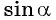
Значения синуса произвольного угла принадлежат отрезку 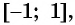
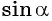
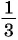
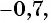
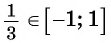
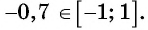
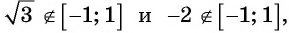
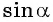
По определению синуса и косинуса угла 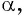
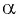
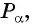
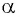
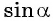
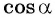
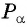
Пример №1
Определите знак выражения:
Решение:
а) Так как 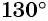
б) Так как 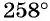
в) Так как 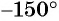
г) Так как 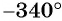
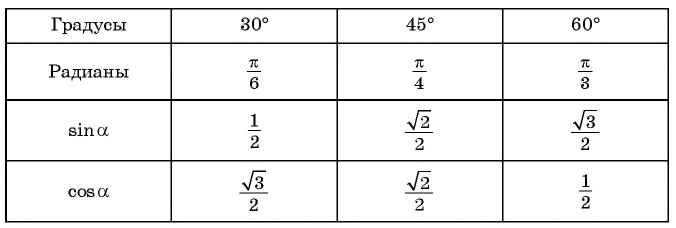
Из геометрии нам известны значения синусов и косинусов острых углов (см. табл.).
С помощью этих значений можно находить значения синусов и косинусов некоторых других углов
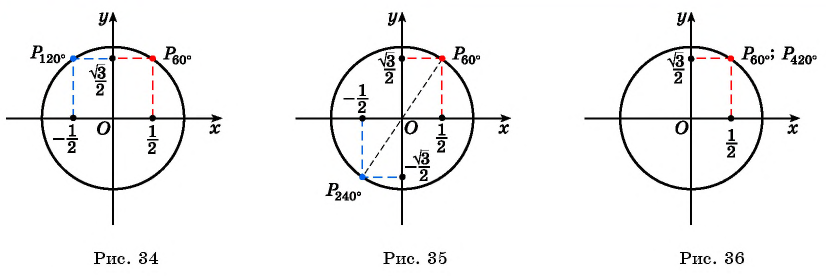
Пример №2
Вычислите:
Решение:
а) Отметим на единичной окружности точку 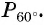
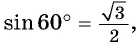
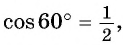
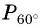
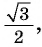
Точки 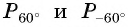
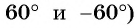
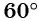
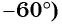
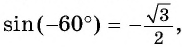
б) Так как 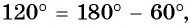
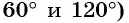
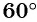
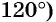
в) Точки 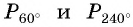
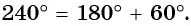
г) Поскольку 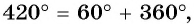
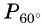
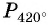
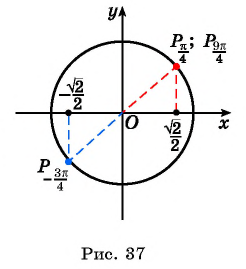
Пример №3
Вычислите:
Решение:
а) Так как 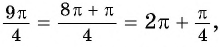
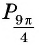
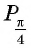
Поскольку
б) Точки 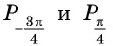
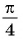
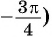
Пример №4
Постройте один из углов, если:
Решение:
а) Так как 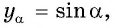
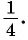
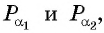
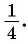
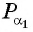
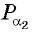
б) Так как 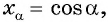
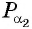
- Заказать решение задач по высшей математике
Примеры заданий и их решения:
Пример №5
Точка 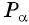
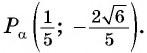
Решение:
Синусом угла 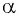
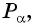
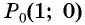
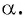
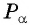
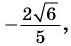
Косинусом угла 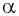
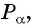
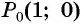
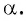
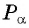
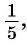
Пример №6
Если 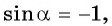
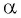
Выберите правильный ответ.
Решение:
Так как синусом угла 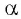
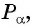
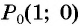
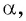
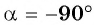
Пример №7
Если 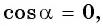
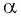
Выберите правильный ответ.
Решение:
Так как косинусом угла 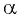
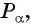
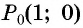
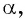
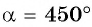
Пример №8
Найдите значение выражения:
Решение:
а) Абсцисса точки 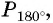
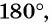
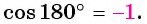
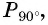
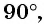

б) 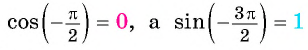
Может ли 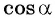
Решение:
Поскольку
а) не может быть равным 1,2, так как
б) может быть равным 0,89, так как
в) не может быть равным 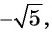
г) может быть равным 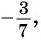
Пример №9
Определите знак выражения:
Решение:
а) 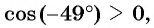
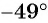
б) 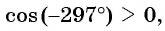
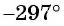
в) 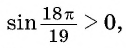
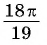
г) 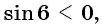
Пример №10
Сравните:
Решение:
а) Отметим на единичной окружности точки, соответствующие углам 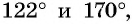
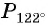
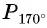
б) Сравним абсциссы точек единичной окружности 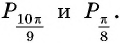
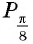
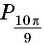
Пример №11
С помощью единичной окружности найдите значение:
Решение:
а) Ордината точки 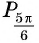
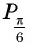
б) Абсцисса точки 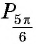
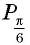
- Определение тангенса и котангенса произвольного угла
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
- Функция y=sin x и её свойства и график
- Функция y=cos x и её свойства и график
- Дробно-рациональные уравнения
- Дробно-рациональные неравенства
- Прогрессии в математике — арифметическая, геометрическая
- Единичная окружность — в тригонометрии
Как найти синус, зная угол
Одной из фундаментальных основ точных наук является понятие о тригонометрических функциях. Они определяют простые отношения между сторонами прямоугольного треугольника. К семейству данных функций относится синус. Найти его, зная угол, можно большим количеством способов, включающих экспериментальные, вычислительные методы, а также использование справочной информации.

Вам понадобится
- — калькулятор;
- — компьютер;
- — электронные таблицы;
- — таблицы брадиса;
- — бумага;
- — карандаш.
Инструкция
Используйте калькулятор с функцией вычисления синуса для получения нужных значений на основании знания угла. Подобный функционал сегодня имеют даже самые простые устройства. При этом вычисления производятся с очень высокой степенью точности (как правило, до восьми и более знаков после запятой).
Примените программное обеспечение, представляющее собой среду для работы с электронными таблицами, запущенное на персональном компьютере. Примерами подобных приложений являются Microsoft Office Excel и OpenOffice.org Calc. Введите в любую ячейку формулу, состоящую из вызова функции вычисления синуса с нужным аргументом. Нажмите Enter. В ячейке отобразится искомая величина. Преимуществом электронных таблиц является возможность быстрого расчета значений функций для большого набора аргументов.
Узнайте приближенное значение синуса угла из таблиц Брадиса, если они имеются в наличии. Их недостатком является точность значений, ограниченная четырьмя знаками после запятой.
Найдите приближенное значение синуса угла, совершив геометрические построения. На листе бумаги вычертите отрезок. При помощи транспортира отложите от него угол, синус которого необходимо найти. Начертите еще один отрезок, пересекающий первый в некоторой точке. Перпендикулярно первому же отрезку проведите прямую линию, пересекающую два уже существующих отрезка. Получится прямоугольный треугольник. Измерьте длину его гипотенузы и катета, противолежащего углу, построенному при помощи транспортира. Разделите второе значение на первое. Это и будет искомая величина.
Рассчитайте синус угла, используя разложение в ряд Тейлора. Если значение угла представлено в градусах, переведите его в радианы. Используйте формулу вида: sin(х) = х — (х^3)/3! + (х^5)/5! — (х^7)/7! + (х^9)/9! — … Для повышения скорости расчетов записывайте текущее значение числителя и знаменателя последнего члена ряда, производя вычисление следующего значения на основе предыдущего. Увеличивайте длину ряда для получения более точной величины.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
В статье мы расскажем, как находить значения:
(cos300^°), (sin(-540^°)), (cos 510^°), (sin(-135^°))
и других тригонометрических выражений без тригонометрической таблицы.
Как вычисляются синусы и косинусы углов?
Чтобы вычислить косинус и синус некоторого угла нужно:
1. Отложить этот угол на тригонометрическом круге и определить какая точка соответствует этому углу;
2. Найти абсциссу и ординату этой точки. Косинус угла равен — абсциссе, а синус угла — ординате.
Предположим, стоит задача найти косинус и синус угла (30^°). Отложим на круге угол в (30^°) и найдем какая точка соответствует этому углу.
Если построить все точно, то видно, что абсцисса точки равна (0,866)… , что равно числу (frac{sqrt{3}}{2}) , а ордината равна (0,5), то есть (frac{1}{2}).

Получается, (cos 30^° = frac{sqrt{3}}{2}), а (sin30^° =frac{1}{2}).
Аналогично и для любой другой точки на круге: значение абсциссы равно косинусу угла, а ординаты – синусу угла. Поэтому:
В тригонометрии ось абсцисс (ось x) часто называют «ось косинусов», а ординат (ось y) – «ось синусов».
Обычно на осях не отмечают (0,1); (0,2); (0,3) и т.д., а сразу наносят стандартные значения для синуса и косинуса: (±frac{1}{2}=±0,5); (±frac{sqrt{2}}{2} ≈±0,707); (±frac{sqrt{3}}{2} ≈±0,866).
Первый шаг к тому, чтобы находить синусы и косинусы стандартных углов – научится отмечать эти углы на тригонометрическом круге.
Как отметить любой угол на тригонометрическом круге?
Для этого нужно знать несколько фактов:
- Начало отсчета находится в крайней правой точке окружности;
-
Чтоб отложить положительный угол нужно двигаться против часовой стрелки от начала отсчета, чтобы отметить отрицательный – по часовой стрелке;
-
Градусная мера окружности равна (360^°), полуокружности (180^°), а четверти (90^°);
-
Углы в (0^°), (30^°), (45^°) и (60^°) выглядят так:


- Одна точка может соответствовать разным углам;
- Угол может быть больше (360^°). В этом случае он просто сделает полный оборот и пойдет дальше. Фактически, можно (360^°) просто отбросить и откладывать тот угол, который останется – в итоге вы всё равно окажетесь в той же точке.
Пример. Отметьте угол в (90^° ) и (-90^°).
Решение:

Пример. Отметьте угол в (225^° ) и (-135^°).
Решение: (225^°=180^°+45^°)
(-135^°=-90^°-45^°)

Пример. Отметьте угол в (420^° ) и (-390^°).
Решение: (420^°=360^°+60^°)
(-390^°=-360^°-30^°)


Задание 1. Отметьте на окружности точки соответствующие углам: (720^°), (225^°), (300^°), (870^°), (900^°), (-330^°), (-630^°), (-210^°).
Как находить синус и косинус любого угла?
Простой алгоритм:
- Начертите тригонометрический круг и оси косинусов и синусов (не обязательно рисовать прям аккуратно, как на картинке ниже, можно и некрасиво – главное не запутаться какая точка к какому значению относится).
- Отложите на круге угол, синус и косинус которого надо найти, и определите точку на круге, соответствующую этому углу.
- Найдите координаты точки, используя картинку ниже.

Пример. Вычислите (sin300^°) и (cos300^°) .
Решение: (300^°=360^°-60^°)

(cos 300^°=frac{1}{2}), (sin{300^°}=-frac{sqrt{3}}{2}).
Пример . Вычислите (sin(-540^°)) и (cos(-540^°)) .
Решение. (-540^°=-360^°-180^°).

(-540^°) на тригонометрическом круге совпадает с (-1) на оси косинусов. То есть, координаты этой точки: ((-1;0)). Значит, (cos(-540^°)=-1), а (sin(-540^° )=0).
Да, имея перед глазами тригонометрический круг, вычислять синусы и косинусы любых углов легко. Возможно, у вас возник вопрос: «а что делать, если круга нет? Как делать такие вычисления на ЕГЭ?». Ответ очевиден – нарисовать круг самому! Для этого надо понять, как располагаются значения на нем. Подробную методику того, как это делается я рассказывала в этой статье.
Есть и другой способ запомнить тригонометрический круг – внимательно посмотреть на картинку ниже и запомнить максимальное количество элементов. После прикройте страницу и по памяти нарисуйте круг и отметьте всё, что смогли запомнить. Сверьте, что у вас получилось с тем, что было на картинке. Повторяйте эту последовательность действий пока по памяти не получится нарисовать тригонометрический круг со всеми значениями. Это займет 15 минут вашего времени, но сильно поможет в 13 задаче ЕГЭ (и не только в ней).

Примеры вычисления синуса и косинуса из ЕГЭ
В двух следующих примерах я специально рисовала круг от руки, чтобы вы увидели, как выглядят реальные решения.
Пример . Найдите значение выражения (-18sqrt{2}sin(-135^°)).
Решение. (-135^°=-90^°-45^°)

Получается (-18sqrt{2} sin(-135^° )=-18sqrt{2}cdot-frac{sqrt{2}}{2}=frac{18cdotsqrt{2}cdotsqrt{2}}{2}=9cdot 2=18.)
Ответ: (18).
Пример . Найдите значение выражения (54sqrt{3}cos(510^°)).
Решение. (510^°=360^°+150^°=360^°+180^°-30^°.)

(54sqrt{3}cos(510^°)=54sqrt{3}cdot(-frac{sqrt{3}}{2})=-frac{54cdot sqrt{3}cdot sqrt{3}}{2}=-27cdot 3=-81.)
Ответ: (-81).
Смотрите также:
Как найти тангенс и котангенс без тригонометрической таблицы? Из градусов в радианы и наборот
Тригонометрическая таблица с кругом
Почему в тригонометрической таблице такие числа?
Для тех кто хочет закрепить знания:
Задание на вычисление синусов, косинусов, тангенсов и котангенсов
Синус угла. Таблица синусов.
Синус угла через градусы, минуты и секунды
Синус угла через десятичную запись угла
Как найти угол зная синус этого угла
У синуса есть обратная тригонометрическая функция — arcsin(y)=x
sin(arcsin(y))=y
Пример sin(30°) = 1/2; arcsin(1/2) = 30°
Рассчитать арксинус
Определение синуса
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Синусом угла α называется ордината точки B единичной окружности, полученной при повороте точки P(1;0) на угол α.
sin(α) = BC/AB
sin(-α) = -sin(α)
Периодичность синуса
Функция y = sin(x) периодична, с периодом 2π
sin(α ± 2π) = sin(α)
Пример sin(5π) = sin(4π + π) = sin(π)
Таблица синусов в радианах
sin(0°) = 0sin(π/12) = sin(15°) = 0.2588190451sin(π/6) = sin(30°) = 0.5sin(π/4) = sin(45°) = 0.7071067812sin(π/3) = sin(60°) = 0.8660254038sin(5π/12) = sin(75°) = 0.9659258263sin(π/2) = sin(90°) = 1sin(7π/12) = sin(105°) = 0.9659258263sin(2π/3) = sin(120°) = 0.8660254038sin(3π/4) = sin(135°) = 0.7071067812sin(5π/6) = sin(150°) = 0.5sin(11π/12) = sin(165°) = 0.2588190451sin(π) = sin(180°) = 0sin(13π/12) = sin(195°) = -0.2588190451sin(7π/6) = sin(210°) = -0.5sin(5π/4) = sin(225°) = -0.7071067812sin(4π/3) = sin(240°) = -0.8660254038sin(17π/12) = sin(255°) = -0.9659258263sin(3π/2) = sin(270°) = -1sin(19π/12) = sin(285°) = -0.9659258263sin(5π/3) = sin(300°) = -0.8660254038sin(7π/4) = sin(315°) = -0.7071067812sin(11π/6) = sin(330°) = -0.5sin(23π/12) = sin(345°) = -0.2588190451
Таблица Брадиса синусы
| sin(0) = 0 | sin(120) = 0.8660254038 | sin(240) = -0.8660254038 |
| sin(1) = 0.01745240644 | sin(121) = 0.8571673007 | sin(241) = -0.8746197071 |
| sin(2) = 0.0348994967 | sin(122) = 0.8480480962 | sin(242) = -0.8829475929 |
| sin(3) = 0.05233595624 | sin(123) = 0.8386705679 | sin(243) = -0.8910065242 |
| sin(4) = 0.06975647374 | sin(124) = 0.8290375726 | sin(244) = -0.8987940463 |
| sin(5) = 0.08715574275 | sin(125) = 0.8191520443 | sin(245) = -0.906307787 |
| sin(6) = 0.1045284633 | sin(126) = 0.8090169944 | sin(246) = -0.9135454576 |
| sin(7) = 0.1218693434 | sin(127) = 0.79863551 | sin(247) = -0.9205048535 |
| sin(8) = 0.139173101 | sin(128) = 0.7880107536 | sin(248) = -0.9271838546 |
| sin(9) = 0.156434465 | sin(129) = 0.7771459615 | sin(249) = -0.9335804265 |
| sin(10) = 0.1736481777 | sin(130) = 0.7660444431 | sin(250) = -0.9396926208 |
| sin(11) = 0.1908089954 | sin(131) = 0.7547095802 | sin(251) = -0.9455185756 |
| sin(12) = 0.2079116908 | sin(132) = 0.7431448255 | sin(252) = -0.9510565163 |
| sin(13) = 0.2249510543 | sin(133) = 0.7313537016 | sin(253) = -0.956304756 |
| sin(14) = 0.2419218956 | sin(134) = 0.7193398003 | sin(254) = -0.9612616959 |
| sin(15) = 0.2588190451 | sin(135) = 0.7071067812 | sin(255) = -0.9659258263 |
| sin(16) = 0.2756373558 | sin(136) = 0.6946583705 | sin(256) = -0.9702957263 |
| sin(17) = 0.2923717047 | sin(137) = 0.6819983601 | sin(257) = -0.9743700648 |
| sin(18) = 0.3090169944 | sin(138) = 0.6691306064 | sin(258) = -0.9781476007 |
| sin(19) = 0.3255681545 | sin(139) = 0.656059029 | sin(259) = -0.9816271834 |
| sin(20) = 0.3420201433 | sin(140) = 0.6427876097 | sin(260) = -0.984807753 |
| sin(21) = 0.3583679495 | sin(141) = 0.629320391 | sin(261) = -0.9876883406 |
| sin(22) = 0.3746065934 | sin(142) = 0.6156614753 | sin(262) = -0.9902680687 |
| sin(23) = 0.3907311285 | sin(143) = 0.6018150232 | sin(263) = -0.9925461516 |
| sin(24) = 0.4067366431 | sin(144) = 0.5877852523 | sin(264) = -0.9945218954 |
| sin(25) = 0.4226182617 | sin(145) = 0.5735764364 | sin(265) = -0.9961946981 |
| sin(26) = 0.4383711468 | sin(146) = 0.5591929035 | sin(266) = -0.9975640503 |
| sin(27) = 0.4539904997 | sin(147) = 0.544639035 | sin(267) = -0.9986295348 |
| sin(28) = 0.4694715628 | sin(148) = 0.5299192642 | sin(268) = -0.999390827 |
| sin(29) = 0.4848096202 | sin(149) = 0.5150380749 | sin(269) = -0.9998476952 |
| sin(30) = 0.5 | sin(150) = 0.5 | sin(270) = -1 |
| sin(31) = 0.5150380749 | sin(151) = 0.4848096202 | sin(271) = -0.9998476952 |
| sin(32) = 0.5299192642 | sin(152) = 0.4694715628 | sin(272) = -0.999390827 |
| sin(33) = 0.544639035 | sin(153) = 0.4539904997 | sin(273) = -0.9986295348 |
| sin(34) = 0.5591929035 | sin(154) = 0.4383711468 | sin(274) = -0.9975640503 |
| sin(35) = 0.5735764364 | sin(155) = 0.4226182617 | sin(275) = -0.9961946981 |
| sin(36) = 0.5877852523 | sin(156) = 0.4067366431 | sin(276) = -0.9945218954 |
| sin(37) = 0.6018150232 | sin(157) = 0.3907311285 | sin(277) = -0.9925461516 |
| sin(38) = 0.6156614753 | sin(158) = 0.3746065934 | sin(278) = -0.9902680687 |
| sin(39) = 0.629320391 | sin(159) = 0.3583679495 | sin(279) = -0.9876883406 |
| sin(40) = 0.6427876097 | sin(160) = 0.3420201433 | sin(280) = -0.984807753 |
| sin(41) = 0.656059029 | sin(161) = 0.3255681545 | sin(281) = -0.9816271834 |
| sin(42) = 0.6691306064 | sin(162) = 0.3090169944 | sin(282) = -0.9781476007 |
| sin(43) = 0.6819983601 | sin(163) = 0.2923717047 | sin(283) = -0.9743700648 |
| sin(44) = 0.6946583705 | sin(164) = 0.2756373558 | sin(284) = -0.9702957263 |
| sin(45) = 0.7071067812 | sin(165) = 0.2588190451 | sin(285) = -0.9659258263 |
| sin(46) = 0.7193398003 | sin(166) = 0.2419218956 | sin(286) = -0.9612616959 |
| sin(47) = 0.7313537016 | sin(167) = 0.2249510543 | sin(287) = -0.956304756 |
| sin(48) = 0.7431448255 | sin(168) = 0.2079116908 | sin(288) = -0.9510565163 |
| sin(49) = 0.7547095802 | sin(169) = 0.1908089954 | sin(289) = -0.9455185756 |
| sin(50) = 0.7660444431 | sin(170) = 0.1736481777 | sin(290) = -0.9396926208 |
| sin(51) = 0.7771459615 | sin(171) = 0.156434465 | sin(291) = -0.9335804265 |
| sin(52) = 0.7880107536 | sin(172) = 0.139173101 | sin(292) = -0.9271838546 |
| sin(53) = 0.79863551 | sin(173) = 0.1218693434 | sin(293) = -0.9205048535 |
| sin(54) = 0.8090169944 | sin(174) = 0.1045284633 | sin(294) = -0.9135454576 |
| sin(55) = 0.8191520443 | sin(175) = 0.08715574275 | sin(295) = -0.906307787 |
| sin(56) = 0.8290375726 | sin(176) = 0.06975647374 | sin(296) = -0.8987940463 |
| sin(57) = 0.8386705679 | sin(177) = 0.05233595624 | sin(297) = -0.8910065242 |
| sin(58) = 0.8480480962 | sin(178) = 0.0348994967 | sin(298) = -0.8829475929 |
| sin(59) = 0.8571673007 | sin(179) = 0.01745240644 | sin(299) = -0.8746197071 |
| sin(60) = 0.8660254038 | sin(180) = 0 | sin(300) = -0.8660254038 |
| sin(61) = 0.8746197071 | sin(181) = -0.01745240644 | sin(301) = -0.8571673007 |
| sin(62) = 0.8829475929 | sin(182) = -0.0348994967 | sin(302) = -0.8480480962 |
| sin(63) = 0.8910065242 | sin(183) = -0.05233595624 | sin(303) = -0.8386705679 |
| sin(64) = 0.8987940463 | sin(184) = -0.06975647374 | sin(304) = -0.8290375726 |
| sin(65) = 0.906307787 | sin(185) = -0.08715574275 | sin(305) = -0.8191520443 |
| sin(66) = 0.9135454576 | sin(186) = -0.1045284633 | sin(306) = -0.8090169944 |
| sin(67) = 0.9205048535 | sin(187) = -0.1218693434 | sin(307) = -0.79863551 |
| sin(68) = 0.9271838546 | sin(188) = -0.139173101 | sin(308) = -0.7880107536 |
| sin(69) = 0.9335804265 | sin(189) = -0.156434465 | sin(309) = -0.7771459615 |
| sin(70) = 0.9396926208 | sin(190) = -0.1736481777 | sin(310) = -0.7660444431 |
| sin(71) = 0.9455185756 | sin(191) = -0.1908089954 | sin(311) = -0.7547095802 |
| sin(72) = 0.9510565163 | sin(192) = -0.2079116908 | sin(312) = -0.7431448255 |
| sin(73) = 0.956304756 | sin(193) = -0.2249510543 | sin(313) = -0.7313537016 |
| sin(74) = 0.9612616959 | sin(194) = -0.2419218956 | sin(314) = -0.7193398003 |
| sin(75) = 0.9659258263 | sin(195) = -0.2588190451 | sin(315) = -0.7071067812 |
| sin(76) = 0.9702957263 | sin(196) = -0.2756373558 | sin(316) = -0.6946583705 |
| sin(77) = 0.9743700648 | sin(197) = -0.2923717047 | sin(317) = -0.6819983601 |
| sin(78) = 0.9781476007 | sin(198) = -0.3090169944 | sin(318) = -0.6691306064 |
| sin(79) = 0.9816271834 | sin(199) = -0.3255681545 | sin(319) = -0.656059029 |
| sin(80) = 0.984807753 | sin(200) = -0.3420201433 | sin(320) = -0.6427876097 |
| sin(81) = 0.9876883406 | sin(201) = -0.3583679495 | sin(321) = -0.629320391 |
| sin(82) = 0.9902680687 | sin(202) = -0.3746065934 | sin(322) = -0.6156614753 |
| sin(83) = 0.9925461516 | sin(203) = -0.3907311285 | sin(323) = -0.6018150232 |
| sin(84) = 0.9945218954 | sin(204) = -0.4067366431 | sin(324) = -0.5877852523 |
| sin(85) = 0.9961946981 | sin(205) = -0.4226182617 | sin(325) = -0.5735764364 |
| sin(86) = 0.9975640503 | sin(206) = -0.4383711468 | sin(326) = -0.5591929035 |
| sin(87) = 0.9986295348 | sin(207) = -0.4539904997 | sin(327) = -0.544639035 |
| sin(88) = 0.999390827 | sin(208) = -0.4694715628 | sin(328) = -0.5299192642 |
| sin(89) = 0.9998476952 | sin(209) = -0.4848096202 | sin(329) = -0.5150380749 |
| sin(90) = 1 | sin(210) = -0.5 | sin(330) = -0.5 |
| sin(91) = 0.9998476952 | sin(211) = -0.5150380749 | sin(331) = -0.4848096202 |
| sin(92) = 0.999390827 | sin(212) = -0.5299192642 | sin(332) = -0.4694715628 |
| sin(93) = 0.9986295348 | sin(213) = -0.544639035 | sin(333) = -0.4539904997 |
| sin(94) = 0.9975640503 | sin(214) = -0.5591929035 | sin(334) = -0.4383711468 |
| sin(95) = 0.9961946981 | sin(215) = -0.5735764364 | sin(335) = -0.4226182617 |
| sin(96) = 0.9945218954 | sin(216) = -0.5877852523 | sin(336) = -0.4067366431 |
| sin(97) = 0.9925461516 | sin(217) = -0.6018150232 | sin(337) = -0.3907311285 |
| sin(98) = 0.9902680687 | sin(218) = -0.6156614753 | sin(338) = -0.3746065934 |
| sin(99) = 0.9876883406 | sin(219) = -0.629320391 | sin(339) = -0.3583679495 |
| sin(100) = 0.984807753 | sin(220) = -0.6427876097 | sin(340) = -0.3420201433 |
| sin(101) = 0.9816271834 | sin(221) = -0.656059029 | sin(341) = -0.3255681545 |
| sin(102) = 0.9781476007 | sin(222) = -0.6691306064 | sin(342) = -0.3090169944 |
| sin(103) = 0.9743700648 | sin(223) = -0.6819983601 | sin(343) = -0.2923717047 |
| sin(104) = 0.9702957263 | sin(224) = -0.6946583705 | sin(344) = -0.2756373558 |
| sin(105) = 0.9659258263 | sin(225) = -0.7071067812 | sin(345) = -0.2588190451 |
| sin(106) = 0.9612616959 | sin(226) = -0.7193398003 | sin(346) = -0.2419218956 |
| sin(107) = 0.956304756 | sin(227) = -0.7313537016 | sin(347) = -0.2249510543 |
| sin(108) = 0.9510565163 | sin(228) = -0.7431448255 | sin(348) = -0.2079116908 |
| sin(109) = 0.9455185756 | sin(229) = -0.7547095802 | sin(349) = -0.1908089954 |
| sin(110) = 0.9396926208 | sin(230) = -0.7660444431 | sin(350) = -0.1736481777 |
| sin(111) = 0.9335804265 | sin(231) = -0.7771459615 | sin(351) = -0.156434465 |
| sin(112) = 0.9271838546 | sin(232) = -0.7880107536 | sin(352) = -0.139173101 |
| sin(113) = 0.9205048535 | sin(233) = -0.79863551 | sin(353) = -0.1218693434 |
| sin(114) = 0.9135454576 | sin(234) = -0.8090169944 | sin(354) = -0.1045284633 |
| sin(115) = 0.906307787 | sin(235) = -0.8191520443 | sin(355) = -0.08715574275 |
| sin(116) = 0.8987940463 | sin(236) = -0.8290375726 | sin(356) = -0.06975647374 |
| sin(117) = 0.8910065242 | sin(237) = -0.8386705679 | sin(357) = -0.05233595624 |
| sin(118) = 0.8829475929 | sin(238) = -0.8480480962 | sin(358) = -0.0348994967 |
| sin(119) = 0.8746197071 | sin(239) = -0.8571673007 | sin(359) = -0.01745240644 |
Похожие калькуляторы

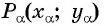
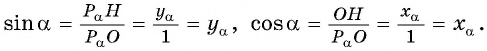
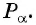
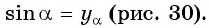
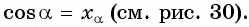
 единичной окружности.
единичной окружности.