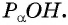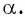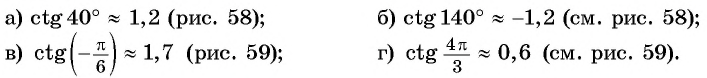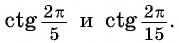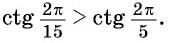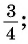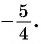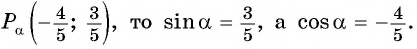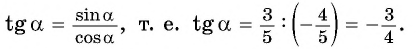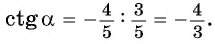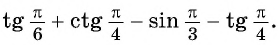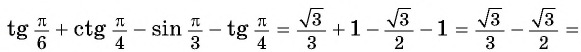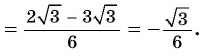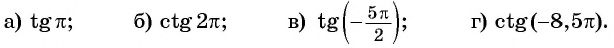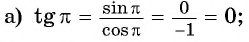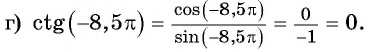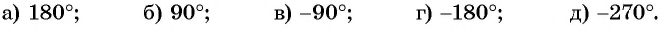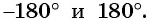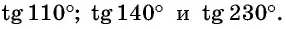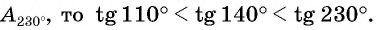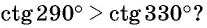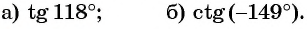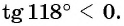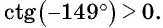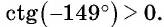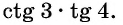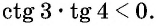Содержание:
Построим точку
По определению тангенса острого угла получим:
Определение тангенса угла
Определение:
Тангенсом угла 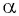
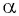
Например,
Используя определение тангенса угла и значения синуса и косинуса этого угла, найдем также значения тангенсов углов
Поскольку 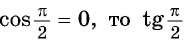
Через точку 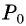
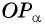
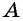
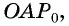
Из подобия треугольников 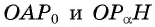
Поскольку 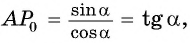
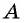
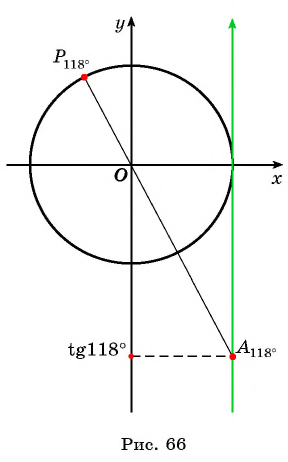
Прямая, перпендикулярная оси абсцисс, проходящая через точку 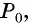
Нахождение тангенса произвольного угла
Для того чтобы найти тангенс произвольного угла а с помощью оси тангенсов, нужно:
- Построить точку
на единичной окружности.
- Продолжить прямую
до пересечения с осью тангенсов.
- Найти ординату точки пересечения прямой
с осью тангенсов.
Найдите тангенс угла
Значения тангенса произвольного угла с помощью оси тангенсов можно указать только приближенно. Для нахождения значения тангенса произвольного угла используют четырехзначные таблицы значений тангенса (синуса, косинуса)* или калькулятор. Методы высшей математики позволяют вычислять значения тангенса (синуса, косинуса) с любой заданной степенью точности.
Пример №1
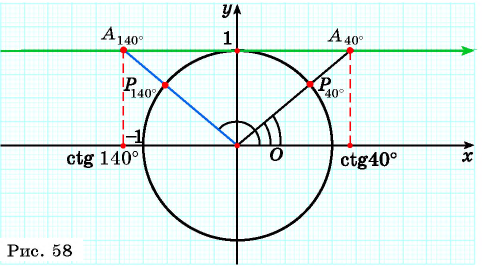
Определите с помощью оси тангенсов:
Решение:
Пример №2
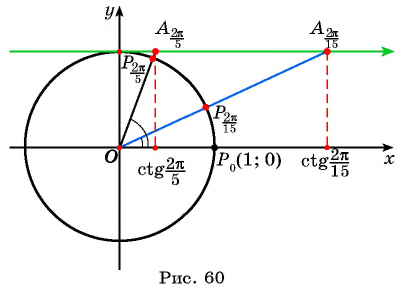
С помощью оси тангенсов сравните значения выражений
Решение:
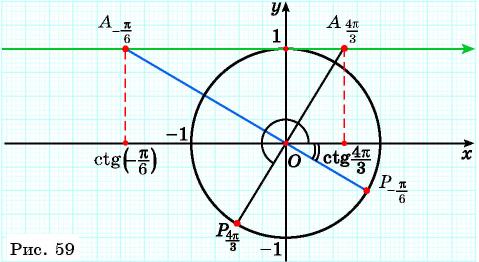
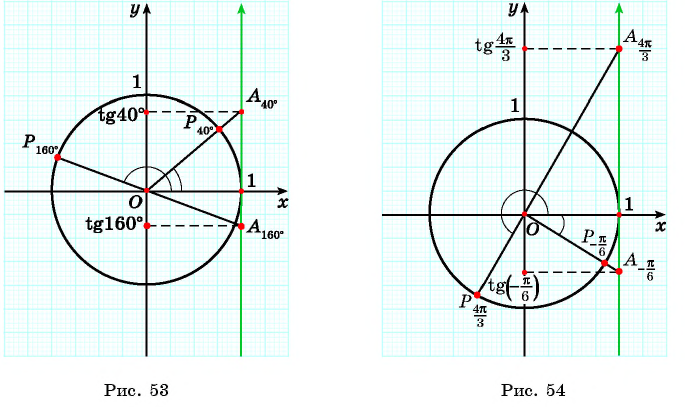
Отметим на оси тангенсов точки, соответствующие углам 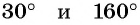
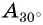
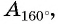
Для углов 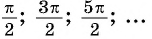
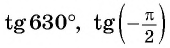
Построим точку 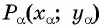
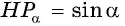
По определению котангенса острого угла получим:
Определение котангенса угла
Определение:
Котангенсом угла 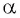
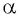
Например,
Поскольку
Воспользуемся полученным равенством и найдем значения котангенсов углов
Поскольку 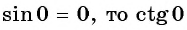
Найденные значения синуса, косинуса, тангенса и котангенса углов 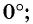
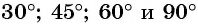
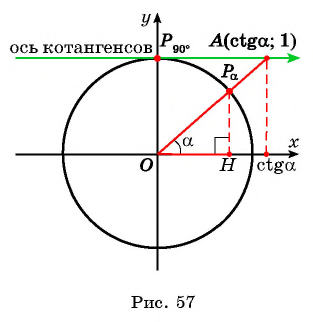
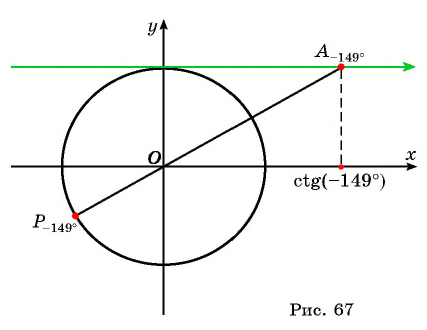
Нахождение котангенса произвольного угла
Для того чтобы найти котангенс произвольного угла 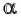
- Построить точку
на единичной окружности.
- Продолжить прямую
до пересечения с осью котангенсов.
- Найти абсциссу точки пересечения прямой
с осью котангенсов.
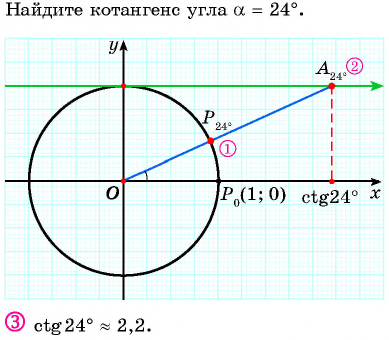
Значения котангенса произвольного угла с помощью оси котангенсов можно указать только приближенно.
- Заказать решение задач по высшей математике
Пример №3
Найдите значение выражения
Решение:
Через точку 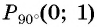
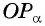
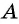
Получим треугольник 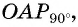
Из подобия треугольников 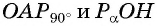
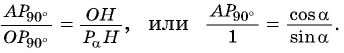
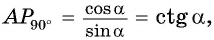
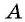
Прямая, перпендикулярная оси ординат, проходящая через точку 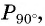
Пример №4
Определите с помощью оси котангенсов:
Решение:
Пример №5
С помощью оси котангенсов сравните значения выражений
Решение:
Отметим на оси котангенсов точки, соответствующие углам 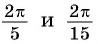
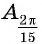
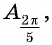
Для углов 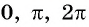
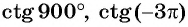
Пример №6
С помощью оси:
а) тангенсов найдите один из углов, тангенс которого равен
б) котангенсов найдите один из углов, котангенс которого равен
Решение:
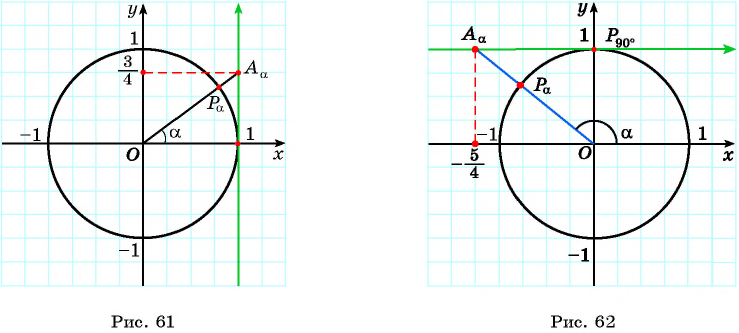
а) 1 Отметим на оси тангенсов точку 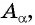
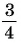
2 Соединим эту точку с началом координат.
3 Найдем соответствующую точку 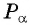
4 Отметим один из углов, соответствующий этой точке (см. рис. 61).
б) 1 Отметим на оси котангенсов точку 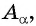
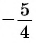
2 Соединим эту точку с началом координат.
3 Найдем соответствующую точку 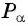
4 Отметим один из углов, соответствующий этой точке (см. рис. 62).
Пример №7
Точка 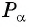
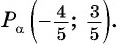
Решение:
Так как точка 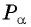
По определению тангенса:
По определению котангенса: 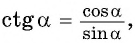
Пример №8
Найдите значение выражения
Решение:
Пример №9
Найдите, если это возможно, значение выражения:
Решение:
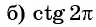
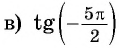
Пример №10
Если 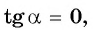
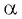
Выберите правильные ответы.
Решение:
Так как тангенсом угла 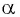
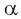
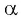
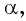
Можно также использовать ось тангенсов: найти точку на оси тангенсов, у которой ордината равна нулю (рис. 63), и определить соответствующие углы. Правильные ответы а) и г).
Пример №11
Расположите в порядке возрастания:
Решение:
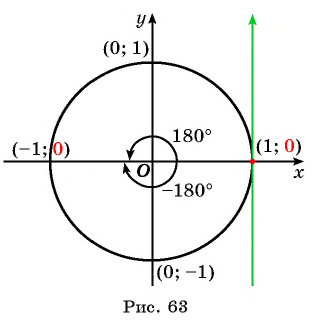
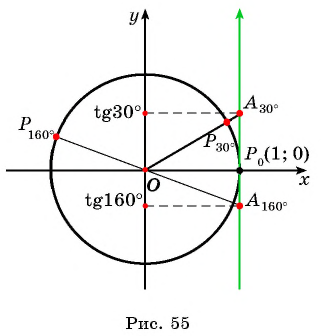
Отметим на оси тангенсов точки, соответствующие углам 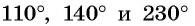
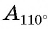
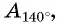
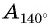
Пример №12
Верно ли, что
Решение:
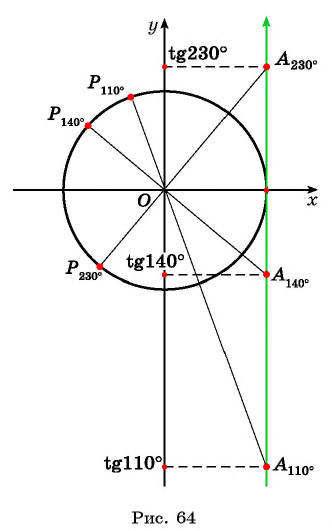
Отметим на оси котангенсов точки, соответствующие углам 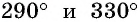
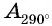
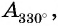
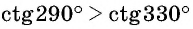
Пример №13
Определите знак выражения:
Решение:
а) Первый способ. По определению тангенса: 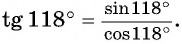
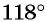
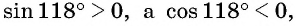
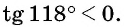
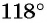
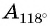
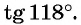
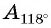
б) Первый способ. По определению котангенса 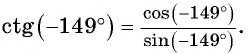
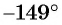
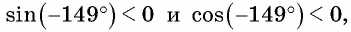
Второй способ. Отметим на оси котангенсов точку, соответствующую углу 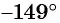
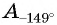
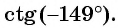
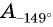
Пример №14
Определите знак произведения
Решение:
Так как угол 3 радиана находится во второй четверти, а угол 4 радиана — в третьей, то 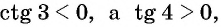
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
- Функция y=sin x и её свойства и график
- Функция y=cos x и её свойства и график
- Функции y=tg x и y=ctg x — их свойства, графики
- Дробно-рациональные неравенства
- Прогрессии в математике — арифметическая, геометрическая
- Единичная окружность — в тригонометрии
- Определение синуса и косинуса произвольного угла
|
Рис. 1.6. |
Рис. 2.1. Тангенс. |
§ 2. Тангенс
В предыдущем параграфе мы научились измерять крутизну с помощью синуса угла. Есть и другой способ измерения крутизны, составляющий, как пока еще говорят, альтернативу синусу.
Представим себе, что человек, поднимаясь по тропе, приближается к крутому берегу (рис. 2.1). Если измерять крутизну подъема с помощью отношения высоты подъема к длине пути, то получится уже знакомый нам синус. Давайте теперь вместо длины пройденного человеком пути измерять, насколько он приблизился к берегу по горизонтали. Иными словами, рассмотрим расстояние AC — проекцию пути на горизонталь. В качестве характеристики крутизны возьмем отношение BC/AC. Это отношение называется тангенсом угла.
Определение. Тангенсом острого угла в прямоугольном треугольнике называется отношение катета этого треугольника, лежащего против угла, к катету треугольника, прилежащему к углу (рис. 2.1).
Как и синус угла, тангенс не зависит от выбора прямоугольного треугольника, содержащего этот угол.
Обозначается тангенс угла α так: tg α (читается «тангенс альфа»).
Задача 2.1. Докажите, что тангенс угла не зависит от размеров прямоугольного треугольника, содержащего этот угол.
Задача 2.2. Для данного острого угла α что больше: sin α или tg α?
9

Выясним, как связаны синус и тангенс угла. Пусть, например, известен тангенс угла α; как найти его синус? Воспользуемся тем, что для вычисления tg α годится любой прямоугольный треугольник с углом α; выберем тот из них, что изображен на рис. 2.1. По
p
теореме Пифагора его гипотенуза равна 1 + tg2 α, так что
|
sin α = |
tg α |
|||||
|
p |
||||||
|
1 + tg2 α |
||||||
|
Рис. 2.1. |
Задача 2.3. Пусть α — острый угол; выведите формулу, выражающую tg α через sin α.
Задача 2.4. Для каждого из углов 10◦, 30◦, 60◦ найдите приближенные значения их тангенса. Что больше: тангенс или радианная мера? И на сколько процентов больше?
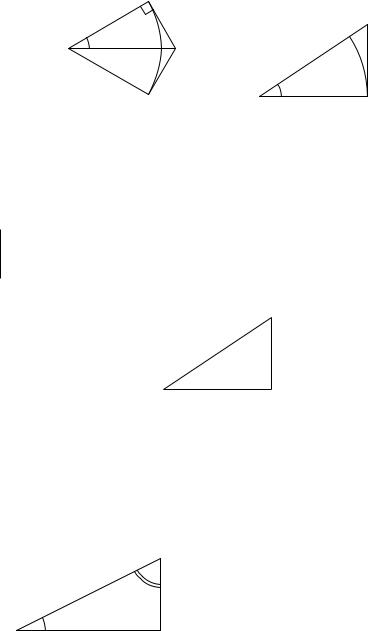
Из предыдущей задачи вы должны были увидеть, что тангенсы фигурировавших в ней углов больше, чем их радианная мера. На самом деле это верно для любых острых углов. Наглядно это можно пояснить с помощью рис. 2.2а. На нем AC = 1, так что длина дуги CMC0 равна 2α (мы считаем, что угол измерен в радианах), а длина ломаной CBC0 равна 2 tg α. Из рисунка ясно, что длина ломаной CBC0 больше, чем длина дуги CMC0,1 так что 2 tg α > 2α, откуда tg α > α.
Аккуратное доказательство этого неравенства вы узнаете, решив следующую задачу.
Задача 2.5. Докажите неравенство tg α > α.
Указание. Сравните площадь треугольника ABC и сектора AMC (рис. 2.2б). Площадь сектора равна половине произведения длины дуги, ограничивающей этот сектор, на радиус окружности.
1Веревочку CBC0 надо укоротить, чтобы она облегала дугу CMC0 вплотную.
10
|
а) |
б) |
Рис. 2.2. tg α > α.
§ 3. Косинус
Определение. Косинусом острого угла α в прямоугольном треугольнике называется отношение катета, прилежащего к углу α, к гипотенузе треугольника (рис. 3.1).

Рис. 3.1. cos α = AC/AB.
От выбора прямоугольного треугольника, содержащего угол α, это отношение не зависит.
Косинус угла α обозначается cos α («косинус альфа»).
Задача 3.1. Докажите следующие формулы:
|
а) |
sin(90◦ − α) = cos α; |
|||
|
б) |
cos(90◦ − α) = sin α; |
|||
|
в) |
tg α = sin α/ cos α. |
|||
11
|
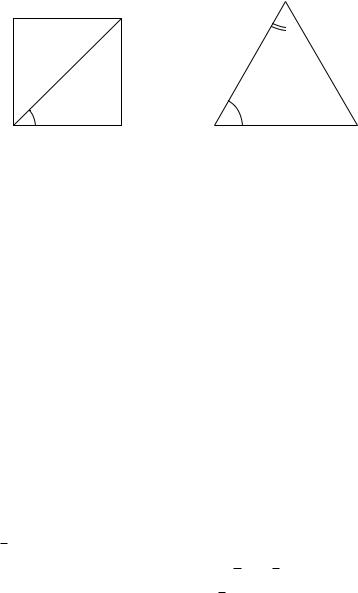
Рис. 3.2. Функции угла 45◦. |
Рис. 3.3. Углы 30◦ и 60◦. |
Задача 3.2. Докажите формулу: sin2 α + cos2 α = 1.
Указание. Воспользуйтесь теоремой Пифагора.
Задача 3.3. Пусть α — острый угол. Выведите формулу, выража-
p
ющую cos α через tg α: cos α = 1/ 1 + tg2 α.
Указание. Воспользуйтесь рис. 2.1 из предыдущего параграфа.
Задача 3.4. Боковая сторона равнобедренного треугольника равна a, угол при основании равен α. Найдите: а) основание; б) высоту, опущенную на боковую сторону; в) высоту, опущенную на основание.
Не существует простой формулы, позволяющей по величине угла найти точное значение его синуса или косинуса. Тем не менее для некоторых углов точные значения синуса, косинуса и тангенса легко вычислить. Сделаем это для углов 30◦, 45◦ и 60◦.
Начнем с угла 45◦. Чтобы посчитать его синус, косинус и тангенс, надо, согласно нашим определениям, взять прямоугольный треугольник с углом 45◦. В качестве такого треугольника можно взять половинку квадрата со стороной 1 (рис. 3.2).
Из теоремы Пифагора ясно, что диагональ этого квадрата рав-
√
на 2. Следовательно, из треугольника ACD получаем:
√ √
sin 45◦ = CD/AC = 1/ 2 = 2/2;
√
cos 45◦ = AD/AC = 2/2; tg 45◦ = CD/AD = 1.
12
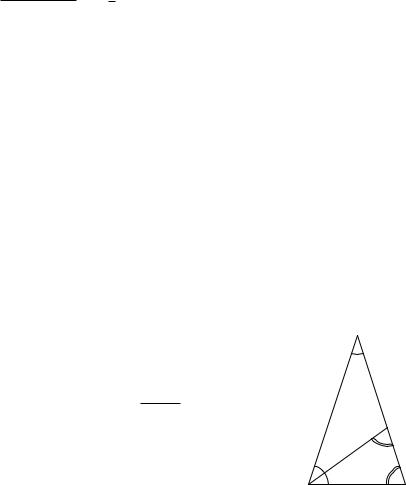
Теперь займемся углами 30◦ и 60◦. Рассмотрим равносторонний треугольник со стороной 1 и опустим в нем высоту (рис. 3.3). Эта высота разделит его на два прямоугольных треугольника с гипотенузой 1 и острыми углами 60◦ и 30◦; при этом AD = 1/2 (высота BD в равностороннем треугольнике является также бис-
сектрисой и медианой). По теореме Пифагора находим BD =
√ √
AB2 − AD2 = 3/2. Теперь, когда длины всех сторон треугольника ABD нам известны, остается только выписать:
|
sin 30◦ = AD/AB = 1/2; |
sin 60◦ = BD/AB = |
√ |
/2; |
|||||||||
|
3 |
||||||||||||
|
cos 30◦ = BD/AB = √ |
/2; |
cos 60◦ = AD/AB = 1/2; |
||||||||||
|
3 |
||||||||||||
|
tg 30◦ = AD/BD = 1/√ |
= √ |
/3; |
tg 60◦ = BD/AD = √ |
. |
||||||||
|
3 |
3 |
3 |
Кстати, тот факт, что sin 30◦ = 1/2, был известен вам и раньше, только в другом обличье, как теорема о том, что катет, лежащий против угла 30◦, равен половине гипотенузы.
Приведем более сложный пример явного вычисления синуса и косинуса. Для этого рассмотрим равнобедренный треугольник ABC с углом при основании 72◦ и углом при вершине 36◦ (рис 3.4). Проведем в нем биссектрису AM угла A и подсчитаем все углы. Из рисунка видно, что треугольники ABM и ACM равнобедренные и AC = AM = BM. Если AB = a, то AC = 2a cos 72◦, MC = 2AC cos 72◦ = 4a cos2 72◦; так как AB = BC = MC + BM = MC + AC, получаем равенство
|
a = 4a cos2 72◦ + 2a cos 72◦, |
|||||||
|
откуда 4 cos2 72◦ + 2 cos 72◦ − 1 = 0. Решая это |
|||||||
|
(квадратное) уравнение |
относительно cos 72◦, |
||||||
|
получаем |
√ |
||||||
|
cos 72◦ = |
5 − 1 |
. |
|||||
|
4 |
|||||||
|
Задача 3.5. Найдите cos 36◦. |
|||||||
|
Задача 3.6. В окружность вписан правильный |
|||||||
|
пятиугольник. Найдите отношение его стороны |
|
к радиусу окружности. |
Рис. 3.4. |
Можно доказать, что правильный многоугольник можно построить с помощью циркуля и линейки в том и только в том случае, когда
13
отношение его стороны к радиусу описанной окружности можно выразить через целые числа с помощью четырех арифметических действий и извлечения квадратного корня. Решив задачу 3.6, вы убедитесь, что правильный пятиугольник именно таков. В 1796 году К. Ф. Гаусс окончательно выяснил, какие правильные многоугольники можно построить с помощью циркуля и линейки (будущему великому немецкому математику было тогда всего 19 лет, и это была его первая научная работа). В частности, оказалось, что циркулем и линейкой можно построить правильный 17-угольник.
Для практических применений нужны не столько точные формулы, сколько приближенные значения синусов и косинусов конкретных углов. В прежние времена эти значения собирались в таблицы тригонометрических функций. Пример такой таблицы мы приводим ниже. Излишне объяснять, что таблицы, использовавшиеся на практике, давали значения тригонометрических функций не через 5◦, а с гораздо более мелким шагом. В настоящее время тригонометрические таблицы утратили былое значение: чтобы приближенно найти синус или косинус угла, достаточно нажать несколько клавиш на микрокалькуляторе или компьютере.
Таблица 3.1. Значения тригонометрических функций (с двумя знаками после запятой)
|
α |
5◦ |
10◦ |
15◦ |
20◦ |
25◦ |
30◦ |
35◦ |
40◦ |
||||||||||||||||||||||||||||
|
sin α |
0,09 |
0,17 |
0,26 |
0,34 |
0,42 |
0,50 |
0,57 |
0,64 |
||||||||||||||||||||||||||||
|
tg α |
0,09 |
0,18 |
0,27 |
0,36 |
0,47 |
0,58 |
0,70 |
0,84 |
||||||||||||||||||||||||||||
|
α |
45◦ |
50◦ |
55◦ |
60◦ |
65◦ |
70◦ |
75◦ |
80◦ |
85◦ |
|||||||||||||||||||||||||||
|
sin α |
0,71 |
0,77 |
0,82 |
0,87 |
0,91 |
0,94 |
0,97 |
0,98 |
0,99 |
|||||||||||||||||||||||||||
|
tg α |
1,00 |
1,19 |
1,43 |
1,73 |
2,14 |
2,75 |
3,73 |
5,67 |
11,43 |
|||||||||||||||||||||||||||
Задача 3.7. Найдите с помощью таблицы 3.1 приближенное значение cos 25◦.
14
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Тангенс
Тангенс – одна из тригонометрических функций. Как и для всех других функций, значение тангенса определяется для конкретного угла или числа (в этом случае используют числовую окружность.
Аргумент и значение тангенса
Аргументом тангенса может быть:
— как число или выражение с Пи: (1,3), (frac<π><4>), (π), (-frac<π><3>) и т.п.
— так и угол в градусах: (45^°), (360^°),(-800^°), (1^° ) и т.п.
Для обоих случаев тангенс вычисляется одинаковым способом – либо через значения синуса и косинуса, либо через тригонометрический круг (см. ниже).
Тангенс острого угла
Тангенс можно определить с помощью прямоугольного треугольника — он равен отношению противолежащего катета к прилежащему.
1) Пусть дан угол и нужно определить тагенс этого угла.
2) Достроим на этом угле любой прямоугольный треугольник.
3) Измерив, нужные стороны, можем вычислить тангенс.
Вычисление тангенса числа или любого угла
Для чисел, а также для тупых, развернутых углов и углов больших (360°) тангенс чаще всего определяют с помощью синуса и косинуса, через их отношение:
Пример. Вычислите (tg:0).
Решение: Чтобы найти тангенс нуля нужно найти сначала синус и косинус (0). И то, и другое найдем с помощью тригонометрического круга :
Точка (0) на числовой окружности совпадает с (1) на оси косинусов, значит (cos:0=1). Если из точки (0) на числовой окружности провести перпендикуляр к оси синусов, то мы попадем в точку (0), значит (sin:0=0). Получается: (tg:0=) (frac) (=) (frac<0><1>) (=0).
Пример. Вычислите (tg:(-765^circ)).
Решение: (tg: (-765^circ)=) (frac)
Что бы вычислить синус и косинус (-765^°). Отложим (-765^°) на тригонометрическом круге. Для этого надо повернуть в отрицательную сторону на (720^°) , а потом еще на (45^°).
Однако можно определять тангенс и напрямую через тригонометрический круг — для этого надо на нем построить дополнительную ось:
Прямая проходящая через начало отсчета на числовой окружности и параллельная оси ординат (синусов) называется осью тангенсов. Направление оси тангенсов и оси синусов совпадает.
Ось тангенсов – это фактически копия оси синусов, только сдвинутая. Поэтому все числа на ней расставляются так же как на оси синусов.
Чтобы определить тангенс с помощью числовой окружности, нужно:
1) Отметить соответствующую аргументу тангенса точку на числовой окружности.
2) Провести прямую через эту точку и начало координат и продлить её до оси тангенсов.
3) Найти координату пересечения этой прямой и оси тангенсов.
2) Проводим через данную точку и начало координат прямую.
3) В данном случае координату долго искать не придется – она равняется (1).
Пример. Вычислите (tg: 45°) и (tg: (-240°)).
Решение:
Для угла (45°) ((∠KOA)) тангенс будет равен (1), потому что именно в таком значении сторона угла, проходящая через начало координат и точку (A), пересекает ось тангесов. А для угла (-240°) ((∠KOB)) тангенс равен (-sqrt<3>) (приблизительно (-1,73)).
Значения для других часто встречающихся в практике углов смотри в тригонометрической таблице.
В отличие от синуса и косинуса значение тангенса не ограничено и лежит в пределах от (-∞) до (+∞), то есть может быть любым.
При этом тангенс не определен для:
1) всех точек (A) (значение в Пи: …(-) (frac<7π><2>) ,(-) (frac<3π><2>) , (frac<π><2>) , (frac<5π><2>) , (frac<9π><2>) …; и значение в градусах: …(-630°),(-270°),(90°),(450°),(810°)…)
2) всех точек (B) (значение в Пи: …(-) (frac<9π><2>) ,(-) (frac<5π><2>) ,(-) (frac<π><2>) , (frac<3π><2>) , (frac<7π><2>) …; и значение в градусах: …(-810°),(-450°),(-90°),(270°)…) .
Так происходит потому, что прямая проходящая через начало координат и любую из этих точек никогда не пересечет ось тангенсов, т.к. будет идти параллельно ей. Поэтому в этих точках тангенс – НЕ СУЩЕСТВУЕТ (для всех остальных значений тангенс может быть найден).
Из-за этого при решении тригонометрических уравнений и неравенств с тангенсом необходимо учитывать ограничения на ОДЗ .
Знаки по четвертям
С помощью оси тангенсов легко определить знаки по четвертям тригонометрической окружности. Для этого надо взять любую точку на четверти и определить знак тангенса для нее описанным выше способом. У всей четверти знак будет такой же.
Для примера на рисунке нанесены две зеленые точки в I и III четвертях. Для них значение тангенса положительно (зеленые пунктирные прямые приходят в положительную часть оси), значит и для любой точки из I и III четверти значение тангенса будет положительно (знак плюс).
С двумя фиолетовыми точками в II и IV четвертях – аналогично, но с минусом.
Связь с другими тригонометрическими функциями:
— котангенсом того же угла: формулой (ctg:x=) (frac<1>)
Другие наиболее часто применяемые формулы смотри здесь .
Значения тангенса и котангенса на тригонометрическом круге
В прошлой статье мы познакомились с тригонометрическим кругом и научились находить значения синуса и косинуса основных углов.
Как же быть с тангенсом и котангенсом ? Об этом и поговорим сегодня.
Где же на тригонометрическом круге оси тангенсов и котангенсов?
Ось тангенсов параллельна оси синусов (имеет тоже направление, что ось синусов) и проходит через точку (1; 0).
Ось котангенсов параллельна оси косинусов (имеет тоже направление, что ось косинусов) и проходит через точку (0; 1).
На каждой из осей располагается вот такая цепочка основных значений тангенса и котангенса: Почему так?
Я думаю, вы легко сообразите и сами. 
Собственно, картинка за себя сама говорит.
Если не очень все же понятно, разберем примеры:
Пример 1.
Вычислить
Находим на круге . Эту точку соединяем с точкой (0;0) лучом (начало – точка (0;0)) и смотрим, где этот луч пересекает ось тангенсов. Видим, что
Ответ:
Пример 2.
Вычислить
Находим на круге . Точку (0;0) соединяем с указанной точкой лучом. И видим, что луч никогда не пересечет ось тангенсов.
не существует.
Ответ: не существует
Пример 3.
Вычислить
Находим на круге точку (это та же точка, что и ) и от нее по часовой стрелке (знак минус!) откладываем (). Куда попадаем? Мы окажемся в точке, что на круге у нас (см. рис.) названа как . Эту точку соединяем с точкой (0;0) лучом. Вышли на ось тангенсов в значение .
Так значит,
Ответ:
Пример 4.
Вычислить
Поэтому от точки (именно там будет ) откладываем против часовой стрелки .
Выходим на ось котангенсов, получаем, что
Ответ:
Пример 5.
Вычислить
Находим на круге . Эту точку соединяем с точкой (0; 0). Выходим на ось котангенсов. Видим, что
Ответ:
Теперь, умея находить по тригонометрическому кругу значения тригонометрических функций (а я надеюсь, что статья, где мы начинали знакомство с кругом и учились вычислять значения синусов и косинусов, вами прочитана…), вы можете пройт и тест по теме «Нахождение значений косинуса, синуса, тангенса и котангенса различных углов».
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Нахождение значений синуса, косинуса, тангенса и котангенса
Для того, чтобы определить значение угла α, необходимо воспользоваться подходящей функции из тригонометрии. Во время решения задач постоянно возникает необходимость в том, чтобы узнать значение углов. Для некоторых углов можно найти точные значения, для других сложно определить точную цифру и можно вывести только приблизительное значение.
В этой статье мы подробно поговорим о функциях из тригонометрии. Мы не только расскажем о свойствах синуса, тангенса и других функций, но и узнаем, как правильно вычислять значения для каждого отдельного случая.
Рассмотрим подробно каждый случай.
Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других – только приблизительные.
Соотношения сторон и углов фигуры используются для того, чтобы определить значения для 30 ° , 45 ° , 60 ° . Если угол выходит за пределы 90 ° , то перед вычислением значения следует воспользоваться специальной формулой для того, чтобы привести угол к нужному виду.
Если известно значение синуса для α , можно быстро узнать значение косинуса для этого же угла. Это легко выполнить с помощью основных тождеств, которые представлены в геометрии.
В некоторых случаях для того, чтобы узнать sin или cos угла, можно использовать подходящую тригонометрическую формулу. Например, по известному значению синуса 45 ° , мы сможем определить значение синуса 30 ° , воспользовавшись правилом из тригонометрии.
Если для примера не подходит ни одно из приведенных выше решений, можно найти приближенное значение. В этом вам помогут таблицы основных тригонометрических функций, которые легко можно найти.
Если взять за основу определения, возможно определить значения для определенного угла α . Также можно вычислить значения тангенса и котангенса для определенного случая. Можно найти значений основных функций из тригонометрии для частных вариантов. Это углы 0 ° , 90 ° , 180 ° , 270 ° , 360 ° .
Разобьем эти углы на четыре группы: 360 · z градусов ( 2 π · z рад), 90 + 360 · z градусов ( π 2 + 2 π · z рад), 180 + 360 · z градусов ( π + 2 π · z рад) и 270 + 360 · z градусов ( 3 π 2 + 2 π · z рад), где z — любое целое число.
Изобразим данные формулы на рисунке:
Для каждой группы соответствуют свои значения.
При повороте из точки A на 360 · z ° , она переходит в себя. А 1 ( 1 , 0 ) . Синус 0 ° , 360 ° , 720 ° равен 0 , а косинус равен 1 . Представим это в виде формулы: sin ( 360 ° · z ) = 0 и cos ( 360 ° · z ) = 1 .
Можно определить, что t g ( 360 ° · z ) = 0 1 = 0 , а котангенс не определен.
Если А ( 1 , 0 ) повернуть на 90 + 360 · z ° , то она перейдет в А 1 ( 0 , 1 ) . По определению: sin ( 90 ° + 360 ° · z ) = 1 и cos ( 90 ° + 360 ° · z ) = 0 . Мы не сможем определить значение тангенса, но котангенс рассчитывается по данной формуле: c t g ( 90 ° + 360 ° · z ) = 0 1 = 0 .
Рассмотрим особенности для третьей группы углов. После поворота точки А ( 1 , 0 ) на любой из углов 180 + 360 · z ° , она перейдет в A 1 ( − 1 , 0 ) . Мы находим значения функций кроме тангенса.
Рассмотрим правила для четвертой группы углов. При повороте точки на 270 + 360 · z ° мы попадем в A 1 ( 0 , − 1 ) . Мы находим значения всех функций кроме тангенса.
Для углов, которые не относятся к перечню от 0 ° , 90 ° , 180 ° , 270 ° , 360 ° … , точных значений нет. Мы можем найти лишь приближенные значения. Рассмотрим пример. Условия – найти основные значения для угла − 52 ° . Выполним построения.
Согласно рисунку, абсцисса А 1 ≈ 0 , 62 , а ордината ≈ − 0 , 78 . Соответственно, sin ( — 52 ° ) ≈ — 0 , 78 и cos ( — 52 ° ) ≈ 0 , 62 . Осталось определиться с тангенсом и котангенсом.
Выполняем вычисления: t g ( — 52 ° ) ≈ — 0 , 78 0 , 62 ≈ — 1 , 26 и c t g ( — 52 ° ) ≈ 0 , 62 — 0 , 78 ≈ — 0 , 79 .
Чем точнее выполняется чертеж, тем более точными будут значения для каждого индивидуального случая. Выполнять вычисления удобно только в теории, так как на практике довольно сложно и долго выполнять рисунки.
Линии тригонометрических функций
Линии тригонометрических функций – это линии, которые изображаются вместе с единичной окружностью. Они имеют точку отсчета и единичный отрезок, которая равна единице в координатной системе. Они используются для наглядного изображения значений.
Рассмотрим их на подробном рисунке
Как найти sin α , cos α , t g α , c t g α
Для тридцати-, сорокопяти-, шестидесятиградусных углов мы имеем определенные значения. Чтобы найти их, можно воспользоваться правилами о прямоугольном треугольнике с острыми углами. Для этого используется теорема Пифагора.
Для того, чтобы узнать значения для углов тридцати- и шестидесятиградусных углов изображаем прямоугольный треугольник с углами данной величины. Длина гипотенузы должна быть равна 1 . Согласно теореме Пифагора, катет, лежащий напротив тридцатиградусного угла, равен половине гипотенузы. Воспользуемся теоремой: 1 2 — 1 2 2 = 3 2 . Так как синус угла – это катет, деленный на гипотенузу, вычисляем, что sin 30 ° = 1 2 1 = 1 2 и sin 60 ° = 3 2 1 = 3 2 .
Косинус можно найти по формуле, которая предполагает деление прилежащего катета на гипотенузу. Вычисляем: cos 30 ° = 3 2 1 = 3 2 и cos 60 ° = 1 2 1 = 1 2 .
Тангенс можно найти по формуле, которая предполагает деление противолежащего катета на прилежащий. Котангенс находим по такой же схеме – делим прилежащий катет на противолежащий.
Вычисляем: t g 30 ° = 1 2 3 2 = 1 3 = 3 3 и t g 60 ° = 3 2 1 2 = 3 . Находим котангенс по подобной схеме: с t g 30 ° = 3 2 1 2 = 3 и с t g 60 ° = 1 2 3 2 = 1 3 = 3 3 . После этого приступаем к вычислению значений основных тригонометрических функций для сорока пятиградусного угла. Используем равнобедренный треугольник с углами 45 ° и гипотенузой, которая равна 1 . Используем теорему Пифагора. Согласно формуле, длины катетов равны 2 2 . Т
Теперь мы сможем найти значения для основных тригонометрических функций. Используем формулу, которая предполагает деление длин соответствующих сторон рассматриваемого треугольника.
Выводим формулу: c t g 45 ° = 2 2 2 2 = 1 .
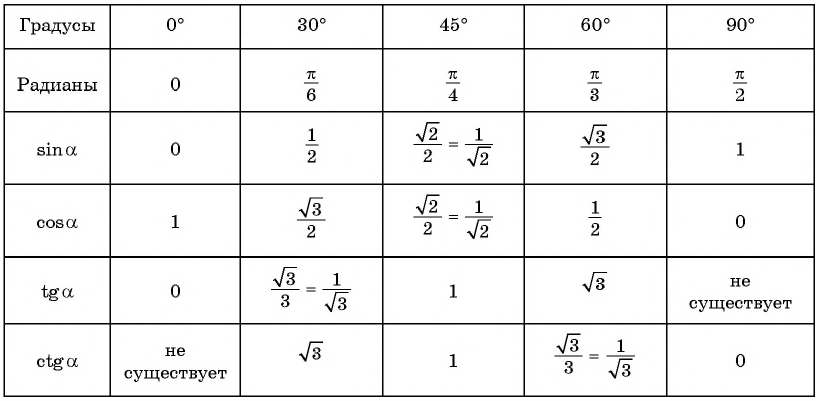
Полученные значения для тридцати-, сорокапяти-, шестидесятиградусных углов будут использоваться для решения различных задач. Запишите их – они часто будут использоваться. Для удобства можно использовать таблицу значений.
Проиллюстрируем значения для тридцати-, сорокапяти-, шестидесятиградусных углов с использованием окружности и линий.
Значения основных функций тригонометрии
Основные тождества из геометрии связывают с собой sin α , cos α , t g α , c t g α для определенного угла. С помощью одной функции вы легко сможете найти другую.
Для того, чтобы найти синус по известному косинусу, sin 2 α + cos 2 α = 1 .
Тангенс по известному косинусу t g 2 α + 1 = 1 cos 2 α .
Котангенс по известному синусу или наоборот 1 + c t g 2 α = 1 sin 2 α .
Тангенс через котангенс или наоборот можно найти благодаря удобной формуле: t g α · c t g α = 1 .
Для того, чтобы закрепить полученные знания, рассмотрим их на подробном примере
Необходимо найти значение синуса угла π 8 , если t g π 8 = 2 — 1 .
Сначала найдем котангенс угла: c t g π 8 = 1 t g π 8 = 1 2 — 1 = 2 + 1 ( 2 — 1 ) · ( 2 + 1 ) = 2 + 1 ( 2 ) 2 — 1 2 = 2 + 1 Воспользуемся формулой 1 + c t g 2 α = 1 sin 2 α . Благодаря этому мы вычисляем значение синуса. Имеем
sin 2 π 8 = 1 1 + c t g 2 π 8 = 1 1 + ( 2 + 1 ) 2 = 1 4 + 2 2 = 1 2 · ( 2 + 2 ) = 2 — 2 2 · ( 2 + 2 ) · ( 2 — 2 ) = = 2 — 2 2 · ( 2 2 — ( 2 ) 2 ) = 2 — 2 4
Для завершения необходимо определить значение синуса. Угол π 8 является углом первой четверти, то синус является положительным. Чтобы точно определить знак, вы можете воспользоваться таблицей, в которой определены знаки по четвертям координатной плоскости. Таким образом, sin π 8 = sin 2 π 8 = 2 — 2 4 = 2 — 2 2 . sin π 8 = 2 — 2 2 .
Сведение к углу
Удобнее всего находить значения для угла от 0 до 90 ° . Сведение к углу из интервала от 0 до 90 ° . Если угол не соответствует заданному интервалу, можно использовать законы и тождества, которые мы учили на уроках геометрии. Тогда мы сможем найти значение, которое будет равно для угла указанных пределах.
Задача заключается в том, чтобы найти синус 210 ° . Представим 210 как разность или сумму, разложив число на несколько. Воспользуемся соответствующей формулой для приведения. Используем формулу для нахождения значения синуса 30 ° : sin 210 ° = sin ( 180 ° + 30 ° ) = — sin 30 ° = — 1 2 , или косинуса 60 ° sin 210 ° = sin ( 270 ° — 60 ° ) = — cos 60 ° = — 1 2 .
Для того, чтобы решать задачи было намного проще, при нахождении значений переходите к углам из интервала от 0 до 90 ° с помощью формул приведения, если угол не находится в этих пределах.
Использование формул
Раннее мы рассмотрели подробности, касающиеся нахождению значений основных функций с использованием формул тригонометрии. Для того, чтобы определить значение для определенного угла, используйте формулы и значения основных функций для известных углов.
Для примера вычислим значение тангенса π 8 , который был использован в предыдущем примере. Возьмем за основу основные формулы тригонометрии.
Найдите значение t g π 8 .
Используя формулу тангенса, преобразуем уравнение до следующего равенства t g 2 π 8 = 1 — cos π 4 1 + cos π 4 . Значения косинуса угла π 4 известны из предыдущего примера. Благодаря этому мы быстро найдем значения тангенса.
t g 2 π 8 = 1 — cos π 4 1 + cos π 4 = 1 — 2 2 1 + 2 2 = 2 — 2 2 + 2 = = ( 2 — 2 ) 2 ( 2 + 2 ) · ( 2 — 2 ) = ( 2 — 2 ) 2 2 2 — ( 2 ) 2 = ( 2 — 2 ) 2 2
Угол π 8 является углом первой четверти. Согласно таблице основных тригонометрических функций по четвертям координатной плоскости, тангенс этого угла положителен. Продолжаем вычисления для дальнейшего решения: t g π 8 = t g 2 π 8 = ( 2 — 2 ) 2 2 = 2 — 2 2 = 2 — 1
Частные случаи
Тригонометрия – довольно сложная наука. Далеко не всегда можно найти формулы, используемые для вычисления. Существует множество уравнений, которые не поддаются стандартным формулам. Некоторые значения очень сложно обозначить точной цифрой. Это не так просто, как может показаться.
Однако точные значения не всегда нужны. Хватает и тех, что не претендуют на высокую точность. Благодаря существующим таблицам, которые можно найти в математических учебниках, можно найти любое приближенное значение основных функций. Благодаря справочным материалам вычислять формулы будет намного проще. В таблицах содержатся значения с высокой точностью.
http://zaochnik.com/spravochnik/matematika/trigonometrija/nahozhdenie-znachenij-sinusa-kosinusa-tangensa-i-k/
Калькулятор тангенса | Calculators.vip
Тангенс острого угла в прямоугольном треугольнике равняется отношение противолежащего катета к прилежащему катету.
.
Поделиться расчетом:
Найти величину
X=SIN(A)X=COS(A)X=TAN(A)X=CTN(A)
A=ARC SIN(X)A=ARC COS(A)A=ARC TAN(X)A=ARC CTN(X)
Первоначальные данные
Градус
Радиан
| Угол в градусах | tg (Тангенс) |
|---|---|
| 0° | 0 |
| 1° | 0.0175 |
| 2° | 0.0349 |
| 3° | 0.0524 |
| 4° | 0.0699 |
| 5° | 0.0875 |
| 6° | 0.1051 |
| 7° | 0.1228 |
| 8° | 0.1405 |
| 9° | 0.1584 |
| 10° | 0.1763 |
| 11° | 0.1944 |
| 12° | 0. |
| 13° | 0.2309 |
| 14° | 0.2493 |
| 15° | 0.2679 |
| 16° | 0.2867 |
| 17° | 0.3057 |
| 18° | 0.3249 |
| 19° | 0.3443 |
| 20° | 0.364 |
| 21° | 0.3839 |
| 22° | 0.404 |
| 23° | 0.4245 |
| 24° | 0.4452 |
| 25° | 0.4663 |
| 26° | 0.4877 |
| 27° | 0.5095 |
| 28° | 0.5317 |
| 29° | 0.5543 |
| 30° | 0.5774 |
| 31° | 0.6009 |
| 32° | 0.6249 |
| 33° | 0.6494 |
| 34° | 0.6745 |
| 35° | 0.7002 |
| 36° | 0.7265 |
| 37° | 0.7536 |
| 38° | 0.7813 |
| 39° | 0.8098 |
| 40° | 0.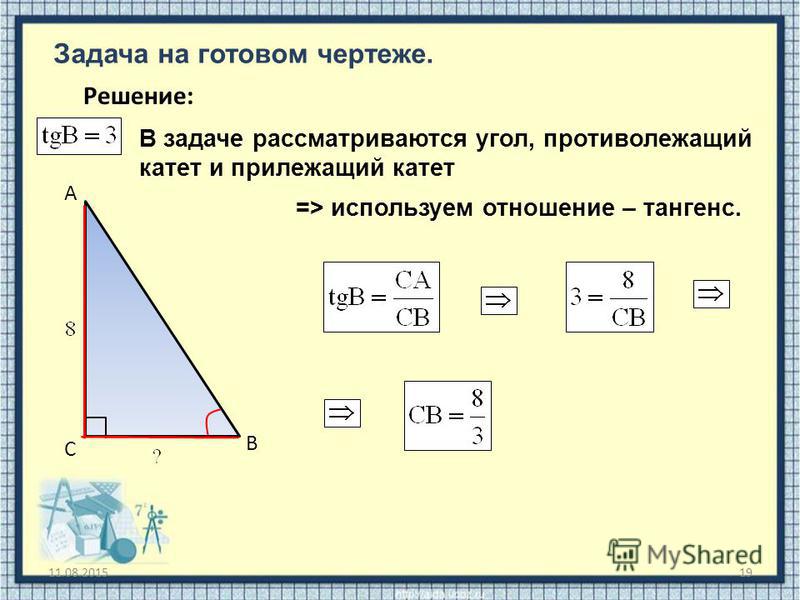 8391 8391 |
| 41° | 0.8693 |
| 42° | 0.9004 |
| 43° | 0.9325 |
| 44° | 0.9657 |
| 45° | 1 |
| 46° | 1.0355 |
| 47° | 1.0724 |
| 48° | 1.1106 |
| 49° | 1.1504 |
| 50° | 1.1918 |
| 51° | 1.2349 |
| 52° | 1.2799 |
| 53° | 1.327 |
| 54° | 1.3764 |
| 55° | 1.4281 |
| 56° | 1.4826 |
| 57° | 1.5399 |
| 58° | 1.6003 |
| 59° | 1.6643 |
| 60° | 1.7321 |
| 61° | 1.804 |
| 62° | 1.8807 |
| 63° | 1.9626 |
| 64° | 2.0503 |
| 65° | 2.1445 |
| 66° | 2.246 |
| 67° | 2.3559 |
| 68° | 2.4751 |
| 69° | 2. 6051 6051 |
| 70° | 2.7475 |
| 71° | 2.9042 |
| 72° | 3.0777 |
| 73° | 3.2709 |
| 74° | 3.4874 |
| 75° | 3.7321 |
| 76° | 4.0108 |
| 77° | 4.3315 |
| 78° | 4.7046 |
| 79° | 5.1446 |
| 80° | 5.6713 |
| 81° | 6.3138 |
| 82° | 7.1154 |
| 83° | 8.1443 |
| 84° | 9.5144 |
| 85° | 11.4301 |
| 86° | 14.3007 |
| 87° | 19.0811 |
| 88° | 28.6363 |
| 89° | 57.29 |
| 90° | ∞ |
Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
ataman |
Заголовок сообщения: Найти приближенное значение тангенса
|
||
|
Как найти приближенное значение тангенса и корня: 1) [math]operatorname{tg}{46^circ}[/math] 2) [math]sqrt[4]{15.8}[/math] Заранее спасибо!
|
||
| Вернуться к началу |
|
||
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Найти приближенное значение функции в точке x=4.06
в форуме Дифференциальное исчисление |
MoonGoosT |
1 |
649 |
09 янв 2014, 23:58 |
|
Найти приближенное значение функции и интегралов
в форуме Ряды |
Evgeny124 |
1 |
551 |
08 июн 2013, 10:17 |
|
С помощью дифференциала найти приближенное значение функции
в форуме Дифференциальные и Интегральные уравнения |
vano888 |
5 |
1576 |
24 янв 2014, 09:47 |
|
Найти приближенное значение вероятности того, что среди
в форуме Теория вероятностей |
vika19 |
13 |
260 |
13 янв 2022, 15:22 |
|
Приближённое значение
в форуме Дифференциальное исчисление |
marinamkg |
6 |
383 |
28 янв 2020, 09:07 |
|
Приближенное значение
в форуме Дифференциальное исчисление |
allochka |
1 |
405 |
30 сен 2014, 18:08 |
|
Приближенное значение числа
в форуме Алгебра |
vladislavmurencov |
4 |
310 |
12 янв 2017, 21:44 |
|
ВЫЧИСЛИТЬ ПРИБЛИЖЕННОЕ ЗНАЧЕНИЕ
в форуме Дифференциальное исчисление |
Irishka09 |
6 |
6765 |
18 дек 2014, 17:19 |
|
Вычислить приближенное значение функции
в форуме Дифференциальное исчисление |
natali0168 |
1 |
707 |
03 июл 2013, 00:56 |
|
Вычислить приближенное значение выражения
в форуме Численные методы |
Adel2015 |
19 |
1049 |
28 окт 2016, 20:59 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 1 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Powered by phpBB © 2000, 2002, 2005, 2007 phpBB Group
Вы можете создать форум бесплатно PHPBB3 на Getbb.Ru, Также возможно сделать готовый форум PHPBB2 на Mybb2.ru
Русская поддержка phpBB

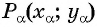
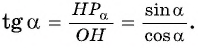
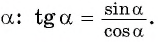
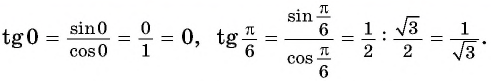
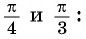
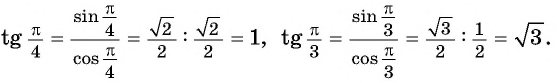
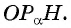
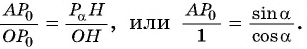
 на единичной окружности.
на единичной окружности. до пересечения с осью тангенсов.
до пересечения с осью тангенсов.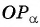 с осью тангенсов.
с осью тангенсов.

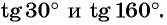
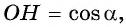
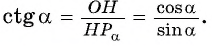
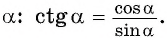
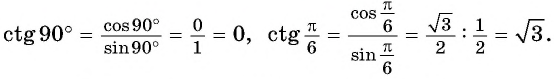
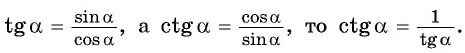
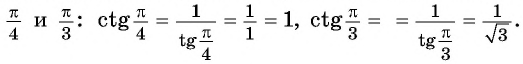
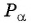 на единичной окружности.
на единичной окружности.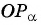 до пересечения с осью котангенсов.
до пересечения с осью котангенсов.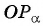 с осью котангенсов.
с осью котангенсов.