Как найти прилежащий угол в параллелограмме - Исправление недочетов и поиск решений вместе с Examum.ru

Углы параллелограмма

Угол

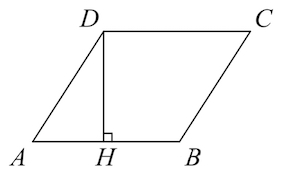
Параллелограмм представляет собой четырехугольник, противоположные стороны которого параллельны и равны друг другу. Два угла, прилежащие к одной стороне параллелограмма, в сумме составляют 180°. Если известен один угол параллелограмма, несложно найти смежный с ним угол путем вычитания из 180° величину известного угла.

α = 180°-β

Таким образом, мы нашли значения всех углов, т.к. известно, что противолежащие углы параллелограмма равны.

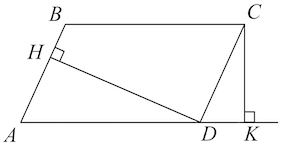
Отрезок, проведенный из двух противоположных вершин параллелограмма, является его диагональю. Если заданы стороны и диагональ, можно определить углы параллелограмма. Диагональ делит параллелограмм на два одинаковых треугольника. Основанием треугольника является диагональ, боковыми сторонами — смежные стороны параллелограмма. Для определения угла используем теорему косинусов, по которой квадрат стороны треугольника (в нашем треугольнике это диагональ) равен сумме квадратов двух его сторон, образующих искомый угол, плюс удвоенное произведение этих сторон на косинус угла. Отсюда, косинус искомого угла равен сумме квадратов смежных сторон (а, b) минус квадрат третей стороны треугольника (в нашем случае — диагонали), противолежащей искомому углу, и все это деленное на удвоенное произведение смежных сторон:

d² = a² + b² + 2ab cos (α)

cos (α) = (a² + b² — d²) / 2ab

,
где а, b — стороны параллелограмма, d — диагональ.
Воспользовавшись таблицей косинусов находим величину искомого угла. После чего находим смежный с ним угол.

Рассчитать углы параллелограмма зная стороны и диагональ

Источник

Решение задач на углы параллелограмма опирается на свойства параллелограмма.

Сумма двух углов параллелограмма, прилежащих к одной стороне, равны 180º (так как они являются внутренними односторонними при параллельных прямых (противолежащих сторонах параллелограмма) и секущей (пересекающей их стороне).

Противоположные углы параллелограмма равны.

Поэтому, если в задаче дана сумма углов параллелограмма (не 180º ), то речь идет о его противолежащих углах.

Если сказано, что один из углов параллелограмма больше или меньше другого на некоторое количество градусов (или в несколько раз, или углы относятся в некотором отношении), то речь идет об углах, прилежащих к одной стороне параллелограмма.

Если в задаче требуется найти все углы параллелограмма, в начале изучения темы ищут все четыре угла.

В дальнейшем обычно находят только два из них (прилежащие к одной стороне), поскольку другие два им равны.

Рассмотрим некоторые задачи на нахождение углов параллелограмма.

Задача 1.

Найти углы параллелограмма, если один из его углов на 40º больше другого.

Дано: ABCD — параллелограмм,

∠B на 40º больше ∠A.

Найти: ∠A, ∠B, ∠C,∠D.

Решение:

Пусть ∠A=хº, тогда ∠B=х+40º.

Так как противоположные стороны параллелограмма параллельны, то

∠A+∠B=180º (как внутренние односторонние при AD ∥ BC и секущей AB).

Имеем уравнение:

х+х+40=180

2х=180-40

2х=140

х=70

Значит, ∠A=70º, тогда ∠B=70+40=110º.

∠C=∠A=70º, ∠D=∠B=110º (как противолежащие углы параллелограмма).

Ответ: 70º, 70º, 110º, 110º.

Задача 2.

Найти углы параллелограмма, если два из них относятся как 2:3.

Дано: ABCD — параллелограмм,

∠A:∠B=2:3.

Найти: ∠A, ∠B, ∠C,∠D.

Решение:

Пусть k — коэффициент пропорциональности. Тогда ∠A=2kº, ∠B=3kº.

∠A+∠B=180º (как внутренние односторонние при AD ∥ BC и секущей AB).

Составим уравнение и решим его:

2k+3k=180

5k=180

k=36

Значит, ∠A=2∙36=72º, ∠B=3∙36=108º.

∠C=∠A=72º, ∠D=∠B=108º (как противолежащие углы параллелограмма).

Ответ: 72º, 72º, 108º, 108º.

Задача 3.

Найти углы параллелограмма, если сумма двух из них равна 150º.

Дано: ABCD — параллелограмм,

∠A+∠C=150º.

Найти: ∠A, ∠B, ∠C,∠D.

Решение:

∠A=∠C=150:2=75º (как противолежащие углы параллелограмма).

∠A+∠B=180º (как внутренние односторонние при AD ∥ BC и секущей AB).

Следовательно, ∠B=180º-∠A=180-75=105º.

∠D=∠B=105º (как противолежащие углы параллелограмма).

Ответ: 75º, 75º, 105º, 105º.

Источник

На чтение 3 мин. Просмотров 23.5k.

Задача 1. Один из углов параллелограмма равен 65°. Найти остальные углы параллелограмма.

Решение.

∠C =∠A = 65° как противоположные углы параллелограмма.

∠А +∠В = 180° как углы, прилежащие к одной стороне параллелограмма.

∠В = 180° — ∠А = 180° — 65° = 115°.

∠D =∠B = 115° как противолежащие углы параллелограмма.

Ответ: ∠А =∠С = 65°; ∠В =∠D = 115°.

Задача 2. Сумма двух углов параллелограмма равна 220°. Найти углы параллелограмма.

Решение.

Так как у параллелограмма имеется 2 равных острых угла и 2 равных тупых угла, то нам дана сумма двух тупых углов, т.е. ∠В +∠D = 220°. Тогда ∠В =∠D = 220°: 2 = 110°.

∠А +∠В = 180° как углы, прилежащие к одной стороне параллелограмма, поэтому ∠А = 180° — ∠В = 180° — 110° = 70°. Тогда ∠C =∠A = 70°.

Ответ: ∠А =∠С = 70°; ∠В =∠D = 110°.

Задача 3. Один из углов параллелограмма в 3 раза больше другого. Найти углы параллелограмма.

Решение.

Пусть ∠А =х. Тогда ∠В = 3х. Зная, что сумма углов параллелограмма, прилежащих к одной его стороне равна 180°, составим уравнение.

х + 3х = 180;

4х = 180;

х = 180 : 4;

х = 45.

Получаем: ∠А =х = 45°, а ∠В = 3х = 3 ∙ 45° = 135°.

Противолежащие углы параллелограмма равны, следовательно,

∠А =∠С = 45°; ∠В =∠D = 135°.

Ответ: ∠А =∠С = 45°; ∠В =∠D = 135°.

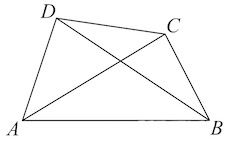
Задача 4. Докажите, что если у четырехугольника две стороны параллельны и равны, то этот четырехугольник – параллелограмм.

Доказательство.

Проведем диагональ BD и рассмотрим Δ ADB и Δ CBD.

AD = BC по условию. Сторона BD – общая. ∠1 = ∠2 как внутренние накрест лежащие при параллельных (по условию) прямых AD и BC и секущей BD. Следовательно, Δ ADB = Δ CBD по двум сторонам и углу между ними (1-й признак равенства треугольников). В равных треугольниках соответственные углы равны, значит, ∠3 =∠4. А эти углы являются внутренними накрест лежащими при прямых AB и CD и секущей BD. Отсюда следует параллельность прямых AB и CD. Таким образом, в данном четырехугольнике ABCD противолежащие стороны попарно параллельны, следовательно, по определению ABCD – параллелограмм, что и требовалось доказать.

Задача 5. Две стороны параллелограмма относятся как 2 : 5, а периметр равен 3,5 м. Найти стороны параллелограмма.

Решение.

Периметр параллелограмма P_ABCD= 2 ∙ (AB + AD).

Обозначим одну часть через х. тогда AB = 2x, AD = 5x метров. Зная, что периметр параллелограмма равен 3,5 м, составим уравнение:

2 ∙ (2x + 5x) = 3,5;

2 ∙ 7x = 3,5;

14x = 3,5;

x = 3,5 : 14;

x = 0,25.

Одна часть составляет 0,25 м. Тогда AB = 2 ∙ 0,25 = 0,5 м; AD = 5 ∙ 0,25 = 1,25 м.

Проверка.

Периметр параллелограмма P_ABCD= 2 ∙ (AB + AD) = 2 ∙ (0,25 + 1,25) = 2 ∙ 1,75 = 3,5 (м).

Так как противоположные стороны параллелограмма равны, то CD = AB = 0,25 м; BC = AD = 1,25 м.

Ответ: CD = AB = 0,25 м; BC = AD = 1,25 м.

Источник

Углы параллелограмма

Обновлено 01.02.2022

Параллелограмм — это геометрическая фигура,
у которой четыре угла и противоположные
стороны попарно параллельны и равны.

Так, как противоположные стороны параллельны,
значит они лежат на параллельных прямых.

Градусные меры противолежащих углов равны.

Сумма двух углов параллелограмма прилежащих к одной
из сторон равна 180 градусам. Внутренние односторонние
углы при параллельных прямых. Это одно из свойств
параллельных прямых для параллелограмма.

Сумма четырех углов параллелограмма — 360 градусов,
как у любого другого четырехугольника.

Формула нахождение углов параллелограмма, если известен только один угол:

[ 2x + 2y = 360 ]

Где x, y — два угла при какой-либо стороне.

Частными случаями параллелограмма являются ромб, прямоугольник, квадрат.

Параллелограмм можно условно разделить на два треугольника.
А как мы знаем сумма углов одного треугольника — 180 градусов,
двух — 360 градусов, поэтому сумма углов параллелограмма — 360 градусов.

Источник

24
Июл 2013

Категория: 01 Геометрия

01. Параллелограмм

2013-07-24
2022-09-11

Задача 1. Сумма двух углов параллелограмма равна $62^{circ}$ . Найдите один из оставшихся углов. Ответ дайте в градусах.

Решение: + показать

Задача 2. Один угол параллелограмма больше другого на $70^{circ}$ . Найдите больший угол. Ответ дайте в градусах.

Решение: + показать

Задача 3. Найдите больший угол параллелограмма, если два его угла относятся как Ответ дайте в градусах.

Решение: + показать

Задача 4. Диагональ параллелограмма образует с двумя его сторонами углы $5^{circ}$ и $38^{circ}.$ Найдите больший угол параллелограмма. Ответ дайте в градусах.

Решение: + показать

Задача 5. Периметр параллелограмма равен Меньшая сторона равна Найдите большую сторону параллелограмма.

Решение: + показать

Задача 6. Две стороны параллелограмма относятся как а периметр его равен Найдите большую сторону параллелограмма.

Решение: + показать

Задача 7. Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна Найдите его большую сторону.

Решение: + показать

Задача 8. Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне. Ответ дайте в градусах.

Решение: + показать

Задача 9. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен

Решение: + показать

Задача 10. В параллелограмме высота, опущенная на сторону из точки равна . Найдите синус угла .

Решение: + показать

Задача 11. В параллелограмме $sinC=frac{5}{7},;AD=7.$ Найдите высоту, опущенную на сторону

Решение: + показать

Задача 12. В параллелограмме $AB=6,;AD=14,;sinA=frac{6}{7}.$ Найдите большую высоту параллелограмма.

Решение: + показать

Задача 13. Площадь параллелограмма равна две его стороны равны и Найдите большую высоту этого параллелограмма.

Решение: + показать

Задача 14. В параллелограмме $sinA=frac{sqrt{561}}{25}$ . Найдите .

Решение: + показать

Задача 15. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.

Решение: + показать

Задача 16. Площадь параллелограмма равна Точка — середина стороны . Найдите площадь трапеции .

Решение: + показать

Задача 17. Площадь параллелограмма равна Найдите площадь параллелограмма вершинами которого являются середины сторон данного параллелограмма.

Решение: + показать

Задача 18. Найдите диагональ параллелограмма , если стороны квадратных клеток равны 1.

Решение: + показать

Задача 19. Диагонали четырехугольника равны и Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.

Решение: + показать

Вы можете пройти тест по теме «Параллелограмм. Вычисление углов и длин».

Автор: egeMax |

комментария 2

Источник