|
12 / 12 / 3 Регистрация: 09.05.2010 Сообщений: 384 |
|
|
1 |
|
Как проверить принадлежит ли точка треугольнику?13.06.2010, 02:17. Показов 218387. Ответов 17
Как проверить принадлежит ли двумерная точка треугольнику с двумерными координатами?
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
13.06.2010, 02:17 |
|
Ответы с готовыми решениями: Как проверить, принадлежит ли точка треугольнику Проверить, принадлежит ли точка M(x,y) треугольнику с заданными вершинами Проверить, принадлежит ли точка M(x,y) треугольнику с… Проверить принадлежит ли точка плоскости с координатами (x,y) треугольнику с заданными вершинами Принадлежит ли точка треугольнику 17 |
|
4 / 4 / 2 Регистрация: 17.04.2010 Сообщений: 55 |
|
|
13.06.2010, 02:56 |
2 |
|
пусть твоя точка имеет координаты (х,у), а вершины треугольника — (х1,у1), (х2,у2), (х3,у3). точка будет принадлежать треугольнику, если будет принадлежать одновременно трем полуплоскостям, пересечение которых и есть треугольник. точка с координатами (х,у) принадлежит полуплоскости, когда находится по одну из сторон некоторой прямой, а именно y-(kx+b)>=0 , где k, b — параметры данной прямой. далее нужно найти уравнения прямых, которые содержат стороны треугольника, составить 3 неравенства, и решить систему из этих 3х неравенств. составить уравнение прямых можно с помощью уравнения прямой, проходящей через 2 точки на плоскости
1 |
|
2833 / 1642 / 254 Регистрация: 03.12.2007 Сообщений: 4,222 |
|
|
13.06.2010, 14:33 |
3 |
|
Решение Уже было — https://www.cyberforum.ru/showthread.php?t=8234.
22 |
|
12 / 12 / 3 Регистрация: 09.05.2010 Сообщений: 384 |
|
|
13.06.2010, 22:18 [ТС] |
4 |
|
junkier, Somebody — спасибо…
1 |
|
pro100saniok 42 / 42 / 3 Регистрация: 11.04.2010 Сообщений: 177 |
||||||||
|
22.06.2010, 22:15 |
5 |
|||||||
|
Уже было — https://www.cyberforum.ru/showthread.php?t=8234. вот решения по данной формуле выше
Добавлено через 13 минут
3 |
|
12 / 12 / 2 Регистрация: 09.03.2011 Сообщений: 38 |
|
|
09.03.2011, 23:26 |
6 |
|
Хотел бы прокоментировать сообщение последнего автора. Первое решение, на мой взгляд в разы лучше второго по одной простой причине. Известно, что квадратный корень есть очень медленная функция. Решение 2 прокатит, если нужно проверить один треугольник, и все. Но если мы программируем графику, к примеру, или что-нибудь еще, где нам это надо считать на каждом кадре и/или для каждого пикселя, то есть очень много раз, то оно совершенно неприемлимо. Тут скорость не спасет даже замена на Fast Inverse Square Root(см. Википедия), хотя она же и ужасно снизит нам точность.
2 |
|
Українець 424 / 318 / 16 Регистрация: 26.09.2009 Сообщений: 844 |
|
|
10.03.2011, 04:41 |
7 |
|
.спасибо
0 |
|
294 / 206 / 2 Регистрация: 20.02.2011 Сообщений: 551 |
|
|
10.03.2011, 14:01 |
8 |
|
[QUOTE=cgsg11;1435009]Хотел бы прокоментировать сообщение последнего автора. Первое решение, на мой взгляд в разы лучше второго по одной простой причине. Известно, что квадратный корень есть очень медленная функция. Решение 2 прокатит, если нужно проверить один треугольник, и все. Но если мы программируем графику, к примеру, или что-нибудь еще, где нам это надо считать на каждом кадре и/или для каждого пикселя, то есть очень много раз, то оно совершенно неприемлимо. Тут скорость не спасет даже замена на Fast Inverse Square Root(см. Википедия), хотя она же и ужасно снизит нам точность. Любое вычисление более-менее извращенных функций, вроде синуса-косинуса, или квадратного корня, явно снизит скорость выполнения данного алгоритма. Тут без вопросов, и спорить не о чем. Остается только согласиться. С другой стороны, задача-то простая. Не элементарная, но достаточно простая. Somebody уже показал, что все решается без особого выпендрежа. Ну, и нафиг оно, усложнение!
0 |
|
Почетный модератор 64287 / 47586 / 32739 Регистрация: 18.05.2008 Сообщений: 115,182 |
|
|
10.03.2011, 14:11 |
9 |
|
Мне кажется аналогично по сложности решение через площади треугольников, естественно не по Герону…
1 |
|
cgsg11 12 / 12 / 2 Регистрация: 09.03.2011 Сообщений: 38 |
||||
|
11.03.2011, 01:26 |
10 |
|||
|
Решение Господа. Должен заметить, что код первого решения вроде как неверен… Я не знаю, проверял ли ПроСтоСанек свое решение, но он в цикле явно «гадит» мимо массива (из-за ++i вместо i++)
3 |
|
476 / 444 / 34 Регистрация: 20.11.2009 Сообщений: 1,293 |
|
|
11.03.2011, 19:55 |
11 |
|
«гадит» мимо массива (из-за ++i вместо i++) Конкретно в данном случае они эквивалентны, лол.
0 |
|
12 / 12 / 2 Регистрация: 09.03.2011 Сообщений: 38 |
|
|
12.03.2011, 00:07 |
12 |
|
Я подозревал, что облажаюсь так. ) При обнаружении в программе цикла for первым выполняется инициализирующее_выражение, в котором обычно устанавливается счетчик цикла. Это происходит только один раз перед запуском цикла. Затем анализируется условное_выражение, которое также называется условием прекращения цикла. Пока оно равно true, цикл не прекращается. Каждый раз после всех строк тела цикла выполняется модифицирующее_выражение, в котором происходит изменение счетчика цикла. Как только проверка условного_выражения даст результат false, все строки тела цикла и модифицирующее_выражение будут пропущены и управление будет передано первому выражению, следующему за телом цикла. Я почему-то решил, что ++ выполнится до условного выражения и до тела цикла. Но по мне так писать ++i в форе все равно моветон. никогда такого изврата не встречал. имхо это нелогично.
0 |
|
1 / 1 / 0 Регистрация: 27.02.2011 Сообщений: 25 |
|
|
11.05.2011, 21:40 |
13 |
|
Спасибо за методы. Очень пригодились!
0 |
|
7 / 7 / 3 Регистрация: 11.01.2011 Сообщений: 73 |
|
|
16.05.2011, 15:07 |
14 |
|
есть ище лучший для понимание!
0 |
|
12 / 12 / 2 Регистрация: 09.03.2011 Сообщений: 38 |
|
|
28.05.2011, 19:41 |
15 |
|
Если бы вы посмотрели чуточку выше в чате, там была фраза «не по Герону, разумеется». Вас это на мысль не навело? В свое время в этой теме был холивар про использование квадратного корня. Герон использует его, по вашему алгоритму, четырежды. Это совершенно неприемлемо по нескольким причинам:
1 |
|
5 / 5 / 2 Регистрация: 07.05.2018 Сообщений: 14 |
|
|
07.05.2018, 17:53 |
16 |
|
Вот решение для С++ Это в ООП
0 |
|
EviLordus 0 / 0 / 0 Регистрация: 26.04.2020 Сообщений: 13 |
||||||||||||||||
|
14.07.2021, 14:05 |
17 |
|||||||||||||||
|
Я написал, это так на c#. По-моему красота. Можно ли еще улучшить и оптимизировать этот метод?
Добавлено через 32 минуты
Добавлено через 9 минут
Добавлено через 46 минут
0 |
|
0 / 0 / 0 Регистрация: 26.04.2020 Сообщений: 13 |
|
|
14.07.2021, 14:09 |
18 |
|
По факту первый метод действительно быстрее Герона. Тут один миллион случайных треугольников и точек, с float координатами в диапазоне [0, 1); Изображения
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
14.07.2021, 14:09 |
|
Помогаю со студенческими работами здесь
Точка принадлежит треугольнику Private _abs As Integer Private Property Abs(ByVal p1 As Integer)…
Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 18 |
Дано: у нас есть треугольник, нам известны только координаты его вершин. У нас есть точка, нам известны её координаты.
Что нужно узнать: нужно установить принадлежность точки треугольнику.
В данной статье разбирается несколько разных методов определения принадлежности точки треугольнику.
Метод сравнения площадей
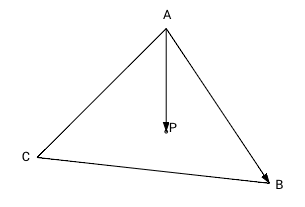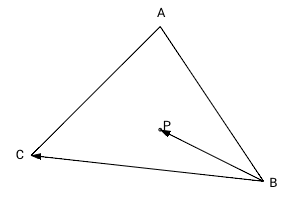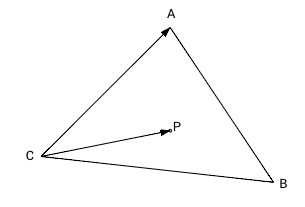
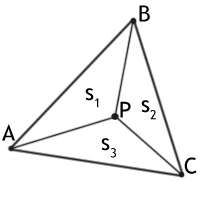
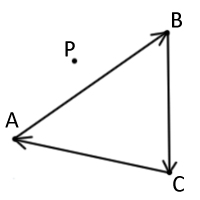
В данном методе сначала находятся площади 3-х треугольников, которые образует данная точка с каждой стороной треугольника. В нашем случае(рис. 1) это треугольники ABP, BCP, CAP и их площади s1, s2, s3 соответственно.
Затем находится площадь самого треугольника ABC.
Найденный площади сравниваются — если сумма 3-х площадей равна площади всего треугольника, то значит точка принадлежит треугольнику. При сравнении, как правило, задаётся погрешность.
Так как у нас известны только координаты точек, то все площади, находятся по формуле Герона, от обильности операций которой становится ясно, почему этот метод очень трудоёмкий.
Простейшая реализация алгоритма:
|
// проверка принадлежности точки треугольнику формулами Герона function IsPointIn_Geron(aAx, aAy, aBx, aBy, aCx, aCy, aPx, aPy: single): boolean; // funcs // площадь треугольника по точкам function Square(aAx, aAy, aBx, aBy, aCx, aCy: single): single; begin Result := abs(aBx*aCy — aCx*aBy — aAx*aCy + aCx*aAy + aAx*aBy — aBx*aAy); end; var s : single; begin s := Square(aPx, aPy, aAx, aAy, aBx, aBy) + Square(aPx, aPy, aBx, aBy, aCx, aCy) + Square(aPx, aPy, aCx, aCy, aAx, aAy); Result := abs(Square(aAx, aAy, aBx, aBy, aCx, aCy) — s) <= 0.01{погрешность}; end; |
Атрибуты функции: aAx, aAy, aBx, aBy, aCx, aCy — координаты точек A, B, C треугольника; aPx, aPy — координаты точки, принадлежность которой надо определить.
Метод относительности
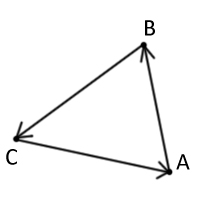
Данный метод заключается в следующем. Сначала выбирается ориентация движения по вершинам треугольника(по часовой или против часовой стрелке). Я выбираю по часовой. На рисунке 2 выбранная ориентация движения(по часовой) показана стрелками. По данной ориентации проходим все стороны треугольника, рассматривая их как прямые, и рассчитываем по какую сторону от текущей прямой лежит наша точка. Не трудно догадаться, что если точка для всех прямых, при нашей ориентации, лежит с правой стороны, то значит точка принадлежит треугольнику, а если хоть для какой-то прямой она лежит с левой стороны, то значит условие принадлежности не выполняется.
На рисунке 2 продемонстрирована ситуация, когда точка только для одной прямой AB лежит по левую сторону, а значит не принадлежит треугольнику.
Реализация алгоритма:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
// проверка прин. точки треуг. методом относительности положения function IsPointIn_Relat(aAx, aAy, aBx, aBy, aCx, aCy, aPx, aPy: single): boolean; // funcs function Q(ax, ay, bx, by, atx, aty: single): single; begin Result := atx * (by — ay) + aty * (ax — bx) + ay * bx — ax * by; end; var q1, q2, q3 : single; begin // выбираем определённую ориентацию по вершинам(чтоб было по порядку) // универсальный q1 := Q(aAx, aAy, aBx, aBy, aPx, aPy); q2 := Q(aBx, aBy, aCx, aCy, aPx, aPy); q3 := Q(aCx, aCy, aAx, aAy, aPx, aPy); Result := ((q1 >= 0) and (q2 >= 0) and (q3 >= 0)) or ((q1 < 0) and (q2 < 0) and (q3 < 0)); //} { // для строгой ориентации по часовой Result := (Q(ftx1, fty1, ftx2, fty2, fpx, fpy) >= 0) and (Q(ftx2, fty2, ftx3, fty3, fpx, fpy) >= 0) and (Q(ftx3, fty3, ftx1, fty1, fpx, fpy) >= 0); //} { // для строгой ориентации против часовой Result := (Q(ftx1, fty1, ftx2, fty2, fpx, fpy) <= 0) and (Q(ftx2, fty2, ftx3, fty3, fpx, fpy) <= 0) and (Q(ftx3, fty3, ftx1, fty1, fpx, fpy) <= 0); //} end; |
Всё относительно!
Тут надо кое что пояснить, весьма не маловажное, что может сыграть роль в оптимизации и выборе алгоритма. Обратите внимание, что в приведённом коде есть закомментированные блоки кода с комментариями «для строгой ориентации», в то время как рабочий код универсален — он предназначен для любой ориентации. Т.е. представленный код определит принадлежность точки для любого заданного треугольника. В моей тестирующей программе треугольники как раз таки строятся по random()-у координат вершин, а ориентация идёт по вершинам(A>B>C>A). Для рисунка 2 — это по часовой стрелки, но для рисунка 3 — это против часовой.
Так вот, в случае рисунка 3 точка должна лежать по левую сторону векторов, чтобы принадлежать треугольнику.
Вот тут и получается важный момент! Если вы уверены, что в вашем проекте все треугольники будут ориентированы по часовой стрелке(а т.е. вершина C будет всегда правее вектора AB), то вам можно закомментировать блок универсального решения и раскомментировать блок «для строгой ориентации по часовой» и данный алгоритм упрощается аж на 3 логических операции!
Векторный метод
Третий метод который я освещаю для меня самый интересный.
Идея его применения зарождается если взглянуть на треугольник как на половинку параллелограмма…
Данный метод я сначала проверил на бумаге. После всех оптимизаций формул, как всё сошлось, я реализовал его в коде, где он показал себя вполне успешным и результативным. Аж эффективнее 2-х предыдущих методов :]
Алгоритм такой:
1) одну вершину треугольника помещаем в координаты (0;0);
2) две стороны, выходящие из этой вершины, представляем как вектора.
Таким образом из всего этого появляется система простых условий нахождения точки P между векторами b и c.(рис. 4)
Смотрим код:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
function IsPIn_Vector(aAx, aAy, aBx, aBy, aCx, aCy, aPx, aPy: single): boolean; var Bx, By, Cx, Cy, Px, Py : single; m, l : single; // мю и лямбда begin Result := False; // переносим треугольник точкой А в (0;0). Bx := aBx — aAx; By := aBy — aAy; Cx := aCx — aAx; Cy := aCy — aAy; Px := aPx — aAx; Py := aPy — aAy; // m := (Px*By — Bx*Py) / (Cx*By — Bx*Cy); if (m >= 0) and (m <= 1) then begin l := (Px — m*Cx) / Bx; if (l >= 0) and ((m + l) <= 1) then Result := True; end; end; |
По коду можно увидеть, что находятся новые координаты точек B и C, которые одновременно являются векторами b и c (рис. 4.). А новые координаты точки P являются вектором (Px, Py). Далее идёт формула, которую я предварительно свёл к общему виду и упростил.
Кол-во основных операций получается 13(+4). Совсем не плохо :]
Метод геометрического луча
Это достаточно известный метод, особенно когда определяется принадлежность точки многоугольникам. Часто данный метод называют «трассировка луча», хотя это не совсем правильно, т.к. трассировка луча — это расчёт хода световых лучей в 3D сцене.
Суть в том, что из данной точки пускается луч по какой-либо оси в каком-либо направлении.
Затем проверяются пересечения со сторонами многоугольника и ведётся подсчёт пересечений.
Таким образом если кол-во пересечений чётное, то значит точка лежит вне многоугольника, если же кол-во НЕчётное, то значит точка лежит внутри.
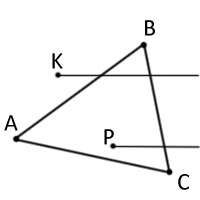
На рисунке 5 изображены две подопытные точки P и K, у луча из точки P одно пересечение со сторонами треугольника, таким образом точка P принадлежит фигуре, а точке K не повезло — у неё два пересечения.
Реализация алгоритма:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
function IsPIn_RayCast(aAx, aAy, aBx, aBy, aCx, aCy, aPx, aPy: single): boolean; // funcs // p1 — начало 1ого отрезка, p2 — конец 1ого отрезка, p3 — начало 2ого отрезка, p4 — конец 2ого отрезка function peresechenie(p1, p2, p3, p4: TPoint): boolean; var zn, ua, ub : single; begin // 25 операций zn := (p4.y — p3.y) * (p2.x — p1.x) — (p4.x — p3.x) * (p2.y — p1.y); ua := ((p4.x—p3.x)*(p1.y—p3.y) — (p4.y—p3.y)*(p1.x—p3.x)) / zn; ub := ((p2.x—p1.x)*(p1.y—p3.y) — (p2.y—p1.y)*(p1.x—p3.x)) / zn; // если ‘ua’ и ‘ub’ принадлежат [0,1] то отрезки пересекаются Result := (ua >= 0) and (ua <= 1) and (ub >= 0) and (ub <= 1); end; var cros_cnt : integer; s1, s2 : single; // коэф. begin cros_cnt := 0; // кол-во пересечений граней (лучом из точки) // луч пускаем по оси X вправо // 1-я сторона треугла s2 := (aPy — aAy) / (aBy — aAy); s1 := aAx — aPx + s2 * (aBx — aAx); if (s1 >= 0) and (s2 >= 0) and (s2 <= 1) then inc(cros_cnt); // 2-я сторона треугла s2 := (aPy — aBy) / (aCy — aBy); s1 := aBx — aPx + s2 * (aCx — aBx); if (s1 >= 0) and (s2 >= 0) and (s2 <= 1) then inc(cros_cnt); // 3-я сторона треугла if cros_cnt < 2 then begin s2 := (aPy — aCy) / (aAy — aCy); s1 := aCx — aPx + s2 * (aAx — aCx); if (s1 >= 0) and (s2 >= 0) and (s2 <= 1) then inc(cros_cnt); end; Result := cros_cnt = 1; end; |
Вроде нормально упростил(для треугольника имею ввиду), но что-то мне кажется, что может быть и по круче…
А так, получается примерно 30 операций.
Сравнение скоростей
Ну вот мы и подошли к самому интересному! Кто быстрее и сильнее!? :]
Я провёл тест со следующими параметрами(хотя всё зависит от процессора):
- кол-во повторений алгоритма за 1 имитацию = 4 миллиона.
- кол-во имитаций для каждого алгоритма = 1000.
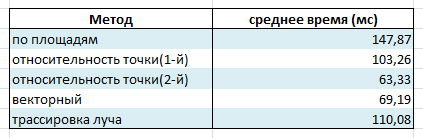
Таблица результатов:
Ну что сказать, векторный метод хорош)
С ним конечно соперничает второй способ относительности точки, но главное отличие в том, что для отн. точки необходима строгая ориентация сторон треугольника, а для векторного это не важно, поэтому он круче)
Так же можно скачать написанную в ходе экспериментов программу: prin_tochki_proga. Программа реализована на Delphi 2007.
Точка внутри треугольника
| Координаты треугольника |
| Координаты точки |
| Вы ввели следующие координаты многоугольника |
Определение, принадлежит ли произвольная точка какому либо треугольнику (находится ли она внутри треугольника, на самом деле очень важная задача. Для нас она важна в контексте разбиения многоугольника на треугольники. Решение этой промежуточной задачи, позволит нам определять координаты центра тяжести многоугольника.
Итак, существует достаточно много вариантов определения принадлежности точки треугольнику. Могу порекомендовать ссылку. Написано достаточно подробно и рассмотрены практически все варианты.
Мы в своей реализации будем придерживаться следующего алгоритма
Пусть у нас есть треугольник
Высчитаем значение трех нижеуказанных выражений
где x0,y0 — координаты произвольной точки
Если все три значения одинакового знака, то точка внутри треугольника,
если значение равно нулю, значит точка лежит на стороне треугольника
В ином случае (если значения различные по знаку) , точка вне треугольника.
Теперь проверим наше предположение
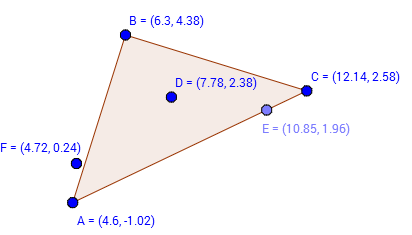
Точка D
Точка лежит внутри треугольника так как результат трех вычислений одинаков по знаку ( все они отрицательные)
Точка F
В этом случае точка F лежит вне треугольника, так как знаки результирующих вычислений различны.
Хотелось бы заметить, что в случае точки Е наш бот, скажет что точка также находится внутри треугольника, хотя и находится на стороне треугольника( или как вариант в одной из вершин) . Это как уже было сказано связано с использованием этого бота, для расчета центра тяжести многоугольников.
Удачных расчетов!
Время на прочтение
2 мин
Количество просмотров 23K
Серия постов [Неочевидные алгоритмы очевидных вещей] будет содержать алгоритмы действий, которые кажутся очевидными и простыми, но если задать себе вопрос «как это делается?», то ответ является далеко не очевидным. Разумеется, все эти алгоритмы можно найти в литературе. Под катом располагается алгоритм определения принадлежности точки P треугольнику ABC в пространстве.
Принадлежность точки P треугольнику ABC в пространстве
Идея
Иногда встречается необходимость определения принадлежности точки какой-нибудь геометрической фигуре. Самой простейшей является треугольник ABC.
Дано:
Точка P(P_x,P_y,P_z), треугольник с вершинами: A(A_x,A_y,A_z), B(B_x,B_y,B_z), C(C_x,C_y,C_z).
методика
Формируются три треугольника: ABP, ACP, BCP. После вычисляются их площади SABP,SACP,SBCP. После этого сверяется сумма этих площадей с площадью треугольника SABC. Если точка лежит на треугольнике ABC, то треугольники ABP, ACP, BCP будут просто частями треугольника ABC, и сумма их площадей будет равна его площади SABC. Если же точка не принадлежит треугольнику, сумма площадей SABP,SACP,SBCP превысит площадь треугольника ABC.
Легкое лирическое отступление для тех, кто не помнит, чему равна площадь треугольника: проще всего использовать формулу Герона, которая позволяет найти площадь треугольника, зная только его стороны, оч. удобно
Код функции:
#define EPS 1e-10
float triangle_square(float a,float b, float c){
float p=(a+b+c)/2;
return sqrt(p*(p-a)*(p-b)*(p-c));
}
float inside_triangle(float P_x,float P_y, float P_z, float A_x, float A_y, float A_z, float B_x, float B_y, float B_z, float C_x, float C_y, float C_z){
int inside=0;
float AB=sqrt( (A_x-B_x)*(A_x-B_x) + (A_y-B_y)*(A_y-B_y) + (A_z-B_z)*(A_z-B_z) );
float BC=sqrt( (B_x-C_x)*(B_x-C_x) + (B_y-C_y)*(B_y-C_y) + (B_z-C_z)*(B_z-C_z) );
float CA=sqrt( (A_x-C_x)*(A_x-C_x) + (A_y-C_y)*(A_y-C_y) + (A_z-C_z)*(A_z-C_z) );
float AP=sqrt( (P_x-A_x)*(P_x-A_x) + (P_y-A_y)*(P_y-A_y) + (P_z-A_z)*(P_z-A_z) );
float BP=sqrt( (P_x-B_x)*(P_x-B_x) + (P_y-B_y)*(P_y-B_y) + (P_z-B_z)*(P_z-B_z) );
float CP=sqrt( (P_x-C_x)*(P_x-C_x) + (P_y-C_y)*(P_y-C_y) + (P_z-C_z)*(P_z-C_z) );
float diff=(triangle_square(AP,BP,AB)+triangle_square(AP,CP,CA)+triangle_square(BP,CP,BC))-triangle_square(AB,BC,CA);
if (fabs(diff)<EPS) inside=1;
return inside;
}
Если вдруг кому лень прикреплять math.h, то можете воспользоваться функцией корня из этого поста.
Этот калькулятор определит где находится заданная точка внутри 2-мерного треугольника или вовне. Калькулятор использует простой алгоритм, основанный на свойствах векторного произведения. Описание этого алгоритма можно найти сразу за калькулятором.
Точка в треугольнике
Точность вычисления
Знаков после запятой: 2
Точка вниутри треугольника?
Векторное произведение ( z — координата )
Точка внутри треугольника. Описание алгоритма.
Векторное произведение векторов a и b, заданного декартовыми координатами в пространстве для 3-х мерного правого ортонормального базиса можно выразить так:
[1].
Векторное произведение обладает свойством антикоммутативности:
Это важное свойство мы будем использовать для решения нашей задачи.
Для того чтобы определить лежит ли точка P внутри треугольника ABC мы вычислим 3 векторных произведения: ABxAP, BCxBP and CAxCP. Так как наш треугольник и точка в 2-мерном пространстве на плоскости, третья координата z для трехмерного пространства равна нулю. Согласно формуле [1] мы можем не вычислять координаты x и y для векторного произведения, если координата z векторов-множителей равна нулю — координаты x и y результата в этом случае всегда равны нулю (результирующий псевдо-вектор перпендикулярен плоскости треугольника). Знак результата произведения для оставшейся координаты (z) зависит от относительного положения умножаемых векторов. Если первый вектор (в нашем случае это сторона треугольника) находится правее второго вектора (вектор из вершины в точку P), то координата z результата будет положительна, если первый вектор будет левее второго — отрицательна, и в противном случае, если оба вектора идут в одном и том же направлении, результат будет равен нулю.
Получив результаты по трем векторным произведениям, нам остается их проанализировать, чтобы понять лежит ли точка внутри треугольника:
Если мы имеем и положительные и отрицательные результаты, точка лежит вне треугольника, если результаты только положительные или только отрицательные, точка — внутри.
Таблица далее иллюстрирует все возможные варианты результатов векторного произведения:
| Рисунок | Описание |
|---|---|
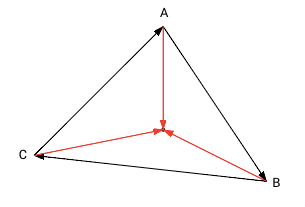 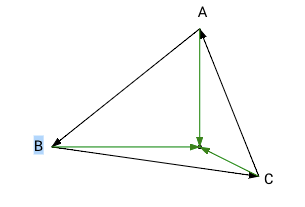 |
Все результаты положительные или все результаты отрицательные. Точка — внутри треугольника. |
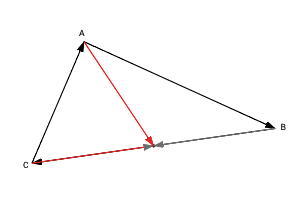 |
Один результат равен нулю, остальные все либо положительны, либо все отрицательны. Точка лежит на стороне треугольника. Если два результата равны нулю, точка совпадает с вершиной треугольника. |
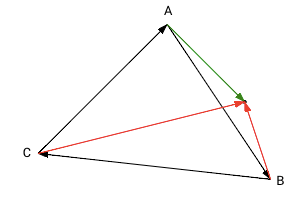 |
Если имеются и положительные и отрицательные результаты. Точка лежит вне треугольника. |


 Сообщение было отмечено как решение
Сообщение было отмечено как решение



%20*%20(y_b%20-%20y_a)%20-%20(x_b%20-%20x_a)%20*%20(y_a%20-%20y0)%20(x_b%20-%20x0)%20*%20(y_c%20-%20y_b)%20-%20(x_c%20-%20x_b)%20*%20(y_b%20-%20y0)%20(x_c%20-%20x0)%20*%20(y_a%20-%20y_c)%20-%20(x_a%20-%20x_c)%20*%20(y_c%20-%20y0))
%20*%20(4.38%20+1.02)%20-%20(6.3%20-%204.6)%20*%20(-1.02%20-%202.38)=-11.392%20(6.3%20-%207.78)%20*%20(2.58%20-%204.38)%20-%20(12.14%20-%206.3)%20*%20(4.38%20-%202.38)=-9.016%20(12.14%20-%207.78)%20*%20(-1.02%20-%202.58)%20-%20(4.6%20-%2012.14)%20*%20(2.58%20-2.38)=-14.188)
%20*%20(4.38%20+1.02)%20-%20(6.3%20-%204.6)%20*%20(-1.02%20-%200.24)=1.494(6.3%20-%204.72)%20*%20(2.58%20-%204.38)%20-%20(12.14%20-%206.3)%20*%20(4.38%20-%200.24)=%20-27.0216(12.14%20-%204.72)%20*%20(-1.02%20-%202.58)%20-%20(4.6%20-%2012.14)%20*%20(2.58%20-0.24)=-9.0684)