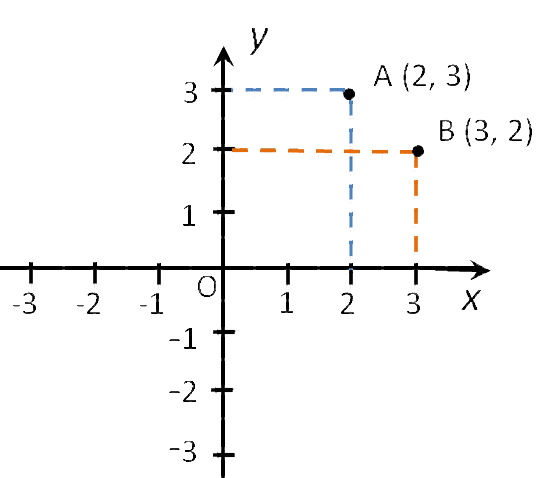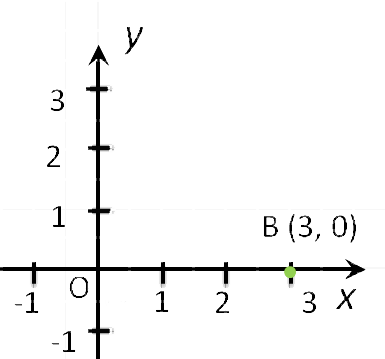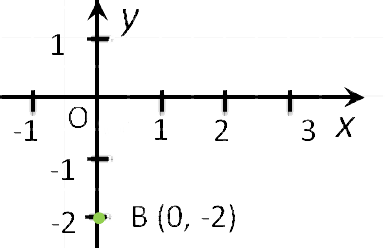Как найти принадлежит точка системе координат

Вычислительная геометрия, или как я стал заниматься олимпиадным программированием. Часть 2

Вступление

Это вторая часть моей статьи посвящена вычислительной геометрии. Думаю, эта статья будет интереснее предыдущей, поскольку задачки будут чуть сложнее.

Начнем с взаимного расположения точки относительно прямой, луча и отрезка.

Задача №1

Определить взаимное расположении точки и прямой: лежит выше прямой, на прямой, под прямой.

Решение
Понятно, что если прямая задана своим уравнением ax + by + c = 0, то тут и решать нечего. Достаточно подставить координаты точки в уравнение прямой и проверить чему оно равно. Если больше нуля, то точка находится в верхней полуплоскости, если равна нулю, то точка находится на прямой и если меньше нуля, то точка находится в нижней полуплоскости. Интереснее случай, когда прямая задана, задана координатами двух точек назовем их P₁(x₁, y₁), P₂(x₂, y₂). В этом случае можно спокойно найти коэффициенты a, b и c и применить предыдущее рассуждение. Но надо сначала подумать, оно нам надо? Конечно, нет! Как я говорил косое произведения — это просто жемчужина вычислительной геометрии. Давайте применим его. Известно, что косое произведение двух векторов положительно, если поворот от первого вектора ко второму идет против часовой стрелки, равно нулю, если векторы коллинеарны и отрицательно, если поворот идет по часовой стрелки. Поэтому нам достаточно посчитать косое произведение векторов P₁P₂ и P₁M и по его знаку сделать вывод.

Задача №2

Определить принадлежит ли точка лучу.

Решение
Давайте вспомним, что такое луч: луч — это прямая, ограниченная точкой с одной стороны, а с другой стороны бесконечная. То есть луч задается некоторой начальной точкой и любой точкой лежащей на нем. Пусть точка P₁(x₁, y₁) — начало луча, а P₂(x₂, y₂) — любая точка принадлежащая лучу. Понятно, что если точка принадлежит лучу, то она принадлежит и прямой проходящей через эти точки, но не наоборот. Поэтому принадлежность прямой является необходимым, но не достаточным условием для принадлежности лучу. Поэтому от проверки косового произведения нам никуда не деться. Для достаточного условия нужно вычислить еще и скалярное произведение тех же векторов. Если оно меньше нуля, то точка не принадлежит лучу, если же оно не отрицательно, то точка лежит на луче. Почему так? Давайте посмотрим на рисунок.

Итак, для того чтобы точка M(x, y) лежала на луче с начальной точкой P₁(x₁, y₁), где P₂(x₂, y₂) лежит на луче необходимо и достаточно выполнения двух условий:
1. [P₁P₂, P₁M] = 0 – косое произведение (точка лежит на прямой)
2. (P₁P₂, P₁M) ≥ 0 – скалярное произведение (точка лежит на луче)

Задача №3

Определить принадлежит ли точка отрезку.

Решение
Пусть точки P₁(x₁, y₁), P₂(x₂, y₂) концы заданного отрезка. Опять-таки необходимым условием принадлежности точки отрезку является ее принадлежность прямой проходящей через P₁, P₂. Далее нам нужно определить лежит ли точка между точками P₁ и P₂, для этого нам на помощь приходит скалярное произведение векторов только на этот раз других: (MP₁, MP₂). Если оно меньше либо равно нуля, то точка лежит на отрезке, иначе вне отрезка. Почему так? Посмотрим на рисунок.

Итак, для того чтобы точка M(x, y) лежала на отрезке с концами P₁(x₁, y₁), P₂(x₂, y₂) необходимо и достаточно выполнения условий:
1. [P₁P₂, P₁M] = 0 – косое произведение (точка лежит на прямой)
2. (MP₁,MP₂) ≤ 0 – скалярное произведение (точка лежит между P₁ и P₂)

Задача №4

Взаимное расположение двух точек относительно прямой.

Решение
В этой задаче необходимо определить по одну или по разные стороны относительно прямой находятся две точки.

Если точки находятся по разные стороны относительно прямой, то косые произведения имеют разные знаки, а значит их произведение отрицательно. Если же точки лежат по одну сторону относительно прямой, то знаки косых произведений совпадают, значит, их произведение положительно.
Итак:
1. [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] 0 – точки лежат по одну сторону.
3. [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] = 0 – одна (или две) из точек лежит на прямой.

Кстати, задача об определении наличия точки пересечения у прямой и отрезка решается точно также. Точнее, это и есть эта же задача: отрезок и прямая пересекаются, когда концы отрезка находятся по разные стороны относительно прямой или когда концы отрезка лежат на прямой, то есть необходимо потребовать [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] ≤ 0.

Задача №5

Определить пересекаются ли две прямые.

Решение
Будем считать, что прямые не совпадают. Понятно, что прямые не пересекаются, только если они параллельны. Поэтому, найдя условие параллельности, мы можем, определить пересекаются ли прямые.
Допустим прямые заданы своими уравнениями a₁x + b₁y + c₁ = 0 и a₂x + b₂y + c₂ = 0. Тогда условие параллельности прямых заключается в том, что a₁b₂ — a₂b₁ = 0.
Если же прямые заданы точками P₁(x₁, y₁), P₂(x₂, y₂), M₁(x₃, y₃), M₂(x₄, y₄), то условие их параллельности заключается в проверки косого произведения векторов P₁P₂ и M₁M₂: если оно равно нулю, то прямые параллельны.

В общем, то когда прямые заданы своими уравнениями мы тоже проверяем косое произведение векторов (-b₁, a₁), (-b₂, a₂) которые называются направляющими векторами.

Задача №6

Определить пересекаются ли два отрезка.

Решение
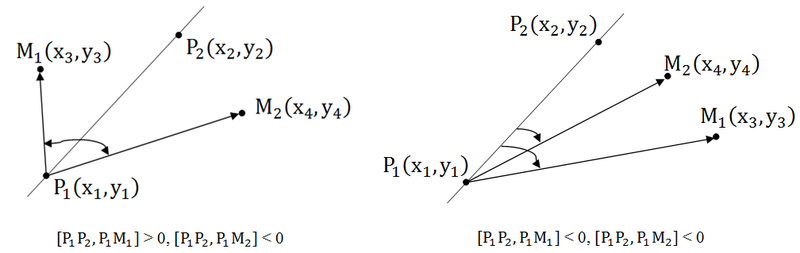
Вот эта задача мне, действительно, нравится. Отрезки пересекаются тогда, когда, концы каждого отрезка лежат по разные стороны от другого отрезка. Посмотрим на рисунок:

Итак, нам нужно проверить, чтобы концы каждого из отрезков лежали по разные стороны относительного концов другого отрезка. Пользуемся косым произведением векторов. Посмотрите на первый рисунок: [P₁P₂, P₁M₂] > 0, [P₁P₂, P₁M₁] [P₁P₂, P₁M₂] * [P₁P₂, P₁M₁] 2 + b 2 ).

Задача №8

Расстояние от точки до луча.

Решение
Эта задача отличается от предыдущей тем, что в этом случае может получиться, так что перпендикуляр из точки не падает на луч, а падает на его продолжение.

В случае, когда перпендикуляр не падает на луч необходимо найти расстояние от точки до начала луча – это и будет ответом на задачу.

Как же определить падает ли перпендикуляр на луч или нет? Если перпендикуляр не падает на луч, то угол MP₁P₂ – тупой иначе острый (прямой). Поэтому по знаку скалярного произведения векторов мы можем определить попадает ли перпендикуляр на луч или нет:
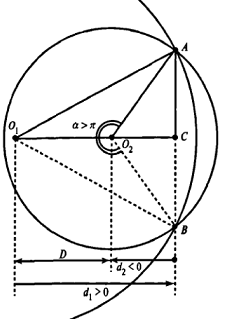
1. (P₁M, P₁P₂) 2 .

Теперь рассмотрим случай, когда центр второго круга O₂ находится между точками O₁ и C. В этом случае получим отрицательное значение величины d₂. Использование отрицательного значения d₂ приводит к отрицательному значению α. В этом случае необходимо для правильного ответа прибавить к α 2π.

Заключение

Ну вот и все. Мы рассмотрели не все, но наиболее часто встречаемые задачи вычислительной геометрии касающиеся взаимного расположения объектов.

Уравнения прямой в пространстве — это уравнения двух пересекающихся плоскостей

В данном разделе продолжим изучение темы уравнения прямой в пространстве с позиции стереометрии. Это значит, что мы будем рассматривать прямую линию в трехмерном пространстве как линию пересечения двух плоскостей.

Согласно аксиомам стереометрии, если две плоскости не совпадают и имеют одну общую точку, то они также имею одну общую прямую, на которой лежат все точки, которые являются общими для двух плоскостей. Используя уравнения двух пересекающихся плоскостей, мы можем определить прямую линию в прямоугольной системе координат.

По ходу рассмотрения темы приведем многочисленные примеры, ряд графических иллюстраций и развернутых решений, необходимых для лучшего усвоения материала.

Уравнения двух плоскостей, задающих прямую линию в пространстве

Пусть даны две плоскости, которые не совпадают между собой и пересекаются. Обозначим их как плоскость α и плоскость β . Разместим их в прямоугольной системе координат O х у z трехмерного пространства.

Как мы помним, любую плоскость в прямоугольной системе координат задает общее уравнение плоскости вида A x + B y + C z + D = 0 . Будем считать, что плоскости α соотвествует уравнение A 1 x + B 1 y + C 1 z + D 1 = 0 , а плоскости β уравнение A 2 x + B 2 y + C 2 z + D 2 = 0 . В этом случае нормальные вектора плоскостей α и β n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) не коллинеарны, так как плоскости не совпадают между собой и е размещаются параллельно друг другу. Запишем это условие следующим образом:

n 1 → ≠ λ · n 2 → ⇔ A 1 , B 1 , C 1 ≠ λ · A 2 , λ · B 2 , λ · C 2 , λ ∈ R

Чтобы освежить в памяти материал по теме «Параллельность плоскостей», смотрите соответствующий раздел нашего сайта.

Линию пересечения плоскостей обозначим буквой a . Т.е. a = α ∩ β . Эта прямая представляет собой множество точек, которые являются общими для обеих плоскостей α и β . Это значит, что все точки прямой линии a удовлетворяют обоим уравнениям плоскости A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 . Фактически, они являются частным решением системы уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 .

Общее решение системы линейных уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 определяет координаты всех точек линии, по которой происходит пересечение двух плоскостей α и β . Это значит, что с его помощью мы можем определить положение прямой в прямоугольной системе координат O x y z .

Рассмотрим описанную теорию еще раз, теперь уже на конкретном примере.

Прямая O x – это прямая, по которой пересекаются координатные плоскости O x y и O x z . Зададим плоскость O x y уравнением z = 0 , а плоскость O x z уравнением у = 0 . Такой подход мы подробно разобрали в разделе «Неполное общее уравнение плоскости», так что, в случае затруднений, можно обратиться к этому материалу повторно. В этом случае координатная прямая O x определяется в трехмерной системе координат системой из двух уравнений вида y = 0 z = 0 .

Нахождение координат точки, лежащей на прямой, по которой пересекаются плоскости

Рассмотрим задачу. Пусть в трехмерном пространстве задана прямоугольная система координат O х у z . Линия, по которой пересекаются две плоскости a , задана системой уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 . Дана точка трехмерного пространства M 0 x 0 , y 0 , z 0 .

Давайте определим, принадлежит ли точка M 0 x 0 , y 0 , z 0 заданной прямой линии a .

Для того, чтобы получить ответ на вопрос задачи, подставим координаты точки М 0 в каждое из двух уравнений плоскости. Если в результате подстановки оба уравнения превратятся в верные равенства A 1 x 0 + B 1 y 0 + C 1 z 0 + D 1 = 0 и A 2 x 0 + B 2 y 0 + C 2 z 0 + D 2 = 0 , то точка М 0 принадлежит каждой из плоскостей и принадлежит заданной линии. Если хотя бы одно из равенств A 1 x 0 + B 1 y 0 + C 1 z 0 + D 1 = 0 и A 2 x 0 + B 2 y 0 + C 2 z 0 + D 2 = 0 окажется неверным, то точка М 0 не принадлежит прямой линии.

Рассмотрим решение примера

Прямая линия задана в пространстве уравнениями двух пересекающихся плоскостей вида 2 x + 3 y + 1 = 0 x — 2 y + z — 3 = 0 . Определите, принадлежат ли точки M 0 ( 1 , — 1 , 0 ) и N 0 ( 0 , — 1 3 , 1 ) прямой линии пересечения плоскостей.

Решение

Начнем с точки М 0 _. Подставим ее координаты в оба уравнения системы 2 · 1 + 3 · ( — 1 ) + 1 = 0 1 — 2 · ( — 1 ) + 0 — 3 = 0 ⇔ 0 = 0 0 = 0 .

В результате подстановки мы получили верные равенства. Это значит, что точка М 0 принадлежит обеим плоскостям и расположена на линии их пересечения.

Подставим в оба уравнения плоскости координаты точки N 0 ( 0 , — 1 3 , 1 ) . Получаем 2 · 0 + 3 · — 1 3 + 1 = 0 0 — 2 · — 1 3 + 1 — 3 = 0 ⇔ 0 = 0 — 1 1 3 = 0 .

Как вы видите, второе уравнение системы превратилось в неверное равенство. Это значит, что точка N 0 не принадлежит заданной прямой.

Ответ: точка М 0 принадлежит прямой линии, а точка N 0 не принадлежит.

Теперь предлагаем вам алгоритм нахождения координат некоторой точки, принадлежащей прямой линии, если прямая в пространстве в прямоугольной системе координат O x y z определяется уравнениями пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 .

Количество решений системы из двух линейных уравнений с темя неизвестными A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 бесконечно. Любое из этих решений может стать решением задачи.

Пусть в трехмерном пространстве задана прямая линия уравнениями двух пересекающихся плоскостей вида x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 . Найдите координаты любой из точек этой прямой.

Решение

Перепишем систему уравнений x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 ⇔ x + 0 y + 3 z = — 7 2 x + 3 y + 3 z = — 2 .

Возьмем отличный от нуля минор второго порядка в качестве базисного минора основной матрицы системы 1 0 2 3 = 3 ≠ 0 . Это значит, что z – это свободная неизвестная переменная.

Перенесем слагаемые, содержащие свободную неизвестную переменную z в правые части уравнений:

x + 0 y + 3 z = — 7 2 x + 3 y + 3 z = — 2 ⇔ x + 0 y = — 7 — 3 z 2 x + 3 y = — 2 — 3 z

Введем произвольное действительное число λ и примем, что z = λ .

Тогда x + 0 y = — 7 — 3 z 2 x + 3 y = — 2 — 3 z ⇔ x + 0 y = — 7 — 3 λ 2 x + 3 y = — 2 — 3 λ .

Для решения полученной системы уравнений применим метод Крамера:

∆ = 1 0 2 3 = 1 · 3 — 0 · 1 = 2 ∆ x = — 7 — 3 λ 0 — — 3 λ 3 = — 7 — 3 λ · 3 — 0 · ( — 2 — 3 λ ) = 21 — 9 λ ⇒ x = ∆ x ∆ = — 7 — 3 λ ∆ y = 1 — 7 — 3 λ 2 — 2 — 3 λ = 1 · — 2 — 3 λ — — 7 — 3 λ · = 12 + 3 λ ⇒ y = ∆ y ∆ = 4 + λ

Общее решение системы уравнений x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 будет иметь вид x = — 7 — 3 λ y = 4 + λ z = λ , где λ ∈ R .

Для получения частного решения системы уравнений, которое даст нам искомые координаты точки, принадлежащей заданной прямой, нам необходимо взять конкретное значение параметра λ . Если λ = 0 , то x = — 7 — 3 · 0 y = 4 + 0 z = 0 ⇔ x = — 7 y = 4 z = 0 .

Это позволяет нам получить координаты искомой точки — 7 , 4 , 0 .

Проверим верность найденных координат точки методом подстановки их в исходные уравнения двух пересекающихся плоскостей — 7 + 3 · 0 + 7 = 0 2 · ( — 7 ) + 3 · 4 + 3 · 0 + 2 = 0 ⇔ 0 = 0 0 = 0 .

Ответ: — 7 , 4 , 0

Направляющий вектор прямой, по которой пересекаются две плоскости

Давайте рассмотрим, как определить координаты направляющего вектора прямой, которая задана уравнениями двух пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 . В прямоугольной системе координат 0хуz направляющий вектор прямой неотделим от прямой линии.

Как мы знаем, прямая перпендикулярна по отношению к плоскости в том случае, когда она перпендикулярна по отношению к любой прямой, лежащей в данной плоскости. Исходя из вышесказанного, нормальный вектор плоскости перпендикулярен любому ненулевому вектору, лежащему в данной плоскости. Эти два факта помогут нам в нахождении направляющего вектора прямой.

Плоскости α и β пересекаются по линии a . Направляющий вектор a → прямой линии a расположен перпендикулярно по отношению к нормальному вектору n 1 → = ( A 1 , B 1 , C 1 ) плоскости A 1 x + B 1 y + C 1 z + D 1 = 0 и нормальному вектору n 2 → = ( A 2 , B 2 , C 2 ) плоскости A 2 x + B 2 y + C 2 z + D 2 = 0 .

Направляющий вектор прямой a представляет собой векторное произведение векторов n → 1 = ( A 1 , B 1 , C 1 ) и n 2 → = A 2 , B 2 , C 2 .

a → = n → 1 × n 2 → = i → j → k → A 1 B 1 C 1 A 2 B 2 C 2

Зададим множество всех направляющих векторов прямой как λ · a → = λ · n 1 → × n 2 → , где λ — это параметр, который может принимать любые действительные значения, отличные от нуля.

Пусть прямая в пространстве в прямоугольной системе координат O х у z задана уравнениями двух пересекающихся плоскостей x + 2 y — 3 z — 2 = 0 x — z + 4 = 0 . Найдем координаты любого направляющего вектора этой прямой.

Решение

Плоскости x + 2 y — 3 z — 2 = 0 и x — z + 4 = 0 имеют нормальные векторы n 1 → = 1 , 2 , — 3 и n 2 → = 1 , 0 , — 1 . Примем за направляющий вектор прямой линии, являющейся пересечением двух заданных плоскостей, векторное произведение нормальных векторов:

a → = n → 1 × n 2 → = i → j → k → 1 2 — 3 1 0 — 1 = i → · 2 · ( — 1 ) + j → · ( — 3 ) · 1 + k → · 1 · 0 — — k → · 2 · 1 — j → · 1 · ( — 1 ) — i → · ( — 3 ) · 0 = — 2 · i → — 2 j → — 2 k →

Запишем ответ в координатной форме a → = — 2 , — 2 , — 2 . Тем, кто не помнит, как это делается, рекомендуем обратиться к теме «Координаты вектора в прямоугольной системе координат».

Ответ: a → = — 2 , — 2 , — 2

Переход к параметрическим и каноническим уравнениям прямой в пространстве

Для решения ряда задач проще использовать параметрические уравнения прямой в пространстве вида x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ или канонические уравнения прямой в пространстве вида x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ . В этих уравнениях a x , a y , a z — координаты направляющего вектора прямой, x 1 , y 1 , z 1 — координаты некоторой точки прямой, а λ — параметр, принимающий произвольные действительные значения.

От уравнения прямой вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 можно перейти к каноническим и параметрическим уравнениям прямой линии в пространстве. Для записи канонических и параметрических уравнений прямой нам понадобятся навыки нахождения координат некоторой точки прямой, а также координат некоторого направляющего вектора прямой, заданной уравнениями двух пересекающихся плоскостей.

Рассмотрим написанное выше на примере.

Зададим прямую линию в трехмерной системе координат уравнениями двух пересекающихся плоскостей 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0 . Напишем канонические и параметрические уравнения этой прямой.

Решение

Найдем координаты направляющего вектора прямой, который является векторным произведением нормальных векторов n 1 → = 2 , 1 , — 1 плоскости 2 x + y — z — 1 = 0 и n 2 → = ( 1 , 3 , — 2 ) плоскости x + 3 y — 2 z = 0 :

a → = n 1 → × n 2 → = i → j → k → 2 1 — 1 1 3 — 2 = i → · 1 · ( — 2 ) + j → · ( — 1 ) · 1 + k → · 2 · 3 — — k → · 1 · 1 — j → · 2 · ( — 2 ) — i → · ( — 1 ) · 3 = i → + 3 · j → + 5 · k →

Координаты направляющего вектора прямой a → = ( 1 , 2 , 5 ) .

Следующим шагом является определение координат некоторой точки заданной прямой линии, которыми является одно из решений системы уравнений: 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0 ⇔ 2 x + y — z = 1 x + 3 y — 2 z = 0 .

Возьмем в качестве минорной матрицы системы определитель 2 1 1 3 = 2 · 3 — 1 · 1 = 5 , который отличен от нуля. В этом случае переменная z является свободной. Перенесем слагаемые с ней в правые части каждого уравнения и придаем переменной произвольное значение λ :

2 x + y — z = 1 x + 3 y — 2 z = 0 ⇔ 2 x + y = 1 + z x + 3 y = 2 z ⇔ 2 x + y = 1 + λ x + 3 y = 2 λ , λ ∈ R

Применяем для решения полученной системы уравнений метод Крамера:

∆ = 2 1 1 3 = 2 · 3 — 1 · 1 = 5 ∆ x = 1 + λ 1 2 λ 3 = ( 1 + λ ) · 3 — 1 · 2 λ = 3 + λ ⇒ x = ∆ x ∆ = 3 + λ 5 = 3 5 + 1 5 · λ ∆ y = 2 1 + λ 1 2 λ = 2 · 2 λ — ( 1 + λ ) · 1 = — 1 + 3 λ ⇒ y = ∆ y ∆ = — 1 + 3 λ 5 = — 1 5 + 3 5 · λ

Получаем: 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0 ⇔ x = 3 5 + 1 5 y = — 1 5 + 3 5 z = λ

Примем λ = 2 для того, чтобы получить координаты точки прямой линии: x 1 = 3 5 + 1 5 · 2 y 1 = — 1 5 + 3 5 · 2 z 1 = 2 ⇔ x 1 = 1 y 1 = 1 z 1 = 2 . Теперь мы имеем достаточно данных для того, чтобы записать канонические и параметрические уравнения данной прямой в пространстве: x — x 1 a x = y — y 1 a y = z — z 1 a z ⇔ x — 1 1 = y — 1 3 = z — 2 5 x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ ⇔ x = 1 + 1 · λ y = 1 + 3 · λ z = 2 + 5 · λ ⇔ x = 1 + λ y = 1 + 3 · λ z = 2 + 5 · λ

Ответ: x — 1 1 = y — 1 3 = z — 2 5 и x = 1 + λ y = 1 + 3 · λ z = 2 + 5 · λ

Данная задача имеет еще один способ решения.

Нахождение координат некоторой точки прямой проводится при решении системы уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 .

В общем случае ее решения можно записать в виде искомых параметрических уравнений прямой в пространстве x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ .

Получение канонических уравнений проводится следующим образом: решаем каждое из полученных уравнений относительно параметра λ , приравниваем правые части равенства.

x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ ⇔ λ = x — x 1 a x λ = y — y 1 a y λ = z — z 1 a z ⇔ x — x 1 a x = y — y 1 a y = z — z 1 a z

Применим данный способ к решению задачи.

Зададим положение прямой линии уравнениями двух пересекающихся плоскостей 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0 . Напишем параметрическое и каноническое уравнения для этой прямой линии.

Решение

Решение системы из двух уравнений с тремя неизвестными проводится аналогично тому, как мы делали это в предыдущем примере. Получаем: 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0 ⇔ x = 3 5 + 1 5 · λ y = — 1 5 + 3 5 · λ z = λ .

Это параметрические уравнения прямой в пространстве.

Канонические уравнения получаем следующим образом: x = 3 5 + 1 5 · λ y = — 1 5 + 3 5 · λ z = λ ⇔ λ = x — 3 5 1 5 λ = y + 1 5 3 5 λ = z 1 ⇔ x — 3 5 1 5 = y + 1 5 3 5 = z 1

Полученные в обоих примерах уравнения отличаются внешне, однако они эквивалентны, так как определяют одно и то же множество точек трехмерного пространства, а следовательно и одну и ту же прямую линию.

Ответ: x — 3 5 1 5 = y + 1 5 3 5 = z 1 и x = 3 5 + 1 5 · λ y = — 1 5 + 3 5 · λ z = λ

Принадлежность точки отрезку. Почему не работает классика?

IP76 > Векторная графика > Принадлежность точки отрезку. Почему не работает классика?

Определить принадлежность точки отрезку, казалось бы, вполне себе тривиальная задача из школьного курса геометрии. Однако, есть определенные нюансы, которые заставляют усомниться в верности классической формулы:

Причины и постановка задачи

Запросы «как найти принадлежность точки отрезку» уводят на страницу «Пересечение прямых, угол и координаты пересечения», где есть пункт «Принадлежность точки отрезку». В нем рассматривается факт принадлежности точки отрезку, уже после того, как мы определили точку пересечения прямых. То есть точка уже принадлежит прямым, и это абсолютно точно. Осталось только определиться, точка в отрезке между двумя точками отрезка, либо где-то на прямой мимо них.

Людям свойственно искать готовые решения, и код, представленный в статье вряд ли удовлетворит запросу «как найти принадлежность точки отрезку, заданный двумя точками«. Поэтому здесь задачу так и сформулируем:

Есть отрезок, заданный точками P1(x1,y1) и P2 (x2,y2) . Необходимо определить, принадлежит ли точка P(x,y) этому отрезку.

Классическое уравнение

Предположим, вы делаете векторный редактор. Необходимо по курсору мыши определить попадает ли точка в ранее нарисованный отрезок. В этом многотрудном деле такая задача возникает всегда.

Для совместимости с Delphi 7 введем тип вещественной точки:

Почему бы не сделать сразу TPointF вместо типа TxPoint? Просто у меня гора старых исходников, где используется этот тип, а никакого TPointF не было ни в помине, ни в планах. Delphi 7 казалась вершиной инженерной мысли на тот момент.

В предложение uses дописываем следующее (ради TPointF, и чтобы компилятор XE не доставал хинтами):

Почему именно XE5? Если честно, нет возможности проверить, не ставить же ради этого всю линейку дельфей. Но в XE5 вещественная точка точно есть, а в Delphi 7 ее точно нет. Вот этим и объясняется выбор версии компилятора в директиве. Одни говорят, что TPointF появился в XE2, другие — аж в Delphi 2010. Короче, с таким директивным условием будет работать везде и точка.

Пишем небольшую функцию, которая использует классическое уравнение прямой, проходящей через две различные точки на плоскости, представленное выше.

SameValue — сравнивает два вещественных числа с учетом погрешности Epsilon. Находится в модуле Math, который надо подключить в предложении uses секции implementation.

Что происходит. Вначале проверяется допустимость координаты точки внутри координат отрезка. Условие необходимое, но недостаточное. Если координата может принадлежать отрезку, третьим условием проверяем нахождение точки на прямой, проходящей через точки отрезка.

Рис.1. Курсор точно на линии, но не определяет, что точка принадлежит отрезку

Если мы попытаемся по координатам курсора мыши определить, попала ли точка в отрезок, нас ждет фиаско. Складывается ощущение, что формула не работает, алгебра — отстой, все в жизни не так.

Расширенная классика

Для начала навесим на функцию еще пару условий, чтобы определить попадание в точки, задающие отрезок.

Ну, во-первых, вот и разгадка, куда делись значения 1 и 2 из результатов предыдущей функции. Во-вторых, теперь в конечные точки отрезка попадает отлично, но между ними по-прежнему не хочет работать.

На самом деле — математика по-прежнему царица наук, а мы пытаемся повенчать розу белую с черной жабой.

Выведем в интерфейс значения dx = (p2.x-p1.x), dy = (p2.y-p1.y) и т.д. Плюс результат работы функции (p.x-p1.x)*(p2.y-p1.y) — (p.y-p1.y)*(p2.x-p1.x). И убедимся, что при самых казалось бы максимально возможных приближениях к отрезку, результат ошеломляет своей двух- или трехзначной непохожестью на ноль.

Рис.2. Теперь определяет конечные точки, но между ними по-прежнему работает так себе…

Конечно, используя операцию умножения вместо деления, мы избегаем деления на ноль, укорачиваем код. Но при этом надо помнить, что умножение даже 1 на 12, это уже далеко от нуля, а если появляется еще и минус в разницах, то от нуля мы улетаем очень быстро и очень ощутимо.

На рисунке 2 прицел точно на линии, но разность координат, которую получаем из классического уравнения, и которая должна быть равна нулю, между тем равна:

Функция применима в точных расчетах, но не в векторном редакторе.

Модификация уравнения

Очевидно, надо вычислять как-то иначе. Например вычислять Y по имеющейся координате X и сравнивать с имеющейся координатой Y. Если разница меньше заданного Epsilon — точка принадлежит отрезку. Выразим Y из используемого уравнения прямой. Итак, дано:

Выразим Y:

И напишем еще одну функцию, в которой учтем ситуацию, когда (X₂-X₁) может быть равно нулю. Это ситуация вертикальной (или почти вертикальной) прямой.

Epsilon уже выступает, и как точность вычислений, и как допуск, при котором мы считаем, что точка на отрезке. Невозможно скрупулезно попасть мышкой в нужную точку отрезка, которая сама по себе уже есть огромное приближение к действительности. Все мы помним и любим Брезенхэма.

Рис.3. Все здорово определяет с учетом погрешности Epsilon=12 pix

Но, даже если мы упростили себе процесс «попадания» в отрезок, мы должны знать точные координаты на отрезке. Для этого у нас и появился тип вещественной точки TxPoint и возвращаемый параметр res. В этой версии функции мы производим расчет реальной точки на отрезке.

На рисунке 3 расчетная точка и ее координаты выделена коричневым цветом.

Однако, все равно есть нюанс. Если линия сильно вертикальна, то есть расстояние (X₂-X₁) невелико, попадать в линию все равно трудно.

Рис.3.1. На почти вертикальной линии функция снова капризничает

Связано с тем, что при уменьшении делителя, коим разность по X выступает в нашем случае, сильно вырастает результат, и чем расстояние (X₂-X₁) меньше, тем труднее попасть в Epsilon.

Итоговая функция

В стремлении к совершенству, всегда что-то незамысловатое, в пару строк кода, разрастается в какую-то все учитывающую портянку листинга.

Давайте проверять, что больше (X₂-X₁) или (Y₂-Y₁), и в зависимости от результата, будем высчитывать либо Y, либо X. Формулу для X не привожу, он очевидна.

Почему такая большая функция получилась?

В функции помимо факта принадлежности точки отрезку, также осуществляется проверка на конечные точки — чтобы можно было менять их расположение мышкой. Также, функция возвращает «истинную» точку на отрезке, полученную из приближенной, содержащую погрешность Epsilon.

Можно сократить, не считать конечные точки, не анализировать «вертикальность» и «горизонтальность». Можно взять за настоящую ту точку, которую анализируем и не считать «истинную». Код в этом случае сильно сократиться. Поэтому лучше иметь полный комплект, из которого можно удалить «лишнее» на ваш взгляд.

Зачем нужны такие ощутимо большие проверки на вертикальность и горизонтальность. Ну, во-первых мы освобождаем от условий последний блок вычислений, во-вторых, если убрать, скажем, проверку на dy, погрешность станет в два раза меньше. Потому что отработает это условие: Abs(p1.Y-p.Y) + Abs(p2.Y-p.Y). Имея идеальную горизонтальную линию, подведя курсор на Epsilon допустимый интервал, мы получим в итоге Epsilon + Epsilon = 2 * Epsilon и условие конечно не сработает. Сработает, если подведем на расстояние в два раза меньшее Epsilon.

Если всех этих тонкостей не требуется, можно смело использовать либо эту, либо вообще эту функцию.

Классика всегда в моде или Математика — царица наук

Теперь давайте полученную в результате предыдущей функции вещественную точку res подставим в первую функцию. И убедимся, что теоретическая принадлежность точки отрезку работает прекрасно, просто в пространстве грубых целочисленных точек мы не в состоянии гарантированно получить такую точку, которая удовлетворила бы уравнению. Но если мы ее рассчитаем и получим значения с плавающей запятой — все заработает как надо.

Рис.5. Результат применения рассчитанной точки для первой функции

На рисунке 5 добавлен результат функции f(x,y)=(x-x₁) * (y₂-y₁) — (y-y₁) * (x₂-x₁) для рассчитанной точки на отрезке. Он равен, как и следовало ожидать, нулю. А также результат вызова первой функции, которая использует это уравнение и возвращает 3, если точка принадлежит отрезку. Что мы воочию и видим.

1)Поэтому в графике надо избегать типов TPoint, даже если это вызывает необходимость постоянно их округлять для функций GDI.

2)Поэтому функция правильная, классическая формула работает, просто в пространстве компьютерных упрощений надо использовать ту же самую формулу, но в другом качестве.

Скачать

Друзья, спасибо за внимание!

Надеюсь, материал был полезен.

Не пропустите новых интересных штуковин, подписывайтесь на телегу. )))

Если есть вопросы, с удовольствием отвечу.

Исходники и исполняемый файл для GDI и Delphi 7. Проверен в XE 7, XE 10.

Исходники (Delphi 7, XE7, XE10) 11 Кб

Исполняемый файл (zip) 213 Кб

Как подключить GDI+ в Delphi 7 и без проблем скомпилировать в XE 7, XE 10 читаем в этой статье. Там же забираем исходники.

Чтобы нарисовать отрезок, нажмите мышь и, не отпуская, ведите курсор. При отпускании отрезок зафиксируется. При повторном нажатии начнет рисоваться новый отрезок.

За концы отрезка можно таскать. Если попали на отрезок, т.е. видна коричневая точка, можно таскать весь отрезок.

Исходники намеренно выложены в D7 варианте.

При компиляции в XE10 следует снять галочку с Enable High-DPI

Какой координатной четверти принадлежит точка?

Определить четверть координатной плоскости, которой принадлежит точка. Координаты точки ввести с клавиатуры.

• Если у точки обе координаты ( x и y ) положительны, то она принадлежит первой четверти.
• Если координата x отрицательна, а y положительна, то точка находится во второй четверти.
• Если обе координаты отрицательны, то точка принадлежит третьей координатной четверти.
• Если x положительна, а y отрицательна, то точка находится в IV четверти.

Следует иметь в виду, что использовать в программе четыре отдельные инструкции if не совсем правильно. Хотя такое решение даст верный результат, программу нельзя будет назвать эффективной, т.к. даже если первая проверка дала «правду», дальнейшие проверки будут продолжены, хотя в них нет никакого смысла. Поэтому правильным решением будет использование вложенных конструкций if-else. Это замечание не касается языка Python, т.к. в нем есть конструкция множественного ветвления (if-elif-else).

Поскольку точка может лежать на одной из двух координатных осей или находиться в начале координат, то значит могут быть ситуации, когда точка не принадлежит ни одной из четвертей. Эти случаи обрабатываются в отдельных ветках, либо опускаются. Из этого также следует, что если первые три проверки не сработали, то нельзя делать однозначный вывод, что точка принадлежит оставшейся четверти. Поэтому в программе сообщение о том, в какой четверти находится точка может быть только в теле if, но не else.

Как найти координаты точки?

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.

Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

• Координатные оси — это прямые, образующие систему координат.
• Ось абсцисс Ox — горизонтальная ось.
• Ось ординат Oy — вертикальная ось.
• Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
• Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.

Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

• верхний правый угол — первая четверть I;
• верхний левый угол — вторая четверть II;
• нижний левый угол — третья четверть III;
• нижний правый угол — четвертая четверть IV;

• Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
• Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
• Если обе координаты отрицательны, то число находится в третьей четверти.
• Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.

Определение координат точки

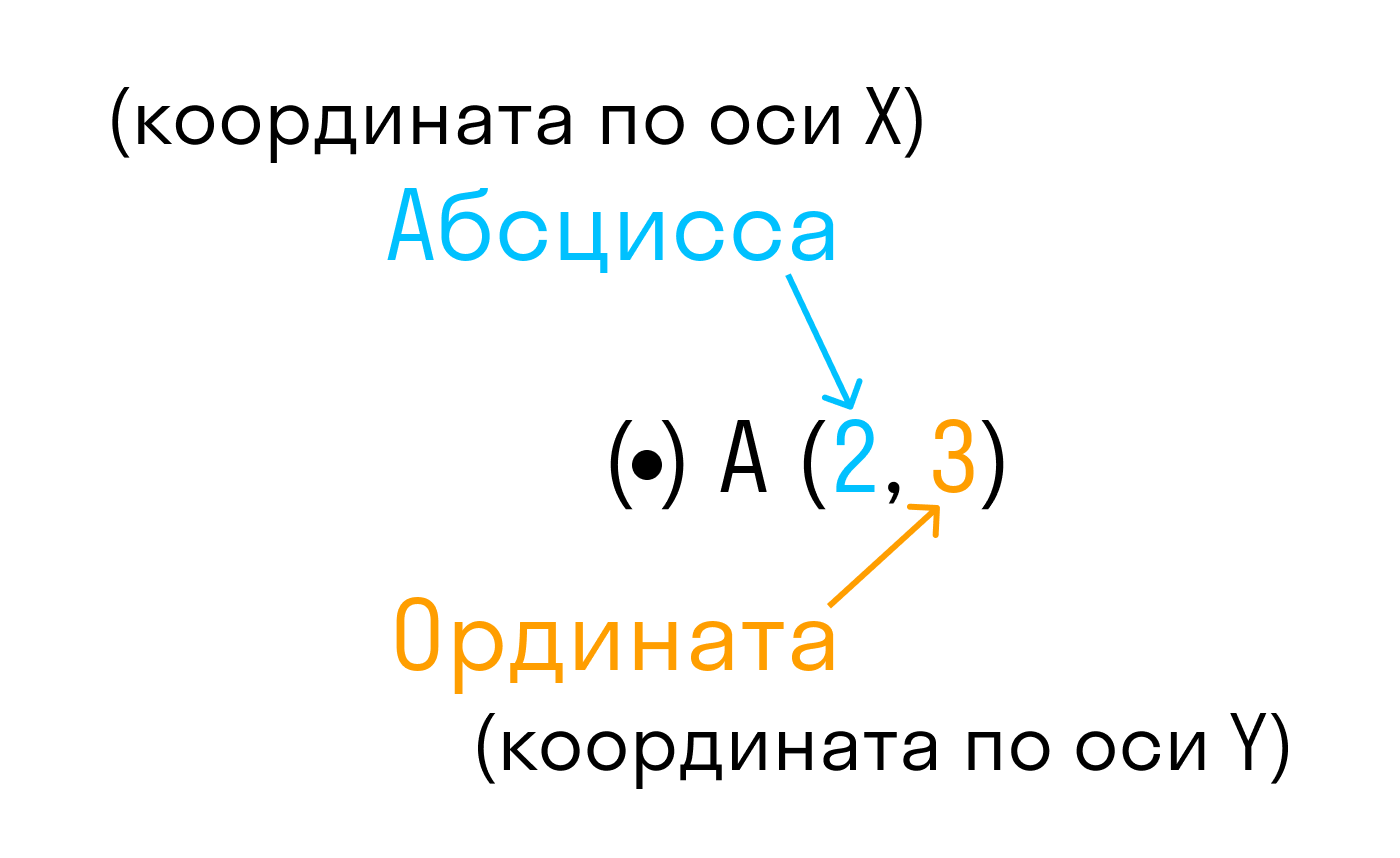
Каждой точке координатной плоскости соответствуют две координаты.

Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.

Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.

Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.

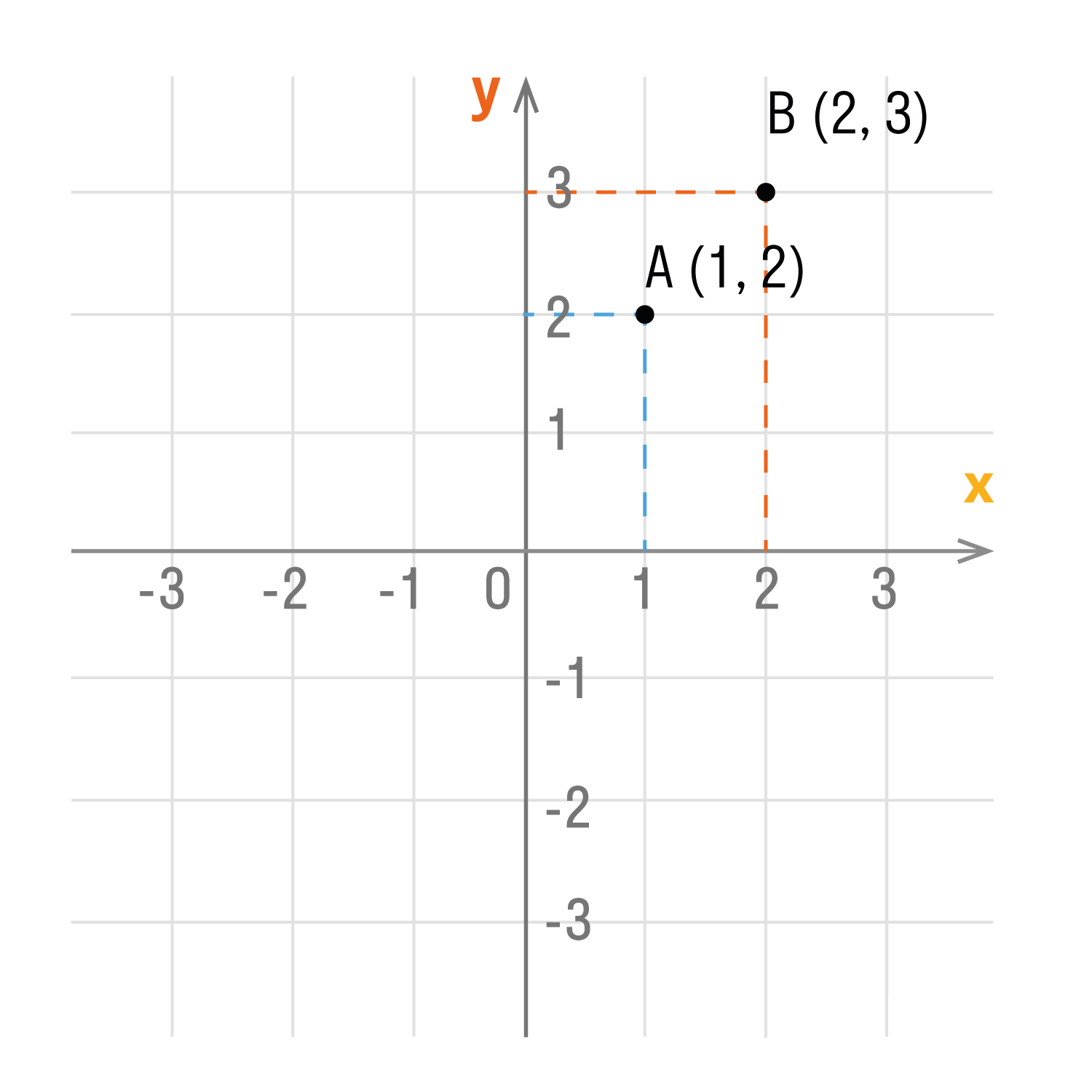
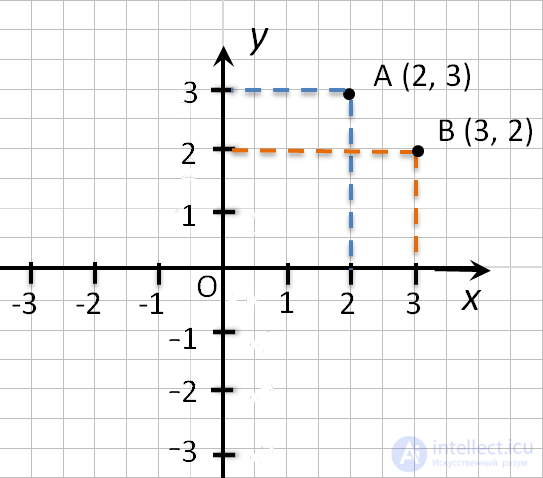
Смотрим на график и фиксируем: A (1; 2) и B (2; 3).

Особые случаи расположения точек

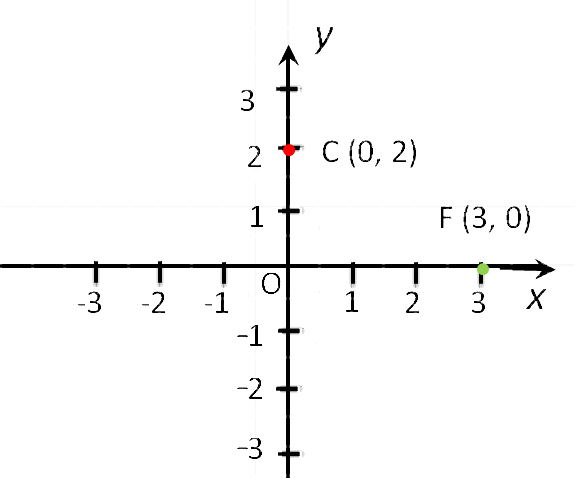
В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:

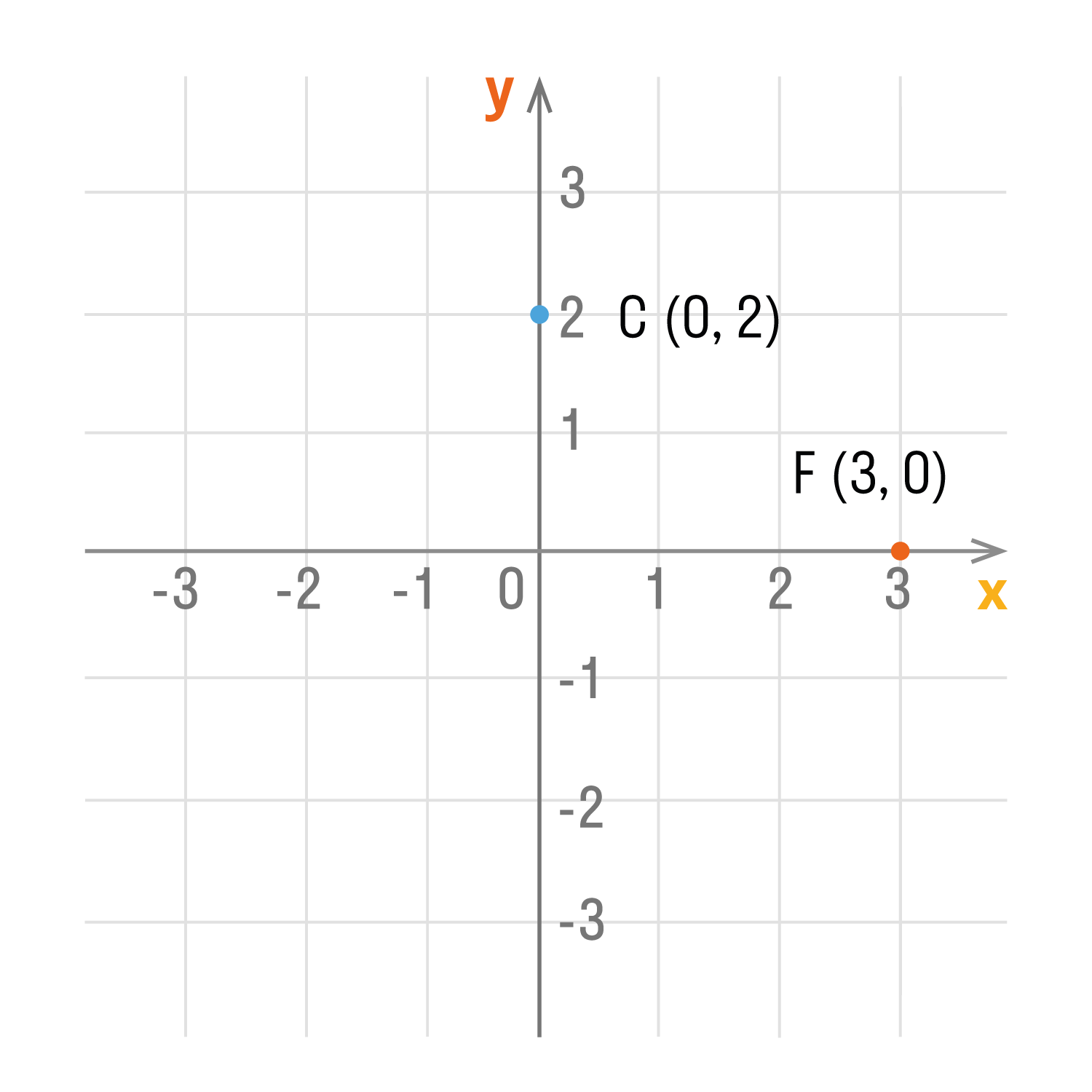
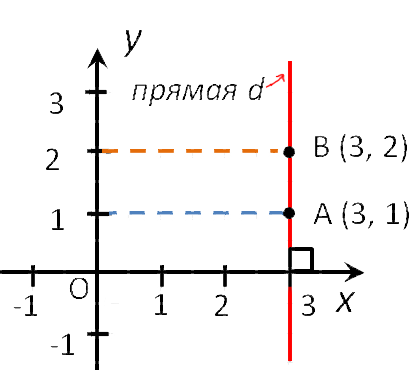
1. Если точка лежит на оси Oy, то ее абсцисса равна 0. Например,
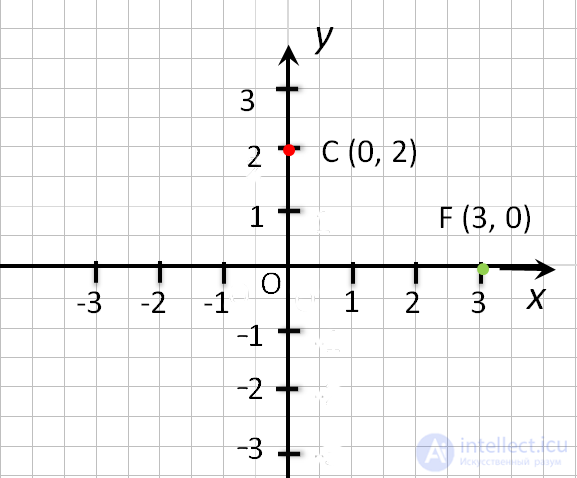
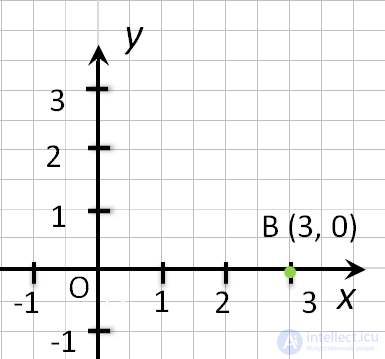
   точка С (0, 2).
2. Если точка лежит на оси Ox, то ее ордината равна 0. Например,
   точка F (3, 0).
3. Начало координат — точка O. Ее координаты равны нулю: O (0,0).
   
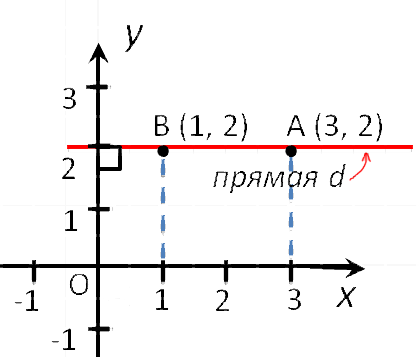
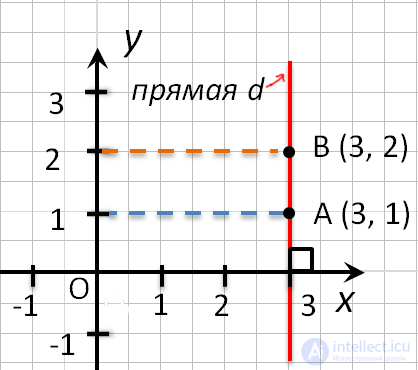
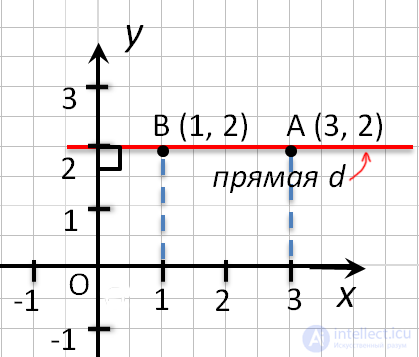
4. Точки любой прямой, которая перпендикулярна оси абсцисс, имеют одинаковые абсциссы.
   
5. Точки любой прямой, которая перпендикулярна оси ординат, имеют одинаковые ординаты.
   
6. Если точка лежит на оси абсцисс, то ее координаты будут иметь вид: (x, 0).
   
7. Если точка лежит на оси ординат, то ее координаты будут иметь вид: (0, y).
   

Способы нахождения точки по её координатам

Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.

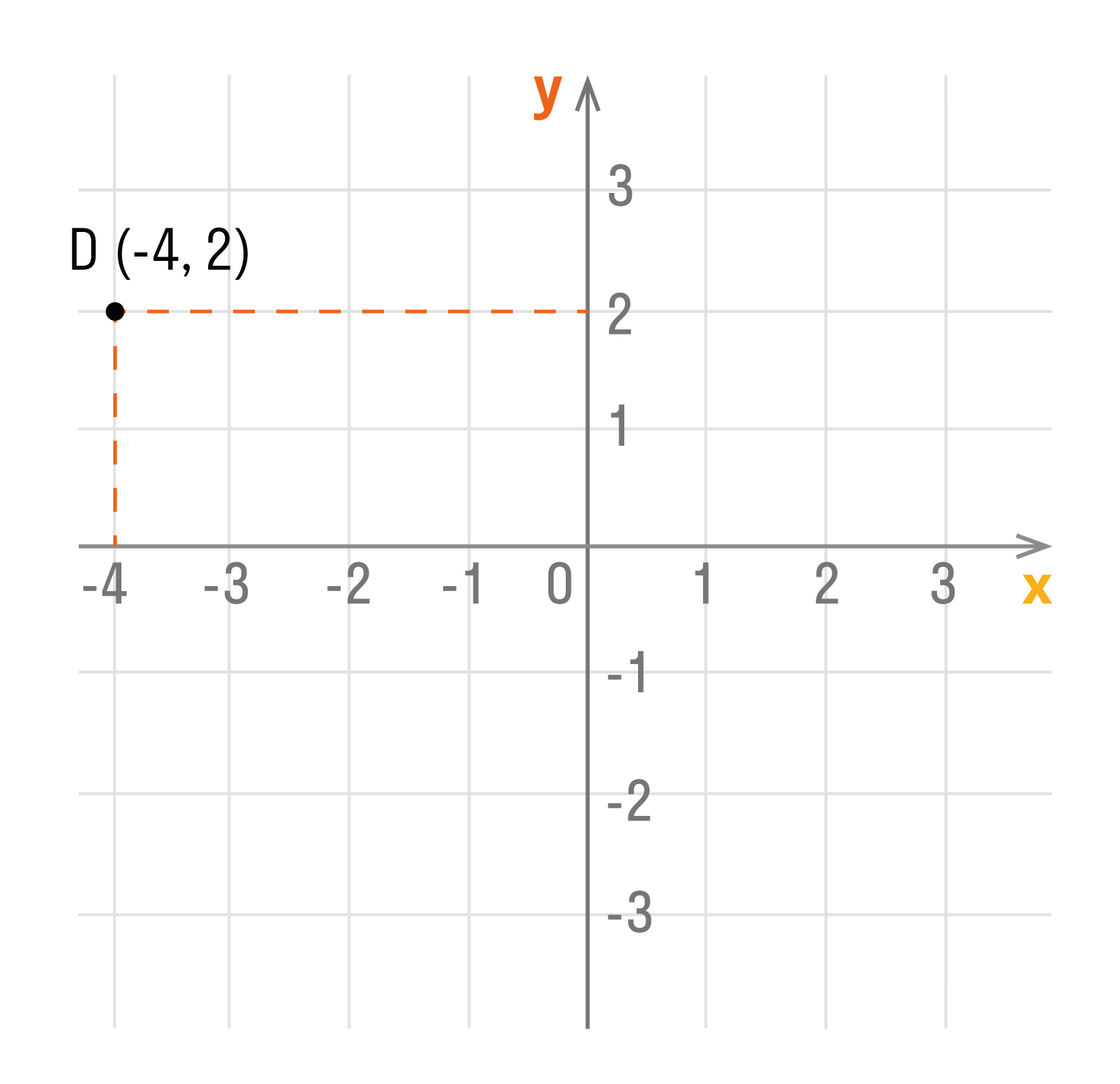
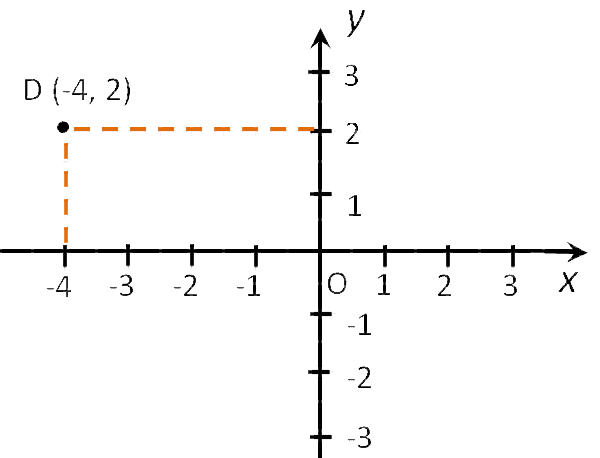
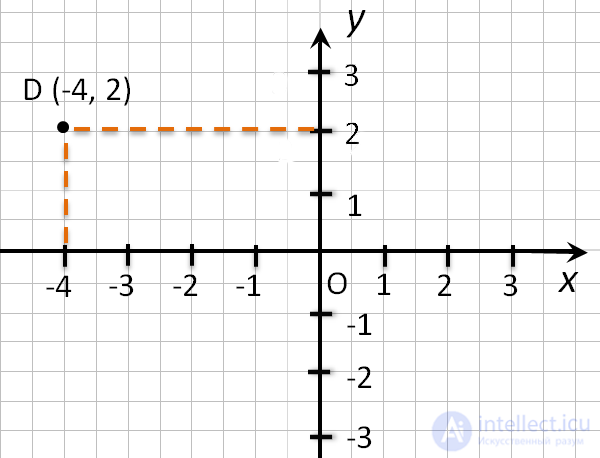
Способ первый. Как определить положение точки D по её координатам (-4, 2):

1. Отметить на оси Ox, точку с координатой -4, и провести через нее прямую перпендикулярную оси Ox.
2. Отметить на оси Oy, точку с координатой 2, и провести через нее прямую перпендикулярную оси Oy.
3. Точка пересечения перпендикуляров и есть искомая точка D. Ее абсцисса равна -4, а ордината — 2.
   

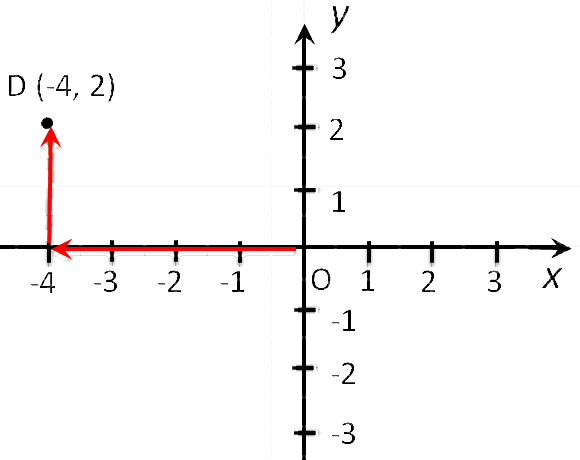
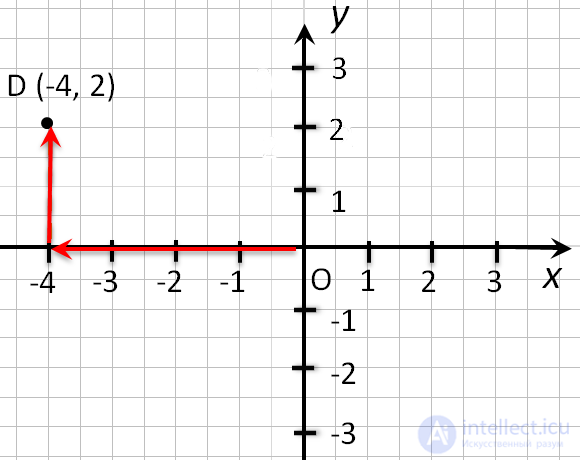
Способ второй. Как определить положение точки D (-4, 2):

1. Сместить прямую по оси Ox влево на 4 единицы, так как у нас
   перед 4 стоит знак минус.
2. Подняться из этой точки параллельно оси Oy вверх на 2 единицы, так как у нас перед 2 стоит знак плюс.
   

Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:

Люди добрые помогите с математикой. ПОЖАЛУЙСТА, УМОЛЯЮ.

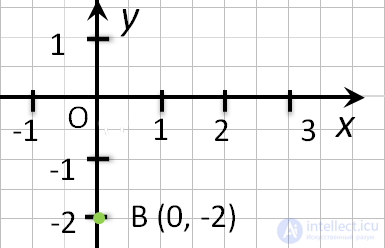
1.Определи ординату данной точки: C(−3;−1).
Даны координаты точки. Определи, на которой координатной оси находится данная точка.

Точка P(0;18) находится на оси ординат или абсцисс.

2.Даны координаты точки. Определи, в какой координатной четверти находится данная точка.

Точка E(20;−12) находится в 1,2,3 или 4 четверти.

Определи, которая из данных точек находится в I квадранте координатной плоскости:

4.На координатной плоскости дана точка с координатами (5;5) .

Которые из данных координат являются координатами точки, симметричной данной точке относительно начальной точки системы координат?

1.Определи ординату данной точки: C(−3;−1). y=-1
Даны координаты точки. Определи, на которой координатной оси находится данная точка.

Точка P(0;18) находится на оси ординат

2.Даны координаты точки. Определи, в какой координатной четверти находится данная точка.

Точка E(20;−12) находится в 4 четверти.

Определи, которая из данных точек находится в I квадранте координатной плоскости:

4.На координатной плоскости дана точка с координатами (5;5) .

Которые из данных координат являются координатами точки, симметричной данной точке относительно начальной точки системы координат?

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

на главную

Как найти координаты точки

Поддержать сайт

Привет, мой друг, тебе интересно узнать все про координаты точки, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое
координаты точки , настоятельно рекомендую прочитать все из категории Арифметика.

каждой точке координатной плоскости соответствуют две координаты.

координаты точки на плоскости — это пара чисел, в которой на первомместе стоит абсцисса,
а на втором — ордината точки.

Рассмотрим как в системе координат (на координатной плоскости):

• находить координаты точки;
• найти положение точки.

Чтобы найти координаты точки на плоскости, нужно опустить из этой точки перпендикуляры на оси координат.

Точка пересечения с осью x называется абсциссой точки А, а с осью y называется ординатой точки А.

Обозначают координаты точки, как указано выше (•) A (2; 3).

Пример (•) A (2; 3) и (•) B (3; 2).

Особые случаи расположения точек

1. Если точка лежит на оси Oy, то ее абсцисса равна 0 . Об этом говорит сайт https://intellect.icu . Например, точка С (0, 2).
2. Если точка лежит на оси Ox, то ее ордината равна 0. Например, точка F (3, 0).
3. Начало координат — точка O имеет координаты, равные нулю O (0,0).
4. Точки любой прямой перпендикулярной оси абсцисс, имеют одинаковые абсциссы.
5. Точки любой прямой перпендикулярной оси ординат, имеют одинаковые ординаты.
6. Координаты любой точки, лежащей на оси абсцисс имеют вид (x, 0).
7. Координаты любой точки, лежащей на оси ординат имеют вид (0, y).

Как найти положение точки по ее координатам

Найти точку в системе координат можно двумя способами.

Первый способ

Чтобы определить положение точки по ее координатам, например, точки D (-4 , 2), надо:

1. Отметить на оси Ox, точку с координатой (-4), и провести через нее прямую перпендикулярную оси 0x.
2. Отметить на оси Oy, точку с координатой (2), и провести через нее прямую перпендикулярную оси 0y.
3. Точка пересечения перпендикуляров (•) D — искомая точка. У нее абсцисса равна (-4), а ордината равна (2).

Второй способ

Чтобы найти точку D (-4 , 2) надо:

1. Сместиться по оси x влево на 4 единицы, так как у нас перед 4 стоит «-».
2. Подняться из этой точки параллельно оси y вверх на 2 единицы, так как у нас перед 2 стоит «+».

Чтобы быстрее и удобнее было находить координаты точек или строить точки по координатам на листе формата A4 в клеточку, можно скачать и использовать готовую систему координат на нашем сайте.

Как ты считаеешь, будет ли теория про координаты точки улучшена в обозримом будующем? Надеюсь, что теперь ты понял что такое координаты точки
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Арифметика

Из статьи мы узнали кратко, но емко про координаты точки

Общее уравнение плоскости : описание, примеры, решение задач

В статье рассмотрим такой тип уравнений плоскости как общее уравнение, получим его вид и разберем на практических примерах. Рассмотрим частные случаи и понятие общего неполного уравнения плоскости.

Общее уравнение плоскости: основные сведения

Перед началом разбора темы вспомним, что такое уравнение плоскости в прямоугольной системе координат в трёхмерном пространстве. Пусть нам дана прямоугольная система координат O x y z в трехмерном пространстве, уравнением плоскости в заданной системе координат будет такое уравнение с тремя неизвестными x , y , и z , которому отвечали бы координаты всех точек этой плоскости и не отвечали бы координаты никаких прочих точек. Иначе говоря, подставив в уравнение плоскости координаты некоторой точки этой плоскости, получаем тождество. Если же в уравнение подставить координаты какой-то другой точки, не принадлежащей заданной плоскости, равенство станет неверным.

Также вспомним определение прямой, перпендикулярной к плоскости: прямая является перпендикулярной к заданной плоскости, если она перпендикулярна любой прямой, принадлежащей этой плоскости.

Любую плоскость, заданную в прямоугольной системе координат O x y z трехмерного пространства, можно определить уравнением A x + B y + C z + D = 0 . В свою очередь, любое уравнение A x + B y + C z + D = 0 определяет некоторую плоскость в данной прямоугольной системе координат трехмерного пространства. A , B , C , D – некоторые действительные числа, и числа A , B , C не равны одновременно нулю.

Теорема состоит из двух частей. Разберем доказательство каждой из них.

1. Первая часть теоремы гласит, что любую заданную плоскость возможно описать уравнением вида A x + B y + C z + D = 0 . Допустим, задана некоторая плоскость и точка M 0 ( x 0 , y 0 , z 0 ) , через которую эта плоскость проходит. Нормальным вектором этой плоскости является n → = ( A , B , C ) . Приведем доказательство, что указанную плоскость в прямоугольной системе координат O x y z задает уравнение A x + B y + C z + D = 0 .

Возьмем произвольную точку заданной плоскости M ( x , y , z ) .В таком случае векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) будут перпендикулярны друг другу, а значит их скалярное произведение равно нулю:

n → , M 0 M → = A x — x 0 + B ( y — y 0 ) + C ( z — z 0 ) = A x + B y + C z — ( A x 0 + B y 0 + C z 0 )

Примем D = — ( A x 0 + B y 0 + C z 0 ) , тогда уравнение преобразуется в следующий вид: A x + B y + C z + D = 0 . Оно и будет задавать исходную плоскость. Первая часть теоремы доказана.

1. Во второй части теоремы утверждается, что любое уравнение вида A x + B y + C z + D = 0 задает некоторую плоскость в прямоугольной системе координат O x y z трехмерного пространства. Докажем это.

В теореме также указано, что действительные числа А , B , C одновременно не являются равными нулю. Тогда существует некоторая точка M 0 ( x 0 , y 0 , z 0 ) , координаты которой отвечают уравнению A x + B y + C z + D = 0 , т.е. верным будет равенство A x 0 + B y 0 + C z 0 + D = 0 . Отнимем левую и правую части этого равенства от левой и правой частей уравнения A x + B y + C z + D = 0 . Получим уравнение вида

A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 , и оно эквивалентно уравнению A x + B y + C z + D = 0 . Докажем, что уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 задает некоторую плоскость.

Уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 являет собой условие, необходимое и достаточное для перпендикулярности векторов n → = ( A , B , C ) и M 0 M → = x — x 0 , y — y 0 , z — z 0 . Опираясь на утверждение, указанное перед теоремой, возможно утверждать, что при справедливом равенстве A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 множество точек M ( x , y , z ) задает плоскость, у которой нормальный вектор n → = ( A , B , C ) . При этом плоскость проходит через точку M ( x 0 , y 0 , z 0 ) . Иначе говоря, уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 задает в прямоугольной системе координат O x y z трехмерного пространства некоторую плоскость. Таким, образом, эквивалентное этому уравнению уравнение A x + B y + C z + D = 0 также определяет эту плоскость. Теорема доказана полностью.

Уравнение вида A x + B y + C z + D = 0 называют общим уравнением плоскости в прямоугольной системе координат O x y z трехмерного пространства.

Допустим, задано некоторое общее уравнение плоскости λ · A x + λ · B y + λ · C z + λ · D = 0 , где λ – некое действительное число, не равное нулю. Это уравнение также задает в прямоугольной системе координат некоторую плоскость, совпадающую с плоскостью, определяемую уравнением A x + B y + C z + D = 0 , поскольку описывает то же самое множество точек трехмерного пространства. Например, уравнения x — 2 · y + 3 · z — 7 = 0 и — 2 · x + 4 · y — 2 3 · z + 14 = 0 задают одну и ту же плоскость, поскольку им обоим отвечают координаты одних и тех же точек трехмерного пространства.

Раскроем чуть шире смысл теорем.

В пределах заданной системы координат плоскость и общее уравнение, ее определяющее, неразрывно связаны: каждой плоскости отвечает общее уравнение плоскости вида A x + B y + C z + D = 0 ( при конкретных значениях чисел A , B , C , D ). В свою очередь, этому уравнению отвечает заданная плоскость в заданной прямоугольной системе координат.

Укажем пример как иллюстрацию этих утверждений.

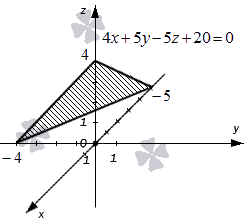
Ниже приведен чертеж, на котором изображена плоскость в фиксированной прямоугольной системе координат трехмерного пространства. Заданной плоскости отвечает общее уравнение вида 4 x + 5 y – 5 z + 20 = 0 , и ему соответствуют координаты любой точки этой плоскости. В свою очередь, уравнение 4 x + 5 y – 5 z + 20 = 0 описывает в заданной системе координат множество точек, которые составляют изображенную плоскость.

Общее уравнение плоскости, проходящей через точку

Повторимся: точка M 0 ( x 0 , y 0 , z 0 ) лежит на плоскости, заданной в прямоугольной системе координат трехмерного пространства уравнением A x + B y + C z + D = 0 в том случае, когда подставив координаты точки M 0 ( x 0 , y 0 , z 0 ) в уравнение A x + B y + C z + D = 0 , мы получим тождество.

Заданы точки M 0 ( 1 , — 1 , — 3 ) и N 0 ( 0 , 2 , — 8 ) и плоскость, определяемая уравнением 2 x + 3 y — z — 2 = 0 . Необходимо проверить, принадлежат ли заданные точки заданной плоскости.

Решение

Подставим координаты точки М 0 в исходной уравнение плоскости:

2 · 1 + 3 · ( — 1 ) — ( — 3 ) — 2 = 0 ⇔ 0 = 0

Мы видим, что получено верное равенство, значит точка M 0 ( 1 , — 1 , — 3 ) принадлежит заданной плоскости.

Аналогично проверим точку N 0 . Подставим ее координаты в исходное уравнение:

2 · 0 + 3 · 2 — ( — 8 ) — 2 = 0 ⇔ 12 = 0

Равенство неверно. Таким, образом, точка N 0 ( 0 , 2 , — 8 ) не принадлежит заданной плоскости.

Ответ: точка М 0 принадлежит заданной плоскости; точка N 0 – не принадлежит.

Приведенное выше доказательство теоремы об общем уравнении дает нам возможность использовать важный факт: вектор n → = ( A , B , C ) — нормальный вектор для плоскости, определяемой уравнением A x + B y + C z + D = 0 . Так, если нам известен вид общего уравнения, то возможно записать координаты нормального вектора заданной плоскости.

В прямоугольной системе координат задана плоскость 2 x + 3 y — z + 5 = 0 . Необходимо записать координаты всех нормальных векторов заданной плоскости.

Решение

Мы знаем, что заданные общим уравнением коэффициенты при переменных x , y , z служат координатами нормального вектора заданной плоскости. Тогда, нормальный вектор n → исходной плоскости имеет координаты 2 , 3 , — 1 . В свою очередь, множество нормальных векторов запишем так:

λ · n → = λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0

Ответ: λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0

Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора.

Очевидным фактом является то, что нормальный вектор n → = ( A , B , C ) является нормальным вектором бесконечного множества параллельных плоскостей. Поэтому для обозначения конкретной плоскости введем дополнительное условие: зададим некоторую точку M 0 ( x 0 , y 0 , z 0 ) , принадлежащую плоскости. Так, задавая в условии нормальный вектор и некоторую точку плоскости, мы ее зафиксировали.

Общее уравнение плоскости с нормальным вектором n → = ( A , B , C ) будет выглядеть так: A x + B y + C z + D = 0 . По условию задачи точка M 0 ( x 0 , y 0 , z 0 ) принадлежит заданной плоскости, т.е. ее координаты отвечают уравнению плоскости, а значит верно равенство: A x 0 + B y 0 + C z 0 + D = 0

Вычитая соответственно правые и левые части исходного уравнения и уравнения A x 0 + B y 0 + C z 0 + D = 0 , получим уравнение вида A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 . Оно и будет уравнением плоскости, проходящей через точку M 0 ( x 0 , y 0 , z 0 ) и имеющей нормальный вектор n → = ( A , B , C ) .

Возможно получить это уравнение другим способом.

Очевидным фактом является то, что все точки М ( x , y , z ) трехмерного пространства задают данную плоскость тогда и только тогда, когда векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) перпендикулярны или, иначе говоря, когда скалярное произведение этих векторов равно нулю:

n → , M 0 M → = A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0

Задана точка М 0 ( — 1 , 2 , — 3 ) , через которую в прямоугольной системе координат проходит плоскость, а также задан нормальный вектор этой плоскости n → = ( 3 , 7 , — 5 ) . Необходимо записать уравнение заданной плоскости.

Решение

Рассмотрим два способа решения.

1. Исходные условия позволяют получить следующие данные:

x 0 = — 1 , y 0 = 2 , z 0 = — 3 , A = 3 , B = 7 , C = — 5

Подставим их в общее уравнение плоскости, проходящей через точку, т.е. в A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0

3 ( x — ( — 1 ) ) + 7 ( y — 2 ) — 5 ( z — ( — 3 ) ) = 0 ⇔ 3 x + 7 y — 5 z — 26 = 0

1. Допустим, М ( x , y , z ) – некоторая точки заданной плоскости. Определим координаты вектора M 0 M → по координатам точек начала и конца:

M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) = ( x + 1 , y — 2 , z + 3 )

Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда:

n → , M 0 M → = 0 ⇔ 3 ( x + 1 ) + 7 ( y — 2 ) — 5 ( z + 3 ) = 0 ⇔ ⇔ 3 x + 7 y — 5 z — 26 = 0

Ответ: 3 x + 7 y — 5 z — 26 = 0

Неполное общее уравнение плоскости

Выше мы говорили о том, что, когда все числа А , B , C , D отличны от нуля, общее уравнение плоскости A x + B y + C z + D = 0 называют полным. В ином случае общее уравнение плоскости является неполным.

Разберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства.

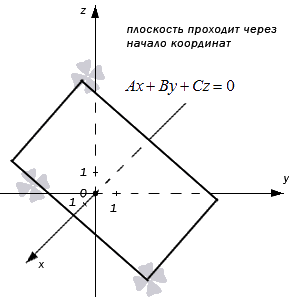
1. В случае, когда D = 0 , мы получаем общее неполное уравнение плоскости: A x + B y + C z + D = 0 ⇔ A x + B y + C z = 0

Такая плоскость в прямоугольной системе координат проходит через начало координат. В самом деле, если подставим в полученное неполное уравнение плоскости координаты точки О ( 0 , 0 , 0 ) , то придем к тождеству:

A · 0 + B · 0 + C · 0 = 0 ⇔ 0 ≡ 0

1. Если А = 0 , В ≠ 0 , С ≠ 0 , или А ≠ 0 , В = 0 , С ≠ 0 , или А ≠ 0 , В ≠ 0 , С = 0 , то общие уравнения плоскостей имеют вид соответственно: B y + C z + D = 0 , или A x + C z + D = 0 , или A x + B y + D = 0 . Такие плоскости параллельны координатным осям О x , O y , O z соответственно. Когда D = 0 , плоскости проходят через эти координатные оси соответственно. Также заметим, что неполные общие уравнения плоскостей B y + C z + D = 0 , A x + C z + D = 0 и A x + B y + D = 0 задают плоскости, которые перпендикулярны плоскостям O y z , O x z , O z y соответственно.

1. При А = 0 , В = 0 , С ≠ 0 , или А = 0 , В ≠ 0 , С = 0 , или А ≠ 0 , В = 0 , С = 0 получим общие неполные уравнения плоскостей: C z + D = 0 ⇔ z + D C = 0 ⇔ z = — D C ⇔ z = λ , λ ∈ R или B y + D = 0 ⇔ y + D B = 0 ⇔ y = — D B ⇔ y = λ , λ ∈ R или A x + D = 0 ⇔ x + D A = 0 ⇔ x = — D A ⇔ x = λ , λ ∈ R соответственно.

Эти уравнения определяют плоскости, которые параллельны координатным плоскостям O x y , O x z , O y z соответственно и проходят через точки 0 , 0 , — D C , 0 , — D B , 0 и — D A , 0 , 0 соответственно. При D = 0 уравнения самих координатных плоскостей O x y , O x z , O y z выглядят так: z = 0 , y = 0 , x = 0

Задана плоскость, параллельная координатной плоскости O y z и проходящая через точку М 0 ( 7 , — 2 , 3 ) . Необходимо составить общее уравнение заданной плоскости.

Р​​ешение

У​​​​​словием задачи определено, что заданная плоскость параллельна координатной плоскости O y z , а, следовательно, может быть задана общим неполным уравнением плоскости A x + D = 0 , A ≠ 0 ⇔ x + D A = 0 . Поскольку точка M 0 ( 7 , — 2 , 3 ) лежит на плоскости по условию задачи, то очевидно, что координаты этой точки должны отвечать уравнению плоскости x + D A = 0 , иначе говоря, должно быть верным равенство 7 + D A = 0 . Преобразуем: D A = — 7 , тогда требуемое уравнение имеет вид: x — 7 = 0 .

Задачу возможно решить еще одним способом.

Вновь обратим внимание на заданную условием задачи параллельность данной плоскости координатной плоскости O y z . Из этого условия понятно, что возможно в качестве нормального вектора заданной плоскости использовать нормальный вектор плоскости O y z : i → = ( 1 , 0 , 0 ) . Так, нам известны и точка, принадлежащая плоскости (задана условием задачи) и ее нормальный вектор. Таким образом, становится возможно записать общее уравнение заданной плоскости:

A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 ⇔ ⇔ 1 · ( x — 7 ) + 0 · ( y + 2 ) + 0 · ( z — 3 ) = 0 ⇔ ⇔ x — 7 = 0

Ответ: x — 7 = 0

Задана плоскость, перпендикулярная плоскости O x y и проходящая через начало координат и точку М 0 ( — 3 , 1 , 2 ) .

Решение

Плоскость, которая перпендикулярна координатной плоскости O x y определяется общим неполным уравнением плоскости A x + B y + D = 0 ( А ≠ 0 , В ≠ 0 ) . Условием задачи дано, что плоскость проходит через начало координат, тогда D = 0 и уравнение плоскости принимает вид A x + B y = 0 ⇔ x + B A y = 0 .

Найдем значение B A . В исходных данных фигурирует точка М 0 ( — 3 , 1 , 2 ) , координаты которой должны отвечать уравнению плоскости. Подставим координаты, получим верное равенство: — 3 + B A · 1 = 0 , откуда определяем B A = 3 .

Так, мы имеем все данные, чтобы записать требуемое общее уравнение плоскости: x + 3 y = 0 .

Онлайн калькулятор. Уравнение плоскости

Предлагаю вам воспользоваться онлайн калькулятором чтобы найти уравнение плоскости.

Воспользовавшись онлайн калькулятором, вы получите детальное пошаговое решение вашей задачи, которое позволит понять алгоритм решения задач на составление уравнения плоскости и закрепить пройденный материал.

Найти уравнение плоскости

Выберите метод решения исходя из имеющихся в задаче данных:

В задаче известны:

Ввод данных в калькулятор для составления уравнения плоскости

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора для вычисления уравнения плоскости

• Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.

Теория. Уравнение плоскости.

Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки

В зависимости от условий задачи уравнение плоскости можно составить следующими способами:

Если заданы координаты трех точек A( x ₁, y ₁, z ₁), B( x ₂, y ₂, z ₂) и C( x ₃, y ₃, z ₃), лежащих на плоскости, то уравнение плоскости можно составить по следующей формуле

x — x 1	y — y 1	z — z 1	= 0
x 2 — x 1	y 2 — y 1	z 2 — z 1
x 3 — x 1	y 3 — y 1	z 3 — z 1

Если заданы координаты точки A( x ₁, y ₁, z ₁) лежащей на плоскости и вектор нормали n = , то уравнение плоскости можно составить по следующей формуле:

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Уравнения плоскости: общее, через три точки, нормальное

Плоскость, общее уравнение плоскости

Чтобы получить общее уравнение плоскости, разберём плоскость, проходящую через заданную точку.

Пусть в пространстве есть три уже известные нам оси координат — Ox, Oy и Oz. Подержим лист бумаги так, чтобы он оставался плоским. Плоскостью будет сам лист и его продолжение во всех направлениях.

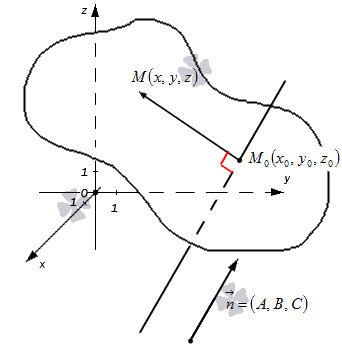
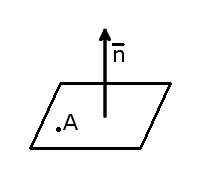
Пусть P произвольная плоскость в пространстве. Всякий перпендикулярный ей вектор называется вектором нормали к этой плоскости. Естественно, речь идёт о ненулевом векторе.

Если известна какая-нибудь точка плоскости P и какой-нибудь вектор нормали к ней, то этими двумя условиями плоскость в пространстве вполне определена (через заданную точку можно провести единственную плоскость, перпендикулярную данному вектору). Общее уравнение плоскости будет иметь вид:

Итак, условия, которыми задаётся уравнение плоскости, есть. Чтобы получить само уравнение плоскости, имеющее приведённый выше вид, возьмём на плоскости P произвольную точку M с переменными координатами x, y, z. Эта точка принадлежит плоскости только в том случае, когда вектор перпендикулярен вектору (рис. 1). Для этого, согласно условию перпендикулярности векторов, необходимо и достаточно, чтобы скалярное произведение этих векторов было равно нулю, то есть

.

Вектор задан по условию. Координаты вектора найдём по формуле :

.

Теперь, используя формулу скалярного произведения векторов , выразим скалярное произведение в координатной форме:

. (1)

Так как точка M(x; y; z) выбрана на плоскости произвольно, то последнему уравнению удовлетворяют координаты любой точки, лежащей на плоскости P. Для точки N, не лежащей на заданной плоскости, , т.е. равенство (1) нарушается.

Перед решением задач может пригодиться урок о декартовой системе координат. Также хорошо бы владеть материалом о скалярном произведении векторов.

Пример 1. Составить уравнение плоскости, проходящей через точку и перпендикулярной вектору .

Решение. Используем формулу (1), еще раз посмотрим на неё:

.

В этой формуле числа A , B и C координаты вектора , а числа x 0 , y 0 и z 0 — координаты точки .

Вычисления очень простые: подставляем эти числа в формулу и получаем

.

Умножаем всё, что нужно умножить и складываем просто числа (которые без букв). Результат:

.

Требуемое уравнение плоскости в этом примере оказалось выражено общим уравнением первой степени относительно переменных координат x, y, z произвольной точки плоскости.

Итак, уравнение вида

(2)

называется общим уравнением плоскости.

Пример 2. Построить в прямоугольной декартовой системе координат плоскость, заданную уравнением .

Решение. Для построения плоскости необходимо и достаточно знать какие-либо три её точки, не лежащие на одной прямой, например, точки пересечения плоскости с осями координат.

Как найти эти точки? Чтобы найти точку пересечения с осью Oz , нужно в уравнение, данное в условии задачи, вместо икс и игрека подставить нули: x = y = 0 . Поэтому получаем z = 6 . Таким образом, заданная плоскость пересекает ось Oz в точке A(0; 0; 6) .

Точно так же находим точку пересечения плоскости с осью Oy . При x = z = 0 получаем y = −3 , то есть точку B(0; −3; 0) .

И, наконец, находим точку пересечения нашей плоскости с осью Ox . При y = z = 0 получим x = 2 , то есть точку C(2; 0; 0) . По трём полученным в нашем решении точкам A(0; 0; 6) , B(0; −3; 0) и C(2; 0; 0) строим заданную плоскость.

Рассмотрим теперь частные случаи общего уравнения плоскости. Это случаи, когда те или иные коэффициенты уравнения (2) обращаются в нуль.

1. При D = 0 уравнение определяет плоскость, проходящую через начало координат, так как координаты точки 0(0; 0; 0) удовлетворяют этому уравнению.

2. При A = 0 уравнение определяет плоскость, параллельную оси Ox, поскольку вектор нормали этой плоскости перпендикулярен оси Ox (его проекция на ось Ox равна нулю). Аналогично, при B = 0 плоскость параллельная оси Oy, а при C = 0 плоскость параллельна оси Oz.

3. При A = D = 0 уравнение определяет плоскость, проходящую через ось Ox, поскольку она параллельна оси Ox (A = 0) и проходит через начало координат (D = 0). Аналогично, плоскость проходит через ось Oy, а плоскость через ось Oz.

4. При A = B = 0 уравнение определяет плоскость, параллельную координатной плоскости xOy, поскольку она параллельна осям Ox (A = 0) и Oy (B = 0). Аналогично, плоскость параллельна плоскости yOz, а плоскость — плоскости xOz.

5. При A = B = D = 0 уравнение (или z = 0) определяет координатную плоскость xOy, так как она параллельна плоскости xOy (A = B = 0) и проходит через начало координат (D = 0). Аналогично, уравнение y = 0 в пространстве определяет координатную плоскость xOz, а уравнение x = 0 — координатную плоскость yOz.

Пример 3. Составить уравнение плоскости P , проходящей через ось Oy и точку .

Решение. Итак, плоскость проходит через ось Oy . Поэтому в её уравнении y = 0 и это уравнение имеет вид . Для определения коэффициентов A и C воспользуемся тем, что точка принадлежит плоскости P .

Поэтому среди её координат есть такие, которые можно подставить в уравнению плоскости, которое мы уже вывели (). Смотрим ещё раз на координаты точки:

Среди них x = 2 , z = 3 . Подставляем их в уравнение общего вида и получаем уравнение для нашего частного случая:

Оставляем 2A в левой части уравнения, переносим 3C в правую часть и получаем

Подставив найденное значение A в уравнение , получим

или .

Это и есть уравнение, требуемое в условии примера.

Решить задачу на уравнения плоскости самостоятельно, а затем посмотреть решение

Пример 4. Определить плоскость (или плоскости, если больше одной) относительно координатных осей или координатных плоскостей, если плоскость (плоскости) задана уравнением .

Уравнение плоскости, проходящей через три точки

Как уже упоминалось, необходимым и достаточным условием для построения плоскости, кроме одной точки и вектора нормали, являются также три точки, не лежащие на одной прямой.

Пусть даны три различные точки , и , не лежащие на одной прямой. Так как указанные три точки не лежат на одной прямой, векторы и не коллинеарны, а поэтому любая точка плоскости лежит в одной плоскости с точками , и тогда и только тогда, когда векторы , и компланарны, т.е. тогда и только тогда, когда смешанное произведение этих векторов равно нулю.

Используя выражение смешанного произведения в координатах, получим уравнение плоскости

(3)

После раскрытия определителя это уравнение становится уравнением вида (2), т.е. общим уравнением плоскости.

Пример 5. Составить уравнение плоскости, проходящей через три данные точки, не лежащие на одной прямой:

, ,

и определить частный случай общего уравнения прямой, если такой имеет место.

Решение. По формуле (3) имеем:

Получили общее уравнение плоскости

или после деления на -2:

.

Это уравнение, в котором A = 0, т.е. оно определяет плоскость, параллельную оси Ox.

Нормальное уравнение плоскости. Расстояние от точки до плоскости

Нормальным уравнением плоскости называется её уравнение, записанное в виде

,

где — направляющие косинусы нормали плоскости, — расстояние от начала координат до плоскости.

Нормалью к плоскости называется вектор, направление которого совпадает с направлением прямой, проведённой через начало координат перпендикулярно данной плоскости. (Есть полная аналогия с нормалью к прямой на плоскости, с той лишь разницей, что нормальное уравнение прямой существует в двух измерениях, а нормальное уравнение плоскости — в трёх).

Пусть M — какая угодно точка пространства. Для нахождения отклонения точки M от плоскости следует в левую часть нормального уравнения плоскости подставить на место x, y и z подставить координаты этой точки.

Это правило позволяет найти и расстояние от точки M до плоскости: расстояние равно модулю отклонения, т.е.

,

так как расстояние не может быть отрицательным числом.

Общее уравнение плоскости

приводится к нормальному виду почленным умножением на нормирующий множитель, определяемый формулой

.

Знак нормирующего множителя берётся противоположным знаку свободного члена в общем уравнении плоскости.

Пример 6. Привести уравнение плоскости к нормальному виду.

Решение. Вычислим нормирующий множитель:

.

Знак нормирующего множителя положительный, то есть, противоположен знаку свободного члена в общем уравнении плоскости. Умножим общее уравнение почленно на нормирующий множитель и получим требуемое в условии примера нормальное уравнение плоскости:

.

Пример 7. Вычислить величину отклонения и расстояния от точки до прямой, если точка задана координатами (-2; -4; 3) , а плоскость задана общим уравнением .

Решение. Сначала приведём уравнение плоскости к нормальному виду. Вычислим нормирующий множитель:

.

Знак нормирующего множителя отрицательный, то есть, противоположен знаку свободного члена в общем уравнении плоскости. Умножим общее уравнение почленно на нормирующий множитель и получим нормальное уравнение плоскости:

.

Вычислим отклонение точки от плоскости:

Найдём теперь расстояние от точки до плоскости как модуль отклонения: