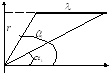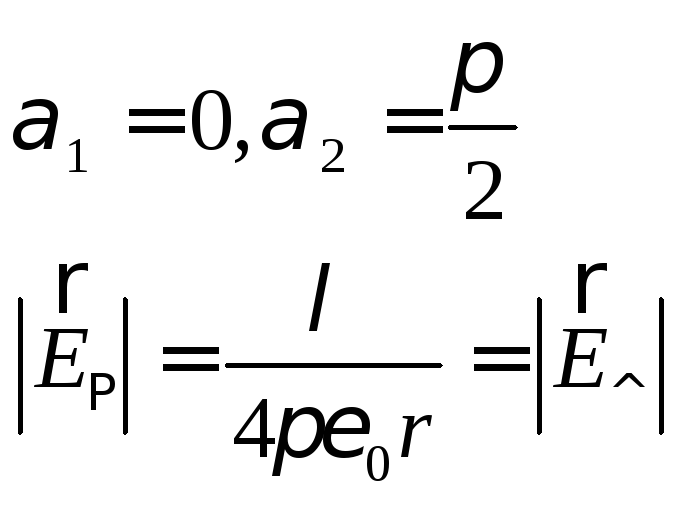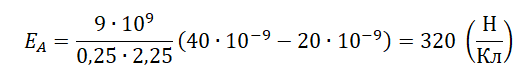From Wikipedia, the free encyclopedia
Superposition of almost plane waves (diagonal lines) from a distant source and waves from the wake of the ducks. Linearity holds only approximately in water and only for waves with small amplitudes relative to their wavelengths.
Rolling motion as superposition of two motions. The rolling motion of the wheel can be described as a combination of two separate motions: translation without rotation, and rotation without translation.
The superposition principle,[1] also known as superposition property, states that, for all linear systems, the net response caused by two or more stimuli is the sum of the responses that would have been caused by each stimulus individually. So that if input A produces response X and input B produces response Y then input (A + B) produces response (X + Y).
A function 
that satisfies the superposition principle is called a linear function. Superposition can be defined by two simpler properties: additivity
and homogeneity
for scalar a.
This principle has many applications in physics and engineering because many physical systems can be modeled as linear systems. For example, a beam can be modeled as a linear system where the input stimulus is the load on the beam and the output response is the deflection of the beam. The importance of linear systems is that they are easier to analyze mathematically; there is a large body of mathematical techniques, frequency domain linear transform methods such as Fourier and Laplace transforms, and linear operator theory, that are applicable. Because physical systems are generally only approximately linear, the superposition principle is only an approximation of the true physical behavior.
The superposition principle applies to any linear system, including algebraic equations, linear differential equations, and systems of equations of those forms. The stimuli and responses could be numbers, functions, vectors, vector fields, time-varying signals, or any other object that satisfies certain axioms. Note that when vectors or vector fields are involved, a superposition is interpreted as a vector sum. If the superposition holds, then it automatically also holds for all linear operations applied on these functions (due to definition), such as gradients, differentials or integrals (if they exist).
Relation to Fourier analysis and similar methods[edit]
By writing a very general stimulus (in a linear system) as the superposition of stimuli of a specific and simple form, often the response becomes easier to compute.
For example, in Fourier analysis, the stimulus is written as the superposition of infinitely many sinusoids. Due to the superposition principle, each of these sinusoids can be analyzed separately, and its individual response can be computed. (The response is itself a sinusoid, with the same frequency as the stimulus, but generally a different amplitude and phase.) According to the superposition principle, the response to the original stimulus is the sum (or integral) of all the individual sinusoidal responses.
As another common example, in Green’s function analysis, the stimulus is written as the superposition of infinitely many impulse functions, and the response is then a superposition of impulse responses.
Fourier analysis is particularly common for waves. For example, in electromagnetic theory, ordinary light is described as a superposition of plane waves (waves of fixed frequency, polarization, and direction). As long as the superposition principle holds (which is often but not always; see nonlinear optics), the behavior of any light wave can be understood as a superposition of the behavior of these simpler plane waves.
Wave superposition[edit]
Two waves traveling in opposite directions across the same medium combine linearly. In this animation, both waves have the same wavelength and the sum of amplitudes results in a standing wave.
two waves permeate without influencing each other
Waves are usually described by variations in some parameters through space and time—for example, height in a water wave, pressure in a sound wave, or the electromagnetic field in a light wave. The value of this parameter is called the amplitude of the wave and the wave itself is a function specifying the amplitude at each point.
In any system with waves, the waveform at a given time is a function of the sources (i.e., external forces, if any, that create or affect the wave) and initial conditions of the system. In many cases (for example, in the classic wave equation), the equation describing the wave is linear. When this is true, the superposition principle can be applied. That means that the net amplitude caused by two or more waves traversing the same space is the sum of the amplitudes that would have been produced by the individual waves separately. For example, two waves traveling towards each other will pass right through each other without any distortion on the other side. (See image at the top.)
Wave diffraction vs. wave interference[edit]
With regard to wave superposition, Richard Feynman wrote:[2]
No-one has ever been able to define the difference between interference and diffraction satisfactorily. It is just a question of usage, and there is no specific, important physical difference between them. The best we can do, roughly speaking, is to say that when there are only a few sources, say two, interfering, then the result is usually called interference, but if there is a large number of them, it seems that the word diffraction is more often used.
Other authors elaborate:[3]
The difference is one of convenience and convention. If the waves to be superposed originate from a few coherent sources, say, two, the effect is called interference. On the other hand, if the waves to be superposed originate by subdividing a wavefront into infinitesimal coherent wavelets (sources), the effect is called diffraction. That is the difference between the two phenomena is [a matter] of degree only, and basically, they are two limiting cases of superposition effects.
Yet another source concurs:[4]
In as much as the interference fringes observed by Young were the diffraction pattern of the double slit, this chapter [Fraunhofer diffraction] is, therefore, a continuation of Chapter 8 [Interference]. On the other hand, few opticians would regard the Michelson interferometer as an example of diffraction. Some of the important categories of diffraction relate to the interference that accompanies division of the wavefront, so Feynman’s observation to some extent reflects the difficulty that we may have in distinguishing division of amplitude and division of wavefront.
Wave interference[edit]
The phenomenon of interference between waves is based on this idea. When two or more waves traverse the same space, the net amplitude at each point is the sum of the amplitudes of the individual waves. In some cases, such as in noise-canceling headphones, the summed variation has a smaller amplitude than the component variations; this is called destructive interference. In other cases, such as in a line array, the summed variation will have a bigger amplitude than any of the components individually; this is called constructive interference.
green wave traverse to the right while blue wave traverse left, the net red wave amplitude at each point is the sum of the amplitudes of the individual waves.
| combined waveform |
|
|
| wave 1 | ||
| wave 2 | ||
| Two waves in phase | Two waves 180° out of phase |
Departures from linearity[edit]
In most realistic physical situations, the equation governing the wave is only approximately linear. In these situations, the superposition principle only approximately holds. As a rule, the accuracy of the approximation tends to improve as the amplitude of the wave gets smaller. For examples of phenomena that arise when the superposition principle does not exactly hold, see the articles nonlinear optics and nonlinear acoustics.
Quantum superposition[edit]
In quantum mechanics, a principal task is to compute how a certain type of wave propagates and behaves. The wave is described by a wave function, and the equation governing its behavior is called the Schrödinger equation. A primary approach to computing the behavior of a wave function is to write it as a superposition (called «quantum superposition») of (possibly infinitely many) other wave functions of a certain type—stationary states whose behavior is particularly simple. Since the Schrödinger equation is linear, the behavior of the original wave function can be computed through the superposition principle this way.[5]
The projective nature of quantum-mechanical-state space causes some confusion, because a quantum mechanical state is a ray in projective Hilbert space, not a vector.
According to Dirac: «if the ket vector corresponding to a state is multiplied by any complex number, not zero, the resulting ket vector will correspond to the same state [italics in original].»[6]
However, the sum of two rays to compose a superpositioned ray is undefined. As a result, Dirac himself
uses ket vector representations of states to decompose or split,
for example, a ket vector 
into superposition of component ket vectors 
as:
where the 
.
The equivalence class of the allows a well-defined meaning to be given to the relative phases of the 
.[7], but an absolute (same amount
for all the ) phase change on the
does not affect the equivalence class of the .
There are exact correspondences between the superposition presented in the main on this page and the quantum superposition.
For example, the Bloch sphere to represent pure state of a two-level quantum mechanical system
(qubit) is also known as the Poincaré sphere representing different types of classical
pure polarization states.
Nevertheless, on the topic of quantum superposition, Kramers writes: «The principle of [quantum] superposition … has no analogy in classical physics»[citation needed].
According to Dirac: «the superposition that occurs in quantum mechanics is of an essentially different nature from any occurring in the classical theory [italics in original].»[8]
Though reasoning by Dirac includes atomicity of observation, which is valid, as for phase,
they actually mean phase translation symmetry derived from time translation symmetry, which is also
applicable to classical states, as shown above with classical polarization states.
Boundary value problems[edit]
A common type of boundary value problem is (to put it abstractly) finding a function y that satisfies some equation
with some boundary specification
For example, in Laplace’s equation with Dirichlet boundary conditions, F would be the Laplacian operator in a region R, G would be an operator that restricts y to the boundary of R, and z would be the function that y is required to equal on the boundary of R.
In the case that F and G are both linear operators, then the superposition principle says that a superposition of solutions to the first equation is another solution to the first equation:
while the boundary values superpose:
Using these facts, if a list can be compiled of solutions to the first equation, then these solutions can be carefully put into a superposition such that it will satisfy the second equation. This is one common method of approaching boundary value problems.
Additive state decomposition[edit]
Consider a simple linear system:
By superposition principle, the system can be decomposed into
with
Superposition principle is only available for linear systems. However, the additive state decomposition can be applied to both linear and nonlinear systems. Next, consider a nonlinear system
where 
is a nonlinear function. By the additive state decomposition, the system can be additively decomposed into
with
This decomposition can help to simplify controller design.
Other example applications[edit]
- In electrical engineering, in a linear circuit, the input (an applied time-varying voltage signal) is related to the output (a current or voltage anywhere in the circuit) by a linear transformation. Thus, a superposition (i.e., sum) of input signals will yield the superposition of the responses. The use of Fourier analysis on this basis is particularly common. For another, a related technique in circuit analysis, see Superposition theorem.
- In physics, Maxwell’s equations imply that the (possibly time-varying) distributions of charges and currents are related to the electric and magnetic fields by a linear transformation. Thus, the superposition principle can be used to simplify the computation of fields that arise from a given charge and current distribution. The principle also applies to other linear differential equations arising in physics, such as the heat equation.
- In engineering, superposition is used to solve for beam and structure deflections of combined loads when the effects are linear (i.e., each load does not affect the results of the other loads, and the effect of each load does not significantly alter the geometry of the structural system).[9] Mode superposition method uses the natural frequencies and mode shapes to characterize the dynamic response of a linear structure.[10]
- In hydrogeology, the superposition principle is applied to the drawdown of two or more water wells pumping in an ideal aquifer. This principle is used in the analytic element method to develop analytical elements capable of being combined in a single model.
- In process control, the superposition principle is used in model predictive control.
- The superposition principle can be applied when small deviations from a known solution to a nonlinear system are analyzed by linearization.
- In music, theorist Joseph Schillinger used a form of the superposition principle as one basis of his Theory of Rhythm in his Schillinger System of Musical Composition.
- In computing, superposition of multiple code paths, code and data, or multiple data structures is sometimes seen in shared memory, fat binaries, as well as overlapping instructions in highly optimized self-modifying code and executable text.
History[edit]
According to Léon Brillouin, the principle of superposition was first stated by Daniel Bernoulli in 1753: «The general motion of a vibrating system is given by a superposition of its proper vibrations.» The principle was rejected by Leonhard Euler and then by Joseph Lagrange. Bernoulli argued that any sonorous body could vibrate in a series of simple modes with a well-defined frequency of oscillation. As he had earlier indicated, these modes could be superposed to produce more complex vibrations. In his reaction to Bernoulli’s memoirs, Euler praised his colleague for having best developed the physical part of the problem of vibrating strings, but denied the generality and superiority of the multi-modes solution.[11]
Later it became accepted, largely through the work of Joseph Fourier.[12]
See also[edit]
- Additive state decomposition
- Beat (acoustics)
- Coherence (physics)
- Convolution
- Green’s function
- Impulse response
- Interference
- Quantum superposition
References[edit]
- ^ The Penguin Dictionary of Physics, ed. Valerie Illingworth, 1991, Penguin Books, London
- ^ Lectures in Physics, Vol, 1, 1963, pg. 30-1, Addison Wesley Publishing Company Reading, Mass [1]
- ^ N. K. VERMA, Physics for Engineers, PHI Learning Pvt. Ltd., Oct 18, 2013, p. 361. [2]
- ^ Tim Freegarde, Introduction to the Physics of Waves, Cambridge University Press, Nov 8, 2012. [3]
- ^ Quantum Mechanics, Kramers, H.A. publisher Dover, 1957, p. 62 ISBN 978-0-486-66772-0
- ^ Dirac, P. A. M. (1958). The Principles of Quantum Mechanics, 4th edition, Oxford, UK: Oxford University Press, p. 17.
- ^ Solem, J. C.; Biedenharn, L. C. (1993). «Understanding geometrical phases in quantum mechanics: An elementary example». Foundations of Physics. 23 (2): 185–195. Bibcode:1993FoPh…23..185S. doi:10.1007/BF01883623. S2CID 121930907.
- ^ Dirac, P. A. M. (1958). The Principles of Quantum Mechanics, 4th edition, Oxford, UK: Oxford University Press, p. 14.
- ^ Mechanical Engineering Design, By Joseph Edward Shigley, Charles R. Mischke, Richard Gordon Budynas, Published 2004 McGraw-Hill Professional, p. 192 ISBN 0-07-252036-1
- ^ Finite Element Procedures, Bathe, K. J., Prentice-Hall, Englewood Cliffs, 1996, p. 785 ISBN 0-13-301458-4
- ^ Topics on Numerics for Wave Propagation, Basque Center for Applied Mathematics, 2012, Spain, p. 39
- ^ Brillouin, L. (1946). Wave propagation in Periodic Structures: Electric Filters and Crystal Lattices, McGraw–Hill, New York, p. 2.
Further reading[edit]
- Haberman, Richard (2004). Applied Partial Differential Equations. Prentice Hall. ISBN 978-0-13-065243-0.
- Superposition of sound waves
External links[edit]
Принцип суперпозиции полей
4.9
Средняя оценка: 4.9
Всего получено оценок: 206.
4.9
Средняя оценка: 4.9
Всего получено оценок: 206.
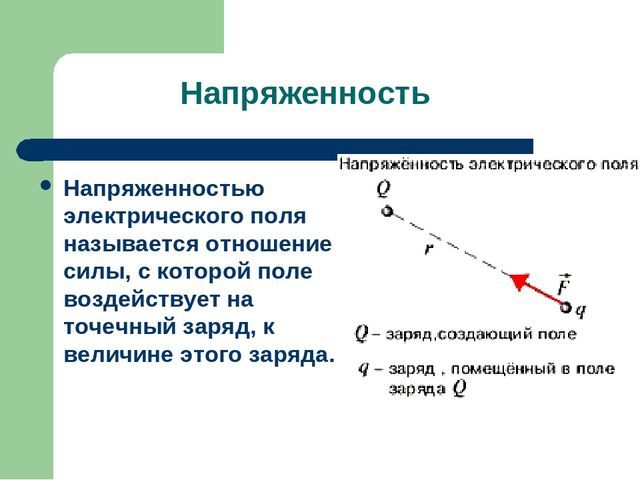
Одним из важнейших принципов, существующих в электростатике, является принцип суперпозиции полей. Кратко рассмотрим суть этого принципа, выведем его математическую формулу.
Действие силового поля
Силовое поле – это особая форма материи, действие которого заключается в силовом влиянии на носители заряда. То есть, если у тела есть некоторый электрический заряд, и оно находится в силовом электрическом поле, то со стороны этого поля на тело будет действовать определенная сила, тем большая, чем больше напряженность поля.
Природа поля не обязательно должна быть электрической. Действие гравитационного силового поля заключается в силовом воздействии на тела, имеющие массу (носители «гравитационного заряда»).
Даже силы трения можно представить в виде поля сил трения, поскольку трение также оказывает на движущиеся соприкасающиеся тела силовое действие.
Сложение действия полей
Что произойдет с зарядом, на который действует несколько полей ?
Опыт показывает, что сила, действующая на заряд со стороны поля, не зависит от других сил, тоже действующих на заряд. При этом их источником могут являться другие поля. Фактически, несколько полей будут действовать на заряд независимо, каждое будет создавать силу, точно такую же, как если бы это поле в точке было бы единственным.
Таким образом, если заряд помещен одновременно в несколько электрических полей, он испытывает одновременное действие нескольких сил. А если на материальную точку действует несколько сил, то результатом их действия будет одна равнодействующая сила, которая находится векторным сложением исходных сил:
$$overrightarrow{F}_{равн} = overrightarrow{F}_{1}+overrightarrow{F}_{2}+…$$
Сила, действующая на заряд, равна произведению напряженности поля на величину заряда:
$$overrightarrow{F}_{n} = { overrightarrow{E}_{n} q}$$
Поскольку заряд в рассматриваемой ситуации один и тот же, то:
$$overrightarrow{F}_{равн} = (overrightarrow{E}_{1}+overrightarrow{E}_{2}+…)q$$
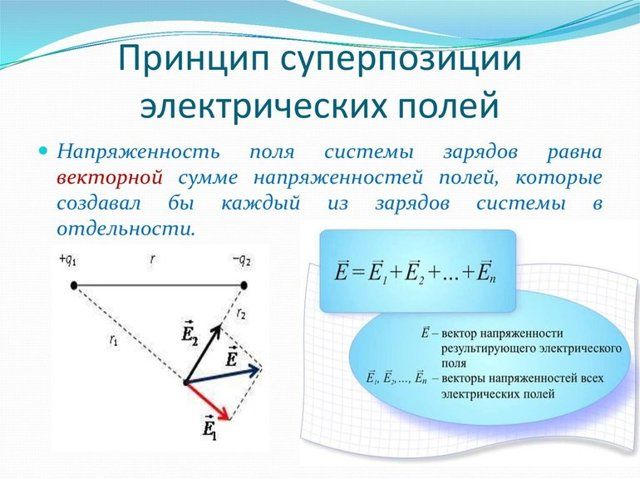
Принцип суперпозиции
Выражение в скобках представляет собой векторную сумму напряженностей всех полей, действующих на заряд. Получается, что результат действия на заряд нескольких полей эквивалентен действию одного поля, напряженность которого равна векторной сумме напряженностей всех полей, действующих на заряд. Иначе можно сказать, что результирующее поле, существующее в точке, является векторной суммой всех полей, его составляющих. В этом и состоит принцип суперпозиции (наложения) полей.
Если в данной точке пространства электрическое поле создано несколькими зарядами, и напряженность поля каждого по отдельности равна $overrightarrow{E}_{1},overrightarrow{E}_{2},…$, то результирующая напряженность этого поля равна векторной сумме напряженностей составляющих его полей.
То есть, формула принципа суперпозиции полей записывается следующим образом:
$$overrightarrow{E}_{общ}=overrightarrow{E}_{1}+overrightarrow{E}_{2}+…$$
Отметим, что потенциал результирующего поля не обязательно равен сумме потенциалов исходных полей. Это происходит потому, что потенциал – скалярная величина, не учитывающая направление.
Принцип суперпозиции полей позволяет не только находить напряженность поля, создаваемые несколькими зарядами. Гораздо чаще возникает ситуация, когда заряд распределен по телу неравномерно. В этом случае тело можно разбить на множество элементарных тел, каждое из которых имеет свой заряд, отличный от прочих. А потом поле в любой точке пространства вычисляется, как векторная сумма полей всех элементарных зарядов. При уменьшении размера элементарного тела до нуля сумма заменяется интегралом по объему. Данный способ используется при определении картины картину сложных электрических полей, например, при проектировании электровакуумных приборов.
Принцип суперпозиции вовсе не так очевиден и универсален, как кажется на первый взгляд. Он действует лишь для линейных полей. Если поле нелинейно – принцип суперпозиции не работает. Примером нелинейного поля является поле сил трения. Если на тело действует несколько внешних сил, то, пока оно не сдвинется, сила трения равна векторной сумме отдельных составляющих. Но, как только тело сдвинулось, сила трения останется неизменной по модулю, даже если мы будем увеличивать количество действующих на тело сил.
Что мы узнали?
Принцип суперпозиции полей заключается в том, что результирующая напряженность поля, состоящего из нескольких исходных полей равна векторной сумме их напряженностей. Принцип суперпозиции выполняется для всех линейных полей, к числу которых относится и электрическое.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.9
Средняя оценка: 4.9
Всего получено оценок: 206.
А какая ваша оценка?
Закон Кулона описывает электрическое
взаимодействие только двух покоящихся
зарядов. Как же найти силу, действующую
на некий заряд со стороны нескольких
других зарядов? Ответ на этот вопрос
дает принцип суперпозиции
электрических полей:Напряженность
электрического поля
,
созданного несколькими неподвижными
точечными зарядами q1,
q2,…, qn,
равна векторной сумме напряженностей
электрических полей
,
которые создавал бы каждый из этих
зарядов в той же точке наблюдения в
отсутствие остальных:
(1.5)
Другими словами, принцип суперпозиции
утверждает, что сила взаимодействия
двух точечных зарядов не зависит от
того, подвергаются эти заряды действию
других зарядов или нет.
Рис.1.6. Электрическое поле системы
зарядов как суперпозиция полей отдельных
зарядов
Итак, для системы Nточечных зарядов
(рис.1.6) на основании принципа суперпозиции
результирующее поле определяется
выражением
.
Напряженность электрического поля
созданного в точке наблюдения системой
зарядов равна векторной сумменапряженностей электрических полей,
созданных в этой же точке наблюдения
отдельными зарядами упомянутой системы.
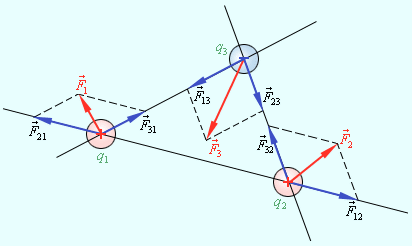
Рис. поясняет принцип
суперпозиции на примере электростатического
взаимодействия трех заряженных тел.
Здесь важны 2
момента: векторное сложение и независимость
поля каждого заряда от присутствия
других зарядов. Если это мы будем говорить
о достаточно точечных телах, о достаточно
небольших размерах, тогда суперпозиция
работает. Однако известно, что в достаточно
сильных электрических полях этот принцип
уже не работает.
1.7. Распределение зарядов
Часто дискретность распределения
электрических зарядов бывает несущественна
при расчете полей. При этом математические
расчеты существенно упрощаются, если
истинное распределение точечных зарядов
заменить фиктивным непрерывным
распределением.
Если дискретные заряды распределены в
объеме, то при переходе к непрерывному
распределению вводят понятие объемной
плотности заряда по определению
,
где dq— заряд, сосредоточенный в
объемеdV(рис.1.8,а).
а) б) в)
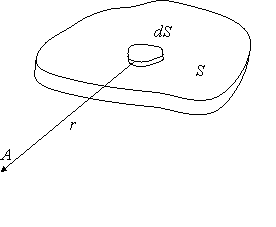
Рис.1.8. Выделение
элементарного заряда в случаях объемно
заряженной области (а); поверхностно
заряженной области (б); линейно заряженной
области (в)
Если дискретные
заряды расположены в тонком слое, то
вводят понятие поверхностной плотности
заряда по определению
,
где dq
— заряд, приходящийся на элемент
поверхности dS
(рис.1.8,б).
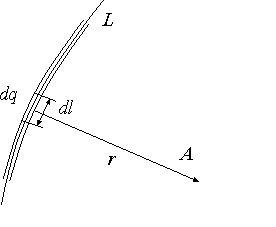
Если дискретные
заряды локализованы внутри тонкого
цилиндра, вводят понятие линейной
плотности заряда
,
где dq
— заряд на элементе длины цилиндра dl
(рис.1.8,в). С использованием введенных
распределений выражение для электрического
поля в точке А
системы зарядов (1.5) запишется в виде
1.8. Примеры расчета электростатических полей в вакууме.
1.8.1. Полепрямолинейного отрезка нити (см. Орокс , примеры 1.9, 1.10) (Пример 1).
Найти напряженность
электрического поля, созданного отрезком
тонкой, однородно заряженной с линейной
плотностью
нити (см.рис).Углы
1,
2
и расстояние r
известны.
О
трезок
разбивают на небольшие отрезки, каждый
из которых относительно точки наблюдения
можно считать точечным.
;
Случай полубесконечной
нити;
Случай бесконечной
нити:
Соседние файлы в папке Лекции
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Принцип суперпозиции сил
Определение
Результирующая, или равнодействующая, сила равна векторной сумме всех сил, действующих на тело:
−R=∑−Fi
Fi — сила, с которой электрическое поле зарядом q действует на пробный заряд qi, помещенный в это поле на расстоянии ri от этого заряда. Численно ее можно вычислить по формуле:
Fi=kqiqr2i
Алгоритм решения задач на определение равнодействующей силы (точечный заряд находится в поле, созданном другими точечными зарядами):
- Сделать чертеж. Указать расположение всех зарядов и их знаки.
- Выделить заряд, для которого определяют равнодействующую.
- Пронумеровать остальные заряды.
- Определить расстояния от выделенного заряда до всех остальных.
- Построить все силы, действующие на интересующий нас заряд. При этом необходимо учитывать знаки зарядов, их модули и расстояния между зарядами.
- Найти геометрическую (векторную) сумму всех сил, действующих на выделенный заряд.
- Пользуясь формулами геометрии и законом Кулона, определить модуль равнодействующей.
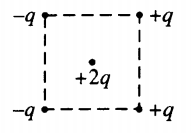
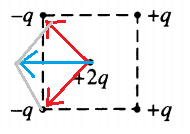
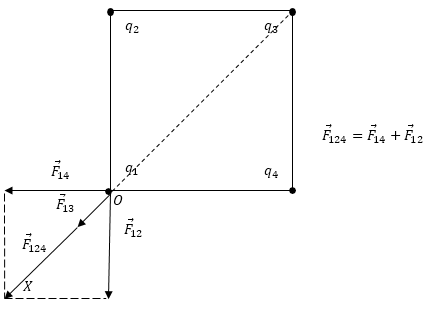
Пример №1. Как направлена (вправо, влево, вверх, вниз) кулоновская сила −FK, действующая на положительный точечный электрический заряд +2q, помещенный в центр квадрата, в вершинах которого находятся заряды +q, +q, –q, –q?
Известно, что одноименные заряды отталкиваются, а разноименные – притягиваются. Из рисунка видно, что заряд +2q, находящийся в центре квадрата, будет отталкиваться от зарядов +q, находящихся справа, и будет притягиваться к зарядам –q, находящимся слева.
Сила Кулона обратно пропорциональна квадрату расстояния между зарядами, то есть с увеличением расстояния r убывает по квадратическому закону. Так как заряд +q находится точно в центре квадрата, то расстояния от зарядов +q, +q, -q, -q будут равны, следовательно, равна по модулю и сила Кулона, действующая на заряд +2q. Суперпозиция сил, действующих на заряд +2q:
Из рисунка видно, что кулоновская сила −FK, действующая на положительный точечный электрический заряд +2q, направлена влево.
Принцип суперпозиции полей
Определение
Если в некоторой точке пространства складываются электрические поля от нескольких зарядов, то результирующая напряженность находится как векторная сумма напряженностей отдельных полей:
−E=∑−Ei
−Ei — напряженность, создаваемая зарядом qi в точке, находящейся на расстоянии ri:
−Ei=kqir2i
Векторное сложение напряженностей аналогично нахождению равнодействующей сил Кулона, только в интересующую нас точку пространства помещают положительный пробный заряд. Чтобы найти результирующий потенциал в точке, необходимо алгебраически сложить потенциалы всех полей. Нельзя забывать, что знак потенциала определяется знаком заряда, создающим электрическое поле:
φ=∑φi
φi — потенциал электростатического поля, создаваемого зарядом qi на расстоянии ri от него. Численно он равен:
φi=±kqiri
Для определения полной энергии надо сложить потенциальные энергии всех пар зарядов:
Wp=∑Wip
Wip — потенциальная энергия взаимодействия зарядов qi и qn, находящихся на расстоянии ri друг от друга. Численно она равна:
Wip=±kqiqnri
Примеры определения расстояний
 |
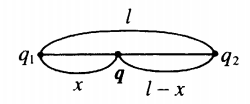Два заряда лежат на одной прямой на расстоянии l друг от друга. Изучаемый заряд лежит между ними:
r1=x; r2=l−x |
 |
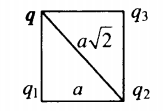Изучаемый заряд лежит в вершине квадрата со стороной a:
r1=r3=a; r2=a√2 |
 |
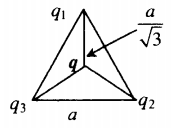Изучаемый заряд лежит в центре равностороннего треугольника со стороной a:
r1=r2=r3=a√3 |
 |
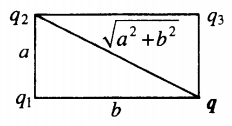Изучаемый заряд лежит в вершине прямоугольника со сторонами a и b:
r1=b; r2=√a2+b2; r3=a |
 |
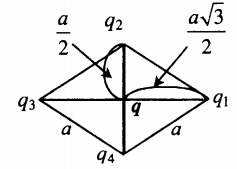Изучаемый заряд лежит в точке пересечения диагоналей ромба со стороной a. Угол при вершине ромба 120о:
r1=r3=a√32; r2=r4=a2 |
 |
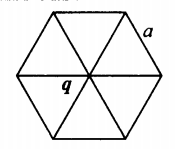Изучаемый заряд лежит в центре правильного шестиугольника со стороной a:
r1=r2=r3=r4=r5=r6=a |
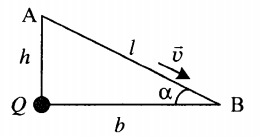
Пример №2. Маленький заряженный шарик массой m, имеющий заряд q, движется с высоты h по наклонной плоскости с углом наклона α. В вершине прямого угла, образованного высотой и горизонталью, находится неподвижный заряд Q. Какова скорость шарика у основания наклонной плоскости v, если его начальная скорость равна нулю? Трением пренебречь.
Построим чертеж:
Применим закон сохранения энергии, согласно которому полная энергия шарика в точке А равна полной энергии шарика в точке В (трением пренебрегаем):
EA=EB
Полная энергия шарика с зарядом qв точке А равна сумме его механической потенциальной энергии и потенциальной энергии взаимодействия с зарядом Q:
EA=mgh+kqQh
В точке В механическая потенциальная энергия шарика равна нулю, но в этой точке максимальная его кинетическая энергия. Полная энергия шарика в точке В равна:
EB=mv22+kqQb
Расстояние между точкой В и местом, где находится заряд Q:
b=htanα
Приравняем правые части уравнений:
mgh+kqQh=mv22+kqQb
mgh+kqQh=mv22+kqQtanαh
mv22=mgh+kqQh−kqQtanαh=mgh+kqQh(1−tanα)
v=⎷2(mgh+kqQh(1−tanα))m=√2gh+2kQmh(1−tanα)
Задание EF17563
Точка В находится в середине отрезка АС. Неподвижные точечные заряды + q и −2q расположены в точках А и С соответственно (см. рисунок). Какой заряд надо поместить в точку С взамен заряда −2q, чтобы напряжённость электрического поля в точке В увеличилась в 2 раза?
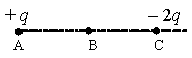
Ответ:
а) − 5q
б) − 4q
в) 4q
г) 5q
Алгоритм решения
1.Определить направление вектора напряженности для зарядов в точках А и С.
2.Определить напряженность поля в точке В, используя принцип суперпозиции.
3.Найти, какой заряд нужно поместить в точку С вместо имеющегося, чтобы напряженность электростатического поля в точке В увеличилась вдвое.
Решение
Вектор напряженности заряда в точке А направлен в направлении от этого заряда, так как он положительный. Это значит, что в точке В вектор напряженности EA направлен вправо. Вектор напряженности заряда в точке С направлен к этому заряду, так как он отрицательный. Поэтому в точке В вектор напряженности EC тоже направлен вправо. Следовательно, при векторном сложении модули напряженностей должны складываться:
E=EA+EC=k|q|r2+k|−2q|r2=3kqr2
Найдем, какой нужно поместить заряд в точку С, чтобы напряженность увеличилась вдвое:
k|q|r2+k|x|r2=2·3kqr2=6kqr2
Преобразуем выражение и получим:
|q|+|x|=6q
Отсюда:
|x|=5q
Этот заряд должен быть отрицательным, так как в этом случае линии напряженности поля, создаваемого зарядом в точке С, будут складываться с линиями напряженности поля, создаваемыми положительным зарядом в точке А. Следовательно, x = –5q.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17967
На рисунке показано направление вектора напряжённости электрического поля E в точке А, равноудалённой от равных по модулю точечных зарядов q1 и q2. Какие знаки имеют заряды?
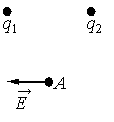
Ответ:
а) q1 > 0; q2 < 0
б) q1 < 0; q2 > 0
в) q1 > 0; q2 > 0
г) q1 < 0; q2 < 0
Алгоритм решения
1.Вспомнить, как направлены векторы напряженности полей, созданных положительным и отрицательным зарядами.
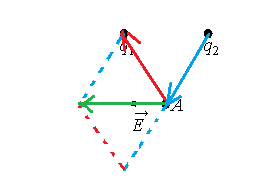
2.Построить параллелограмм, сторонами которого являются отрезки, равные длинам векторов напряженности полей, создаваемыми двумя точечными зарядами.
3.Определить, какое направление должны иметь векторы напряженности, чтобы результатом их вычитания/сложения был вектор −E.
4.Определить знаки зарядов с учетом направления векторов напряженности полей.
Решение
Векторы напряженности электростатического поля, создаваемого положительным точечным зарядом, направлены по радиусным линиям от заряда. Векторы напряженности электростатического поля, создаваемого отрицательным точечным зарядом, направлены по радиусным линиям к заряду.
Построим параллелограмм. Чтобы получить вектор −E, нужно вычесть из вектора −E1 вектор −E2. Причем первый должен быть направлен в сторону заряда, а второй — от заряда.
Следовательно, заряд q1 отрицательный (q1 < 0), а заряд q2 положительный (q2 > 0).
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18357
Два точечных отрицательных заряда: q1=−20 нКл и q2=−40 нКл находятся в вакууме на расстоянии L=1,5м друг от друга. Определите величину напряжённости электрического поля этих зарядов в точке А, расположенной на прямой, соединяющей заряды, на одинаковом расстоянии от обоих зарядов.
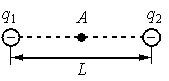
Ответ:
а) 160 Н/Кл
б) 320 Н/Кл
в) 125 Н/Кл
г) 640 Н/Кл
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Определить направление векторов напряженности в точке А.
3.Выполнить общее решение задачи, применив принцип суперпозиции полей.
4.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Величина первого заряда: q1 = –20 нКл.
• Величина второго заряда: q2 = –40 нКл.
• Расстояние между зарядами: L = 1,5 м.
–20 нКл = –20∙10–9 Кл
–40 нКл = –40∙10–9 Кл
Вектор напряженности поля, создаваемого первым зарядом в точке А, направлен влево (в сторону заряда), так как он отрицательный. Второй заряд тоже отрицательный, но он лежит по другую сторону от точки А. Поэтому в ней вектор напряженности поля, создаваемого вторым зарядом, будет направлен вправо. Так как модуль второго заряда больше модуля первого, результирующая напряженность будет направлена вправо. Напряженность в точке А в этом случае будет вычисляться как разность двух напряженности:
EA=E2−E1
Напряженность определяется формулой:
E=k|q|r2
Следовательно:
EA=k|q2|(0,5L)2−k|q1|(0,5L)2=k(0,5L)2(|q2|−|q1|)
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 3.3k
Алексей . Малеев
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Принцип суперпозиции
Допустим, что у нас есть три точечных заряда. Эти заряды взаимодействуют. Можно провести эксперимент и измерить силы, которые действуют на каждый заряд. Для того чтобы найти суммарную силу, с которой на один заряд действует второй и третий, необходимо силы, с которыми действуют каждый из них сложить по правилу параллелограмма. Возникает вопрос, равна ли измеряемая сила, которая действует на каждый из зарядов, сумме сил со стороны двух других, если силы рассчитаны по закону Кулона. Исследования показали, что измеряемая сила равна сумме вычисляемых сил в соответствии с законом Кулона со стороны двух зарядов. Такой эмпирический результат выражается в виде утверждений:
- сила взаимодействия двух точечных зарядов не изменяется, если присутствуют другие заряды;
- сила, действующая на точечный заряд со стороны двух точечных зарядов, равна сумме сил, действующих на него со стороны каждого из точечных зарядов при отсутствии другого.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Данное утверждение называется принципом суперпозиции. Этот принцип является одной из основ учения об электричестве. Он так же важен, как и закон Кулона. Его обобщение на случай множества зарядов очевидно. Если имеется несколько источников поля (количество зарядов N), то результирующую силу, действующую на пробный заряд q можно найти как:
[overrightarrow{F}=sumlimits^N_{i=1}{overrightarrow{F_{ia}}}left(1right),]
где $overrightarrow{F_{ia}}$ — сила, с которой действует на заряд q заряд $q_i$ если остальные N-1 заряд отсутствуют.
Принцип суперпозиции (1) позволяет, используя закон взаимодействия между точечными зарядами, вычислить силу взаимодействия между зарядами, находящимися на теле конечных размеров. Для этого необходимо разбить каждый из зарядов на малые заряды dq, которые можно считать точечными, взять из попарно, вычислить силу взаимодействия и провести векторное сложение полученных сил.
Полевая трактовка принципа суперпозиции
Принцип суперпозиции имеет полевую трактовку: напряженность поля двух точечных зарядов равна сумме напряженностей, которые создаются каждым из зарядов, при отсутствии другого.
«Принцип суперпозиции электрических полей» 👇
В общем случае принцип суперпозиции относительно напряженностей можно записать так:
[overrightarrow{E}=sum{overrightarrow{E_i}}left(2right).]
где ${overrightarrow{E}}_i=frac{1}{4pi {varepsilon }_0}frac{q_i}{varepsilon r^3_i}overrightarrow{r_i} $- напряжённость i-го точечного заряда, $overrightarrow{r_i} $- радиус-вектор, проведённый от i-го заряда в точку пространства. Выражение (1) означает, что напряженность поля любого числа точечных зарядов равна сумме напряженностей полей каждого из точечных зарядов, если другие отсутствуют.
Подтверждено инженерной практикой, что принцип суперпозиции соблюдается вплоть до очень больших напряженностей полей. Очень значительные напряженности имеют поля в атомах и ядрах (порядка ${10}^{11}-{10}^{17}frac{B}{м}$), но и для них использовали принцип суперпозиции в расчетах энергетических уровней атомов и данные расчетов совпали с данными экспериментов с большой точностью. Однако надо отметить, что при очень малых расстояниях (порядка $sim {10}^{-15}м$) и экстремально сильных полях принцип суперпозиции, возможно, не выполняется. Так, к примеру, на поверхности тяжелых ядер напряженности достигают порядка $sim {10}^{22}frac{В}{м}$ принцип суперпозиции выполняется, но при напряженности ${10}^{20}frac{В}{м}$ возникают квантово — механические нелинейности взаимодействия.
Если заряд распределен непрерывно (нет необходимости учитывать дискретность), то суммарная напряженность поля найдется как:
[overrightarrow{E}=int{doverrightarrow{E}} left(3right).]
В уравнении (3) интегрирование проводят по области распределения зарядов. Если заряды распределены по линии ($tau =frac{dq }{dl}-линейная плотность распределения заряда$), то интегрирование в (3) проводят по линии. Если заряды распределены по поверхности и поверхностная плотность распределения $sigma =frac{dq }{dS}$, то интегрируют по поверхности. Интегрирование проводят по объему, если имеют дело с объемным распределением заряда: $rho =frac{dq }{dV}$, где $rho $ — объемная плотность распределения заряда.
Принцип суперпозиции в принципе позволяет определить $overrightarrow{E}$ для любой точки пространства по известному пространственному распределению заряда.
Пример 1
Задание: Одинаковые точечные заряды q находятся в вершинах квадрата со стороной a. Определите, какая сила, действует на каждый заряд со стороны других трех зарядов.
Решение:
Изобразим силы, действующие на один из зарядов в вершине квадрата (выбор не важен, так как заряды одинаковы) (рис.1). Результирующую силу, действующую на заряд $q_1$, запишем как:
[overrightarrow{F}={overrightarrow{F}}_{12}+{overrightarrow{F}}_{14}+{overrightarrow{F}}_{13} left(1.1right).]
Силы ${overrightarrow{F}}_{12}$ и ${overrightarrow{F}}_{14}$ равны по модулю и могут быть найдены как:
[left|{overrightarrow{F}}_{12}right|=left|{overrightarrow{F}}_{14}right|=kfrac{q^2}{a^2} left(1.2right),]
где $k=9•{10}^9frac{Нм^2}{{Кл}^2}.$
Модуль силы ${overrightarrow{F}}_{13}$ найдем, также по закону Кулона, зная, что диагональ квадрата равна:
[d=sqrt{2}a left(1.3right),]
следовательно, имеем:
[left|{overrightarrow{F}}_{13}right|=kfrac{q^2}{2a^2} left(1.4right)]
Рис. 1
Направим ось OX как указано на рис. 1, спроектируем уравнение (1.1), подставим полученные модули сил, получим:
[F=2kfrac{q^2}{a^2}cdot frac{sqrt{2}}{2}+kfrac{q^2}{2a^2}=frac{kq^2}{a^2}left(frac{2sqrt{2}+1}{2}right).]
Ответ: Сила, действующая на каждый из зарядов в вершинах квадрата равна: $F=frac{kq^2}{a^2}left(frac{2sqrt{2}+1}{2}right).$
Пример 2
Задание: Электрический заряд равномерно распределен вдоль тонкой нити в равномерной линейной плотностью $tau $. Найдите выражение для напряженности поля на расстоянии $а$ от конца нити на ее продолжении. Длина нити равна $l$.
Рис. 2
Решение:
Выделим на нити точечный заряд $dq$, запишем для него из закона Кулона выражение для напряженности электростатического поля:
[doverrightarrow{E}=kfrac{dq}{r^3}overrightarrow{r }left(2.1right).]
В заданной точке все векторы напряженности направлены одинаково, вдоль оси Х, поэтому, имеем:
[dE_x=kfrac{dq}{r^2}=dEleft(2.2right).]
Так как заряд по условию задачи равномерно распределен по нити с линейной плотностью $tau $, то можно записать следующее:
[dq=tau drleft(2.4right).]
Подставим (2.4) в уравнение (2.1), проинтегрируем:
[E=kintlimits^{l+a}_a{frac{tau dr}{r^2}}=ktau left(-{left.frac{1}{r}right|}^{l+a}_aright)=frac{ktau l}{a(l+a)}.]
Ответ: Напряженность поля нити в указанной точке вычисляется по формуле: $E=frac{ktau l}{a(l+a)}.$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме