Приращение
функции
Не всегда в жизни нас интересуют точные
значения каких-либо величин. Иногда интересно узнать изменение этой величины,
например, средняя скорость автобуса, отношение величины перемещения к
промежутку времени и т.д. Для сравнения значения функции в некоторой точке со
значениями этой же функции в других точках, удобно использовать такие понятия,
как «приращение функции» и «приращение аргумента».
Понятия «приращение функции» и «приращение
аргумента»
Допустим, х – некоторая
произвольная точка, которая лежит в какой-либо окрестности точки х0.
Приращением аргумента в точке х0 называется разность х-х0.
Обозначается приращение следующим образом: ∆х.
·
∆х=х-х0.
Иногда эту величину еще
называют приращением независимой переменной в точке х0. Из формулы
следует: х = х0+∆х. В таких случаях говорят, что начальное значение
независимой переменной х0, получило приращение ∆х.
Если мы изменяем аргумент, то
и значение функции тоже будет изменяться.
·
f(x) – f(x0) = f(x0 + ∆х) – f(x0).
Приращением
функции f в точке x0, соответствующим
приращению ∆х называется разность f(x0 + ∆х) – f(x0).
Приращение функции обозначается следующим образом ∆f. Таким образом получаем,
по определению:
·
∆f= f(x0 +∆x) – f(x0).
Иногда, ∆f еще называют
приращением зависимой переменной и для обозначения используют ∆у, если функция
была, к примеру, у=f(x).
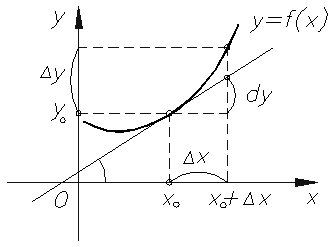
Геометрический смысл приращения
Посмотрите на следующий
рисунок.
Как видите, приращение
показывает изменение ординаты и абсциссы точки. А отношение приращения функции
к приращению аргумента определяет угол наклона секущей, проходящей через
начальное и конечное положение точки.
Рассмотрим примеры приращения функции и аргумента
Пример
1. Найти приращение аргумента ∆х и приращение функции ∆f в
точке х0, если f(х) = х2, x0=2 a) x=1.9
b) x =2.1
Воспользуемся формулами,
приведенными выше:
a) ∆х=х-х0 = 1.9 –
2 = -0.1;
·
∆f=f(1.9) – f(2) = 1.92 – 22 =
-0.39;
b) ∆x=x-x0=2.1-2=0.1;
·
∆f=f(2.1) – f(2) = 2.12 – 22 =
0.41.
Пример
2. Вычислить приращение ∆f для функции
f(x) = 1/x в точке х0, если приращение аргумента равняется ∆х.
Опять же, воспользуемся
формулами, полученными выше.
·
∆f = f(x0 + ∆x) – f(x0) =1/(x0-∆x)
– 1/x0 = (x0 – (x0+∆x))/(x0*(x0+∆x))
= -∆x/((x0*(x0+∆x)).
Пример
3.. Найти приращение функции y=2x2 при x0=3 и Δx=0,1
Решение. Подставляя
в формулу, получаем, что приращение функции:
Δy=y(3+0,1)−y(3)=2⋅(3+0,1)2−2⋅32=1,22
Ответ. Δy=1,22
Приращение функции
Понятие
приращения аргумента и приращения
функции.
Пусть
x – произвольная точка, ледащая в
некоторой окрестности фиксированной
точки x0.
разность x – x0 называется приращение
независимой переменной (
или приращением
аргумента)
в точке x0 и
обозначается Δx. Таким образом,
Δx = x –x0,
откуда
следует, что
x = x0 +
Δx.
Говорят
также, что первоначальное значение
аргумента x0 получило
приращение Δx. Вследствие этого значение
функции f изменится на величину
f(x) – f(x0)
= f (x0 +Δx)
– f(x0).
Эта
разность называется приращением
функции f
в точке x0,
соответствующим приращению Δx, и
обозначается символом Δf (читается
«дельта эф»), т.е. по определению
Δf = f (x0 +
Δx) – f (x0),
откуда
f (x) = f (x0 +Δx)
= f (x0)
+ Δf.
При
фиксированном x0 приращение Δf есть
функция от Δx. Δf называют также приращение
зависимой переменной и обозначают через
Δy для функции y = f(x) .
Определение
непрерывной в точке функции через
приращение.
Функция f(x) называется непрерывной
в точке x0,
если существует limx → x0 f(x) ,
равный значению функции f(x) в
этой точке:
f(x) = f(x0), |
(1) |
т.е.
|
» O( f(x0) ) $ O(x0) |
Производная функции одной переменной
Определение
производной функции в точке.
Пусть
в некоторой окрестности точки
определена функция
Производной
функции
в
точке
называется предел,
если он существует,
Геометрический
смысл производной и дифференциала.
Если
функция у = f(x) дифференцируема в точке
x0,
то ее производная в этой точке равна
тангенсу угла наклона касательной к
оси Ох, а дифференциал равен приращению
ординаты касательной
f'(x0)
= tg a.
Уравнения
касательной и нормали к графику функции.
Уравнение
касательной имеет вид:
У
= f'(x0)
• (x — x0)
+ f(x0)
Если
функция у = f(x) имеет в точке x0бесконечную
производную, то ее касательной является
вертикальная прямая х = х0.
Под
нормалью к кривой понимается прямая,
перпендикулярная касательной и проходящая
через точку касания. Если f'(x0)
0,
то уравнение нормали имеет вид:
Понятие
дифференцируемости функции в точке.
Функция y=f(x) называется дифференцируемой в
точке x0,
если ее приращение Δy в
точке x0 может
быть представлено в виде: Δy=A·Δx+α(Δx)·Δx,
где A — некоторое число, независящее
от Δx,
а α(Δx)—
бесконечно малая функция от переменной Δx,
т.е. limΔx→0α(Δx)=0.
Теорема
о необходимом и достаточном условии
дифференцируемости .
Теорема
Для
того, чтобы функция y=f(x) была дифференцируема в
точке x0,
необходимо и достаточно, чтобы она в
этой точке имела конечную
производную.
Доказательство
Необходимость.
Предположим: функция дифференцируема
в точке x0,
т.е. Δy=A·Δx+α(Δx)·Δx.
Разделив обе части данного равенства
на Δx,
получим: ΔxΔy=A+α(Δx).
Из
определения производной функции в
точке: y/(x0)=limΔx→0ΔxΔy=limΔx→0(A+α(Δx))=A.
Т.е.
получили, что существует конечная
производная функции в
точке x0 и y/(x0)=A.
Достаточность.
Пусть существует конечная
производная y/(x0)∈R .
Покажем дифференцируемость
функции. y/(x0)=limΔx→0ΔxΔy.
Если
функция f(x) имеет
конечный предел b при Δx→0 ,
то ее можно представить: f(x)=b+α(x)
(α(x)→0) .
Исходя из этого: ΔxΔy=y/(x0)+α(Δx),
где limΔx→0α(Δx)=0, Δy=y/(x0)·Δx+α(Δx)·Δx→ A=y/(x0) .
Теорема доказана.
Связь
свойств дифференцируемости и непрерывности
.
Если
функция y=y(x) дифференцируема
в точке x0,
то она и непрерывна в этой
точке.
Справедливость
утверждения следует
из Δy=y/(x0)·Δx+α(Δx)·Δx и limΔx→0Δy=0,
а по определению функция непрерывна,
если малому приращению аргумента
соответствует малое приращение
функции.
Обратное
утверждение не верно.
Например,
функция y=∣x∣ непрерывна
в точкеx=0,
но не дифференцируема в этой точке.
Таким
образом, не всякая непрерывная функция
дифференцируема, а любая дифференцируемая
функция непрерывна.
Дифференциал
функции. Физический смысл производной.
Дифференциалом функции f(x)
в точке х называется главня линейная
часть приращения функции.
Обозначается dy или df(x)
Производная
функции пути по времени есть мгновенная
скорость материальной точки в момент
времени х:
v(x)
= f'(x).
Поскольку
dy = f'(x)dx = v(x)dx, то дифференциал функции
пути равен расстоянию, которое прошла
бы точка за бесконечно малый промежуток
времени dx, если бы она двигалась равномерно
со скоростью, равной величине мгновенной
скорости в момент времени х.
Вторая
производная функции пройденного пути
также имеет простой смысл — это мгновенное
ускорение точки в данный момент времени
a(x)=v'(x)
= f»(x).
Производная
суммы, разности, произведения и частного
функций (все с доказательством кроме
последнего).
Производная
суммы (разности) функций
Производная
алгебраической суммы функций выражается
следующей теоремой.
Производная
суммы (разности) двух
дифференцируемых функций равна сумме
(разности) производных этих функций:
Производная
произведения функций.
Пусть u(x) и u(x) —
дифференцируемые функции. Тогда
произведение функций u(x)v(x) также
дифференцируемо и
Производная
произведения двух функций не равана
произведению производных этих функций.
Производная
частного функций.
Пусть u(x) и u(x) —
дифференцируемые функции. Тогда,
если v(x)
≠ 0,
то производная частного этих функций
вычисляется по формуле
Производная
сложной функции .
«Двухслойная»
сложная функция записывается в виде
где u
= g(x) —
внутренняя функция, являющаяся, в свою
очередь, аргументом для внешней
функции f.
Если f и g —
дифференцируемые функции, то сложная
функция
также
дифференцируема по x и
ее производная равна
Данная
формула показывает, что производная
сложной функции равна произведению
производной внешней функции на производную
от внутренней функции. Важно, однако,
что производная внутренней функции
вычисляется в точке x,
а производная внешней функции — в точке u
= g(x)!
Определение
логарифмической производной функции.
Логарифмической
производной функции y=f(x) называется
производная ее логарифма.
тогда
производная функции y=f(x) может
быть найдена так:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- Приращение аргумента и функции
- Определение производной
- Дифференцирование функции
Пусть задана некоторая функция $y=f(x)$. Возьмем какое-нибудь
значение $x_{0}$ из области определения этой функции:
$x_{0} in D[f]$ . Соответствующее значение функции в этой точке
будет равно $y_{0}=fleft(x_{0}right)$ .
Приращение аргумента и функции
Определение
Приращением аргумента называется разность между двумя значениями аргумента: «новым» и «старым».
Обычно обозначается как $Delta x=x_{1}-x_{0}$ .
Пример
Задание. Найти приращение аргумента $x$, если он переходит от значения 3 к значению 3,2.
Решение. Искомое приращение: $Delta x=3,2-3=0,2$ .
Ответ. $Delta x=0,2$
Зададим аргументу $x_{0}$ приращение
$Delta x$. А тогда значение функции в новой точке
$fleft(x_{0}+Delta xright)$.
Определение
Приращением функции $y=f(x)$ в точке
$x_{0}$, соответствующее приращению аргумента
$Delta x=x-x_{0}$, называется величина:
$Delta y=fleft(x_{0}+Delta xright)-fleft(x_{0}right)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти приращение функции $y=2 x^{2}$
при $x_{0}=3$ и
$Delta x=0,1$
Решение. Подставляя в формулу, получаем, что приращение функции:
$Delta y=y(3+0,1)-y(3)=2 cdot(3+0,1)^{2}-2 cdot 3^{2}=1,22$
Ответ. $Delta y=1,22$
Определение производной
Определение
Производной $y^{prime}(x)$ от функции
$y=f(x)$ в точке
$x_{0}$ называется предел отношения
приращения функции $Delta y$ к приращению аргумента
$Delta x$ :
$frac{Delta y}{Delta x}$ при
$Delta x rightarrow 0$, если он существует, то есть:
$y^{prime}left(x_{0}right)=f^{prime}left(x_{0}right)=lim _{Delta x rightarrow 0} frac{Delta y}{Delta x}=lim _{Delta x rightarrow 0} frac{fleft(x_{0}+Delta xright)-fleft(x_{0}right)}{Delta x}$
или
$y^{prime}left(x_{0}right)=lim _{x rightarrow x_{0}} frac{f(x)-fleft(x_{0}right)}{x-x_{0}}$
Пример
Задание. Найти производную функции $y=x^{2}+3 x$
в точке $x_{0}=0$.
Решение. Найдем приращение заданной функции в точке $x_{0}$ :
$Delta y=y(0+Delta x)-y(0)=y(Delta x)-y(0)=$
$=(Delta x)^{2}+3 Delta x-0=Delta x(Delta x+3)$
Тогда
$y^{prime}(0)=lim _{Delta x rightarrow 0} frac{Delta x(Delta x+3)}{Delta x}=lim _{Delta x rightarrow 0}(Delta x+3)=0+3=3$
Ответ. $y^{prime}(0)=3$
Дифференцирование функции
Определение
Операция нахождения производной функции называется дифференцированием этой функции.
Функция $y=f(x)$ имеет производную на интервале
$(a ; b)$ или называется дифференцируемой в этом
интервале, если производная $f^{prime}(x)$ существует в каждой точке этого интервала.
Функция $y=f(x)$ имеет в точке
$x$ бесконечную производную, если в этой точке
$f^{prime}(x)=lim _{Delta x rightarrow 0} frac{Delta y}{Delta x}=infty$ .
Теорема
(О непрерывности функции в точке)
Если функция $y=f(x)$ имеет конечную производную в
точке $x_{0}$ , то она непрерывна в этой точке.
Замечание. Обратное заключение не всегда верно: если функция $y=f(x)$
непрерывна в некоторой точке $x_{0}$ , то она может
и не иметь производной в этой точке.
Определение
Функция $y=f(x)$ называется дифференцируемой
в точке $x$, если приращение функции,
соответствующее приращению аргумента, можно представить в виде:
$Delta y=A cdot Delta x+alpha(Delta x) cdot Delta x$
где $A$ — число, не зависящее от
$Delta x$,
$alpha(Delta x)$ — б.м. функция при
$Delta x rightarrow 0$.
Теорема
(О необходимом и достаточном условии дифференцируемости)
Для того чтобы функция $y=f(x)$ была дифференцируемой
в точке $x$, необходимо и достаточно,
чтобы $y=f(x)$ имела в этой точке конечную производную.
Теорема устанавливает, что для функции $y=f(x)$
дифференцируемость в данной точке $x$ и существование конечной производной в этой точке — понятия равносильные.
Читать дальше: односторонние производные.
- Приращение аргумента и приращение функции
- Определение производной
- Физический смысл производной
- Геометрический смысл производной
- Алгоритм поиска значения производной в заданной точке
- Алгоритм поиска уравнения производной
- Примеры
п.1. Приращение аргумента и приращение функции
Приращением аргумента называют разность $$ triangle x=x-x_0 $$ где (x) — произвольное число, которое мало отличается от начальной точки (x_0). Приращение аргумента может быть как положительным, так и отрицательным.
Приращением функции называют соответствующую разность $$ triangle y=f(x)-f(x_0 )=f(x_0+triangle x)-f(x_0) $$ Приращение функции может быть как положительным, так и отрицательным.
Например:
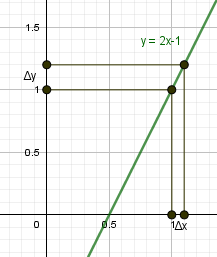 |
begin{gather*} y=2x-1\ x_0=1, x=1,1 end{gather*} Найдем приращение аргумента и функции. begin{gather*} triangle x= x-x_0=1,1-1=0,1gt 0\ \ f(x)=f(1,1)=2cdot 1,1-1=1,2\ f(x_0 )=f(1)=2cdot 1-1=1\ triangle y=f(x)-f(x_0 )=1,2-1=0,2gt 0 end{gather*} |
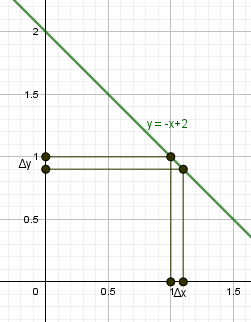 |
begin{gather*} y=-x+2\ x_0=1, x=1,1 end{gather*} Найдем приращение аргумента и функции. begin{gather*} triangle x= x-x_0=1,1-1=0,1gt 0\ \ f(x)=f(1,1)=-1,1+2=0,9\ f(x_0 )=f(1)=-1+2=1\ triangle y=f(x)-f(x_0)=0,9-1=-0,1lt 0 end{gather*} |
Если функция возрастает, приращение аргумента и приращение функции имеют один и тот же знак: $$ begin{cases} y=f(x) — text{возрастает}\ triangle xgt 0 end{cases} Rightarrow triangle ygt 0 $$ Если функция убывает, приращение аргумента и приращение функции имеют разные знаки: $$ begin{cases} y=f(x) — text{убывает}\ triangle xgt 0 end{cases} Rightarrow triangle ylt 0 $$
п.2. Определение производной
Производной функции (f(x)) в точке (x_0) называют предел отношения приращения функции в точке (x_0) к приращению аргумента, если приращение аргумента стремится к нулю, а предел существует: $$ f'(x_0)=lim_{triangle xrightarrow 0}frac{triangle y}{triangle x} $$
Например:
Найдем производную функции (f(x)=x^2-4) в точке (x_0=3)
Значение функции в точке: (f(x_0 )=3^2-4=5)
Пусть (triangle x) — некоторое приращение аргумента. Тогда: begin{gather*} f(x)=f(x_0+triangle x)=(x_0+triangle x)^2-4=(3+triangle x)^2-4=9+6triangle x+triangle x^2-4=\ =5+6triangle x+triangle x^2 end{gather*} Приращение функции: $$ triangle y=f(x)-f(x_0)=5+6triangle x+triangle x^2-5=6triangle x+triangle x^2=triangle x(6+triangle x) $$ Производная: $$ f'(x_0)=lim_{triangle xrightarrow 0}frac{triangle x}{triangle y}=lim_{triangle xrightarrow 0}frac{triangle x(6+triangle x)}{triangle x}=lim_{triangle xrightarrow 0}(6+triangle x)=6+0=6 $$ Ответ: 6
п.3. Физический смысл производной
Рассмотрим прямолинейное движение.
Пусть расстояние по прямой между городами (triangle x=) 300 км поезд преодолевает за (triangle t=)4 часа. Мы легко можем найти его среднюю скорость: $$ v_{cp}=frac{triangle x}{triangle t}, v_{cp}=frac{300}{4}=75 (text{км/ч}) $$ Но поезд не едет все время с одной и той же скоростью: где-то ускоряется, где-то замедляется, где-то и вовсе останавливается.
Если мы захотим определить скорость как можно точнее, нам понадобится уменьшать интервалы времени и измерять соответствующий путь. Уменьшив время до «мгновений», мы получим «мгновенную скорость» для каждой точки траектории в каждый момент времени.
Мгновенная скорость это скорость тела в данный момент времени (t_0): $$ v(t_0)=lim_{triangle trightarrow 0}frac{triangle x}{triangle t}=x'(t_0) $$ где (triangle x=x-x_0) — путь тела за время (triangle t=t-t_0, x(t)) – уравнение движения.
Мгновенная скорость равна первой производной от уравнения движения при (t=t_0).
Сравнивая определения мгновенной скорости и производной функции, мы можем сформулировать физический смысл производной:
Производная функции (y=f(x)) в точке (x_0) равна скорости изменения функции в этой точке.
Или, ближе к физике/химии/биологии:
Производная уравнения процесса (s=f(t)) в момент времени (t_0) равна скорости протекания процесса в этот момент.
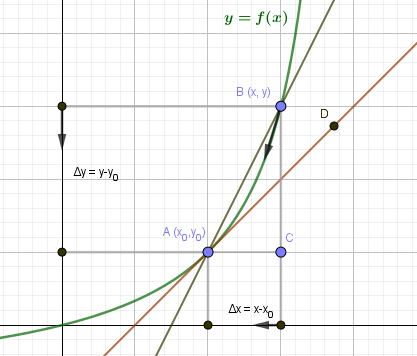
п.4. Геометрический смысл производной
Пусть на плоскости задана кривая (y=f(x)).
Выберем на кривой две точки (A(x_0,y_0)) и (B(x,y)). Прямая AB будет секущей для кривой (y=f(x)). Угол наклона прямой AB определяется угловым коэффициентом: $$ k_{AB}=tgangle A=frac{BC}{AC}=frac{triangle y}{triangle x} $$ Начнем движение точки B вдоль кривой по направлению к точке A. Приращение аргумента при этом будет уменьшаться: (triangle x=ACrightarrow 0). В тот момент, когда B совпадет с A, секущая AB превратится в касательную AD. Угловой коэффициент касательной: $$ k_{AD}=lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=y'(x_0) $$
Мы можем сформулировать геометрический смысл производной:
Производная функции (y=f(x)) в точке (x_0) равна угловому коэффициенту касательной к графику этой функции в этой точке.
п.5. Алгоритм поиска значения производной в заданной точке
На входе: уравнение функции (y=f(x)), точка (x_0)
Шаг 1. Найти значение функции в заданной точке (y_0=f(x_0)).
Шаг 2. Задать приращение аргумента (triangle x=x-x_0), найти приращение функции (triangle y=f(x)-f(x_0)=f(x_0+triangle x)-f(x_0)).
Шаг 3. Найти предел (lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=f'(x_0))
На выходе: значение производной в точке (x_0)
Например:
Найдем значение производной в точке (x_0=1) для функции (y=x^2-3).
Значение функции в заданной точке: (f(x_0)=1^2-3=-2)
Пусть (∆x) — некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x_0+triangle x)-f(x_0)=((1+triangle x)^2-3)-(-2)=\ =1+2triangle x+(triangle x)^2-1=2triangle x+(triangle x)^2=triangle x(2+triangle x) end{gather*} Ищем предел: begin{gather*} lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{triangle x(2+triangle x)}{triangle x}=lim_{triangle xrightarrow 0}(2+triangle x)=2+0=2 end{gather*} Искомая производная в заданной точке: (f'(1)=2)
Ответ: 2
п.6. Алгоритм поиска уравнения производной
На входе: уравнение функции (y=f(x))
Шаг 1. Задать приращение аргумента (triangle x), найти выражение для приращения функции (triangle y=f(x+triangle x)-f(x)).
Шаг 2. Найти предел выражения (lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=f'(x))
На выходе: уравнение производной (y ‘=f'(x)) в любой точке (x).
Например:
Найдем общее уравнение производной для функции (y=x^2-3).
Пусть (∆x) — некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x+triangle x)-f(x)=((x+triangle x)^2-3)-(x^2-3)=\ =(x+triangle x)^2-x^2=(x+triangle x-x)(x+triangle x+x)=triangle x(2x+triangle x) end{gather*} Ищем предел: begin{gather*} lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{triangle x(2x+triangle x)}{triangle x}=lim_{triangle xrightarrow 0}(2x+triangle x)=2x+0=2x end{gather*} Ответ: уравнение производной (y ‘=2x)
п.7. Примеры
Пример 1. Пользуясь алгоритмом поиска значения производной в заданной точке, найдите:
a) ( f'(1), text{если} f(x)=2x )
По условию (x_0=1)
Значение функции в заданной точке: (f(x_0 )=2cdot 1=2)
Пусть (triangle x) — некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x_0+triangle x)-f(x_0)=2(1+triangle x)-2=2+2triangle x-2=2triangle x end{gather*} Ищем предел: begin{gather*} lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{2triangle x}{triangle x}=2 end{gather*} Искомая производная в заданной точке: (f'(1)=2)
б) ( f'(3), text{если} f(x)=3x^2 )
По условию (x_0=3)
Значение функции в заданной точке: (f(x_0 )=3cdot 3^2=27)
Пусть (triangle x) — некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x_0+triangle x)-f(x_0)=3(3+triangle x)^2-27=3(9+6triangle x+(triangle x)^2)-27=\ =27+18triangle x+3(triangle x)^2-27=3triangle x(6+triangle x) end{gather*} Ищем предел: begin{gather*} lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{3triangle x(6+triangle x)}{triangle x}=3lim_{triangle xrightarrow 0}(6+triangle x)=3(6+0)=18 end{gather*} Искомая производная в заданной точке: (f'(3)=18)
в) ( f'(-1), text{если} f(x)=4x-1 )
По условию (x_0=-1)
Значение функции в заданной точке: (f(x_0)=4cdot (-1)-1=-5)
Пусть (triangle x) — некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x_0+triangle x)-f(x_0)=(4(-1+triangle x)-1)-(-5)=-5+4triangle x+5=4triangle x end{gather*} Ищем предел: begin{gather*} lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{4triangle x}{triangle x}=4 end{gather*} Искомая производная в заданной точке: (f'(-1)=4)
г) ( f'(2), text{если} f(x)=x^3 )
По условию (x_0=2)
Значение функции в заданной точке: (f(x_0)=2^3=8)
Пусть (triangle x) — некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x_0+triangle x)-f(x_0)=(2+triangle x)^3-8=\ =2^3+3cdot 2^2cdot triangle x+3cdot 2cdot (triangle x)^2+(triangle x)^3-8=\ =12triangle x+6(triangle x)^2+(triangle x)^3=triangle xcdot (12+6triangle x+(triangle x)^2 ) end{gather*} Ищем предел: begin{gather*} lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{triangle xcdot(12+6triangle x+(triangle x)^2)}{triangle x}=lim_{triangle xrightarrow 0}(12+6triangle x+(triangle x)^2)=12+0+0=12 end{gather*} Искомая производная в заданной точке: (f'(2)=12)
Ответ: а) 2; б) 18; в) 4; г) 12
Пример 2. Пользуясь алгоритмом поиска уравнения производной, найдите общее уравнение производной для функции (y=f(x)):
a) ( f(x)=C), где C – постоянная величина
Пусть (triangle x) — некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x+triangle x)-f(x)=C-C=0 end{gather*} Отношение (frac{triangle y}{triangle x}=frac{0}{triangle x}=0)
Предел (lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}0=0)
Производная (y ‘=C’=0)
Производная постоянной равна нулю: (C ‘=0)
б) ( f(x)=x)
Пусть (triangle x) — некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x+triangle x)-f(x)=x+triangle x-x=triangle x end{gather*} Ищем предел: (lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{triangle x}{triangle x}=lim_{triangle xrightarrow 0}1=1)
Производная (x ‘=1)
Производная аргумента равна единице: (x ‘=1)
в) ( f(x)=x^2)
Пусть (triangle x) — некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x+triangle x)-f(x)=(x+triangle x)^2-x^2=(x+triangle x-x)(x+triangle x+x)=triangle x(2x+triangle x) end{gather*} Ищем предел: begin{gather*} lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{triangle x(2x+triangle x)}{triangle x}=lim_{triangle xrightarrow 0}(2x+triangle x)=2x+0=2x end{gather*} Производная ((x^2) ‘=2x)
г) ( f(x)=x^3)
Пусть (triangle x) — некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x+triangle x)-f(x)=(x+triangle x)^3-x^3=\ =(x+triangle x-x)((x+triangle x)^2+x(x+triangle x)+x^2)=triangle x((x+triangle x)^2+x(x+triangle x)+x^2) end{gather*} Ищем предел: begin{gather*} lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{triangle x((x+triangle x)^2+x(x+triangle x)+x^2)}{triangle x}=\ =lim_{triangle xrightarrow 0}((x+triangle x)^2+x(x+triangle x)+x^2)=(x+0)^2+x(x+0)+x^2=3x^2 end{gather*} Производная ((x^3) ‘=3x^2)
д) ( f(x)=frac1x)
Пусть (triangle x) — некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x+triangle x)-f(x)=frac{1}{x+triangle x}-frac1x=frac{x-(x+triangle x)}{x(x+triangle x)}=-frac{triangle x}{x(x+triangle x)} end{gather*} Ищем предел: begin{gather*} lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}left(-frac{triangle x}{triangle xcdot x(x+triangle x)}right)=-lim_{triangle xrightarrow 0}frac{1}{x(x+triangle x)}=-frac{1}{x(x+0)}=-frac{1}{x^2} end{gather*} Производная (left(frac1xright) ‘=-frac{1}{x^2})
e) ( f(x)=kx+b)
Пусть (triangle x) — некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x+triangle x)-f(x)=k(x+triangle x)+b-kx-b=ktriangle x end{gather*} Ищем предел: begin{gather*} lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{ktriangle x}{triangle x}=lim_{triangle xrightarrow 0}k=k end{gather*} Производная ((kx+b) ‘=k)
ж) ( f(x)=sqrt{x})
Пусть (triangle x) — некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x+triangle x)-f(x)=sqrt{x+triangle x}-sqrt{x} end{gather*} Ищем предел, умножив числитель и знаменатель на сопряженное выражение: begin{gather*} lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{sqrt{x+triangle x}-sqrt{x}}{triangle x}= lim_{triangle xrightarrow 0}frac{(sqrt{x+triangle x}-sqrt{x})(sqrt{x+triangle x}+sqrt{x})}{triangle x(sqrt{x+triangle x}+sqrt{x})}=\ =lim_{triangle xrightarrow 0}frac{x+triangle x-x}{triangle x(sqrt{x+triangle x}+sqrt{x})}=lim_{triangle xrightarrow 0}frac{1}{(sqrt{x+triangle x}+sqrt{x})}=frac{1}{sqrt{x+0}+sqrt{x}}=frac{1}{2sqrt{x}} end{gather*} Производная ((sqrt{x}) ‘=frac{1}{2sqrt{x}})
Дата публикации: 09 апреля 2017.
Алгебра – 10 класс. Приращение аргумента, приращение функции
Урок на тему: «Приращение аргумента, приращение функции»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Скачать:
Приращение аргумента, приращение функции (PDF)
Что будем изучать:
1.Определение приращения аргумента, приращения функции.
2. Непрерывная функция и приращение.
3. Примеры.
Определение приращения аргумента и приращения функции
Ребята, мы с вами научились находить пределы функции в точке. Важным остается вопрос, как изменяется значение функции при изменении значения аргумента около этой точки?
Математики ввели такое понятие – приращение аргумента и функции. Давайте запишем определение.
Определение: Пусть функция $y=f(x)$ определена в точках $x_0$ и $x_1$. Разность $x_1-x_0$ называют приращением аргумента, а разность $f(x_1)-f(x_0)$–приращением функции.
Иначе говоря, узнаем прирост точки $x_0$ в точке $x_1$. Приращение аргумента обозначают как $Δx$, читается как дельта x.
Приращение функции обозначают, как $Δy$ или $Δf(x)$.
Из нашего определения следует: $x_1-x_0=Δx$ => $x_1= Δx+x_0$ и $f(x_1)-f(x_0)=Δy$. Тогда получаем важное равенство: $Δy=f(x_0+ Δx)-f(x_0)$.
Приращение функции может быть как положительным, так и отрицательным.
Давайте рассмотрим пример.
Найти приращение функции $y=х^3$ при переходе от $x_0=2$ к точке:
а) $x=2,1$; б) $x=1,9$.
Решение:
Обозначим $f(x)=х^3$.
Имеем: $f(2)=2^3=8$.
а) Воспользуемся формулой $Δy=f(x_0+ Δx)-f(x_0)$.
Нам надо найти значение $f(2,1)$.
$f(2,1)=2,1^3=9,261$.
$Δy= f(2,1)- f(2)= 9,261-8=1,261$.
б) $f(2)=8$.
$f(1,9)=1,9^3=6,859$.
$Δy= f(1,9)- f(2)= 6,859-8=-1,141$.
Ответ: а) $1,261$; б) $-1,141$.
Непрерывная функция и приращение
Ребята, давайте вернемся к определению непрерывной функции, и посмотрим на него с помощью приращений.
Вспомним определение непрерывной функции.
Определение. Функцию $y=f(x)$ называют непрерывной в точке $x=a$, если выполняется тождество:
[lim_{x rightarrow a}f(x)=f(a)]
Обратим внимание: $x →a$, тогда $(x-a) →0$ т.е. $Δx → 0$.
Также заметим: $f(x) → f(a)$ , значит $f(x) — f (a) → 0$ т.е. $Δy → 0$.
Определение непрерывности функции в точке можно записать так.
Функция $y=f(x)$ непрерывна в точке $x=a$, если в этой точке выполняется следующее условие:
если $Δx→0$, то $Δy → 0$.
Примеры
1. Для функции $y=kx+b$ найти:
а) приращение функции при переходе от фиксированной точки $x$ к $x+ Δx$;
б)предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю.
Решение:
а) $f(x)= kx+b$.
$f(x+ Δx)=k(x+Δx)+b$;
$Δy= f(x+ Δx)-f(x)= k(x+Δx)+b-( kx+b)= kx+kΔx+b – kx-b= kΔx$.
б) Найдем требуемый предел: $lim_{Δx rightarrow 0}frac{Δy}{Δx}=lim_{Δx rightarrow 0}frac{kΔx}{Δx}=lim_{Δx rightarrow 0}k=k$.
2. Для функции $y=x^3$ найти:
а) приращение функции при переходе от фиксированной точки $x$ к $x+ Δx$.
б)предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю.
Решение:
а) $f(x)= x^3$.
$f(x+ Δx)=(x+Δx)^3=x^3+3x^2Δx+3xΔx^2+Δx^3$.
$Δy= f(x+Δx)-f(x)= x^3+3x^2Δx+3xΔx^2+Δx^3-x^3=3x^2Δx+3xΔx^2+Δx^3$.
б) Найдем требуемый предел: $lim_{Δx rightarrow 0}frac{Δy}{Δx}=lim_{Δx rightarrow 0}frac{3x^2Δx+3xΔx^2+Δx^3}{Δx}=lim_{Δx rightarrow 0}(3x^2+3xΔx+Δx^2)=3x^2$.
Задачи для самостоятельного решения:
1) Найти приращение функции $y=x^4$ при переходе от $x_0=3$ к точке:
а) $x=3,2$;
б) $x=2,8$.
2) Для функции $y=3x+5$ найти приращение функции при переходе от фиксированной точки $x$ к $x+ Δx$.
3) Для функции $y=x^2$ найти приращение функции при переходе от фиксированной точки $x$ к $x+ Δx$.
4) Для функции $y=2x^3$ найти приращение функции при переходе от фиксированной точки $x$ к $x+ Δx$.