Как найти приращение энтропии системы

Из полученного в разделе Error: Reference source not found
соотношения
следует, что

и

.

Другими словами, отношение количества
тепла, полученного системой в ходе
изотермического расширения к температуре
Т₁равно отношению тепла,
выделенного системой в ходе изотермического
сжатия к температуреТ₂.

Такая взаимосвязь отношений Q/Tнаводит на мысль о том, что за этим
отношением скрыта какая-то характеристика
тепловых процессов.

Поскольку Q₁>0,
постольку при получении системой тепла
она получает положительное приращение.

В процессе изотермического сжатия
система выделяет тепло, поэтому Q₂<0.
Следовательно, при отдаче тепла эта
характеристика получает отрицательное
приращение.

Поскольку
,
постольку эта характеристика в ходе
цикла Карно не изменяется:.

В 60^хгодахXIXвека
немецкий физик Рудольф Клаузиус
опубликовал ряд работ, в которых
говорилось об этой характеристике
тепловых процессов.

Клаузиус присвоил ей название энтропияи показал, что энтропияSесть функция состояния системы (это
означает, что значение энтропии
определяется состоянием системы и не
зависит от того, как система пришла в
это состояние).

Произвольный обратимый круговой процесс
Клаузиус представил как сумму множества
элементарных циклов Карно. В каждом из
них газ получает элементарное количество
тепла Qпри некоторой температуреТа затем
отдаёт теплоQпри температуре Т.

В каждом из элементарных циклов Карно
приращение энтропии
.

Суммарное приращение энтропии во всех
элементарных циклах Карно, образующих
рассматриваемый круговой процесс, также
должно быть равно нулю.

Поскольку вид обратимого кругового
процесса не оговаривался, полученный
вывод справедлив для всех циклических
обратимых процессов:

.

Величина, стоящая под знаком интеграла
является приращением энтропии:

.

Это выражение и является определением
энтропии.

Следует отметить, что такое определение
является не совсем полным. Оно позволяет
определить значение энтропии с точностью
до произвольной постоянной (так же, как
и значение потенциальной энергии в
механике). Но приращение энтропии в ходе
любого обратимого процесса с помощью
такого определения рассчитывается
точно:

.

Клаузиус не ограничился рассмотрением
обратимых процессов. Им были проанализированы
и реальные, т.е. необратимые процессы.
Анализ показал, что в результате
циклического необратимого процесса
энтропия системы возрастает:

S>0.

В качестве примера рассмотрим расчёт
приращения энтропии идеального газа.

Пусть идеальный газ переходит из
состояния с температурой Т₁и объёмомV₁в
состояние с температуройТ₂и объёмомV₂.
Начальное и конечное состояние газа
считаем равновесным.

Приращение энтропии можно найти следующим
образом:

(здесь учтено, что в соответствии с
первым началом термодинамики Q=dU+A).

В разделе Error: Reference source not found показано,
что приращение внутренней энергии
идеального газа
.

Элементарная работа
(здесь учтено, что в соответствии с
уравнением Менделеева-Клапейрона).

Используя эти выражения, получаем
приращение энтропии идеального газа:

.

При изотермическом процессе dT=0,
поэтому приращение энтропии

.

При изохорическом процессе dV=0
и приращение энтропии

.

При адиабатическом процессе Q=0.

Из определения энтропии Q=TdS.
Это означает, что при адиабатическом
процессе приращение энтропииdS=0
и энтропияS=const.
Поэтому адиабатический процесс также
называютизоэнтропийным.

Открытие энтропии позволило решить ещё
одну термодинамическую проблему.

Первое начало термодинамики показывает,
какими способами можно изменить
внутреннюю энергию системы. Однако оно
не позволяет определить направление
термодинамических процессов.

Между тем из экспериментального опыта
известно, что далеко не любой процесс
можно осуществить на практике. Например,
энергия не перейдёт самопроизвольно
от более холодного тела к более горячему.

Поэтому физики искали критерий, по
которому можно определить, в каком
направлении может протекать
термодинамический процесс. Таким
критерием оказалась энтропия. Использование
этого параметра состояния позволило
сформулировать в наиболее общей форме
второе начало термодинамики:в
замкнутой макроскопической системе
энтропия при любом реальном процессе
либо возрастает, либо остаётся неизменной.

Другими словами, термодинамические
процессы идут в том направлении, которое
сопровождается возрастанием энтропии.

Например, рассчитаем приращение энтропии
замкнутой системы, состоящей из двух
тел. Пусть одно из тел имеет более высокую
температуру Т₁. Температура
второго тела равнаТ₂.

Более горячее тело передаст второму
телу некоторое количество тепла Q.

Энтропия более горячего тела при этом
изменится на
(первое тело отдаёт тепло, поэтому
приращение энтропии отрицательное).

Энтропия холодного тела возрастёт на
.

Приращение полной энтропии системы
равно сумме приращений энтропии каждого
из тела:

.

Поскольку Т₁>Т₂,
постолькуS>0,
т.е. при переходе энергии от более
горячего тела к более холодному энтропия
системы возрастает.

Если допустить, что энергия пойдёт от
более холодного тела к более горячему,
то приращение энтропии системы будет
отрицательным, энтропия системы
уменьшится. Это запрещено вторым началом
термодинамики и поэтому подобные
процессы самопроизвольно не происходят.

Энтропия – это фундаментальная физическая величина. Введение этого понятия завершило этап становления понятийного аппарата термодинамики. Следующим этапом развития этой науки было выяснение физического смысла энтропии.

Установление принципа Больцмана (формулы Больцмана) и таким образом связи между термодинамикой и статистической физикой, позволило энтропии покинуть пределы физики и войти в другие области знаний.

Энтропия – это общезначимое понятие, применяемое во множестве наук, например, в:

• физике;
• химии;
• билогии;
• космологии;
• теории информации.

Введено это понятие было Р. Клаузиусом. Важные работы посвятил энтропии Л. Больцман, М. Планк.

Важно, что выражение (1) определяет не саму энтропию, а ее изменение, или разность энтропий. При помощи данной формулы можно вычислить, каково изменение энтропии, если термодинамическая система переходит из одного состояния в другое, но нельзя понять, какова энтропия каждого из этих состояний.

Напомним формулу Больцмана для энтропии, так как она нам поможет понять физический смысл, процессов, которые происходят с энтропией:

$S=klnW, left( 2 right)$

где ($W$) – термодинамическая вероятность (статистический вес состояния), то есть количество способов, реализации данного состояния термодинамической системы. $W$ ≥1; $k$- постоянная Больцмана.

Изменение энтропии, исходя из статистической формулы Больцмана, найдем как:

$S_{2}-S_{1}=klnfrac{W_{2}}{W_{1}}left( 2.1 right)$).

«Изменение энтропии» 👇

Вычисление изменения энтропии в изотермическом процессе

Вычислим изменение энтропии в одном моле идеального газа при изотермическом процессе ($T=const$). Оттолкнемся от первого начала термодинамики в дифференциальной форме:

$delta Q=dU+pdV, left( 3 right)$,

где $dU$ — изменение внутренней энергии идеального газа; $pdV$=$delta A$ – работа, совершаемая газом.

Найдем отношение всех слагаемых выражения (3) и температуры:

$frac{delta Q}{T}=C_{V}frac{dT}{T}+frac{p}{T}dVleft( 4 right)$.

где $C_V$ – теплоемкость газа при $V=const$.

Для идеального газа справедливо уравнение Менделеева – Клапейрона, учитывая, что у нас 1 моль газа:

$pV=RTto frac{p}{T}=frac{R}{V}left( 5 right)$.

Учтем:

$frac{dT}{T}=dleft( ln T right),, frac{dV}{V}=dleft( ln V right)left( 6 right)$.

в этом случае мы можем записать для уравнения (4):

$frac{delta Q}{T}=dleft( C_{V}lnT+RlnV right)left( 7 right)$.

По определению (1), и принимая во внимание (7), запишем:

$dS=dleft( C_{V}lnT+RlnV right)left( 8 right)$.

Формула (8) показывает нам, что в изотермическом процессе изменяется только второе слагаемое правой части:

• при увеличении объема энтропия увеличивается,
• с уменьшением объема энтропия уменьшается.

Данный результат очевиден, так как если увеличивается объем, то возрастает количество мест, которое смогут занять частицы при неизменяющемся их количестве. Следовательно, растет число разных возможностей расположения на этих местах (увеличивается количество пространственных микросостояний). Увеличение числа микросостояний означает увеличение энтропии (см формулу (2)).

Изменение энтропии в изохорическом процессе

Рассмотрим изохорный процесс в идеальном газе ($V=const$ или $dV=0$). Из формулы (7) для изохорного процесса следует:

$dS=dleft( C_{V}lnT+RlnV right)=d(C_{V}lnT)left( 9 right)$.

После интегрирования (9), получим:

$S_{2}-S_{1}=C_{V}ln left( frac{T_{2}}{T_{1}} right)left( 10 right)$.

Формула (10) показывает, что в изохорическом процессе при увеличении температуры происходит рост энтропии. Данный результат можно пояснить так:

1. при увеличении температуры растет средняя энергия частиц газа;
2. увеличивается количество возможных энергетических состояний.

Изменение энтропии в адиабатном процессе

Адиабатный процесс характеризуется тем, что он происходит без теплообмена (δQ=0). Исследуя адиабатный процесс в идеальном газе, за основу для вычисления энтропии примем выражение (8). Найдем интеграл правой и левой частей этого выражения, получим:

$S_{2}-S_{1}=C_{V}ln left( frac{T_{2}}{T_{1}} right)+Rln {left( frac{V_{2}}{V_{1}} right)left( 11 right).}$

Запишем уравнение адиабатного процесса в параметрах $T,V$:

$T_{1}V_{1}^{gamma -1}=T_{2}V_{2}^{gamma -1}left( 12 right)$.,

где $gamma =frac{C_{p}}{C_{V}}-$ показатель адиабаты. Возьмем натуральные логарифмы от обеих частей выражения (12), имеем:

$ln left( frac{T_{2}}{T_{1}} right)=left( gamma -1 right)ln left( frac{V_{1}}{V_{2}} right)=-left( gamma -1 right)ln left( frac{V_{2}}{V_{1}} right)left( 13 right)$.

Преобразуем выражение (11), приняв во внимание формулу (13):

$S_{2}-S_{1}=C_{V}left[ -left( gamma -1 right)ln left(frac{V_{2}}{V_{1}} right) right]+Rln left( frac{V_{2}}{V_{1}} right)=-C_{V}left( frac{C_{p}}{C_{V}}-1 right)ln left( frac{V_{2}}{V_{1}}right)$
$+Rln {left( frac{V_{2}}{V_{1}} right)=left[ -C_{V}left(frac{C_{p}}{C_{V}}-1 right)+R right]ln {left( frac{V_{2}}{V_{1}}right)=left[ C_{V}-C_{p}+R right]ln left( frac{V_{2}}{V_{1}} right)}}left( 14 right)$.

Вспомним соотношение Майера:

$R=C_{p}-C_{V}left( 15 right)$

и сделаем вывод о том, что изменение энтропии в адиабатном процессе нет:

$S_{2}-S_{1}=0.$

Адиабатный процесс является изоэнтропийным ($S=const$).

При адиабатном расширении газа увеличение энтропии может идти только за счет увеличения объема, но при этом происходит уменьшение температуры, и энтропия уменьшается из-за уменьшения температуры. Данные тенденции взаимно компенсируют друг друга.

Рассмотрим пример. Два сосуда разного объема содержат по $nu$ молей одинакового идеального газа. Температуры газов равны $ T_1$ и $ T_2$. Сосуды соединяют, газы перемешиваются. Система приходит в состояние равновесия. Определим изменение энтропии в этом процессе.

Будем считать, что изобарное расширение каждого из газов до конечного объема является обратимым. В этом процессе температура каждой из газовых компонент изменяется до конечной температуры $frac{T_{1}+T_{2}}{2}$. Найдем изменение энтропии каждого из газов по отдельности:

$Delta S_{1}=intlimits_a^b frac{dT}{T} =nu c_{p}ln left(frac{T_{1}+T_{2}}{2T_{1}} right)left( 16 right)$,

где $a=T_{1};b=frac{T_{1}+T_{2}}{2}$ $c_p$ – молярная теплоемкость газа при постоянном давлении.

Изменение энтропии второго газа запишем аналогично:

$Delta S_{2}=nu c_{p}ln left( frac{T_{1}+T_{2}}{2T_{2}} right)left( 17right)$.

Поскольку энтропия является аддитивной величиной, то полное изменение энтропии найдем как сумму:

$Delta S_{2}=Delta S_{1}+Delta S_{2}=nu c_{p}ln left( frac{T_{1}+T_{2}}{2T_{1}} right)+c_{p}ln left(frac{T_{1}+T_{2}}{2T_{2}} right)=nu c_{p}ln frac{left( T_{1}+T_{2} right)^{2}}{4T_{1}T_{2}}=2nu$ $c_{p}lnleft( frac{T_{1}+T_{2}}{2sqrt {T_{1}T_{2}} } right)$.

Приращение — энтропия — система

Cтраница 1

Приращение энтропии системы, поскольку рабочее тело совершает круговой процесс, равно сумме приращений энтропии источников теплоты.
 [1]

Найдем теперь приращение энтропии системы, обусловленное действием сил вязкости.
 [2]

Здесь вместо приращения энтропии системы минимизируется приращение энтропии рабочего тела, что не влияет на оптимальное решение.
 [3]

Таким образом, приращение энтропии системы рабочее тело — источники теплоты для обратимого цикла Карно равно нулю.
 [4]

Выделим из As ту часть приращения энтропии системы, которая обусловлена необратимостью процессов теплообмена между рабочим телом и теплоотдатчиком или теплоприемником.
 [5]

Легко показать, что SAs — приращение энтропии системы тел, участвовавших в процессе.
 [6]

Поскольку энтропия — функция состояния, то приращение энтропии системы при переходе ее от одного состояния в другое не зависит от пути, пройденного системой между этими состояниями и определяется лишь начальными и конечными значениями параметров состояния системы.
 [7]

Легко показать, что величина 2As есть именно приращение энтропии системы тел, участвовавших в процессе.
 [8]

Таким образом, разность Sj — sj равна приращению энтропии системы при переходе единицы массы компонента А1 из фазы Ф в фазу Ф, когда температура и давления р и р ( или общее давление р на обе фазы) постоянны.
 [9]

Разность энтропии в точках 7 и 5 представляет собой приращение энтропии системы из-за необратимости процесса теплообмена.
 [10]

Согласно второму закону термодинамики в формулировке ( 1.19.1 — 1) приращение энтропии системы dtS за счет внутренних причин никогда не бывает отрицательным, оно всегда больше нуля при наличии в системе тех или иных процессов и равно нулю при их отсутствии.
 [11]

Уменьшение работоспособности изолированной системы, в которой происходят необратимые процессы, равно произведению приращения энтропии системы на минимальную абсолютную температуру в системе. Все необратимые процессы в изолированной системе сопровождаются обесценением энергии, которая из более полезной формы переходит в менее полезную. Происходит рассеивание энергии и ее деградация. Энтропия системы при этом увеличивается. Таким образом, принцип возрастания энтропии изолированной системы представляет собой общее выражение второго закона термодинамики.
 [12]

Этот прием имеет самое общее значение и может применяться и в тех случаях, когда необходимо вычислить приращение энтропии системы As из-за необратимости какого-либо определенного процесса, входящего в цикл.
 [13]

Потеря работоспособности энергии изолированной системы из-за необратимости любых процессов, происходящих в ней, равна минимальной температуре системы, умноженной на приращение энтропии системы, вызванное необратимостью.
 [14]

Здесь As — прирост энтропии системы рабочее тело окружающая среда, отнесенный к единице массы рабочего тела: величина As равна сумме приращений энтропии системы в процессах теплообмена при подводе и отводе теплоты и производства полезной работы. Обычно прирост энтропии в процессе подвода теплоты не принимают во внимание, рассматривая количество подведенной теплоты 7i и температуру 7 рабочего тела в процессе подвода теплоты как заданные величины, имеющие смысл исходных данных для термодинамического анализа.
 [15]

Страницы:  

   1

   2

Мы уже решали задачи на первый закон термодинамики. Как известно, где первый – там и второй. В сегодняшней статье занимаемся физикой и разбираем примеры задач на второе начало термодинамики.

Хотите ежедневно получать интересную и полезную для студентов рассылку? Присоединяйтесь к нам в телеграме.

Второй закон термодинамики: задачи с решениями

Задача на второй закон термодинамики №1

Условие

Определить изменение энтропии 14 г азота при изобарном нагревании eгo oт 27°C дo 127°C.

Решение

Изменение энтропии вычисляем по формуле:

Для элементарного количества теплоты в изобарном процессе можно записать:

Удельная теплоемкость при постоянном давлении:

Для двухатомного газа число степеней свободы молекулы i=5 (три поступательных и две вращательных).

С учетом сказанного, формулу для энтропии можно переписать так:

Выполним проверку размерности и подставим значения, не забывая переводить Цельсии в Кельвины:

Ответ: 4,18 кДж/К.

Задача на второй закон термодинамики №2

Условие

1 кмоль гелия, изобарически расширяясь, увеличил объем в 4 раза. Найти изменение энтропии при этом расширении.

Решение

Изменение энтропии:

При постоянном давлении (в изобарном процессе) элементарное количество теплоты, полученное газом при температуре Т и молярная теплоемкость, запишутся так:

где ν — число молей газа, i – число степеней свободы молекулы газа (для молекулы инертного газе Не i=3). С учетом этого можно записать выражение для изменения энтропии:

При изобарном процессе справедлив закон Гей-Люссака:

По условию задачи:

Решая уравнения, получаем ответ:

Ответ: 29 Дж/К.

Задача на второй закон термодинамики №3

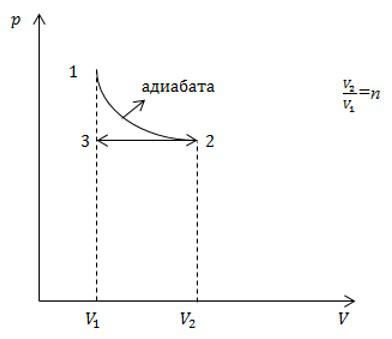
Условие

С идеальным газом определенного числа молей последовательно провели два процесса, указанных на рисунке. Какое приращение энтропии в результате получили? Считать, что число степеней свободы молекулы газа равно i.

Решение

Процесс 1-2 является адиабатным. Энтропия в адиабатном процессе не изменяется, следовательно, изменение энтропии происходит только в процессе 2-3, который является изобарным. Запишем в соответствии со вторым началом термодинамики:

Теперь запишем первое начало термодинамики для изобарного процесса:

Давление в процессе остается постоянным, поэтому:

Подставим это выражение в выражение для энтропии, и с учетом первого начала, запишем:

Для изобарного процесса выполняется закон Гей-Люссака:

С учетом этого, запишем окончательное решение:

Ответ: см. выше.

Задача на второй закон термодинамики №4

Условие

Найдите изменение энтропии двухатомного азота массой 0,560 кг при изотермическом расширении. Известно, что объем увеличился в 5 раз.

Решение

Запишем первое начало термодинамики для изотермического процесса:

Изменение энтропии вычислим следующим образом:

Ответ: 268 Дж/К.

Задача на второй закон термодинамики №5

Условие

Как изменилась энтропия воды массой 0,1 кг при ее охлаждении с Т1=293 К до Т2=273 К?

Решение

Изменение энтропии находим в соответствии со вторым началом термодинамики:

Считая, что изменение происходит при постоянном объеме, для элементарного этапа можно записать:

Ответ: -29,3 Дж/ К.

Вопросы на 2 закон термодинамики

Вопрос 1. Сформулируйте второй закон (второе начало) термодинамики.

Ответ. Второй закон термодинамики устанавливает: 

В изолированных системах самопроизвольно могут протекать только такие процессы, при которых энтропия системы возрастает, и процесс может идти самопроизвольно до такого состояния, при котором энтропия обладает максимальным для данных условий значением.

Второе начало термодинамики имеет несколько формулировок, первая из которых принадлежит Сади Карно. Вот пример второго закона термодинамики в его формулировке: теплота не может самоприозвольно переходить от холодного (менее нагретого) тела к горячему (более нагретому).

Хотите больше объяснений и примеров второго закона термодинамики? Читайте нашу отдельную статью на эту тему.

Вопрос 2. Что такое энтропия?

Ответ. Энтропия – физическая величина, одна из функций состояния термодинамической системы. Приращение энтропии вычисляется по формуле:

Энтропия показывает направление процессов и является мерой неупорядоченности в системе. Например, сахар в стакане лежит в виде кусочка, а потом его размешивают по всему стакану. В первом случае энтропия мала, а во втором – велика.

Вопрос 3. Что такое вечный двигатель второго рода?

Ответ. Вечный двигатель второго рода, или перпетум мобиле второго рода – это такая тепловая машина, которая превращает всю теплоту, полученную от нагревателя, в работу. По сути, это тепловая машина, которая работает без холодильника, а коэффициент ее полезного действия равен единице.

Эмпирически установлено, что создание такой машины невозможно.

Вопрос 4. Сформулируйте постулат второго начала термодинамики.

Ответ. Это постулат, вытекающий из невозможности построения вечного двигателя второго рода:

Невозможен круговой процесс, единственным результатом которого было бы произведение работы за счет охлаждения теплового резервуара.

Данная формулировка принадлежит Томсону.

Вопрос 5. Что такое тепловая смерть Вселенной?

Ответ. Это гипотеза, предложенная Клаузиусом в 1865 году. Главная ее идея состоит в том, что энтропия Вселенной, согласно 2 началу термодинамики, постоянно растет. Это значит, что со временем все макроскопические процессы прекратятся, и Вселенная придет в состояние термодинамического равновесия с температурой абсолютного нуля. Данная гипотеза считается ошибочной, так как Больцман объяснил, что Вселенную нельзя рассматривать как замкнутую систему.

Нужна помощь в решении задач на 2 закон термодинамики и написании студенческих работ? Обращайтесь в проверенный студенческий сервис с любыми заданиями в любое время.

Термодинамические величины
Статья является частью серии «Термодинамика».
Энтропия
Количество теплоты
Термодинамическая работа
Химический потенциал
См. также: Термодинамические потенциалы.
Разделы термодинамики
Начала термодинамики
Уравнение состояния
Термодинамические величины
Термодинамические потенциалы
Термодинамические циклы
Фазовые переходы
править
См. также «Физический портал»

Термодинамическая энтропия S, часто просто именуемая энтропия, — физическая величина, используемая для описания термодинамической системы, одна из основных термодинамических величин. Энтропия является функцией состояния и широко используется в термодинамике, в том числе химической.

Термодинамическое определение энтропии[править | править вики-текст]

Понятие энтропии было впервые введено в 1865 году Рудольфом Клаузиусом. Он определил изменение энтропии термодинамической системы при обратимом процессе как отношение общего количества тепла к величине абсолютной температуры  :

.

Например, при температуре 0 °C, вода может находиться в жидком состоянии и при незначительном внешнем воздействии начинает быстро превращаться в лед, выделяя при этом некоторое количество теплоты. При этом температура вещества так и остается 0 °C. Изменяется состояние вещества, сопровождающееся выделением тепла, вследствие изменения структуры.

Рудольф Клаузиус дал величине имя «энтропия», происходящее от греческого слова τρoπή, «изменение» (изменение, превращение, преобразование). Данное равенство относится к изменению энтропии, не определяя полностью саму энтропию.

Эта формула применима только для изотермического процесса (происходящего при постоянной температуре). Её обобщение на случай произвольного квазистатического процесса выглядит так:

,

где  — приращение (дифференциал) энтропии некоторой системы, а  — бесконечно малое количество теплоты, полученное этой системой.

Необходимо обратить внимание на то, что рассматриваемое термодинамическое определение применимо только к квазистатическим процессам (состоящим из непрерывно следующих друг за другом состояний равновесия).

Поскольку энтропия является функцией состояния, в левой части равенства стоит её полный дифференциал. Напротив, количество теплоты является функцией процесса, в котором эта теплота была передана, поэтому считать полным дифференциалом нельзя.

Энтропия, таким образом, согласно вышеописанному, определена вплоть до произвольной аддитивной постоянной. Третье начало термодинамики позволяет определить её точнее: предел величины энтропии равновесной системы при стремлении температуры к абсолютному нулю полагают равным нулю.

Статистическое определение энтропии: принцип Больцмана[править | править вики-текст]

В 1877 году Людвиг Больцман установил связь энтропии с вероятностью данного состояния. Позднее эту связь представил в виде формулы Макс Планк:

где константа 1,38·10⁻²³ Дж/К названа Планком постоянной Больцмана, а  — статистический вес состояния, является числом возможных микросостояний (способов), с помощью которых можно составить данное макроскопическое состояние. Этот постулат, названный Альбертом Эйнштейном принципом Больцмана, положил начало статистической механике, которая описывает термодинамические системы, используя статистическое поведение составляющих их компонентов. Принцип Больцмана связывает микроскопические свойства системы () с одним из её термодинамических свойств ().

Рассмотрим, например, идеальный газ в сосуде. Микросостояние определено как позиции и импульсы (моменты движения) каждого составляющего систему атома. Связность предъявляет к нам требования рассматривать только те микросостояния, для которых: (I) месторасположения всех частей расположены в рамках сосуда, (II) для получения общей энергии газа кинетические энергии атомов суммируются.

Согласно определению, энтропия является функцией состояния, то есть не зависит от способа достижения этого состояния, а определяется параметрами этого состояния. Так как может быть только натуральным числом (1, 2, 3, …), то энтропия Больцмана должна быть неотрицательной — исходя из свойств логарифма.

Понимание энтропии как меры беспорядка[править | править вики-текст]

Существует мнение, что мы можем смотреть на S и как на меру беспорядка в системе. В определённом смысле это может быть оправдано, потому что мы думаем об «упорядоченных» системах как о системах, имеющих очень малую возможность конфигурирования, а о «беспорядочных» системах как об имеющих очень много возможных состояний. Собственно, это просто переформулированное определение энтропии как числа микросостояний на данное макросостояние.

Рассмотрим, например, распределение молекул идеального газа. В случае идеального газа наиболее вероятным состоянием, соответствующим максимуму энтропии, будет равномерное распределение молекул. При этом реализуется и максимальный «беспорядок», так как при этом будут максимальные возможности конфигурирования.

Границы применимости понимания энтропии как меры беспорядка[править | править вики-текст]

Подобное определение беспорядка термодинамической системы как количества возможностей конфигурирования системы фактически дословно соответствует определению энтропии как числа микросостояний на данное макросостояние. Проблемы начинаются в двух случаях:

• когда начинают смешивать различные понимания беспорядка, и энтропия становится мерой беспорядка вообще;
• когда понятие энтропии применяется для систем, не являющихся термодинамическими.

В обоих этих случаях применение понятия термодинамической энтропии совершенно неправомерно^[1].

Рассмотрим оба пункта подробнее.

Рассмотрим пример термодинамической системы — распределение молекул в поле тяготения. В этом случае наиболее вероятным распределением молекул будет распределение согласно барометрической формуле Больцмана. Другой пример — учёт электромагнитных сил взаимодействия между ионами. В этом случае наиболее вероятным состоянием, соответствующим минимуму свободной энергии, будет упорядоченное кристаллическое состояние, а совсем не «хаос», хотя в состоянии «хаоса» значение конфигурационной энтропии системы и ниже. (Термин «хаос» здесь понимается в смысле беспорядка — в наивном смысле. К хаосу в математическом смысле как сильно неустойчивой нелинейной системе это не имеет отношения, конечно.)

Рассмотрим случай с кристаллической решёткой более подробно. Кристаллическая решётка может быть и в равновесном, и в неравновесном состоянии, как и любая термодинамическая система. Скажем, возьмём следующую модель — совокупность взаимодействующих осцилляторов. Рассмотрим некоторое неравновесное состояние: все осцилляторы имеют одинаковое отклонение от положения равновесия. С течением времени эта система перейдёт в состояние ТД равновесия, в котором отклонения (в каждый момент времени) будут подчинены некоторому распределению типа Максвелла (только это распределение будет для отклонений, и оно будет зависеть от типа взаимодействия осцилляторов). В таком случае максимум энтропии будет действительно реализовывать максимум возможностей конфигурирования, то есть — беспорядок согласно вышеуказанному определению. Но данный «беспорядок» вовсе не соответствует «беспорядку» в каком-либо другом понимании, например, информационному. Такая же ситуация возникает и в примере с кристаллизацией переохлаждённой жидкости, в которой образование структур из «хаотичной» жидкости идёт параллельно с увеличением энтропии.

То есть при образовании кристалла из переохлажденной жидкости энтропия увеличивается с одновременным ростом температуры. Если кристаллизация сопровождается отводом тепла из системы, то энтропия при этом уменьшится.

Это неверное понимание энтропии появилось во время развития теории информации, в связи с парадоксом термодинамики, связанным с мысленным экспериментом т. н. «демона Максвелла». Суть парадокса заключалась в том, что рассматривалось два сосуда с разными температурами, соединённых узкой трубкой с затворками, которыми управлял т. н. «демон». «Демон» мог измерять скорость отдельных летящих молекул, и таким образом избирательно пропускать более быстрые в сосуд с высокой температурой, а более медленные — в сосуд с низкой. Из этого мысленного эксперимента вытекало кажущееся противоречие со вторым началом термодинамики.

Парадокс может быть разрешён при помощи теории информации. Для измерения скорости молекулы «демон» должен был бы получить информацию о её скорости. Но всякое получение информации — материальный процесс, сопровождающийся возрастанием энтропии. Количественный анализ^[2] показал, что приращение энтропии при измерении превосходит по абсолютной величине уменьшение энтропии, вызванное перераспределением молекул «демоном».

Энтропия в открытых системах[править | править вики-текст]

В силу второго начала термодинамики, энтропия замкнутой системы не может уменьшаться» (закон неубывания энтропии). Математически это можно записать так: , индекс обозначает так называемую внутреннюю энтропию, соответствующую замкнутой системе. В открытой системе возможны потоки тепла как из системы, так и внутрь неё. В случае наличия потока тепла в систему приходит количество тепла при температуре и уходит количество тепла при температуре . Приращение энтропии, связанное с данными тепловыми потоками, равно:

В стационарных системах обычно , , так что . Поскольку здесь изменение энтропии отрицательно, то часто употребляют выражение «приток негэнтропии», вместо оттока энтропии из системы. Негэнтропия определяется таким образом как «отрицательная энтропия».

Суммарное изменение энтропии открытой системы будет равно:

Если всё время , то рост внутренней энтропии не компенсируется притоком внешней негэнтропии, система движется к ближайшему состоянию равновесия. Если , то мы имеем стационарный процесс с неизменной общей энтропией. В этом случае в системе осуществляется некоторая внутренняя работа с генерацией внутренней энтропии, которая преобразует, например, температуру внешнего потока тепла в температуру уходящего из системы потока тепла.

Измерение энтропии[править | править вики-текст]

В реальных экспериментах очень трудно измерить энтропию системы. Техники измерения базируются на термодинамическом определении энтропии и требуют экстремально аккуратной калориметрии.

Для упрощения мы будем исследовать механическую систему, термодинамические состояния которой будут определены через её объем V и давление P. Для измерения энтропии определенного состояния мы должны сперва измерить теплоёмкость при постоянных объёме и давлении (обозначенную C_V и C_P соответственно), для успешного набора состояний между первоначальным состоянием и требуемым. Тепловые ёмкости связаны с энтропией S и с температурой T согласно формуле:

где нижний индекс X относится к постоянным объёму и давлению. Мы можем проинтегрировать для получения изменения энтропии:

Таким образом, мы можем получить значение энтропии любого состояния (P,V) по отношению к первоначальному состоянию (P₀,V₀). Точная формула зависит от нашего выбора промежуточных состояний. Для примера, если первоначальное состояние имеет такое же давление, как и конечное состояние, то

В добавление, если путь между первым и последним состояниями лежит сквозь любой фазовый переход первого рода, скрытая теплота, ассоциированная с переходом, должна также учитываться.

Энтропия первоначального состояния должна быть определена независимо. В идеальном варианте выбирается первоначальное состояние как состояние при экстремально высокой температуре, при которой система существует в виде газа. Энтропия в этом состоянии подобна энтропии классического идеального газа плюс взнос от молекулярных вращений и колебаний, которые могут быть определены спектроскопически.

Построение графика изменения энтропии[править | править вики-текст]

Следующее уравнение может быть использовано для построения графика изменения энтропии на диаграмме P—V для идеального газа:

Здесь два замечания:

См. также[править | править вики-текст]

• Термодинамика чёрных дыр
• Тепловая смерть
• Демон Максвелла
• Термодинамические потенциалы
• Стрела времени
• Информационная энтропия
• Негэнтропия

Примечания[править | править вики-текст]

Литература[править | править вики-текст]

• Осипов А.И., Уваров А.В. Энтропия и ее роль в науке // Сетевой образовательный журнал. — 2004. — Т. 8. — № 1. — С. 70-79.
• Fermi, E., Thermodynamics, Prentice Hall (1937). — Русский перевод: Ферми, Энрико, Термодинамика, Харьков: Изд-во Харьковского ун-та, 1969. — 140 с.
• Reif, F., Fundamentals of statistical and thermal physics, McGraw-Hill (1965)
• Wehrl Alfred General properties of entropy (англ.) // Reviews of Modern Physics. — American Physical Society, 1978. — Vol. 50. — № 2. — P. 221–260. — DOI:http://dx.doi.org/10.1103/RevModPhys.50.221
• Шамбадаль П. Развитие и приложение понятия энтропии. — М.: Наука, 1967. — 280 с.
• Волькенштейн М. В. Энтропия и информация. — М.: Наука, 1986. — 192 с.

Ссылки[править | править вики-текст]

• Термодинамическая энтропия
• Статья «Эволюция как сопротивление энтропии»
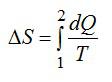
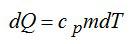
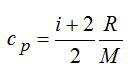
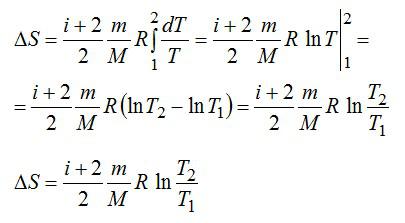
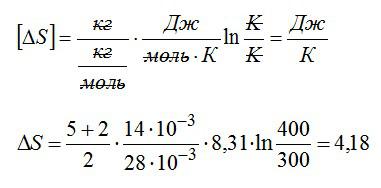
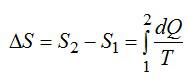
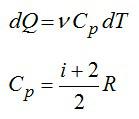
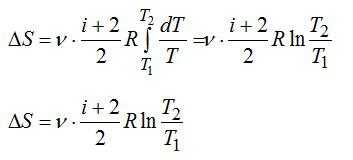
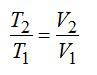
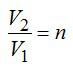
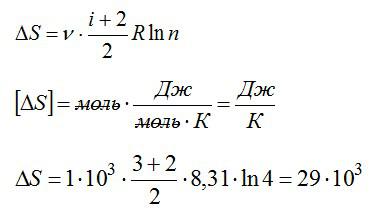
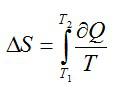
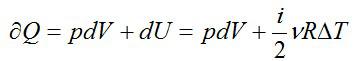
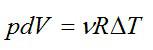
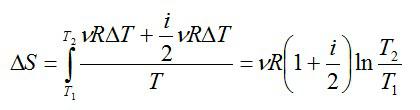
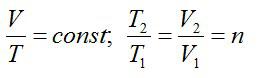
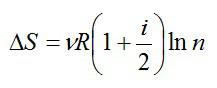
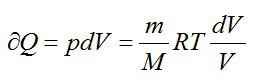
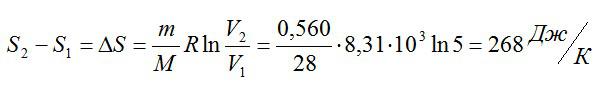
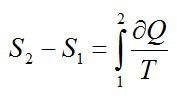
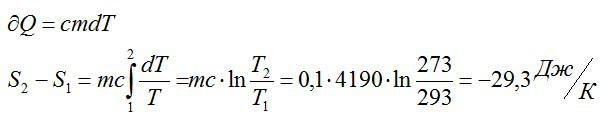
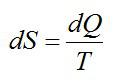