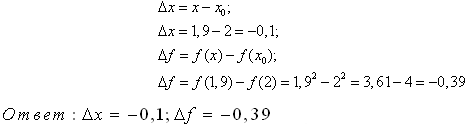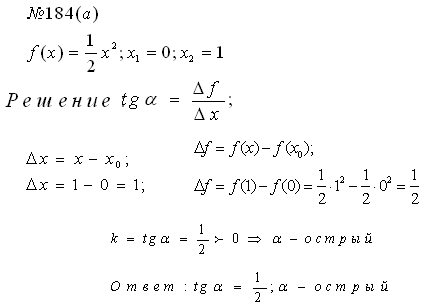Дата публикации: 09 апреля 2017.
Алгебра – 10 класс. Приращение аргумента, приращение функции
Урок на тему: «Приращение аргумента, приращение функции»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Скачать:
Приращение аргумента, приращение функции (PDF)
Что будем изучать:
1.Определение приращения аргумента, приращения функции.
2. Непрерывная функция и приращение.
3. Примеры.
Определение приращения аргумента и приращения функции
Ребята, мы с вами научились находить пределы функции в точке. Важным остается вопрос, как изменяется значение функции при изменении значения аргумента около этой точки?
Математики ввели такое понятие – приращение аргумента и функции. Давайте запишем определение.
Определение: Пусть функция $y=f(x)$ определена в точках $x_0$ и $x_1$. Разность $x_1-x_0$ называют приращением аргумента, а разность $f(x_1)-f(x_0)$–приращением функции.
Иначе говоря, узнаем прирост точки $x_0$ в точке $x_1$. Приращение аргумента обозначают как $Δx$, читается как дельта x.
Приращение функции обозначают, как $Δy$ или $Δf(x)$.
Из нашего определения следует: $x_1-x_0=Δx$ => $x_1= Δx+x_0$ и $f(x_1)-f(x_0)=Δy$. Тогда получаем важное равенство: $Δy=f(x_0+ Δx)-f(x_0)$.
Приращение функции может быть как положительным, так и отрицательным.
Давайте рассмотрим пример.
Найти приращение функции $y=х^3$ при переходе от $x_0=2$ к точке:
а) $x=2,1$; б) $x=1,9$.
Решение:
Обозначим $f(x)=х^3$.
Имеем: $f(2)=2^3=8$.
а) Воспользуемся формулой $Δy=f(x_0+ Δx)-f(x_0)$.
Нам надо найти значение $f(2,1)$.
$f(2,1)=2,1^3=9,261$.
$Δy= f(2,1)- f(2)= 9,261-8=1,261$.
б) $f(2)=8$.
$f(1,9)=1,9^3=6,859$.
$Δy= f(1,9)- f(2)= 6,859-8=-1,141$.
Ответ: а) $1,261$; б) $-1,141$.
Непрерывная функция и приращение
Ребята, давайте вернемся к определению непрерывной функции, и посмотрим на него с помощью приращений.
Вспомним определение непрерывной функции.
Определение. Функцию $y=f(x)$ называют непрерывной в точке $x=a$, если выполняется тождество:
[lim_{x rightarrow a}f(x)=f(a)]
Обратим внимание: $x →a$, тогда $(x-a) →0$ т.е. $Δx → 0$.
Также заметим: $f(x) → f(a)$ , значит $f(x) — f (a) → 0$ т.е. $Δy → 0$.
Определение непрерывности функции в точке можно записать так.
Функция $y=f(x)$ непрерывна в точке $x=a$, если в этой точке выполняется следующее условие:
если $Δx→0$, то $Δy → 0$.
Примеры
1. Для функции $y=kx+b$ найти:
а) приращение функции при переходе от фиксированной точки $x$ к $x+ Δx$;
б)предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю.
Решение:
а) $f(x)= kx+b$.
$f(x+ Δx)=k(x+Δx)+b$;
$Δy= f(x+ Δx)-f(x)= k(x+Δx)+b-( kx+b)= kx+kΔx+b – kx-b= kΔx$.
б) Найдем требуемый предел: $lim_{Δx rightarrow 0}frac{Δy}{Δx}=lim_{Δx rightarrow 0}frac{kΔx}{Δx}=lim_{Δx rightarrow 0}k=k$.
2. Для функции $y=x^3$ найти:
а) приращение функции при переходе от фиксированной точки $x$ к $x+ Δx$.
б)предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю.
Решение:
а) $f(x)= x^3$.
$f(x+ Δx)=(x+Δx)^3=x^3+3x^2Δx+3xΔx^2+Δx^3$.
$Δy= f(x+Δx)-f(x)= x^3+3x^2Δx+3xΔx^2+Δx^3-x^3=3x^2Δx+3xΔx^2+Δx^3$.
б) Найдем требуемый предел: $lim_{Δx rightarrow 0}frac{Δy}{Δx}=lim_{Δx rightarrow 0}frac{3x^2Δx+3xΔx^2+Δx^3}{Δx}=lim_{Δx rightarrow 0}(3x^2+3xΔx+Δx^2)=3x^2$.
Задачи для самостоятельного решения:
1) Найти приращение функции $y=x^4$ при переходе от $x_0=3$ к точке:
а) $x=3,2$;
б) $x=2,8$.
2) Для функции $y=3x+5$ найти приращение функции при переходе от фиксированной точки $x$ к $x+ Δx$.
3) Для функции $y=x^2$ найти приращение функции при переходе от фиксированной точки $x$ к $x+ Δx$.
4) Для функции $y=2x^3$ найти приращение функции при переходе от фиксированной точки $x$ к $x+ Δx$.
МБОУ «СОШ № 90» г.Саратова
Учитель:
Манахова Е.А.
Предмет: математика
Класс: 10
Тип урока:
урок получения нового
знания.
Тема: «
Приращение аргумента, приращение функции».
Цели:
образовательные:
сформировать понятия приращения функции и приращения аргумента, секущей,
геометрического смысла приращения функции; показать применение данных понятий
при решении задач.
развивающие:
развитие вычислительных навыков, умений логически и аргументированно
рассуждать, обобщать и абстрагировать.
воспитательные:
воспитание познавательного интереса к предмету.
.
Оборудование:
учебник; компьютер, проектор и экран.
Ход урока
1.Организационный момент
1)
Взаимное приветствие преподавателя и обучающихся, проверка готовности
обучающихся к уроку.
Обсуждение
темы и целей урока. (Слайд 1 и 2.)
2.Подготовка к восприятию нового материала
(устная работа с целью актуализации знаний):
Как
найти значение функции в данной точке?
Пример: (Слайд 3)
Найти
значение функции f(x) = x2 + 2x в точке x0 = -3.
Решение:
f(x0) = f(-3) = (-3)2+ 2∙(-3) = 9 — 6 = 3
Ответ:
f(-3) = 3
3)
Итак, мы поработали устно и вспомнили некоторые теоретические сведения, которые
нам будут нужны при изучении нового материала. А теперь мы выясним, что же
такое приращение аргумента и приращение функции.
2. Изучение
нового материала:

ее изменение. Например: как быстро изменяется температура, как быстро
дорожают цены на билеты и так далее…
Давайте рассмотрим с Вами
основные понятия которые относятся к приращению функции.
(работа с раздаточным материалом)
Например:
Дан график функции у = 4 -х2 (Слайд 4)
По
графику найти значение функции в точке х1= 1 и
х2
= 2.
Разность
х2 – х1 = 2 — 1 = 1; ∆x =1
f
(1) = 3; f(2) = 0; f(2) – f(1) = 0 — 3 = -3
∆f
= -3
2).
В приведенном примере мы не только вычислили значения функции f(x) в некоторых
точках, но и оценили изменения ∆f этой функции при заданных изменениях
аргумента ∆х.
При
сравнении значений функции f в некоторой фиксированной точке х0 со
значениями этой функции в различных точках х, лежащих в окрестности х0,
удобно выражать разность f(x) — f(x0) через разность х-х0,
пользуясь понятиями “приращение функции” и “приращение аргумента”.
Рассмотрим
функцию у = f(x). Пусть х – произвольная точка, лежащая в некоторой окрестности
фиксированной точки х0. Разность х — х0 называется
приращением независимой переменной (или приращением аргумента) в точке х0
и обозначается ∆х. Таким образом, ∆х= х -х0, откуда следует,
что х = х0+∆х. (Слайд 5)
Говорят
также, что первоначальное значение аргумента х0 получило приращение ∆х.
Вследствие этого значение функции f изменится на величину f(x) — f(x0)
= f(х0 +х)– f(x0).
Эта
разность называется приращением функции f в точке х0, соответствующим
приращению ∆х, и обозначается ∆f, т. е. по определению
∆f
= f (х0+∆х) – f(x0), откуда f (х0 +∆х) = f(x0)
+∆f.
Обратите
внимание: при фиксированном значении х0 приращение ∆f есть функция
от ∆х.
2)
Что такое приращение аргумента?
Что такое
приращение функции? (Слайд6)
•
Определение.
Приращением аргумента функции называется величина, равная разности
между конечным и начальным значением аргумента: ∆ x =x-х0
•
Определение.
Приращением
функции называется величина, равная разности между конечным и начальным
значением функции ∆f =f(x) — f(x0) = f(х0 + х)–
f(x0).
Пример
1. Найти приращение функции y=x3
при переходе от х0=1,2 к точке х=2,5 (Слайд
7)
Решение:
∆ x=2,5-1,2=1,3,
∆f=2,52-1,22=6,25-1,44=
4,81
Ответ:
1,3; 4,81
Пример
2. Найти приращение аргумента и приращение функции в точке х0, если f(x)=
x2,
если х0= 2, х=1,9. (Слайд 
Решение:
∆ x=1,9-2=-0,1,
∆f=1,92-22=3,61-4=
-0,39
Ответ:
-0,1; -0,39
Вывод:
Приращение функции может быть как положительным так и отрицательным.
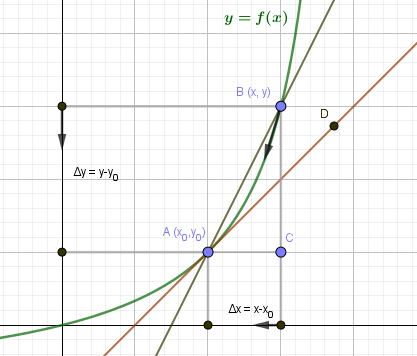
Теперь выясним геометрический смысл приращения аргумента, приращения
функции.
(Слайд 9.)
Рассмотрим
график функции у = f (x). Геометрический смысл приращения функции можно понять,
рассмотрев рисунок. Прямую l, проходящую через любые две точки графика
функции f, называют секущей к графику f. Уравнение прямой на плоскости
имеет вид у = кх + b. Угловой
коэффициент k секущей, проходящей через точки (х0; f(x0)
и (х; f(x)), равен tga. ∆ABC – прямоугольный.
или
k
= tgα =
Пример
3. Найти угловой коэффициент секущей к графику функции f(x)
= , проходящей через точки
с данными абсциссами х1 и х2. Какой угол (острый или
тупой) образует секущая с осью Ох, если f(x)
= x2;
x1
= 0; x2
= 1 (Слайд 10)
Решение:
tgα
=
Δx
= x – x0; Δf = f(x) — f(x0);
Δx = 1 – 0 = 1; Δf = f(1) — f(0) = · 12
— · 02
=
k = tgα = > 0, значит
α
– острый
Ответ:
tgα
= ; α
— острый
5)
Итак, мы выяснили что такое приращение аргумента и приращение функции и в чём
состоит их геометрический смысл. Теперь мы научимся применять данные
определения при решении задач.
3.Закрепление изученного материала
1.
Решение задач у доски преподавателем.
а)
Найдите приращение функции f
в точке х0, если
f(x)
= 3x+1
x0
= 5 ∆x
= 0, 01.
Решение:
х=х0+∆x, х= 5+0,01=5,01
f(х0)=f(5)=3·5+1=16;
f
(x)=f(5,01)=
3·5,01+1=16,03
Δf
= f(x)
— f(x0);
Δf
= 16,03-16=0,03 Ответ: 0,03 (Слайд 11)
б)
Найти приращение функции y=f(x)
при переходе от точки х к точке х+ ∆x,
если f(x)=
х2.
Решение:
Δf
= f(x)
— f(x0)=f(х+
∆x)-f(x)=
(х+ ∆x)2—x2=x2+2x∆x+∆x2—x2=2x∆x+∆x2
Ответ:
2x∆x+∆x2
(Слайд 12)
5. Проверка усвоения материала.
Самостоятельная работа
(Слайд 13)
1
вариант № 26.20(а), 26.22 (а), 26.24 (а)
2
вариант №26.20(б), 26.22(б), 26.24(б)
(1 вар- №26.20 0,4 №26.22 0,2; №26.24 3 ∆x
2 вар- №26.20 2,8
№26.22 —
0,1; №26.24 -2х
∆x—
(∆x)2 )
6. Подведение итогов урока.
Домашнее
задание: П.26, №26.20-26.21(вг), 26.22(вг),
26.24 (вг)
Вопросы
занятия:
·
познакомиться
с понятием непрерывной функции;
·
познакомиться
с понятием предел функции в точке;
·
рассмотреть
примеры использования данных понятий для решения задач.
Материал
урока.
Прежде
чем приступить к изучению нового материала, давайте выполним упражнение.
Упражнение.
Не всегда нам надо знать точные значения
тех или иных параметров. Иногда нам достаточно знать, как они изменяются.
Например, если мы в течение одного дня выйдем на улицу, то нам не важно, на
сколько именно изменилась температура воздуха, а нам важно похолодало или
потеплело. Или при движении автомобиля нам, не важно, знать точную скорость, а
важно определить разгоняется автомобиль или тормозит.
Причём, если на улице потеплело, то
изменения будут со знаком плюс и наоборот если похолодало, то изменения будут
со знаком минус.
Если автомобиль разгоняется, то изменения
будут со знаком плюс, если тормозит – то со знаком минус.
Для описания таких изменений было введено
понятие приращение.
Определение.
Пусть функция y = f(x) определена в
точках x0
и x1.
Разность x1 –
x0
называют приращением аргумента, а разность f(x1) –
f(x0)
называют приращением функции.
Приращение аргумента обозначают так:
Приращение функции обозначают
так:
Давайте рассмотрим, что же такое
приращение аргумента и функции на графике.
Рассмотрим пример.
Пример.
Рассмотрим ещё один пример.
Пример.
Давайте вспомним определение непрерывной
функции, которое мы формулировали ранее.
Определение непрерывности функции в точке x
= a выглядит так:
Определение непрерывности функции в точке
можно записать так:
Когда мы вводили определение непрерывной
функции, то мы говорили, что функция непрерывна на промежутке X, если
она непрерывна в каждой точке промежутка. Давайте уточним, что означает
непрерывность функции в концевых точках промежутка, например, как понимать
непрерывность функции в точках a
и b отрезка [a;
b].
Рассмотрим пример.
Пример.
Давайте изобразим график линейной функции.
Отметим приращение аргумента и функции. И найдём чему равно отношение
приращения аргумента к приращению функции.
Рассмотрим пример.
Пример.
- Приращение аргумента и приращение функции
- Определение производной
- Физический смысл производной
- Геометрический смысл производной
- Алгоритм поиска значения производной в заданной точке
- Алгоритм поиска уравнения производной
- Примеры
п.1. Приращение аргумента и приращение функции
Приращением аргумента называют разность $$ triangle x=x-x_0 $$ где (x) — произвольное число, которое мало отличается от начальной точки (x_0). Приращение аргумента может быть как положительным, так и отрицательным.
Приращением функции называют соответствующую разность $$ triangle y=f(x)-f(x_0 )=f(x_0+triangle x)-f(x_0) $$ Приращение функции может быть как положительным, так и отрицательным.
Например:
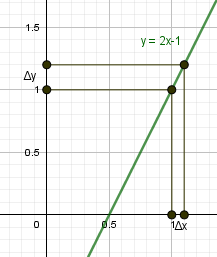 |
begin{gather*} y=2x-1\ x_0=1, x=1,1 end{gather*} Найдем приращение аргумента и функции. begin{gather*} triangle x= x-x_0=1,1-1=0,1gt 0\ \ f(x)=f(1,1)=2cdot 1,1-1=1,2\ f(x_0 )=f(1)=2cdot 1-1=1\ triangle y=f(x)-f(x_0 )=1,2-1=0,2gt 0 end{gather*} |
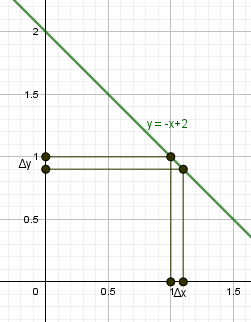 |
begin{gather*} y=-x+2\ x_0=1, x=1,1 end{gather*} Найдем приращение аргумента и функции. begin{gather*} triangle x= x-x_0=1,1-1=0,1gt 0\ \ f(x)=f(1,1)=-1,1+2=0,9\ f(x_0 )=f(1)=-1+2=1\ triangle y=f(x)-f(x_0)=0,9-1=-0,1lt 0 end{gather*} |
Если функция возрастает, приращение аргумента и приращение функции имеют один и тот же знак: $$ begin{cases} y=f(x) — text{возрастает}\ triangle xgt 0 end{cases} Rightarrow triangle ygt 0 $$ Если функция убывает, приращение аргумента и приращение функции имеют разные знаки: $$ begin{cases} y=f(x) — text{убывает}\ triangle xgt 0 end{cases} Rightarrow triangle ylt 0 $$
п.2. Определение производной
Производной функции (f(x)) в точке (x_0) называют предел отношения приращения функции в точке (x_0) к приращению аргумента, если приращение аргумента стремится к нулю, а предел существует: $$ f'(x_0)=lim_{triangle xrightarrow 0}frac{triangle y}{triangle x} $$
Например:
Найдем производную функции (f(x)=x^2-4) в точке (x_0=3)
Значение функции в точке: (f(x_0 )=3^2-4=5)
Пусть (triangle x) — некоторое приращение аргумента. Тогда: begin{gather*} f(x)=f(x_0+triangle x)=(x_0+triangle x)^2-4=(3+triangle x)^2-4=9+6triangle x+triangle x^2-4=\ =5+6triangle x+triangle x^2 end{gather*} Приращение функции: $$ triangle y=f(x)-f(x_0)=5+6triangle x+triangle x^2-5=6triangle x+triangle x^2=triangle x(6+triangle x) $$ Производная: $$ f'(x_0)=lim_{triangle xrightarrow 0}frac{triangle x}{triangle y}=lim_{triangle xrightarrow 0}frac{triangle x(6+triangle x)}{triangle x}=lim_{triangle xrightarrow 0}(6+triangle x)=6+0=6 $$ Ответ: 6
п.3. Физический смысл производной
Рассмотрим прямолинейное движение.
Пусть расстояние по прямой между городами (triangle x=) 300 км поезд преодолевает за (triangle t=)4 часа. Мы легко можем найти его среднюю скорость: $$ v_{cp}=frac{triangle x}{triangle t}, v_{cp}=frac{300}{4}=75 (text{км/ч}) $$ Но поезд не едет все время с одной и той же скоростью: где-то ускоряется, где-то замедляется, где-то и вовсе останавливается.
Если мы захотим определить скорость как можно точнее, нам понадобится уменьшать интервалы времени и измерять соответствующий путь. Уменьшив время до «мгновений», мы получим «мгновенную скорость» для каждой точки траектории в каждый момент времени.
Мгновенная скорость это скорость тела в данный момент времени (t_0): $$ v(t_0)=lim_{triangle trightarrow 0}frac{triangle x}{triangle t}=x'(t_0) $$ где (triangle x=x-x_0) — путь тела за время (triangle t=t-t_0, x(t)) – уравнение движения.
Мгновенная скорость равна первой производной от уравнения движения при (t=t_0).
Сравнивая определения мгновенной скорости и производной функции, мы можем сформулировать физический смысл производной:
Производная функции (y=f(x)) в точке (x_0) равна скорости изменения функции в этой точке.
Или, ближе к физике/химии/биологии:
Производная уравнения процесса (s=f(t)) в момент времени (t_0) равна скорости протекания процесса в этот момент.
п.4. Геометрический смысл производной
Пусть на плоскости задана кривая (y=f(x)).
Выберем на кривой две точки (A(x_0,y_0)) и (B(x,y)). Прямая AB будет секущей для кривой (y=f(x)). Угол наклона прямой AB определяется угловым коэффициентом: $$ k_{AB}=tgangle A=frac{BC}{AC}=frac{triangle y}{triangle x} $$ Начнем движение точки B вдоль кривой по направлению к точке A. Приращение аргумента при этом будет уменьшаться: (triangle x=ACrightarrow 0). В тот момент, когда B совпадет с A, секущая AB превратится в касательную AD. Угловой коэффициент касательной: $$ k_{AD}=lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=y'(x_0) $$
Мы можем сформулировать геометрический смысл производной:
Производная функции (y=f(x)) в точке (x_0) равна угловому коэффициенту касательной к графику этой функции в этой точке.
п.5. Алгоритм поиска значения производной в заданной точке
На входе: уравнение функции (y=f(x)), точка (x_0)
Шаг 1. Найти значение функции в заданной точке (y_0=f(x_0)).
Шаг 2. Задать приращение аргумента (triangle x=x-x_0), найти приращение функции (triangle y=f(x)-f(x_0)=f(x_0+triangle x)-f(x_0)).
Шаг 3. Найти предел (lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=f'(x_0))
На выходе: значение производной в точке (x_0)
Например:
Найдем значение производной в точке (x_0=1) для функции (y=x^2-3).
Значение функции в заданной точке: (f(x_0)=1^2-3=-2)
Пусть (∆x) — некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x_0+triangle x)-f(x_0)=((1+triangle x)^2-3)-(-2)=\ =1+2triangle x+(triangle x)^2-1=2triangle x+(triangle x)^2=triangle x(2+triangle x) end{gather*} Ищем предел: begin{gather*} lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{triangle x(2+triangle x)}{triangle x}=lim_{triangle xrightarrow 0}(2+triangle x)=2+0=2 end{gather*} Искомая производная в заданной точке: (f'(1)=2)
Ответ: 2
п.6. Алгоритм поиска уравнения производной
На входе: уравнение функции (y=f(x))
Шаг 1. Задать приращение аргумента (triangle x), найти выражение для приращения функции (triangle y=f(x+triangle x)-f(x)).
Шаг 2. Найти предел выражения (lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=f'(x))
На выходе: уравнение производной (y ‘=f'(x)) в любой точке (x).
Например:
Найдем общее уравнение производной для функции (y=x^2-3).
Пусть (∆x) — некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x+triangle x)-f(x)=((x+triangle x)^2-3)-(x^2-3)=\ =(x+triangle x)^2-x^2=(x+triangle x-x)(x+triangle x+x)=triangle x(2x+triangle x) end{gather*} Ищем предел: begin{gather*} lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{triangle x(2x+triangle x)}{triangle x}=lim_{triangle xrightarrow 0}(2x+triangle x)=2x+0=2x end{gather*} Ответ: уравнение производной (y ‘=2x)
п.7. Примеры
Пример 1. Пользуясь алгоритмом поиска значения производной в заданной точке, найдите:
a) ( f'(1), text{если} f(x)=2x )
По условию (x_0=1)
Значение функции в заданной точке: (f(x_0 )=2cdot 1=2)
Пусть (triangle x) — некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x_0+triangle x)-f(x_0)=2(1+triangle x)-2=2+2triangle x-2=2triangle x end{gather*} Ищем предел: begin{gather*} lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{2triangle x}{triangle x}=2 end{gather*} Искомая производная в заданной точке: (f'(1)=2)
б) ( f'(3), text{если} f(x)=3x^2 )
По условию (x_0=3)
Значение функции в заданной точке: (f(x_0 )=3cdot 3^2=27)
Пусть (triangle x) — некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x_0+triangle x)-f(x_0)=3(3+triangle x)^2-27=3(9+6triangle x+(triangle x)^2)-27=\ =27+18triangle x+3(triangle x)^2-27=3triangle x(6+triangle x) end{gather*} Ищем предел: begin{gather*} lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{3triangle x(6+triangle x)}{triangle x}=3lim_{triangle xrightarrow 0}(6+triangle x)=3(6+0)=18 end{gather*} Искомая производная в заданной точке: (f'(3)=18)
в) ( f'(-1), text{если} f(x)=4x-1 )
По условию (x_0=-1)
Значение функции в заданной точке: (f(x_0)=4cdot (-1)-1=-5)
Пусть (triangle x) — некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x_0+triangle x)-f(x_0)=(4(-1+triangle x)-1)-(-5)=-5+4triangle x+5=4triangle x end{gather*} Ищем предел: begin{gather*} lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{4triangle x}{triangle x}=4 end{gather*} Искомая производная в заданной точке: (f'(-1)=4)
г) ( f'(2), text{если} f(x)=x^3 )
По условию (x_0=2)
Значение функции в заданной точке: (f(x_0)=2^3=8)
Пусть (triangle x) — некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x_0+triangle x)-f(x_0)=(2+triangle x)^3-8=\ =2^3+3cdot 2^2cdot triangle x+3cdot 2cdot (triangle x)^2+(triangle x)^3-8=\ =12triangle x+6(triangle x)^2+(triangle x)^3=triangle xcdot (12+6triangle x+(triangle x)^2 ) end{gather*} Ищем предел: begin{gather*} lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{triangle xcdot(12+6triangle x+(triangle x)^2)}{triangle x}=lim_{triangle xrightarrow 0}(12+6triangle x+(triangle x)^2)=12+0+0=12 end{gather*} Искомая производная в заданной точке: (f'(2)=12)
Ответ: а) 2; б) 18; в) 4; г) 12
Пример 2. Пользуясь алгоритмом поиска уравнения производной, найдите общее уравнение производной для функции (y=f(x)):
a) ( f(x)=C), где C – постоянная величина
Пусть (triangle x) — некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x+triangle x)-f(x)=C-C=0 end{gather*} Отношение (frac{triangle y}{triangle x}=frac{0}{triangle x}=0)
Предел (lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}0=0)
Производная (y ‘=C’=0)
Производная постоянной равна нулю: (C ‘=0)
б) ( f(x)=x)
Пусть (triangle x) — некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x+triangle x)-f(x)=x+triangle x-x=triangle x end{gather*} Ищем предел: (lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{triangle x}{triangle x}=lim_{triangle xrightarrow 0}1=1)
Производная (x ‘=1)
Производная аргумента равна единице: (x ‘=1)
в) ( f(x)=x^2)
Пусть (triangle x) — некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x+triangle x)-f(x)=(x+triangle x)^2-x^2=(x+triangle x-x)(x+triangle x+x)=triangle x(2x+triangle x) end{gather*} Ищем предел: begin{gather*} lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{triangle x(2x+triangle x)}{triangle x}=lim_{triangle xrightarrow 0}(2x+triangle x)=2x+0=2x end{gather*} Производная ((x^2) ‘=2x)
г) ( f(x)=x^3)
Пусть (triangle x) — некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x+triangle x)-f(x)=(x+triangle x)^3-x^3=\ =(x+triangle x-x)((x+triangle x)^2+x(x+triangle x)+x^2)=triangle x((x+triangle x)^2+x(x+triangle x)+x^2) end{gather*} Ищем предел: begin{gather*} lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{triangle x((x+triangle x)^2+x(x+triangle x)+x^2)}{triangle x}=\ =lim_{triangle xrightarrow 0}((x+triangle x)^2+x(x+triangle x)+x^2)=(x+0)^2+x(x+0)+x^2=3x^2 end{gather*} Производная ((x^3) ‘=3x^2)
д) ( f(x)=frac1x)
Пусть (triangle x) — некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x+triangle x)-f(x)=frac{1}{x+triangle x}-frac1x=frac{x-(x+triangle x)}{x(x+triangle x)}=-frac{triangle x}{x(x+triangle x)} end{gather*} Ищем предел: begin{gather*} lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}left(-frac{triangle x}{triangle xcdot x(x+triangle x)}right)=-lim_{triangle xrightarrow 0}frac{1}{x(x+triangle x)}=-frac{1}{x(x+0)}=-frac{1}{x^2} end{gather*} Производная (left(frac1xright) ‘=-frac{1}{x^2})
e) ( f(x)=kx+b)
Пусть (triangle x) — некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x+triangle x)-f(x)=k(x+triangle x)+b-kx-b=ktriangle x end{gather*} Ищем предел: begin{gather*} lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{ktriangle x}{triangle x}=lim_{triangle xrightarrow 0}k=k end{gather*} Производная ((kx+b) ‘=k)
ж) ( f(x)=sqrt{x})
Пусть (triangle x) — некоторое приращение аргумента. Тогда приращение функции: begin{gather*} triangle y=f(x+triangle x)-f(x)=sqrt{x+triangle x}-sqrt{x} end{gather*} Ищем предел, умножив числитель и знаменатель на сопряженное выражение: begin{gather*} lim_{triangle xrightarrow 0}frac{triangle y}{triangle x}=lim_{triangle xrightarrow 0}frac{sqrt{x+triangle x}-sqrt{x}}{triangle x}= lim_{triangle xrightarrow 0}frac{(sqrt{x+triangle x}-sqrt{x})(sqrt{x+triangle x}+sqrt{x})}{triangle x(sqrt{x+triangle x}+sqrt{x})}=\ =lim_{triangle xrightarrow 0}frac{x+triangle x-x}{triangle x(sqrt{x+triangle x}+sqrt{x})}=lim_{triangle xrightarrow 0}frac{1}{(sqrt{x+triangle x}+sqrt{x})}=frac{1}{sqrt{x+0}+sqrt{x}}=frac{1}{2sqrt{x}} end{gather*} Производная ((sqrt{x}) ‘=frac{1}{2sqrt{x}})
Цели урока:
- Формирование понятий приращения функции и приращения аргумента, секущей,
геометрического смысла приращения функции; - Развитие вычислительных навыков;
- Воспитание познавательного интереса к предмету. (Презентация.
Слайд 2.)
Тип урока: формирование новых понятий.
Метод обучения: обучающая беседа.
Оборудование: учебник А.Н. Колмогорова “Алгебра и начала анализа”
10-11 кл.; мультимедийный проектор и экран.
Ход урока
I. Организационный момент:
Взаимное приветствие учителя и учащихся, проверка готовности учащихся к
уроку.
II. Анализ контрольной работы по теме:
“Решение тригонометрических уравнений и неравенств”/
Сообщение темы и целей урока. (Слайд 1 и 2.)
III. Актуализация знаний:
- Формула периметра прямоугольника;
- Формула площади прямоугольника;
- Определение функции, определение тангенса угла;
- Как найти значение функции в данной точке?
Пример: Найти значение функции f(x) =
x2 + 2x в
точке x0 = -3.
Решение: f(x0) =
f(-3) = (-3)2
+ 2∙(-3) =
9 — 6
= 3
Ответ: f(-3) = 3
IV. Изучение нового материала:
Часто нас интересует не значение какой-либо величины, а ее изменение.
Например: Дан график функции у =
4 -х2
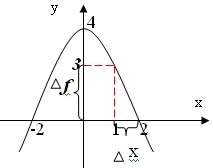 |
По графику найти значение функции в точке х1 = 1 и х2 = 2. Разность х2 – х1 = f (1) = 3; f(2)
|
В приведенном примере мы не только
вычислили значения функции f(x) в некоторых точках, но и оценили изменения
f этой
функции при заданных изменениях аргумента
х.
При
сравнении значений функции f в некоторой фиксированной точке х0 со
значениями этой функции в различных точках х, лежащих в окрестности х0,
удобно выражать разность f(x) —
f(x0) через разность х —
х0, пользуясь понятиями “приращение функции” и “приращение
аргумента”.
Рассмотрим функцию у = f(x). Пусть х – произвольная
точка, лежащая в некоторой окрестности фиксированной точки х0.
Разность х — х0
называется приращением независимой переменной (или приращением аргумента)
в точке х0 и обозначается
х. Таким
образом, х
= х —
х0, откуда следует, что х = х0
+х.
Говорят также, что первоначальное значение аргумента х0 получило
приращение х.
Вследствие этого значение функции f изменится на величину
f(x) — f(x0)
= f(х0 +
х)
– f(x0).
Эта разность называется приращением функции f в точке х0,
соответствующим приращению
х, и
обозначается
f, т. е. по
определению
f
= f (х0+х)
– f(x0), откуда f (х0 +
х)
= f(x0) +
f.
Обратите внимание: при фиксированном значении х0 приращение
f есть
функция от х.
(Слайд 4.)
Пример 1:
Найти приращение аргумента и приращение функции в точке х0, если
Решение:
(Слайд 5.)
Рассмотрим график функции у = f (x). Геометрический смысл приращения функции
можно понять, рассмотрев рисунок. (Слайд 6.) Прямую l, проходящую
через любые две точки графика функции f, называют секущей к графику f.
Уравнение прямой на плоскости имеет вид у = кх + в. Угловой коэффициент k
секущей, проходящей через точки (х0; f(x0) и (х; f(x)),
равен tga. ABC
– прямоугольный.
(Слайд 7.)
V. Закрепление материала: № 177 (а,1)
– (решение на Cлайде
8), 178(а,в) , 180 (устно)
VI. Домашнее задание: п.12, №177(б), 178(б, г)
VII. Подведение итогов урока.