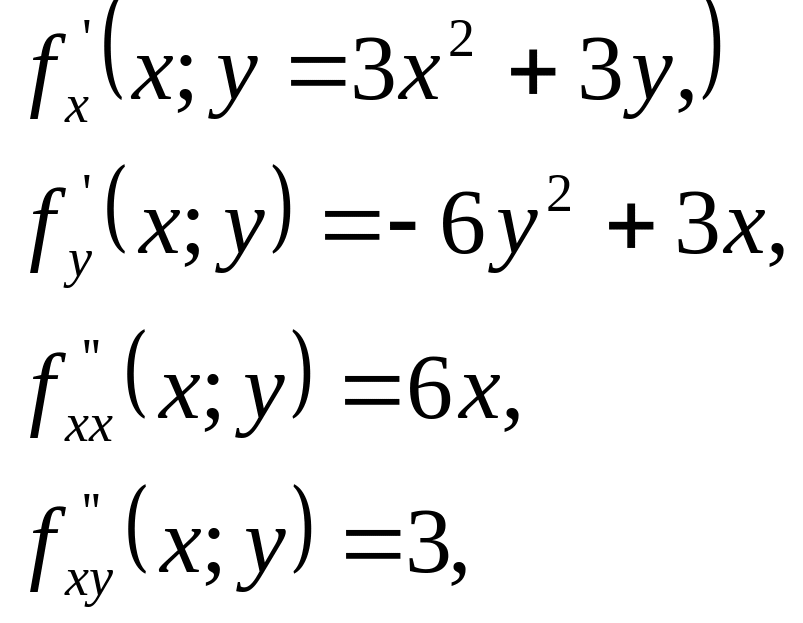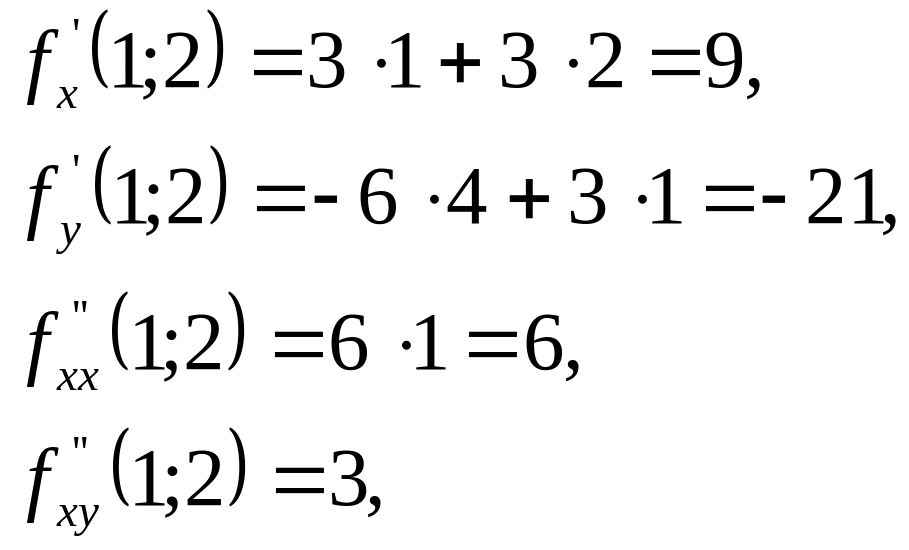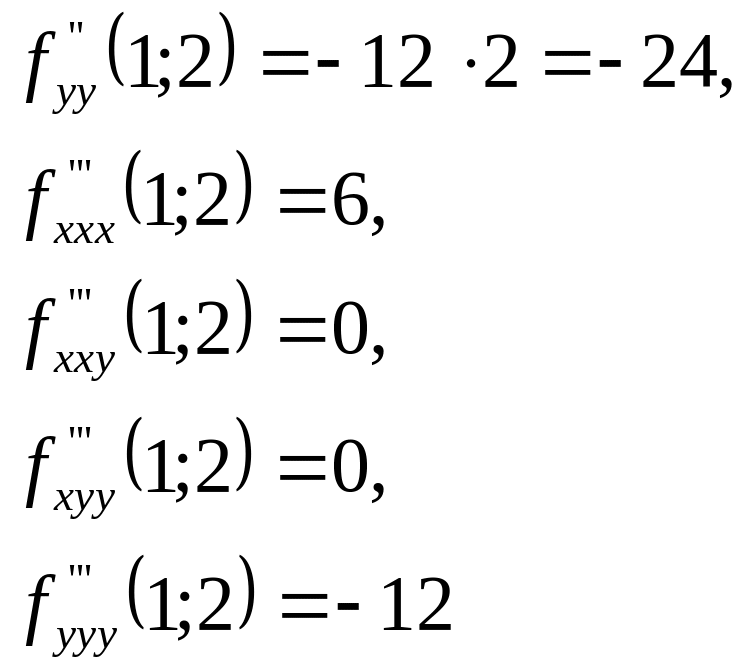Дата публикации: 09 апреля 2017.
Алгебра – 10 класс. Приращение аргумента, приращение функции
Урок на тему: «Приращение аргумента, приращение функции»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Скачать:
Приращение аргумента, приращение функции (PDF)
Что будем изучать:
1.Определение приращения аргумента, приращения функции.
2. Непрерывная функция и приращение.
3. Примеры.
Определение приращения аргумента и приращения функции
Ребята, мы с вами научились находить пределы функции в точке. Важным остается вопрос, как изменяется значение функции при изменении значения аргумента около этой точки?
Математики ввели такое понятие – приращение аргумента и функции. Давайте запишем определение.
Определение: Пусть функция $y=f(x)$ определена в точках $x_0$ и $x_1$. Разность $x_1-x_0$ называют приращением аргумента, а разность $f(x_1)-f(x_0)$–приращением функции.
Иначе говоря, узнаем прирост точки $x_0$ в точке $x_1$. Приращение аргумента обозначают как $Δx$, читается как дельта x.
Приращение функции обозначают, как $Δy$ или $Δf(x)$.
Из нашего определения следует: $x_1-x_0=Δx$ => $x_1= Δx+x_0$ и $f(x_1)-f(x_0)=Δy$. Тогда получаем важное равенство: $Δy=f(x_0+ Δx)-f(x_0)$.
Приращение функции может быть как положительным, так и отрицательным.
Давайте рассмотрим пример.
Найти приращение функции $y=х^3$ при переходе от $x_0=2$ к точке:
а) $x=2,1$; б) $x=1,9$.
Решение:
Обозначим $f(x)=х^3$.
Имеем: $f(2)=2^3=8$.
а) Воспользуемся формулой $Δy=f(x_0+ Δx)-f(x_0)$.
Нам надо найти значение $f(2,1)$.
$f(2,1)=2,1^3=9,261$.
$Δy= f(2,1)- f(2)= 9,261-8=1,261$.
б) $f(2)=8$.
$f(1,9)=1,9^3=6,859$.
$Δy= f(1,9)- f(2)= 6,859-8=-1,141$.
Ответ: а) $1,261$; б) $-1,141$.
Непрерывная функция и приращение
Ребята, давайте вернемся к определению непрерывной функции, и посмотрим на него с помощью приращений.
Вспомним определение непрерывной функции.
Определение. Функцию $y=f(x)$ называют непрерывной в точке $x=a$, если выполняется тождество:
[lim_{x rightarrow a}f(x)=f(a)]
Обратим внимание: $x →a$, тогда $(x-a) →0$ т.е. $Δx → 0$.
Также заметим: $f(x) → f(a)$ , значит $f(x) — f (a) → 0$ т.е. $Δy → 0$.
Определение непрерывности функции в точке можно записать так.
Функция $y=f(x)$ непрерывна в точке $x=a$, если в этой точке выполняется следующее условие:
если $Δx→0$, то $Δy → 0$.
Примеры
1. Для функции $y=kx+b$ найти:
а) приращение функции при переходе от фиксированной точки $x$ к $x+ Δx$;
б)предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю.
Решение:
а) $f(x)= kx+b$.
$f(x+ Δx)=k(x+Δx)+b$;
$Δy= f(x+ Δx)-f(x)= k(x+Δx)+b-( kx+b)= kx+kΔx+b – kx-b= kΔx$.
б) Найдем требуемый предел: $lim_{Δx rightarrow 0}frac{Δy}{Δx}=lim_{Δx rightarrow 0}frac{kΔx}{Δx}=lim_{Δx rightarrow 0}k=k$.
2. Для функции $y=x^3$ найти:
а) приращение функции при переходе от фиксированной точки $x$ к $x+ Δx$.
б)предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю.
Решение:
а) $f(x)= x^3$.
$f(x+ Δx)=(x+Δx)^3=x^3+3x^2Δx+3xΔx^2+Δx^3$.
$Δy= f(x+Δx)-f(x)= x^3+3x^2Δx+3xΔx^2+Δx^3-x^3=3x^2Δx+3xΔx^2+Δx^3$.
б) Найдем требуемый предел: $lim_{Δx rightarrow 0}frac{Δy}{Δx}=lim_{Δx rightarrow 0}frac{3x^2Δx+3xΔx^2+Δx^3}{Δx}=lim_{Δx rightarrow 0}(3x^2+3xΔx+Δx^2)=3x^2$.
Задачи для самостоятельного решения:
1) Найти приращение функции $y=x^4$ при переходе от $x_0=3$ к точке:
а) $x=3,2$;
б) $x=2,8$.
2) Для функции $y=3x+5$ найти приращение функции при переходе от фиксированной точки $x$ к $x+ Δx$.
3) Для функции $y=x^2$ найти приращение функции при переходе от фиксированной точки $x$ к $x+ Δx$.
4) Для функции $y=2x^3$ найти приращение функции при переходе от фиксированной точки $x$ к $x+ Δx$.
При изучении поведения функции y=f(x) около конкретной точки x0, необходимо знать, как меняется значение функции при изменении значения аргумента. Введём следующие понятия.
Пусть функция y=f(x) определена в точках x0 и x1. Разность x1−x0 называют приращением аргумента (при переходе от точки x0 к точке x1), а разность f(x1)−f(x0) называют приращением функции.
Приращение аргумента обозначают Δx, произносят: дельта икс ( Δ — прописная буква; δ — строчная буква греческого алфавита «дельта»). Приращение функции обозначают Δy или Δf.
Итак, x1−x0=Δx, значит, x1=x0+Δx.
f(x1)−f(x0)=Δy, значит, Δy=f(x0+Δx)−f(x0).
Функция
y=f(x)
непрерывна в точке (x=a), когда в этой точке выполняется условие: если
Δx→0
, то
Δy→0
,
-
Формула Тейлора
Пусть
функция двух переменных z
=
непрерывна
вместе со всеми своими частными
производными до (n+1)-го
порядка
включительно в некоторой окрестности
точки (a,b).
Тогда представим эту функцию в виде
суммы многочлена п-го
порядка по степеням (х-а)
и (у-b)
и
некоторого остаточного члена. В
рассматриваемой окрестности справедлива
формула
Тейлора:
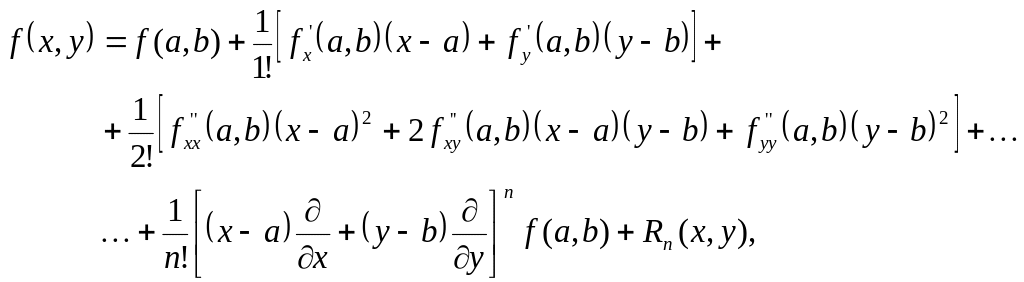
где
остаточный член представлен в форме
Лагранжа
В
других обозначениях эта формула прозвучит
так:

Или
же через полные дифференциалы различных
порядков:
Частный
случай формулы Тейлора получаем при
,
что носит название формулы
Маклорена.
Пример.
Найти приращение, получаемое функцией
при переходе от значений х=1,
у=2
к значениям
.
Решение
Искомое
приращение можно найти, применяя формулу
Вычислим
предварительно последовательные частные
производные и их значения в данной точке
(1; 2):
|
|
|
Все
дальнейшие производные тождественно
равны нулю. Подставляя найденные
результаты в исходную формулу, получим:
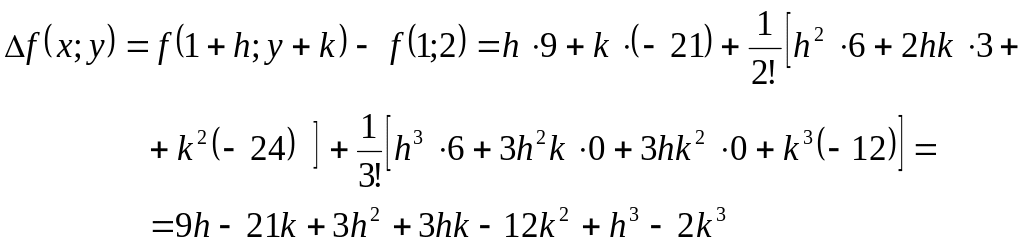
-
Экстремум функции нескольких переменных
Говорят,
что функция z
=
имеет
максимум
в
точке
,
если для всех точек
,
достаточно близких к точке
и отличных от неё выполняется неравенство
.
Аналогично
говорят, что функция z
=
имеет
минимум
в точке
,
если для всех точек
,
достаточно близких к точке
и отличных от неё выполняется неравенство
.
Максимум
или минимум функции называется её
экстремумом.
Аналогично
определяется экстремум функции трех и
большего числа переменных.
Теорема
1
(Необходимые
условия экстремума).
Если
функция z
=
достигает
экстремума
при
,
,
то каждая частная производная первого
порядка или обращается в нуль при этих
значениях аргументов, или не существует.
Точки,
в которых дифференцируемая функция z
=
может
достигать экстремума, называются
стационарными
точками
и находятся путём решения системы
уравнений:
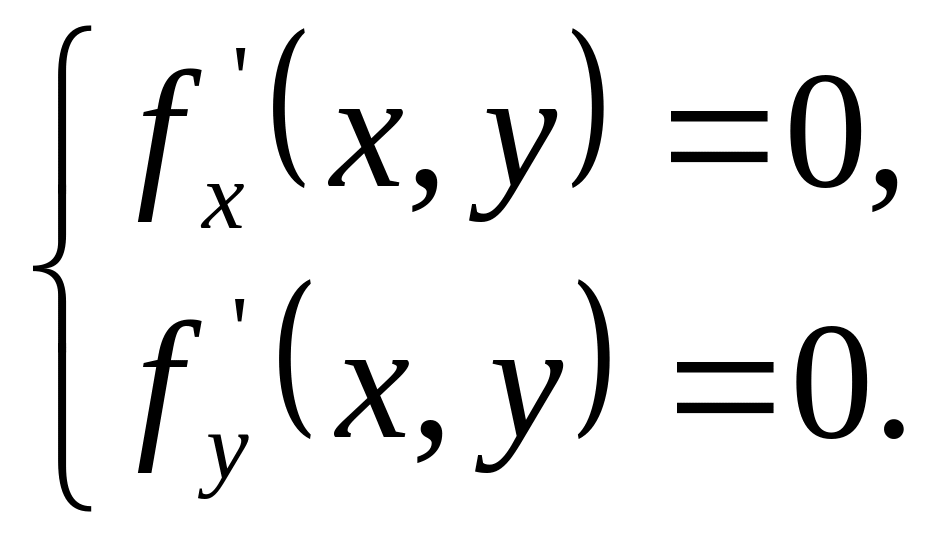
Данная
система эквивалентна одному уравнению
.
В
общем случае необходимые условия
позволяют отыскать критические
точки,
т.е. подозрительные
на экстремум
(стационарные точки и точки из области
определения функции, в которых частные
производные не существуют). Не всякая
«подозрительная» точка оказывается
точкой экстремума. Для исследования
функции в таких точках установим
достаточные условия экстремума функции
двух переменных.
Теорема
2
(Достаточные условия экстремума).
Пусть
в некоторой области, содержащей точку
,
функция
имеет
непрерывные частные производные до
третьего порядка включительно; пусть,
кроме того, точка
является критической точкой функции
,
т.е.
.
Обозначим:
.
Составим определитель
.
Тогда:
1) если
то
функция имеет экстремум в точке
,
а именно максимум, если А < 0 (или C
< 0), и минимум, если А > 0 (или C
> 0);
2)
если
то
экстремума в точке
нет;
3)
если
то вопрос о наличии экстремума функции
в точке
остаётся открытым.
11. Условный экстремум
В
простейшем случае условным
экстремумом
функции
называется максимум или минимум этой
функции, достигнутый при условии, что
её аргументы связаны уравнением
(уравнение
связи).
Чтобы
найти условный экстремум функции
при
наличии соотношения
,
составляют так называемую функцию
Лагранжа
,
где
— неопределенный постоянный множитель,
и ищут обычный экстремум этой
вспомогательной функции. Необходимые
условия экстремума сводятся к системе
трех уравнений 
с
тремя неизвестными
,
из которой можно определить эти
неизвестные.
Вопрос
о существовании и характере условного
экстремума решается на основании
изучения знака второго дифференциала
функции Лагранжа
для
испытуемой системы значений
,
полученной при решении исходной системы
при условии, что
.
А
именно, функция
имеет
условный максимум, если
,
и условный минимум, если
.
В частности, если определитель
для
функции
в стационарной точке положителен, то в
этой точке имеется условный максимум
функции
,
если А < 0 (или C
< 0), и условный минимум, если А > 0 (или
C
> 0).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Производная функции — это понятие дифференциального исчисления, характеризующее скорость изменения функции в данной точке. Определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует.
Содержание:
- Приращение аргумента. Приращение функции
- Определение производной
- Формулы дифференцирования. Таблица производных
- Дифференцирование суммы, произведения, частного
- Сложная функция и ее дифференцирование
- Физический смысл производной
- Вторая производная и ее физический смысл
- Касательная к графику функции
- Применение производной к исследованию функций на монотонность
- Применение производной к исследованию функций на экстремум
- Отыскание наибольшего и наименьшего значений непрерывной функции на отрезке
- Отыскание наибольшего или наименьшего значения непрерывной функции на незамкнутом промежутке
- Задачи на отыскание наибольших или наименьших значений величин
- Применение производной для доказательства неравенств
- Общая схема построения графика функции
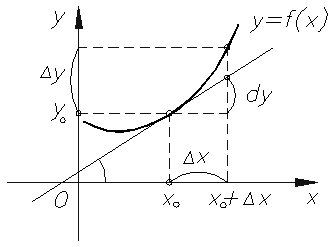
Приращение аргумента. Приращение функции
Пусть функция у = f(x) определена в точках х и 







Пример 1.
Найти приращение функции 

Решение:
Имеем 
Итак, 



при х = 1, 
Пример 2.
Доказать, что для линейной функции 

Решение:
Имеем f(x) = kx + b,
Значит, 

Геометрический смысл доказанного равенства проиллюстрирован на рисунке 1.151: из треугольника АМВ получаем
Определение производной
Пусть функция у = f(х) определена в точке х и в некоторой окрестности этой точки. Пусть 


Если существует предел отношения приращения функции 


Итак,
f'(x) — это новая функция, определенная во всех таких точках х, в которых существует указанный выше предел; эту функцию называют производной функции у = f(x).
Пример 1.
Найти f'(2), если 
Решение:
Тогда
Значит, f'(2) = 4.
Опираясь на определение, можно рекомендовать следующий план отыскания производной функции у = f(x):
1) фиксируем значение х, находим Дх);
2) даем аргументу х приращение 

3) вычисляем приращение функции
4) составляем отношение 
5) находим предел отношения 
Пример 2.
Найти производную функции 
Решение:
Формулы дифференцирования. Таблица производных
Операцию отыскания производной называют дифференцированием. В п. 209 получена одна из формул дифференцирования: 
Например, (2х — 3)’ = 2 (формула 2); 


Дифференцирование суммы, произведения, частного
Если функции 
1°. Их сумма дифференцируема в точке х и
(теорема о дифференцировании суммы).
2°. Функция 
(теорема о вынесении постоянного множителя за знак производной).
3°. Произведение функций 
(теорема о дифференцировании произведения).
4°. Частное функций 
(теорема о дифференцировании частного; здесь 
Пример 1.
Найти производную функции
Решение:
Воспользовавшись теоремами 1° и 2°, получим
Осталось применить соответствующие формулы дифференцирования (см. п. 210). Получим
Пример 2.
Найти
Решение:
Воспользовавшись теоремой о дифференцировании произведения, получим
Осталось применить соответствующие формулы дифференцирования (см. п. 210). Получим
Итак,
Пример 3.
Вычислить f'(0), если
Решение:
Сначала найдем f'(x). Воспользовавшись теоремой о дифференцировании частного, получим
Теперь вычислим f'(0):
Сложная функция и ее дифференцирование
Рассмотрим функцию 
1) вычислить 
2) найти значение синуса от полученного значения 


Пример 1.
Составить сложную функцию у = = f(g(x)), если g(x) = In х,
Решение:
Пример 2.
Из каких функций составлена сложная функция
Решение:
Эта функция — композиция составляющих: 
Пусть у = f(g(x)) — сложная функция, причем функция 
Запись f'(g(x)) означает, что производная вычисляется по формуле для f'(x), но вместо х подставляется g(x).
Пример 3.
Найти
Решение:
Здесь 
Пример 4.
Найти
Решение:
Так как 
Физический смысл производной
Если s = s(t) — закон прямолинейного движения, то s'(t) выражает скорость движения в момент времени t, т. е. 
Например, закон свободного падения тела выражается зависимостью 
Вообще производная функции у = f(х) в точке х выражает скорость изменения функции в точке х, т. е. скорость протекания процесса, описываемого зависимостью у = f(х). В этом состоит физический смысл производной. Например, для функции 
Вторая производная и ее физический смысл
Пусть функция у = f(х) имеет производную. Производная — это новая функция, которая, в свою очередь, может иметь производную. Производную f'(х) называют второй производной функции у = f(х) и обозначают f»(х) или у».
Пример 1.
Найти у», если
Решение:
Имеем 
Если s = s(t) — закон прямолинейного движения, то вторая производная выражает скорость изменения скорости этого движения, т. е. ускорение 
Пример 2.
Материальная точка движется прямолинейно по закону 
действующая на тело, пропорциональна кубу пройденного пути.
Решение:
По второму закону Ньютона, 



Значит, 

Касательная к графику функции
Касательной к графику функция у = f(x), дифференцируемой в точке х = 


Геометрический смысл этого определения состоит в следующем. Рассмотрим график функции у = f(x), дифференцируемой в точке 






Если точку Р двигать по графику, приближая ее к точке М, то прямая MP начнет поворачиваться вокруг точки М (на рис. 1.152 указаны два положения точки Р — 

Но условие 



Но 


Итак, k = 


Если функция у = f(x) дифференцируема в точке 


Это позволяет по графику функции находить точки, в которых функция имеет или не имеет производную. Так, функция, график которой изображен на рисунке 1.154, дифференцируема во всех точках, кроме точки х = 1; в этой точке график имеет заострение и касательную провести нельзя.
Уравнение касательной к графику функции у = f(x) в точке 
Пример 1.
Составить уравнение касательной к графику функции 
Решение:
Имеем:
Подставив найденные значения 
Пример 2.
Найти угол, который образует с осью х касательная к графику функции 
Решение:
Имеем:
Значит, 
Пример З.
К графику функции 
Решение:
Две прямые параллельны тогда и только тогда, когда их угловые коэффициенты равны (см. п. 81). Угловой коэффициент прямой у = -х + 2 равен -1, а угловой коэффициент касательной равен 

Имеем 
Решим уравнение 


Если 

Если 

Пример 4.
Через точку О (0; 0) провести касательную к графику функции у = In х.
Решение:
Здесь, как и в предыдущем примере, неизвестна точка касания 



По условию касательная должна проходить через точку О (0; 0), т. е. координаты точки О (0; 0) должны удовлетворять уравнению (2). Подставив х = 0, у = 0 в уравнение (2), получим 



Это — уравнение искомой касательной (рис. 1.155).
Применение производной к исследованию функций на монотонность
Производная позволяет во многих случаях сравнительно просто исследовать функцию на монотонность. Достигается это с помощью следующих двух теорем:
Теорема 6.
Пусть функция у = f(x) определена и непрерывна в промежутке X и во всех внутренних точках этого промежутка имеет неотрицательную производную (f'(x) > 0), причем равенство f'(x) = 0 выполняется не более чем в конечном числе точек этого промежутка. Тогда функция у = f(x) возрастает на промежутке X.
Теорема 7.
Пусть функция у = f(x) определена и непрерывна в промежутке ж и во всех внутренних точках этого промежутка имеет неположительную производную (f'(x) < 0), причем равенство f'(x) = 0 выполняется не более чем в конечном числе точек этого промежутка. Тогда функция у = f(x) убывает на промежутке X.
Пример 1.
Исследовать на монотонность функцию

Решение:
Имеем 


Пример 2.
Исследовать на монотонность функцию
у = 2 sin х — Зх.
Решение:
Имеем у’ = 2 cos х — 3. Так как 
Пример 3.
Исследовать на монотонность функцию
Решение:
Имеем
Знаки выражения 
Но область определения исследуемой функции задается неравенством х > 2. Значит, из показанных на рисунке четырех промежутков нас интересуют только два: промежуток (2; 3) — на нем у’ < 0 и, следовательно, функция на этом интервале убывает, — и промежуток 
Указанные два промежутка имеют общую концевую точку х = 3. В точке х = 3 заданная функция определена и непрерывна. В таких случаях при исследовании функции на монотонность концевую точку включают в промежуток монотонности.
Ответ: Функция убывает на полуинтервале (2; 3] и возрастает на луче
Применение производной к исследованию функций на экстремум
Говорят, что функция у = f(x) имеет максимум (минимум) в точке 
Так, функция, график которой изображен на у-рисунке 1.157, имеет максимум в точках 

Точки максимума и минимума объединяют общим термином — точки экстремума.
Обратимся еще раз к рисунку 1.157. Замечаем, что в точках 


Теорема 8.
Если функция у = f(x) имеет экстремум в точке 

Точки, в которых 




Как узнать, когда стационарная или критическая точка функции является точкой экстремума? Ответ на этот вопрос дает следующая теорема.
Теорема 9.
Пусть 



1) если на 


2) если на 


3) если и на 


Из теорем 8 и 9 вытекает следующее правило исследования функции у = f(x) на экстремум:
1) найти область определения функции;
2) найти f'(x);
3) найти точки, в которых выполняется равенство f'(x) = 0;
4) найти точки, в которых f'(x) не существует;
5) отметить на координатной прямой все стационарные и критические точки и область определения функции у = f(x); получатся промежутки области определения функции, на каждом из которых производная функции у = f(x) сохраняет постоянный знак;
6) определить знак у’ на каждом из промежутков, полученных в п. 5;
7) сделать выводы о наличии или отсутствии экстремума в каждой из выделенных точек в соответствии с теоремой 9.
Пример 1.
Исследовать на экстремум функцию
Решение:
1) Функция определена при всех х.
2)
3) Из уравнения 

4) у’ существует при всех х (критических точек нет).
5) Отметим точки 
6) у’ = 6(х — 2)(х — 3). Знаки ■ -х производной на полученных промежутках отмечены на рисунке 1.159.
7) При переходе через точку х = 2 слева направо производная у’ меняет знак с «+» на « — », значит, х = 2 — точка максимума; при переходе через точку х = 3 производная меняет знак с «—» на «+», значит, х = 3 — точка минимума. В точке х = 2 имеем 
Пример 2.
Исследовать на экстремум функцию
Решение:
1) Область определения функции задается неравенством х > 2.
2)
3) в области определения функции, т. е. при х > 2, нет ни стационарных, ни критических точек; значит точек экстремума у функции нет.
Пример 3.
Исследовать на экстремум функцию
Решение:
1) Область определения
2)
3) у’ = 0 при х = 3 или при х = -1.
4) у’ не существует при х = 1, но эта точка не принадлежит области определения функции.
5) Отметим на координатной прямой точки х = -1, х = 3 и точку х = 1 (рис. 1.160).
6) Знаки производной на полученных промежутках отмечены на рисунке 1.160.
7) х = -1 — точка максимума,
х = 3 — точка минимума,
Отыскание наибольшего и наименьшего значений непрерывной функции на отрезке
Говорят, что функция у = f(x), определенная на промежутке X, достигает на нем своего наибольшего (наименыиего) значения, если существует точка а, принадлежащая этому промежутку, такая, что для всех х из X выполняется неравенство
Обозначения соответственно:
Теорема 10.
Функция, непрерывная на отрезке, достигает на нем своего наибольшего и наименьшего значений.
Наибольшее значение М и наименьшее значение 
Алгоритм отыскания наибольшего и наименьшего значений непрерывной функции у = f(х) на отрезке 
1) найти f'(x);
2) найти точки, в которых f'(x) = 0 или f'(x) не существует, и отобрать из них те, что лежат внутри отрезка 
3) вычислить значения функции у = f(x) в точках, полученных в п. 2, и на концах отрезка и выбрать из них наибольшее и наименьшее; они и будут соответственно наибольшим и наименьшим значениями функции у = f(x) на отрезке 
Пример:
Найти наибольшее и наименьшее значения непрерывной функции 
Решение:
1)
2) у’ существует при всех х. Найдем точки, в которых у’ = 0. Имеем:
Отрезку [0; 6] принадлежит лишь точка х = 5.
3) вычислим значения функции в точках 0, 5, 6:
Наибольшим из найденных значений функции является число 225, наименьшим — число 50. Итак,
Отыскание наибольшего или наименьшего значения непрерывной функции на незамкнутом промежутке
Задача отыскания наибольшего (наименьшего) значения непрерывной функции на незамкнутом промежутке, например на интервале 






Если поставлена задача найти 


Пример:
Найти наименьшее значение функции 

Решение:
1) Найдем производную данной функции:
2) у’ = 0, если 1 + 2 cos x = 0 или 2 + cos x = 0. Но второе уравнение не имеет решений, так как 


Производная у’ не существует, если 


3) Если
При приближении к концам интервала, т. е. при 



Поскольку при приближении к концам интервала 

Иногда для отыскания наибольшего или наименьшего значения непрерывной функции у = f(x) на промежутке 
Теорема 11.
Если функция у = f(x) имеет в промежутке X только одну стационарную или критическую точку 

Теорема 12.
Если функция у = f(x) имеет в промежутке X только одну стационарную или критическую точку 

Так, в рассмотренном выше примере функция имела в интервале 




Задачи на отыскание наибольших или наименьших значений величин
Задачи на отыскание наибольших или наименьших значений величин удобно решать по следующему плану.
1) Выявляют оптимизируемую величину (т. е. величину, наибольшее или наименьшее значение которой требуется найти) и обозначают ее буквой у (или S, р, г, R и т. д. в зависимости от сюжета задачи).
2) Одну из неизвестных величин (сторону, угол и т. д.) объявляют независимой переменной и обозначают буквой х; устанавливают реальные границы изменения х в соответствии с условиями задачи.
3) Исходя из конкретных условий данной задачи, выражают у через х и известные величины.
4) Для полученной на третьем шаге функции у = f(x) находят наибольшее или наименьшее значение (в зависимости от требований задачи) по промежутку реального изменения х, найденному на втором шаге.
5) Интерпретируют результат, полученный на четвертом шаге, для данной конкретной задачи.
На первых трех этапах составляется, как принято говорить, математическая модель задачи. Здесь часто успех решения зависит от разумного выбора независимой переменной. Важно, чтобы было сравнительно нетрудно выразить у через х. На четвертом этапе составленная математическая модель исследуется чаще всего с помощью производной, реже элементарными способами. В момент такого исследования сюжет самой задачи, послужившей отправной точкой для математической модели, исследователя не интересует. И лишь когда закончится решение задачи в рамках составленной математической модели, полученный результат интерпретируется для исходной задачи (пятый этап).
Пример 1.
В степи, в 9 км к северу от шоссе, идущего с запада на восток, находится поисковая партия. В 15 км к востоку от ближайшей к поисковой партии точки шоссе, находится райцентр. Поисковая партия отправляет курьера-велосипедиста в райцентр. Каков должен быть маршрут следования курьера, чтобы он прибыл в райцентр в кратчайший срок, если известно, что по степи он едет со скоростью 8 км/ч, а по шоссе — 10 км/ч?
Решение:
Сделаем чертеж. На рисунке 1.165 точка Р означает местонахождение поисковой партии, прямая 
Будем решать задачу поэтапно.
1. Оптимизируемая величина — время t движения курьера из Р в В; надо найти
2. Положим AM = х. По смыслу задачи точка М может занять любое положение между A и В, не исключая самих точек А и В. Значит, реальные границы изменения х таковы: 
3. Выразим t через х. Имеем 





4. Нужно найти наименьшее значение функции
на отрезке [0; 15]. Используем для этого план из п. 218:
1)
2) t’ существует при всех х. Найдем точки, в которых t’ = 0. Имеем:
Значение х = 12 принадлежит отрезку [0; 15].
3) Составим таблицу значений функции, куда включим значения функции на концах отрезка и в найденной стационарной точке:
Четвертый этап решения задачи закончен, нам осталось интерпретировать полученный результат применительно к исходной задаче.
5. Время 
Пример 2.
Через фиксированную точку М внутри данного угла провести прямую, отсекающую от этого угла треугольник наименьшей площади (рис. 1.166).
Решение (по этапам):
1. Оптимизируемая величина — площадь S треугольника АОВ.
2. Проведем DM || ОВ, МК || OA. Положим KB = х; реальные границы изменения х таковы:
3. Поскольку М — фиксированная точка, отрезки DM и КМ тоже фиксированы; положим 
Рассмотрим треугольники МКВ и АОВ, они подобны; значит, 

Далее имеем
Значит, 
4. Рассмотрим функцию 
Найдем ее наименьшее значение:
1)
2) производная не существует в точке х = 0, а обращается в нуль в точках 


3) 


5. Вернемся к исходной геометрической задаче. Если 

Применение производной для доказательства неравенств
Пример 1.
Доказать, что при 
Решение:
Рассмотрим функцию у = f(x), где 



Но
Итак, f(х) > 5, т. е. 
Пример 2.
Доказать, что если 
Решение:
Рассмотрим функцию у = f(х), где f(х) = х + cos х, и найдем ее производную: f'(x) = 1 — sin х. Замечаем, что 


Пример 3.
Доказать, что при всех х справедливо неравенство
Решение:
Рассмотрим функцию у = f(x), где 
f'(х) = 0 при 





Итак,
Общая схема построения графика функции
Пусть нужно построить график функции у = f(x). Для этого нужно рассмотреть некоторые свойства функции, что обычно сопровождается соответствующей иллюстрацией на координатной плоскости. Это помогает создать графический образ функции. В то же время графические представления помогают лучше понять свойства функции, а иногда и предвидеть их. Полезно придерживаться следующего плана;
1) найти область определения функции у = f(x);
2) найти точки, в которых f(x) = 0 (точки пересечения графика с осью абсцисс);
3) отметить на оси х точки, найденные в п. 2, и точки, в которых функция не определена, найденные в п. 1; эти точки разбивают ось абсцисс на несколько промежутков, на каждом из которых функция сохраняет постоянный знак, установить знак функции на каждом из промежутков;
4) исследовать функцию на четность и нечетность (в случае четности или нечетности функции можно ограничиться исследованием и построением графика при 
5) найти вертикальные и горизонтальные асимптоты (см. п. 203, 206);
6) исследовать функцию на экстремум;
7) найти несколько дополнительных контрольных точек и построить график.
Для периодических функций полезно с самого начала найти основной период Т (см. п. 76), с тем чтобы, исследовав функцию и построив ветвь графика на промежутке 
Если выполнение каких-либо шагов предложенной схемы сопряжено с техническими трудностями, их иногда можно опустить.
Пример 1.
Построить график функции
Решение:
1) Функция определена при всех х.
2) Из уравнения 
3) Точки -2; 0; 2 разбивают ось абсцисс на 4 промежутка. Изменение знаков функции 
4) 
5) Асимптот у графика нет. 6)
Точка 
Аналогично, в точке 
7) В качестве дополнительных возьмем две точки х = 3, х = -3. Имеем f(3) = 15, f(-3) = -15.
Использовав найденные 7 точек, строим график функции (рис. 1.169).
Пример 2.
Построить график функции
Решение:
1) Область определения:
2) Из уравнения 
3) Точки 2, -2, 3, -3 разбивают ось абсцисс на 5 промежутков. Изменение знаков функции 
4) Функция четна, так как f(-x) = f(x). Значит, график функции симметричен относительно оси ординат. 5) х = 2, х = -2 — вертикальные асимптоты (см. п. 206).
Чтобы найти горизонтальную асимптоту, вычислим 

Итак, 
6)
Производная обращается в нуль в точке х = 0 и не существует в точках х = ±2. Но эти последние не принадлежат области определения функции; значит, функция имеет лишь одну стационарную точку х = 0. При переходе через эту точку производная меняет знак с «-» на «+»; значит, х = 0 — точка минимума;
7) В качестве дополнительных возьмем следующие точки: х = ±1, х = ±4. Имеем 
Использовав найденные 7 точек, строим график функции (рис. 1.172).
Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:
- Математика решение заданий и задач
Смотрите также дополнительные лекции по предмету «Математика»:
Лекции:
- Интеграл примеры решения
- Интеграл от экспоненты
- Распределение Пуассона
- Метод Симпсона
- Контрольная производная и ее геометрический смысл
- Симплекс метод: примеры решения
- Частная производная функции
- Показательные комплексные числа
- Матрица смежности графа
- Точки перегиба функции
Содержание:
- Приращение аргумента и функции
- Определение производной
- Дифференцирование функции
Пусть задана некоторая функция $y=f(x)$. Возьмем какое-нибудь
значение $x_{0}$ из области определения этой функции:
$x_{0} in D[f]$ . Соответствующее значение функции в этой точке
будет равно $y_{0}=fleft(x_{0}right)$ .
Приращение аргумента и функции
Определение
Приращением аргумента называется разность между двумя значениями аргумента: «новым» и «старым».
Обычно обозначается как $Delta x=x_{1}-x_{0}$ .
Пример
Задание. Найти приращение аргумента $x$, если он переходит от значения 3 к значению 3,2.
Решение. Искомое приращение: $Delta x=3,2-3=0,2$ .
Ответ. $Delta x=0,2$
Зададим аргументу $x_{0}$ приращение
$Delta x$. А тогда значение функции в новой точке
$fleft(x_{0}+Delta xright)$.
Определение
Приращением функции $y=f(x)$ в точке
$x_{0}$, соответствующее приращению аргумента
$Delta x=x-x_{0}$, называется величина:
$Delta y=fleft(x_{0}+Delta xright)-fleft(x_{0}right)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти приращение функции $y=2 x^{2}$
при $x_{0}=3$ и
$Delta x=0,1$
Решение. Подставляя в формулу, получаем, что приращение функции:
$Delta y=y(3+0,1)-y(3)=2 cdot(3+0,1)^{2}-2 cdot 3^{2}=1,22$
Ответ. $Delta y=1,22$
Определение производной
Определение
Производной $y^{prime}(x)$ от функции
$y=f(x)$ в точке
$x_{0}$ называется предел отношения
приращения функции $Delta y$ к приращению аргумента
$Delta x$ :
$frac{Delta y}{Delta x}$ при
$Delta x rightarrow 0$, если он существует, то есть:
$y^{prime}left(x_{0}right)=f^{prime}left(x_{0}right)=lim _{Delta x rightarrow 0} frac{Delta y}{Delta x}=lim _{Delta x rightarrow 0} frac{fleft(x_{0}+Delta xright)-fleft(x_{0}right)}{Delta x}$
или
$y^{prime}left(x_{0}right)=lim _{x rightarrow x_{0}} frac{f(x)-fleft(x_{0}right)}{x-x_{0}}$
Пример
Задание. Найти производную функции $y=x^{2}+3 x$
в точке $x_{0}=0$.
Решение. Найдем приращение заданной функции в точке $x_{0}$ :
$Delta y=y(0+Delta x)-y(0)=y(Delta x)-y(0)=$
$=(Delta x)^{2}+3 Delta x-0=Delta x(Delta x+3)$
Тогда
$y^{prime}(0)=lim _{Delta x rightarrow 0} frac{Delta x(Delta x+3)}{Delta x}=lim _{Delta x rightarrow 0}(Delta x+3)=0+3=3$
Ответ. $y^{prime}(0)=3$
Дифференцирование функции
Определение
Операция нахождения производной функции называется дифференцированием этой функции.
Функция $y=f(x)$ имеет производную на интервале
$(a ; b)$ или называется дифференцируемой в этом
интервале, если производная $f^{prime}(x)$ существует в каждой точке этого интервала.
Функция $y=f(x)$ имеет в точке
$x$ бесконечную производную, если в этой точке
$f^{prime}(x)=lim _{Delta x rightarrow 0} frac{Delta y}{Delta x}=infty$ .
Теорема
(О непрерывности функции в точке)
Если функция $y=f(x)$ имеет конечную производную в
точке $x_{0}$ , то она непрерывна в этой точке.
Замечание. Обратное заключение не всегда верно: если функция $y=f(x)$
непрерывна в некоторой точке $x_{0}$ , то она может
и не иметь производной в этой точке.
Определение
Функция $y=f(x)$ называется дифференцируемой
в точке $x$, если приращение функции,
соответствующее приращению аргумента, можно представить в виде:
$Delta y=A cdot Delta x+alpha(Delta x) cdot Delta x$
где $A$ — число, не зависящее от
$Delta x$,
$alpha(Delta x)$ — б.м. функция при
$Delta x rightarrow 0$.
Теорема
(О необходимом и достаточном условии дифференцируемости)
Для того чтобы функция $y=f(x)$ была дифференцируемой
в точке $x$, необходимо и достаточно,
чтобы $y=f(x)$ имела в этой точке конечную производную.
Теорема устанавливает, что для функции $y=f(x)$
дифференцируемость в данной точке $x$ и существование конечной производной в этой точке — понятия равносильные.
Читать дальше: односторонние производные.